1 Introduction

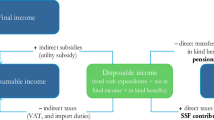
The under-five mortality rate (which is the probability that a liveborn child dies before reaching the fifth birthday), henceforth U5M, is a valid measure of the economic and social development of a country (Wang 2003). U5M has been declining across the world since the beginning of the twentieth Century. This trend began in western countries following the industrial revolution and has subsequently spread across the globe in association with increasing wealth. (French 2016). However, there is an alarming disparity between and within countries in U5M and maternal mortality rate (MMR). The critical determinants of child and maternal survival are access to public services such as clean water, sanitation, education, and health services (Dersarkissian et al. 2013; Bishai et al. 2016). These rely on adequate levels of both gross domestic product (GDP) per capita (GDPpc) and government revenue (GR) per capita (GRpc). However, GDPpc in low-income countries (LICs) and lower-middle-income countries (LMICs) is a fraction of that of wealthier nations. Also, GR is a much smaller proportion of GDP in LICs, than in high-income countries (HICs): for LICs the figure is around 20%, compared with 40% for HICs. Thus, the mean GRpc in LICs and LMICs is USD 100 and USD 450 (constant USD 2010) respectively (ICTD/UNU-WIDER 2018a), as shown in Fig. 1. Furthermore, LICs allocate a smaller proportion of their GR to social sectors (Long and Miller 2017).

Fig. 1
figure 1

Gross domestic product per capita and government revenue per capita by income group in 2015

Full size image

Here we examine the relationship between GRpc and U5M and MMR (U5M/MMR) using a panel data analysis. The article is as follows: section 2 gives our rationale, section 3 reviews the literature on the determinants of U5M/MMR, section 4 explains our modelling strategy, section 5 outlines the data, variables and models, section 6 gives the econometric results, section 7 discusses the results, section 8 discusses the limitations and section 9 concludes.

2 Rationale

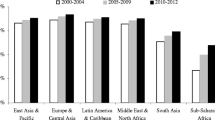
Determinants of health, including clean water, sanitation, education, and healthcare, are among the Sustainable Development Goals (SDGs) (The United Nations 2018). Although, widely available in upper-middle-income countries (UMICs) and high-income countries (HICs), large proportions of the populations of LMICs and LICs do not have access to them, as shown for the year 2015 in Fig. 2.

Fig. 2
figure 2

Percentage of the population with access to the determinants of health by income group in 2015

Full size image

Governments are responsible for either the provision of public services or the effective regulation of private providers (WHO Commission on the Social Determinants of Health 2008). Increasing GR could increase the resources available for public services and the determinants of health. A better understanding of the relationship between GRpc and health outcomes affected by population access to the determinants of health, such as mortality, is useful because the policies and practices of national and international actors directly influences GR. For example, a multinational company (MNC) may significantly increase GR in a country in which it is based, as a result of tax and royalties, or decrease GR as a result of aggressive tax planning.

Many of the models in the literature use a log formulation, which makes deriving elasticities convenient (Jamison et al. 2016). However, the disadvantage is that the elasticity is then constrained to be the same across all countries. We find that this specification is not sufficiently non-linear to describe the substantial differences we observe across the world, and we suggest an alternative specification which we believe is superior. This study contributes to a better understanding of the complex relationship between GRpc and U5M/MMR at a country-year level.

Thus, the findings of this study help assess the impact on health of increasing or decreasing GR at a country level and could contribute to evidence-based policymaking, advocacy and economic, social and governance reporting.

3 Literature Review

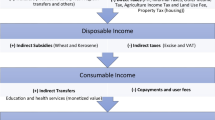
Figure 3 summarises the conceptual framework applied in this study that relates GDP, GR and U5M/MMR. We briefly review the literature for the steps along this pathway.

Fig. 3
figure 3

Conceptual framework for the pathways between gross domestic product, government revenue and mortality

Full size image

The literature on the relationship between GDP and mortality suggests that as GDP increases, mortality decreases (Filmer and Pritchett 1999; Bhalotra 2006; Schell et al. 2007; French 2016). The impact acts through two main pathways, as shown in fig. 3: (1) Increased GR, government spending (GS) and public services, and (2) Increased household income (O’Hare et al. 2014). Mortality does not decrease uniformly as GDP increases across countries. One of the explanations may be that the GR/GDP ratio varies widely.

Generally, increases in GR result in increased GS. However, this is not consistent across countries or income groups (Reeves et al. 2015; Carter and Cobham 2016), for example, an increase in GR by 10% leads to a 17% increase in GS on public services for health in LICs, a 4% increase in LMICs and a 3% increase in UMICs (Tamarappoo et al. 2016). However, GS on social sectors constitutes a small proportion of total GS; in 2016 the average (mean) percentage of general GS on health in LICs was 7% (range 2–17%), and for LMICs 8% (0–21%), for education, the figures are 14% (1–21%) and 16% (9–23%) respectively (The World Bank. 2018). Generally, a rise in GS on public services is associated with a positive impact on the human development index (Haile and Niño-Zarazúa 2017), and GS on public health services reduces maternal and child mortality (Gupta et al. 2002; Bokhari et al. 2007; Anyanwu and Erhijakpor 2009; Maruthappu et al. 2015). Others confirm this and also find that that GS is more effective in countries with better governance (Rajkumar and Swaroop 2008; Makuta and O’Hare 2015). Concerning education, Gupta et al. found that an increase in GS on education by 1% of GDP increased enrolment in secondary school by 2.6%, while the elasticity for U5M is 0.21. Others found that an increase of 1% of GDP is associated with an increase in the average duration of schooling by three years (Gupta et al. 2002; Baldacci et al. 2008). Improved coverage of the critical determinants of health, including, water and sanitation, healthcare and education, reduces mortality (Fewtrell et al. 2005; Gakidou et al. 2010; Jeuland et al. 2013). A virtuous circle results from increased and efficient GS on social sectors, as a better educated and a healthier population drives economic growth and increases tax return and GR (Woessmann 2016). There are several steps in the causal chain between GRpc and U5M/MMR, including the percentage of GS allocated to the social sectors and the efficiency of use. These factors result in variation between countries, which makes modelling at the country level essential, and such modelling may capture the combined impact of allocation decisions and the efficacy of different sectors (see fig. 3).

4 Modelling Strategy

The seminal paper by Filmer and Pritchett identified the relationship between GDP and U5M (i.e. the elasticity or the amount which one variable changes in response to another variable) to be between −0.51 to −0.61 (Filmer and Pritchett 1999). Other researchers have confirmed a strong negative association, and a meta-analysis of 38 estimates found the pooled elasticity to be −0.45 (O’Hare et al., 2013). All these studies use a similar basic generic panel data model of the form

$$ \log \left(U5{M}_{tj}\right)={\beta}_0+\sum \limits_{i=1}^n{\beta}_i\log \left({x}_{itj}\right)+\gamma T+{\varepsilon}_{tj}, $$
(1)

where xitj is a vector of n explanatory variables (i = 1 …n) including GDP or GS on healthcare and other relevant factors. Here t is the time index, and j is the cross-section index, T is a deterministic time trend,εtj is a standard error term which is assumed to be normally distributed with no serial correlation and βi is the elasticity with respect to each variable. There are several points to discuss about the generic formulation used in the literature (1) above.

The first is the general assumption regarding the double log specification: this has the advantage of making the coefficients easily interpretable as elasticities. However, it limits the degree of non-linearity, as the same elasticity applies across countries. It is improbable that the pooling assumption will hold across a large number of countries. To illustrate this, in South Sudan in 1980, the U5M was 292 per 1000 births while in Germany in 2016 it was 3.8. It does not appear reasonable to believe that the same elasticity can accurately reflect the association in both countries. To mitigate the issue, researchers often split the panel by income levels. Indeed, once the mortality rate decreases to low levels as recently observed in Germany, there is little scope for improvement. So, we argue for the exploration of other non-linear formulations.

The second point regarding the specification of (1) is the inclusion of a deterministic time trend. This is described in the literature as a technical progress effect in health care, analogous to the technical progress term in a standard production function (Preston 1975; Jamison et al. 2016). The important contribution of Jamison, Murphy and Sandbu is to include a country-specific time trend elasticity so that different countries may adopt health technology at different rates, and to introduce a country-specific constant term (a standard fixed effect in panel data terms)(Jamison et al. 2016), so that (1) is re-specified as follows:

$$ \log \left(U5{M}_{tj}\right)={\beta}_{0j}+\sum \limits_{i=1}^n{\beta}_i\log \left({x}_{itj}\right)+{\gamma}_jT+{\varepsilon}_{tj}. $$
(2)

The fixed effect is likely to play an important role as this will capture everything about a country which does not vary over time – things such as geography and natural resources. It is also clear to see how the country-specific trend will produce a much-improved fit: ‘We find that there is a high variation across countries in the rate of improvement over time’ (Jamison et al. 2016). The problem with this deterministic trend treatment is that it has no policy implications. That is to say, if South Sudan is different from Germany simply because they have different trends, then there is nothing to be done about it. We reject this view and believe that proactive policies can bring countries with high U5M/MMR rates into line with the rest of the world.

We will focus on a model which explains U5M/MMR through government resources, measured by GRpc, a range of health care indicators drawn from the SDGs, and we will also adopt a two-way fixed-effects specification and explore a range of non-linear functions to link GRpc:

$$ U5{M}_{tj}={\beta}_{0j}+f\left({\beta}_{1,} GR\right)+\sum \limits_{i=2}^n{\beta}_i{x}_{itj}+\sum \limits_{k=t0}^T{\gamma}_k{D}_k+{\varepsilon}_{tj}. $$
(3)

Here the termf(β1,GR) is a non-linear function of GR to be explored, and we have a country-specific intercept term (the standard fixed effect) and a set of time-specific dummy variables \( \sum \limits_{k=t0}^T{\gamma}_k{D}_k \) where Dk = 0, k ≠ t and Dk = 1, k = t – that is, these are a set of dummy variables taking the value zero everywhere except for period t where they take the value 1. This then makes our model a standard two-way fixed-effects specification in terms of these two effects. To further explain the set of dummy variables: this part of the model will capture any common effects which affect all countries over time. So, it will fully capture global improvements in health care; it is, in fact, more general than the deterministic trend in (1) as productivity is not constrained to rise in a simple linear way. It will also capture any other events which affect the world as a whole, such as climate change and global conflicts. Deviations from this global trend for each country will then be explained by GR and other specific health care factors. The next section will consider the specification of our variables.

5 Data, Variables and Models

5.1 Dependent Variables

U5M, which is the probability that a liveborn child dies before reaching the fifth birthday, is regarded as representative of a country’s health status and has been widely applied (Wang 2003). The other investigated dependent variable associated with health outcomes is the maternal mortality ratio (MMR). A maternal death is the death of a woman while pregnant or within 42 days of termination of pregnancy (The World Bank. 2018). Many low-income countries have no or very little data and use statistical approaches to compute a national estimate for the number of mothers who die in childbirth per 100,000 live births.

5.2 Selection of Independent Variables

We compared World Development Indicators data with GR data from the 2018 UNU WIDER Government Revenue Dataset (GRD) (Prichard 2016). We found the latter to have more data points, with data for 191 countries available (ICTD/UNU-WIDER 2018a). The dataset has both general GR and central GR, and we used the former as the latter would underestimate total revenue in fiscally decentralised states. Data which includes and excludes grants are available, and we used total general government revenue, excluding grants as this variable best reflects the capacity of domestic revenue. For the same reason, we used data which includes social contributions. The GRD expresses all data as a percentage of GDP taken from the World Economic Outlook (WEO), in Local Currency Units (ICTD/UNU-WIDER 2018b). GR as % of GDP was multiplied by the GDPpc in constant 2010 US$ (taken from the WDI), to convert to GRpc.

The categories of independent variables commonly controlled for in other studies include demography, education, geography, governance, and specific health challenges. Within each category, the variable chosen depended on two factors. First, data availability: our data set, taken from the World Development Indicators, is annual from 1980 to 2016 for 191 countries giving a total of 7067 observations (The World Bank. 2018). However, many observations selected as candidate independent variables are missing, and the panel is an unbalanced one. As a result, the best we could hope for is around 2500 observations available for analysis. Within each category of independent variables, there are several choices of a specific variable. Still, in some cases, a given variable would reduce the total available sample to under 400 observations, most of which would be for developed countries. Hence, we rule out any variables which reduce the total sample size too drastically. Second, where there are suitable choices, we choose the best fitting variable in a general to a specific approach to modelling.

5.2.1 Demography

The standard independent variables studied include the percentage of the population living in urban areas, the fertility rate, and gender inequality. Amouzou and Hill showed that the higher the urbanisation rate, the lower the U5M in Africa (Amouzou and Hill 2004). Baldacci et al. found that a decrease in the average fertility rate by one birth per woman in developing countries is associated with a reduction of U5M by 11.75 per 1000 live births (Baldacci et al. 2008). Further, Brinda et al. determined an association between gender inequality and mortality (Brinda et al. 2015).

5.2.2 Education

Multiple studies use primary school completion and progression to secondary school and find lower mortality is associated with higher education levels (Gupta et al. 2002; Gakidou et al. 2010; Anyamele et al. 2017).

5.2.3 Geography

Rural populations are often underserved. Haile and Niño-Zarazúa found that agriculture as a percentage of the GDP was negatively correlated with social spending, and concluded that agriculture in LICs and LMICs is generally small in scale and dispersed thus presenting challenges to the imposition of taxes (Haile and Niño-Zarazúa 2017).

5.2.4 Governance

Health is generally better, and mortality is lower when the needs of the majority drive public policy, which is more likely in a democracy and countries which depend on the collection of taxes for revenue (Welander et al. 2015; Wigley 2017).

5.2.5 Specific Health Challenges

Countries with high levels of HIV have increased child mortality; for example, in Botswana, half of all children who die before 24 months are exposed to HIV (Zash et al. 2016).

5.3 Models

The two models we will then be investigating are

$$ U5{M}_{tj}={\beta}_{0j}+f\left({\beta}_{1,} GR\right)+{\beta}_2 Demograph{y}_{tj}+{\beta}_3 Educatio{n}_{tj}+{\beta}_4{Geography}_{tj}+{\beta}_5 Governanc{e}_{tj}+{\beta}_6 Healt{h}_{tj}+{\sum}_{k=t0}^T{\gamma}_k{D}_k+{\varepsilon}_{tj} $$
(5)

and

$$ MM{R}_{tj}={\beta}_{0j}+f\left({\beta}_{1,} GR\right)+{\beta}_2 Demograph{y}_{tj}+{\beta}_3 Educatio{n}_{tj}+{\beta}_4{Geography}_{tj}+{\beta}_5 Governanc{e}_{tj}+{\beta}_6 Healt{h}_{tj}+{\sum}_{k=t0}^T{\gamma}_k{D}_k+{\varepsilon}_{tj}. $$
(6)

5.3.1 Estimation

The first step before implementing (5) and (6) is the functional specification of the non-linear term between GR and the two dependent variables U5M and MMR. Our theoretical expectation for the shape of this relationship seems very clear: we want something which initially has a substantial return to increasing GR in terms of U5M and MMR when a country has very low GR and development levels. As these increase, we then want an increase in GR always to have a negative effect on U5M and MMR, but for the size of this effect to fall rapidly and at least asymptotically approach zero, without turning negative. Graphically, therefore, we want something like the relationship shown in fig. 4.

Fig. 4
figure 4

Representation of relationship between U5M and government revenue

Full size image

The association is given by the multiplicative inverse function, that is

$$ U5M=\frac{\beta }{GR} $$
(7)

and the marginal effect of an increase in GR on U5M is given by the partial derivative of this function with respect to GR, that is

$$ \frac{\partial U5M}{\partial GR}=-\frac{\beta }{GR^2} $$
(8)

which is always negative as long as β > 0 (so as GR increases, U5M always decreases) but the size of the effect falls in proportion to the square of GR. As GR becomes very large, this term tends to zero, that is

$$ {\lim}_{GR\to \infty}\left(-\beta /{GR}^2\right)\to 0. $$
(9)

There are variants we could try to alter the shape of the curve and its rate of descent, and we experimented with the following two options

$$ U5M=\frac{\beta }{\log (GR)} $$
(10)

and

$$ U5M=\frac{\beta }{GR^{\alpha }} $$
(11)

Footnote 1where α may be either less than or greater than 1.

6 Results

We now present our estimated equations for the determination of U5M and MMR. Table 1 gives the findings for U5M.

Table 1 Model Estimates for the dependent variable U5M
Full size table

Absolute ‘t’ statistics in parenthesis. All models contain fixed effects and time dummies.

Models 1, 2 and 4 in Table 1 above show the effect of using the log of GR, the inverse of the log of GR and the simple inverse. We can formally judge between these models purely based on the model, which gives the highest log-likelihood function as each of them has the same number of parameters and dependent variables. Model 4 has the best log-likelihood function of the three models, 1, 2 and 4.

Furthermore, while most of the coefficients of the other variables have similar signs and magnitude across the three models, the level of significance is generally considerably higher in model 4. Model 3 gives a direct comparison between the inverse function (model 4) and the log specification (model 1) by including both variables in the regression. We cannot use the log-likelihood function to judge between model 3 and the other models as there is a different number of parameters in 3 than the other models and hence the log-likelihood function will increase by construction. However, it is striking that the inverse function retains its positive coefficient (meaning that the marginal effect on U5M is negative) while the semi elasticity from the log variable turns positive so that the effect here would be for an increase in GR to increase U5M. This may indicate that an even more complex non-linear function may improve on the simple inverse function, but the combined effect of these two could undoubtedly go positive for a sufficiently large level of GR. Our preferred model for U5M is, therefore, model 4.

We now turn to the determination of the maternal mortality rate MMR in Table 2.

Table 2 Model Estimates for the dependent variable MMR
Full size table

Absolute ‘t’ statistics in parenthesis. All models contain fixed effects and time dummies.

In this case, the highest log-likelihood function between the three options (1, 2, and 4) is given by model 2, which uses the inverse of the log of government revenue. As model 2 is the best of the three, we then introduce both the log of GR and the inverse of the log of GR in model 3. This again shows the superiority of the log inverse specification which remains positive (the correct sign) and statistically significant while the simple log of GR turns positive (opposite sign) and is not statistically significant. Our preferred model is model 2 in this case.

Interpreting these results is not as simple as in the usual case where we derive elasticities for all countries. Despite this, these models give a much richer set of results as the marginal effects of increasing GR will be quite different for each country and even at different points in time (where GR has changed significantly over time). We can do this for every country at every point in time using either

$$ \frac{\partial U5M}{\partial GR}=-\frac{\beta }{G{R}^2} $$

Or in the case of MMR, the log inverse

$$ \frac{\partial MMR}{\partial \mathit{\log}(GR)}=-\frac{\beta }{\mathit{\log}{(GR)}^2} $$

Table 3 shows the estimated effect of a 10% increase in GR on U5M and MMR for a selected group of countries.Footnote 2

Table 3 Effect of a 10% increase in GR on U5M and MMR with associated total lives saved
Full size table

7 Discussion

An increase in GR is associated with a reduction in U5M/MMR. We have made no assumptions about the allocation of GR or the efficiency of its use. Instead, we have modelled based on the past relationship. The pathways between GR and mortality are likely to act via GS on public services and access to the determinants of health, as shown in fig. 3. The relationship between GR and U5M/MMR is more robust in some countries than others, and this may be due to differences in allocation decisions and levels of efficiency.

Previous analyses have studied the relationship between GDP, GS and access to the determinants of health and mortality, but not the relationship between GR and mortality.

Governments could increase GR by curtailing leaks which include the use of tax incentives and treaties, international corporate tax avoidance, and an informal economy that is undertaxed (Mick Moore et al. 2018). Establishing the relationship between GRpc and U5M/MMR allows us to appreciate the scale of the human costs of these leaks. Repayment of debt and corruption also results in decreased GR (O’Hare and Makuta 2015).

Policymakers need to consider the impact of granting tax incentives in terms of foregone GR and the human costs. To reduce international corporate tax avoidance, governments may need to establish specialist units within their revenue authorities (Waris 2017). The estimates reported here could be used by civil society to advocate such action by their governments. Tax treaties may result in losses of 15% of corporate income tax in some regions (Beer and Loeprick 2018). The estimates we have presented may help those advocating for a review of tax treaties.

Institutional investors routinely analyse the environmental, social, and governance (ESG) performance of companies (London Stock Exchange Group 2018). These estimates could inform the ESG reports of MNCs, as many contribute significantly to GR in many LICs and LMICs. Advocates could also use the estimates to influence MNCs that engage in aggressive tax planning, as companies are obliged to avoid adversely affecting the local communities where they operate (Office of the United Nations High Commissioner for Human Rights 2011). Equally, HICs must regulate the entities over which they have control to ensure MNCs pay tax where economic activities take place and to meet their international human rights obligations. These estimates could help advocate for this (Economic and Social Council 2017).

Debt repayment drains GR and in conjunction with the conditions attached to the loan makes it almost impossible for countries to achieve economic growth and human development (Ilias Bantekas and Cephas Lumina 2018). Target 4 of SDG 17 refers to assisting developing countries in attaining long-term debt sustainability through coordinated policies aimed at fostering debt financing, debt relief, and debt restructuring. These estimates could help to model the benefit of debt reduction during renegotiation procedures.

SDG 17 pledges global partnership for the attainment of the goals and target 17.1 aims to strengthen domestic resource mobilisation, including through international support, to improve capacity for tax revenue collection. Curtailing some leaks will require actions within countries but some issues, such as international tax avoidance and foreign debt, will require action by multiple stakeholders, including national governments, MNCs, HICs, and international organisations. Estimates of the human cost of leaks from GR using models such as this one may help garner support to address gaps in global governance, including tax cooperation and sovereign debt resolution (Antonio Alonso 2019).

8 Limitations

The main limitation is data availability. We could not use many of the candidate independent variables due to a lack of data. The model assumes that effects due to increased government revenue are instantaneous, and there is no attempt to quantify cumulative and lasting improvements, and this will be a focus of future work.

9 Conclusions

The modelling summarised here and shown in an easily accessible format online can be used to give a sense of the potential impact of increasing or decreasing GR in each country. The possible uses are many. For example, it could assist in evidence-based policymaking when ministries are making decisions which will impact GR. Such choices include the granting of tax incentives or taking out loans. Other uses include the use by civil society to advocate for evidence-based policymaking and equitable redistribution policies. Multinational companies could use this tool to report on their ESG contributions for the countries where they work.