Is Hard Brexit Detrimental to EU Integration? Theory and Evidence

Abstract

In the struggle between the forces of free trade and the restrictive influence of insularism the latter recently seems to have the upper hand. This is illustrated by the referendum of June 23, 2016 where the United Kingdom (UK) voted to leave the European Union (EU). In this paper we evaluate the consequences of this event for EU integration. In particular, we analyze how the extent of EU economic integration would change once the UK leaves the Union. To that end we develop an integration benchmark that consists of the steady state production equilibrium characterized by arbitrage pricing and perfect factor mobility. We apply metrics to measure the distance between this benchmark and the data. We find that the integration in the EU is incomplete and its trend is non-linear while Brexit would not bring negative consequences to its development.

1 Introduction

Since the mid-1980s there has been a surge of regional trade agreements (RTAs) around the globe as subsets of countries seek deeper integration among themselves. Lately, the announced RTA between Mongolia and Japan in June 2016 represents an important milestone in the history of the World Trade Organization (WTO) in that all its members now have an RTA in force (see the WTO website). June 2016 also marks another rare event, namely Brexit, the UK departure from the European Union (EU) voted during the historic referendum of June 23, 2016. One of the prime motivations for Brexit is UK’s desire to re-establish sovereignty of its own borders (and territorial waters). It wishes to form regional trading agreements with countries of their choice, namely the USA. More importantly, advocates of Brexit are against the free movement of people and wish to retain control of immigration. As these are key pillars of EU integration, other EU members are not inclined to accept any British proposal to keep access to the European single market.

Though the future design of economic relations between the UK and EU can take different forms, three options are frequently cited: the Norwegian scenario, the Swiss scenario and Hard Brexit. Both Norway and Switzerland have in common that they are part of Schengen but are not customs union members. Switzerland differs in that its agreement exempts the financial sector. However, both countries gained access to the internal market by allowing for the free labor mobility with the EU. As the latter aspect is not acceptable to the UK, the third option, Hard Brexit, seems a realistic option. UK would then leave EU-28 but be released from any obligation to allow for the free mobility of labor with the EU. Bilateral trade would operate according to the WTO rules, e.g. with no special agreement on tariffs and non-tariff barriers. This outcome is favoured by “Hard Brexiteers” since any future RTA would be negotiated freely with no EU interference. Summing up:

”We cannot leave the club and continue to use its facilities” (Lord Mandelson, The Guardian; June 10, 2016).

A number of studies have looked into the implications of the UK leaving the European Union. For example, Ebell et al. (2016) analyse the costs and benefits for the UK if it no longer participates to a free trade agreement for goods and services with the EU. Ebell and Warren (2016) evaluate the scenario where the UK obtains the same status as Norway and Switzerland. Both scenarios lead to a reduction in projected GDP for the UK compared to the status quo. Differently, Dhingra et al. (2018) analyse the multilateral trade effects of the various options and in all cases obtain negative welfare losses. While most studies mainly evaluate the long-term implications of different trade patterns for the UK, a focus of this paper is to analyse the re-allocation of productive resources for remaining EU members following Hard Brexit in terms of arbitrage pricing and factor mobility. Specifically, the question is: What would be the extent of integration for the remaining EU countries once the UK leaves the Union?

Results of the 2016 referendum cannot be seen independently of the public’s discontent with the European Union. The latter is currently being criticized by scholars, politicians, and the popular press who demand reforms.¹ The claim is that member countries bear the financial costs of very costly bureaucracies that in many cases fail to benefit European citizens because of, for example, a lack of common approaches to tax evasion, cheap labor migration and harmonization of corporate income tax. This demand for value from the EU is triggered by numerous factors like shaky economic conditions, migration from Eastern member countries, the waves of war refugees but also a lack of transparency. This is happening worldwide but is more pronounced in some Western countries where populism is on the rise (e.g., France, the Netherlands, Hungary and Poland). Given this background, the following questions are often raised: (i) What are the objective grounds for challenging the model proposed by EU over time? (ii) Is the conjecture correct that the EU shows symptoms of reduced economic integration over time? Therefore, the answer to how the sequence of enlargements experienced since the 1957 Treaty of Rome affects the time pattern of EU integration assumes importance. While we are aware of previous research on the comparison between the USA, European Union and Eurozone for a few years (e.g. Rogers 2007), we have not seen any empirical estimation in the literature of such a time profile of European integration over several decades.

Through a RTA, a group of countries agrees to enjoy freer international economic relations among themselves. In the extreme, this allows for the free movement of goods and services, capital, and labour within the integrated area. However, the institutional arrangements under which countries open their borders will differ in reality. As a result, the global economy looks complex beyond comprehension, with a web of treaties and rules whose reallocation of global production is poorly understood. Taken together these observations point to the need to construct a single measure of regional integration that goes beyond trade statistics but includes goods and factor flows. The idea is to build a simple model that generates testable predictions about EU integration and performs the Brexit counterfactual analysis. Specifically, we develop an integration benchmark that consists of a steady state equilibrium characterized by both free trade and perfect mobility of physical and human capital. A metric is then developed to measure the distance between this benchmark and the observed equilibrium characterized by the data, namely with barriers to trade and to factor mobility. This metric allows for comparison of integration over time and across regions. In addition, it is used to analyse the effects of Brexit on EU integration (excl. UK).

Another important application measures economic integration in the EU-28 and compares the outcomes with two control groups namely, the European Monetary Union (EMU or Eurozone) and Latin America (specifically the Latin American Integration Association or ALADI). WTO provides details regarding the institutional arrangements of these RTAs. ALADI is defined as a free trade area, EU-28 a common market and EMU a monetary union, in order of increasing economic integration according to the WTO criteria (e.g., Table C.1 of WTO 2011). ALADI is a form of ‘shallow’ integration as it mainly refers to border measures whereas EU-28 and, even more so, the Eurozone are characterized by ‘deep’ integration since agreements go well beyond the removal of border measures and include, for example, the coordination of policies.

Our analysis focuses on the distribution of output and the stocks of productive factors within a particular region. Particularly, the variables of interest are country output shares of regional output and country factor shares of regional factor supplies that have been shown to be important both theoretically and empirically (see, for example, Helpman and Krugman 1985; Bowen et al.1987; Viaene and Zilcha 2002). In this paper, shares behave randomly and their path is assumed to be described by (possibly correlated) reflected geometric Brownian motions with a lower and upper bound. A random process modelled as a Brownian motion is a framework that is popular in the empirical trade and economic geography literature because it has the property of being parsimonious in terms of number of parameters (e.g. Albornoz et al. 2016). A lower bound is justified since nowadays countries are unlikely to disappear; an upper bound matters as the sum of shares must be one. Given this, starting from some initial conditions, we derive the steady state distribution of shares across member countries of a particular region.

Assuming fully integrated goods and factor markets and comparing dynamic paths, we obtain the following results: (i) Using variable elasticity production function, we develop and empirically support the equality between output and factor shares of economies that are member of an integrated area; (ii) Using metrics of distance, we construct an integration measure that includes both goods and factor flows and show that EU integration is still incomplete; (iii) Besides, the estimated time profile of EU integration is non-linear, exhibiting a w-pattern. Except for 1957, none of the enlargement dates are endogenously selected as being breakpoints; (iv) While UK’s membership (together with Ireland and Denmark) has initiated a quarter century of EU integration growth, we find that its departure would enhance EU integration (excl. UK).

The paper is organized as follows. Section 2 discusses the related literature. Section 3 outlines the model and establishes key theoretical results; in addition, it describes the data and discusses the empirical method used. Section 4 derives the steady state equilibrium distribution of shares and applies Maximum Likelihood on available data. Section 5 includes the derivation of the steady state distribution of shares and the computation of integration measures for each region. Section 6 explores the quantitative implications of our results by computing the effects of Brexit on EU integration (excl. Britain). Section 7 concludes. The Appendix contains all the proofs, describes the data sources and methods and outlines our bootstrap replications.

2 Related Literature

The literature has demonstrated the benefits of international trade for the growth experience of open economies (Harrison and Rodríguez-Clare 2009). Particularly, integration among economies plays an important role in that it increases the long-run rate of growth. For example, the essential idea of Rivera-Batiz and Romer (1991) is that integration stimulates the worldwide exploitation of increasing returns to scale in research and development. Factor mobility is also a powerful instrument in the allocation of resources and some regions of the world have fewer barriers to labour mobility than to goods trade. The complex nature of the relationship between trade and factor mobility is found in two classic papers in the literature, namely Mundell (1957) and Markusen (1983). Mundell (1957) shows that if factors are internationally mobile, in the extreme form, trade in goods will cease, which implies that goods trade and factor flows are substitutes. Markusen (1983) challenged the idea of substitution between trade and factor movements. Assuming similar endowments, he relaxes a number of assumptions of the Heckscher-Ohlin model, one by one, and concludes that eliminating barriers to factor movement results in the complementarity between trade and the movements of both labour and physical capital. Felbermayr et al. (2015) reviews the literature and derives new conditions for substitutability and complementarity in numerous settings. A major conclusion is that the way international factors directly influence the allocation of resources is an empirical question.

A vast literature has also contributed to our understanding of the various dimensions of international labour migration. For example, recent topics include interest groups and immigration (Facchini et al. 2011), policy interactions between host and source countries facing skilled-worker migration (Djajić et al. 2012) and temporary low-skilled migration and welfare (Djajić 2014). Closer to our work Borjas (2001) tests the hypothesis of immigration being ”the grease on the wheels” of the labour market. Likewise, in our model migration leads to greater labour market efficiency in that the geographic sorting of migrants ensures that the value marginal products of labour are equalized across countries. Labour migration can also alter the market for physical capital and aggregate production. Galor and Stark (1990) show that the probability of return migration results in migrants saving more than comparable local residents. Kugler and Rapoport (2007), Javorcik et al. (2011) find that the presence of migrants in the US causes US foreign direct investment in the migrants’ countries of origin. In contrast, calibrating a dynamic general equilibrium model to match Canadian data over 1861 - 1913 Wilson (2003) shows that labour force growth through immigration is responsible for up to three quarters of the rise in the foreign capital inflows. Similarly, the driving force behind international capital flows in our framework is the impact of international labour migration on the value of marginal products of physical capital.

Integration over time can also be assessed in other ways. For example, Riezman et al. (2011) assess how far the world economy is between autarky and free trade and develop methodologies to answer the question using a global general equilibrium model. Riezman et al. (2013) discuss metrics of globalization for individual economies as distance measures between fully integrated and trade restricted equilibria. Bowen et al. (2011) test empirically the properties of the distribution of outputs and stocks of productive factors expected to arise between members of a fully integrated economic area. Other studies focus on prices of homogeneous goods and homogeneous assets assuming that price differentials reflect market frictions and/or lack of arbitrage. For example, Volosovych (2011) looks at patterns of nominal and real long-term bonds; Uebele (2013) analyses wheat prices in Europe and the USA; Hoeberichts and Stokman (2018) provide evidence of increased price dispersion since 2010 within the Eurozone. Though these studies do not fully control for successive EU enlargements, they provide important signals regarding the allocation of productive resources across regions and countries.

3 Equality of Output and Factor Shares

Given this background the analysis of this section focuses on how the distribution of output and stocks of productive factors would look like if an economic area were characterized by fully integrated goods and factor markets. Particularly, we show the importance of each member’s share of an area’s total output and its share of the area’s total stock of physical capital and of human capital, concepts which have been shown to be important both theoretically and empirically.

3.1 The Economic Framework

We consider an economic area consisting of N countries. As our model considers two types of international factor flows, we take the aggregate production function of any country n, Y_nt, to depend on both sorts of capital: Y_nt = F_n(K_nt,H_nt) where K_nt stands for the stock of physical capital and H_nt for the stock of human capital, n = 1,...,N is a country, t = 1,...,T is a time index. Production is carried out by competitive firms which combine these two production factors to produce a single commodity. The aggregate level of human capital at each date t has a direct effect upon the production possibilities at that period.

Upon the integration of capital markets, physical capital will flow from the low return to the high return country until value marginal products of physical capital are all equal to the equilibrium rental rate $\bar {r}$ of the integrated economy at any date t. Particularly:

$$ p_{1}F_{1K}= ... = p_{j}F_{jK} = ... = p_{N}F_{NK}=\bar{r}, $$

(1)

where F_nK is the marginal product of physical capital in country n and p_n is the price of country n goods (expressed in the same currency, e.g. euro). Likewise, upon the integration of labor markets, human capital will flow until marginal products of human capital are equal to $\bar {w}$, the equilibrium wage rate per unit of effective labor at date t. In particular we take this production function to be the following constant returns to scale but variable elasticity of substitution (VES) production function (Revankar 1971). The function, which is a generalized Cobb-Douglas production function, reads:

$$ Y_{nt}=\gamma K_{nt}^{1-\delta \rho} \left( H_{nt}+(\rho -1)K_{nt}\right)^{\delta \rho} , $$

(2)

where parameter values satisfy γ > 0, 0 < δ < 1, 0 < δρ < 1. The corresponding share of human capital in total output is $\delta \rho \lbrack 1+(\rho -1)\frac {K_{nt}}{H_{nt}}]^{-1}$, decreasing in ρ and K_nt/H_nt. The elasticity of substitution υ depends linearly on the physical-to-human capital ratio:

$$ \upsilon =1+\frac{\rho -1}{1-\delta \rho} \frac{K_{nt}}{H_{nt}}. $$

Our interest in production function (2) lies in a number of useful properties associated with parameter values. With ρ = 0 the VES function degenerates to the fixed-coefficient production function as a special case: Y_nt = γK_nt. This implies redundancy of human capital in the n th economy as the employment of human capital (and labour) is below its endowment H_nt, a common observation in many developing countries. When ρ = 1 the VES function reduces to the Cobb-Douglas function with a unitary elasticity of substitution (υ = 1), a popular specification in developed economies.²

We assume υ > 0 which implies that the human-to-physical capital ratio is such that $\frac { H_{nt}}{K_{nt}}>\frac {1-\rho } {1-\delta \rho }$. The function spelled out in Eq. 2 is therefore different from the constant elasticity of substitution production function in that the elasticity of substitution implied by the VES production function varies along the isoquant. With ρ > 1, the latter is generally steeper as K_nt/H_nt increases.

Assuming homogeneous goods and perfect arbitrage (p₁ = ... = p_j = ... = p_N), free goods trade and perfect factor mobility within an economic area lead to an equality between shares:

Proposition 1

Given the production function (2), if no barriers to the free movement of goods, physical and human capital exist then

$$ \frac{Y_{nt}}{{\sum}_{k=1}^{N}Y_{kt}}=\frac{K_{nt}}{{\sum}_{k=1}^{N}K_{kt}}= \frac{H_{nt}}{{\sum}_{k=1}^{N}H_{kt}}. $$

(3)

The shares of output, physical and human capital fully equalize for every country n = 1,...,N. Particularly, each member’s share of an area’s total output will equal its share of the area’s total stock of physical capital and of human capital.

The proof is included in the Appendix to facilitate the reading. Relationship (3) gives rise to a number of observations, two of which we highlight here. First, Proposition 1 assumes that integrated economies like EU are similar except for their human capital intensities. However, EU countries possess many levels of heterogeneity like different production functions, barriers to capital mobility (e.g., corporate income tax differentials) or to labor mobility (e.g., language, differing pension systems). It can be shown that differences in technology or factor market imperfections lead to a multiplicative scaling of observable variables that is different for each ratio but the equality obtained in Eq. 3 remains the same. Second, to strengthen Proposition 1, let us consider the other extreme model where goods are differentiated by place of origin like in gravity models of Anderson and van Wincoop (2003), Anderson et al. (2015) and others. Prices did not explicitly enter in expression (3), because, with free trade, arbitrage eliminates any price differentials across countries and a single price will prevail. With equal value marginal products, this price cancels in the expressions. Now, as each of the N regions is specialized in the production of a single commodity, it charges a different price p_n with n = 1,2,...,N. In this setting, we obtain:

$$ \frac{{{Y}_{n}}}{\sum\nolimits_{k=1}^{N}{Q_{nk}^{{\Psi}} {{Y}_{k}}}}=\frac{{{K}_{n}}}{\sum\nolimits_{k=1}^{N}{{{K}_{k}}}}=\frac{{{H}_{n}}}{\sum\nolimits_{k=1}^{N}{Q_{nk}^{{\Omega}} {{H}_{k}}}} $$

(4)

The derivation of Eq. 4 is described in Appendix A to facilitate the reading. In this expression, Ψ = δρ/(δρ − 1), Ω = 1/(δρ − 1) are composite parameters. Importantly, Q_nj = S_njp_j/p_n is the real bilateral exchange rate with S_nj being the nominal bilateral exchange rate expressed as units of n currency per unit of j currency (so that Q_nj = 1 when n = j). Identity (4) states that with identical technologies and perfect factor mobility, a model with differentiation by place of origin maintains the equal-share relationship, though it rescales variables (Y_n,H_n) with real exchange rates. Hence, with perfect factor mobility, the value marginal product of each factor will be equal across origins but since goods are differentiated relative prices will appear explicitly. Interestingly the type of exchange rate system plays a role here. If S_nj are equilibrium exchange rates such that absolute purchasing parity holds, Q_nj = S_njp_j/p_n = 1, expression (3) is restored. If exchange rates are fixed or common to all countries like in the Eurozone, then relative prices will appear explicitly.

Having established the equality of output and factor shares in integrated areas, we now verify its empirical validity. To that end we outline the construction of our data set and then perform empirical tests.

3.2 Data Sources and Methods

3.2.1 Defining Geographic Units

Through a RTA, a group of countries agrees to enjoy freer international economic relations among themselves. However, the institutional arrangements under which countries open their borders will differ in reality. The following describes the three blocks of countries in our sample.

ALADI, a Spanish acronym for the Latin American Integration Association (Asociación Latinoamericana de Integración) was founded in 1980 to promote trade in the region. It is a free trade area whose member countries eliminate tariffs among themselves but keep individual tariff schedules (and tariff revenues) on imports from non-member countries. As members maintain their own external tariff, imports could enter through the member country with the lowest tariff and then be re-exported to other members. Member countries therefore agree to ’rules of origin’ that determine whether a good is eligible for a tariff-free treatment. These rules often require that goods contain a high percentage of domestic content to prevent the simple repackaging of goods. ALADI fits this definition. Initially it included 11 member countries (Argentina, Bolivia, Brazil, Chile, Colombia, Ecuador, Mexico, Paraguay, Peru, Uruguay and Venezuela). Three other countries joined the association in the year noted: Cuba (1999), Nicaragua (2011) and Panama (2012).

The European Communities were established by the 1957 Treaties of Rome with 6 founding member states, namely Belgium, France, Germany, Italy, Luxembourg, and the Netherlands. Later the European Union formed to become a common market to promote the free mobility of goods, services, persons and capital within the area. The number of members has steadily grown to the present 28 countries. Members eliminate tariffs among themselves but establish a common external tariff against non-members. Customs revenues mostly accrue to a common fund that finances, besides large institutions, social and regional projects in poor European regions. Table 1 reproduces the historical sequence of enlargements whose inputs are essential for the construction of our measure of regional integration.

Table 1 European Union: historical enlargements

In a parallel manner, 19 of the 28 EU countries have the ambition to form an economic union, where members of a common market unify all other economic (fiscal, monetary) and socio-economic (labor, social security) policies. While this is the ultimate goal of the EU, only the ”Eurozone” has unified its monetary policy with member states adopting the euro as their common currency. The Eurozone was created in 1999 by 11 member states: Austria, Belgium, Finland, France, Germany, Ireland, Italy, Luxembourg, Netherlands, Portugal and Spain. Later enlargements include: Greece (2001), Slovenia (2007), Cyprus (2008), Malta (2008), Slovakia (2009), Estonia (2011), Latvia (2014) and Lithuania (2015).

WTO provides detailed information regarding the institutional arrangements of the above RTAs (see trade topics at https://www.wto.org/english). Current economic conditions of Latin America are described by the World Bank (see economic indicators at https://data.worldbank.org/indicators); those of European countries are also portrayed in Eurostat (http://ec.europa.eu/eurostat/data/database).

3.2.2 Data Methods

Let us denote a share of a variable j ∈{Y,K,H} by S_jnt. Thus, to compute output shares S_Ynt we use:

$$ S_{Ynt}=\frac{Y_{nt}}{{\sum}_{k=1}^{N}Y_{kt}} $$

Factor shares S_Knt and S_Hnt are computed analogously. Hence, our sample includes country data on outputs and stocks of physical and human capital. Our data set is an unbalanced panel of annual data ranging from 1957 till 2016. The data for ALADI ends in 2014, the last year for which physical capital data is available for the countries of this region.

We measure output as gross domestic product (GDP) expressed in international dollars and valued at constant 2000 prices. The main source of data on output is Penn World Tables (PWT) 7.0. We use PWT 9.0, World Bank and Eurostat as additional data sources where information is unavailable in PWT 7.0. The data on the stock of physical capital is obtained from the version 6.2 of PWT and extended to more recent years using the growth rates of data from PWT 9.0 and European Commission. Just as output, physical capital is expressed in international dollars and valued at constant 2000 prices. Human capital is measured as total population aged 15 and over that has at least completed secondary education. The data is obtained from the version 2.1 of the Barro and Lee’s data set on educational attainment. Because the data is only available on a five-year interval basis and because it most of the time exhibits a clear exponential growth we use cubic splines to interpolate missing observations. A more detailed description of the data and the methods employed for interpolation and extrapolation is contained in the Appendix.

For the purpose of our empirical analysis we further compute the shares of output, physical and human capital separately for the countries of the EU. Figure 1 illustrates the distribution of all three sets of shares in 2016 where it is clear that Germany takes the highest intra-regional share of all the variables. Likewise, sets of shares are also computed for ALADI and EMU and are reproduced in Figs. 2 and 3 respectively.

Fig. 1

Note: Year 2016. Source: Own calculations based on Penn World Tables 7.0, 9.0 and Barro and Lee (2013)

Distribution of output and factor shares in EU-28.

Fig. 2

Note: Year 2014. Source: Own calculations based on Penn World Tables 6.2, 9.0 and Barro and Lee (2013)

Distribution of output and factor shares in ALADI-14.

Fig. 3

Note: Year 2016. Source: Own calculations based on Penn World Tables 7.0, 9.0 and Barro and Lee (2013)

Distribution of output and factor shares in EMU-19.

3.3 Tests of Proposition 1

To test whether there is conformity between the ranks of the output and factor shares we compute Spearman rank-order correlation coefficients at every time point and compare them across regions and over time. Contrary to Pearson correlation, rank correlation also allows for non linearities to be present in a relationship.

Table 2 reports pairwise Spearman rank correlations computed for the three regions at different time points. Although reported correlation coefficients are population values and as such are not subject to sampling errors we nevertheless report bootstrap confidence intervals in the brackets to take into account possible data measurement errors. The table reveals a significant positive relationship between any pair of shares. All the coefficients are close to or above 0.9. Thus, a country with a higher ranked output share tends to also have higher ranked factor shares. Particularly high, close to unity, coefficients are observed for EU and EMU indicating a nearly perfect rank conformity. Correlations are also relatively stable over time with some but minor over time variation, which means that a country that takes a certain rank position is unlikely to change it quickly.

Table 2 Spearman rank correlations

To strengthen the result on the equality of shares we also report per region the fraction of countries whose shares are similar (see Table 3). For calculations we consider pairwise Y − K, Y − H and K − H comparisons for each region and each year. For each pairwise comparison we compute the fraction of countries whose shares differ in absolute by no more than 1 percentage point. We then aggregate the numbers by taking the average of the three pairwise comparisons. The results indicate that the proportion of countries whose shares are almost equal is increasing over time for all regions, the highest being in EMU and EU with ALADI lagging behind.

Table 3 Fraction of countries with equal shares

Though Proposition 1 established the equality of shares, its underlying assumptions can be used to explain why deviations from equality might be observed in empirics. For example, part of the equality of shares in Eq. 3 breaks down when the parameter space includes δρ = 0. With ρ = 0 the VES function degenerates to Y_nt = γK_nt and the human capital share in Eq. 3 no longer equals the other two. Alternatively, human capital might be the constraining factor instead. In this case, the physical capital share in Eq. 3 is no longer equal to the other two.

4 Steady State Equilibrium Distribution of Shares

4.1 Dynamics of Shares

We assume that changes in shares are the realization of some particular states of nature. There are numerous reasons why shares could be random. Innovation and discoveries of natural resources are usually believed to follow a random process once investments in those activities have been made. Also, upheavals, military conflicts and natural disasters hit output, stocks of human and physical capital at random. To characterize such randomness we assume that both output and factor shares evolve according to a reflected geometric Brownian motion (RGBM), a framework that is widely used in theoretical and empirical studies (e.g. Gabaix 1999; Albornoz et al. 2016). The motion is characterized by a drift parameter μ, volatility σ, lower bound b = minS_jnt and upper bound c = maxS_jnt. That is, we assume:

$$ \frac{dS_{jnt}}{S_{jnt}}=\mu dt+\sigma dB_{t}+dL_{t}-dU_{t}, $$

(5)

where B_t is a Wiener process, while L_t and U_t denote non-negative, non-decreasing, right-continuous processes, guaranteeing reflections every time S_jnt goes below the lower or above the upper bound (Harrison 1985). Lower bound b is a solidarity parameter that represents the principle of solidarity of the European Union as identified in its Charter: it is a fundamental principle based on sharing both the burdens and the advantages like prosperity equally. The parameter prevents the economic collapse of member countries below a certain threshold. The evolution of shares spelled out in Eq. 5 recognizes a link between output and primary factors in that the process from which shocks to the shares are derived is common to all. Though the process is similar, the realization of the states of nature might differ across shares. For example, strikes, technical breakdowns and political upheavals disrupt the production of goods with minor impacts on the stocks of production factors. Later in this section, however, we discuss the case of explicitly modelled correlations. Given this we show:

Proposition 2

If shares evolve according to a reflected Brownian motion given by Eq. 5 and its drift and volatility parameters satisfy $\mu <\frac { \sigma ^{2}}{2}$, there exists a steady state cumulative distribution of these shares that has the following form:

$$ F_{jn\infty} (S)=P(S_{jn\infty} \leq S)=1-\frac{S^{\frac{2\mu} {\sigma^{2}} -1}-c^{\frac{2\mu} {\sigma^{2}}-1}}{b^{\frac{2\mu} {\sigma^{2}}-1}-c^{\frac{2\mu} {\sigma^{2}}-1}},\quad S\in \lbrack b,c]. $$

(6)

See the Appendix for the proof. It is clear from Eq. 6 that though realizations of states of nature differ distributions of output and factor shares are similar when μ = 0.

An important extension of the proposition is that the steady state distribution exhibits power law behaviour even when shares of country i and country j and/or output and factor shares are correlated. The shares must follow RGBM with a sole lower barrier and a certain pattern of correlations described by the so called skew symmetry condition: $\mathbf {R}\hspace {2pt}diag\hspace {1pt}\boldsymbol {{\Sigma }} +diag \hspace {1pt}\boldsymbol {{\Sigma }} \hspace {2pt}\mathbf {R}^{\intercal } =2\boldsymbol {{\Sigma }}$, where Σ is the variance-covariance matrix of shares, diagΣ is a diagonal matrix whose entries are the variance of each share and R is a reflection matrix that corrects correlations when one of the single components hits the barrier (see Harrison and Williams 1987; Dai and Harrison 1992).

Proposition 2 is very general in that it applies to a vast class of economic environments. However, since shares are the key concepts of our analysis, we have to impose a normalization constraint at every time to ensure summation to one:

$$ \sum\limits_{n=1}^{N}S_{jnt}=1,\qquad t=1,...,T. $$

(7)

It turns out that this constraint leads to a number of simplifications:

Proposition 3

If shares evolve according to the reflected Brownian motion given by Eq. 5 subject to the normalization constraint (7), the steady state is characterized by μ = 0 and by the cumulative distribution of shares of the following form:

$$ {{F}_{jn\infty} }(S)=P({{S}_{jn\infty} }\le S)=1-\frac{{{S}^{-1}}-{{c}^{-1}}}{{{b}^{-1}}-{{c}^{-1}}},\qquad S\in \left[ b,c \right]. $$

(8)

See the Appendix for the proof. To illustrate the properties of this proposition, let us focus on the steady state analysis of shares S_nj and therefore omit the time index t. We rank shares in a descending order attributing the highest rank to the country having the largest share of variable of interest within the area. Then a country ranked the n th has the n th largest share within the area or, equivalently, n countries have their shares larger or equal to the n th largest share. This allows to deduce the following relationship between the cumulative distribution function and a rank:

$$ P(S_{jk}\geq S_{jn})=\frac{R_{jn}}{N}. $$

(9)

Using the cumulative distribution function of shares (8) with c = ∞ we obtain:

$$ P(S_{jk}\geq S_{jn})=1-P(S_{jk}<S_{jn})=\frac{S_{jn}^{-1} }{b^{-1}}. $$

(10)

Using expressions (9) and (10) we obtain a non-linear relationship between a rank and a share:

$$ S_{jn}=\frac{\lambda}{R_{jn}}, $$

(11)

where λ = Nb.

4.2 Maximum Likelihood Estimation of RGBM Parameters

Having described the properties of our fully integrated group of economies through Propositions 1 and 2, we now seek empirical support for the law of motion (5). Particularly, we follow the estimation approach outlined in Aït-Sahalia (2002) and apply Maximum Likelihood (ML) on available data for output and factor shares to estimate the parameters μ and σ.

Let 𝜃 = (μ,σ)^′ denote a vector of RGBM parameters. A critical step is the derivation of the conditional density function of normalized RGBM. No such density in its analytical form exists in the literature. To obtain approximate estimates we use the density of RGBM with a sole lower barrier derived in Veestraeten (2008) . In this case the density reads:

$$ \begin{array}{lll} P(S_{jnt}|S_{jn,t-{\Delta}} ;\theta ) & = & \frac{1}{\sigma S_{jnt}\sqrt{2\pi {\Delta}} }\exp \left[-\frac{\left( \ln S_{jnt}-\ln S_{jn,t-{\Delta}} -\gamma_{1}{\Delta} \right)^{2}}{2\sigma^{2}{\Delta}} \right] \\ &&+ \frac{1}{\sigma S_{jnt}\sqrt{2\pi {\Delta}} }\exp\left [\gamma_{2}\ \left( \ln b-\ln S_{jn,t-{\Delta}} \right) \right]\\ &&\exp \left[-\frac{\left( \ln S_{jnt}+\ln S_{jn,t-{\Delta}} -2\ln b-\gamma_{1}{\Delta} \right)^{2}}{2\sigma^{2}{\Delta}} \right] \\ && - \gamma_{2}\frac{1}{S_{jnt}}\exp\left [\gamma_{2}\left( \ln S_{jnt}-\ln b\right) \right]\\ &&\times\left( 1-{\Phi} \left[\frac{\ln S_{jnt}+\ln S_{jn,t-{\Delta}} -2\ln b+\gamma_{1}{\Delta}} {\sigma \sqrt{{\Delta}} }\right]\right) , \end{array} $$

where

$$ \begin{array}{lll} \gamma_{1} & = & \mu -\frac{\sigma^{2}}{2} \\ \gamma_{2} & = & \frac{2}{\sigma^{2}}\gamma_{1}. \end{array} $$

S_jnt denotes as before country’s n share of variable j at time point t and Δ is a time step equalling 1 for annual data. ML therefore solves:

$$ \hat{\theta}=\underset{\theta}{\arg\max} \ell (\theta ) $$

(12)

with the log-likelihood function ℓ being:

$$ \ell (\theta )=\sum\limits_{t={\Delta}}^{T}\sum\limits_{n=1}^{N}\ln [P(S_{jnt}|S_{jn,t-{\Delta}} ;\theta )]. $$

Solution to Eq. 12 can be obtained by various numerical optimization algorithms such as, for example, the algorithm of Broyden-Fletcher-Goldfarb-Shanno (BFGS).

Estimation results of model parameters μ and σ for each set of shares are presented in Table 4.³ From the table it is clear that the estimated drift parameters are significantly non-positive as successive enlargements cause observed shares to decline over time. Also, the volatility of output shares is generally the largest in all three regions. This is partly due to output being a flow variable and therefore more volatile than the more steady stocks of physical and human capital. That volatility in EU (and even more so in EMU) is so low and decreasing can be explained by policy coordination that is a key to the region. For example, consider the scenario where all N countries in the integrated area put in place a coordinated policy such that the human capital of each member country increases by a factor λ (λ > 1). Then, using Eq. 3:

$$ \frac{Y_{nt}}{{\sum}_{k=1}^{N}Y_{kt}}=\frac{K_{nt}}{{\sum}_{k=1}^{N}K_{kt}}= \frac{\lambda H_{nt}}{{\sum}_{k=1}^{N}\lambda H_{kt}}=\frac{H_{nt}}{ {\sum}_{k=1}^{N}H_{kt}}. $$

In this situation shares are not modified and the relative position of each country in the total remains unchanged. It is clear from the above equation that complete harmonization of policies, expressed in growth factors, makes these shares deterministic and does not modify the distribution of shares of member countries. Hence, if one abstracts from random shocks then the volatility of shares would be zero according to this result. This is a useful benchmark for our empirical analysis.

Table 4 Estimates of drift and volatility parameters

Though integration in ALADI is characterized as “shallow” (WTO 2011), estimates of our economic framework offer a valid representation of its data. As expected, Spearman rank correlations of Table 2 are generally lower and estimates of the volatility parameters in Table 4 are higher, definitely compared to the Eurozone. As a result, we have gained confidence that the properties of the model are supported by the data. The following sections will therefore focus on EU-28 and the Eurozone only.⁴

5 Assessing the Degree of Economic Integration

5.1 Theoretical Shares

Assume further without loss of generality that country 1 has the largest and country N has the smallest share of variable j in the area. That is, assume the following:

$$ S_{j1}\geq S_{j2}\geq ...\geq S_{jN}, j\in \{Y,K,H\}. $$

Given the above information, we derive the shares that describe the steady state equilibrium of an integrated area:

Proposition 4

The steady state distribution of shares is uniquely determined by the number of countries N. Particularly, shares are the solution to the following set of equations

$$ \frac{S_{j1}}{S_{j2}}=2, \frac{S_{j1}}{S_{j3}}=3, ...,\frac{S_{j1}}{S_{jN}}=N. $$

(13)

and

$$ S_{j1}=\frac{1}{{\sum}_{n=1}^{N} n^{-1}} $$

(14)

See the proof in the Appendix. The steady-state distribution of shares among integrated economies obtained in Proposition 4 has a number of implications. It reproduces the main outcome of neo-classical growth theory in that the steady state capital-labor ratios are equal among countries that share the same technology. Besides this well-known result, the main contribution of Proposition 4 is to show that for integrated economies the distribution of shares is uniquely determined once the number of member countries is known, a feature shared by all RTAs since the number of member countries is always finite. For example, Table 5 applies the proposition to the EU and gives the complete distribution of shares for the successive EU enlargements. Assuming μ = 0 implies Zipf’s law: the share of the first ranked country is twice as large as the share of the second ranked country, three times as large as the share of the third country and so on. Lastly, it is worth noting that as long as the drift parameter μ is zero, the steady state distribution is unaffected by volatility. This allows for heterogeneity of volatility parameters across variables and across countries. We denote the steady state distribution as $\bar {S}$.

Table 5 Steady state distribution of shares for the European Union (μ = 0)

5.2 Measurement of Integration

Given the theory and the empirical analysis thus far we are in a position to verify a first conjecture, namely that the integration pattern achieved by EU institutions is unsatisfactory. To that end, we measure the degree of economic integration by an integration index $I_{E}(\bar {S},S_{t})$ which is a transformed Euclidean distance. It is defined as

$$ I_{E}(\bar{S},S_{t})=e^{-E(\bar{S},S_{t})}, $$

(15)

where $E(\bar {S},S_{t})$ is the Euclidean distance, measuring the deviation of observed shares S_jnt from their theoretical counterparts $\bar {S} _{jn}$ found by applying Proposition 4:

$$ E(\bar{S},S_{t})=\frac{1}{3}\sum\limits_{j=Y,K,H}\sqrt{\sum\limits_{n=1}^{N}(\bar{S} _{jn}-S_{jnt})^{2}}. $$

(16)

The Euclidean distance (16) has the properties of a metric. For example, it is always non-negative and takes the value zero when for each variable j and for each n ranked country, $S_{jnt}=\bar {S}_{jn}$ : this is the property that arises under full integration. The lower is the degree of economic integration the greater is the deviation of the measure from zero, the lower is the value of $I_{E}(\bar {S},S_{t})$.⁵

Computation of $I_{E}(\bar {S},S_{t})$ makes use of the following information: (1) We use the results of Proposition 4 to compute theoretical shares for the varying number of countries that became member of the European Union. These values are found in Table 5; (2) Observed shares are ranked in the descending order so that rank 1 (n = 1) is attributed to the country with the largest share in the area; rank 2 (n = 2) to the second largest share, etc. Each enlargement requires the re-computation of output and factor shares based on new data; (3) At any date and for each set of countries, confidence bounds are constructed using 10000 bootstrap samples with replacement.⁶

Figure 4 displays the computed index values. The results suggest that most of the time the degree of economic integration fluctuates around 0.9. The time pattern is non-linear indicating that the different enlargements have a differentiated impact on EU integration and that the latter is also responsive to world economic conditions. The values of the index are however, all significantly lower than unity at the 5% significance level suggesting that although high, integration is incomplete. What follows will not change these conclusions.

Fig. 4

Note: Shaded area denotes a 95% confidence interval obtained by taking 10000 bootstrap samples with replacement. See also Appendix C

Integration measure I_E for the EU with estimated confidence bounds.

5.3 Additional Results

5.3.1 Revision of Integration Measure

Spearman rank correlations of Table 2 indicate that the conformity of ranks is not perfect, i.e. the equal-share relationship that should hold in our fully integrated benchmark does not always hold in the data. Our index (15) does not take that into account so far; specifically we miss to assure that the country that ranks n th in the output distribution of shares is also n th in the distribution of primary factors. It is therefore important to re-compute index (15) so that this distortion is accounted for.

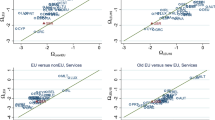
For example, let us consider the UK in 2016. Figure 1 reveals that it is ranked second in EU-28 for output (Y ) and human capital (H) but fourth for its share of physical capital (K): the equal-share relationship is clearly violated in this case and penalties for such violations must be introduced in Eq. 15. Our correction is as follows. To preserve the equality of shares between H, K and Y, UK physical capital share (K) is positioned second though it is not, which introduces larger gaps between $\bar {S}_{Kn}$ and S_Kn,2016 (see Table 6). Hence, this correction increases $E(\bar {S},S_{t})$ and decreases the integration measure. The more a country violates the equal-share relationship the larger are the deviations and the smaller is the value of the integration index.⁷ Let $I_{R}(\bar {S},S_{t})$ denote the revised measure. Figure 5 contains information regarding the extent of the revision for EU and EMU. Panel (a) shows the index values computed using Eq. 15; panel (b) shows revised integration index values. As it is clear, revised index values are slightly lower than the original ones. However, the decline in the integration measure is not very large. This is because of the relatively high correlations between different pairs of shares. The results suggest that the extent of economic integration is higher in the Eurozone and clearly more stable.

Table 6 Corrections to the integration measure based on the observed ranking of Y

Fig. 5

Note: Revision of the index is performed using observed ranking of output shares

Integration in the EU and Eurozone: a comparison.

5.3.2 Assessing Trends in EU Integration

The integration performance of the EU and the sequence of enlargements experienced since the 1957 Treaty of Rome raise the following important issue: What is the time pattern of EU integration: increasing or decreasing? The answer to this question uses segmented regression in which the integration index $I_{R}(\bar {S},S_{t})$ is partitioned into intervals whose boundaries are integration breakpoints. The estimation technique thus endogenously detects over which period the integration variable stagnates, shows a positive or negative trend (Muggeo 2003).⁸

Initially we enter seven enlargement dates as potential breakpoints to the analysis and let the algorithm determine how many of them are actual breakpoints. Except for 1957, none of enlargement dates are selected as containing breakpoints, though some are close. Figure 6 shows the optimization results that display a distorted w-shape.

After more than 60 years of the Rome Treaty and 25 years of the Maastricht Treaty, the time profile of European integration is rather unknown and our analysis tries to fill this gap. The difficulty arises from the lack of specification of the limits to integration. When the latter are not defined, episodes of European integration are compared to the USA as analysts and policymakers often refer explicitly or implicitly to the union of US states as the benchmark of complete integration. For example, Bowen et al. (2011) reveal that by 2000 the measured extent of integration of EU countries was essentially the same as that of the US states. Rogers (2007) provides evidence of a striking decline in dispersion for traded goods prices in Europe over the period 1990-2004. By 2004 dispersion in the euro area is quite close to that of the USA. On the whole, the patterns of Figs. 5b and 6 support this empirical evidence.

Fig. 6

Integration measure I_R for the EU with the estimated non-linear trend

Specifically, the membership of the UK, Ireland and Denmark has initiated a very long period of integration growth (likewise for Greece, Spain and Portugal). EU integration peaked in the period 1995 - 2000 but collapsed afterwards following drastic events like the dot-com bubble, September 11th attacks, stock market downturns of 2002 and the second Persian Gulf War. The opening of EU to Eastern countries in 2004 and 2007 also contributed positively to EU integration. However, since 2011, integration in the EU-28 has stalled. This is clear from the regression slope estimates of Table 7 where the slope of the last segment is not significantly different from zero.

Table 7 Breakpoints and slope estimates of the segmented regression

6 Brexit

The first part of this section explores the quantitative implications of Brexit using the comparative statics results of our theory. This is followed by a direct application of our framework by computing the effect of the UK departure from the European Union on integration levels.

6.1 Labour Exodus

Consider for a moment the relative position of the UK within the European Union by looking at outflows of UK productive factors that are likely to occur in the transition to the official Brexit date. The focus is on human capital though physical capital can be coped with by analogy. The reason for this emphasis is the planned relocation on the continent of European agencies like the European Medicines Agency (EMA) and European Banking Authority (EBA) currently located in London. Simultaneously, multinationals and international banks are taking similar steps to relocate some affiliates elsewhere within EU-27.

Let the n th economic unit be the UK. Consider an exogenous outflow ΔH > 0 of human capital out of the n th economic unit that relocates in the rest of the region. This outflow, at impact, will affect relationship (3) for the n th country as follows:

$$ \frac{{{Y}_{n}}}{\sum\nolimits_{k=1}^{N}{{{Y}_{k}}}}=\frac{{{K}_{n}}}{\sum\nolimits_{k=1}^{N}{{{K}_{k}}}}>\frac{{{H}_{n}}-{\Delta} H}{\sum\nolimits_{k=1}^{N}{{{H}_{k}}+({\Delta} H-{\Delta} H)}} $$

This outflow of labour out of the UK decreases its share of the total stock of human capital. Since this drop in human capital decreases country UK’s marginal return to physical capital, incentives arise to decrease investment in physical capital. Given the decrease in both stocks of productive factors, country n’s output and share in total area output will decrease. These adjustments in both output and factor stocks continue until the equality of shares in Eq. 3 is restored, but now with UK achieving a relatively lower level of economic activity than originally.

6.2 Integration Measures

The computation of the new integration index in Eq. 15 is performed by repeating steps of previous sections: (1) With Brexit, firms in EU-27 maximize profits in a new environment with no international labor mobility with the UK, with a wedge between EU and UK prices resulting from tariff and non-tariff barriers and no solidarity via Regional and Social Funds; (2) The new steady state of EU-27 is computed using Proposition 4; (3) Observed shares are re-computed for this new set of EU-27 countries; (4) These are ranked in descending order so that rank 1 (n = 1) is attributed to the country with the largest share in the new area; rank 2 (n = 2) to the second largest share; etc. Figure 7 displays the computed index values for both scenarios, EU-28 and EU-27 (excl. UK).

Fig. 7

Note: Revised measure of integration I_R is used in the figure

Integration measure in EU and EU excl. UK.

From Fig. 7 it is clear that the extent of economic integration measured by the integration index is higher in the EU-27 (excl. UK) scenario. This is because the distribution of productive resources across countries in the new situation comes closer to the ideal distribution obtained in an integrated area with free trade and free factor mobility. Technically, with the United Kingdom being comparable in size to some other EU economies like France or Italy, the EU-27 scenario would bring the actual distribution of shares closer to its steady state values. This suggests the absence of negative consequences of Brexit on EU’s integration.

7 Concluding Remarks

In response to the perception that Brexit involves a process of economic dis-integration, the paper developed a theoretical framework that enables the measurement of economic integration among a group of countries. The objective was to construct an integration benchmark that consists of a steady state equilibrium distribution of economic activity that was characterized by arbitrage pricing and perfect factor mobility. The model predictions were then tested with respect to the members of EU and for two other control groups, the Eurozone and Latin America (ALADI). In all cases, the empirical results strongly supported the theoretical predictions. Given this, metrics were then used to measure the distance between the benchmark and the data.

Measurement allowed for a comparison of integration indices over time and across regions. It was performed on the various enlargements of the European Union and Eurozone, regions characterized by different institutional arrangements. The results suggest that the extent of economic integration is clearly the highest in the Eurozone but values are all very close to each other.

In response to the title of the paper, the results of our framework inferred the quantitative implications of Brexit. It turns out that the UK departure from the European Union has no negative consequence on integration levels of EU excl. UK.

Appendices

Appendix A: Proofs of Results

1.1 A.1 Proof of Proposition 1

Marginal products of human capital implied by Eq. 2 can be expressed as a function f of human-to-physical capital (x) and as a function g of output-to-physical capital (y). In particular, at any date t:

$$ \frac{\partial Y_{n}}{\partial H_{n}}=f\left( \frac{H_{n}}{K_{n}}\right) =g\left( \frac{Y_{n}}{K_{n}}\right) , $$

where

$$ f\left( x\right) =\gamma \delta \rho \left( x+\rho -1\right)^{\delta \rho -1} $$

and

$$ g\left( y\right) =\gamma^{\frac{1}{\delta \rho }}\delta \rho y^{1-\frac{1}{ \delta \rho }}. $$

Functions f and g are strictly decreasing. In particular,

$$ \frac{\partial f}{\partial x}=\gamma \delta \rho \left( \delta \rho -1\right) \left( x+\rho -1\right)^{\delta \rho -2}<0 $$

as the first two terms of the product have opposite signs while the last term is always positive. Namely, γδρ > 0 and δρ − 1 < 0, which follows directly from the domain over which parameters γ, δ, ρ are defined, and

$$ x+\rho -1>\frac{1-\rho }{1-\delta \rho }\delta \rho >0, $$

which follows from the fact that x > 0 and $x>\frac {1-\rho }{1-\delta \rho }$. Similarly,

$$ \frac{\partial g}{\partial y}=\gamma^{\frac{1}{\delta \rho }}\delta \rho \left( 1-\frac{1}{\delta \rho }\right) y^{-\frac{1}{\delta \rho }}<0, $$

which follows again from the definition of the domain of parameters γ, δ, ρ.

Perfect mobility of labour brings about the equalization of value marginal products of human capital across member countries as human capital from the low-return country flows to the high-return country until efficiency wages fully equalize. With free trade the price of the single good are similar across countries. Given this and the strict monotonicity of f and g, equality of marginal products implies equality of human-to-physical capital ratios and output-to-capital ratios between any two members of the economic area. Namely, for any pair of countries j and n we obtain the following equality:

$$ \frac{H_{n}}{K_{n}}=\frac{H_{j}}{K_{j}} \text{ and } \frac{Y_{n}}{K_{n}}= \frac{Y_{j}}{K_{j}}, $$

(A.17)

which is sufficient to conclude that for any country n within a fully integrated economic area the human capital share coincides with that of physical capital and the physical capital share coincides with that of output. Specifically, employing (A.17) gives:

$$ \frac{H_{n}}{{\sum}_{k=1}^{N}H_{k}}=\frac{1}{{\sum}_{k=1}^{N}\frac{H_{k}}{H_{n}}} =\frac{1}{{\sum}_{k=1}^{N}\frac{K_{k}}{K_{n}}}=\frac{K_{n}}{{\sum}_{k=1}^{N}K_{k}} $$

and

$$ \frac{K_{n}}{{\sum}_{k=1}^{N}K_{k}}=\frac{1}{{\sum}_{k=1}^{N}\frac{K_{k}}{K_{n}}} =\frac{1}{{\sum}_{k=1}^{N}\frac{Y_{k}}{Y_{n}}}=\frac{Y_{n}}{{\sum}_{k=1}^{N}Y_{k}}, $$

from where the equal-share relationship (3) follows. __

1.2 A.2 Derivation of Eq. 4

Using elements of the proof of Proposition 1, we know for region n:

$$\frac{\partial {{Y}_{n}}}{\partial {{H}_{n}}}=f({{x}_{n}})=g({{y}_{n}})$$

where ${{x}_{n}}=\frac {{{H}_{n}}}{{{K}_{n}}}$ and ${{y}_{n}}=\frac {{{Y}_{n}}}{{{K}_{n}}}$. From (1), expressions f(⋅) and g(⋅) for region n are:

$$f({{x}_{n}})=\gamma \delta \rho {{({{x}_{n}}+\rho -1)}^{(\delta \rho -1)}}$$

and

$$g({{y}_{n}})={{\gamma }^{{1}/{\delta \rho } }}\delta \rho y_{n}^{(\delta \rho -1)/\delta \rho }.$$

Likewise for any region j:

$$f({{x}_{j}})=\gamma \delta \rho {{({{x}_{j}}+\rho -1)}^{(\delta \rho -1)}}$$

and

$$g({{y}_{j}})={{\gamma }^{{1}/{\delta \rho } }}\delta \rho y_{j}^{(\delta \rho -1)/\delta \rho }.$$

First order conditions imply equal value marginal products of physical capital across regions:

$${{S}_{n1}}{{p}_{1}}g({{y}_{1}})=...={{S}_{nj}}{{p}_{j}}g({{y}_{j}})=...={{S}_{nn}}{{p}_{n}}g({{y}_{n}})=...={{S}_{nN}}{{p}_{N}}g({{y}_{N}}),$$

where S_nj is the nominal bilateral exchange rate expressed as units of n currency per unit of j currency (so that S_nn = 1). Isolating regions j and n:

$$....={{p}_{n}}{{\gamma }^{{1}/{\delta \rho } }}\delta \rho y_{n}^{(\delta \rho -1)/\delta \rho }={{S}_{nj}}{{p}_{j}}{{\gamma }^{{1}/{\delta \rho } }}\delta \rho y_{j}^{(\delta \rho -1)/\delta \rho }=...$$

Let us scale all prices with respect to good n and define Q_nj = S_njp_j/p_n as the real bilateral exchange rate (so that Q_nj = 1 with n = j). Taking the power δρ/(δρ − 1) common to all countries:

$$...={{y}_{n}}=Q_{j}^{\delta \rho /(\delta \rho -1)}{{y}_{j}}=...$$

or

$$...=\frac{{{Y}_{n}}}{{{K}_{n}}}=\frac{Q_{j}^{{\Psi} }{{Y}_{j}}}{{{K}_{j}}}=...$$

where Ψ = δρ/(δρ − 1). Altogether:

$$...=\frac{{{Y}_{n}}}{{{K}_{n}}}=\frac{Q_{j}^{{\Psi} }{{Y}_{j}}}{{{K}_{j}}}=...=\frac{\sum\nolimits_{k=1}^{N}{Q_{k}^{{\Psi} }{{Y}_{k}}}}{\sum\nolimits_{k=1}^{N}{{{K}_{k}}}}$$

For region n, a transformation of this equality gives the following relationships between ratios of output and physical capital:

$$ \frac{{{K}_{n}}}{\sum\nolimits_{k=1}^{N}{{{K}_{k}}}}=\frac{{{Y}_{n}}}{\sum\nolimits_{k=1}^{N}{Q_{k}^{{\Psi} }{{Y}_{k}}}} $$

(A.18)

The equality of rates of return to human capital across the N members can be written:

$${{S}_{n1}}{{p}_{1}}f({{x}_{1}})=...={{S}_{nj}}{{p}_{j}}f({{x}_{j}})=...={{S}_{nn}}{{p}_{n}}f({{x}_{n}})=...={{S}_{nN}}{{p}_{N}}f({{x}_{N}})$$

Focusing on j and n:

$$...={{S}_{nn}}{{p}_{n}}\gamma \delta \rho {{({{x}_{n}}+\rho -1)}^{(\delta \rho -1)}}={{S}_{nj}}{{p}_{j}}\gamma \delta \rho {{({{x}_{j}}+\rho -1)}^{(\delta \rho -1)}}=...$$

In compliance with Anderson et al. (2015) we assume a Cobb Douglas production function (ρ = 1):

$$...={{S}_{nn}}{{p}_{n}}x_{n}^{(\delta \rho -1)}={{S}_{nj}}{{p}_{j}}x_{j}^{(\delta \rho -1)}=...$$

Like before, let us scale all prices with respect to good n and use Q_nj = S_njp_j/p_n with Q_nn = S_nnp_n/p_n = 1. Taking the power 1/(δρ − 1) common to all countries:

$$...={{x}_{n}}=Q_{nj}^{1/(\delta \rho -1)}{{x}_{j}}=...$$

or

$$...=\frac{{{H}_{n}}}{{{K}_{n}}}=\frac{Q_{nj}^{{\Omega} }{{H}_{j}}}{{{K}_{j}}}=...$$

where Ω = 1/(δρ − 1). Altogether:

$$...=\frac{{{H}_{n}}}{{{K}_{n}}}=\frac{Q_{nj}^{{\Omega} }{{H}_{j}}}{{{K}_{j}}}=...=\frac{\sum\nolimits_{k=1}^{N}{Q_{nk}^{{\Omega} }{{H}_{k}}}}{\sum\nolimits_{k=1}^{N}{{{K}_{k}}}}.$$

For region n, a transformation of this equality gives the following relationships between ratios of human and physical capital:

$$ \frac{{{K}_{n}}}{\sum\nolimits_{k=1}^{N}{{{K}_{k}}}}=\frac{{{H}_{n}}}{\sum\nolimits_{k=1}^{N}{Q_{nk}^{{\Omega} }{{H}_{k}}}}. $$

(A.19)

Combining (A.18) and (A.19):

$$ \frac{{{Y}_{n}}}{\sum\nolimits_{k=1}^{N}{Q_{nk}^{{\Psi} }{{Y}_{k}}}}=\frac{{{K}_{n}}}{\sum\nolimits_{k=1}^{N}{{{K}_{k}}}}=\frac{{{H}_{n}}}{\sum\nolimits_{k=1}^{N}{Q_{nk}^{{\Omega} }{{H}_{k}}}}. $$

(A.20)

Thus, the introduction of a model with differentiation by place of origin though it rescales variables (Y_n,H_n) by relative prices maintain the equal-share relationship. Now assume purchasing power parity, that is S_nj = p_n/p_j and Q_nj = 1 as the real bilateral exchange rate becomes unity. Then:

$$ \frac{{{Y}_{n}}}{\sum\nolimits_{k=1}^{N}{{{Y}_{k}}}}=\frac{{{K}_{n}}}{\sum\nolimits_{k=1}^{N}{{{K}_{k}}}}=\frac{{{H}_{n}}}{\sum\nolimits_{k=1}^{N}{{{H}_{k}}}} $$

(A.21)

That reproduces expression (3) of Proposition 1.

1.3 A.3 Proof of Proposition 2

Itô lemma applied to log S_jnt yields the following expression for Eq. 5 for any initial value S_jn0 :

$$ \left\{ \begin{array}{ll} \log {\ S_{jnt}} & =X_{nt}+L_{t}-U_{t} \\ X_{nt} & =\log {S_{jn0}}+\left( \mu -\frac{\sigma^{2}}{2}\right) t+\sigma B_{t} \end{array} \right. $$

(A.22)

A convenient way to model reflections is to use Skorokhod maps that restrict shares to take values within a given interval. In particular, L_t and U_t are defined as

$$ \left\{ \begin{array}{ll} L_{t} & =-\inf_{0\leq s\leq t}\left( \{X_{ns}-\log {b}\}\wedge \{0\}\right) \\ U_{t} & =-\inf_{0\leq s\leq t}\left( \{\log {c}-X_{ns}\}\wedge \{0\}\right) \end{array} \right. $$

where inf stands for the infimum of a set so that reflections occur now at log b and log c. For μ and σ such that $\mu <\frac { \sigma ^{2}}{2}$ there exists a steady state distribution of Eq. A.22. Zhang and Du (2010) derive the steady state density function of RGBM with two barriers. The function reads:

$$ f_{jn\infty }(S)=\left( 1-\frac{2\mu }{\sigma^{2}}\right) \frac{S^{\frac{ 2\mu }{\sigma^{2}}-2}}{b^{\frac{2\mu }{\sigma^{2}}-1}-c^{\frac{2\mu }{ \sigma^{2}}-1}}. $$

The corresponding cumulative distribution is then given by Eq. 6.⁹ __

1.4 A.4 Proof of Proposition 3

μ = 0 follows from the adding-up constraint (7). Let $g_{jnt}=\frac {S_{jnt}}{S_{jn,t-1}}-1$ denote the growth rate of factor j, country n at time point t. Then Eq. 7 implies ${\sum }_{n=1}^{N}S_{jn,t-1}g_{jnt}=0$. Taking average of this expression over time gives $E_{t} {\sum }_{n=1}^{N}S_{jn,t-1}g_{jnt}={\sum }_{n=1}^{N}S_{jn,t-1}E_{t}g_{jnt}=0$ and because in our model the drift parameter μ does not vary across countries, this holds only if E_tg_jnt = 0. Therefore, the average growth rate must be zero. __

1.5 A.5 Proof of Proposition 4

Using (11) and taking the ratio of the first share over the second share, the first share over the third, etc. gives the sequence of ratios (13) in the proposition:

$$ \frac{{{S}_{j1}}}{{{S}_{j2}}} = \frac{\lambda /{{R}_{j1}}}{\lambda /{{R}_{j2}}} = \frac{{{R}_{j2}}}{{{R}_{j1}}} = 2,\frac{{{S}_{j1}}}{{{S}_{j3}}} = \frac{\lambda /{{R}_{j1}}}{\lambda /{{R}_{j3}}} = \frac{{{R}_{j3}}}{{{R}_{j1}}} = 3,...,\frac{{{S}_{j1}}}{{{S}_{jN}}} = \frac{\lambda /{{R}_{j1}}}{\lambda /{{R}_{jN}}} = \frac{{{R}_{jN}}}{{{R}_{j1}}} = N. $$

The definition of shares implies also that the same rule holds not only for shares but also for the levels of the variables j ∈ {Y,K,H}. Without loss of generality assume j = H:

$$ \frac{{{H}_{1}}}{{{H}_{2}}}=2,\frac{{{H}_{1}}}{{{H}_{3}}}=3,...,\frac{{{H}_{1}}}{{{H}_{N}}}=N. $$

This in turn together with the definition of shares uniquely determines the share of the first ranked country or the largest share as a function of the number of countries only. Namely:

$$ {{S}_{H1}}=\frac{{{H}_{1}}}{\sum\nolimits_{n=1}^{N}{{{H}_{n}}}}=\frac{1}{\sum\nolimits_{n=1}^{N}{\frac{{{H}_{n}}}{{{H}_{1}}}}}=\frac{1}{\sum\nolimits_{n=1}^{N}{{{n}^{-1}}}} $$

that is (14). Shares of other countries can be determined similarly. Likewise for j = K,Y. __

Appendix B: Data Sources and Methods

2.1 B.1 Human Capital

For the three groups of countries (ALADI, EU and Eurozone), human capital is measured as total population aged 15 and over with at least completed secondary education¹⁰ and is obtained from Barro and Lee’s data set on educational attainment (version 2.1). The data is on the 5-year interval basis covering the period 1950 - 2010 and is available for all the countries under analysis. We use cubic spline interpolation to obtain annual data. The method is illustrated in Fig. 8 with points representing original figures before interpolation.

Fig. 8

Human capital data interpolation. The example of Lithuania and the Netherlands

To extend interpolation until 2016 we need human capital data for 2015 and 2020. The data for 2015 and 2020 is obtained from Barro and Lee’s projections of educational attainment for the population aged 15–64. We compute the percentage of population aged 15–64 with at least completed secondary education and use it as a proxy for the percentage of population aged 15+ with at least completed secondary education. We then multiply it by the population aged 15+ in 2015 and 2020 to obtain human capital in those years. Population aged 15+ is obtained from the World Bank population projections. We download 2010, 2015 and 2020 data points, compute growth rates and apply them to extend Barro and Lee data on population aged 15 and over.

2.2 B.2 Physical Capital

Data for physical capital in all regions come from Penn World Tables, version 6.2 (PWT 6.2) and cover the period of 1950–2004. The data is in constant prices with the base year of 2000. Measurement units are international dollars.

There were two problems associated with the capital stock data in hand. First, the data was available until the year 2004 only or even until 2003 for some of the countries. Second, no data was available for Bulgaria, Croatia, Czech Republic, Estonia, Latvia, Lithuania, Slovakia and Slovenia.

To solve the first above mentioned problem we applied the growth rates of PWT 9.0 physical capital stock data (variable rkna). This extended the data till 2014. To extend it further till 2016 we used the growth rates of physical capital stock from European Commission’s AMECO database (variable oknd).

To solve the second problem we relied on PWT 9.0 data for the year 2011. In that year we computed the ratio of physical capital for missing countries to Dutch physical capital and multiplied it by 2011 Dutch physical capital from PWT 6.2. Thus, for example, Lithuanian physical capital in 2011 was obtained as:

$$ K_{LT, 2011} = \frac{K^{PWT 9.0}_{LT, 2011}}{K^{PWT 9.0}_{NL, 2011}}K^{PWT 6.2}_{NL, 2011}. $$

To extend the series backwards and forwards we used the growth rates of physical capital from PWT 9.0 (variable rkna) and AMECO.

2.3 B.3 Output

Output in all country groupings, measured by real GDP, is obtained from PWT 7.0. The data ranges from 1950 to 2009 and is expressed in international dollars to equalize the purchasing power of different currencies and allow for cross-country level data comparison. PWT 7.0 uses the year 2005 as a base year for all constant price variables. We use 2000 as the base year in our study. Hence, to convert the base year of real output to 2000 we find the implicit deflator in 2000 for each of the countries and rescale 2005 constant price series accordingly. To extend the series till 2014 we use the growth rates of real GDP from PWT 9.0 (variable rgdpna). We also use the growth rates from the same source to extend German GDP backwards till 1950. To extend Cuban data till 2015 we apply the growth rates of GDP in constant 2011 USD obtained from the World Bank WDI database. Finally, we use Eurostat real GDP growth rates to compute 2015 - 2016 data for the EU countries (code: tec00115).

Appendix C: Bootstrap Samples

We construct the confidence interval for the integration measure using the bootstrap technique. To implement the bootstrap we draw random samples with replacement from the data on output and production factors. For illustration purposes let us consider the EU-6 in 1958. We have three sets of variables {Y₁,Y₂,...,Y₆}, {K₁,K₂,...,K₆} and {H₁,H₂,...,H₆}. We draw 10000 random samples from each of the sets. Our samples are of the same size as the data and the possibility of replacement means that a variable of a particular country can be selected more than once. An example of a sample for output could therefore be {Y₂,Y₂,Y₄,Y₄,Y₄,Y₁}. Once 10000 samples are drawn, for each of the samples we compute output and production factor shares and rank them in descending order. Further, we generate theoretical shares given in Table 5. This allows us to compute 10000 integration indices. To find the 95% confidence interval we rank computed integration indices and take the lower 2.5% and the upper 97.5% data points. The 2.5% and the 97.5% points define our confidence interval. We compute confidence intervals for the Spearman rank correlations in Table 2 in a similar manner.