Skip to main content

Advertisement

SpringerLink
Log in

Productivity, Demand, and the Home Market Effect

  • Research Article
  • Published:
Open Economies Review Aims and scope Submit manuscript

Abstract

The nature of causality between international trade and industrialization remains ambiguous. We consider a model of international trade that features the home market effect—where there are differences in income and productivity between sectors and between countries—to identify additional channels by which to determine the effects of international trade on industrialization. The introduction of non-homothetic preferences and differences in productivity can aid in interpreting of some apparent paradoxes within international trade, such as the commercial relations between more populated countries as China and India and large economies in term of their GDP as the U.S. Population size, demand composition, and productivity levels constitute the three main channels by which to determine the effects of international trade. Interactions among these channels define the results obtained, especially in terms of the countries’ industrialization levels. Additionally, we find that welfare levels under trade are always higher than those under autarky.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. World Bank data (2013).

  2. Hereafter,thevariablesthatcorrespondtoforeignregionsbearasuperscriptasterisk.

  3. γ∗ > 1

  4. This consumption is equal across all countries, thus indicating that everybody needs the same minimum consumption of food to survive.

  5. γ represents the relationship between the population and labour—in other words, the dependency factor.

  6. The level of industrialization can also be measured by the amount of labour available in the manufactured goods sector (Desdoigts and Jaramillo 2009).

  7. The supernumerary income is defined as the wage minus subsistence consumption of X good.

  8. This is a simplified assumption that is widely used (Helpman and Krugman 1985; Krugman 1991, etc.) and which does not affect the essential argument of the model. Ottaviano and Thisse (2004) and Zeng and Kikuchi (2009) each shows that the HME and conclusions pertaining to differentiated goods persist, while bearing in mind transportation costs on homogeneous goods.

  9. $$\mathcal{L=}\left( \sum\limits_{i = 1}^{n}y_{i}^{\sigma }+\sum\limits_{j = 1}^{n^{\ast }}y_{j}^{\ast \sigma }\right)^{\frac{1}{\sigma }}-\lambda \left( \sum\limits_{i = 1}^{n}p_{i}y_{i}+\sum\limits_{i = 1}^{n}\widehat{p_{j}^{\ast }}y_{j}^{\ast }-\left( 1-\alpha \right) \left( \frac{w}{\gamma }-P_{x}\overline{X}\right) \right) $$

  10. The results can be modified relative to those of the closed economy, only if wages between the countries differ; this is a central element in the following section.

  11. D is determined by the zero-profit condition: \(D_{i}=D=\frac {\mu \sigma }{\left (1-\sigma \right ) \beta }\)

  12. Barrios et al. (2003) show evidence of this establishment of firms in the largest market.

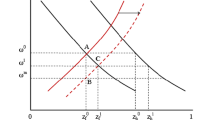
  13. In the Appendix, we show that even when international trade reduces the degree of industrialization in a country, the welfare of the representative agent improves, because the international market offers a greater number of varieties.

  14. This is true so long as worker remuneration exceeds the survival consumption of the agricultural good; this is one of the assumptions made herein.

  15. See Appendix 1.

  16. See Kikuchi (2001) for more details on welfare levels in a monopolistic competition model. Candau and Fleurbaey (2011) show how this result is robust to heterogeneous preferences.

  17. It is always true that productivity is higher than the minimum level of consumption of homogeneous goods.

  18. These results are always true under the interest interval.

  19. These standard values are used in the studies of Krugman (1991), Martin and Ottaviano (1999), and Corsetti et al. (2007), among others.

  20. When productivity is equal among sectors, total productivity determines the wages of workers.

References

  • Antweiler W, Trefler D (2002) Increasing returns and all that: a view from trade. Am Econ Rev 92:93–119

    Article  Google Scholar 

  • Barrios S, Görg H, Strobl E (2003) Multinational enterprises and new trade theory: evidence for the convergence hypothesis. Open Econ Rev 14:397–418

    Article  Google Scholar 

  • Bohman H, Nilsson D (2007) Income inequality as a determinant of trade flows. Int J Appl Econ 4:40–59

    Google Scholar 

  • Candau F, Fleurbaey M (2011) Agglomeration and welfare with heterogeneous preferences. Open Econ Rev 22:685–708

    Article  Google Scholar 

  • Chung C (2006) Nonhomothetic preferences and the home market effect: does relative market size matter? Mimeo. Georgia Institute of Technology

  • Corden W (1970) A note on economies of scale, the size of the domestic market and the pattern of trade. In: Studies in international economics

  • Corsetti G, Martin P, Pesenti P (2007) Productivity, terms of trade and the “home market effect”. J Int Econ 73:99–127

    Article  Google Scholar 

  • Crozet M, Trionfetti F (2008) Trade costs and the home market effect. J Int Econ 76:309–321

    Article  Google Scholar 

  • Dalgin M, Mitra D, Trindade V (2008) Inequality, nonhomothetic preferences, and trade: a gravity approach. South Econ J 74:747–774

    Google Scholar 

  • Davis D (1998) The home market, trade, and industrial structure. Am Econ Rev 88:1264–1276

    Google Scholar 

  • Davis D, Weinstein D (1996) Does economic geography matter for international specialization? NBER working paper 5706

  • Davis D, Weinstein D (2003) Market access, economic geography and comparative advantage: an empirical assessment. J Int Econ 59:1–23

    Article  Google Scholar 

  • Desdoigts A, Jaramillo F (2009) Trade, demand spillovers, and industralization: the emerging global middle class in perspective. J Int Econ 79:248–258

    Article  Google Scholar 

  • Felbermayr G, Jung B (2011) Home market effects and the single-sector Melitz model. Mimeo. CESifo working paper no.3695

  • Hanson G, Xiang C (2004) The home market effect and bilateral trade patterns. Am Econ Rev 94:1108–1129

    Article  Google Scholar 

  • Helpman E, Krugman P (1985) Market structure and foreing trade. The MIT Press, Cambridge

    Google Scholar 

  • Huang D-S, Huang Y-Y (2011) Technology advantage and home-market effect: an empirical investigation. J Econ Integr 26:81–109

    Article  Google Scholar 

  • Kikuchi T (2001) A note on the distribution of trade gains in a model of monopolistic competition. Open Econ Rev 12:415–421

    Article  Google Scholar 

  • Krugman P (1980) Scale economies, product differentiation, and the pattern of trade. Am Econ Rev 70:950–959

    Google Scholar 

  • Krugman P (1991) Increasing returns and economic geography. J Polit Econ 99:483–499

    Article  Google Scholar 

  • Linder B (1961) An essay on trade and transformation. Garland Pub, New York

    Google Scholar 

  • Markusen J (1986) Explaining the volume of trade: an eclectic approach. Am Econ Rev 76:1002–1011

    Google Scholar 

  • Martin P, Ottaviano G (1999) Growing locations: industry location in a model of endogenous growth. Eur Econ Rev 43:281–302

    Article  Google Scholar 

  • Melitz MJ (2005) When and how should infant industries be protected? J Int Econ 66:177–196

    Article  Google Scholar 

  • Mitra D, Trindade V (2005) Inequality and trade. Can J Econ 38:1253–1271

    Article  Google Scholar 

  • Ottaviano G, Thisse J-F (2004) Agglomeration and economic geography. Handbook of regional and urban economics 4:2563–2608

    Article  Google Scholar 

  • Romer P (1990) Endogenous technological change. J Polit Econ 98:71–102

    Article  Google Scholar 

  • Young A (1991) Learning by doing and the dynamic effects of international trade. Q J Econ 106:369–405

    Article  Google Scholar 

  • Yu Z (2005) Trade, market size, and industrial structure: revisiting the home-market effect. Can J Econ 38:255–272

    Article  Google Scholar 

  • Zeng D-Z, Kikuchi T (2009) home market effect and trade costs. Jpn Econ Rev 60:253–270

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Business, Colegio de Estudios Superiores de Administración-CESA, Cra 6 #34-51, Bogotá, Colombia

    Iader Giraldo

  2. Economics Department, Universidad del Rosario, Cl 12c #4-69, Bogotá, Colombia

    Fernando Jaramillo

Authors
  1. Iader Giraldo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fernando Jaramillo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Iader Giraldo.

Additional information

We wish to thank two anonymous referees and the editor for helpful comments and suggestions. We also thank Thierry Verdier, Matthieu Crozet, Cecilia García-Peñalosa, Alain Desdoigts, Hernando Zuleta, and Ricardo Argüello for their pertinent comments.

Appendix

Appendix

In this section, we demonstrate that welfare levels are always better after trade, relative to autarky levels. The next equation relates the utility levels under trade and under autarky:

$$ \frac{U}{U_{A}}=\left( \frac{n}{n_{A}}+\frac{n^{\ast }\tau^{\frac{\sigma }{ 1-\sigma }}}{n_{A}}\left( \frac{p}{p^{\ast }}\right)^{\frac{\sigma }{ 1-\sigma }}\right)^{\frac{(1-\sigma )(1-\alpha )}{\sigma }}. $$
(71)

Using Eqs. 17, 21, 33, 36, 37 and 38,

$$\begin{array}{@{}rcl@{}} \frac{n}{n^{A}} \!&=&\!\left( \frac{\frac{n}{n^{\ast }}}{\frac{n}{n^{\ast }} \!+\!\theta \frac{p^{\ast }}{p}}\right) \!+\!\left( \frac{\theta^{\ast }\frac{n}{ n^{\ast }}}{\frac{p^{\ast }}{p}\!+\!\theta^{\ast }\frac{n}{n^{\ast }}}\right) \frac{1}{Z}\!=\!\frac{1}{1\!-\!\theta^{\ast }}\!-\!\frac{\theta }{1\!-\!\theta }\left( \frac{1}{Z}\right) \end{array} $$
(72)
$$\begin{array}{@{}rcl@{}} \frac{n^{\ast }}{n^{A}} \!&=&\!\left[ \left( \frac{\theta }{\frac{n}{n^{\ast }} \frac{p}{p^{\ast }}\!+\!\theta }\right) \!+\!\left( \frac{1}{1\!+\!\theta^{\ast }\frac{n }{n^{\ast }}\frac{p}{p^{\ast }}}\right) \frac{1}{Z}\right] \!\frac{p}{p^{\ast } }\!=\!\theta \left( \! \frac{1}{\left( 1\!-\!\theta \right) Z}\!-\!\frac{\theta^{\ast }}{ 1\!-\!\theta^{\ast }}\!\right). \end{array} $$
(73)

Entering the final equations in (71), we have

$$ \frac{U}{U_{A}}=\left( \frac{1-\theta \theta^{\ast }}{1-\theta^{\ast }} \right)^{\frac{(1-\sigma )(1-\alpha )}{\sigma }}. $$
(74)

Given that 𝜃 < 1 ⇒ U > UA, welfare is always better after trade, relative to that under autarky.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Giraldo, I., Jaramillo, F. Productivity, Demand, and the Home Market Effect. Open Econ Rev 29, 517–545 (2018). https://doi.org/10.1007/s11079-018-9476-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11079-018-9476-1

Keywords

JEL Classification

Search

Navigation