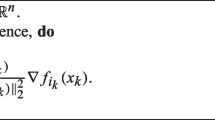Abstract
The randomized Kaczmarz method, along with its recently developed variants, has become a popular tool for dealing with large-scale linear systems. However, these methods usually fail to converge when the linear systems are affected by heavy corruption, which is common in many practical applications. In this study, we develop a new variant of the randomized sparse Kaczmarz method with linear convergence guarantees, by making use of the quantile technique to detect corruptions. Moreover, we incorporate the averaged block technique into the proposed method to achieve parallel computation and acceleration. Finally, the proposed algorithms are illustrated to be very efficient through extensive numerical experiments.









Similar content being viewed by others
Availability of supporting data
The data that support the findings of this study are divided into two kinds: simulated data generated by Matlab code and public data generated by AIRtools toolbox (http://www.imm.dtu.dk/~pcha/Regutools/).
References
Lorenz, D.A., Wenger, S., Schöpfer, F., Magnor, M.: A sparse Kaczmarz solver and a linearized Bregman method for online compressed sensing. In: 2014 IEEE International Conference on Image Processing (ICIP), pp. 1347–1351 (2014). https://doi.org/10.1109/ICIP.2014.7025269. IEEE
Tan, Y.S., Vershynin, R.: Phase retrieval via randomized Kaczmarz: theoretical guarantees. Inf. Inference: J. IMA 8(1), 97–123 (2019). https://doi.org/10.1093/imaiai/iay005
Xian, Y., Liu, H.G., Tai, X.C., Wang, Y.: Randomized Kaczmarz Method for Single-Particle X-Ray Image Phase Retrieval[M]//Handbook of Mathematical Models and Algorithms in Computer Vision and Imaging: Mathematical Imaging and Vision. Cham: Springer International Publishing, pp. 1–16 (2022). https://doi.org/10.1007/978-3-030-98661-2112
Römer, P., Filbir, F., Krahmer, F.: On the randomized Kaczmarz algorithm for phase retrieval. In: 2021 55th Asilomar Conference on Signals, Systems, and Computers, pp. 847–851 (2021). https://doi.org/10.1109/IEEECONF53345.2021.9723291. IEEE
Chen, X., Qin, J.: Regularized Kaczmarz algorithms for tensor recovery. SIAM J. Imaging Sci. 14(4), 1439–1471 (2021). https://doi.org/10.1137/21M1398562
Du, K., Sun, X.H.: Randomized regularized extended Kaczmarz algorithms for tensor recovery. Preprint at arXiv:2112.08566 (2021)
Gordon, R., Bender, R., Herman, G.T.: Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography. J. Theor. Biol. 29(3), 471–481 (1970). https://doi.org/10.1016/0022-5193(70)90109-8
Jarman, B., Needell, D.: QuantileRK: Solving large-scale linear systems with corrupted, noisy data. In: 2021 55th Asilomar Conference on Signals, Systems, and Computers, pp. 1312–1316 (2021). https://doi.org/10.1109/IEEECONF53345.2021.9723338. IEEE
Needell, D.: Randomized Kaczmarz solver for noisy linear systems. BIT Numer. Math. 50, 395–403 (2010). https://doi.org/10.1007/s10543-010-0265-5
Schöpfer, F., Lorenz, D.A.: Linear convergence of the randomized sparse Kaczmarz method. Math. Program. 173(1), 509–536 (2019). https://doi.org/10.1007/s10107-017-1229-1
Yuan, Z.Y., Zhang, H., Wang, H.X.: Sparse sampling Kaczmarz-Motzkin method with linear convergence. Math. Methods Appl. Sci. 45(7), 3463–3478 (2022). https://doi.org/10.1002/mma.7990
Yuan, Z.Y., Zhang, L., Wang, H.X., Zhang, H.: Adaptively sketched Bregman projection methods for linear systems. Inverse Probl. 38(6), 065005 (2022). https://doi.org/10.1088/1361-6420/ac5f76
Zhang, L., Yuan, Z.Y., Wang, H.X., Zhang, H.: A weighted randomized sparse Kaczmarz method for solving linear systems. Comput. Appl. Math. 41(8), 1–18 (2022). https://doi.org/10.1007/s40314-022-02105-9
Haddock, J., Needell, D., Rebrova, E., Swartworth, W.: Quantile-based iterative methods for corrupted systems of linear equations. SIAM J. Matrix Anal. Appl. 43(2), 605–637 (2022). https://doi.org/10.1137/21M1429187
Steinerberger, S.: Quantile-based random Kaczmarz for corrupted linear systems of equations. Inf. Inference: J. IMA 12(1), 448–465 (2023). https://doi.org/10.1093/imaiai/iaab029
Tondji, L., Lorenz, D.A.: Faster randomized block sparse Kaczmarz by averaging. Numer. Algorithms 93(4), 1417–1451 (2023). https://doi.org/10.1007/s11075-022-01473-x
Merzlyakov, Y.I.: On a relaxation method of solving systems of linear inequalities. USSR Comput. Math. and Math. Phys. 2(3), 504–510 (1963). https://doi.org/10.1016/0041-5553(63)90463-4
Necoara, I.: Faster randomized block Kaczmarz algorithms. SIAM J. Matrix Anal. Appl. 40(4), 1425–1452 (2019). https://doi.org/10.1137/19M1251643
Karczmarz, S.: Angenaherte auflosung von systemen linearer glei-chungen. Bull. Int. Acad. Pol. Sic. Let., Cl. Sci. Math. Nat., 355–357 (1937)
Hounsfield, G.N.: Computerized transverse axial scanning (tomography): Part 1. description of system. Brit. J. Radiol. 46(552), 1016–1022 (1973). https://doi.org/10.1259/0007-1285-46-552-1016
Neumann, J.V.: Functional operators, vol. ii. the geometry of orthogonal spaces (this is a reprint of mimeographed lecture notes first distributed in 1933) annals of math. Studies Nr. 22 Princeton Univ. Press (1950). https://doi.org/10.1515/9781400882250
Halperin, I.: The product of projection operators. Acta Sci. Math. (Szeged) 23(1), 96–99 (1962)
Deutsch, F., Hundal, H.: The rate of convergence for the method of alternating projections, ii. J. Math. Anal. Appl. 205(2), 381–405 (1997). https://doi.org/10.1006/jmaa.1997.5202
Galántai, A.: On the rate of convergence of the alternating projection method in finite dimensional spaces. J. Math. Anal. Appl. 310(1), 30–44 (2005). https://doi.org/10.1016/j.jmaa.2004.12.050
Strohmer, T., Vershynin, R.: A randomized Kaczmarz algorithm with exponential convergence. J. Fourier Anal. Appl. 15(2), 262–278 (2009). https://doi.org/10.1007/s00041-008-9030-4
Lorenz, D.A., Schopfer, F., Wenger, S.: The linearized Bregman method via split feasibility problems: analysis and generalizations. SIAM J. Imaging Sci. 7(2), 1237–1262 (2014). https://doi.org/10.1137/130936269
Chen, S.S., Donoho, D.L., Saunders, M.A.: Atomic decomposition by basis pursuit. SIAM Rev. 43(1), 129–159 (2001). https://doi.org/10.1137/S003614450037906X
Cai, J.F., Osher, S., Shen, Z.: Convergence of the linearized Bregman iteration for \(l_1\)-norm minimization. Math. Comput. 78(268), 2127–2136 (2009). https://doi.org/10.1090/S0025-5718-09-02242-X
Petra, S.: Randomized sparse block Kaczmarz as randomized dual block-coordinate descent. Anal. ştiin. ale Univ. Ovidius Constanţa. Seria Mat. 23(3), 129–149 (2015). https://doi.org/10.1515/auom-2015-0052
Jiang, Y.T., Wu, G., Jiang, L.: A Kaczmarz method with simple random sampling for solving large linear systems. Preprint at arXiv:2011.14693 (2020)
Needell, D., Tropp, J.A.: Paved with good intentions: analysis of a randomized block Kaczmarz method. Linear Algebra Appl. 441, 199–221 (2014). https://doi.org/10.1016/j.laa.2012.12.022
Moorman, J.D., Tu, T.K., Molitor, D., Needell, D.: Randomized Kaczmarz with averaging. BIT Numer. Math. 61(1), 337–359 (2021). https://doi.org/10.1007/s10543-020-00824-1
Miao, C.Q., Wu, W.T.: On greedy randomized average block Kaczmarz method for solving large linear systems. J. Comput. Appl. Math. 413, 114372 (2022). https://doi.org/10.1016/j.cam.2022.114372
Yin, W.T.: Analysis and generalizations of the linearized bregman method. SIAM J. Imaging Sci 3(4), 856–877 (2010). https://doi.org/10.1137/090760350
Haddock, J., Needell, D.: Randomized projection methods for linear systems with arbitrarily large sparse corruptions. SIAM J. Sci. Comput. 41(5), 19–36 (2019). https://doi.org/10.1137/18M1179213
Cheng, L., Jarman, B., Needell, D., Rebrova, E.: On block accelerations of quantile randomized Kaczmarz for corrupted systems of linear equations. Inverse Probl. 39(2), 024002 (2022). https://doi.org/10.1088/1361-6420/aca78a
Zhang, L., Wang, H.X., Zhang, H.: Quantile-based random sparse Kaczmarz for corrupted, noisy linear inverse systems. Preprint at arXiv:2206.07356 (2022)
Hansen, P.C.: Regularization tools version 4.0 for matlab 7.3. Numer. Algorithms 46(2), 189–194 (2007). https://doi.org/10.1007/s11075-007-9136-9
Polyak, B.T.: Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. and Math. Phys. 4(5), 1–17 (1964). https://doi.org/10.1016/0041-5553(64)90137-5
Schöpfer, F.: Exact regularization of polyhedral norms. SIAM J. Optim. 22(4), 1206–1223 (2012). https://doi.org/10.1137/11085236X
Acknowledgements
The authors thank the editor and reviewers of this manuscript for their thoughtful suggestions.
Funding
This work was supported by the National Natural Science Foundation of China (No.11971480, No.61977065), the Natural Science Fund of Hunan for Excellent Youth (No.2020JJ3038), and the Fund for NUDT Young Innovator Awards (No.20190105).
Author information
Authors and Affiliations
Contributions
All authors contributed to the study’s conception and design. The first draft of the manuscript was written by Lu Zhang and all authors commented on previous versions of the manuscript. All authors read and approve the final manuscript and are all aware of the current submission.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Lemma 5
Denote the set of all the indices of corrupted equations as C. The set excluding the \(\beta m\) corrupted rows is denoted as E. For all \(i\in E\), we have \(b_i=\tilde{b}_i+r_i\) and \(\langle a_i,\hat{x}\rangle =\tilde{b}_i=b_i-r_i\). Hence,
Thus,
Recall that \(Q_k=Q_q(x_{k},1\le i\le m )\) and \(|E|=(1-\beta )m\), meaning that at least \((1-\beta -q)m\) numbers of residuals \(|\langle a_i,x_k\rangle -b_i|_{i=1}^m\) are at least \(Q_k\) and have not been corrupted. Then,
Therefore,
which completes the proof. \(\square \)
Proof of Theorem 1
We start by introducing some useful notations. Denote the set consisting of all acceptable indices in the k-th iterate as
The subset consisting of corrupted indices in B is denoted as S; then the other indices in B are in subset \(B\backslash S\). Apparently, \((q-\beta )m\le |B\backslash S|\le qm\) and \(0\le |S|\le \beta m\). Note that the used index in each iterate is sampled from the acceptable set B in each iterate. This observation inspires us to consider the following splitting:
Our remainder assignment is to estimate the split terms above. For clarity, we respectively take both inexact and exact steps into account, which are all divided into three steps.
(a) In the inexact-step case, firstly we consider the uncorrupted equations indexed \(i\in B\backslash S\). Since \(b_{B\backslash S}^c=0\), the equations indexed \(i\in B\backslash S\) satisfy
According to the convergence rate of RaSK in noisy case in Lemma 4(a), we have
where the last inequality follows from \(\Vert r_{B\backslash S}\Vert ^2\le |B\backslash S|\cdot \Vert r\Vert _{\infty }^2\) and
Second, we consider the conditional expectation in S. In this case,
Denote the orthogonal projection of true solution \(\hat{x}\in H(a_{i_k},\tilde{b}_{i_k})\) onto corrupted hyperplane \(H(a_{i_k},b_{i_k})\) as \(x_k^c\) [9], implying that
Note that \(x_{k+1}\) is the Bregman projection of \(x_k\) onto the hyperplane \(H(a_{i_k},b_{i_k})\). According to Lemma 2 and the 1-strong convexity of f, it follows that
By reformulating it, we obtain that
For Quantile-RaSK with inexact step, we have \(x_{k+1}^*-x_{k}^*=-(\langle a_{i_k},x_k\rangle -b_{i_k})a_{i_k}\), obtained from the 11-step of Algorithm 1. Hence, (8) can be rewritten as
Now fix the values of the indices \(i_0,\ldots ,i_{k-1}\) and consider only \(i_k\) as a random variable with values in \(\{1,\ldots ,m\}\). According to \(|\langle a_{i_k},x_k\rangle -b_{i_k}|\le Q_k\), we have
where
Combining (3), (10) and (1), we have that
To handle the \(\Vert x_k-\hat{x}\Vert \cdot \Vert r\Vert _{\infty }\) term we split into two cases: \(\Vert x_k-\hat{x}\Vert \ge \sqrt{n} \Vert r\Vert _{\infty }\) and \(\Vert x_k-\hat{x}\Vert \le \sqrt{n} \Vert r\Vert _{\infty }\). It is easy to obtain that
where
Finally, combining (4), (5) and (13) we have
where
We consider all indices \(i_0,i_1,\ldots ,i_k\) as random variables, and take full expectation on both sides. Thus,
(b) In the exact-step case, first we consider the uncorrupted equations indexed \(i\in B\backslash S\). Since \(b_{B\backslash S}^c=0\), the equations indexed \(i\in B\backslash S\) satisfy
It follows from the convergence rate of ERaSK for noisy case in Lemma 4(b) that
Second, we consider the conditional expectation in corrupted set S. In this case, we have
For Quantile-RaSK with exact step, we have \(x_{k}^*=x_{k}+\lambda s_k\) with \(\Vert s_k\Vert _{\infty }\le 1\) and \(\Vert s_{k+1}\Vert _{\infty }\le 1\); then \(x_{k+1}^*-x_{k}^*=(x_{k+1}-x_{k})+\lambda (s_{k+1}-s_{k})\). Note that the exact linesearch guarantees \(\langle a_{i_k},x_{k+1}\rangle =b_{i_k}\). Thus, (8) can be rewritten as
Viewing \(i_k\) as a random variable with fixed \(i_0,\ldots ,i_{k-1}\), yields
And recall the conclusion (13) in (a), we obtain
Finally, combining all ingredients: (4), (16) and (19), and taking full expectation, we have that
The constants \(C_1\) and \(C_2\) are placed in Theorem 1.
(c) To ensure the decay in expectation, we require
which holds for a small enough parameter \(\beta \) since the left-hand side of it tends to zero as \(\beta \) tends to zero. Therefore, we obtain the conclusion. \(\square \)
The proof of Theorem 3
Similar to the proof of Theorem 1, we first denote the set of row indices less than the quantile \(Q_k\) at iteration k as \(T=\{i\in [m]\mid |\langle a_i,x_k\rangle -b_i|<Q_k\},|T|=\eta =qm\). The uncorrupted and corrupted rows in T are respectively denoted as \(T_1\) and \(T_2\). Then \((q-\beta )m\le |T_1|\le qm,|T_2|\le \beta m\). Using the constant stepsize, the update in Algorithm 2 is as follows:
Denote
Now use Lemma 8 with \(f(x)=\lambda \Vert x\Vert _{1}+\frac{1}{2}\Vert x\Vert ^2\), \(\Phi (x)=\langle x_k^*-x_{k+1}^*,x-x_k\rangle \) and \(y=x_k^{\delta }\), and it holds that
Unfolding the expression of \(x_k^{\delta }\) in (21), we obtain
We divide it into two steps: the scalar product and the quadratic term.
Step 1: For the inner product term, we can derive that
From the first term in (22), we obtain
From the second term in (22), we get
The last inequality makes use of Lemma 5. Combining (22), (23) and (24), we obtain
Step 2: For the quadratic term, we have
where \(u=\frac{w}{\eta }\sum _{i\in T_1} (\langle a_i,x_k\rangle -b_i) a_{i},v=\frac{w}{\eta }\sum _{i\in T_2} (\langle a_i,x_k\rangle -b_i) a_{i}\).
We have
and
Bring (27) and (28) together, we obtain
Combining (25) and (29) yields
where \(c_i,i=1,\ldots ,6\) are positive constants only related to q and \(\beta \); they can be directly obtained and we omit it. For the term \(\Vert r\Vert _{\infty }\cdot \Vert x_k-\hat{x}\Vert \), we use average inequality
Denote \(\alpha =\frac{|\hat{x}|_{\text {min}}}{ |\hat{x}|_{\text {min}} +2 \lambda }\), and use Lemma 9, we have
where
\(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhang, L., Wang, H. & Zhang, H. Quantile-based random sparse Kaczmarz for corrupted and noisy linear systems. Numer Algor (2024). https://doi.org/10.1007/s11075-024-01844-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11075-024-01844-6