Error analysis of the exponential wave integrator sine pseudo-spectral method for the higher-order Boussinesq equation

Abstract

In this paper, we derive a new exponential wave integrator sine pseudo-spectral (EWI-SP) method for the higher-order Boussinesq equation involving the higher-order effects of dispersion. The method is fully-explicit and it has fourth order accuracy in time and spectral accuracy in space. We rigorously carry out error analysis and establish error bounds in the Sobolev spaces. The performance of the EWI-SP method is illustrated by examining the long-time evolution of the single solitary wave, single wave splitting, and head-on collision of solitary waves. Numerical experiments confirm the theoretical results.

1 Introduction

In this paper, we study the higher-order Boussinesq (HBq) equation

$$\begin{aligned} u_{tt}= u_{xx}+ \eta _1u_{xxtt}-\eta _2u_{xxxxtt}+(f(u))_{xx} \end{aligned}$$

(1.1)

with initial and homogeneous boundary conditions. Here, u(x, t) denotes the unknown function, $\eta _1$ and $\eta _2$ are real positive constants. We consider a single power-type nonlinearity as $f (u)=u^p$. The HBq equation was first derived by Rosenau for the continuum limit of a dense chain of particles with elastic couplings in [1]. The propagation of longitudinal waves in an infinite elastic medium with nonlinear and non-local properties is also described by the HBq equation in [2]. Choosing the parameter $\eta _2=0$, (1.1) reduces the improved Boussinesq (IBq) equation

$$\begin{aligned} u_{tt}=u_{xx}+ \eta _1 u_{xxtt}+(f(u))_{xx}, \end{aligned}$$

(1.2)

which models the water wave problem with zero surface tension [3]. The most well-known classical Boussinesq equation [4] is given by

$$\begin{aligned} u_{tt}=u_{xx} +\alpha u_{xxxx}+ (u^2)_{xx}. \end{aligned}$$

(1.3)

When $\alpha =-1$, (1.3) is called the “good” Boussinesq equation, and when $\alpha =1$, it is known as the “bad” Boussinesq equation. Bogolubsky revealed that contrary to the “good” Boussinesq equation, the “bad” Boussinesq equation is unstable under short-wave perturbation and has no local well-posedness result in [5]. The improved Boussinesq equation has been shown as an approach for the “bad” Boussinesq equation by replacing the term $u_{xxxx}$ with $u_{xxtt}$, which is physically stable [5, 6].

Assume that u and all its derivatives converge to zero as $x \rightarrow \pm \infty$. For the solutions of the HBq equation subjected to these boundary conditions, the conserved quantity (mass) is given in [7] as

$$\begin{aligned} \mathcal {M}(t)=\int _{-\infty }^{\infty }v_t ~dx, \end{aligned}$$

(1.4)

where $u=v_x$.

Regarding the existence of local/global solutions of the Cauchy problem concerning (1.1), the authors in [2] used the fixed-point technique for the initial data in $H^s$ with $s>1/2$. The local and global existence of solutions to the initial and boundary value problems corresponding to the initial data in (i) the Sobolev space $W^{3,\infty }(0,1)$ for the nonlinear function $f(s)\in C^1(\mathbb {R})$ with $f(0)=0$ and (ii) the Sobolev space $H^{m+3}(0,1)$,  $m\ge 1$ for the nonlinear function $f(s)\in C^m (\mathbb {R})$ with $f(0)=0$ are established in [8]. Considering a general nonlinearity, the group classification and exact solutions of the HBq equation are obtained in [9].

From the numerical point of view, a variety of numerical schemes for approximating the time evolution of the solutions of the “good” Boussinesq equation have been proposed including the finite difference methods [10, 11], pseudo-spectral methods [12, 13], splitting methods [14] and the exponential wave integrators [15]. There are also a large number of studies in the literature on the IBq equation involving finite difference methods [10, 16], finite element methods [17, 18], spectral methods [19], meshless methods [20], Runge–Kutta type exponential integrators [21], energy preserving methods [22, 23] and exponential wave integrators [24]. To the best of our knowledge, there is only one numerical study [7] in the literature considering the HBq equation. The convergence of the semi-discrete scheme is only proved in [7] and the authors focus on the quadratic nonlinearity.

The exponential wave integrator pseudo-spectral method has recently become very popular for solving time-dependent PDEs due to its superior properties. The method can be implemented efficiently by applying the fast discrete Fourier or Sine transform for the spatial discretization combined with an exponential wave integrator based on some efficient quadrature rules. Bao and Dong proposed a method based on the Fourier pseudo-spectral approach to spatial discretization followed by a Gautschi-type exponential integrator for the Klein-Gordon equation in the non-relativistic limit regime [25]. Zhao studied an exponential wave integrator sine pseudo-spectral method for solving the Klein-Gordon-Zakharov system in [26] and an exponential wave integrator Fourier pseudo-spectral method for solving symmetric regularized-long-wave equation in [27]. The numerical method is based on a Deuflhard-type and Gautschi-type exponential wave integrator for temporal integrations, respectively. Exponential wave integrator methods are also applied successfully for the nonlinear Schrödinger equation [28], the extended Fisher-Kolmogorov equation [29]. As far as we know, the methods given in above mentioned studies have second-order accuracy in time and spectral accuracy in space. A fourth-order exponential wave integrator Fourier pseudo-spectral method for the nonlinear Dirac equation and the nonlinear Schrödinger equation are proposed in [30] and [31], respectively. For approximating the integral terms, the authors in [30, 31] use the Simpson quadrature formula. However, the proposed schemes are implicit schemes that require solving a nonlinear system for each step. Ji and Zhang presented a fourth-order exponential wave integrator Fourier pseudo-spectral method for solving the Klein-Gordon equation in [32]. The scheme is explicit and the corrected trapezoidal formula is used for approximating the integral term. They proved the fourth-order convergence in time under the restriction $\tau \le \frac{\pi h}{3\sqrt{2\pi ^2+h^2}}$, where $\tau$ is the time step and h is the spatial step size. Wang and Zhao introduce a group of symmetric Gautschi-type exponential wave integrators for the Klein-Gordon equation [33] in nonrelativistic limit regime. The scheme has fourth-order convergence in time. However, this scheme involves a rather complicated procedure due to the approximation of the second-order time derivative of the nonlinear function.

To the best of our knowledge, the exponential wave integrator methods applied to “good” Boussinesq [15] and Improved Bousinesq equation [24] are both second-order accurate in time. In order to demonstrate higher-order calculations for the Boussinesq-type equations, we derive a new fourth-order accurate scheme in time. The scheme is easy to implement since it is explicit. We also avoid the approximation of the time derivative of nonlinear function only except for initial time. Most of the studies in the literature focus on the only convergence of the semi-discrete scheme, conservation properties, and stability analysis. Our aim is to prove error analysis of the exponential wave integrator sine pseudo-spectral method for the higher-order Boussinesq equation involving the higher-order effects of dispersion. We obtain optimal error estimates of the fully discrete scheme in the Sobolev space $H^m$.

This article is outlined as follows. In Sect. 2, we propose a new exponential integrator sine pseudo-spectral method for the HBq equation. In Sect. 3, the error estimate is proved in detail. Sect. 4 is devoted to the numerical accuracy of the method. The scheme is tested for various problems, like the propagation of the single solitary wave, single wave splitting, and head-on collision of two solitary waves. Throughout this article, we use the notation $A\lesssim B$ to represent that there exists a generic constant $C>0$, which is independent of the time step $\tau$ and spatial step size h, such that $|A|\le CB$.

2 Numerical methods

In this section, we solve the HBq equation by combining a sine pseudo-spectral method for spatial derivatives with the fourth-order exponential wave integrator for temporal derivatives. We consider the HBq equation on a bounded domain $\Omega =(a, b)$ with initial and homogeneous boundary conditions given by

$$\begin{aligned} \left\{ \begin{aligned}&u_{tt}= u_{xx}+ \eta _1 u_{xxtt} - \eta _2 u_{xxxxtt}+(f(u))_{xx},\quad x\in \Omega ,\quad t>0, \\&u(x,0)=u_0(x), \quad u_t(x,0)=u_1(x), \\&u(a,t)=u(b,t)=0,\quad t\ge 0, \end{aligned} \right. \end{aligned}$$

(2.1)

where $f\in C^\infty (\mathbb {R}, \mathbb {R})$. The space interval is chosen large enough so that the truncation error is negligible.

Now, we start introducing some notations employed throughout the paper. The interval [a, b] is divided into M equal subintervals with grid spacing $h=(b-a)/M$, where M is a positive integer. The spatial grid points are given by $x_{j}=a+jh$, $j=0,1,2,\ldots ,M$. The time interval [0, T] is divided into N equal subintervals with time step $\tau =T/N$ and temporal grid points $t_n=n\tau$,  $n=0,\ldots ,N$. Denote

$$\begin{aligned}&X_M:=\{u=(u_0,u_1,\ldots ,u_M)\in \mathbb {R}^{M+1} |u_0=u_M=0\}, \\&Y_M:=\text{ span } \{ \sin (\mu _l(x-a)), \quad l=1,2,\ldots ,M-1 \}, \end{aligned}$$

with $\mu _l=\frac{l\pi }{b-a}$. For a general function u(x) on $\overline{\Omega }=[a,b]$ and a vector $u\in X_M$, let $P_M: L^2(\Omega ) \rightarrow Y_M$ be the standard $L^2$-projection operator and $I_M: C_0(\overline{\Omega })\rightarrow Y_M$ or $I_M: X_M\rightarrow Y_M$ be the trigonometric interpolation operator as

$$\begin{aligned} (P_M u)(x)=\sum _{l=1}^{M-1} \widehat{u}_l \sin (\mu _l (x-a)), \hspace{20pt} (I_M u)(x)=\sum _{l=1}^{M-1} \widetilde{u}_l \sin (\mu _l (x-a)), \end{aligned}$$

(2.2)

where $\widehat{u}_l$ and $\widetilde{u}_l$ are the sine and discrete sine transform coefficients, respectively, given by

$$\begin{aligned} \widehat{u}_l=\frac{2}{b-a} \int _a^b u(x) \sin (\mu _l (x-a)) dx, \hspace{20pt} \widetilde{u}_l=\frac{2}{M}\sum _{j=1}^{M-1} u_j \sin \bigg (\frac{jl\pi }{M}\bigg ) , \end{aligned}$$

(2.3)

with $u_j=u(x_j)$ when involved. The sine pseudo-spectral approximation

$$\begin{aligned} u_M(x,t_n+s)=\sum _{l=1}^{M-1} \widehat{u}_l(t_n+s) \sin (\mu _l(x-a)), \hspace{20pt} x\in \Omega , s\in \mathbb {R} \end{aligned}$$

(2.4)

for the solution of (2.1) satisfies

$$\begin{aligned} \partial _{ss} u_M(x,t_n+s)= & {} \partial _{xx} u_M(x,t_n+s)+ \eta _1\partial _{xxss}u_M(x,t_n+s) \nonumber \\{} & {} - \eta _2\partial _{xxxxss}u_M(x,t_n+s)\nonumber \\{} & {} + \partial _{xx} P_M(f(u_M(x,t_n+s)). \end{aligned}$$

(2.5)

Substituting (2.4) into (2.5) and noticing the orthogonality of $\sin (\mu _l(x-a))$ for $l=1,...,M-1$, one gets

$$\begin{aligned} \frac{d^2}{ds^2}\widehat{u}_l(t_n+s)+\theta _l^2\widehat{u}_l(t_n+s)+\theta _l^2\widehat{(f_M^n)}_l(s)=0,\hspace{20 pt}s\in \mathbb {R} \end{aligned}$$

(2.6)

where $f_M^n(x,s)=P_M f(u_M(x,t_n+s))$ and $\theta _l=\mu _l/\sqrt{1+\eta _1\mu _l^2+\eta _2\mu _l^4}$.

By using the well-known variation of the parameters formula, the general solution of the (2.6) is given by

$$\begin{aligned} \widehat{u}_l(t_n+s)=\cos {(\theta _ls)\widehat{u}_l}(t_n)+\frac{\sin {(\theta _ls)}}{\theta _l}\widehat{u}_l^\prime (t_n) -\theta _l\int _0^s\sin {\big (\theta _l(s-\omega )\big )}\widehat{(f_M^n)}_l(\omega )d\omega . \end{aligned}$$

(2.7)

Differentiating (2.7) with respect to s, we obtain

$$\begin{aligned} \widehat{u}_l^{\prime }(t_n+s)=-\theta _l \sin (\theta _l s) \widehat{u}_l(t_n) +{\cos (\theta _l s)}\widehat{u}_l^{\prime }(t_n) -\theta _l^2\int _0^s\cos {\big (\theta _l(s-\omega )\big )}\widehat{(f_M^n)}_l (\omega )d\omega . \end{aligned}$$

(2.8)

Plugging $s=2\tau$ and replacing n by $n-1$, one gets

$$\begin{aligned} \widehat{u}_l(t_{n+1})= & {} \cos {(2\theta _l\tau )\widehat{u}_l}(t_{n-1})+\frac{\sin {(2\theta _l\tau )}}{\theta _l}\widehat{u}_l^\prime (t_{n-1})\nonumber \\{} & {} -\theta _l\int _0^{2\tau }\sin {(\theta _l(2\tau -\omega ))}\widehat{(f_M^{n-1})_l}(\omega )d\omega . \end{aligned}$$

(2.9)

In order to obtain the fourth-order accuracy method, we approximate the integral term in (2.9) by the Simpson rule as

$$\begin{aligned} \int _0^{2\tau }\sin {\big (\theta _l(2\tau \!-\!\omega )\big )}\widehat{(f_M^{n-1})}_l(\omega )d\omega \!\approx \!\frac{\tau }{3}\Big [\sin {(2\theta _l\tau )}\widehat{(f_M^{n-1}})_l(0)+4\sin {(\theta _l\tau )}\widehat{(f_M^n)}_l(0)\Big ] \end{aligned}$$

(2.10)

noticing that $\widehat{(f_M^{n-1})}_l(\tau )=\widehat{(f_M^n)}_l(0)$. Similarly, plugging $s=2\tau$ and replacing n by $n-1$ in (2.8), we obtain

$$\begin{aligned} \widehat{u}_l^{\prime }(t_{n+1})= & {} -\theta _l \sin (2\theta _l\tau )\widehat{u}_l(t_{n-1}) +{\cos (\theta _ls)}\widehat{u}_l^{\prime }(t_{n-1})\nonumber \\{} & {} -\theta _l^2\int _0^{2\tau }\cos (\theta _l(2\tau -\omega ))\widehat{(f_M^{n-1})}_l(w)d\omega . \end{aligned}$$

(2.11)

Applying Simpson’s rule for approximating the integration in (2.11) yields

$$\begin{aligned} \int _0^{2\tau }\cos {\big (\theta _l(2\tau -\omega )\big )}\widehat{(f_M^{n-1})}_l(\omega )d\omega\approx & {} \frac{\tau }{3}\Big [\cos {(2\theta _l\tau )}\widehat{(f_M^{n-1})}_l(0)\nonumber \\{} & {} +4\cos {(\theta _l\tau )}\widehat{(f_M^n)}_l(0)+\widehat{(f_M^{n+1})}_l(0)\Big ]. \end{aligned}$$

(2.12)

In practice, computing the continuous sine coefficients in (2.9)-(2.12) is difficult. Therefore, we replace the continuous sine coefficients with the discrete sine coefficients as in (2.2) and (2.3). Now, we introduce the fourth-order EWI-SP scheme: Let $u_j^n$ and $\dot{u}_j^n (j=0, 1, \ldots , M, n=0, 1, \ldots )$ be the approximations to $u(x_j, t_n)$ and $u_t (x_j, t_n)$, respectively. Setting $u_j^0=u_0(x_j)$, $\dot{u}_j^0=u_1(x_j)$, the numerical approximations $u^{n+1},\dot{u}^{n+1}\in X_M$ are computed as

$$\begin{aligned} u_j^{n+1}=\sum \limits _{l=1}^{M-1}\widetilde{u_l^{n+1}} \sin \left( \frac{jl\pi }{M}\right) ,\quad \dot{u}_j^{n+1}=\sum \limits _{l=1}^{M-1}\widetilde{\dot{u}_l^{n+1}} \sin \left( \frac{jl\pi }{M}\right) , \end{aligned}$$

(2.13)

where the discrete sine coefficients are computed as follows for $n\ge 1$:

$$\begin{aligned} \widetilde{u_l^{n+1}}= & {} \cos {(2\theta _l\tau )}\widetilde{u_l^{n-1}}+\frac{\sin {(2\theta _l\tau )}}{\theta _l}\widetilde{\dot{u}_l^{n-1}} -\frac{\theta _l\tau }{3}\Big [\sin {(2\theta _l\tau )}\widetilde{f_l^{n-1}}+4\sin {(\theta _l\tau )}\widetilde{f_l^n}\Big ],\nonumber \\ \widetilde{\dot{u}_l^{n+1}}= & {} -\theta _l\sin {(2\theta _l\tau )}\widetilde{u_l^{n-1}}+\cos {(2\theta _l\tau )}\widetilde{\dot{u}_l^{n-1}}\nonumber \\{} & {} -\frac{\theta _l^2\tau }{3}\Big [\cos {(2\theta _l\tau )}\widetilde{f_l^{n-1}}+4\cos {(\theta _l\tau )}\widetilde{f_l^n}+\widetilde{f_l^{n+1}}\Big ], \end{aligned}$$

(2.14)

with

$$\begin{aligned} \widetilde{u_l^n}=\frac{2}{M}\sum \limits _{j=1}^{M-1}u_j^n \sin \left( \frac{jl\pi }{M}\right) , \hspace{20pt} \widetilde{\dot{u}_l^n}=\frac{2}{M}\sum \limits _{j=1}^{M-1}\dot{u}_j^n\sin \left( \frac{jl\pi }{M}\right) , \hspace{20pt} \widetilde{f_l^n}=\frac{2}{M}\sum \limits _{j=1}^{M-1}f(u_j^n) \sin \left( \frac{jl\pi }{M}\right) . \end{aligned}$$

(2.15)

In order to start the iteration, we need the initial values $u^1$ and $\dot{u}^1$.

Computation of $\widehat{u}_l(t_1)$: If we differentiate (2.6) with respect to s, we obtain

$$\begin{aligned} \frac{d^3}{ds^3}\widehat{u}_l(t_n+s)+\theta _l^2\frac{d}{ds} \widehat{u}_l(t_n+s)+\theta _l^2\frac{d}{ds}\widehat{(f_M^n)}_l(s)=0,\hspace{20 pt}s\in \mathbb {R}. \end{aligned}$$

(2.16)

By using (2.6) and (2.16) in Taylor’s expansion, the fourth-order approximation can be written as

$$\begin{aligned} \widehat{u}_l(t_1)=\widehat{u}_l(0)+\tau \widehat{u}_l^\prime (0)-\frac{\theta _l^2\tau ^2}{2}\Big [\widehat{u}_l(0)+\widehat{(f_M^0)_l}(0)\Big ]-\frac{\theta _l^2\tau ^3}{6}\Big [\widehat{u}_l^\prime (0)+\widehat{(f_M^0)}^{\prime }_l(0)\Big ]+\frac{\tau ^4}{24}\widehat{u}_l^{\prime \prime \prime \prime }(s_{l,1}), \end{aligned}$$

(2.17)

where $s_{l,1}\in (0,\tau )$. Since $f\in C^\infty (\mathbb {R}, \mathbb {R})$, the sine coefficients $\widehat{(f_M^0)}^{\prime }_l(0)$ for $l=0,1,\ldots M-1$ are computed as

$$\begin{aligned} \widehat{(f_M^0)}^{\prime }_l(0)=\widehat{\bigg [f'\big (u_M(x,0)\big )\partial _s u_M(x,0)\bigg ]}_l. \end{aligned}$$

(2.18)

Computation of $\widehat{u}_l^\prime (t_1)$: Approximating $\widehat{u}_l(t_0)$ and $\widehat{u}_l(t_2)$ by using Taylor’s expansion around $t_1$, and taking their difference, one can get

$$\begin{aligned} \widehat{u}_l(t_2)-\widehat{u}_l(0)=2\tau \widehat{u}_l^\prime (t_1) +\frac{\tau ^3}{3}\widehat{u}_l^{\prime \prime \prime }(t_1)+\frac{\tau ^5}{60}\widehat{u}_l^{\prime \prime \prime \prime \prime }(s_{l,2}), \end{aligned}$$

(2.19)

where $s_{l,2}\in (0,2\tau )$. Using

$$\begin{aligned} \widehat{u}_l^{\prime \prime \prime }(t_1)=\frac{\widehat{u}_l^{\prime \prime }(t_2)-\widehat{u}_l^{\prime \prime }(0)}{2\tau }-\frac{\tau ^2}{6}\widehat{u}_l^{\prime \prime \prime \prime \prime }(s_{l,3}), \end{aligned}$$

(2.20)

where $s_{l,3}\in (0,2\tau )$, (2.19) becomes

$$\begin{aligned} \widehat{u}_l(t_2)-\widehat{u}_l(0)=2\tau \widehat{u}_l^\prime (t_1)+\frac{\tau ^2}{6}\left[ {\widehat{u}_l^{\prime \prime }(t_2)-\widehat{u}_l^{\prime \prime }(0)}\right] +\frac{\tau ^5}{60}\widehat{u}_l^{\prime \prime \prime \prime \prime }(s_{l,2})-\frac{\tau ^5}{18}\widehat{u}_l^{\prime \prime \prime \prime \prime }(s_{l,3}). \end{aligned}$$

(2.21)

By (2.6)

$$\begin{aligned} {\widehat{u}_l^{\prime \prime }(t_2)-\widehat{u}_l^{\prime \prime }(0)} =-{\theta _l^2}\Big [\widehat{u}_l(t_2)-\widehat{u}_l(0) +\widehat{(f_M^2)}_l(0)-\widehat{(f_M^0)}_l(0)\Big ], \nonumber \end{aligned}$$

(2.22)

we obtain

$$\begin{aligned} \widehat{u}_l^\prime (t_1)=\Big (\frac{1}{2\tau }+\frac{\theta _l^2\tau }{12}\Big )\Big [\widehat{u}_l(t_2)-\widehat{u}_l(0)\Big ]+\frac{\theta _l^2\tau }{12}\Big [\widehat{(f_M^2)}_l(0)-\widehat{(f_M^0)}_l(0)\Big ]+\frac{7\tau ^4}{360}\widehat{u}_l^{\prime \prime \prime \prime \prime }(s_{l,4}), \end{aligned}$$

(2.23)

where $s_{l,4}\in (0,2\tau )$.

By replacing the continuous sine coefficients with the discrete sine coefficients, the discrete sine coefficients at the first time step are obtained as follows:

$$\begin{aligned} \widetilde{u_l^1}= & {} \widetilde{u_l^0}+\tau \widetilde{\dot{u}_l^0}-\frac{\theta _l^2\tau ^2}{2}\Big [\widetilde{u_l^0}+\widetilde{f_l^0}\Big ]-\frac{\theta _l^2\tau ^3}{6}\Big [\widetilde{\dot{u}_l^0}+\widetilde{\dot{f}_l^0}\Big ], \nonumber \\ \widetilde{\dot{u}_l^1}= & {} \Big (\frac{1}{2\tau }+\frac{\theta _l^2\tau }{12}\Big )\Big (\widetilde{u_l^2}-\widetilde{u_l^0}\Big )+\frac{\theta _l^2\tau }{12}\Big (\widetilde{f_l^2}-\widetilde{f_l^0}\Big ), \end{aligned}$$

(2.24)

where

$$\begin{aligned} \widetilde{\dot{f}_l^0}=\frac{2}{M}\sum \limits _{j=1}^{M-1}\Big [f^\prime (u_j^0)\dot{u}_j^0\Big ]\sin \left( \frac{jl\pi }{M}\right) . \end{aligned}$$

(3.1)

To summarize, the scheme is based on the following steps:

Step 1::

The discrete sine coefficients $\widetilde{u_l^0}$, $\widetilde{\dot{u}_l^0}$, $\widetilde{f_l^0}$, $\widetilde{\dot{f}_l^0}$ are found by using the formulas (2.15) and (2.24).

Step 2::

$\widetilde{u_l^1}$ is computed by using (2.23).

Step 3::

$\widetilde{f_l^1}$ is calculated by using (2.15) after constructing the approximate solution $u^1$.

Step 4::

$\widetilde{u_l^{2}}$ is evaluated by using (2.14).

Step 5::

$\widetilde{f_l^2}$ is obtained by using (2.15) after constructing the approximate solution $u^2$.

Step 6::

$\widetilde{\dot{u}_l^1}$ and $\widetilde{\dot{u}_l^2}$ are evaluated by using (2.23) and (2.14), respectively, and then $\dot{u}^1$ and $\dot{u}^2$ are constructed.

Step 7::

$u^n$ and $\dot{u}^n$ can be found for $n\ge 3$ by using (2.13)-(2.15).

3 Error estimates

In this section, we give the error analysis for the fully discretized scheme (2.14) and (2.23). We denote the standard Sobolev space by $H^m(\Omega )$. We define its subspace $H^m \cap H_0^1$ as

$$\begin{aligned} {\widetilde{H}^m(\Omega )}=\{ u\in H^m(\Omega ): u^{(2k)}(a)=u^{(2k)}(b)=0, \quad k\in \mathbb {N}, \quad 0\le {2k<m}\}, \end{aligned}$$

for some integer $m\ge 1$. For any function $u(x)={\sum \limits _{l=1}^\infty } \widehat{u}_l \sin (\mu _l(x-a))\in \widetilde{H}^m(\Omega )$, we define its norm as

$$\begin{aligned} \Vert u\Vert _m^2={\sum \limits _{l=1}^\infty } \big (1+|\mu _l|^2\big )^m|\widehat{u}_l|^2. \end{aligned}$$

(3.2)

Particularly, for $m=0$, the space is exactly $L^2(\Omega )$ and the corresponding norm is denoted as $\Vert \cdot \Vert$. In order to obtain the convergence of the fully discrete scheme, we need the following auxiliary lemmas.

Lemma 3.1

[26] For any $0 \le \mu \le k$ with $k>1/2$, there exists a constant C such that

$$\begin{aligned} \Vert u-P_M u\Vert _{\mu } \le Ch^{k-\mu }\Vert u\Vert _{k}, \quad \Vert u-I_M u\Vert _{\mu } \le C h^{k-\mu } \Vert u\Vert _{k},\quad \forall u\in {\widetilde{H}^k(\Omega )}. \end{aligned}$$

(3.3)

Lemma 3.2

[34] For $m >1/2$, $H^m (\mathbb {R})$ is an algebra with respect to the product of functions. That is, if $u, v \in H^m(\mathbb {R})$ then $uv \in H^m(\mathbb {R})$ and

$$\begin{aligned} \Vert uv \Vert _m \le C \Vert u\Vert _ m \Vert v \Vert _m. \end{aligned}$$

(3.4)

Lemma 3.3

[35] For any function $g\in C^\infty (\mathbb {C}, \mathbb {C})$ and $\sigma >1/2$, there exists a nondecreasing function $\chi _g: \mathbb {R}^+\rightarrow \mathbb {R}^+$ such that

$$\begin{aligned} \Vert g(u)\Vert _\sigma \le \Vert g(0)\Vert _\sigma +\chi _g(\Vert u\Vert _{L^\infty })\Vert u\Vert _\sigma ,\quad \forall u\in H^\sigma . \end{aligned}$$

(3.5)

For all $v, w\in B_R^\sigma :=\{u\in H^\sigma : \Vert u\Vert _{\sigma }\le R\}$, we have

$$\begin{aligned} \Vert g(v)-g(w)\Vert _\sigma \le \alpha (g, R)\Vert v-w\Vert _{\sigma }, \end{aligned}$$

(3.6)

where $\alpha (g, R)=\Vert g'(0)\Vert _\sigma +R\chi _{g'}(cR)$ is nondecreasing with respect to R, with $c>0$ being the constant for the Sobolev imbedding $\Vert \cdot \Vert _{L^\infty }\le c\Vert \cdot \Vert _\sigma$.

For simplicity of notation, we denote the interpolations of the numerical solutions by

$$ u^n_I(x)=I_M(u^n)(x), \quad \dot{u}^n_I(x)=I_M(\dot{u}^n)(x), \quad x\in (a,b), $$

and the error functions by

$$ e^n(x)=u(x,t_n)-u^n_I(x), \quad \dot{e}^n(x)=\partial _t u(x,t_n)-\dot{u}^n_I(x), \quad x\in (a,b). $$

Theorem 3.1

Let the solution of the HBq equation (2.1) satisfy the regularity properties ${u\in C^1\big ([0,T];\widetilde{H}^{m+\sigma }\big )\cap C^5\big ([0,T];\widetilde{H}^m\big )(m>\frac{1}{2}, \sigma >0)}$. Then, there exist $h_0>0$ and $0<\tau _0\le 1$ such that when $\tau \le \tau _0$ and $h\le h_0$, the numerical solutions $u^n$ and $\dot{u}^n$ obtained from the EWI-SP scheme (2.13)-(2.15) with (2.23) and (2.24) converge to the solution of the problem (2.1) with the convergence rate

$$\begin{aligned} \Vert e^n\Vert _m +\Vert \dot{e}^n\Vert _m\lesssim \tau ^4+h^\sigma ,\hspace{20pt} n=0,1,\ldots ,N, \end{aligned}$$

(3.7)

with $\Vert \partial _t^k u\Vert _{L^\infty ([0,T];H^m)}\le K_k$ for $(k=0,1,\ldots ,5)$ and $\Vert \partial _t^k u\Vert _{L^\infty ([0,T];H^{m+\sigma })}\le R_k$ for $(k=0,1)$. Furthermore, we have

$$\begin{aligned} \Vert u_I^n\Vert _m\le K_0+1,\quad \Vert \dot{u}_I^n\Vert _m\le K_1+1. \end{aligned}$$

(3.8)

Proof

We give the proof for (3.6) and (3.7) by mathematical induction. For $n=0$, noticing that ${e^0=u_0-I_M(u_0)}$, $\dot{e}^0=u_1-I_M(u_1)$, applying Lemma 3.1, one gets

$$\begin{aligned} \Vert e^0\Vert _m+\Vert \dot{e}^0\Vert _m\lesssim h^\sigma . \end{aligned}$$

(3.9)

There exists a constant $h_1>\!0$ such that, when $0<\!h\le \! h_1$, the inequality (3.7) is valid for $n=0$. Assuming (3.6) and (3.7) are true for $n\le \! k\!<T/\tau$, we show that (3.6) and (3.7) are valid for $n=k\!+\!1$. The projected error functions are introduced by

$$\begin{aligned}&e^n_M(x)=P_M(e^n(x))=\sum \limits _{l=1}^{M-1}\widehat{e_l^n}\sin (\mu _l(x-a)),\\&\dot{e}^n_M(x)=P_M(\dot{e}^n(x))=\sum \limits _{l=1}^{M-1}\widehat{\dot{e}_l^{n}} \sin (\mu _l(x-a)), \end{aligned}$$

where the corresponding coefficients in the frequency satisfy

$$ \widehat{e_l^n}=\widehat{u}_l(t_n)-\widetilde{u_l^n}, \qquad \widehat{\dot{e}_l^n}=\widehat{u_l}'(t_n)-\widetilde{\dot{u}_l^n}. $$

We define the local truncation errors

$$\begin{aligned} \xi ^n(x)=\sum \limits _{l=1}^{M-1}\widehat{\xi _l^n}\sin (\mu _l(x-a)), \hspace{20 pt} \dot{\xi }^n(x)=\sum \limits _{l=1}^{M-1}\widehat{\dot{\xi }_l^{n}} \sin (\mu _l(x-a)), \end{aligned}$$

where

$$\begin{aligned} \widehat{\xi _l^n}= & {} \widehat{u}_l(t_{n+1})-\cos (2\theta _l\tau )\widehat{u}_l(t_{n-1})-\frac{\sin (2\theta _l\tau )}{\theta _l}\widehat{u}_l^\prime (t_{n-1})\nonumber \\{} & {} +\frac{\theta _l\tau }{3}\Bigl [\sin (2\theta _l\tau )\widehat{f_l^{n-1}}(0)+4\sin (\theta _l\tau )\widehat{f_l^n}(0)\Bigr ], \nonumber \\ \widehat{\dot{\xi }_l^n}= & {} \widehat{u}_l^\prime (t_{n+1})+\theta _l\sin (2\theta _l\tau )\widehat{u}_l(t_{n-1})-\cos (2\theta _l\tau )\widehat{u}_l^\prime (t_{n-1}) \nonumber \\{} & {} +\frac{\theta _l^2\tau }{3}\Bigl [\cos (2\theta _l\tau )\widehat{f_l^{n-1}}(0)+4\cos (\theta _l\tau )\widehat{f_l^n}(0)+\widehat{f_l^{n+1}}(0)\Bigr ], \end{aligned}$$

(3.10)

for $n\ge 1$ and

$$\begin{aligned} \widehat{\xi _l^0}= & {} \widehat{u}_l(t_1)-\widehat{u}_l(0)-\tau \widehat{u}_l^\prime (0)+\frac{\theta _l^2\tau ^2}{2}\Bigl [\widehat{u}_l(0)+\widehat{f_l^0}(0)\Bigr ] +\frac{\theta _l^2\tau ^3}{6}\Bigl [\widehat{u}_l^\prime (0)+\widehat{(f_l^0)}^\prime (0)\Bigr ], \nonumber \\ \widehat{\dot{\xi }_l^0}= & {} \widehat{u}_l^\prime (t_1)-\Big (\frac{1}{2\tau }+\frac{\theta _l^2\tau }{12}\Big )\Big [\widehat{u}_l(t_2)-\widehat{u}_l(0)\Big ] -\frac{\theta _l^2\tau }{12}\Bigl [\widehat{f^2_l}(0)-\widehat{f_l^0}(0)\Bigr ], \end{aligned}$$

(3.11)

with $\widehat{f}^n_l(s)=\widehat{f(u(t_n+s))}_l$.

If we subtract (2.14) and (2.23) from (3.9) and (3.10) respectively, the resulting error equations for $n\ge 1$ become

$$\begin{aligned} \widehat{e_l^{n+1}}= & {} \cos (2\theta _l\tau )\widehat{e_l^{n-1}}+\frac{\sin (2\theta _l\tau )}{\theta _l}\widehat{\dot{e}_l^{n-1}}+\widehat{\xi _l^{n}}\nonumber \\{} & {} -\frac{\theta _l\tau }{3}\Bigl [\sin (2\theta _l\tau )\widehat{\eta _l^{n-1}}+4\sin (\theta _l\tau )\widehat{\eta _l^n}\Bigr ] \\ \widehat{\dot{e}_l^{n+1}}= & {} -\theta _l\sin (2\theta _l\tau )\widehat{e_l^{n-1}} +\cos (2\theta _l\tau )\widehat{\dot{e}_l^{n-1}}\nonumber \\{} & {} +\widehat{\dot{\xi }_l^n} -\frac{\theta _l^2\tau }{3}\Bigl [\cos (2\theta _l\tau )\widehat{\eta _l^{n-1}} +4\cos (\theta _l\tau )\widehat{\eta _l^n}+\widehat{\eta _l^{n+1}}\Bigr ]. \end{aligned}$$

(3.12)

and

$$\begin{aligned} \widehat{e_l^1}= & {} \widehat{e_l^0}+\tau \widehat{\dot{e}_l^0}+\widehat{\xi _l^0}-\frac{\theta _l^2\tau ^2}{2}\Bigl [\widehat{e_l^0} +\widehat{\eta _l^0}\Bigr ]-\frac{\theta _l^2\tau ^3}{2}\Bigl [\widehat{\dot{e}_l^0} +\widehat{\dot{\eta }_l^0}\Bigr ], \end{aligned}$$

(3.13)

$$\begin{aligned} \widehat{\dot{e}_l^1}= & {} \Big (\frac{1}{2\tau } +\frac{\theta _l^2\tau }{12}\Big )\Big (\widehat{e_l^2} -\widehat{e_l^0}\Big )+\widehat{\dot{\xi }_l^0} +\frac{\theta _l^2\tau }{12}\Bigl [\widehat{\eta _l^2}-\widehat{\eta _l^0}\Bigr ], \end{aligned}$$

(3.14)

where the nonlinear errors are

$$\begin{aligned} \eta ^n(x)=\sum \limits _{l=1}^{M-1}\widehat{\eta _l^n}\sin (\mu _l(x-a)),\hspace{30 pt}\dot{\eta }^0(x)=\sum \limits _{l=1}^{M-1}\widehat{\dot{\eta }_l^{0}} \sin (\mu _l(x-a)) \end{aligned}$$

with $\widehat{\eta _l^n}=\widehat{f_l^n}(0)-\widetilde{f_l^n}$ and $\widehat{\dot{\eta }_l^0}=\widehat{(f_l^0)^\prime }(0)-\widetilde{\dot{f}_l^0}$.

Step 1: Estimation of local truncation errors

Substituting (2.9) and (2.11) into (3.9), (2.17) and (2.22) into (3.10) respectively, the resulting truncation errors for $n\ge 1$ become

$$\begin{aligned} \widehat{\xi _l^n}= & {} -\theta _l\int _0^{2\tau }\sin \big (\theta _l(2\tau -\omega )\big )\widehat{f_l^{n-1}}(\omega )d\omega \nonumber \\{} & {} +\frac{\theta _l\tau }{3}\Bigl [\sin (2\theta _l\tau )\widehat{f_l^{n-1}}(0)+4\sin (\theta _l\tau )\widehat{f_l^n}(0)\Bigr ], \nonumber \\ \widehat{\dot{\xi }_l^n}= & {} -\theta _l^2\int _0^{2\tau }\cos \big (\theta _l(2\tau -\omega )\big )\widehat{f_l^{n-1}}(\omega )d\omega \nonumber \\{} & {} +\frac{\theta _l^2\tau }{3}\Bigl [\cos (2\theta _l\tau )\widehat{f_l^{n-1}}(0)+4\cos (\theta _l\tau )\widehat{f_l^n}(0)+\widehat{f_l^{n+1}}(0)\Bigr ] \end{aligned}$$

(3.15)

and

$$\begin{aligned} \widehat{\xi _l^0}=\frac{\tau ^4}{24}\widehat{u}_l^{\prime \prime \prime \prime }(s_{l,1}), \hspace{20pt} \widehat{\dot{\xi }_l^0}=\frac{7\tau ^4}{360}\widehat{u}_l^{\prime \prime \prime \prime \prime }(s_{l,4}). \end{aligned}$$

It is clear that

$$\begin{aligned} \Vert \xi ^0\Vert _m^2+\Vert \dot{\xi }^0\Vert _m^2\lesssim \tau ^{8}. \end{aligned}$$

(3.16)

Thus, the local truncation errors in (3.15) actually come from the error using the Simpson rule. By the standard error formula of the Simpson rule for a general function $v(s)\in C^4 [0,2\tau ]$

$$ \int _0^{2\tau }v(s)ds-\frac{\tau }{3}\big [v(0)+4v(\tau )+v(2\tau )\big ]=-\frac{8\tau ^5}{45}v^{(4)}(c),\hspace{20 pt} c\in (0,2\tau ), $$

the local truncation errors (3.15) become

$$\begin{aligned} \widehat{\xi _l^n}= & {} \frac{8\theta _l}{45}\tau ^5\Bigg (\frac{d^4}{d\omega ^4}\Big [\sin \big (\theta _l(2\tau -\omega )\big )\widehat{(f_l^{n-1})}(\omega )\Big ]\bigg |_{\omega =s_{l,5}}\Bigg ) \\= & {} \frac{8\theta _l}{45}\tau ^5\bigg [\theta _l^4\sin \big (\theta _l(2\tau -s_{l,5})\big )\widehat{f}_l^{n-1}(s_{l,5})+4\theta _l^3\cos \big (\theta _l(2\tau -s_{l,5})\big )\widehat{(f_l^{n-1})}^\prime (s_{l,5}) \\{} & {} -6\theta _l^2\sin \big (\theta _l(2\tau -s_{l,5})\big )\widehat{(f_l^{n-1})}^{\prime \prime }(s_{l,5})-4\theta _l\cos \big (\theta _l(2\tau -s_{l,5})\big )\widehat{(f_l^{n-1})}^{\prime \prime \prime }(s_{l,5}) \\{} & {} +\sin \big (\theta _l(2\tau -s_{l,5})\big )\widehat{(f_l^{n-1})}^{\prime \prime \prime \prime }(s_{l,5})\bigg ], \\ \widehat{\dot{\xi }_l^n}= & {} \frac{8\theta _l^2}{45}\tau ^5\Bigg (\frac{d^4}{d\omega ^4}\Big [\cos \big (\theta _l(2\tau -\omega )\big )\widehat{(f_l^{n-1})}(\omega )\Big ]\bigg |_{\omega =s_{l,6}}\Bigg ) \\= & {} \frac{8\theta _l^2}{45}\tau ^5\bigg [\theta _l^4\cos \big (\theta _l(2\tau -s_{l,6})\big )\widehat{f}_l^{n-1}(s_{l,6})-4\theta _l^3\sin \big (\theta _l(2\tau -s_{l,6})\big )\widehat{(f_l^{n-1})}^\prime (s_{l,6}) \\{} & {} -6\theta _l^2\cos \big (\theta _l(2\tau -s_{l,6})\big )\widehat{(f_l^{n-1})}^{\prime \prime }(s_{l,6})+4\theta _l\sin \big (\theta _l(2\tau -s_{l,6})\big )\widehat{(f_l^{n-1})}^{\prime \prime \prime }(s_{l,6}) \\{} & {} +\cos \big (\theta _l(2\tau -s_{l,6})\big )\widehat{(f_l^{n-1})}^{\prime \prime \prime \prime }(s_{l,6})\bigg ] \end{aligned}$$

where $s_{l,5},s_{l,6}\in (0,2\tau )$. Since $\eta _1$ and $\eta _2$ are positive real numbers, we have $|\theta _l|\le 1/\sqrt{\eta _1}$. Applying Young’s inequality to the above equations, we deduce

$$\begin{aligned} |\widehat{\xi _l^n}|^2\le & {} C\tau ^{10}\bigg [\big |\widehat{f}_l^{n-1}(s_{l,5})\big |^2+\big |\widehat{(f_l^{n-1})}^\prime (s_{l,5})\big |^2+\big |\widehat{(f_l^{n-1})}^{\prime \prime }(s_{l,5})\big |^2\\{} & {} +\big |\widehat{(f_l^{n-1})}^{\prime \prime \prime }(s_{l,5})\big |^2+\big |\widehat{(f_l^{n-1})}^{\prime \prime \prime \prime }(s_{l,5})\big |^2\bigg ],\\ |\widehat{\dot{\xi }_l^n}|^2\le & {} C\tau ^{10}\bigg [\big |\widehat{f}_l^{n-1}(s_{l,6})\big |^2+\big |\widehat{(f_l^{n-1})}^\prime (s_{l,6})\big |^2+\big |\widehat{(f_l^{n-1})}^{\prime \prime }(s_{l,6})\big |^2\\{} & {} +\big |\widehat{(f_l^{n-1})}^{\prime \prime \prime }(s_{l,6})\big |^2+\big |\widehat{(f_l^{n-1})}^{\prime \prime \prime \prime }(s_{l,6})\big |^2\bigg ]. \end{aligned}$$

Using the assumptions $\Vert \partial _t^k u\Vert _{L^\infty ([0,T];H^m)}\le K_k$ for $(k=0,1,\ldots ,4)$ and $f\in C^\infty (\mathbb {R},\mathbb {R})$, it follows that

$$\begin{aligned} \Vert \xi ^n\Vert _m^2+\Vert \dot{\xi }^n\Vert _m^2\le C(f,K_0,K_1,K_2,K_3,K_4)\tau ^{10}\lesssim \tau ^{10} \end{aligned}$$

(3.17)

for $n\ge 1$.

Step 2: Estimation of nonlinear errors

Now, we show that $\dot{\eta }^0$ and $\eta ^n$ are bounded in $H^m$ with $m > 1/2$. We use Lemmas 3.1$-$3.3 and $u_I^n,u(\cdot ,t_n)\in B^m_{K_0+1}$ to obtain

$$\begin{aligned} \Vert \dot{\eta }^0\Vert _m= & {} \Big \Vert I_M\big (f^\prime (u_I^0)\dot{u}_I^0\big )-P_M\big (f^\prime (u(\cdot ,0))\partial _t u(\cdot ,0)\big )\Big \Vert _m \nonumber \\\le & {} \Big \Vert I_M\Big [f^\prime (u_I^0)\dot{u}_I^0-f^\prime (u(\cdot ,0))\dot{u}_I^0\Big ]\Big \Vert _m+\Big \Vert I_M\Big [f^\prime (u(\cdot ,0))\dot{u}_I^0-f^\prime (u(\cdot ,0))\partial _t u(\cdot ,0)\Big ]\Big \Vert _m \nonumber \\{} & {} +\Big \Vert I_M\big (f^\prime (u(\cdot ,0))\partial _t u(\cdot ,0)\big )-P_M\big (f^\prime (u(\cdot ,0))\partial _t u(\cdot ,0)\big )\Big \Vert _m, \nonumber \\\le & {} C\Big \Vert f^\prime \big (u_I^0\big )\dot{u}_I^0-f^\prime \big (u(\cdot ,0)\big )\dot{u}_I^0\Big \Vert _m+C\Big \Vert f^\prime \big (u(\cdot ,0)\big )\dot{u}_I^0-f^\prime \big (u(\cdot ,0)\big )\partial _t u(\cdot ,0)\Big \Vert _m \nonumber \\{} & {} +Ch^\sigma \Big \Vert f^\prime \big (u(\cdot ,0)\big )\partial _t u(\cdot ,0)\Big \Vert _{m+\sigma } \nonumber \\\le & {} C\Vert \dot{u}_I^0\Vert _m\Big \Vert f^\prime \big (u_I^0\big )-f^\prime \big (u(\cdot ,0)\big )\Big \Vert _m+C\Big \Vert f^\prime \big (u(\cdot ,0)\big )\Big \Vert _m\Big \Vert \dot{u}_I^0-\partial _t u(\cdot ,0)\Big \Vert _m \nonumber \\{} & {} +Ch^\sigma \Big \Vert f^\prime \big (u(\cdot ,0)\big )\Big \Vert _{m+\sigma }\Big \Vert \partial _t u(\cdot ,0)\Big \Vert _{m+\sigma } \nonumber \\\le & {} C\alpha \Big (f^\prime ,K_0+1\Big )\Vert \dot{u}_I^0\Vert _m\Vert u_I^0-u(\cdot ,0)\Vert _m \nonumber \\{} & {} +C\Big [\Vert f^\prime (0)\Vert _m+\chi _{f^\prime }\big (\Vert u(\cdot ,0)\Vert _{L^\infty }\big )\Vert u(\cdot ,0)\Vert _m\Big ]\Vert \dot{u}_I^0-\partial _t u(\cdot ,0)\Vert _m \nonumber \\{} & {} +Ch^\sigma \Big [\Vert f^\prime (0)\Vert _{m+\sigma }+\chi _{f^\prime }\big (\Vert u(\cdot ,0)\Vert _{L^\infty }\big )\Vert u(\cdot ,0)\Vert _{m+\sigma }\Big ]\Vert \partial _t u(\cdot ,0)\Vert _{m+\sigma } \nonumber \\\le & {} C\alpha \Big (f^\prime ,K_0+1\Big )\Vert \dot{u}_I^0\Vert _m\Vert e_M^0\Vert _m+C\Big [\Vert f^\prime (0)\Vert _m+\chi _{f^\prime }(cK_0)K_0\Big ]\Vert \dot{e}_M^0\Vert _m \nonumber \\{} & {} +Ch^\sigma \Big [\Vert f^\prime (0)\Vert _{m+\sigma }+\chi _{f^\prime }(cR_0)R_0\Big ]R_1, \nonumber \\\le & {} C(f,K_0)\big (\Vert e_M^0\Vert _m+\Vert \dot{e}_M^0\Vert _m\big )+C(f,R_0,R_1)h^\sigma . \end{aligned}$$

(3.18)

On the other hand,

$$\begin{aligned} \Vert \eta ^n\Vert _m= & {} \Big \Vert I_M\big (f(u_I^n)\big )-P_M\big (f(u(\cdot ,t_n))\big )\Big \Vert _m \\\le & {} \Big \Vert I_M\Big [f(u_I^n)-f(u(\cdot ,t_n))\Big ]\Big \Vert _m+\Big \Vert I_M\big (f(u(\cdot ,t_n))\big )-P_M\big (f(u(\cdot ,t_n))\big )\Big \Vert _m \\\le & {} C\Big \Vert f\big (u_I^n\big )-f\big (u(\cdot ,t_n)\big )\Big \Vert _m+Ch^\sigma \Big \Vert f\big (u(\cdot ,t_n)\big )\Big \Vert _{m+\sigma } \\\le & {} C\alpha \Big (f,K_0+1\Big )\Vert u_I^n-u(\cdot ,t_n)\Vert _m\\{} & {} +Ch^\sigma \Big (\Vert f(0)\Vert _{m+\sigma }+\chi _f\big (\Vert u(\cdot ,t_n)\Vert _{L^\infty }\big )\Vert u(\cdot ,t_n)\Vert _{m+\sigma }\Big ) \\\le & {} C\alpha \Big (f,K_0+1\Big )\Vert e_M^n\Vert _m+C(f,R_0)h^\sigma . \end{aligned}$$

In order to estimate $\Vert \eta ^{n+1}\Vert _m$, we need to find an upper bound for $\Vert u_I^{n+1}\Vert _m$. It follows that

$$\begin{aligned} \Vert u_I^{n+1}\Vert _m\le & {} \Vert u_I^{n-1}\Vert _m+2\tau \Vert \dot{u}_I^{n-1}\Vert _m+C\tau \Big (\Vert I_M(f(u_I^{n-1}))\Vert _m+\Vert I_M(f(u_I^n))\Vert _m\Big ) \\\le & {} K_0+2\tau K_1+C\tau \Big (\Vert f(u_I^{n-1})\Vert _m+\Vert f(u_I^n)\Vert _m\Big ) \\\le & {} K_0+2\tau K_1+C\tau \bigg (2\Vert f(0)\Vert _m+\chi _f(c\Vert u_I^{n-1}\Vert _m)\Vert u_I^{n-1}\Vert _m+\chi _f(c\Vert u_I^n\Vert _m)\Vert u_I^n\Vert _m\bigg ) \\\le & {} C(f,K_0,K_1). \end{aligned}$$

Therefore, we deduce that

$$\begin{aligned} \Vert \eta ^{n+1}\Vert _m\lesssim \Vert e^{n+1}_M\Vert _m+h^\sigma . \end{aligned}$$

(3.19)

Step 3: Error equations

From (3.13), one gets

$$\begin{aligned} |\widehat{e_l^1}|^2\lesssim (1+\tau ^2+\tau ^4)|\widehat{e_l^0}|^2+(\tau ^2+\tau ^4+\tau ^6)|\widehat{\dot{e}_l^0}|^2+|\widehat{\xi _l^0}|^2+\tau ^4|\widehat{\eta _l^0}|^2+\tau ^6|\widehat{\dot{\eta }_l^0}|^2. \end{aligned}$$

Substituting (3.11) with $n=1$ into (3.14) yields

$$\begin{aligned} \widehat{\dot{e}_l^1}= & {} \bigg (1+\frac{\theta _l^2\tau ^2}{6}\bigg )\Bigg [-\bigg (\frac{1-\cos {(2\theta _l\tau )}}{2\theta _l\tau }\bigg )\theta _l\widehat{e_l^0}+\bigg (\frac{\sin {(2\theta _l\tau )}}{2\theta _l\tau }\bigg )\widehat{\dot{e}_l^0}+\frac{1}{2\tau }\widehat{\xi _l^1} \\{} & {} -\frac{\theta _l^2\tau }{3}\bigg (\frac{\sin {(2\theta _l\tau )}}{2\theta _l\tau }\bigg )\widehat{\eta _l^0}-\frac{2\theta _l^2\tau }{3}\bigg (\frac{\sin {(\theta _l\tau )}}{\theta _l\tau }\bigg )\widehat{\eta _l^1}\Bigg ] +\widehat{\dot{\xi }_l^0}+\frac{\theta _l^2\tau }{12}\Bigl [\widehat{\eta _l^2}-\widehat{\eta _l^0}\Bigr ]. \end{aligned}$$

This implies that

$$\begin{aligned} |\widehat{\dot{e}_l^1}|^2\lesssim & {} (1+\tau ^2+\tau ^4)\big (\theta _l^2|\widehat{e_l^0}|^2+|\widehat{\dot{e}_l^0}|^2\big )+|\widehat{\dot{\xi }_l^0}|^2+\Big (\frac{1}{\tau ^2}+1+\tau ^2\Big )|\widehat{\xi _l^1}|^2 \\{} & {} +(\tau ^2+\tau ^4+\tau ^6)|\widehat{\eta _l^0}|^2+(\tau ^2+\tau ^4+\tau ^6)|\widehat{\eta _l^1}|^2+\tau ^2|\widehat{\eta _l^2}|^2. \end{aligned}$$

Hence,

$$\begin{aligned} \theta _l^2|\widehat{e_l^1}|^2+|\widehat{\dot{e}_l^1}|^2\lesssim & {} (1+\tau ^2+\tau ^4+\tau ^6)\big (\theta _l^2|\widehat{e_l^0}|^2+|\widehat{\dot{e}_l^0}|^2\big )+|\widehat{\xi _l^0}|^2+|\widehat{\dot{\xi }_l^0}|^2 \nonumber \\{} & {} +\Big (\frac{1}{\tau ^2}+1+\tau ^2\Big )|\widehat{\xi _l^1}|^2+(\tau ^2+\tau ^4+\tau ^6)|\widehat{\eta _l^0}|^2\nonumber \\{} & {} +(\tau ^2+\tau ^4+\tau ^6)|\widehat{\eta _l^1}|^2+\tau ^2|\widehat{\eta _l^2}|^2+\tau ^6|\widehat{\dot{\eta }_l^0}|^2 \nonumber \\\lesssim & {} \big (\theta _l^2|\widehat{e_l^0}|^2+|\widehat{\dot{e}_l^0}|^2\big )+|\widehat{\xi _l^0}|^2+|\widehat{\dot{\xi }_l^0}|^2+\frac{1}{\tau ^2}|\widehat{\xi _l^1}|^2\nonumber \\{} & {} +\tau ^2\big (|\widehat{\eta _l^0}|^2+|\widehat{\eta _l^1}|^2+|\widehat{\eta _l^2}|^2\big )+\tau ^6|\widehat{\dot{\eta }_l^0}|^2 \end{aligned}$$

(3.20)

for $\tau \le 1$. Applying the triangle and Young’s inequalities to (3.11) and (3.12), we obtain

$$\begin{aligned} |\widehat{e_l^{n+1}}|^2\le & {} \big (1+\tau \big )\frac{\big |\theta _l\cos (2\theta _l\tau )\widehat{e_l^{n-1}}+\sin (2\theta _l\tau )\widehat{\dot{e}_l^{n-1}}\big |^2}{\theta _l^2}\\{} & {} +C\bigg (1+\frac{1}{\tau }\bigg )\bigg [|\widehat{\xi _l^n}|^2+\tau ^2\big (|\widehat{\eta _l^{n-1}}|^2+|\widehat{\eta _l^n}|^2\big )\bigg ], \\ |\widehat{\dot{e}_l^{n+1}}|^2\le & {} \big (1+\tau \big )\big |-\theta _l\sin (2\theta _l\tau )\widehat{e_l^{n-1}}+\cos (2\theta _l\tau )\widehat{\dot{e}_l^{n-1}}\big |^2 \\{} & {} +C\bigg (1+\frac{1}{\tau }\bigg )\bigg [|\widehat{\dot{\xi }_l^n}|^2+\tau ^2\big (|\widehat{\eta _l^{n-1}}|^2+|\widehat{\eta _l^n}|^2+|\widehat{\eta _l^{n+1}}|^2\big )\bigg ] \end{aligned}$$

for $n\ge 1$. Hence,

$$\begin{aligned} \theta _l^2|\widehat{e_l^{n+1}}|^2+|\widehat{\dot{e}_l^{n+1}}|^2\le & {} (1+\tau )\big (\theta _l^2|\widehat{e_l^{n-1}}|^2+|\widehat{\dot{e}_l^{n-1}}|^2\big )+C\bigg (\frac{1}{\tau }+1\bigg )\big (|\widehat{\xi _l^n}|^2+|\widehat{\dot{\xi }_l^n}|^2\big ) \nonumber \\{} & {} +(\tau +\tau ^2)\big (|\widehat{\eta _l^{n-1}}|^2+|\widehat{\eta _l^n}|^2+|\widehat{\eta _l^{n+1}}|^2\big ). \end{aligned}$$

(3.21)

Moreover, we define

$$\begin{aligned} \mathcal {E}^n=\sum _{l=1}^{M-1}\big (1+|\mu _l|^2\big )^m\Big (\theta _l^2|\widehat{e_l^n}|^2+|\widehat{\dot{e}_l^n}|^2\Big ). \end{aligned}$$

(3.22)

It is easy to see that

$$\begin{aligned} \mathcal {E}^0\lesssim \Vert e^0_M\Vert _m^2+\Vert \dot{e}^0_M\Vert _m^2\lesssim \Vert e^0\Vert _m^2+\Vert \dot{e}^0\Vert _m^2\lesssim h^{2\sigma }, \end{aligned}$$

(3.23)

by Lemma 3.1 and (3.8). Combining the inequalities (3.16), (3.17) and

$$\begin{aligned} \Vert \dot{\eta }^0\Vert _m^2\lesssim h^{2\sigma },\hspace{20 pt}\Vert \eta ^n\Vert _m^2\lesssim \mathcal {E}^n+h^{2\sigma }, \end{aligned}$$

(3.24)

one can estimate

$$\begin{aligned} \mathcal {E}^1\lesssim & {} \mathcal {E}^0+\!\Vert \xi ^0\Vert _m^2+\!\Vert \dot{\xi }^0\Vert _m^2+\!\frac{1}{\tau ^2}\Vert \xi ^1\Vert _m^2\!+\tau ^2\big (\Vert \eta ^0\Vert _m^2\!+\Vert \eta ^1\Vert _m^2\!+\Vert \eta ^2\Vert _m^2\big )\!+\tau ^6\Vert \dot{\eta }^0\Vert _m^2 \nonumber \\\lesssim & {} \tau ^8+(1+\tau ^2+\tau ^6)h^{2\sigma }+\tau ^2(\mathcal {E}^1+\mathcal {E}^2) \nonumber \\\lesssim & {} \tau ^8+h^{2\sigma }+\tau ^2\mathcal {E}^2. \end{aligned}$$

(3.25)

for $0<\tau \le \tau _1$. Using (3.21), we obtain

$$\begin{aligned} \mathcal {E}^{n+1}\le (1+\tau )\mathcal {E}^{n-1}+C\bigg (\frac{1}{\tau }+1\bigg )\big (\Vert \xi ^n\Vert _m^2+\Vert \dot{\xi }^n\Vert _m^2\big )+(\tau +\tau ^2)\big (\Vert \eta ^{n-1}\Vert _m^2+\Vert \eta ^n\Vert _m^2+\Vert \eta ^{n+1}\Vert _m^2\big ) \end{aligned}$$

for $n\ge 1$. This implies that

$$\begin{aligned} \mathcal {E}^{n+1}-\mathcal {E}^{n-1}\lesssim \tau \mathcal {E}^{n-1}+\frac{1}{\tau }\big (\Vert \xi ^n\Vert _m^2+\Vert \dot{\xi }^n\Vert _m^2\big )+\tau \big (\Vert \eta ^{n-1}|_m^2+\Vert \eta ^n\Vert _m^2+\Vert \eta ^{n+1}\Vert _m^2\big ). \end{aligned}$$

(3.26)

Substituting (3.17) and (3.24) into (3.26), we get

$$\begin{aligned} \mathcal {E}^{n+1}-\mathcal {E}^{n-1}\lesssim & {} \tau \big (\mathcal {E}^{n-1}+\mathcal {E}^n+\mathcal {E}^{n+1}\big )+\tau ^9+\tau h^{2\sigma }. \end{aligned}$$

Summing the above inequalities from $n=1$ to $n=k$ such that $k\le T/\tau$, one can find

$$\begin{aligned} \mathcal {E}^{k+1}+\mathcal {E}^k-\mathcal {E}^1-\mathcal {E}^0\lesssim & {} k\tau ^9+k\tau h^{2\sigma }+\tau \sum _{n=0}^{k+1}\mathcal {E}^n\\\lesssim & {} \tau ^8+h^{2\sigma }+\tau \sum _{n=0}^{k+1}\mathcal {E}^n. \end{aligned}$$

In view of (3.23), (3.25), one may estimate

$$\begin{aligned} \mathcal {E}^{k+1}\lesssim & {} \mathcal {E}^0+\mathcal {E}^1+\tau ^8+h^{2\sigma }+\tau \sum _{n=0}^{k+1}\mathcal {E}^n-\mathcal {E}^k \nonumber \\\lesssim & {} \tau ^8+h^{2\sigma }+\tau \sum _{n=0}^k\mathcal {E}^n+\tau ^2\mathcal {E}^2+\tau \mathcal {E}^{k+1} \nonumber \\\lesssim & {} \tau ^8+h^{2\sigma }+\tau \sum _{n=0}^k\mathcal {E}^n \end{aligned}$$

(3.27)

for $0<\tau \le \tau _2$. When the discrete Gronwall’s Lemma is applied to (3.27), we finally show that

$$\begin{aligned} \mathcal {E}^{k+1}\lesssim \big (\tau ^8+h^{2\sigma }\big )\exp {\Big (\sum _{n=0}^{k}\tau \Big )}\lesssim \tau ^8+h^{2\sigma }. \end{aligned}$$

(3.28)

Moreover, using Lemma 3.1 and (3.28), we deduce that

$$\begin{aligned} \Vert e^{k+1}\Vert _m+\Vert \dot{e}^{k+1}\Vert _m\lesssim & {} \Vert e^{k+1}_M\Vert _m+\big \Vert u(\cdot ,t_{k+1})-P_M\big (u(\cdot ,t_{k+1})\big )\big \Vert _m \\{} & {} +\Vert \dot{e}^{k+1}_M\Vert _m+\big \Vert \partial _t u(\cdot ,t_{k+1})-P_M\big (\partial _t u(\cdot ,t_{k+1})\big )\big \Vert _m \\\lesssim & {} \tau ^4+h^\sigma . \end{aligned}$$

There exist sufficiently small $h_2$ and $\tau _3$ such that the following inequalities hold

$$\begin{aligned} \Vert u_I^{k+1}\Vert _m\le & {} \Vert e^{k+1}_M\Vert _m+\Vert u(\cdot ,t_{k+1})\Vert _m\le K_0+1, \\ \Vert \dot{u}_I^{k+1}\Vert _m\le & {} \Vert \dot{e}^{k+1}_M\Vert _m+\Vert \partial _t u(\cdot ,t_{k+1})\Vert _m\le K_1+1, \end{aligned}$$

when $0<h\le h_2$ and $0<\tau \le \tau _3$. The proof of the Theorem 3.1 is completed by choosing $h_0=\min \{h_1,h_2\}$ and $\tau _0=\min \{1,\tau _1,\tau _2,\tau _3\}$.$\square$

4 Numerical experiments

To investigate the performance of the proposed EWI-SP method, we now consider the propagation of a single solitary wave, the single wave splitting, the head-on collision of two solitary waves. For all the numerical experiments, we choose the nonlinear function $f(u)=u^p$ with $p=2$ or $p=3$. To quantify the error, we use the following error function

$$\begin{aligned} e_{\tau ,h}(t_n)=\big \Vert u^n_{\tau ,h}-u(\cdot ,t_n)\big \Vert _1+\big \Vert \dot{u}^n_{\tau ,h}-\partial _tu(\cdot ,t_n)\big \Vert _1, \end{aligned}$$

where $u^n_{\tau ,h}$ and $\dot{u}^n_{\tau ,h}$ are the numerical solutions obtained by the EWI-SP method.

4.1 Single solitary wave

The exact solitary wave solution of the HBq equation is given in [7] as

$$\begin{aligned} u(x,t)=A\Big [{{\,\textrm{sech}\,}}\big (B(x-ct-x_0)\big )\Big ]^\frac{4}{p-1}, \end{aligned}$$

(4.1)

where

$$\begin{aligned} A=\bigg [\frac{\eta _1^2c^2(p+1)(p+3)(3p+1)}{2\eta _2(p^2+2p+5)^2}\bigg ]^\frac{1}{p-1}, \hspace{20pt}B=\bigg [\frac{\eta _1(p-1)^2}{4\eta _2(p^2+2p+5)}\bigg ]^\frac{1}{2}, \end{aligned}$$

(4.2)

$$\begin{aligned} c^2=\Bigg (1-\bigg [\frac{4\eta _1^2(p+1)^2}{\eta _2(p^2+2p+5)^2}\bigg ]\Bigg )^{-1}. \end{aligned}$$

(4.3)

Here, A is amplitude, B is the inverse width of the solitary wave and c represents the velocity of the solitary wave at $x_0$ with $c^2>1$.

Fig. 1

The spatial errors (left panel) and the temporal errors (right panel) of the EWI-SP method for the solution under different grid spacing and time steps

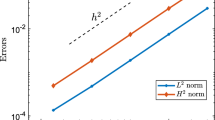
The problem is solved on the space interval $\Omega =(-400,400)$ for times up to $T=10$. We choose the parameters $\eta _1=\eta _2=1$ with $x_0=0$ taking the initial condition corresponding to the exact solitary wave solution in (4.1)-(4.3). To test whether the EWI-SP method exhibits the expected convergence rate in the space, we perform some numerical experiments for various values of h and a fixed value of time step $\tau$. We take a tiny time step $\tau =0.005$ so that the temporal error is negligible. In the left panel of Fig. 1, we present the variation of the error with different values of h. As is seen from the figure, the error decays very rapidly when the spatial step size h decreases. This numerical experiment shows that the EWI-SP method converges rapidly to the accurate solution in space, which is indicative of exponential convergence. In order to confirm the temporal error bound given in Theorem 3.1, the computations are performed for fixed value $h=0.5$ and various values of the time step $\tau$. The right panel of Fig. 1 shows the temporal errors of the EWI-SP method. As we expected, the scheme has fourth-order accuracy in time, which agrees with the theoretical result in Theorem 3.1.

Fig. 2

Conservation of mass (left panel) and long-time errors (right panel) of the EWI-SP method by choosing $h=0.5$ and $\tau =0.005$

The evolution of the change for the conserved quantity $\mathcal {M}$ is depicted in the left panel of Fig. 2. This figure illustrates that the EWI-SP method preserves conserved quantity very well. Next, we investigate the long-time behavior of the EWI-SP method up to $T=100$. The right panel of Fig. 2 shows that the error is about $10^{-12}$, even for the cubic nonlinearity. It can be observed that the EWI-SP method is reliable for long-time dynamics.

4.2 Single wave splitting

In these numerical experiments, we set $\eta _1=\eta _2=1$. The initial data

$$\begin{aligned} u_0(x)=\frac{15}{38}{{\,\textrm{sech}\,}}^4\bigg (\frac{\sqrt{13}}{~26}x\bigg ), \hspace{20 pt} u_1(x)=0 \end{aligned}$$

are chosen for quadratic nonlinearity. We take the following initial data

$$\begin{aligned} u_0(x)=\sqrt{\frac{5}{14}}{{\,\textrm{sech}\,}}^2\bigg (\frac{\sqrt{5}}{~10}x\bigg ), \hspace{20 pt} u_1(x)=0 \end{aligned}$$

for cubic nonlinearity. The computations are performed on the domain $\Omega =(-400,400)$ up to $T=60$ with $h=0.5$ and $\tau =0.005$. In the left panel of Fig. 3, we show the dynamics of the solitary wave with amplitude $A = \displaystyle \frac{15}{38}$ and the null initial velocity for quadratic nonlinearity. Snapshots of the solutions at different times are illustrated in the right panel of Fig. 3. We observe that the initial stationary wave splits up into two smaller diverging waves, one traveling towards the left and the other one to the right and the splitting leads to the creation of secondary solitary waves.

Fig. 3

The contour plot of single wave splitting for the quadratic nonlinearity (left panel), snapshots of the solitary wave at different times (right panel)

Fig. 4

The contour plot of single wave splitting for the cubic nonlinearity (left panel), snapshots of the solitary wave at different times (right panel)

Fig. 5

The evolution of the change in the conserved quantity $\mathcal {M}$ for the single wave splitting

The dynamic of the solitary wave with the amplitude $\displaystyle \sqrt{\frac{5}{14}}$ and the null initial velocity is depicted in Fig. 4 for cubic nonlinearity. We observe that the dynamics are similar to quadratic nonlinearity. However, the secondary waves between the two main splitting waves become more discernible when the power of nonlinearity increases.

Since an analytical solution is not available for the single wave splitting experiments, we cannot present the errors for this experiment. However, we present the evolution of the change in the conserved quantity $\mathcal {M}$ as a numerical check of the proposed scheme in Fig. 5. The conserved quantity remains constant in time and this behavior provides a valuable check on the numerical results.

4.3 Head-on collision

In these numerical experiments, we use the initial data

$$\begin{aligned} u_0(x)= & {} \frac{15}{38}{{\,\textrm{sech}\,}}^4\bigg (\frac{\sqrt{13}}{26}\Big [x+40\Big ]\bigg )+\frac{15}{38}{{\,\textrm{sech}\,}}^4\bigg (\frac{\sqrt{13}}{26}\Big [x-40\Big ]\bigg )\\ u_1(x)= & {} \frac{15\sqrt{1729}}{2527}{{\,\textrm{sech}\,}}^4\bigg (\frac{\sqrt{13}}{26}\Big [x+40\Big ]\bigg )\tanh \bigg (\frac{\sqrt{13}}{26}\Big [x+40\Big ]\bigg )\\{} & {} -\frac{15\sqrt{1729}}{2527}{{\,\textrm{sech}\,}}^4\bigg (\frac{\sqrt{13}}{26}\Big [x-40\Big ]\bigg )\tanh \bigg (\frac{\sqrt{13}}{26}\Big [x-40\Big ]\bigg ) \end{aligned}$$

for quadratic nonlinearity and

$$\begin{aligned} u_0(x)= & {} \sqrt{\frac{5}{14}}{{\,\textrm{sech}\,}}^2\bigg (\frac{\sqrt{5}}{10}\Big [x+40\Big ]\bigg )+\sqrt{\frac{5}{14}}{{\,\textrm{sech}\,}}^2\bigg (\frac{\sqrt{5}}{10}\Big [x-40\Big ]\bigg )\\ u_1(x)= & {} \frac{5\sqrt{6}}{42}{{\,\textrm{sech}\,}}^2\bigg (\frac{\sqrt{5}}{10}\Big [x+40\Big ]\bigg )\tanh \bigg (\frac{\sqrt{5}}{10}\Big [x+40\Big ]\bigg )\\{} & {} -\frac{5\sqrt{6}}{42}{{\,\textrm{sech}\,}}^2\bigg (\frac{\sqrt{5}}{10}\Big [x-40\Big ]\bigg )\tanh \bigg (\frac{\sqrt{5}}{10}\Big [x-40\Big ]\bigg ) \end{aligned}$$

for cubic nonlinearity by taking $\eta _1=\eta _2=1$. The computations are performed on the domain $\Omega =(-400,400)$ up to $T=72$ with $h=0.5$ and $\tau =0.005$. In the left panel of Fig. 6, we show the head-on collision of two solitary waves with equal amplitudes for quadratic nonlinearity. We see the oscillating secondary waves. Therefore, the interaction is inelastic. The numerical solution at different times is shown in the right panel of Fig. 6. The collision occurs at around $t=35.08$ with the largest amplitude which is smaller than the sum of the two initial amplitudes. We observe that the small secondary waves are emitted after collision time. We also compute that the amplitudes of secondary waves are smaller than 0.006.

Fig. 6

The surface plot of the head-on collision of two solitary waves for the quadratic nonlinearity (left panel), snapshots of the solution at different times (right panel)

Fig. 7

The surface plot of the head-on collision of two solitary waves for the cubic nonlinearity (left panel), snapshots of the solution at different times (right panel)

Fig. 8

The evolution of the change in the conserved quantity $\mathcal {M}$ for the head-on collision of two solitary waves

The head-on collision of two solitary waves for cubic nonlinearity is illustrated in Fig. 7, we see that the collision is inelastic and the interaction is similar to quadratic nonlinearity. We observe that the amplitudes of secondary waves are smaller than 0.0098. We also observe that the amplitudes of secondary waves which occur after the collision are less than 2% of the amplitude of the waves at the initial time for both quadratic and cubic nonlinearity. Figure 8 shows that the conserved quantities for the head-on collision of two solitary waves remain constant in time for both cases. These results provide a valuable check on the numerical results.