1 Introduction

We investigate the global approximation of solutions of the following stochastic differential equations

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle { \,{\mathrm d}X(t) = a(t,X(t))\,{\mathrm d}t + \sigma (t) \,{\mathrm d}W(t) , \ t\in [0,T]},\\ X(0)=x_0, \end{array} \right. \end{aligned}$$
(1)

where \(T >0\), \(W(t) = [W_1(t), W_2(t), \ldots ]^T\) is a sequence of independent scalar Wiener processes on the probability space with sufficiently rich filtration \((\Omega , \mathcal {F}, \mathbb {P}, \big (\mathcal {F}_t)_{t\in [0,T]}\big ),\) and \(x_0 \in \mathbb {R}.\) For suitable, regular coefficients \(a, \sigma ,\) the uniqueness of the solution \(X=X(t),\) and its finite second-order moments can be assured; see [1, 4, 6, 23] where more general models were considered.

Recently, the global approximation of solutions of SDEs driven by finite-dimensional Wiener process has been studied extensively in the literature. In particular, the algorithms with step-size were introduced in [8, 9, 12, 19, 20]. Generally, the time-step adaptation linked to the equation coefficients instead of leveraging equidistant mesh can significantly decrease the asymptotic constant for the method error in the finite-dimensional models. On the other hand, SDEs driven by countably dimensional Wiener noise can be found in [2, 5, 14], while their applications, e.g., in [3, 18]. Nonetheless, there are still a few papers referring to the exact error behaviour and optimality issues for such SDEs in the global setting. For instance, in [24] authors developed an Euler algorithm and estimated its global error for X being countably dimensional. However, the assumptions were relatively strong, and the proposed algorithm was non-implementable due to infinite dimension of the solution.

In this paper, we extend some asymptotic results for the global approximation from [8, 12] to SDEs with countably dimensional noise structure. To that end, we utilise solution moment bounds and approximation strategy presented in [23], where a pointwise setting was investigated. In our setting, error of an algorithm \({\mathcal A}\) returning a process \(Y = (Y(t))_{t\in [0,T]}\) is measured in the norm \(\Vert \cdot \Vert _2\) defined as follows:

$$\begin{aligned} \Vert X-Y\Vert _2 = \left( \mathbb {E}\int _0^T |X(t)-Y(t)|^2 \,{\mathrm d}t \right) ^{1/2}. \end{aligned}$$

Under suitable conditions imposed on the model coefficients, we analyse asymptotic exact error behaviour in two classes \(\chi _{eq}, \chi _{noneq}\) of admissible algorithms leveraging only finite-dimensional evaluations of the process W; , we refer to [7, 8, 11, 12, 17, 22, 26] where similar approach for generic error analysis was developed. In our setting, permitted truncation levels are determined by non-decreasing sequences leveraging information about how fast \(\sigma \) entries vanish. In Theorem 2, we show that for any fixed, admissible truncation level sequence \(\bar{M}=(M_n)_{n=1}^{\infty }\), an exact asymptotic behaviour of the cost-error relation satisfies

$$\begin{aligned} \big ({\text {cost}}{({\overline{X}_{M_n,\bar{k}_n}})}\big )^{1/2}\,\big \Vert {\overline{X}_{M_n,\bar{k}_n}}- X\big \Vert _{2} \gtrapprox \frac{M_n^{1/2}}{\sqrt{6}}\int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}\,{\mathrm d}t, \end{aligned}$$
(2)

irrespective of the choice of admissible method \(({\overline{X}_{M_n,\bar{k}_n}})_{n\in \mathbb {N}}\in \chi _{noneq}^{\bar{M}}\) based on (possibly) non-equidistant mesh with a suitable number of nodes \(\bar{k_n}+1,\) and such that \({\overline{X}_{M_n,\bar{k}_n}}\) utilises discrete information from \(M_n, n\in \mathbb {N},\) first coordinates of W. When we limit ourselves to methods \(\chi _{eq}^{\bar{M}}\) based on equidistant partitions of the interval [0, T],  we get

$$\begin{aligned} \big ({\text {cost}}{({\overline{X}_{M_n,\bar{k}_n}})}\big )^{1/2}\,\big \Vert {\overline{X}_{M_n,\bar{k}_n}}- X\big \Vert _{2} \gtrapprox M_n^{1/2}\sqrt{\frac{T}{6}}\biggr (\int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}^2\,{\mathrm d}t \biggr )^{1/2}. \end{aligned}$$
(3)

We hereinafter use the notation

$$\begin{aligned} \mathcal {C}_{noneq} = \frac{1}{\sqrt{6}}\int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}\,{\mathrm d}t, \quad \quad \mathcal {C}_{eq} = \sqrt{\frac{T}{6}}\biggr (\int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}^2\,{\mathrm d}t \biggr )^{1/2}. \end{aligned}$$

By the Hölder inequality, we have \(0 \le \mathcal {C}_{noneq}\le \mathcal {C}_{eq}\). We also stress that the lower bounds in (2) and (3) diverge as n tends to infinity, which illustrates significant increase of the informational cost needed to decrease the method error. Next, for fixed \(\bar{M},\) we construct truncated Euler algorithm with adaptive path-independent step-size control \(X^{step}_{M_n,k_n^*}\) which is optimal in class \(\chi _{noneq}^{\bar{M}},\) since it attains asymptotic lower bound in (2). We also provide lower bounds which hold irrespective of the truncation level sequence, see Theorem 3. While those cannot be asymptotically achieved by any admissible algorithm, we show that the errors for the methods proposed in this paper can be arbitrary close in some sense to the obtained bound. We note that both error bounds and optimality are investigated in the spirit of information-based complexity (IBC) framework.

According to our best knowledge, this is the first paper to establish lower bounds for exact asymptotic error in the global approximation setting for SDEs with countably dimensional Wiener process. Moreover, the new constructed algorithms are implementable, and their performance is verified by using the multiprocessing library in Python.

The paper is organised as follows. In Sect. 2, we provide basic notation, model assumptions, and properties of the underlying solution X. Then, in Sect. 3, we investigate lower bounds for exact asymptotic error behaviour. In Sect. 4.1 and in Sect. 4.2, we introduce and show optimality of the truncated dimension Euler schemes in the classes \(\chi _{eq}^{\bar{M}}\) and \(\chi _{noneq}^{\bar{M}},\) respectively. Next, in Sect. 4.3, we extend optimality investigation to the classes \(\chi _{eq}\) and \(\chi _{noneq}.\) Finally, Sect. 5 deals with numerical experiments in Python and alternative solver implementation utilizing Numba compiler.

2 Preliminaries

Let \((\Omega ,\Sigma ,\mathbb {P})\) be a complete probability space and \(\mathcal {N}_0=\{A\in \Sigma \ | \ \mathbb {P}(A)=0\}\). Let also \((\Sigma _t)_{t\ge 0}\) be a filtration on \((\Omega ,\Sigma ,\mathbb {P})\) that satisfies the usual conditions, i.e., \(\mathcal {N}_0\subset \Sigma _0\) and is right-continuous. For a random variable X by \(\Vert X\Vert _{L^2(\Omega )}\), we understand \((\mathbb {E}|X|^2)^{1/2}.\)

Let \(W=[W_1,W_2,\ldots ]^T\) be a countably dimensional \((\Sigma _t)_{t\ge 0}\)-Wiener process defined on \((\Omega ,\Sigma ,\mathbb {P})\). We note that similarly to the finite-dimensional case, stochastic integrals with respect to W enjoy properties such as the Burkholder inequality, Itô isometry, Itô lemma, see e.g. [2, 4, 23].

For \(x\in \ell ^2(\mathbb {R})\), we use the following notation \(x = (x_1, x_2, \ldots ).\) We introduce projection operators \(P_k: \ell ^2 (\mathbb {R}) \mapsto \ell ^2 (\mathbb {R}),\) \(k\in \mathbb {N}\cup \{\infty \}\) with

$$\begin{aligned} P_k v = (v_1, v_2, \ldots , v_k, 0, 0, \ldots ), \quad v\in \ell ^2(\mathbb {R}). \end{aligned}$$

We also set \(P_{\infty }=Id\), hence \(P_{\infty }v=v\) for all \(v\in \ell ^2(\mathbb {R})\). For brevity, in this paper, we write \(\Vert \cdot \Vert _{\ell ^2}\) instead of \(\Vert \cdot \Vert _{\ell ^2(\mathbb {R})}.\)

For vectors \(v = [v_1, \ldots , v_m] \in {\mathbb R}^m,\) \(u = [u_1, \ldots , u_l] \in {\mathbb R}^l,\) we denote by \(v\oplus u\) the vector \([v_1, \ldots , v_m, u_1,\ldots , u_l]\in \mathbb {R}^{m+l}\). By \(\bigoplus _{k=1}^n w_k\), we understand the vector \(w_1 \oplus w_2 \oplus \ldots \oplus w_n.\)

In this paper, we use the following asymptotic notation. For two real-valued sequences \((a_n)_{n=1}^\infty ,\, (b_n)_{n=1}^\infty ,\) we write \(a_n \lessapprox b_n, n\rightarrow +\infty ,\) if and only if \(\limsup _{n\rightarrow +\infty } a_n/b_n \le 1.\) We also say that \(a_n \approx b_n, n \rightarrow +\infty ,\) if and only if \(\lim _{n\rightarrow +\infty }a_n / b_n = 1.\) Furthermore, the asymptotic symbols \(\Omega , \Theta , \mathcal {O},o\) appearing in this paper are aligned with classical Landau notation for sequences. For a sequence \((c(n))_{n=1}^\infty \) of non-negative numbers converging to zero and \(\epsilon >0,\) we define the inverse \(c^{-1}(\epsilon ) = \sup \{n \in \mathbb {N}\, | \, c(n)>\epsilon \}.\)

We assume that drift coefficient \(a: [0,T]\times \mathbb {R} \mapsto \mathbb {R} \) belongs to \(\mathcal {C}^{1,2}([0,T]\times \mathbb {R})\) and satisfies the following conditions:

  1. (A1)

    \(|a(t,x) - a(s,x)| \le C_1(1+ |x|)|t-s|\) for all \(t,s\in [0,T], \ x\in \mathbb {R}\),

  2. (A2)

    \(|a(t,0)|\le C_1\) for all \(t\in [0,T]\),

  3. (A3)

    \(|a(t,x) - a(t,y)| \le C_1|x-y|\) for all \(x,y \in \mathbb {R}\), \(t \in [0,T]\),

  4. (A4)

    \(|\frac{\partial a}{\partial x}(t,x) - \frac{\partial a}{\partial x}(t,y)| \le C_1|x-y|\) for all pairs \((t,x), (t,y) \in [0,T]\times \mathbb {R}\)

for some \(C_1 > 0.\)

Let \(\delta = (\delta (k))_{k = 1}^{\infty }\subset \mathbb {R}\) be a positive, strictly decreasing sequence vanishing at infinity. For fixed \(\delta ,\) by \(\mathcal {G}_\delta \), we denote a set of all non-decreasing sequences \(G=(G(n))_{n=1}^{\infty } \subset \mathbb {N}\) such that \(G(n)\rightarrow +\infty \) and

$$\begin{aligned} \lim \limits _{n \rightarrow +\infty }n^{1/2}\,\delta \big (G(n)\big ) = 0. \end{aligned}$$
(4)

We assume that diffusion coefficient \(\sigma = (\sigma _1, \sigma _2, \ldots ):[0,T] \mapsto \ell ^2(\mathbb {R})\) satisfies the following conditions:

  1. (S1)

    \(\Vert \sigma (0)\Vert _{\ell ^2} \le C_2,\)

  2. (S2)

    \(\Vert \sigma (t) - \sigma (s)\Vert _{\ell ^2} \le C_2|t-s|\) for all \(t,s\in [0,T]\),

  3. (S3)

    \(\Vert \sigma (t) - P_k \sigma (t)\Vert _{\ell ^2} \le C_2\delta (k)\) for all \(k \in \mathbb {N}, \ t \in [0,T],\)

for \(C_2 > 0\) and some fixed sequence \(\delta \) as above.

Our idea is to first provide the approximation of truncated solution \(X^M = X^M(a,\sigma ,W)\) which depends on the first \(M\in \mathbb {N}\) coordinates of the underlying Wiener process W. In this paper, any method leveraging finite number of Wiener process coordinates will be referred to as ‘truncated dimension method’. Then, we estimate globally the inevitable truncation error resulting from substituting the process X for \(X^M.\) For convenience, we will use the notation \(X^{\infty }:= X.\)

To this end, we consider the family of processes \(X^M, \ M \in \mathbb {N} \cup \{\infty \},\) satisfying

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle { \,{\mathrm d}X^M(t) = a(t,X^M(t))\,{\mathrm d}t + \sigma ^M(t) \,{\mathrm d}W(t) , \ t\in [0,T]},\\ X^M(0)=x_0. \end{array}\right. \end{aligned}$$
(5)

In particular, for \(M=+\infty \), we obtain the main problem (1). For further analysis, we need some properties of the process \(X^M.\) Those are presented below, in a corollary from Lemma 1 in [23].

Lemma 1

For every \(M \in \mathbb {N} \cup \{\infty \}\) the Eq. (5) admits a unique strong solution \(X^M = (X^M(t))_{t\in [0,T]}.\) Moreover, there exists \(K \in (0,+\infty ),\) depending only on the constants \(C_1, C_2,\) such that for every \(M\in \mathbb {N}\ \cup \ \{\infty \}\), we have that

$$\begin{aligned} \mathbb {E}\Bigl (\sup _{0 \le t \le T} |X^M(t)|^2\Bigr ) \le K \end{aligned}$$
(6)

and for all \(s,t \in [0,T]\) the following holds

$$\begin{aligned} \mathbb {E}|X^M(t)-X^M(s)|^2 \le K|t-s|. \end{aligned}$$

We also state truncation error bound for our model. This result is a corollary from Proposition 1 in [23].

Proposition 1

There exists \(K_1\in (0,+\infty )\) such that for any \(M \in \mathbb {N}\) it holds

$$\begin{aligned} \sup \limits _{0 \le t \le T}\Vert X(a,\sigma , W)(t)-X^M(a,\sigma ,W)(t)\Vert _{L^2(\Omega )} \le K_1\delta (M). \end{aligned}$$
(7)

We define truncated dimension time-continuous Euler algorithm \({\widetilde{X}_{M,n}^E}= ({\widetilde{X}_{M,n}^E}\) \((t))_{t\in [0,T]}\) that approximates the process \((X(t))_{t \in [0,T]}\). Take \(M,n \in \mathbb {N}\), and let

$$\begin{aligned} \tau _n: 0 = t_{0,n}< t_{1,n}< \ldots< t_{k_n-1,n} < t_{k_n,n} = T \end{aligned}$$
(8)

be a sequence of partitions of the interval [0, T],  with \(k_n \in \mathbb {N}.\)

We set

$$\begin{aligned} {\left\{ \begin{array}{ll} {\widetilde{X}_{M,n}^E}(0) = x_0 \\ {\widetilde{X}_{M,n}^E}(t) = {\widetilde{X}_{M,n}^E}(t_{j,n}) + a\big (t_{j,n} , {\widetilde{X}_{M,n}^E}(t_{j,n})\big )(t - t_{j,n}) + \sigma ^M(t_{j,n})\big (W(t) - W(t_{j,n})\big ), \\ \quad \quad \quad \quad \quad t \in [t_{j,n}, t_{j+1,n}], \ \ j=0,1,\ldots , k_n-1. \end{array}\right. } \end{aligned}$$
(9)

We stress that \({\widetilde{X}_{M,n}^E}\) is not implementable since it requires complete knowledge of the trajectories of the underlying Wiener process.

Now, we state the upper error bound of the truncated dimension time-continuous Euler algorithm in finite-dimensional setting.

Proposition 2

Under the assumptions (A1)-(A4) and (S1)-(S3), there exists a positive constant \(C_0\), depending only on \(C_1, C_2\), such that for all \(M,n\in \mathbb {N}\) the time-continuous truncated Euler process (9) based on partition (8) satisfies

$$\begin{aligned} \sup _{0 \le t \le T} \Vert {\widetilde{X}_{M,n}^E}(t)-X^M(t)\Vert _{L^2(\Omega )} \le C_0 \max _{0 \le j \le k_n-1}\Delta t_{j,n}, \end{aligned}$$
(10)

where \(\Delta t_{j,n} = t_{j+1,n} - t_{j,n},\) \(j=0,1,\ldots , k_n-1.\)

The proof of Proposition 2 is postponed to the Appendix.

We can state the most important result of this section.

Theorem 1

Let the coefficients \(a,\sigma \) satisfy (A1)-(A4) and (S1)-(S3) with sequence \(\delta \), respectively. Then, there exists a positive constant K, depending on \(C_1, C_2, \delta ,\) such that for every \(M,n\in \mathbb {N}\) and the discretisation (8), it holds

$$\begin{aligned} \sup _{0\le t \le T}\Vert X(t) - {\widetilde{X}_{M,n}^E}(t)\Vert _{L^2(\Omega )}\le K\Bigl (\max \limits _{0\le j \le k_n-1} \,\Delta t_{j,n} + \delta (M)\Bigr ). \end{aligned}$$

Proof

By Proposition 1, Proposition 2, and the triangle equality, we obtain the desired result. \(\square \)

At the end of this section, we present several remarks on the model, imposed assumptions, and suitability of the chosen stochastic scheme.

Remark 1

Generally, the concept of SDEs with integrals with respect to countably dimensional Wiener process is used to describe the evolution driven by countably many risk factors. This modelling choice can be leveraged for a wide range of problems in, e.g., genetics, mathematical finance or physics [3, 18]. From a pragmatic point of view, infinite-dimensional setting can be leveraged when the number of random risks is finite but still too large to be entirely captured by the electronic machines. On the other hand, the integrals appearing in this paper can be viewed as stochastic integrals with respect to cylindrical Brownian motion in Hilbert space of sequences \(\ell ^2(\mathbb {R})\) and hence, our model forms a bridge between ordinary SDEs and stochastic partial differential equations (SPDEs), see [5].

Remark 2

First, the assumptions (A1) - (A4) imply the existence of a constant \(K_0 > 0\) such that

$$\begin{aligned} \max \bigg \{\left| \frac{\partial a}{\partial x}(t,x)\right| , \left| \frac{\partial ^2 a}{\partial x^2}(t,x)\right| \bigg \} \le K_0 \quad \text {for every} \quad (t,x)\in [0,T] \times \mathbb {R}. \end{aligned}$$
(11)

Second, in the presented setting, a crucial role is played by appropriate choice of corresponding truncation levels for admissible methods. Indeed, those are defined in terms of the elements of \(\mathcal {G}_{\delta }\) as per (4). We note that for every \(\delta \) the corresponding set \(\mathcal {G}_\delta \) is nonempty. Furthermore, the slower rate of diffusion decay to zero, the greater values of G(n) need to be taken. We note that \(\delta \) does not need to be optimal in a sense that for fixed \(\sigma \) there might exist \(\delta '\) also satisfying (S3) and \(\delta ' < \delta .\) Nevertheless, sharper bound in (S3) yields greater palette of the corresponding sequences G in (4), as \(\delta ' \le \delta \) implies \(\mathcal {G}_\delta \subset \mathcal {G}_{\delta '}.\)

Remark 3

It is worth mentioning that suitable modifications of the classic Euler scheme for finite-dimensional setting have been investigated in, e.g., [8, 15, 23]. For the problem (1), the method \({\widetilde{X}_{M,n}^E}\) coincides with truncated dimension time-continuous Euler algorithm proposed in [23]. However, the regularity of function a in our case enhances the rate of convergence from 1/2 to 1,  see Theorem 1. Indeed, the proposed method also coincides with the Milstein scheme; see, e.g., [12, 13, 16, 19,20,21,22] where the approximation by modified Milstein schemes for finite-dimensional models was considered.

In the following sections, we investigate lower bounds for exact asymptotic error behaviour and construct optimal methods in suitable subclasses of admissible algorithms. The optimality is defined in the spirit of Information-Based Complexity (IBC) framework, see also [26] for more details.

3 Lower bounds for exact asymptotic error behaviour

In this section, we derive minimal global approximation error for our initial problem (1). The main results are presented in Theorem 2.

Let us fix \((a,\sigma ),\) and a sequence \(\delta \) satisfying (S3). An arbitrary method under consideration is a sequence of the form \(\overline{X} = ({\overline{X}_{M_n,\bar{k}_n}})_{n=1}^{\infty }\) and can be equivalently viewed as a quadruple \(\overline{X} = (\bar{\Delta }, \bar{\mathcal {N}}, \bar{M}, \bar{\phi }),\) where

  • \(\bar{\Delta }=(\bar{\Delta }_{n})_{n=1}^{\infty }\) is a sequence of (possibly) non-expanding partitions of the interval [0, T],  i.e.,

    $$\begin{aligned} \bar{\Delta }_{n}: \quad 0=\bar{t}_{0,n}< \bar{t}_{1,n}< \ldots< \bar{t}_{\bar{k}_n-1,n} < \bar{t}_{\bar{k}_n,n} = T, \end{aligned}$$
    (12)

    where for some \(\overline{C}_1, \overline{C}_2>0\) it holds

    $$\begin{aligned} \overline{C}_1\, n \ge \bar{k}_n \ge \overline{C}_2 \, n^{1/2}, \quad n\ge n_0(\overline{X}) \in \mathbb {N}. \end{aligned}$$
    (13)

  • \(\bar{\mathcal {N}} = (\mathcal {N}_{M_n, \bar{k}_n})_{n=1}^{\infty }\) is a sequence of information vectors. For fixed \(n \in \mathbb {N},\) the vector \(\mathcal {N}_{M_n, \bar{k}_n}\) consists of the points in which the method \({\overline{X}_{M_n,\bar{k}_n}}\) evaluates the values of underlying (scalar) Wiener processes \(W_k,\) \(k=1,\ldots , M_n:\)

    $$\begin{aligned} \mathcal {N}_{M_n, \bar{k}_n} = \bigoplus _{k=1}^{M_n}\,\big [W_k(\bar{t}_{1,n}), W_k(\bar{t}_{2,n}),\ldots , W_k(\bar{t}_{\bar{k}_n,n})\big ]. \end{aligned}$$

  • \(\bar{M} = (M_n)_{n=1}^{\infty } \in \mathcal {G}_\delta \) with \(M_n\) indicating number of initial Wiener process coordinates used by the method \({\overline{X}_{M_n,\bar{k}_n}}, \,n \in {\mathbb N}\).

  • The method \({\overline{X}_{M_n,\bar{k}_n}}\) is assumed to evaluate W in the time points from \(\mathcal {N}_{M_n, \bar{k}_n},\) yielding a process \({\overline{X}_{M_n,\bar{k}_n}}(a,\sigma ,W)\) being an approximation of X. Namely, we assume the existence of Borel measurable mappings \(\bar{\phi } = (\phi _n)_{n=1}^\infty ,\) with \(\phi _n: \mathbb {R}^{\bar{k}_n \cdot M_n} \mapsto L^2([0,T]),\) such that

    $$\begin{aligned} \phi _n(\mathcal {N}_{M_n, \bar{k}_n}(W)) = {\overline{X}_{M_n,\bar{k}_n}}, \quad n \in \mathbb {N}. \end{aligned}$$

    Note that while discrete information about Wiener process is leveraged, the method may use e.g. interpolation techniques to yield a full approximate trajectory of the solution process.

The class of algorithms satisfying above conditions are denoted by \(\chi _{noneq}.\) In this paper, we distinguish a subclass \(\chi _{eq}\subset \chi _{noneq}\) of methods leveraging equidistant partitions

$$\begin{aligned} \chi _{eq} = \big \{\overline{X}\in \chi _{noneq}\,|\, \exists \,n_0 = n_0(\overline{X}): \forall \,n\ge n_0 \ \bar{\Delta }_n = \{jT/\bar{k}_n \ : \ j=0,1,\ldots , \bar{k}_n\}\big \}. \end{aligned}$$
(14)

The optimality in class of methods leveraging equidistant meshes for the global approximation problem in finite-dimensional model has been considered recently in, e.g., [11]. In this paper, we also show the benefit of leveraging adaptive meshes instead of equidistant ones.

The cost of the algorithm \({\overline{X}_{M_n,\bar{k}_n}}\) is defined as a number of evaluations of scalar Wiener processes performed by \({\overline{X}_{M_n,\bar{k}_n}}\). Specifically, we have

$${\text {cost}}({\overline{X}_{M_n,\bar{k}_n}}) = {\left\{ \begin{array}{ll} M_n \cdot \bar{k}_n, \quad \quad \text {when } \sigma \not \equiv 0, \\ 0, \quad \quad \quad \quad \ \ \text {when } \sigma \equiv 0. \end{array}\right. } $$

While in case of \(\sigma \equiv 0\), we actually deal with ordinary differential equations and still some calculations need to be performed, there is no W process involved. In our setting, this is justified by zero cost.

The global approximation error is measured in a product \(L^2(\Omega \times [0,T])\) norm

$$\begin{aligned} \big \Vert X - {\overline{X}_{M_n,\bar{k}_n}}\big \Vert _2 := \bigg (\mathbb {E}\int _{0}^T|X(t) - {\overline{X}_{M_n,\bar{k}_n}}(t)|^2 \,{\mathrm d}t\bigg )^{1/2}. \end{aligned}$$

For a fixed method \({\overline{X}_{M_n,\bar{k}_n}}=(\bar{\Delta }, \bar{\mathcal {N}}, \bar{M}, \bar{\phi }) \in \chi _{noneq}\setminus \chi _{eq},\) we define the sequence of augmented partitions \(\widetilde{\Delta } = (\widetilde{\Delta }_n)_{n=1}^\infty \) with

$$\begin{aligned} \widetilde{\Delta }_n := \bar{\Delta }_n \,\cup \, \Delta _{m_n}^{eq} , \quad n\in {\mathbb N}, \end{aligned}$$
(15)

where \(\bar{k}_n^{1/2}/ m_n \rightarrow 0\) and \(m_n/ \bar{k}_n \rightarrow 0,\) \(n\rightarrow +\infty ,\) and \(\Delta _{m_n}^{eq} = (t_j^{eq})_{j=0}^{m_n}\) is an equidistant partition, \(t_j^{eq} = Tj/m_n, \ j=0, \ldots , m_n.\) In the sequel, by \(\widetilde{k}_n\), we denote the number of distinct time points \(\widetilde{t}_{j,n}\) in \(\widetilde{\Delta }_n.\) Consequently, we get

$$\begin{aligned} \bar{k}_n \le \widetilde{k}_n \le \bar{k}_n + m_n -1, \end{aligned}$$

which in turn implies that

$$\begin{aligned} \lim _{n\rightarrow +\infty }\widetilde{k}_n / \bar{k}_n = 1. \end{aligned}$$
(16)

In addition, we introduce augmented information vectors \(\widetilde{\mathcal {N}} = (\widetilde{\mathcal {N}}_{M_n, \widetilde{k}_n}(W))_{n=1}^{\infty },\) where

$$\begin{aligned} \widetilde{\mathcal {N}}_{M_n, \widetilde{k}_n}(W) = \bigoplus _{k=1}^{M_n}\,\big [W_k(\widetilde{t}_{0,n}), W_k(\widetilde{t}_{1,n}),\ldots , W_k(\widetilde{t}_{\,\widetilde{k}_n,n})\big ]. \end{aligned}$$

For brevity, in the sequel, we will use the notation \(\Delta \widetilde{t}_{j,n} = \widetilde{t}_{j+1,n} - \widetilde{t}_{j,n}, \ n\in {\mathbb N}, \ j = 0,1,\ldots , \widetilde{k}_n-1.\)

Now for fixed \(n\in {\mathbb N}\), we estimate distance between truncated dimension time-continuous Euler process \(\widetilde{X}_{M_n,\widetilde{k}_n}^{E}\) based on partition \(\widetilde{\Delta }_{n}\) and the associated time-continuous conditional Euler process

$$X_{M_n, \widetilde{k}_n}^{cond}(t) = \mathbb {E}\big (\widetilde{X}_{M_n,\widetilde{k}_n}^{E}(t) \big |\,\widetilde{\mathcal {N}}_{M_n,\widetilde{k}_n}(W)\big ),$$

which leverages the augmented information \(\widetilde{\mathcal {N}}_{M_n, \widetilde{k}_n}(W).\) We refer to, e.g., [12] for more details on conditional Euler process in finite-dimensional setting when also jumps modelled by homogeneous Poisson process are considered.

We obtain

$$\begin{aligned} \begin{aligned} \big \Vert \widetilde{X}_{M_n,\widetilde{k}_n}^{E} - \mathbb {E}\big (\widetilde{X}_{M_n,\widetilde{k}_n}^{E} \big |\, \widetilde{\mathcal {N}}_{M_n,\widetilde{k}_n}(W)\big )\big \Vert _2^2&= \mathbb {E}\int _0^T\sum _{j=0}^{\widetilde{k}_n-1}\sum _{k=1}^{M_n} \bigg (W_k(t) - \mathbb {E}\big (W_k(t)\big |\,\widetilde{\mathcal {N}}_{M_n,\widetilde{k}_n}(W)\big )\bigg )^2 \\&\quad \quad \quad \times (\sigma _k(\widetilde{t}_{j,n}))^2\cdot \mathbbm {1}_{(\widetilde{t}_{j,n}, \widetilde{t}_{j+1,n}]}(t)\,{\mathrm d}t \\&= \sum _{j=0}^{\widetilde{k}_n -1} \int _{\widetilde{t}_{j,n}}^{\widetilde{t}_{j+1,n}}\sum _{k=1}^{M_n} (\sigma _k(\widetilde{t}_{j,n}))^2 \ \mathbb {E}\big (\hat{W}_{j,k,n}(t)\big )^2 \,{\mathrm d}t, \end{aligned} \end{aligned}$$
(17)

where \(\hat{W}_{j,k,n}\) is a Brownian bridge on the interval \([\widetilde{t}_{j,n}, \widetilde{t}_{j+1,n}],\) conditioned on \(W_k.\) For more details on Brownian bridge, we refer to e.g. [19]. Furthermore,

$$\begin{aligned} \begin{aligned} \big \Vert \widetilde{X}_{M_n,\widetilde{k}_n}^{E} - \mathbb {E}\big (\widetilde{X}_{M_n,\widetilde{k}_n}^{E} \big | \widetilde{\mathcal {N}}_{M_n,\widetilde{k}_n}(W)\big )\big \Vert _2^2&= \sum _{j=0}^{\widetilde{k}_n -1} \int _{\widetilde{t}_{j,n}}^{\widetilde{t}_{j+1,n}} \frac{(\widetilde{t}_{j+1,n}-t)(t-\widetilde{t}_{j,n})}{\Delta \widetilde{t}_{j,n}}\sum _{k=1}^{M_n} (\sigma _k(\widetilde{t}_{j,n}))^2 \,{\mathrm d}t \\&= \frac{1}{6}\sum _{j=0}^{\widetilde{k}_n-1}\Vert \sigma ^{M_n}(\widetilde{t}_{j,n})\Vert _{\ell ^2}^2(\Delta \widetilde{t}_{j,n})^2. \end{aligned} \end{aligned}$$
(18)

Combining Theorem 1 and the fact that \({\overline{X}_{M_n,\bar{k}_n}}\) is \(\sigma (\bar{\mathcal {N}}_{M_n,\bar{k}_n}(W))\)-measurable, we get

$$\begin{aligned} \begin{aligned} \big \Vert X - {\overline{X}_{M_n,\bar{k}_n}}\big \Vert _2&\ge \big \Vert {\overline{X}_{M_n,\bar{k}_n}}- \widetilde{X}_{M_n,\widetilde{k}_n}^{E}\big \Vert _2 - \big \Vert X - \widetilde{X}_{M_n,\widetilde{k}_n}^{E}\big \Vert _2 \\&\ge \big \Vert \widetilde{X}_{M_n,\widetilde{k}_n}^{E} - \mathbb {E}\big (\widetilde{X}_{M_n,\widetilde{k}_n}^{E} \big |\, \bar{\mathcal {N}}_{M_n,\bar{k}_n}(W)\big )\big \Vert _2 - D_1m_n^{-1} - D_2\delta (M_n). \end{aligned} \end{aligned}$$
(19)

Furthermore, (18), (19), and the relation \(\bar{\mathcal {N}}_{M_n,\bar{k}_n}(W) \subset \widetilde{\mathcal {N}}_{M_n,\widetilde{k}_n}(W)\) yield

$$\begin{aligned} \begin{aligned} \big \Vert X - {\overline{X}_{M_n,\bar{k}_n}}\big \Vert _2&\ge \big \Vert \widetilde{X}_{M_n,\widetilde{k}_n}^{E} - \mathbb {E}\big (\widetilde{X}_{M_n,\widetilde{k}_n}^{E} \big |\, \widetilde{\mathcal {N}}_{M_n,\widetilde{k}_n}(W)\big )\big \Vert _2 - D_1m_n^{-1} - D_2\delta \big (M_n\big ) \\&= \biggr (\frac{1}{6}\sum _{j=0}^{\widetilde{k}_n-1}\Vert \sigma ^{M_n}(\widetilde{t}_{j,n})\Vert _{\ell ^2}^2(\Delta \widetilde{t}_{j,n})^2\biggr )^{1/2} - D_1m_n^{-1} - D_2\delta \big (M_n\big ), \end{aligned} \end{aligned}$$
(20)

where both \(D_1, D_2\) do not depend on n (explicitly or implicitly via \(M_n\) or \(\bar{k}_n, \widetilde{k}_n\)). Hence, by (4), (13), (19), and the definition of \(m_n,\) we have

$$\begin{aligned} \liminf _{n \rightarrow \!+\!\infty } (M_n)^{-1/2}\big ({\text {cost}}({\overline{X}_{M_n,\bar{k}_n}})\big )^{1/2}\big \Vert X \!-\! {\overline{X}_{M_n,\bar{k}_n}}\big \Vert _2&\!\ge \! \liminf \limits _{n \rightarrow \!+\!\infty }\biggr (\frac{\bar{k}_n}{6}\sum _{j=0}^{\widetilde{k}_n \!-\!1}\Vert \sigma ^{M_n}(\widetilde{t}_{j,n})\Vert _{\ell ^2}^2 (\Delta \widetilde{t}_{j,n})^2\bigg )^{1/2}\nonumber \\&- \limsup \limits _{n\rightarrow +\infty }\,\bar{k}_n^{1/2}\big (D_1m_n^{-1} + D_2\,\delta (M_n)\big )\nonumber \\&\hspace{-0.5cm}= \liminf \limits _{n \rightarrow +\infty }\biggr (\frac{\bar{k}_n}{6}\sum _{j=0}^{\widetilde{k}_n -1}\Vert \sigma ^{M_n}(\widetilde{t}_{j,n})\Vert _{\ell ^2}^2 (\Delta \widetilde{t}_{j,n})^2\bigg )^{1/2}. \end{aligned}$$
(21)

By the Hölder inequality, we arrive at

$$\begin{aligned} \begin{aligned} \liminf \limits _{n \rightarrow +\infty }\biggr (\frac{\bar{k}_n}{6}\sum _{j=0}^{\widetilde{k}_n -1}\Vert \sigma ^{M_n}(\widetilde{t}_{j,n})\Vert _{\ell ^2}^2 (\Delta \widetilde{t}_{j,n})^2\bigg )^{1/2} \ge \liminf \limits _{n \rightarrow +\infty }\frac{1}{\sqrt{6}}\,\biggr (\frac{\bar{k}_n}{\widetilde{k}_n}\bigg )^{1/2}\,\sum _{j=0}^{\widetilde{k}_n -1}\Vert \sigma ^{M_n}(\widetilde{t}_{j,n})\Vert _{\ell ^2}\,\Delta \widetilde{t}_{j,n}. \end{aligned} \end{aligned}$$
(22)

Next, by Fact 2 in Appendix, (16), (21), and (22), we obtain

$$\begin{aligned} \begin{aligned} \liminf _{n \rightarrow +\infty } (M_n)^{-1/2}\big (\text {cost}({\overline{X}_{M_n,\bar{k}_n}})\big )^{1/2}\big \Vert X - {\overline{X}_{M_n,\bar{k}_n}}\big \Vert _2&\ge \frac{1}{\sqrt{6}}\int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}\,{\mathrm d}t. \end{aligned} \end{aligned}$$

Since

$$\begin{aligned} \liminf _{n \rightarrow +\infty } \frac{\big (\text {cost}({\overline{X}_{M_n,\bar{k}_n}})\big )^{1/2}\big \Vert X - {\overline{X}_{M_n,\bar{k}_n}}\big \Vert _2}{M_n^{1/2}\mathcal {C}_{noneq}} = \left( \limsup _{n \rightarrow +\infty } \frac{M_n^{1/2}\mathcal {C}_{noneq}}{\big (\text {cost}({\overline{X}_{M_n,\bar{k}_n}})\big )^{1/2}\big \Vert X - {\overline{X}_{M_n,\bar{k}_n}}\big \Vert _2}\right) ^{-1}, \end{aligned}$$

we finally get for all \({\overline{X}_{M_n,\bar{k}_n}}\in \chi _{noneq}\) that

$$\begin{aligned} \big (\text {cost}({\overline{X}_{M_n,\bar{k}_n}})\big )^{1/2}\,\big \Vert X - {\overline{X}_{M_n,\bar{k}_n}}\big \Vert _2 \gtrapprox M_n^{1/2}\,\mathcal {C}_{noneq}, \quad n\rightarrow +\infty . \end{aligned}$$
(23)

For \({\overline{X}_{M_n,\bar{k}_n}}\in \chi _{eq},\) the proof follows analogous steps, except for taking simply \(\widetilde{\Delta }_n = \bar{\Delta }_n\) in (15). Leveraging the fact that \(\Delta \widetilde{t}_{j,n} = \frac{T}{\bar{k}_n}, \ j=0,\ldots , \bar{k}_n -1,\) leads to

$$\begin{aligned} \begin{aligned} \liminf _{n \rightarrow \!+\!\infty } (M_n)^{-1/2}\big ({\text {cost}}({\overline{X}_{M_n,\bar{k}_n}})\big )^{1/2}\big \Vert X \!-\! {\overline{X}_{M_n,\bar{k}_n}}\big \Vert _2&\!\ge \! \liminf \limits _{n \rightarrow +\infty }\biggr (\frac{1}{6}\sum _{j=0}^{\widetilde{k}_n -1}\Vert \sigma ^{M_n}(\widetilde{t}_{j,n})\Vert _{\ell ^2}^2 \Delta \widetilde{t}_{j,n}\bigg )^{1/2}. \end{aligned} \end{aligned}$$
(24)

Consequently, (24) implies that for all \({\overline{X}_{M_n,\bar{k}_n}}\in \chi _{eq}\) it holds

$$\begin{aligned} \big (\text {cost}({\overline{X}_{M_n,\bar{k}_n}})\big )^{1/2}\,\big \Vert X - {\overline{X}_{M_n,\bar{k}_n}}\big \Vert _2 \gtrapprox M_n^{1/2}\,\mathcal {C}_{eq}, \quad n\rightarrow +\infty . \end{aligned}$$
(25)

Considering (23) and (25), we are ready to formulate the main result of this section.

Theorem 2

Let us denote by \(\chi _{noneq}^{\bar{M}}\subset \chi _{noneq}\) a set of all admissible methods with fixed truncation level sequence \(\bar{M}.\) We have the following asymptotic lower bound

$$\begin{aligned} \inf \limits _{\overline{X} \in \chi _{noneq}^{\bar{M}}}\big ({\text {cost}}({\overline{X}_{M_n,\bar{k}_n}})\big )^{1/2}\big \Vert X - {\overline{X}_{M_n,\bar{k}_n}}\big \Vert _2 \gtrapprox \frac{M_n^{1/2}}{\sqrt{6}}\int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}\,{\mathrm d}t. \end{aligned}$$
(26)

In particular, restriction to the subclass \(\chi _{eq}\) gives sharper asymptotic lower bound

$$\begin{aligned} \inf \limits _{\overline{X} \in \chi _{noneq}^{\bar{M}}\,\cap \,\chi _{eq}}\big ({\text {cost}}({\overline{X}_{M_n,\bar{k}_n}})\big )^{1/2}\big \Vert X - {\overline{X}_{M_n,\bar{k}_n}}\big \Vert _{2} \gtrapprox \sqrt{\frac{M_n T}{6}}\biggr (\int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}^2\,{\mathrm d}t \biggr )^{1/2}. \end{aligned}$$
(27)

Remark 4

The restriction (13) imposed on \(\bar{k}_n\) is not limiting, as the majority of algorithms used in practice leverage \(\mathcal {O}(n)\) nodes. We also stress that \(\overline{C}_1, \overline{C}_2,\) as well as the related sequence \(\bar{k}_n,\) depend on the method \(\overline{X}\) and need not be the same across all considered algorithms. Furthermore, we allow only discrete, finite-dimensional evaluations of W. Therefore, for all \(n\in \mathbb {N},\) the vector \(\mathcal {N}_{M_n, \bar{k}_n}\) is \(\sigma \big (W_1, W_2,\ldots ,W_{M_n}\big )\)-measurable. Moreover, different partitions among various coordinates of W are not permitted in our setting.

Remark 5

We stress that while the sequences \(\bar{\Delta }\) and \(\bar{\phi }\) might depend on \(a,\sigma ,\) they cannot base on the trajectory of W. The resulting information about Wiener process is then called non-adaptive, while the associated algorithms are referred to as path-independent. For path-dependent version of Euler algorithm in finite-dimensional setting, see, e.g., [20].

Remark 6

It should be noted that lower bounds in Theorem 2 diverge to infinity when \(n \rightarrow +\infty \) in both subclasses. This significantly differs from finite-dimensional case, when the truncation level sequence was bounded from above. That saying, when \(M_n \equiv 1,\) we have \(\Vert \sigma (t)\Vert _{\ell ^2}^2 = |\sigma _1(t)|^2\) for all \(t\in [0,T],\) and the asymptotic constant appearing in (26) is consistent with the result from Theorem 2 in [8].

Notably, for given sequence \(\overline{M},\) in Sect. 4.1 and Sect. 4.2, we construct algorithms which asymptotically attain lower bounds appearing in Theorem 2. Then, in Sect. 4.3, we discuss the existence of optimal algorithms in a class of methods taking into account all permitted truncation sequences \(\overline{M}.\)

4 Construction of asymptotically optimal methods

4.1 Optimal algorithm in class of methods \(\chi _{eq}^{\bar{M}}\)

First, we fix \(\bar{M} = (M_n^*)_{n=1}^{\infty }\) satisfying (4). Next, for any \(n \in \mathbb {N}\) let us denote by \(X_{M_n^*, n}^{Eq}\in \chi _{eq}\) the truncated dimension Euler method based on equidistant mesh \(\Delta ^{eq}_n: 0 = t_{0,n}^{eq}< \ldots <~t_{n,n}^{eq} =~T,\) where \(t_{j,n}^{eq} = \frac{Tj}{n}, \ j=0,1,\ldots , n.\) The scheme is defined as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} X_{M_n^*, n}^{Eq}(0) = x_0 \\ X_{M_n^*, n}^{Eq}(t) = X_{M_n^*, n}^{Eq}(t_{j,n}^{eq}) + a\big (t_{j,n}^{eq} , X_{M_n^*, n}^{Eq}(t_{j,n}^{eq})\big )(t_{j+1,n}^{eq} - t_{j,n}^{eq}) \\ \hspace{2.0cm} + \sigma ^{M_n^*}(t_{j,n}^{eq})\big (W(t_{j+1,n}^{eq}) - W(t_{j,n}^{eq})\big ), \quad \quad t \in [t_{j,n}, t_{j+1,n}], \ \ j=0,1,\ldots , n-1. \end{array}\right. } \end{aligned}$$
(28)

The outcome of the method is a stochastic process \(\big (X_{M_n^*, n}^{Eq*}(t)\big )_{t\in [0,T]}\) obtained by linear interpolation between two subsequent nodes \(t_{j,n}^{eq}\) and \(t_{j+1,n}^{eq},\) i.e.,

$$\begin{aligned} X_{M_n^*,n}^{Eq*}(t) = \frac{X_{M_n^*,n}^{Eq}(t_{j,n}^{eq})(t_{j+1,n}^{eq} - t) + X_{M_n^*,n}^{Eq}(t_{j+1,n}^{eq})(t - t_{j,n}^{eq})}{t_{j+1,n}^{eq} - t_{j,n}^{eq}}, \quad t\in \big [t_{j,n}^{eq}, t_{j+1,n}^{eq}\big ], \end{aligned}$$
(29)

\(j=0,1,\ldots , n-1.\) Let us also denote by \(\mathcal {N}_{M_n^*,n}^{eq}(W)\) the related information vector. In addition, by \(\widetilde{X}_{M_n^*,n}^{E,eq}\), we understand the truncated dimension time-continuous Euler process based on the mesh \(\Delta ^{eq}_n,\) \(n\in \mathbb {N}.\) Certainly, it holds

$$\begin{aligned} n^{1/2}\bigg |\big \Vert X - X_{M_n^*,n}^{Eq*}\big \Vert _2 - \big \Vert \widetilde{X}_{M_n^*,n}^{E,eq} - X_{M_n^*,n}^{Eq*}\big \Vert _2\bigg | \le n^{1/2}\, \big \Vert X - \widetilde{X}_{M_n^*,n}^{E,eq}\big \Vert _2. \end{aligned}$$
(30)

Consequently, from Theorem 1 and (30) it follows

$$\begin{aligned} \begin{aligned} n^{1/2}\bigg |\big \Vert X - X_{M_n^*,n}^{Eq*}\big \Vert _2 - \big \Vert \widetilde{X}_{M_n^*,n}^{E,eq} - X_{M_n^*,n}^{Eq*}\big \Vert _2\bigg | \le \frac{KT}{n^{1/2}} + Kn^{1/2}\delta (M_n^*). \end{aligned} \end{aligned}$$
(31)

Therefore, by repeating the reasoning as in (18) and the fact that

$$\begin{aligned} X_{M_n^*,n}^{Eq*} = \mathbb {E}\big (\widetilde{X}_{M_n^*,n}^{E,eq}\,|\,\mathcal {N}_{M_n^*,n}^{eq}(W)\big ), \end{aligned}$$

the inequality (31) implies

$$\begin{aligned} \begin{aligned} \lim \limits _{n\rightarrow +\infty }n^{1/2}\big \Vert X - X_{M_n^*,n}^{Eq*}\big \Vert _2&= \lim \limits _{n\rightarrow +\infty }n^{1/2}\big \Vert \widetilde{X}_{M_n^*,n}^{E,eq} - \mathbb {E}\big (\widetilde{X}_{M_n^*,n}^{E,eq}\,|\, \mathcal {N}_{M_n^*,n}^{eq}(W)\big )\big \Vert _2 \\&= \lim \limits _{n\rightarrow +\infty }\biggr (\frac{T}{6}\sum _{j=0}^{n -1}\Vert \sigma ^{M_n^*}(t_{j,n}^{eq})\Vert _{\ell ^2}^2 \,\frac{T}{n}\bigg )^{1/2} \\&= \sqrt{\frac{T}{6}}\biggr (\int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}^2\,{\mathrm d}t \biggr )^{1/2}. \end{aligned} \end{aligned}$$
(32)

Finally, by (32), we have

$$\begin{aligned} \big ({\text {cost}}(X_{M_n^*,n}^{Eq*})\big )^{1/2}\,\big \Vert X - X_{M_n^*,n}^{Eq*}\big \Vert _2 \approx \sqrt{\frac{M_n^*T}{6}}\biggr (\int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}^2\,{\mathrm d}t \biggr )^{1/2}, \end{aligned}$$
(33)

which establishes the lower bound in Theorem 2 for fixed class \(\chi _{eq}^{\bar{M}}\). Note that \(X_{M_n^*,n}^{Eq}\) is an implementable algorithm, and it does not require the knowledge of the trajectories of (truncated) Wiener process.

4.2 Optimal algorithm with adaptive path-independent step-size control in class \(\chi _{noneq}^{\bar{M}}\)

In this section, we construct an optimal method in class \(\chi _{noneq}^{\bar{M}}\) for fixed truncation level sequence \(\bar{M} = (M_n^*)_{n=1}^{\infty }\in \mathcal {G}_\delta \). To this end, we define truncated dimension Euler scheme \((X_{M_n^*,k_n^*}^{step})_{n=1}^{\infty }\) with adaptive path-independent step-size of the following form.

First, let \(\bar{\varepsilon } = (\varepsilon _n)_{n=1}^{\infty } \subset {\mathbb R}_+\) be a non-increasing sequence satisfying

$$\begin{aligned} \lim \limits _{n \rightarrow +\infty }\varepsilon _n = \lim \limits _{n \rightarrow +\infty }\frac{1}{n \,\varepsilon _n^2} = 0. \end{aligned}$$
(34)

We note that the second equality in (34) implies the existence of \(C_0 > 0 \) such that for all \(n\in \mathbb {N}\) it holds \(n\varepsilon _n^2 > C_0.\) Hence,

$$\begin{aligned} n\varepsilon _n \ge \sqrt{C_0}\,n^{1/2}, \ n\in \mathbb {N}. \end{aligned}$$
(35)

For fixed \(n \in \mathbb {N}\) the proposed scheme utilises step-size control with \(\hat{t}_{0,n}:= 0\) and

$$\begin{aligned} \hat{t}_{j+1,n} := \hat{t}_{j,n} + \frac{T}{n\max \{\varepsilon _n, \Vert \sigma ^{M_n^*}(\hat{t}_{j,n})\Vert _{\ell ^2}\}}, \quad j=0,1,\ldots , k_n^*-1, \end{aligned}$$
(36)

where \(k_n^* = \inf \{j \in \mathbb {N} \ | \ \hat{t}_{j,n} \ge T \},\) \(n\in \mathbb {N}.\) We will denote the corresponding mesh by \(\hat{\Delta }_n.\) Then, we set

$$\begin{aligned} {\left\{ \begin{array}{ll} X_{M_n^*,k_n^*}^{step}(0) = x_0 \\ X_{M_n^*,k_n^*}^{step}(\hat{t}_{j+1,n}) = X_{M_n^*,k_n^*}^{step}(\hat{t}_{j,n}) + a(\hat{t}_{j,n} , X_{M_n^*,k_n^*}^{step}(\hat{t}_{j,n}))(\hat{t}_{j+1,n} - \hat{t}_{j,n}) \\ \hspace{5.14cm}+ \ \sigma ^{M_n^*}(\hat{t}_{j,n})(W(\hat{t}_{j+1,n}) - W(\hat{t}_{j,n})), \ \ \\ \quad \quad \quad \quad j=0,1,\ldots , k_n^*-1. \end{array}\right. } \end{aligned}$$

In the sequel, we will use the notation \(\Delta ^*_n = \hat{\Delta }_n \setminus \{\hat{t}_{k_n^*,n}\} \cup \{T\}\) and \(t_{j,n}^* = \hat{t}_{j,n}, \ j=0,1,\ldots , k_n^*-1,\) \(t_{k_n^*,n}^*=T.\) The corresponding information vector will be denoted by \(\mathcal {N}_{M_n^*,k_n^*}^*(W).\) Also, by \(\Delta \hat{t}_{j,n},\) \(\Delta t_{j,n}^*\), we will understand the j–th time step for the discretisation \(\hat{\Delta }_{n}\) and \(\Delta _{n}^*,\) respectively.

The final process \(X^{*}_{M_n^*,k_n^*} = \big (X^{*}_{M_n^*,k_n^*}(t)\big )_{t\in [0,T]}\) approximating X is obtained by piecewise linear interpolation between \(X_{M_n^*,k_n^*}^{step}({t}_{j,n}^*)\) and \(X_{M_n^*,k_n^*}^{step}({t}_{j+1,n}^*).\) We recall that in our model (1), the process \(X^{*}_{M_n^*,k_n^*}\) coincides with the time-continuous conditional Euler process

$$\begin{aligned} \widetilde{X}_{M_n^*,k_n^*}^{cond*}(t) := \mathbb {E}\big (\,\widetilde{X}_{M_n^*,k_n^*}^{E}(t) \ | \ \mathcal {N}_{M_n^*,k_n^*}^*(W)\big ), \quad t\ \in [0,T], \end{aligned}$$
(37)

based on the sequence of partitions \(\Delta ^*_n.\)

Fact 1

 

  1. a)

    The proposed method \(X_{M_n^*,k_n^*}^{step}\) with adaptive step-size control is an element of \(\chi _{noneq}\) and attains point T,  irrespective of prior choice of the sequences \(\bar{M}\) and \(\bar{\varepsilon }.\)

  2. b)

    \(k_n^*\) is deterministic and \(\lim \limits _{n\rightarrow +\infty } k_n^*(\sigma ) = +\infty .\)

  3. c)

    \(\max \limits _{0\le j \le k_n^*-1} (t_{j+1,n}^* - t_{j,n}^*) \le \frac{T}{n\varepsilon _n} \rightarrow 0, \ \ n \rightarrow +\infty .\)

Proof

Since for every \(M,n \in \mathbb {N}\) and \(j = 0, \ldots , k_n^*\), we have

$$\begin{aligned} \Vert \sigma ^M (\hat{t}_{j,n})\Vert _{\ell ^2} \le C_2\delta (M) + \Vert \sigma (\hat{t}_{j,n}) - \sigma (\hat{t}_{0,n})\Vert _{\ell ^2} + \Vert \sigma (0)\Vert _{\ell ^2}\le C_2(\Vert \delta \Vert _{\ell ^\infty (\mathbb {R})} + T + 1) =: \hat{C} < +\infty , \end{aligned}$$

for \(n_0 = \lfloor n (\varepsilon _n + \hat{C})\rfloor + 1\) it holds \(\hat{t}_{n_0,n} \ge T.\) Combining this, (34), and (35), we have that \(n\varepsilon _n^2 \le n\varepsilon _n \le k_n^* \le n_0(n),\) \(n\in \mathbb {N}.\) This, together with the fact that \(n\varepsilon _n = o(n),\) proves both assertions a) and b).

Now, we investigate asymptotic behaviour of the method error. Let us denote

$$\begin{aligned} \widetilde{S}_{M_n^*,n}^{\,l} :=\sum _{j = 0}^{k_n^* - 1}\max \left\{ \varepsilon _n^l, \big \Vert \sigma ^{M_n^*}(t_{j,n}^*)\big \Vert _{\ell ^2}^{l}\right\} (t_{j+1,n}^* - t_{j,n}^*)^l, \quad l\in \{1,2\}, \end{aligned}$$
(38)

and

$$\begin{aligned} \hat{S}_{M_n^*,n}^{\,l} :=\sum _{j = 0}^{k_n^* - 1}\max \left\{ \varepsilon _n^l,\big \Vert \sigma ^{M_n^*}(\hat{t}_{j,n})\big \Vert _{\ell ^2}^l\right\} (\hat{t}_{j+1,n} - \hat{t}_{j,n})^l, \quad l \in \{1,2\}. \end{aligned}$$
(39)

By Fact 2, we get that

$$\begin{aligned} \left| \sum _{j = 0}^{k_n^* - 1} \big \Vert \sigma ^{M_n^*}(t_{j,n}^*)\big \Vert _{\ell ^2}\,\Delta t_{j,n}^* - \int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}\,\text {d}t\right| \le K_1 \left( \frac{T}{n\varepsilon _n} + \delta (M_n^*)\right) . \end{aligned}$$
(40)

Consequently, from (38), (40), and the fact that for all \(a,b \ge 0\)

$$\begin{aligned} \frac{a-b}{2} \le \max \{a,b\} - b \le a, \end{aligned}$$

we obtain

$$\begin{aligned} \begin{aligned} \biggr |\widetilde{S}_{M_n^*,n}^{\,1} - \int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}\,\text {d}t\biggr |&\le \biggr |\sum _{j=0}^{k_n^* - 1}\bigg (\max \left\{ \varepsilon _n,\big \Vert \sigma ^{M_n^*}(t_{j,n}^*)\big \Vert _{\ell ^2}\right\} - \big \Vert \sigma ^{M_n^*}(t_{j,n}^*)\big \Vert _{\ell ^2}\bigg )\,\Delta t_{j,n}^*\biggr | \\&\hspace{0.55cm}+ \biggr |\sum _{j = 0}^{k_n^* - 1} \big \Vert \sigma ^{M_n^*}(t_{j,n}^*)\big \Vert _{\ell ^2}\,\Delta t_{j,n}^* - \int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}\,\text {d}t\biggr | \\&\le \sum _{j=0}^{k_n^* - 1} \varepsilon _n \Delta t_{j,n}^* + K_1\left( \frac{T}{n\varepsilon _n} + \delta (M_n^*)\right) \\&\le K_2 \Big (\varepsilon _n + (n\varepsilon _n)^{-1} + \delta (M_n^*)\Big ). \end{aligned} \end{aligned}$$
(41)

Since from (38) and (39)

$$\begin{aligned}\Big |\widetilde{S}_{M_n^*,n}^{\,1} - \hat{S}_{M_n^*,n}^{\,1}\Big | = \max \left\{ \varepsilon _n, \big \Vert \sigma ^{M_n^*}(\hat{t}_{k_{n}^*-1,n})\big \Vert _{\ell ^2}\right\} \big (\hat{t}_{k_{n}^*,n} - T\big ) \le \frac{K_4}{n\varepsilon _n}, \end{aligned}$$

the inequality (41) implies

$$\begin{aligned} \biggr |\hat{S}_{M_n^*,n}^{\,1} - \int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}\,\text {d}t\,\biggr | \le K_5\Big (\varepsilon _n + (n\varepsilon _n)^{-1} + \delta (M_n^*)\Big ). \end{aligned}$$
(42)

Also, note that (36) results in

$$\begin{aligned} \hat{S}_{M_n^*,n}^{\,l} = \sum _{j = 0}^{k_n^* - 1}\left( \frac{T}{n}\right) ^l = k_n^*\left( \frac{T}{n}\right) ^l, \quad l \in \{1,2\}. \end{aligned}$$
(43)

Consequently, since \(k_n^* = \mathcal {O}(n)\) by Fact 1, from (43) it follows

$$\begin{aligned} \hat{S}_{M_n^*,n}^{\,l} \le \tilde{C}, \quad n\in \mathbb {N}, \ l=1,2, \end{aligned}$$
(44)

for some \(\tilde{C}>0.\) Consequently, (42) together with (43) yield

$$\begin{aligned} \biggr |\frac{k_n^*\,T}{n} - \int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}\,\text {d}t\,\biggr | \le K_5\Big (\varepsilon _n + (n\varepsilon _n)^{-1} + \delta (M_n^*)\Big ). \end{aligned}$$
(45)

Furthermore, by (43) and (45), we arrive at

$$\begin{aligned} \begin{aligned} \biggr |k_n^*\,\hat{S}_{M_n^*,n}^{\,2} - \left( \int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}\,\text {d}t\right) ^2 \biggr |&\le \, \biggr |\hat{S}_{M_n^*,n}^{\,1} + \int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}\,\text {d}t\,\biggr | \times K_5\Big (\varepsilon _n + (n\varepsilon _n)^{-1} + \delta (M_n^*)\Big ) \\&\le K_6\Big (\varepsilon _n + (n\varepsilon _n)^{-1} + \delta (M_n^*)\Big ), \end{aligned} \end{aligned}$$
(46)

where \(K_6\) does not depend on n on the virtue of (44). Since \(t_{k_n^*,n}^* = T,\) we also have

$$\begin{aligned} \begin{aligned} \Big |k_n^* \hat{S}_{M_n^*,n}^{\,2} - k_n^* \widetilde{S}_{M_n^*,n}^{\,2}\Big |&= k_n^* \max \left\{ \varepsilon _n^2, \big \Vert \sigma ^{M_n^*}(\hat{t}_{k_n^*-1,n})\big \Vert _{\ell ^2}^{2}\right\} \Big ((\hat{t}_{k_n^*,n} - \hat{t}_{k_n^*-1,n})^2 - (T - t_{k_n^*-1,n}^*)^2\Big ) \\&\le 2k_n^* \max \left\{ \varepsilon _n^2, \big \Vert \sigma ^{M_n^*}(\hat{t}_{k_n^*-1,n})\big \Vert _{\ell ^2}^{2}\right\} \big (\hat{t}_{k_n^*,n} - \hat{t}_{k_n^*-1,n}\big )^2. \end{aligned} \end{aligned}$$
(47)

By (46), (47), and Fact 1, we obtain

$$\begin{aligned} \Big |k_n^* \hat{S}_{M_n^*,n}^{\,2} - k_n^* \widetilde{S}_{M_n^*,n}^{\,2}\Big | \le K_7 \frac{k_n^*}{(n\varepsilon _n)^2} = K_7 \frac{k_n^*}{n}\,\frac{1}{n\varepsilon _n^2}\le K_8 (n\varepsilon _n^2)^{-1}. \end{aligned}$$
(48)

Combining (46) and (48) results in

$$\begin{aligned} \begin{aligned} \biggr |k_n^*\,\widetilde{S}_{M_n^*,n}^{\,2} - \left( \int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}\,\text {d}t\right) ^2\biggr |&\le K_6\Big (\varepsilon _n + (n\varepsilon _n)^{-1} + \delta (M_n^*)\Big ) + K_8 (n\varepsilon _n^2)^{-1} \\&\le K_9\Big (\varepsilon _n + (n\varepsilon _n^2)^{-1} + \delta (M_n^*)\Big ). \end{aligned} \end{aligned}$$
(49)

On the other hand, by Theorem 1, Fact 1, and (37), we have

$$\begin{aligned} (k_n^*)^{1/2}\bigg |\big \Vert X - X_{M_n^*, k_n^*}^* \big \Vert _2 - \big \Vert \widetilde{X}_{M_n^*, k_n^*}^E- & {} \mathbb {E}\big (\widetilde{X}_{M_n^*, k_n^*}^E \big | \mathcal {N}_{M_n^*, k_n^*}^*(W)\big )\big \Vert _2 \bigg |\nonumber \\\le & {} (k_n^*)^{1/2}\,\big \Vert X - \widetilde{X}_{M_n^*, k_n^*}^E\big \Vert _2\nonumber \\\le & {} K_{10}\Big ((n\varepsilon _n^2)^{-1/2} + (k_n^*)^{1/2}\delta (M_n^*)\Big ), \end{aligned}$$
(50)

for some \(K_{10}>0\) which depends only on the constants \(C_1, C_2, T.\)

Therefore, from (4), (34), and (50) it follows

$$\begin{aligned} \lim \limits _{n\rightarrow +\infty } (k_n^*)^{1/2}\,\big \Vert X - X_{M_n^*, k_n^*}^* \big \Vert _2 = \lim \limits _{n\rightarrow +\infty }(k_n^*)^{1/2}\,\big \Vert \widetilde{X}_{M_n^*, k_n^*}^E - \mathbb {E}\big (\widetilde{X}_{M_n^*, k_n^*}^E \big | \mathcal {N}_{M_n^*, k_n^*}^*(W)\big )\big \Vert _2. \end{aligned}$$
(51)

Rewriting (51) analogously as in (17) and (18), we conclude that (49) and (51) imply

$$\begin{aligned} \lim \limits _{n\rightarrow +\infty } (k_n^*)^{1/2}\,\big \Vert X - X_{M_n^*, k_n^*}^* \big \Vert _2 = \lim \limits _{n\rightarrow +\infty } \biggr (\frac{k_n^*}{6}\,\tilde{S}^2_{M_n^*,n}\biggr )^{1/2} = \mathcal {C}_{noneq}. \end{aligned}$$
(52)

Hence, (52) yields

$$\begin{aligned}\big ({\text {cost}}(X^{step}_{M_n^*,k_n^*})\big )^{1/2}\,\big \Vert X - X^{*}_{M_n^*,k_n^*}\big \Vert _2 \approx (M_n^*)^{1/2}\,\mathcal {C}_{noneq}, \quad n\rightarrow +\infty , \end{aligned}$$

which establishes lower bound in (26) for class \(\chi _{noneq}^{\bar{M}}.\)

4.3 Asymptotically (almost) optimal algorithms for classes \(\chi _{eq}, \chi _{noneq}\)

In this subsection, we extend optimality results obtained for fixed truncation level sequences \(\bar{M}\) to the general classes of considered methods \(\chi _{eq}, \chi _{noneq}\). Our final conclusions are gathered in Theorem 3.

Theorem 3

Let \(a,\sigma \) satisfy conditions (A1)-(A4) and (S1)-(S3) with sequence \(\delta \), respectively. Let also \(\diamond \in \{noneq, eq\}.\) Then, for every method \(\bar{X}=({\overline{X}_{M_n,\bar{k}_n}})_{n=1}^{\infty } \in \chi _{\diamond }\), we have

$$\begin{aligned} \big ({\text {cost}}({\overline{X}_{M_n,\bar{k}_n}})\big )^{1/2}\,\big \Vert X - {\overline{X}_{M_n,\bar{k}_n}}\big \Vert _2 \,\gtrapprox \,\big (\delta ^{-1}(n^{-1/2})\big )^{1/2}\,\mathcal {C}_{\diamond }, \quad n\rightarrow +\infty . \end{aligned}$$
(53)

Moreover, for every truncation level sequence \(M_n\) with \(\delta ^{-1}(n^{-1/2})=o(M_n), \ n\rightarrow +\infty ,\) there exists a sequence \(M^* = (M^*_n)_{n=1}^{\infty }\in \mathcal {G}_{\delta }\) such that \(M_n^* = o (M_n), \ n\rightarrow +\infty ,\) and

(a) the truncated-dimension Euler algorithm with adaptive path-independent step-size \(X^{*} = \big (X^*_{M_n^*, k_n^*}\big )_{n=1}^{\infty }\in \chi _{noneq}\) satisfying

$$\begin{aligned} \big ({\text {cost}}(X_{M_n^*,k_n^*}^*)\big )^{1/2}\big \Vert X - X_{M_n^*,k_n^*}^*\big \Vert _2 \,\lessapprox \,\sqrt{\frac{M_n^*}{6}}\,\int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}\,\,{\mathrm d}t, \quad n\rightarrow +\infty ; \end{aligned}$$
(54)

(b) the truncated-dimension Euler algorithm \(X^{Eq*} = \big (X^{Eq*}_{M_n^*, n}\big )_{n=1}^{\infty }\in \chi _{eq},\) based on the sequence of equidistant meshes, and satisfying

$$\begin{aligned} \big ({\text {cost}}(X^{Eq*}_{M_n^*, n})\big )^{1/2}\big \Vert X - X^{Eq*}_{M_n^*, n}\big \Vert _2 \,\lessapprox \,\sqrt{\frac{M_n^* T}{6}}\,\left( \int _{0}^T \Vert \sigma (t)\Vert _{\ell ^2}^2\,\,{\mathrm d}t\right) ^{1/2}, \quad n\rightarrow +\infty . \end{aligned}$$
(55)

Proof

First, we note that (4) and monotonicity of \(\delta ^{-1}\) imply that for every admissible truncation level sequence \(\bar{M} = (M_n)_{n=1}^{\infty }\in \mathcal {G}_{\delta }\) it holds \(M_n \gtrapprox \delta ^{-1}\big (n^{-1/2}\big )\). This in turn implies that (53) is satified for every \(\bar{M}\) and method \(\overline{X}_{M_n, n}\) in \(\chi _{noneq}\) and \(\chi _{eq},\) respectively.

However, the lower bound in (53) cannot be asymptotically attained by any algorithm. Otherwise, the truncation level would satisfy \(M_n \approx \delta ^{-1}(n^{-1/2}),\) which in turn would violate the property (4). Nevertheless, for every sequence \(\bar{M}:=(M_n)_{n=1}^{\infty }\in \mathcal {G}_\delta \) there exists a constant \(k_0^{\bar{M}} = k_0(\bar{M}) \in \mathbb {N}\) such that for every \(k\ge k_0^{\bar{M}}\), we have

$$\begin{aligned} M_n \gtrapprox \,M_n\big (\log (\ldots \log (\log (n))\ldots )\big )^{-1}, \quad n \rightarrow +\infty , \end{aligned}$$
(56)

and both sequences in (56) belong to \(\mathcal {G}_\delta ,\) with natural logarithm being composed k-times. For fixed k,  denote the sequence on the right side of (56) by \(\bar{M}^k=(\bar{M}^k_n)_{n=1}^{\infty },\) and the output of an optimal method \((X^{*,k}_{\diamond }) = \big (X^{*,k}_{\diamond }(t)\big )_{t\in [0,T]}\) in corresponding class \(\chi _{\diamond }^{\bar{M}^{k}}, \ \diamond \in \{eq, noneq\},\) respectively. For every \(k\in \mathbb {N},\) \(X^{*,k}_{eq}\) is a truncated dimension Euler scheme based on equidistant mesh, while \(X^{*,k}_{noneq}\) is a truncated dimension Euler scheme with adaptive path-independent step-size control (36).

As a result, we have the following relation between the exact asymptotic behaviour of the method errors

$$\begin{aligned} \begin{aligned} \big ({\text {cost}}({\overline{X}_{M_n,\bar{k}_n}})\big )^{1/2}\,\big \Vert X - {\overline{X}_{M_n,\bar{k}_n}}\big \Vert _2&\gtrapprox \,\big (\bar{M}^k_n\big )^{1/2}\,\mathcal {C}_{\diamond }\\&\approx \big ({\text {cost}}(X^{*,k}_{\diamond })\big )^{1/2}\,\big \Vert X - X^{*,k}_{\diamond }\big \Vert _2, \quad k\ge k_0^{\bar{M}}, \quad n\rightarrow +\infty , \end{aligned} \end{aligned}$$

holding for all \({\overline{X}_{M_n,\bar{k}_n}}\in \chi _{\diamond }^{\bar{M}}.\) Since the constructed sequence satisfies \(\bar{M}^k_n = o(M_n), \ n\rightarrow +\infty , \) this concludes the proof. \(\square \)

Remark 7

Due to leveraging the alternative truncation sequence as per (56), the asymptotic benefit is at least of order \(\left( M_n / \bar{M}^k_n\right) ^{1/2},\) which is unbounded and diverges to infinity, as \(n\rightarrow +\infty \). In particular, this ratio can be significant also for smaller values of n,  especially for sequences \(\delta \) converging relatively slowly to zero.

Remark 8

In class \(\chi _{noneq}\), we consider only algorithms which are non-adaptive with respect to the number of leveraged Wiener process coordinates. In particular, this results in lower bound for cost times error terms in (26), (27) diverge to infinity, as the cost rises. On the other hand, this is not the case for finite-dimensional noise structure, see, e.g., [12, 20]. We conjecture that this term can be significantly lowered when additional adaptation with respect to Wiener process coordinates is introduced. We plan to investigate such algorithms in our future work.

5 Numerical experiments and implementation issues in Python

5.1 Solver implementation in Numba

In this section, we exhibit alternative implementation of \(X_{M_n^*,k_n^*}^{step},\) which leverages Numba compiler in Python. This enables us to execute specified functions, called kernels, on the GPU (Graphics Processing Unit) device which supports CUDA API developed by NVIDIA. For more details on parallel computing and kernel execution for a specified grid of blocks and threads, we refer to [10, 23]. Due to the fact that truncated dimension Euler scheme can be executed independently on each thread, we would expect significant decrease of the computation time when compared to the similar calculations on CPU (Central Processing Unit). This is beneficial especially when large number of the trajectories should be simulated.

The crucial part of the code responsible for the algorithm \(X_{M_n^*,k_n^*}^{step}\) execution on GPU, together with relevant comments, can be found in the listing below.

figure a

5.2 Results of numerical experiments in Python

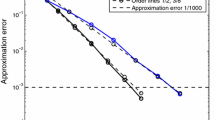
In this section, we present results of numerical experiments performed on CPU by using Multiprocessing library in Python programming language. We analyse the asymptotic error behaviour for both algorithms \(X_{M_n^*,k_n^*}^{step}\) and \(X_{M_n^*,n}^{Eq}\) by verifying if the ratio between constants \(\mathcal {C}_{noneq}\) and \(\mathcal {C}_{eq},\) appearing in Theorem 2, is attained.

To this end, we consider the following parameters: \(T =1.5, \ x_0 = 0.9,\) and the equation coefficients

$$\begin{aligned} a(t,x) = (t+2)(x-1), \quad t\in [0,T], \ x\in \mathbb {R}, \end{aligned}$$
(57)
$$\begin{aligned} \sigma _k(t) = \frac{e^{2t} + 2}{(k+1)^{p}\sqrt{\log (k+1)}}\quad t\in [0,T], \ k = 1,2,\ldots , \end{aligned}$$
(58)

where \(p>1/2.\) One can show that for all \(l\in \mathbb {N}, \ l > 1\) it holds

$$\begin{aligned} \Vert \sigma (t) - P_l(t)\Vert _{\ell ^2}^2 = \left| \sum _{k=l}^{+\infty } \frac{(e^{2t}+ 2)^2}{(k+1)^{2p}\log (k+1)}\right| \le (e^{2T} + 2)^2\left| \int \limits _{l}^{+\infty }\frac{1}{(x+1)^{2p}\log (x+1)}\,{\mathrm d}x\right| . \end{aligned}$$

By substituting \(v = (2p-1)\log (x+1),\) we arrive at

$$\begin{aligned} \Vert \sigma (t) - P_l(t)\Vert _{\ell ^2}^2 \le (e^{2T} + 2)^2\left| \,\int \limits _{(2p-1)\log (l+1)}^{+\infty }e^{-v}\,v^{-1}\,{\mathrm d}v\right| , \end{aligned}$$
(59)

and the integral appearing in (59) is equal to the upper incomplete gamma function \(\Gamma \big (1, (2p-1)\log (l+1)\big ).\) Since for all \(s\in \mathbb {N}, x>0\), we have

$$\begin{aligned} \Gamma (s,x) = (s-1)!\,\,e^{-x}\sum _{k=0}^{s-1}\frac{x^k}{k!}, \end{aligned}$$
(60)

combining (59) and (60) yields

$$\begin{aligned} \Vert \sigma (t) - P_l(t)\Vert _{\ell ^2} \le (e^{2T} + 2)e^{-0.5(2p-1)\log (l+1)} = (e^{2T} + 2)\big (l+1\big )^{1/2-p}. \end{aligned}$$

Therefore, we can assume \(\delta (n) \approx n^{1/2-p},\) which implies \(\delta ^{-1}(n^{-1/2})\approx n^{\frac{1}{2p-1}}.\) In our simulations, we set \(p = 0.9,\) hence \(M_n \gtrapprox n^{5/4 + \varepsilon }\in \mathcal {G}_\delta \) for all \(\varepsilon > 0.\) We decide to choose \(\varepsilon = 0.03.\) Consequently, it suffices to take \(M_n = \Theta (n^{1.28}),\) \(n \rightarrow +\infty \).

Now, we provide the values of the constants \(\mathcal {C}_{noneq}\) and \(\mathcal {C}_{eq}\) in our model. First, for all \(t\in [0,T]\), we have that

$$\Vert \sigma (t)\Vert _{\ell ^2} = \gamma (e^{2t} + 2)\quad \text {with}\quad \gamma = 0.75638883...$$

Finally, the constant appearing in lower bounds for \(\chi _{eq}\) is equal to

$$\begin{aligned} \sqrt{\frac{T}{6}}\big (0.25e^{4T} + 2e^{2T} - 9/4 + 4T\big )^{1/2}\gamma = 4.55058060..., \end{aligned}$$

while in \(\chi _{noneq}\)

$$\begin{aligned} \sqrt{\frac{1}{6}}\big (0.5e^{2T} - 0.5 + 2T\big )\gamma = 3.87313729... . \end{aligned}$$

While the analytical form of the unique solution to the Eq. (1) with coefficients as per (57) and (58) is not known, generation of its trajectories requires simulation of underlying stochastic integrals. Therefore for each \(X^{alg}\in \{X_{M_n^*,k_n^*}^{Eq*}, X_{M_n^*,k_n^*}^{step}\}\), we execute in parallel the algorithm \(X_{W_{ratio}\cdot M_n^*,n^*}^{Eq*}\) based on equidistant mesh with \(n^* = 10^6\) nodes and first \(W_{ratio}\cdot M_n^*\) coordinates of the countably dimensional Wiener process W. Let us denote the corresponding process by \(X_{M_n^*,n^*}.\) The method error, \(\text {err}_K(X^{alg}),\) is estimated by simulating K trajectories of the underlying processes. We measure the difference between each pair of trajectories by using the composite Simpson quadrature Q based on time points for which \(X^{alg}\) is evaluated, together with the midpoints of the corresponding subintervals. To summarise, we take

$$\begin{aligned} \text {err}_K(X^{alg}) := \biggr (\frac{1}{K}\sum _{l=1}^{K}Q\Big (|X^{alg}_l(a,b,W^{(l)}) - X_{W_{ratio} M_n^*,n^*,l}\,(a,b,W^{(l)})|^2\Big )\biggr )^{1/2}, \end{aligned}$$
(61)

where \(X^{alg}_l,\) \(X_{W_{ratio}\cdot M_n^*,n^*,l},\) and \(W^{(l)}\) are the l–th generated trajectories of the corresponding processes. Finally, we compare empirical improvement ratio \(\text {err}_K(X_{M_n^*,k_n^*}^{step}) /\) \(\text {err}_K(X_{M_n^*,k_n^*}^{Eq*})\) with the theoretical value \(\mathcal {C}_{noneq} / \mathcal {C}_{eq} \simeq 0.85113723.\) The testing results are exhibited in Table 1.

Table 1 Simulation results for \(X_{M_n^*,n}^{Eq*}\) and \(X_{M_n^*,k_n^*}^{step}\)
Full size table

The average improvement from leveraging adaptive mesh is generally visible. For \(n\in \{5000,10,000\}\), we executed smaller number of trajectories due to high complexity and time consumption. We also note that the impact of leveraging (61), Monte Carlo simulation, and rare-fine mesh comparison as an approximation of the method error is not quantified. Nevertheless, the obtained ratios are roughly aligned with the expected asymptotic error behaviour.

6 Conclusions

We investigated the global approximation of SDEs driven by countably dimensional Wiener process, where the diffusion term depends only on the time variable. For fixed sequence \(\delta ,\) modelling level of decay for the diffusion term, we derived lower bounds for asymptotic error in suitable classes of algorithms leveraging specified truncation levels of the Wiener process. In particular, we quantified asymptotic benefit from leveraging step-size control instead of equidistant mesh. We also constructed two truncated dimension Euler schemes which are the (almost) optimal algorithms in the respective classes. Our results indicate that the decrease of method error requires significant increase of the cost term, which is illustrated by the product of cost and minimal error diverging to infinity. Nonetheless, we conjecture that the estimates might be beaten in case we allow for additional adaptation with respect to different Wiener process coordinates.