1 Introduction

The Black-Scholes (BS) or Black-Scholes-Merton (BSM) model for option pricing [1, 2] has two common expressions as a stochastic differential equation (SDE) or a partial differential equation (PDE). In this work, we concentrate on the PDE expression of the BS model, namely:

$$\begin{aligned} \frac{\partial V(S,\tau )}{\partial \tau } + \frac{1}{2}\sigma ^2S^2\frac{\partial ^2 V(S,\tau )}{\partial S^2}+rS\frac{\partial V(S,\tau )}{\partial S}-rV(S,\tau )=0 \end{aligned}$$
(1)

where \(V(S,\tau )\) denotes the option value at time \(\tau \) and at asset price S; \(\sigma \) and r represent the volatility and risk-free interest, respectively. The above equation can be used to describe the valuation of European call or put options in terms of different parameters. The traditional BS model imposes strict assumptions and this leads to inadequacy in describing complex financial processes in real markets. For example, it is assumed that the market is frictionless, complete and liquid, but financial assets incur transaction costs from securities trading. Therefore, the BS equation has been modified to relax some of the assumptions, resulting in, for example, jump-diffusion models [3, 4], stochastic volatility models [5, 6], models with transactions costs [7,8,9], stochastic interest models [10, 11] and regime-switching models [12, 13].

These models use standard integer-order derivatives, which can only capture localised information of a function at a particular point and time. Due to the appearance of heavy tails and long memory (or long-range dependence) in stock returns, these equations may underestimate the large price changes in market turbulence. A remedy is to employ a fractional operator, which is known to be global and incorporate memory, meaning that the solution of the equation involves previous time steps as well as the current time step. Many fractional BS equations have been proposed in the literature. Wyss [14] derived a BS equation with a time-fractional derivative. Chen et al. [15] modified a time-fractional BS model for double-barrier options. Two fractional BS equations were proposed by using the Taylor series of fractional order [16]. Prathumwan and Trachoo [17] studied a two-dimensional BS equation for a European put option and derived its analytic solution by the Laplace homotopy perturbation method. Chen and Wang [18] developed a two-dimensional space-fractional BS model governing two-asset option pricing.

Analytical and numerical solutions for fractional BS models have been investigated. Kumar et al. [19] used the homotopy perturbation method and analysis method for the TFBS model. Chen et al. [15] derived an analytical solution of a modified BS equation with a spatial-fractional derivative. Chen et al. [20] proposed a predictor-corrector method based on the spectral collocation method to price American options. Golbabai et al. [21] used the radial basis functions for spatial approximation to deal with the TFBS equation. Zhang et al. [22] derived an implicit discrete scheme with a temporal accuracy of order (\(2-\alpha \)) and spatial accuracy of second order for solving the fractional BS model. Huang et al. [23] developed an adaptive moving mesh approach and carried out error analysis for the proposed scheme for the TFBS model.

For most fractional PDEs, it is not feasible to obtain their analytical form. A common method for approximation of the Caputo derivative is the L1 method with order (\(2-\alpha \)) where piecewise linear interpolating polynomials are used to replace the integrand in the fractional derivative [24, 25]. Several analogs of the Caputo approximation were proposed to achieve higher orders. Gao et al. [26] developed an L1-2 formula to approximate the time-fractional sub-diffusion equations and fractional ordinary differential equations. An L2 scheme with order (\(3-\alpha \)) was constructed by using piecewise quadratic interpolating polynomials [27, 28]. The L2-1\(_\sigma \) method was introduced to approximate the Caputo fractional derivative at a special point; this method can achieve an accuracy of \(\mathcal {O}(3-\alpha )\) [29].

These numerical methods were proposed to obtain the solutions of fractional BS models which is a forward problem. However, the option prices that can be obtained from financial markets are the solutions of many generalised BS equations, and some parameters such as volatility and fractional order are unknown. Therefore, it is necessary to investigate these unknown parameters in order to make the theory into practice, and the process of which is named as an inverse problem. For the BS model, Bayram et al. [30] employed a non-parametric estimation method and maximum likelihood to estimate its parameters. Ota et al. [31] used a Bayesian inference approach to solve an inverse problem of option pricing in the extended BS model. Riane and David [32] considered an inverse BS problem by using a gradient algorithm. In addition, the inverse problems of fractional-order models have been investigated in recent years. Cheng et al. [33] showed the uniqueness of an inverse problem for a one-dimensional fractional diffusion equation. Jin and Rundell [34] used the Mittag-Leffler function and singular value decomposition to examine the degree of ill-posedness of several traditional inverse problems. The MH-NMSS-PSO method was developed and used to solve the inverse problem of fractional dynamical models in biological systems [35, 36]. Fan et al. [37] used the MH-NMSS-PSO algorithm to estimate the parameters for fractional differential equations. Qin et al. [38] solved the multi-term time-fractional Bloch equations for anomalous relaxation processes in human tissue. Li et al. [39] considered a multi-term fractional dynamical epidemic model of dengue fever.

This paper considers a fractional version of the Black-Scholes equation in which the integer-order derivative \(\frac{\partial V}{\partial \tau }\) is replaced by the Caputo fractional derivative \(\frac{\partial ^\alpha V}{\partial \tau ^\alpha }\). The fractional order \(\alpha \) is a key parameter of the TFBS equation, which indicates the long-range dependence property of the solution of the model. To our knowledge, there are many papers discussing developing analytical or numerical methods for solving fractional BS equations. However, the study of investigating the meaning of \(\alpha \) of the TFBS model has not been examined. As a huge amount of options are traded in the market nowadays, how to choose a value of \(\alpha \) under different financial environments is necessary to be studied. Therefore, this paper will estimate \(\alpha \) by using S &P 500 index options data and explore its empirical implications.

This work contributes three main aspects. First, we employ the L2 scheme with an accuracy of \(\mathcal {O}(\tau ^{3-\alpha })\) for approximating the Caputo fractional derivative. This high-order scheme is used to reduce approximation errors in order to obtain more accurate theoretical values of option price. We present stability and convergence analyses as measures to confirm the efficiency and accuracy of the proposed scheme, and present a numerical example to show the maximum errors and convergence order of L2 scheme.

Secondly, this work focuses on exploring the underlying meanings of the fractional order \(\alpha \) of the TFBS model. First, we classify the market conditions into three periods: one stable period and two unstable periods (the Covid-19 economic downturn in 2020 and the global financial crisis in 2008). Then we obtain and analyse the estimated \(\alpha \) of the TFBS equation under different periods by using the S &P 500 monthly and weekly options and discuss our empirical results in three cases. We also compare the mean squared errors (MSEs) of both the TFBS model and the BS model with respect to different strike prices of options on the same expiration date in order to illustrate that the TFBS equation is able to fit the data well under extreme economic conditions. From the empirical experiments, we conclude that the fractional order \(\alpha \) may be seen as an indicator to describe large fluctuations of stock price or even financial markets. This work may provide a general framework for the application of fractional-order option pricing models to fit and interpret real option pricing data.

Thirdly, we find an interesting empirical relation involving \(\alpha \) and implied volatility \(\sigma \) of both the TFBS equation and the BS equation. We introduce the functional parameter \(\rho \) in order to balance the units of the TFBS equation (more details in the next section). Under the assumption of \(\rho =1\), \(\alpha \) is approximately related to the ratio of volatility \(\sigma _F\) of the TFBS model and volatility \(\sigma _{BS}\) of the BS model. We discuss this empirical relation in three angles and hope to provide insights for future research.

The paper is structured as follows. Section 2 presents the TFBS model. The numerical scheme for the TFBS model is proposed in Section 3. Then in Section 4, we carry out the solvability, stability and convergence analyses of the proposed scheme. Section 5 reviews the methodology of the MH-NMSS-PSO algorithm. In Section 6, the empirical results are summarised in four empirical cases and one discussion. Section 7 draws some conclusions on the work.

2 Model description

In this paper, we consider the following time-fractional Black-Scholes model:

$$\begin{aligned} \begin{aligned}&\frac{\partial ^\alpha V(S,\tau )}{\partial \tau ^\alpha } + \frac{1}{2}\sigma ^2 S^2 \frac{\partial ^2 V(S,\tau )}{\partial S^2} + rS \frac{\partial V(S,\tau )}{\partial S} - r V(S,\tau )=0, \\&(S,\tau )\in (S_L,S_R) \times (0,T), \end{aligned} \end{aligned}$$
(2)

subject to the boundary conditions

$$\begin{aligned} V(S_L,\tau )=p(\tau ),\ V(S_R,\tau )=q(\tau ),\end{aligned}$$

and the terminal condition

$$\begin{aligned} V(S,T)=\textrm{Payoff}(S), \end{aligned}$$

where \(V(S,\tau )\) denotes the price of a European option for stock price S at time \(\tau \), and \(\sigma \) represents the volatility of the returns from the underlying asset. r denotes the risk-free rate and T is the maturity date of the contract. \(\frac{\partial ^{\alpha }V(S,\tau )}{\partial \tau ^{\alpha }}\) represents the Caputo derivative. By changing \(x=\textrm{ln}S\) and \(t=T-\tau \), \(u(x,t)=V(S,T-\tau )\), the model (2) can be changed into:

$$\begin{aligned} \left\{ \begin{aligned}&_0 ^C D_t^{\alpha } u(x,t) = \mu \frac{\partial ^2 u(x,t)}{\partial x^2} + \lambda \frac{\partial u(x,t)}{\partial x} - r u(x,t), \ (x,t)\in (x_L,x_R) \times (0,T),\\ {}&u(x,0)=\textrm{Payoff}(e^x),\\ {}&u(x_L,t)= \tilde{p}(t), \ u(x_R,t)=\tilde{q}(t), \end{aligned} \right. \end{aligned}$$
(3)

where \(\mu =\frac{\sigma ^{2}}{2}\), \(\lambda =r-\mu \) and \(_{0}^{C}D_{t}^{\alpha }\) is the Caputo fractional derivative on a finite domain, which is given by:

$$\begin{aligned} _{0}^{C}D_{t}^{\alpha }u(x,t)=\frac{1}{\Gamma (1-\alpha )} \int _{0}^{t} \frac{\partial u(x,\eta )}{\partial \eta } \frac{d\eta }{(t-\eta )^\alpha }, \ 0<\alpha <1. \end{aligned}$$

From Eq. (3), we can find that the left-hand side has the dimensions of \((Year)^{-\alpha }\) while the right-hand side has the dimensions of \((Year)^{-1}\). In order to keep the unit balanced on both sides, a new functional parameter \(\rho \) is introduced with the unit of \((Year)^{\alpha -1}\). For simplification, we let \(\rho = 1\), since adding one more parameter makes computing time longer and it may be too complex to analyse the underlying meaning of \(\alpha \). The property of \(\rho \) can be considered in future research. Then Eq. (3) can be written as:

$$\begin{aligned} \left\{ \begin{aligned}&\rho \ _0 ^C D_t^{\alpha } u(x,t) \!=\! \mu \frac{\partial ^2 u(x,t)}{\partial x^2} \!+\! \lambda \frac{\partial u(x,t)}{\partial x} \!-\! r u(x,t), \ (x,t)\in (x_L,x_R) \times (0,T),\\ {}&u(x,0)=\textrm{Payoff}(e^x),\\ {}&u(x_L,t)= \tilde{p}(t), \ u(x_R,t)=\tilde{q}(t), \end{aligned} \right. \end{aligned}$$
(4)

For a European call option,

$$\begin{aligned} \begin{aligned}&u(x,0) = \max \{e^x-K,0\},\\&\tilde{p}(t) = 0,\\&\tilde{q}(t) = x_R-Ke^{(-r(T-t))}. \end{aligned} \end{aligned}$$
(5)

For a European put option,

$$\begin{aligned} \begin{aligned}&u(x,0) = \max \{K-e^x,0\},\\&\tilde{p}(t) = Ke^{(-r(T-t))},\\&\tilde{q}(t) = 0. \end{aligned} \end{aligned}$$
(6)

3 Numerical approximation

In this section, we discretise the TFBS equation using difference approximation. Let \(h=(x_{R}-x_{L})/M\) be the spatial step and \(x_i=x_L+ih\) \((i=0,1,2,\cdots ,M)\), \(\Delta t=T/N\) be the temporal step and \(t_{k}=k\Delta t\) \((k=0,1,2,\cdots ,N)\). Assume that \(u(x,t)\in \mathcal {C}^3(x_L, x_R)\times (0,T)\) at the fixed point \(t_{k}\). For \(k=1\), L1 scheme is used:

$$\begin{aligned} \begin{aligned} _0 ^C D_{t}^{\alpha }u(x,t_1)= & {} {}&\frac{1}{\Gamma (1-\alpha )} \int _{0}^{t_1} \partial _\eta u(x,\eta )\frac{d\eta }{(t_1-\eta )^\alpha }\\= & {} {}&\frac{1}{\Gamma (1-\alpha )} \frac{u(x,t_1)-u(x,t_0)}{\Delta t} \int _0^{t_1}\frac{d \eta }{(t_1-\eta )^\alpha }+r_1\\= & {} {}&\frac{1}{\Gamma (2-\alpha )\Delta t^\alpha }(u(x,t_1)-u(x,t_0))+r_1, \end{aligned} \end{aligned}$$
(7)

where \(r_1\) is the first step truncation error. Similarly, for \(2\le k \le N\), we have

$$\begin{aligned} \begin{aligned} _0 ^C D_{t}^{\alpha }u(x,t_k)= & {} {}&\frac{1}{\Gamma (1-\alpha )} \int _0^{t_k} \partial _\eta u(x,\eta ) \frac{d\eta }{(t_k-\eta )^\alpha }\\= & {} {}&\frac{1}{\Gamma (1-\alpha )} \left( \sum _{j=1}^{k-1} \int _{t_{j-1}}^{t_j} \partial _\eta u(x,\eta ) \frac{d\eta }{(t_k-\eta )^\alpha }+ \int _{t_{k-1}}^{t_k} \partial _\eta u(x,\eta ) \frac{d\eta }{(t_k-\eta )^\alpha }\right) \\= & {} {}&\frac{1}{\Gamma (1-\alpha )} \left( \sum _{j=1}^{k-1} \int _{t_{j-1}}^{t_j} \partial _\eta \Pi _2^j(\eta ) \frac{d\eta }{(t_k-\eta )^\alpha }+ \int _{t_{k-1}}^{t_k} \partial _\eta \Pi _2^{k-1}(\eta ) \frac{d\eta }{(t_k-\eta )^\alpha }\right) \\{} & {} &+r_k\\= & {} {}&\frac{1}{\Gamma (3-\alpha )\Delta t^\alpha } \left( \sum _{j=1}^{k-1} \left( a_{k-j} u(x,t_{j-1})+b_{k-j} u(x,t_j)+c_{k-j} u(x,t_{j+1})\right) \right. \\{} & {} &\left. +\frac{\alpha }{2}u(x,t_{k-2})-2u(x,t_{k-1})+\frac{4-\alpha }{2}u(x,t_k) \right) + r_k, \end{aligned} \end{aligned}$$
(8)

where

$$\begin{aligned} \Pi _2^j(\eta ) = u(t_j)-\frac{u(t_j)-u(t_{j-1})}{\Delta t}(t_j-\eta )-\frac{u(t_{j+1})-2u(t_j)+u(t_{j-1})}{\Delta t^2}\frac{(t_j-\eta )(\eta -t_{j-1})}{2}, \end{aligned}$$
(9)

which interpolates the function u at the 3 points \(t_{j-1}, t_j, t_{j+1}\), \(1\le j \le N-1\). \(r_k\) is the truncation error of the approximation for \(1\le k \le N\) and it takes the form of \(r_\tau ^{k+1} = \mathcal {O}(\tau ^{3-\alpha })\). We list some notations for convenience,

$$\begin{aligned} \begin{aligned}&a_i = (2-\alpha )\left( \frac{1}{2}i^{1-\alpha }-\frac{3}{2}(i+1)^{1-\alpha }\right) -i^{2-\alpha }+(i+1)^{2-\alpha },\\&b_i = (4-2\alpha )(i+1)^{1-\alpha }+2i^{2-\alpha }-2(i+1)^{2-\alpha },\\&c_i = \left( \frac{1}{2}\alpha -1\right) \left( i^{1-\alpha }+(i+1)^{1-\alpha }\right) -i^{2-\alpha }+(i+1)^{2-\alpha }. \end{aligned} \end{aligned}$$

Lemma 1

[27] For any \(\alpha \in (0,1)\), it holds

$$\begin{aligned} |r_1 |\le c_{\alpha } \tilde{M}(u)\Delta t^{2-\alpha }, \end{aligned}$$
(10)
$$\begin{aligned} |r_k |\le c_{\alpha } M(u)\Delta t^{3-\alpha }, \forall k = 1,2,\cdots , N. \end{aligned}$$
(11)

where \(c_{\alpha }\) depends only on \(\alpha \), \(\tilde{M}(u) \!=\! \max _{x,t\in \Omega } |\partial ^2 u(x,t)|\), \(M(u)\!=\!\max _{x,t\in \Omega }|\partial ^3_t u(t) |\).

Next, for the space derivatives we obtain

$$\begin{aligned} \frac{\partial u(x_i,t_k)}{\partial x} = \frac{u(x_{i+1},t_{k})-u(x_{i-1},t_k)}{2h}+\mathcal {O}(h^2), \end{aligned}$$
(12)
$$\begin{aligned} \frac{\partial ^2 u(x_i,t_k)}{\partial x^2} = \frac{u(x_{i+1},t_k)-2u(x_i,t_k)+u(x_{i-1},t_k)}{h^2}+\mathcal {O}(h^2). \end{aligned}$$
(13)

We let \(\phi _1 = \Gamma (2-\alpha )\Delta t^\alpha \) and \(\phi _2 = \Gamma (3-\alpha )\Delta t^\alpha \). Denoting \(u_i^k\) as the approximation of \(u(x_i,t_k)\), then we construct the implicit discrete scheme for Eq. (3), for \(k=1\),

$$\begin{aligned} \begin{aligned}&- \left( \frac{\mu \phi _1}{h^2}-\frac{\lambda \phi _1}{2h} \right) u_{i-1}^1+ \left( 2\frac{\mu \phi _1}{h^2}+ r\phi _1 +1\right) u_i^1 -\left( \frac{\mu \phi _1}{h^2}+\frac{\lambda \phi _1}{2h} \right) u_{i+1}^1 = u_i^0, \end{aligned} \end{aligned}$$
(14)

for \(k=2\),

$$\begin{aligned} \begin{aligned}&- \left( \frac{\mu \phi _2}{h^2}-\frac{\lambda \phi _2}{2h} \right) u_{i-1}^2 \!+\! \left( 2\frac{\mu \phi _2}{h^2}+ r\phi _2 \!+\! c_1+ \frac{4-\alpha }{2}\right) u_i^2 \!-\!\left( \frac{\mu \phi _2}{h^2}+\frac{\lambda \phi _2}{2h} \right) u_{i+1}^2 \\&= (2-b_1)u_i^1 - \left( \frac{\alpha }{2}+a_1 \right) u_i^0, \end{aligned} \end{aligned}$$
(15)

for \(k=3\),

$$\begin{aligned} \begin{aligned}&- \left( \frac{\mu \phi _2}{h^2}\!-\!\frac{\lambda \phi _2}{2h} \right) u_{i-1}^3 \!+\! \left( 2\frac{\mu \phi _2}{h^2}\!+\! r\phi _2 \!+\! c_1+ \frac{4-\alpha }{2}\right) u_i^3 -\left( \frac{\mu \phi _2}{h^2}+\frac{\lambda \phi _2}{2h} \right) u_{i+1}^3 \\&= (2-b_1-c_2)u_i^2 - \left( \frac{\alpha }{2}+a_1+b_2\right) u_i^1 -a_2 u_i^0, \end{aligned} \end{aligned}$$
(16)

for \(4 \le k \le N\),

$$\begin{aligned} \begin{aligned}&- \left( \frac{\mu \phi _2}{h^2}\!-\!\frac{\lambda \phi _2}{2h} \right) u_{i-1}^k \!+\! \left( 2\frac{\mu \phi _2}{h^2} \!+\!r\phi _2 \!+\! c_1 \!+\! \frac{4-\alpha }{2} \right) u_i^k -\left( \frac{\mu \phi _2}{h^2}+\frac{\lambda \phi _2}{2h} \right) u_{i+1}^k \\&= (2-b_1-c_2)u_i^{k-1} -\frac{\alpha }{2}u_i^{k-2} - \sum _{j=2}^{k-2} (a_{k-j-1}+ b_{k-j}+c_{k-j+1})u_i^j\\&-(a_{k-2}+b_{k-1})u_i^1 -a_{k-1} u_i^0. \end{aligned} \end{aligned}$$
(17)

with the initial and boundary conditions

$$\begin{aligned} u_i^0 = \max \{e^{x_i}-K,0\}, \end{aligned}$$
(18)
$$\begin{aligned} u_0^k = \tilde{p}(t_k), \ u_M^k = \tilde{q}(t_k). \end{aligned}$$
(19)

Equations (14)–(19) can be written as a matrix form,

$$\begin{aligned} A_k\textbf{U}^k = \sum _{i=0}^{k-1} D_i^k \textbf{U}^i, \end{aligned}$$
(20)

where \(A_k\) is a tridiagonal matrix and is expressed by \( A_k = tridiag(p_k,q_k,r_k)\).

$$\begin{aligned} p_1 = - \frac{\mu \phi _1}{h^2}+\frac{\lambda \phi _1}{2h}, \quad q_1 = 2\frac{\mu \phi _1}{h^2}+ r\phi _1 +1, \quad r_1 = -\frac{\mu \phi _1}{h^2}-\frac{\lambda \phi _1}{2h}, \end{aligned}$$

for \(2\le k\le N \),

$$\begin{aligned} p_k = - \frac{\mu \phi _2}{h^2}+\frac{\lambda \phi _2}{2h},\quad q_k = 2\frac{\mu \phi _2}{h^2} +r\phi _2 + c_1 + \frac{4-\alpha }{2},\quad r_k = \frac{\mu \phi _2}{h^2}-\frac{\lambda \phi _2}{2h}, \end{aligned}$$

and \(D_{i}^k\) is a diagonal matrix and is expressed by \(D_{i}^k = diag(d_{i}^k)\) where

$$\begin{aligned} d_1^2 = -(b_1-2), \quad d_0^2 = \left( -a_1-\frac{\alpha }{2}\right) , \end{aligned}$$
$$\begin{aligned} d_2^3 = -(b_1+c_2-2), \quad d_1^3 = \left( -a_1-b_2-\frac{\alpha }{2}\right) , \quad d_0^3 = -a_2 , \end{aligned}$$

and for \(k \ge 4\),

$$\begin{aligned} \begin{aligned}{} & {} {}&d_{k-1}^k = -(b_1+c_2-2), \quad d_{k-2}^k = \left( -a_1-b_2-c_3-\frac{\alpha }{2} \right) ,\\{} & {} {}&d_{k-i}^k = (-a_{i-1}-b_i-c_{i+1}), \ i = 3,4,\cdots ,k-2, \\{} & {} {}&d_1^k = (-a_{k-2}-b_{k-1}), \quad d_0^k = -a_{k-1}. \end{aligned} \end{aligned}$$

4 Theoretical analysis

In this section, we consider the solvability, stability and convergence analyses of the proposed schemes (14)–(19). We write \((\cdot ,\cdot )\) for the inner product on the space \(L^2(\Omega )\) with the \(L^2\) norm \(\Vert \cdot \Vert _{L^2(\Omega )}\). For convenience, we denote \(\Vert \cdot \Vert _{L^2(\Omega )}\) as \(\Vert \cdot \Vert \).

4.1 Solvability

Theorem 1

The difference scheme (14)–(19) has a unique solution for h sufficiently small.

Proof

We already know that \(\mu \) and r are positive, so when \(h\rightarrow 0\), we obtain, for \(k=1\),

$$\begin{aligned} \left|2\frac{\mu \phi _1}{h^2}+ r\phi _1 +1 \right|= 2\frac{\mu \phi _1}{h^2}+ r\phi _1 +1 \end{aligned}$$
$$\begin{aligned} \left|- \frac{\mu \phi _1}{h^2}+\frac{\lambda \phi _1}{2h} \right|+ \left|-\frac{\mu \phi _1}{h^2}-\frac{\lambda \phi _1}{2h} \right|= \frac{\mu \phi _1}{h^2}-\frac{\lambda \phi _1}{2h} +\frac{\mu \phi _1}{h^2}+\frac{\lambda \phi _1}{2h}= \frac{2\mu \phi _1}{h^2} \end{aligned}$$

for \(k \ge 2\)

$$\begin{aligned} \left|2\frac{\mu \phi _2}{h^2}+ r\phi _2 +c_1+\frac{4-\alpha }{2} \right|= 2\frac{\mu \phi _2}{h^2}+ r\phi _2 +c_1+\frac{4-\alpha }{2} \end{aligned}$$
$$\begin{aligned} \left|- \frac{\mu \phi _2}{h^2}+\frac{\lambda \phi _2}{2h} \right|+ \left|-\frac{\mu \phi _2}{h^2}-\frac{\lambda \phi _2}{2h} \right|= \frac{\mu \phi _2}{h^2}-\frac{\lambda \phi _2}{2h} +\frac{\mu \phi _2}{h^2}+\frac{\lambda \phi _2}{2h}= \frac{2\mu \phi _2}{h^2} \end{aligned}$$

Therefore, it is obvious that matrix A is strictly diagonally dominant and nonsingular and thus invertible. The existence and uniqueness of the solution of our scheme (14)–(19) are proved.

4.2 Stability

In this part, we consider the stability of the semidiscretised problem (14)–(19). For convenience, we denote \(\beta := c_1+2-\frac{\alpha }{2}\). Then the scheme (14)–(17) can be written as, for \(k = 1\),

$$\begin{aligned} u^1 - \phi _1 \mu \partial _{xx} u^1 -\phi _1 \lambda \partial _{x} u^1 + \phi _1 r u^1 = u^0, \end{aligned}$$
(21)

for \(k = 2\),

$$\begin{aligned} \begin{aligned}{} & {} &u^2 - \phi _2 \beta ^{-1} \mu \partial _{xx} u^2 -\phi _2 \beta ^{-1} \lambda \partial _{x} u^2 + \phi _2 \beta ^{-1} r u^2\\= & {} {}&\beta ^{-1} \left( -(b_1-2)u^{1}+\left( -a_1-\frac{\alpha }{2}\right) u^{0}\right) , \end{aligned} \end{aligned}$$
(22)

for \(k = 3\),

$$\begin{aligned} \begin{aligned}{} & {} &u^3 - \phi _2 \beta ^{-1} \mu \partial _{xx} u^3 -\phi _2 \beta ^{-1} \lambda \partial _{x} u^3 + \phi _2 \beta ^{-1} r u^3\\= & {} {}&\beta ^{-1} \left( -(b_1+c_2-2)u^{2}+\left( -a_1-b_2-\frac{\alpha }{2}\right) u^{1} -a_2 u^0 \right) , \end{aligned} \end{aligned}$$
(23)

for \(k\ge 4\),

$$\begin{aligned} \begin{aligned}{} & {} &u^k - \phi _2 \beta ^{-1} \mu \partial _{xx} u^k -\phi _2 \beta ^{-1} \lambda \partial _{x} u^k + \phi _2 \beta ^{-1} r u^k\\= & {} {}&\beta ^{-1} \left( -(b_1+c_2-2)u^{k-1}+\left( -a_1-b_2-c_3-\frac{\alpha }{2}\right) u^{k-2} \right. \\{} & {} &\left. + \sum _{i=3}^{k-2}(-a_{i-1}-b_i-c_{i+1})u^{k-i}+(-a_{k-2}-b_{k-1})u^1-a_{k-1}u^0 \right) . \end{aligned} \end{aligned}$$
(24)

The semidiscretised scheme (21)–(24) can be summarised as a compact scheme

$$\begin{aligned} u^1 - \phi _1 \mu \partial _{xx} u^1 -\phi _1 \lambda \partial _{x} u^1 + \phi _1 r u^1 = u^0, \end{aligned}$$
(25)
$$\begin{aligned} u^k - \phi _2 \beta ^{-1} \mu \partial _{xx} u^k -\phi _2 \beta ^{-1} \lambda \partial _{x} u^k + \phi _2 \beta ^{-1} r u^k = \sum _{j=1}^k \tilde{d}_{k-j}^k u^{k-j}, 2\le k \le K, \end{aligned}$$
(26)

where \(\tilde{d}_{k-j}^k = d_{k-j}^k \beta ^{-1}\).

Lemma 2

[27] For any \(0<\alpha <1\), \(k \ge 4\), the coefficients in the scheme (25)–(26) satisfy

  • \(\beta = (1+\frac{\alpha }{2})2^{1-\alpha }>0\), \(0<\phi _2 \beta ^{-1}<\phi _1\),

  • \(\sum _{j=1}^{k}\tilde{d}_{k-j}^{k}=1\),

  • \(\tilde{d}_{k-j}^k >0, i = 3,4,\cdots ,k\),

  • \(0<\tilde{d}_{k-1}^k <\frac{4}{3},\)

  • \(-\frac{1}{2}< \tilde{d}_{k-2}^k <\frac{1}{3}\),

  • \(\frac{1}{4}(\tilde{d}_{k-1}^k)^2+\tilde{d}_{k-2}^k>0\).

From Lemma 2, we know that the coefficient \(\tilde{d}_{k-2}^k\) can either be positive and negative. Then a new parameter is introduced in order to establish stability and convergence for \(\alpha \in (0,1)\), given by

$$\begin{aligned} \eta := \frac{1}{2} \tilde{d}_{k-1}^k. \end{aligned}$$
(27)

Denote

$$\begin{aligned} \bar{d}_{k-i}^k := \eta ^i + \sum _{j=2}^i \eta ^{i-j}\tilde{d}_{k-j}^k, i = 2,3,\cdots ,k, \end{aligned}$$
(28)
$$\begin{aligned} \bar{u}^i := u^i - \eta u^{i-1} , i=1,2,\cdots ,k. \end{aligned}$$
(29)

Then the scheme (26) can be rearranged as

$$\begin{aligned} \bar{u}^k - \alpha _0 \beta _0^{-1} \mu \partial _{xx} u^k - \alpha _0 \beta _0^{-1} \lambda \partial _x u^k + \alpha _0 \beta _0^{-1} r u^k = \eta \bar{u}^{k-1} + \sum _{i=2}^{k-1} \bar{d}_{k-i}^k \bar{u}^{k-i}+\bar{d}_0^k u^0. \end{aligned}$$
(30)

Lemma 3

[27] For \(0<\alpha <1\), \(k \ge 4\), the coefficients of the transformed scheme (30) meets

  • \(0<\eta <\frac{2}{3}\),

  • \( \bar{d}_{k-i}^k >0, i = 2,3, \cdots , k,\)

  • \( \eta + \sum _{i=2}^{k-1} \bar{d}_{k-i}^k + \bar{d}_0^k \le 1\),

  • \(\frac{1}{\bar{d}_0^k} < \frac{k^\alpha }{(2-\alpha )(1-\alpha )}\)

Let \(L^2(\Lambda ), H^1(\Lambda )\), and \(H_0^1(\Lambda )\) be usual Sobolev spaces. The weak formulation of (25)–(26) with the homogeneous boundary conditions is given by, when \(u^k \in H_0^1(\Lambda ), 2\le k\le K\),

$$\begin{aligned} \begin{aligned}{} & {} &(u^k,v)+\phi _2 \beta ^{-1} \mu (\partial _x u^k, \partial _x v^k) -\phi _2 \beta ^{-1} \lambda (\partial _x u^k, v) + \phi _2 \beta ^{-1} r (u^k, v) \\= & {} {}&\sum _{j=1}^k \tilde{d}_{k-j}^k (u^{k-j},v) \ \forall v \in H_0^1(\Lambda ) \end{aligned} \end{aligned}$$
(31)

where \((\cdot ,\cdot )\) is the usual \(L^2\)-inner product.

Theorem 2

Suppose that \(u_i^n\) and \(\tilde{u}_i^n\) are solutions of the finite difference scheme (31) with the initial values \(u_0^n\) and \(\tilde{u}_0^n\). For \(\alpha \in (0,1)\), the proposed scheme is unconditionally stable,

$$\begin{aligned} \left\| u^k \right\| _0 + \sqrt{\phi _2 \beta ^{-1}} \left\| \partial _x u^k \right\| _0 \le 4 \left\| u^0 \right\| _0, \ 1\le k \le N. \end{aligned}$$
(32)

Proof

By using Lemma 2, it is easy to prove the case of \(k=1\). For \(k\ge 2\), the scheme (31) can be rewritten as follows, for \(\forall v \in H_0^1(\Lambda )\):

$$\begin{aligned} \begin{aligned}{} & {} &\left( \bar{u}^k,v\right) +\phi _2 \beta ^{-1} \mu \left( \partial _x u^k, \partial _x v \right) - \phi _2 \beta ^{-1} \lambda \left( \partial _x u^k,v \right) + \phi _2 \beta ^{-1} r \left( u^k,v \right) \\= & {} {}&\sum _{j=1}^k \tilde{d}_{k-j}^k (\bar{u}^{k-j},v)+\bar{d}_0^k(u^0,v). \end{aligned} \end{aligned}$$
(33)

Letting \(v=2\bar{u}^k\), we obtain

$$\begin{aligned} \begin{aligned}{} & {} {}&2\left\| \bar{u}^k \right\| _0^2 +2\phi _2 \beta ^{-1} \mu (\partial _x u^k, \partial _x \bar{u}^x) -2\phi _2 \beta ^{-1} \lambda \left( \partial _x u^k,\bar{u}^k \right) + 2\phi _2 \beta ^{-1} r \left( u^k,\bar{u}^k \right) \\= & {} {}&2\sum _{j=1}^k \tilde{d}_{k-j}^k (\bar{u}^{k-j},\bar{u}^k)+2\bar{d}_0^k(u^0,\bar{u}^k). \end{aligned} \end{aligned}$$
(34)

In virtue of the identity

$$\begin{aligned} 2\left( \partial _x u^k, \partial _x \bar{u}^x \right) = \left\| \partial _x \bar{u}^k \right\| _0^2 + \left\| \partial _x u^k\right\| _0^2-\eta ^2 \left\| \partial _x u^{k-1}\right\| _0^2, \end{aligned}$$
$$\begin{aligned} 2\left( u^k, \bar{u}^x \right) = \left\| \bar{u}^k \right\| _0^2 + \left\| u^k \right\| _0^2-\eta ^2 \left\| u^{k-1}\right\| _0^2, \end{aligned}$$

Here, we assume that \(u^{k-1}\) is equal to \(u^k\) when \(\Delta t \) is sufficiently small, then \(2(\partial _x u^k, \bar{u}^k)=2\eta (\partial _x u^{k-1},u^k)=0\). Next, we use Schwarz inequality and Lemma 3 and obtain

$$\begin{aligned} \begin{aligned}{} & {} {}&2\left\| \bar{u}^k \right\| _0^2 + \phi _2 \beta ^{-1} \mu \Vert \partial _x u^k \Vert _0^2 + \phi _2 \beta ^{-1} r \Vert u^k \Vert _0^2 + \phi _2 \beta ^{-1} r \Vert \bar{u}^k \Vert _0^2 \\\le & {} {}&\eta \Vert \bar{u}^{k-1}\Vert _0^2 + \phi _2 \beta ^{-1} \mu \eta ^2 \Vert \partial _x u^{k-1} \Vert _0^2 + \phi _2 \beta ^{-1} r \eta ^2 \Vert u^{k-1}\Vert _0^2\\{} & {} {}&+ \sum _{j=2}^{k-1} \bar{d}_{k-j}^k\Vert \bar{u}^{k-j}\Vert _0^2 + \bar{d}_0^k \Vert u^0\Vert _0^2 + \left( \eta + \sum _{j=2}^{k-1} \bar{d}_{k-j}^k +\bar{d}_0^k \right) \Vert \bar{u}^k \Vert _0^2. \end{aligned} \end{aligned}$$
(35)

According to Lemma 3, we have

$$\begin{aligned} \begin{aligned}{} & {} {}&\left\| \bar{u}^k \right\| _0^2 + \phi _2 \beta ^{-1} \mu \left\| \partial _x u^k \right\| _0^2 + \phi _2 \beta ^{-1} r \left\| u^k \right\| _0^2 \\\le & {} {}&\eta \left\| \bar{u}^{k-1}\right\| _0^2 + \phi _2 \beta ^{-1} \mu \eta ^2 \left\| \partial _x u^{k-1} \right\| _0^2 + \phi _2 \beta ^{-1} r \eta ^2 \left\| u^{k-1}\right\| _0^2\\{} & {} {}&+ \sum _{j=2}^{k-1} \bar{d}_{k-j}^k \left\| \bar{u}^{k-j}\right\| _0^2 + \bar{d}_0^k \left\| u^0\right\| _0^2 \\\le & {} {}&\eta \left( \left\| \bar{u}^{k-1}\right\| _0^2 + \phi _2 \beta ^{-1} \mu \eta \left\| \partial _x u^{k-1} \right\| _0^2 + \phi _2 \beta ^{-1} r \eta \left\| u^{k-1}\right\| _0^2\right) \\{} & {} {}&+ \sum _{j=2}^{k-1} \bar{d}_{k-j}^k \left( \left\| \bar{u}^{k-j}\right\| _0^2 + \phi _2 \beta ^{-1} \mu \left\| \partial _x u^{k-i} \right\| _0^2 +\phi _2 \beta ^{-1} r \left\| u^{k-i} \right\| _0^2 \right) + \bar{d}_0^k \left\| u^0\right\| _0^2\\\le & {} {}&\eta \left( \left\| \bar{u}^{k-1}\right\| _0^2 + \phi _2 \beta ^{-1} \mu \left\| \partial _x u^{k-1} \right\| _0^2 + \phi _2 \beta ^{-1} r \left\| u^{k-1}\right\| _0^2\right) \\{} & {} {}&+ \sum _{j=2}^{k-1} \bar{d}_{k-j}^k \left( \left\| \bar{u}^{k-j}\right\| _0^2 \!+\! \phi _2 \beta ^{-1} \mu \left\| \partial _x u^{k-i} \right\| _0^2 \!+\!\phi _2 \beta ^{-1} r \left\| u^{k-i} \right\| _0^2 \right) \!+\! \bar{d}_0^k \left\| u^0\right\| _0^2 .\\ \end{aligned} \end{aligned}$$
(36)

Now we want to prove the following estimate by induction:

$$\begin{aligned} \left\| u^k\right\| _0^2 + \phi _2 \beta ^{-1} \mu \left\| \partial _x u^k\right\| _0^2 + \phi _2 \beta ^{-1} r \left\| u^k\right\| _0^2 \le \left\| u^0\right\| _0^2, \quad 2\le k \le N. \end{aligned}$$
(37)

It is easy to check the above inequality when \(k=2\). Then assuming the inequality (37) is valid for \(k=2,\cdots ,j-1\), we can obtain from

$$\begin{aligned} \begin{aligned}&\left\| u^k\right\| _0^2 + \phi _2 \beta ^{-1} \mu \left\| \partial _x u^k\right\| _0^2 + \phi _2 \beta ^{-1} r \left\| u^k\right\| _0^2 \le \left( \eta + \sum _{i=2}^{j-1} \bar{d}_{j-i}^j + \bar{d}_0^j \right) \left\| u^0\right\| _0^2, \\&\forall j = 1,2,\cdots , K. \end{aligned} \end{aligned}$$
(38)

Thus (37) is proven. By the triangle inequality and (37), we obtain \(\Vert u^k\Vert _0 \le 3 \Vert u^0\Vert _0\). Finally, we combine the above estimates. The proof is completed.

4.3 Convergence

Let \(u(x_i,t_k)\) be the exact solution of the TFBS model and \(u_i\) be the semidiscrete solution of the schemes. The error \(\varepsilon _i^k = u(x_i,t_k)-u_i^k \). Similar to the work of [27], the first step scheme can be transformed to obtain a global \((3-\alpha )\) order accuracy.

$$\begin{aligned} \left\| u(t_1)-u^1\right\| + \sqrt{\phi _1} \left\| \partial _x(u(t_1)-u^1)\right\| \le c \left\| \partial _t^2 u\right\| _{L^\infty (L^2)}\Delta t^{3-\alpha }. \end{aligned}$$
(39)

Theorem 3

Suppose \(\partial _t^3 u \in L^{\infty }((0,T];L^2(\Lambda ))\), then the following error estimate holds,

$$\begin{aligned} \left\| u(t_k)u^k\right\| _0+\sqrt{\phi _2 \beta ^{-1}} \left\| \partial _x(u(t_k)-u^k)\right\| _0 \le c_{\alpha ,T} \left\| \partial _t^3 u \right\| _{L^{\infty }(L^2)}\Delta t^{3-\alpha }, \quad 2\le k \le N, \end{aligned}$$
(40)

Proof

Let \(\varepsilon ^k = u(t_k)-u^k\). We derive

$$\begin{aligned} \begin{aligned}{} & {} &\left( \varepsilon ^k,v\right) +\phi _2 \beta ^{-1} \left( \partial _x \varepsilon ^k,\partial _x v\right) -\phi _2 \beta ^{-1} \lambda \left( \partial _x \varepsilon ^k,v\right) +\phi _2 \beta ^{-1} r \left( \varepsilon ^k,v\right) \\= & {} {}&\sum _{j=1}^k \tilde{d}_{k-j}^k \left( \varepsilon ^{k-j},v\right) +\bar{d}_0^k\left( \varepsilon ^0,v\right) . \end{aligned} \end{aligned}$$
(41)

Taking \(v= \bar{\varepsilon }^k\) and following the similar procedure as in Theorem 2 yields

$$\begin{aligned} \begin{aligned}{} & {} {}&\left\| \varepsilon ^k \right\| _0 + \sqrt{\alpha _0 \beta _0^{-1}} \left\| \partial _x \varepsilon ^k \right\| _0 \\{} & {} \le&4 \left( \left\| \varepsilon ^1\right\| _0^2 +\frac{4T^\alpha \Gamma (1-\alpha )}{\beta _0} \max _{2\le i \le N } \left\| r_i \right\| _0^2 \right) ^{\frac{1}{2}}, \ k=2,\cdots ,N. \end{aligned} \end{aligned}$$
(42)

Finally, the proof is completed using Lemma 1 and Eq.(39).

4.4 Numerical example

In this section, we represent a numerical experiment to show the accuracy and efficiency of the proposed scheme (14)–(17) for solving the TFBS model. The Thomas algorithm is used to decrease computational time [47]. The exact solution of problem (3) is

$$\begin{aligned} u=\left( t+1\right) ^2\left( x^3+x^2+1\right) . \end{aligned}$$

Here parameters are \(r=0.5\), \(\mu =1,\lambda = r-\mu \), \(T=1\). The source term is

$$\begin{aligned} \begin{aligned} f= & {} {}&\left( \frac{2\tau ^{2-\alpha }}{\Gamma (3-\alpha )}+\frac{2\tau ^{1-\alpha }}{\Gamma (2-\alpha )}\right) \left( x^3+x^2+1\right) \\{} & {} &-\left( t+1\right) ^2\left[ \mu \left( 6x+2\right) +\lambda \left( 3x^2+2x\right) -r\left( x^3+x^2+1\right) \right] . \end{aligned} \end{aligned}$$

The convergence order is calculated as

$$\begin{aligned} \textrm{Order} = log_{\frac{\Delta t_1}{\Delta t_2}} \frac{\varepsilon _1}{\varepsilon _2}. \end{aligned}$$
Table 1 Errors and convergence order for L2 formula, \(h^2=\Delta t^{3-\alpha }\), with \(\alpha = 0.1,0.5,0.9\)
Full size table

Table 1 describes that when the time step and space step decrease with the rate of \(h^2=\Delta t^{3-\alpha }\), the maximum error decreases as well. The results satisfy the theoretical analyses and show that the convergence order of the proposed scheme is \(\mathcal {O}(h^2)\) or \(\mathcal {O}(\Delta t^{3-\alpha })\). In addition, we carry out a small test to compare the L1 and L2 schemes. In this example, we explain why we choose a high-order scheme rather than the common method for approximating the Caputo derivative. We extend the length of the domain in order to match the requirements for real applications. For instance, the domain of the log form of stock price is \(x_L = -4.6 \approx \log (0.01)\) and \(x_R = 8.4 \approx \log (4000)\). The maximum error of the L1 scheme is 2.7230 but the error of the L2 is only 0.0519. From the result, we can say that a high-order scheme has its advantage in the larger domain and improve the accuracy of the numerical solution to option valuation problems.

5 Parameter estimation

From Sections 3 and 4, we have already considered the forward problem of the TFBS model. In this section, the inverse problem will be considered in order to examine and explore the underlying meanings of the parameters of the TFBS equation. This section begins with introducing the rationale of the NMSS and PSO, followed by a demonstration of how the MH-NMSS-PSO method works on the S &P 500 index option.

The Nelder-Mead simplex search method is a traditional direct search algorithm and is easy to implement in many unconstrained optimization problems [40]. There are four procedures: reflection, expansion, contraction and shrinkage, which are used for re-scaling the simplex. However, this technique is relatively sensitive to the choice of initial points and is possible to be trapped in local optima, and thus is hard to guarantee to reach the global optimum.

The particle swarm optimization algorithm is an evolutionary technique and can be applied in optimizing various continuous nonlinear functions [41]. The concept of PSO comes from social interaction such as bird flocking. The main procedure of PSO has two steps: generating randomly a group of potential solutions and assigning a random velocity to each solution; updating the velocity that is adjusted dynamically to locate the best point. The convergence rate of PSO, however, is slow and can cause huge computational costs.

The rationale of the MH-NMSS-PSO is firstly to generate two groups of particles for the NMSS and PSO, then apply the two algorithms to each group, and eventually rank and evaluate all the updated particles by stopping criterion. The aim of combining the NMSS and PSO algorithms is to utilise their advantages and avoid limitations. Therefore, the PSO can randomly provide good particles in the domain and the NMSS can approach the local optima quickly. The MH-NMSS-PSO algorithm is reviewed in Algorithm 1.

Algorithm 1
figure a

MH-NMSS-PSO [42]

Full size image

In our case, the objective function of the MH-NMSS-PSO method is

$$\begin{aligned} y(\lambda ) = \sqrt{\frac{\sum _{k=0}^N(u(t_k)-u_k(\lambda ))^2}{N+1}}, \end{aligned}$$
(43)

where N is the number of prices of an option, \(u(t_k)\) is the S &P 500 index option prices and \(u_k(\lambda )\) is the numerical solution of the TFBS equation. There are three unknown parameters: fractional order \(\alpha \), volatility \(\sigma \) and the functional parameter \(\rho \) in Eq. (4). As mentioned in Section 2, we assume \(\rho =1\) for convenience. \(\alpha \) and \(\sigma \) cannot be directly calculated from the financial market, hence are to be estimated in this work. Let \(\Omega \) be a given search domain: \(\Omega =\left[ \alpha ^{(\min )},\alpha ^{(\max )}\right] \times \left[ \sigma ^{(\min )},\sigma ^{(\max )}\right] \) and thus \(m=2\) in Algorithm 1. The rationale for the MH-NMSS-PSO method is that 7 particles are evaluated and ranked by their objective function values \(y(\lambda )\) in which the first 3 particles are for the NMSS method and the last 4 particles are for the PSO method. The terminal criterion is defined as

$$\begin{aligned} S_c = \sqrt{\sum _{i=1}^{3}\frac{(\bar{y}-\sqrt{y_i})^2}{m+1}}<\epsilon , \end{aligned}$$
(44)

where \(\bar{y}=\sum _{i=1}^{3} \sqrt{y_i}/(m+1)\), \(f_i=f(\alpha _1,...,\alpha _7,\sigma _1,...\sigma _7)\) and \(\epsilon \) represents a small error parameter.

6 Empirical studies using S &P 500 index option

In this section, we explore the underlying meanings of the fractional order \(\alpha \) of the TFBS model. We first describe the data and the basic ideas about the empirical research and then focus on the empirical results by using the S &P 500 index option. There are four empirical studies and one discussion that presented to discuss the meanings of the parameters \(\alpha \) and \(\sigma \) of the TFBS model.

6.1 Data description

Our empirical research is carried out on a data set of the S &P 500 index option which is obtained from the OptionMetrics. The data set includes the date of the transaction, the bid and ask prices, the expiration date, the strike price, volume, open interest and so on. The S &P 500 index option is the European-style option and has two formats: SPX and SPXW, representing monthly and weekly options, respectively. The SPX options expire only on the third Friday of each month while the SPXW options expire on Monday, Wednesday and Friday.

The idea of filtering raw data is adopted from [43] and [44], but we adjust some measurements to meet our study. Options whose period is less than 10 days and more than 126 trading days are eliminated. To avoid the bid-ask bounce problems in transaction data, we take option prices as the midpoints of bid-ask price quotations. The T-bill rate with a maturity closest to option expiration is used to represent the risk-free interest rate, because the change of interest rate is relatively small on daily basis and the prices of options are not sensitive to the interest rate. We use 252 trading days rather than calendar days to calculate the time (T = L/253, where L is the number of trading days of one option contract).

Fig. 1
figure 1

Daily returns of S &P 500 index for stable and unstable economic condition

Full size image

The procedure of estimating \(\alpha \) for one option is as follows. We collect the bid and ask prices for all trading days and calculate the option prices. Next, we use the option prices, interest rate, strike price and the stock prices to conduct the parameter estimation by Algorithm 1 to obtain the estimated \(\alpha \) and \(\sigma \). The options are divided into different groups according to the same expiration date. In each group, we classify options by moneyness in three types, following the work of [45]. For call options, denote \(S/K \in (0.95,0.98)\) as “Out of the money" (OTM) options, \(S/K \in (0.98,1.02)\) as “At the money" (ATM) options and \(S/K \in (1.02,1.05)\) as “In the money" (ITM) options. Similarly, we can also define the put options. We take the mean of the estimates for each small group and use the notations \(\alpha _I\), \(\alpha _A\) and \(\alpha _O\) to represent the ITM, ATM and OTM options, respectively. After calculating more than 2000 option contracts, the empirical results are summarised as tables in the Appendix. In the following cases, we plot figures to illustrate the results of average estimates of \(\alpha \) for the SPXW and SPX options. Note that, for convenience, we use the format of year-month-date or month-date in the following tables and figures to show the expiration date. For example, 20-03-04 means March 4, 2020.

6.2 Case I: SPXW between stable and unstable financial markets

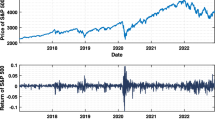
In this case, we explore the estimated \(\alpha \) of the TFBS model under different financial markets. First, we classify the stable and unstable financial environments. Similar to the work of [46], we plot the daily returns of the S &P 500 index under two periods: from January 2019 to June 2019 and from January 2020 to June 2020. Figure 1 shows that the returns of the S &P 500 index in 2019 are between -5% and 5%, which is assumed to be a stable financial market. The daily returns on March 2020 approach -10% or 10% because of the Covid-19 recession that began in most countries in February 2020 and thus we name it as an unstable financial environment.

Fig. 2
figure 2

Normal probability plots of returns of daily S &P 500 index for stable and unstable periods

Full size image
Fig. 3
figure 3

Results of estimated \(\alpha \) for the SPXW calls and puts with the expiration date between March 6, 2019, and April 24, 2019

Full size image

Moreover, we would like to know how the distributions of the two periods behave. We choose two groups of the returns of S &P 500 index data (Jan 29, 2019–April 25, 2019, and Jan 28, 2020–April 30, 2020). Figure 2 contains two Quantile-Quantile plots that compare the distribution of daily returns to the normal distribution. It is seen that the daily returns in the stable period are close to the normal distribution while the unstable period exhibits a heavy tail distribution. We also employ the lillietest built-in function in Matlab to test the two groups of returns. The results show that P = 0.2229 for the stable group and we conclude that it is a normal distribution at the significance of 95%, while for the unstable one, P = 0.0477 and the assumption that the data follow a normal distribution is rejected at the 95% significance level.

Based on the three analyses, we define two types of stock market conditions. We would like to study the estimated values of the fractional order \(\alpha \) of the TFBS model under the global stock market crash which happened on February 20, 2020, and finished on April 7, 2020, caused by the Covid-19 pandemic. Several series of SPXW options that expired in March and April 2020 are collected and analysed. The results are summarised in Tables 2, 3, 4, and 5 in the Appendix.

Fig. 4
figure 4

Results of estimated \(\alpha \) for the SPXW calls and puts with the expiration date between March 4, 2020, and April 29, 2020

Full size image

We plot Fig. 3 and Fig. 4 in order to show the change of estimated \(\alpha \) over time. From Fig. 3, we can see that the difference among the ITM, ATM and OTM call options is not remarkable, but for put options, the OTM puts that expired on April 10 are much lower than the other types of options. This is because the S &P 500 index dropped from 2854 to 2800 on March 22, 2019, and the SPXW options that expired on April 10 include this period of time. Figure 3(b) demonstrates that the OTM put options are more sensitive than the ITM and ATM options when the stock index decreases. In 2020, however, there was a huge stock market crash due to the Covid-19 pandemic. Figure 4 shows that the \(\alpha _I\), \(\alpha _A\) and \(\alpha _O\) for calls and puts are varying significantly over time but both recover back to 1 after April 8, 2020, which is surprisingly consistent with the end date of the sudden decline in the stock market. It is known that the recovery began in early April 2020 and the GDP for most countries had returned to normal levels. For put options, the estimated \(\alpha \) approaches the smallest value on March 18 which is also roughly consistent with the fact that the S &P 500 dropped 1300 points on the date.

The empirical results are interesting and it seems that \(\alpha \) can reflect the performance of the S &P 500 stock index. When the stock price jump is bigger, \(\alpha \) is smaller. In addition, the change in \(\alpha \) not only occurs in the extremely unstable period but also in the stable period with slight price jumps.

Fig. 5
figure 5

Results of estimated \(\alpha \) for the SPX calls and puts with expiration date from January 2020 to December 2020

Full size image
Fig. 6
figure 6

Results of estimated \(\alpha \) for the SPX calls and puts with expiration date from March 2008 to December 2008

Full size image

6.3 Case II: Two extreme stock market crashes

In this case, the SPX monthly options are used to study the meanings of \(\alpha \) over months. We choose the SPX data for 2008 and 2020 in order to identify \(\alpha \) in the two famous stock market crashes: the Covid-19 recession in 2020 and the global financial crisis in 2008. We choose a series of monthly options with the same expiration date. All the empirical results are summarised in Tables 6, 7, 8, and 9 in the Appendix.

Figure 5 illustrates that the results of estimated \(\alpha \) of the TFBS model for the SPX options that expired in each month in 2020. For call options, the data in March is eliminated because there is no sufficient data. The reason is that buyers are less likely to buy the very deep ITM options when the stock price declines significantly. It is shown in Fig. 5(a) that \(\alpha \) has smaller values in April and May. For put options, it is clearly seen that \(\alpha \) reaches the minimum in March, which indicates that high fluctuations of stock markets occurred in this month. For both calls and puts, we can see that \(\alpha \) slightly fluctuates in the interval (0.8, 1) after June 2020.

Unlike Fig. 5, due to the lack of sufficient data in 2008, we do not take the mean of estimated \(\alpha \) under each category but simply choose the most appropriate option from March 2008 to December 2008. It is obvious in Fig. 6 that the estimated \(\alpha \) has the smallest value in October for both call and put options when there was an extreme market crash in October 2008. For call options, \(\alpha \) of the OTM option is the smallest, that of ATM stays in the middle, and that of the ITM is the largest in October. For put options, the difference among the three categories of options is not significant. Based on the two extreme financial markets, we may conclude that \(\alpha \) can reflect huge fluctuations in stock markets.

6.4 Case III: Results of estimated \(\alpha \) with different strike price under unstable period

In the first two cases, we analyse the estimated \(\alpha \) over time under different financial environments. For the third case, we focus on \(\alpha \) over different strike prices for options with the same expiration date. We choose the SPXW options that expired on March 18, 2020, whose strike prices are between 2700 and 2900. Two lengths of options contracts are chosen: one is 15 trading days and the other is 26 trading days. From Fig. 7, we may see that \(\alpha \) behaves differently over strike prices in the two groups. \(\alpha \) with 26 trading days is larger than that with 15 trading days for calls but smaller for puts. Note that we have compared a number of empirical results about the SPX and SPXW options, and there is no strong significance in the relation of \(\alpha \) with the length of options contracts.

Fig. 7
figure 7

Results of estimated \(\alpha \) for the SPXW calls and puts under different strike prices

Full size image

6.5 Case IV: Comparison about the MSE of the TFBS model and the BS model

We choose the call and put options with strike prices from 2980 to 3295 that expired on March 4, 2020. By moneyness, we denote strike prices within (2980, 3065) as ITM calls or OTM puts, within (3065, 3195) as ATM calls and puts, within (3195, 3295) as OTM calls or ITM puts. Figure 8(a) shows that the MSE of the TFBS model is slightly smaller for ITM calls and is close to that of the BS model for ATM and OTM calls. From Fig. 8(b), it is seen that there is a significant difference in MSE between the TFBS and BS models when the put options are OTM. Then the difference between two lines tends to be small over strike price. From the empirical results, we may conclude that the TFBS model has its advantages in fitting data especially for put options during stock market downturns.

We compare the SPXW options and the numerical solution of the TFBS model. We choose a call and a put with a strike price of 3295 which expired on March 4, 2020. Figure 9 shows how the option price changes over the trading days in an option contract. For a call option, the price decreases rapidly on the 20th trading day and approaches 0 until the expiration date, because the stock on the 19th trading day is below 3295 and the value of calls becomes 0. For a put option, it is the opposite and its value rises considerably.

Fig. 8
figure 8

MSE for the SPXW calls and puts that expired on March 4, 2020, under different strike prices

Full size image
Fig. 9
figure 9

The comparison of numerical results and real option data with strike price of 3295 expired on March 4, 2020

Full size image

6.6 Discussion: a relation between fractional order \(\alpha \) and volatility \(\sigma \) in the TFBS equation and the BS equation

We denote by \(\sigma _F\) the volatility in the TFBS model, and by \(\sigma _{BS}\) the volatility in the BS model. From empirical results, we find an interesting result, as follows:

$$\begin{aligned} \alpha \approx \frac{\sigma _F}{\sigma _{BS}}. \end{aligned}$$
(45)

From the above analysis, we can take \(\alpha \) as a big jump indicator of the stock market. Now we find that \(\alpha \) is approximately the ratio of the fractional volatility \(\sigma _F\) to the traditional volatility \(\sigma _{BS}\). The approximation can be rearranged as

$$\begin{aligned} \frac{1}{\sigma _{BS}} \approx \frac{\alpha }{\sigma _F}. \end{aligned}$$
(46)

We may interpret that the ratio of the order of the derivative to its volatility in the BS model is approximately equal to the ratio of the fractional order of the derivative and its volatility in the TFBS models. The third expression is

$$\begin{aligned} \sigma _{BS} \approx \frac{\sigma _F}{\alpha }. \end{aligned}$$
(47)

We may interpret that the ‘true’ volatility of the TFBS model should be the same as \(\sigma _{BS}\). Then we may extend the TFBS model into

$$\begin{aligned} _0 ^C D_t^{\alpha } U(x,t) = \frac{\alpha ^2}{2} \sigma _{BS}^2 \frac{\partial ^2 U(x,t)}{\partial x^2} + (r-\frac{\alpha ^2}{2}\sigma _{BS}^2) \frac{\partial U(x,t)}{\partial x} - r U(x,t). \end{aligned}$$
(48)

If this equation holds, we can estimate the \(\sigma _{BS}\) in the BS model first and then estimate \(\alpha \) in the TFBS model, which can decrease the computation time significantly. Note that we assumed \(\rho =1\) in the TFBS model. An estimate is that \(\rho \) may be set to be equal to \(1/\alpha ^2\). From the three expressions, we may find the potential underlying meaning of the fractional order \(\alpha \). This discussion might provide a basis for studying similar relationships for the coefficients from the fractional-order model and integer-order model. This can be an open problem for further study.

7 Summary and conclusion

This work has provided an implementable framework for identifying the fractional order \(\alpha \) and implied volatility \(\sigma \) of the TFBS model by the MH-NMSS-PSO technique. In this study, we proposed a high-order scheme and carried out theoretical analyses. Then, we used parameter estimation to explore the underlying meaning of \(\alpha \) under different financial environments; the results showed that \(\alpha \) may be regarded as a jump indicator in the option pricing problem. The smaller \(\alpha \) is, the larger the fluctuation in the financial market. Several empirical cases about the properties of \(\alpha \) have been investigated under the Covid-19 recession in 2020 and the global financial crisis in 2008. We found an interesting approximation between \(\alpha \) and \(\sigma \) of both the BS model and TFBS model based on certain assumptions. This work is the first attempt to study the performance of \(\alpha \) for one option contract based on empirical studies.

There are still some issues to consider. The algorithm for parameter estimation is still slow and needs to be developed especially for long-term options (longer than 126 trading days) in the application. The function parameter \(\rho \) is introduced but assumed to be equal to 1 for convenience. The financial meaning of \((Year)^{\alpha -1}\) is still to be further investigated.