Relaxed fixed point iterations for matrix equations arising in Markov chain modeling

Abstract

We present some accelerated variants of fixed point iterations for computing the minimal non-negative solution of the unilateral matrix equation associated with an M/G/1-type Markov chain. These variants derive from certain staircase regular splittings of the block Hessenberg M-matrix associated with the Markov chain. By exploiting the staircase profile, we introduce a two-step fixed point iteration. The iteration can be further accelerated by computing a weighted average between the approximations obtained at two consecutive steps. The convergence of the basic two-step fixed point iteration and of its relaxed modification is proved. Our theoretical analysis, along with several numerical experiments, shows that the proposed variants generally outperform the classical iterations.

1 Introduction

The transition probability matrix of an M/G/1-type Markov chain is a block Hessenberg matrix P of the form

$$ P=\left[\begin{array}{cccc} B_{0} & B_{1}& B_{2} & {\ldots} \\ A_{-1} & A_{0} & A_{1} & {\ldots} \\ & A_{-1} & A_{0} & {\ddots} \\ & & {\ddots} & \ddots \end{array}\right], $$

(1)

with $A_{i}, B_{i} \in \mathbb R^{n\times n}\geq 0$ and ${\sum }_{i=0}^{\infty } B_{i}$ and ${\sum }_{i=-1}^{\infty } A_{i}$ stochastic matrices.

In the sequel, given a real matrix A = (a_ij)_{i= 1,…,m,j= 1,…,n}, we write A ≥ 0 (A > 0) if a_ij ≥ 0 (a_ij > 0) for any i,j. A stochastic matrix is a matrix A ≥ 0 such that Ae = e, where e is the column vector having all the entries equal to 1.

In the positive recurrent case, the computation of the steady state vector π of P, such that

$$ \boldsymbol{\pi}^{T} P=\boldsymbol{\pi}^{T}, \quad \boldsymbol{\pi}^{T}\boldsymbol{e}=1, \quad \boldsymbol{\pi}\geq \boldsymbol{0}, $$

(2)

is related with the solution of the unilateral power series matrix equation

$$ X= A_{-1} + A_{0} X + A_{1} X^{2} + A_{2} X^{3} +\ldots. $$

(3)

Indeed, this equation has a componentwise minimal non-negative solution G which determines, by means of Ramaswami’s formula [1], the vector π.

Among the easy-to-use, but still effective, tools for numerically solving (3), there are fixed point iterations (see [2] and the references given therein for a general review of these methods). The intrinsic simplicity of such schemes makes them attractive in domains where high performance computing is crucial. But they come at a price: the convergence can become very slow especially for problems which are close to null recurrent. The design of acceleration methods (also known as extrapolation methods) for fixed point iterations is a classical topic in numerical analysis [3]. Relaxation techniques are commonly used for the acceleration of classical stationary iterative solvers for large systems. In this paper, we introduce some new coupled fixed point iterations for solving (3), which can be combined with relaxation techniques to speed up their convergence. More specifically, we first observe that computing the solution of the matrix (3) is formally equivalent to solving a semi-infinite block Toeplitz, block Hessenberg linear system. Customary block iterative algorithms applied for the solution of this system yield classical fixed point iterations. In particular, the traditional and the U-based fixed point iterations [2] originate from the block Jacobi and the block Gauss-Seidel method, respectively. Recently, in [4], the authors show that some iterative solvers based on a block staircase partitioning outperform the block Jacobi and the block Gauss-Seidel method for M-matrix linear systems in block Hessenberg form. Indeed, the application of the staircase splitting to the block Toeplitz, block Hessenberg linear system associated with (3) yields the new coupled fixed point iteration (10), starting from an initial approximation X₀. The contribution of this paper is aimed at highlighting the properties of the sequences defined in (10).

We show that, if X₀ = 0, the sequence {X_k}_k defined in (10) converges to G faster than the traditional fixed point iteration. In the case where the starting matrix X₀ of (10) is any row stochastic matrix and G is also row stochastic, we prove that the sequence {X_k}_k still converges to G. Moreover, by comparing the mean asymptotic rates of convergence, we conclude that (10) is asymptotically faster than the traditional fixed point iteration.

Since, at each iteration, the scheme (10) determines two approximations, we propose to combine them by using a relaxation technique. Therefore, the approximation computed at the k th step takes the form of a weighted average between Y_k and X_k+ 1. The modified relaxed variant is defined by the sequence (11), where ω_k+ 1 is the relaxation parameter. The convergence results proved for the sequences (10) can be easily extended to the modified scheme in the case of under-relaxation, that is, when the parameter ω_k is such that 0 ≤ ω_k ≤ 1. Heuristically, it is argued that over-relaxation values (ω_k > 1) can improve the convergence. If X₀ = 0, under some suitable assumptions, a theoretical estimate of the asymptotic convergence rate of (11) is given, which confirms this heuristic. Moreover, an adaptive strategy is devised, which makes possible to perform over-relaxed iterations of (11), by still ensuring the convergence of the overall iterative process. The results of an extensive numerical experimentation confirm the effectiveness of the proposed variants, which generally outperform the U-based fixed point iteration for nearly null recurrent problems. In particular, the over-relaxed scheme (11) with X₀ = 0, combined with the adaptive strategy for parameter estimation, is capable to significantly improve the convergence, without increasing the computational cost.

The paper is organized as follows. In Section 2, we set up the theoretical framework, by briefly recalling some preliminary properties and assumptions. In Section 3, we revisit classical fixed point iterations for solving (3), by establishing the link with the iterative solution of an associated block Toeplitz block Hessenberg linear system. In Section 4, we introduce the new fixed point iteration (10) and we prove some convergence results. The relaxed variant (11), as well as the generalizations of convergence results for this variant, are described in Section 5. Section 6 deals with a formal analysis of the asymptotic convergence rate of both (10) and (11). Adaptive strategies for the choice of the relaxation parameter are discussed in Section 7, together with their cost analysis, under some simplified assumptions. Finally, the results of an extensive numerical experimentation are presented in Section 8, whereas conclusions and future work are the subjects of Section 9.

2 Preliminaries and assumptions

Throughout the paper, we assume that A_i, i ≥− 1, are n × n nonnegative matrices, such that their sum $A={\sum }_{i=-1}^{\infty } A_{i}$ is irreducible and row stochastic, that is, Ae = e, $\boldsymbol {e}=\left [1, \ldots , 1\right ]^{T}$. According to the results of [2, Chapter 4], such assumption implies that (3) has a unique componentwise minimal nonnegative solution G; moreover, I_n − A₀ is a nonsingular M-matrix and, hence, (I − A₀)^− 1 ≥ 0.

Furthermore, in view of the Perron Frobenius Theorem, there exists a unique vector v such that v^TA = v^T and v^Te = 1, v > 0. If the series ${\sum }_{i=-1}^{\infty } iA_{i}$ is convergent, we may define the vector $\boldsymbol {w}={\sum }_{i=-1}^{\infty } iA_{i}\boldsymbol {e}\in \mathbb { R}^{n}$. In the study of M/G/1-type Markov chains, the drift is the scalar number η = v^Tw [5]. The sign of the drift determines the positive recurrence of the M/G/1-type Markov chain [2].

When explicitly stated, we will assume the following additional condition:

A1.:

The series ${\sum }_{i=-1}^{\infty } iA_{i}$ is convergent and η < 0.

Under assumption [A1], the componentwise minimal nonnegative solution G of (3) is stochastic, i.e., Ge = e ([2]). Moreover, G is the only stochastic solution.

3 Nonlinear matrix equations and structured linear systems

In this section, we reinterpret classical fixed point iterations for solving the matrix (3) in terms of iterative methods for solving a structured linear system.

Formally, the power series matrix (3) can be rewritten as the following block Toeplitz, block Hessenberg linear system

$$ \left[\begin{array}{cccc} I_{n}-A_{0} & -A_{1}& -A_{2} & {\ldots} \\ -A_{-1} & I_{n} -A_{0}& -A_{1} & {\ldots} \\ & - A_{-1} & I_{n}-A_{0} & {\ddots} \\ & & {\ddots} & \ddots \end{array}\right]\left[\begin{array}{cccc} X \\ X^{2} \\ X^{3} \\ \vdots \end{array}\right]=\left[\begin{array}{cccc} A_{-1} \\ 0 \\ 0 \\ \vdots \end{array}\right]. $$

The above linear system can be expressed in compact form as

$$ H \hat{\mathbf{X}} = \boldsymbol{E} A_{-1}, \ H=I -\tilde P, $$

(4)

where $\hat {\mathbf {X}}=\left [X^{T}, (X^{T})^{2}, \ldots \right ]^{T}$, $\tilde P$ is the matrix obtained from P in (1) by removing its first block row and block column, and $\boldsymbol {E}=\left [I_{n}, 0_{n}, \ldots \right ]^{T}$.

Classical fixed point iterations for solving (3) can be interpreted as iterative methods for solving (4), based on suitable partitionings of the matrix H. For instance, from the partitioning H = M − N, where M = I and $N=\tilde P$, we find that the block vector $\hat X$ is a solution of the fixed point problem

$$ \hat{\mathbf{X}}=\tilde P \hat{\mathbf{X}} + \boldsymbol{E} A_{-1}. $$

(5)

From this equation, we may generate the sequence of block vectors

$$ \hat{\mathbf{X}}_{k}= \begin{bmatrix} X_{k}\\ {X_{k}^{2}}\\ {X_{k}^{3}}\\ \vdots \end{bmatrix},~~~ \mathbf{Z_{k+1}}= \begin{bmatrix} X_{k+1}\\ X_{k+1} X_{k}\\ X_{k+1} {X_{k}^{2}}\\ \vdots \end{bmatrix}, $$

such that

$$ \boldsymbol{Z}_{k+1}=\tilde P \boldsymbol{\hat X_{k}} + \boldsymbol{E} A_{-1},~~k=0,1,\ldots. $$

We may easily verify that the sequence {X_k}_k coincides with the sequence generated by the so-called natural fixed point iteration $X_{k+1}={\sum }_{i=-1}^{\infty } A_{i} X_{k}^{i+1}$, k = 0,1,,…, applied to (3).

Similarly, the Jacobi partitioning, where M = I ⊗ (I_n − A₀) and N = M − H, which leads to the sequence

$$ M \boldsymbol{Z}_{k+1}= N \boldsymbol{\hat X_{k}} + \boldsymbol{E} A_{-1},~~k=0,1,\ldots, $$

corresponds to the traditional fixed point iteration

$$ (I_{n}-A_{0})X_{k+1}= A_{-1} +\sum\limits_{i=1}^{\infty} A_{i} X_{k}^{i+1},~~k\ge0. $$

(6)

The anti-Gauss-Seidel partitioning, where M is the block upper triangular part of H and N = M − H, determines the fixed point iteration

$$ \left( I_{n}-\sum\limits_{i=0}^{\infty} A_{i}{X_{k}^{i}}\right)X_{k+1}=A_{-1},~~k\ge 0, $$

(7)

introduced and named U-based iteration in [6]. In some references (see for instance [7]), the fixed point iteration (7) is called SS iteration, where the acronym SS stands for Successive Substitution.

The convergence properties of these three fixed point iterations are analyzed in [2]. Among the three iterations, (7) is the fastest and also the most expensive since it requires the solution of a linear system (with multiple right-hand sides) at each iteration. Moreover, it turns out that fixed point iterations exhibit arbitrarily slow convergence for problems which are close to null recurrence. In particular, for positive recurrent Markov chains having a drift η close to zero, the convergence slows down and the number of iterations becomes arbitrarily large. In the next sections, we present some new fixed point iterations which offer several advantages in terms of computational efficiency and convergence properties when compared with (7).

4 A new fixed point iteration

Recently, in [4], a comparative analysis has been performed for the asymptotic convergence rates of some regular splittings of a non-singular block upper Hessenberg M-matrix of finite size. The conclusion is that the staircase splitting is faster than the anti-Gauss-Seidel splitting, that in turn is faster than the Jacobi splitting. The second result is classical, while the first one is somehow surprising since the matrix M in the staircase splitting is much more sparse than the corresponding matrix in the anti-Gauss-Seidel partitioning and the splittings are not comparable. Inspired from these convergence properties, we introduce a new fixed point iteration for solving (3), based on the staircase partitioning of H, namely,

$$ M=\left[\begin{array}{cccccccccc} I_{n}-A_{0} \\ -A_{-1} & I_{n}-A_{0} & -A_{1} \\ & & I_{n}-A_{0} \\ & & -A_{-1} & I_{n}-A_{0} & -A_{1}\\ &&&& I_{n}-A_{0} \\ &&&&\times & \times & \times \\ &&&&&&\times &\phantom{a} \\ \end{array}\right], \quad N=M-H. $$

(8)

The splitting has attracted interest for applications in parallel computing environments [8, 9]. In principle, the alternating structure of the matrix M in (8) suggests several different iterative schemes.

From one hand, the odd block entries of the system $M \boldsymbol {Z}_{k+1}=N\boldsymbol {\hat X_{k}} + \boldsymbol {E} A_{-1}$ yield the traditional fixed point iteration. On the other hand, the even block entries lead to the implicit scheme $-A_{-1} + (I_{n}-A_{0})X_{k+1} -A_{1} X_{k+1} X_{k} ={\sum }_{i=2}^{\infty } A_{i}X_{k}^{i+1}$, where a Sylvester equation should be solved at each step. Differently, by looking at the structure of the matrix M on the whole, we introduce the following composite two-stage iteration:

$$ \left\{\begin{array}{ll} (I_{n} -A_{0}) Y_{k}=A_{-1} +{\sum}_{i=1}^{\infty} A_{i} X_{k}^{i+1}; \\ -A_{-1} + (I_{n}-A_{0})X_{k+1} -A_{1} {Y_{k}^{2}}={\sum}_{i=2}^{\infty} A_{i}X_{k}^{i+1}, \end{array}\right. \quad k\geq 0, $$

(9)

or, equivalently,

$$ \left\{\begin{array}{ll} (I_{n} -A_{0}) Y_{k}=A_{-1} +{\sum}_{i=1}^{\infty} A_{i} X_{k}^{i+1}; \\ X_{k+1}= Y_{k} + (I_{n}-A_{0})^{-1} A_{1} ({Y_{k}^{2}}-{X_{k}^{2}}), \end{array}\right. \quad k\geq 0, $$

(10)

starting from an initial approximation X₀. At each step k, this scheme consists of a traditional fixed point iteration, as (6), that computes Y_k from X_k, followed by a cheap correction step for computing the new approximation X_k+ 1.

Observe that, in the QBD case where A_i = 0 for i ≥ 2, then $Y_{k}=(I-A_{0})^{-1}(A_{-1}+A_{1} {X_{k}^{2}})$ and $X_{k+1}=Y_{k}+(I-A_{0})^{-1}({Y_{k}^{2}}-{X_{k}^{2}})$. By replacing Y_k in the latter expression, we find that X_k+ 1 coincides with the matrix obtained by applying two steps of the traditional fixed point iteration (6), starting from X_k. In the general case, the matrix X_k+ 1 can be interpreted as a refinement of the approximation obtained by the traditional fixed point iteration (6). The computation of such refinement is generally (except for the QBD case) cheaper than applying a second step of traditional fixed point iteration.

As for classical fixed point iterations, the convergence is guaranteed when X₀ = 0.

Proposition 1

Assume that X₀ = 0. Then the sequence $\{X_{k}\}_{k\in \mathbb N}$ generated by (10) converges monotonically to G.

Proof 1

We show by induction on k that 0 ≤ X_k ≤ Y_k ≤ X_k+ 1 ≤ G for any k ≥ 0. For k = 0, we verify easily that

$$ X_{1}\geq Y_{0}=(I_{n}-A_{0})^{-1}A_{-1}\geq 0=X_{0}, \quad (I_{n} -A_{0})X_{1}\leq A_{-1} +A_{1}G^{2}\leq (I_{n} -A_{0})G, $$

which gives G ≥ X₁. Suppose now that G ≥ X_k ≥ Y_k− 1 ≥ X_k− 1, k ≥ 1. We find that

$$ (I_{n} -A_{0}) Y_{k}=A_{-1} +\sum\limits_{i=1}^{\infty} A_{i} X_{k}^{i+1}\geq A_{-1} + A_{1} Y_{k-1}^{2} + \sum\limits_{i=2}^{\infty} A_{i}X_{k-1}^{i+1} =(I_{n} -A_{0}) X_{k} $$

and

$$ (I_{n} -A_{0}) Y_{k}=A_{-1} +\sum\limits_{i=1}^{\infty} A_{i} X_{k}^{i+1}\leq A_{-1} +\sum\limits_{i=1}^{\infty} A_{i} G^{i+1}=(I_{n} -A_{0}) G. $$

By multiplying both sides by the inverse of I − A₀, we obtain that G ≥ Y_k ≥ X_k. This also implies that ${Y_{k}^{2}}-{X_{k}^{2}}\geq 0$ and therefore X_k+ 1 ≥ Y_k. Since

$$ (I_{n} -A_{0}) X_{k+1}=A_{-1} + A_{1} {Y_{k}^{2}}+\sum\limits_{i=2}^{\infty} A_{i} X_{k}^{i+1}\leq (I_{n} -A_{0}) G, $$

we prove similarly that G ≥ X_k+ 1. It follows that $\{X_{k}\}_{k\in \mathbb N}$ is convergent, the limit solves (3) by continuity, and, hence, the limit coincides with the matrix G, since G is the minimal nonnegative solution. □

A similar result is valid also in the case where X₀ is a stochastic matrix, assuming that [A1] holds, so that G is stochastic.

Proposition 2

Assume that condition [A1] is fulfilled and that X₀ is a stochastic matrix. Then, the sequence $\{X_{k}\}_{k\in \mathbb N}$ generated by (10) converges to G.

Proof 2

From (9), we obtain that

$$ \left\{\begin{array}{ll} (I_{n} -A_{0}) Y_{k}=A_{-1} +{\sum}_{i=1}^{\infty} A_{i} X_{k}^{i+1}; \\ (I_{n} -A_{0}) X_{k+1}=A_{-1} + A_{1} {Y_{k}^{2}}+{\sum}_{i=2}^{\infty} A_{i} X_{k}^{i+1} \end{array}\right. \quad k\geq 0, $$

which gives that X_k ≥ 0 and Y_k ≥ 0, for any $k\in \mathbb N$, since X₀ ≥ 0. By assuming that X₀e = e, we may easily show by induction that Y_ke = X_ke = e for any k ≥ 0. Therefore, all the matrices X_k and Y_k, $k\in \mathbb N$, are stochastic. Let $\{\hat X_{k}\}_{k\in \mathbb N}$ be the sequence generated by (10) with $\hat X_{0}=0$. We can easily show by induction that $X_{k}\geq \hat X_{k}$ for any $k\in \mathbb N$. Since $\lim _{k\to \infty }\hat X_{k}=G$, then any convergent subsequence of $\{X_{k}\}_{k\in \mathbb N}$ converges to a stochastic matrix S such that S ≥ G. Since G is also stochastic, it follows that S = G and therefore, by compactness, we conclude that the sequence $\{X_{k}\}_{k\in \mathbb N}$ is also convergent to G. □

Propositions 1 and 2 are global convergence results. An estimate of the rate of convergence of (10) will be provided in Section 6, together with a comparison with other existing methods.

5 A relaxed variant

At each iteration, the scheme (10) determines two approximations which can be combined by using a relaxation technique, that is, the approximation computed at the k-th step takes the form of a weighted average between Y_k and X_k+ 1:

$$ X_{k+1}= \omega_{k+1} (Y_{k} + (I_{n}-A_{0})^{-1} A_{1} ({Y_{k}^{2}}-{X_{k}^{2}})) + (1-\omega_{k+1})Y_{k}, \quad k\geq 0. $$

In matrix terms, the resulting relaxed variant of (10) can be written as

$$ \left\{\begin{array}{ll} (I_{n} -A_{0}) Y_{k}=A_{-1} +{\sum}_{i=1}^{\infty} A_{i} X_{k}^{i+1}; \\ X_{k+1}= Y_{k} + \omega_{k+1} (I_{n}-A_{0})^{-1} A_{1} ({Y_{k}^{2}}-{X_{k}^{2}}), \end{array}\right. \quad k\geq 0. $$

(11)

If ω_k = 0, for k ≥ 1, the relaxed scheme reduces to the traditional fixed point iteration (6). If ω_k = 1, for k ≥ 1, the relaxed scheme coincides with (10). Values of ω_k greater than 1 can speed up the convergence of the iterative scheme.

Concerning convergence, the proof of Proposition 1 can immediately be generalized to show that the sequence {X_k}_k defined by (11), with X₀ = 0, converges for any ω_k = ω, k ≥ 1, such that 0 ≤ ω ≤ 1. Moreover, let $\{X_{k}\}_{k\in \mathbb N}$ and $\{\hat X_{k}\}_{k\in \mathbb N}$ be the sequences generated by (11) for ω_k = ω and $\omega _{k}=\hat \omega$ with $0\leq \omega \leq \hat \omega \leq 1$, respectively. It can be easily shown that $G\geq \hat X_{k} \geq X_{k}$ for any k and, hence, that the iterative scheme (10) converges faster than (11) if 0 ≤ ω_k = ω < 1.

The convergence analysis of the modified scheme (11) for ω_k > 1 is much more involved since the choice of a relaxation parameter ω_k > 1 can destroy the monotonicity and the nonnegativity of the approximation sequence, which are at the core of the proofs of Propositions 1 and 2 . In order to maintain the convergence properties of the modified scheme we introduce the following definition.

Definition 1

The sequence {ω_k}_k≥ 1 is eligible for the scheme (11) if ω_k ≥ 0, k ≥ 1, and the following two conditions are satisfied:

$$ \omega_{k+1}A_{1}({Y_{k}^{2}}-{X_{k}^{2}})\leq A_{1}(X_{k+1}^{2}-{X_{k}^{2}}) +\sum\limits_{i=2}^{\infty} A_{i}(Y_{k}^{i+1}-X_{k}^{i+1}), \quad k\geq 0 $$

(12)

and

$$ X_{k+1}\boldsymbol{e} =Y_{k}\boldsymbol{e} + \omega_{k+1} (I_{n}-A_{0})^{-1} A_{1} ({Y_{k}^{2}}-{X_{k}^{2}})\boldsymbol{e}\leq \boldsymbol{e}, \quad k\geq 0. $$

(13)

It is worth noting that condition (12) is implicit since the construction of X_k+ 1 also depends on the value of ω_k+ 1. By replacing X_k+ 1 in (12) with the expression in the right-hand side of (11), we obtain a quadratic inequality with matrix coefficients in the variable ω_k+ 1. Obviously the constant sequence ω_k = ω, k ≥ 1, with 0 ≤ ω ≤ 1, is an eligible sequence.

The following generalization of Proposition 1 holds.

Proposition 3

Set X₀ = 0 and let condition [A1] be satisfied. If {ω_k}_k≥ 1 is eligible then the sequence $\{X_{k}\}_{k\in \mathbb N}$ generated by (11) converges monotonically to G.

Proof 3

We show by induction that 0 ≤ X_k ≤ Y_k ≤ X_k+ 1 ≤ G. For k = 0, we have

$$ (I_{n}-A_{0})X_{1}\geq (I_{n}-A_{0})Y_{0}=A_{-1}\geq 0=X_{0} $$

which gives immediately X₁ ≥ Y₀ ≥ 0. Moreover, X₁e ≤e. Suppose now that X_k ≥ Y_k− 1 ≥ X_k− 1 ≥ 0, k ≥ 1. We find that

$$ \begin{array}{lll} (I_{n} -A_{0}) X_{k}=A_{-1} + A_{1}(X_{k-1}^{2} +\omega_{k} (Y_{k-1}^{2} -X_{k-1}^{2}))+ {\sum}_{i=2}^{\infty} A_{i} X_{k-1}^{i+1}\leq \\ \leq A_{-1}+A_{1} X_{k-1}^{2} + A_{1} ({X_{k}^{2}} -X_{k-1}^{2}) + {\sum}_{i=2}^{\infty} A_{i}(Y_{k-1}^{i+1}-X_{k-1}^{2})+ {\sum}_{i=2}^{\infty} A_{i} X_{k-1}^{i+1}\leq\\ \leq A_{-1} + A_{1} {X_{k}^{2}} + {\sum}_{i=2}^{\infty} A_{i} Y_{k-1}^{i+1}\leq A_{-1} + {\sum}_{i=1}^{\infty} A_{i} X_{k}^{i+1}=(I_{n} -A_{0}) Y_{k} \end{array} $$

from which it follows Y_k ≥ X_k ≥ 0. This also implies that X_k+ 1 ≥ Y_k. From (13), it follows that X_ke ≤e for all k ≥ 0 and therefore the sequence of approximations is upper bounded and it has a finite limit H. By continuity, we find that H solves the matrix (3) and He ≤e. Since G is the unique stochastic solution, then H = G. □

Remark 1

As previously mentioned, condition (12) is implicit, since X_k+ 1 also depends on ω_k+ 1. An explicit condition can be derived by noting that

$$ A_{1}(X_{k+1}^{2}-{X_{k}^{2}}) \geq A_{1}(({Y_{k}^{2}}-{X_{k}^{2}}) +\omega_{k+1}(Y_{k}{\Gamma}_{k} + {\Gamma}_{k} Y_{k})), $$

with ${\Gamma }_{k}=(I_{n}-A_{0})^{-1} A_{1} ({Y_{k}^{2}}-{X_{k}^{2}})$. There follows that (12) is fulfilled whenever

$$ \frac{\omega_{k+1}-1}{\omega_{k+1}} A_{1}(({Y_{k}^{2}}-{X_{k}^{2}})\leq (Y_{k}{\Gamma}_{k} + {\Gamma}_{k} Y_{k}) + \omega_{k+1}^{-1} \sum\limits_{i=2}^{\infty} A_{i}(Y_{k}^{i+1}-X_{k}^{i+1}) $$

which can be reduced to a linear inequality in ω_k+ 1 over a fixed search interval. Let $\omega \in [1, \hat \omega ]$ be such that

$$ \frac{\omega_{}-1}{\omega_{}} A_{1}(({Y_{k}^{2}}-{X_{k}^{2}})\leq (Y_{k}{\Gamma}_{k} + {\Gamma}_{k} Y_{k}) + {\hat \omega}^{-1} \sum\limits_{i=2}^{\infty} A_{i}(Y_{k}^{i+1}-X_{k}^{i+1}). $$

(14)

Then we can impose that

$$ \omega_{k+1}=\max\{\omega_{}\colon \omega \in [1, \hat \omega] \land (14) \ holds\}. $$

(15)

From a computational viewpoint, the strategy based on (14) and (15) for the choice of the value of ω_k+ 1 can be too much expensive and some weakened criterion should be considered (compare with Section 7 below).

In the following section, we perform a convergence analysis to estimate the convergence rate of (11) in the stationary case ω_k = ω, k ≥ 1, as a function of the relaxation parameter.

6 Estimate of the convergence rate

Relaxation techniques are usually aimed at accelerating the convergence speed of frustratingly slow iterative solvers. Such inefficient behavior is typically exhibited when the solver is applied to a nearly singular problem. Incorporating some relaxation parameter into the iterative scheme (3) can greatly improve its convergence rate. Preliminary insights on the effectiveness of relaxation techniques applied for the solution of the fixed point problem (5) come from the classical analysis for stationary iterative solvers and are developed in Section 6.1. A precise convergence analysis is presented in Section 6.2.

6.1 Finite dimensional convergence analysis

Suppose that H in (5) is block tridiagonal of finite size m = nℓ, ℓ even. We are interested in comparing the iterative algorithm based on the splitting (8) with other classical iterative solvers for the solution of a linear system with coefficient matrix H. As usual, we can write H = D − P₁ − P₂, where D is block diagonal, while P₁ and P₂ are staircase matrices with zero block diagonal. The eigenvalues λ_i of the Jacobi iteration matrix satisfy

$$ 0=\det(\lambda_{i} I_{\ell} -D^{-1}P_{1} -D^{-1}P_{2}). $$

Let us consider a relaxed scheme where the matrix M is obtained from (8) by multiplying the off-diagonal blocks by ω. The eigenvalues μ_i of the iteration matrix associated with the relaxed staircase regular splitting are such that

$$ 0=\det(\mu_{i} (D-\omega P_{1}) -(P_{2}+(1-\omega) P_{1})) $$

and, equivalently,

$$ 0=\det(\mu_{i} I_{\ell} -(\mu_{i} \omega +(1-\omega))D^{-1}P_{1} -D^{-1}P_{2}). $$

By using a similarity transformation induced by the matrix $S=I_{\ell /2} \otimes diag\left [I_{n},\alpha I_{n}\right ]$, we find that

$$ \begin{array}{@{}rcl@{}} &\det(\mu_{i} I -(\mu_{i} \omega +(1-\omega))D^{-1}P_{1} -D^{-1}P_{2})= \\ &\det(\mu_{i} I_{\ell} -\alpha (\mu_{i} \omega +(1-\omega))D^{-1}P_{1} -\frac{1}{\alpha}D^{-1}P_{2}). \end{array} $$

There follows that

$$ \mu_{i}\alpha=\lambda_{i} $$

whenever α fulfills

$$ \alpha (\mu_{i} \omega +(1-\omega))=\frac{1}{\alpha}. $$

Therefore, the eigenvalues of the Jacobi and relaxed staircase regular splittings are related by

$$ {\mu_{i}^{2}} -{\lambda_{i}^{2}} \mu \omega + {\lambda_{i}^{2}} (\omega-1)=0. $$

For ω = 0, the staircase splitting reduces to the Jacobi partitioning. For ω = 1, we find that $\mu _{i}={\lambda _{i}^{2}}$, which yields the classical relation between the spectral radii of Jacobi and Gauss-Seidel methods. It is well known that the asymptotic convergence rates of Gauss-Seidel and the staircase iteration coincide, when applied to a block tridiagonal matrix [11]. For ω > 1, the spectral radius of the relaxed staircase scheme can be significantly smaller than the spectral radius of the same scheme for ω = 1. In Fig. 1, we illustrate the plot of the function

$$ \rho_{S}(\omega)= \left\vert \frac{\lambda^{2} \omega + \sqrt{\lambda^{4} \omega^{2} -4 \lambda^{2} (\omega-1)}}{2}\right\vert, \quad 1\leq \omega \leq 2, $$

for a fixed λ = 0.999. For the best choice $\omega =\omega ^{\star }=2 \frac { 1 + \sqrt {1-\lambda ^{2}}}{\lambda ^{2}}$, we find $\rho _{S}(\omega ^{\star })=1-\sqrt {1-\lambda ^{2}} =\frac {\lambda ^{2}}{1+\sqrt {1-\lambda ^{2}}}$.

Fig. 1

Plot of ρ_S(ω) for ω ∈ [1,2] and λ = 0.999

6.2 Asymptotic convergence rate

A formal analysis of the asymptotic convergence rate of the relaxed variants (11) can be carried out by using the tools described in [12]. In this section, we relate the approximation error at two subsequent steps and we provide an estimate of the asymptotic rate of convergence, expressed as the spectral radius of a suitable matrix depending on ω.

Hereafter, it is assumed that assumption [A1] is verified.

6.2.1 The case X ₀ = 0

Let us introduce the error matrix E_k = G − X_k, where $\{X_{k}\}_{k\in \mathbb N}$ is generated by (11) with X₀ = 0. We also define E_k+ 1/2 = G − Y_k, for k = 0,1,2,…. Suppose that

C0.:

{ω_k}_k is an eligible sequence according to Definition 1.

Under this assumption, from Proposition 3, the sequence {X_k}_k converges monotonically to G and E_k ≥ 0, E_k+ 1/2 ≥ 0. Since E_k ≥ 0 and $\Vert E_{k}\Vert _{\infty }=\Vert E_{k}\boldsymbol {e}\Vert _{\infty }$, we analyze the convergence of the vector 𝜖_k = E_ke, k ≥ 0.

We have

$$ (I_{n}-A_{0}) E_{k+1/2}= \sum\limits_{i=1}^{\infty} A_{i} (G^{i+1}-X_{k}^{i+1})= \sum\limits_{i=1}^{\infty} A_{i}\sum\limits_{j=0}^{i} G^{j} E_{k}X_{k}^{i-j}. $$

(16)

Similarly, for the second equation of (11), we find that

$$ (I_{n}-A_{0}) E_{k+1}= (I_{n}-A_{0}) E_{k+1/2} -\omega_{k+1} A_{1}((G^{2}-{X_{k}^{2}})-(G^{2}-{Y_{k}^{2}})), $$

which gives

$$ \begin{array}{@{}rcl@{}} &&(I_{n}-A_{0}) E_{k+1}= \\ &&(I_{n}\! - \!A_{0}) E_{k+1/2} - \omega_{k+1}A_{1}(E_{k}G + X_{k} E_{k}) + \omega_{k+1}A_{1}(\!GE_{k+1/2} + E_{k+1/2} Y_{k}). \end{array} $$

(17)

Denote by R_k the matrix on the right-hand side of (16), i.e.,

$$R_{k}=\sum\limits_{i=1}^{\infty} A_{i}\sum\limits_{j=0}^{i} G^{j} E_{k}X_{k}^{i-j}. $$

Since Ge = e, (17), together with the monotonicity, yields

$$ (I_{n}-A_{0}) E_{k+1}\boldsymbol{e}\le R_{k}\boldsymbol{e}- \omega_{k+1}A_{1}(I_{n}+X_{k}) E_{k}\boldsymbol{e} +\omega_{k+1}A_{1}(I_{n}+G)(I_{n}-A_{0})^{-1}R_{k} \boldsymbol{e}. $$

(18)

Observe that R_ke ≤ WE_ke, where

$$ W=\sum\limits_{i=1}^{\infty} A_{i}\sum\limits_{j=0}^{i} G^{j}, $$

hence

$$ \boldsymbol{\epsilon}_{k+1}\le P(\omega_{k+1})\boldsymbol{\epsilon}_{k}, \quad k\geq 0, $$

(19)

where

$$ P(\omega)= (I_{n}-A_{0})^{-1}W - \omega(I_{n}-A_{0})^{-1} A_{1}(I_{n}+G)(I_{n}-(I_{n}-A_{0})^{-1}W). $$

(20)

The matrix P(ω) can be written as P(ω) = M^− 1N(ω) where

$$ M=I_{n}-A_{0},~~~ M-N(\omega)=A(\omega), $$

and

$$ A(\omega)=(I_{n}+\omega A_{1}(I_{n}+G)(I_{n}-A_{0})^{-1})(I_{n}-A_{0}-W). $$

Let us assume the following condition holds:

C1.:

The relaxation parameter ω satisfies $\omega \in [0,\hat \omega ]$, with $\hat \omega \ge 1$ such that

$$ \hat \omega A_{1}(I_{n}+G)(I_{n}-A_{0})^{-1}(I_{n}-A_{0}-W)\leq W. $$

Assumption [C1] ensures that N(ω) ≥ 0 and, therefore, P(ω) ≥ 0 and M − N(ω) = A(ω) is a regular splitting of A(ω). If [C1] is satisfied at each iteration of (11), then from (19) we obtain that

$$ \boldsymbol{\epsilon}_{k}\le P(\omega_{k})P(\omega_{k-1}){\cdots} P(\omega_{0})\boldsymbol{\epsilon}_{0},~~k\ge 1. $$

Therefore, the asymptotic rate of convergence, defined as

$$ \sigma=\limsup_{k\to\infty}\left( \frac{\| \boldsymbol{\epsilon}_{k}\|}{ \|\boldsymbol{\epsilon}_{0} \|}\right)^{1/k}, $$

where ∥⋅∥ is any vector norm, is such that

$$ \sigma\le \limsup_{k\to\infty}\| P(\omega_{k})P(\omega_{k-1}){\cdots} P(\omega_{0})\|_{\infty}^{1/k}. $$

The above properties can be summarized in the following result that gives a convergence rate estimate for iteration (11).

Proposition 4

Under Assumptions [A1], [C0] and [C1], for the fixed point iteration (11) applied with ω_k = ω for any k ≥ 0, we have the following convergence rate estimate:

$$ \sigma=\limsup_{k\to\infty}\left( \frac{\|\boldsymbol{\epsilon}_{k}\|}{ \| \boldsymbol{\epsilon}_{0} \|}\right)^{1/k}\leq \rho_{\omega}, $$

where P(ω) is defined in (20) and ρ_ω = ρ(P(ω)) is the spectral radius of P(ω).

When ω = 0, we find that A(0) = I_n − A₀ − W = I_n − V, where $V={\sum }_{i=0}^{\infty } A_{i}{\sum }_{j=0}^{i} G^{j}$. According to Theorem 4.14 in [2], I − V is a nonsingular M-matrix and therefore, since N(0) ≥ 0 and M^− 1 ≥ 0, A(0) = M − N(0) is a regular splitting. Hence, the spectral radius ρ₀ of P(0) is less than 1. More generally, under Assumption [C1] since

$$ I_{n} -V\leq A(\omega) \leq I_{n}-A $$

from characterization F20 in [13], we find that A(ω) is a nonsingular M-matrix and A(ω) = M − N(ω) is a regular splitting. Hence, we deduce that ρ_ω < 1. The following result gives an estimate of ρ_ω, by showing its dependence as function of the relaxation parameter.

Proposition 5

Let ω be such that $0\le \omega \le \hat \omega$ and assume that condition [C1] holds. Assume that the Perron eigenvector v of P(0) is positive. Then we have

$$ \rho_{0}-\omega (1-\rho_{0})\sigma_{\max} \le \rho_{\omega} \le \rho_{0}-\omega (1-\rho_{0})\sigma_{\min} $$

(21)

where $\sigma _{\min \limits }=\min \limits _{i} \frac {u_{i}}{v_{i}}$ and $\sigma _{\max \limits }=\max \limits _{i} \frac {u_{i}}{v_{i}}$, with u = (I_n − A₀)^− 1A₁(I + G)v. Moreover, $0\le \sigma _{\min \limits },\sigma _{\max \limits }\le \rho _{0}$.

Proof 4

In view of the classical Collatz-Wielandt formula (see [14], Chapter 8), if P(ω)v = w, where v > 0 and w ≥ 0, then

$$ \min_{i} \frac{w_{i}}{v_{i}}\le \rho_{\omega}\le \max_{i} \frac{w_{i}}{v_{i}}. $$

Observe that

$$ \begin{array}{l} \boldsymbol{w}=P(\omega)\boldsymbol{v}= P(0)\boldsymbol{v}-\omega (I_{n}-A_{0})^{-1} A_{1}(I_{n}+G)(I-P(0))\boldsymbol{v}=\\ \rho_{0} \boldsymbol{v}-\omega (1-\rho_{0}) (I_{n}-A_{0})^{-1} A_{1}(I_{n}+G)\boldsymbol{v}= \rho_{0} \boldsymbol{v}-\omega (1-\rho_{0})\boldsymbol{u}, \end{array} $$

which leads to (21), since u ≥ 0. Moreover, since A₁(I_n + G) ≤ W, then

$$ \boldsymbol{u}= (I_{n}-A_{0})^{-1} A_{1}(I_{n}+G)\boldsymbol{v}\le (I_{n}-A_{0})^{-1} W\boldsymbol{v}=\rho_{0} \boldsymbol{v}, $$

hence u_i/v_i ≤ ρ₀ for any i. □

Observe that, in the quasi-birth-and-death case, where A_i = 0 for i ≥ 2, we have A₁(I_n + G) = W and, from the proof above, u = ρ₀v. Therefore, we have $\sigma _{\min \limits }=\sigma _{\max \limits }=\rho _{0}$ and, hence, ρ_ω = ρ₀(1 − ω(1 − ρ₀)). In particular, ρ_ω linearly decreases with ω, and $\rho _{1}={\rho _{0}^{2}}$. In the general case, inequality (21) shows that the upper bound to ρ_ω linearly decreases as a function of ω. Therefore, the choice $\omega =\hat \omega$ gives the fastest convergence rate.

Remark 2

For the sake of illustration, we consider a quadratic equation associated with a block tridiagonal Markov chain taken from [15]. We set A_− 1 = W + δI, A₀ = A₁ = W where 0 < δ < 1 and $W\in \mathbb R^{n\times n}$ has zero diagonal entries and all off-diagonal entries equal to a given value α determined so that A_− 1 + A₀ + A₁ is stochastic. We find that N(ω) ≥ 0 for ω_k = ω ∈ [0,6]. In Fig. 2, we plot the spectral radius of P = P(ω). The linear plot is in accordance with Proposition 5.

Fig. 2

Plot of ρ(P(ω)) for ω ∈ [0,6]

6.2.2 The case X ₀ stochastic

In this section, we analyze the convergence of the iterative method (11) starting with a stochastic matrix X₀, that is, X₀ ≥ 0 and X₀e = e. Eligible sequences {ω_k}_k are such that X_k ≥ 0 for any k ≥ 0. This happens for 0 ≤ ω_k ≤ 1, k ≥ 1. Suppose that:

S0.:

The sequence {ω_k}_k in (11) is determined so that ω_k ≥ 0 and X_k ≥ 0 for any k ≥ 1.

Observe that the property X_ke = e, k ≥ 0 is automatically satisfied. Hence, under assumption [S0], all the approximations generated by the iterative scheme (11) are stochastic matrices and therefore, Proposition 2 can be extended in order to prove that the sequence $\{X_{k}\}_{k\in \mathbb N}$ is convergent to G.

The analysis of the speed of convergence follows from relation (17). Let us denote as $\text {vec}(A)\in \mathbb R^{n^{2}}$ the vector obtained by stacking the columns of the matrix $A\in \mathbb R^{n\times n}$ on top of one another. Recall that vec(ABC) = (C^T ⊗ A)vec(B) for any $A,B,C \in \mathbb R^{n\times n}$. By using this property, we can rewrite (17) as follows:

$$ \begin{array}{ll} & \left( I_{n} \otimes (I_{n}-A_{0})\right) \text{vec}(E_{k+1})=\\ & \omega_{k+1}\left( I_{n}\otimes A_{1}G(I_{n}-A_{0})^{-1}A_{1}G \right) \text{vec}(E_{k})+\\ &\omega_{k+1}\left( {X_{k}^{T}}\otimes A_{1}G(I_{n}-A_{0})^{-1}A_{1}\right) \text{vec}(E_{k}) +\\ & \omega_{k+1}\left( {Y_{k}^{T}}\otimes A_{1}(I_{n}-A_{0})^{-1}A_{1}G\right)\text{vec}(E_{k}) +\\ &\omega_{k+1}\left( {Y_{k}^{T}}{X_{k}^{T}} \otimes A_{1}(I_{n}-A_{0})^{-1}A_{1}\right)\text{vec}(E_{k}) +\\ & (1-\omega_{k+1})\left( I_{n} \otimes A_{1}G\right)\text{vec}(E_{k}) + (1-\omega_{k+1})\left( {X_{k}^{T}}\otimes A_{1}\right)\text{vec}(E_{k}) + \\ &\left( \sum\limits_{i=2}^{\infty} \sum\limits_{j=0}^{i}({{X_{k}^{T}}}^{i-j}\otimes A_{i}G^{j})\right)\text{vec}(E_{k}) + \\ &\omega_{k+1}\left( \sum\limits_{i=2}^{\infty} \sum\limits_{j=0}^{i}({{X_{k}^{T}}}^{i-j}\otimes A_{1}G(I_{n}-A_{0})^{-1}A_{i}G^{j})\right)\text{vec}(E_{k}) + \\&\omega_{k+1}\left( \sum\limits_{i=2}^{\infty} \sum\limits_{j=0}^{i}({{Y_{k}^{T}}}{{X_{k}^{T}}}^{i-j}\otimes A_{1}(I_{n}-A_{0})^{-1}A_{i}G^{j})\right)\text{vec}(E_{k}), \end{array} $$

(22)

for k ≥ 0. The convergence of {vec(E_k)}_k depends on the choice of ω_k+ 1, k ≥ 0. Suppose that ω_k = ω for any k ≥ 0 and [S0] holds. Then (22) can be rewritten in a compact form as

$$ \text{vec}(E_{k+1}) =H_{k} \text{vec}(E_{k}), \quad k\geq 0, $$

where H_k = H_ω(X_k,Y_k) and

$$ \lim_{k\rightarrow +\infty} H_{k}=H_{\omega}(G, G)=H_{\omega}. $$

It can be shown that the asymptotic rate of convergence σ satisfies

$$ \sigma=\limsup_{k\to\infty}\left( \frac{\|\text{vec}(E_{k+1})\|}{ \| \text{vec}(E_{0}) \|}\right)^{1/k}\leq \rho(H_{\omega}). $$

In the sequel, we compare the cases ω_k = 0, which corresponds with the traditional fixed point iteration (6), and ω_k = 1 which reduces to the staircase fixed point iteration (10).

For ω_k+ 1 = 0, k ≥ 0, we find that

$$ \text{vec}(E_{k+1})=\left( \sum\limits_{i=1}^{\infty} \sum\limits_{j=0}^{i}({{X_{k}^{T}}}^{i-j}\otimes (I_{n}-A_{0})^{-1}A_{i}G^{j})\right)\text{vec}(E_{k}), \quad k\geq 0, $$

which means that

$$ H_{0}=\sum\limits_{i=1}^{\infty} \sum\limits_{j=0}^{i}({G^{T}}^{i-j}\otimes (I_{n}-A_{0})^{-1}A_{i}G^{j}), \quad k\geq 0. $$

Let U^HG^TU = T be the Schur form of G^T and set W = (U^H ⊗ I_n). Then

$$ W \sum\limits_{i=1}^{\infty} \sum\limits_{j=0}^{i}({G^{T}}^{i-j}\otimes (I_{n}-A_{0})^{-1}A_{i}G^{j}) W^{-1}=\sum\limits_{i=1}^{\infty} \sum\limits_{j=0}^{i}({T}^{i-j}\otimes (I_{n}-A_{0})^{-1}A_{i}G^{j}) $$

which means that H₀ is similar to the matrix on the right-hand side. There follows that the eigenvalues of H₀ belong to the set

$$ \bigcup_{\lambda}\left\{\mu\colon \mu \textrm{ is eigenvalue of } \sum\limits_{i=1}^{\infty} \sum\limits_{j=0}^{i}(\lambda^{i-j}(I_{n}-A_{0})^{-1}A_{i}G^{j})\right\} $$

with λ eigenvalue of G. Since G is stochastic we have |λ|≤ 1. Thus, from

$$ \left\vert\sum\limits_{i=1}^{\infty} \sum\limits_{j=0}^{i}\lambda^{i-j}(I_{n}-A_{0})^{-1}A_{i}G^{j}\right\vert \leq {\sum}_{i=1}^{\infty} \sum\limits_{j=0}^{i}(I_{n}-A_{0})^{-1}A_{i}G^{j} =P(0) $$

we conclude that ρ(H₀) ≤ ρ(P(0)) in view of the Wielandt theorem [14].

A similar analysis can be performed in the case ω_k = 1, k ≥ 0. We find that

$$ \begin{array}{@{}rcl@{}} H_{1} &=& \left( I_{n} \otimes (I_{n}-A_{0})^{-1}\right) \left( \sum\limits_{i=2}^{\infty} \sum\limits_{j=0}^{i}({G^{T}}^{i-j}\otimes A_{i}G^{j})\right.\\ &&+ \left. \sum\limits_{i=1}^{\infty} \sum\limits_{j=0}^{i} \left( ({G^{T}}^{i-j}\otimes A_{1}G(I_{n}-A_{0})^{-1}A_{i}G^{j}) \right.\right.\\&&\left.\left.+ ({G^{T}}^{i-j+1}\otimes A_{1}(I_{n}-A_{0})^{-1}A_{i}G^{j})\right)\vphantom{{\sum}_{i=2}^{\infty}} \right). \end{array} $$

By the same arguments as above, we find that the eigenvalues of H₁ belong to the set

$$ \cup_{\lambda}\{\mu\colon \mu \textrm{ is eigenvalue of } (I_{n}-A_{0})^{-1} N(\lambda)\}, $$

with λ eigenvalue of G^T, and

$$ \begin{array}{ll}N(\lambda)={\sum}_{i=2}^{\infty} {\sum}_{j=0}^{i}(\lambda^{i-j}A_{i}G^{j}) + {\sum}_{i=1}^{\infty} {\sum}_{j=0}^{i}(\lambda^{i-j}A_{1}G(I_{n}-A_{0})^{-1}A_{i}G^{j}) + \\ {\sum}_{i=1}^{\infty} {\sum}_{j=0}^{i}(\lambda^{i-j+1} A_{1}(I_{n}-A_{0})^{-1}A_{i}G^{j}). \end{array} $$

Since

$$ \vert(I_{n}-A_{0})^{-1} N(\lambda)\vert\leq P(1) $$

we conclude that

$$ \rho(H_{1})\leq \rho(P(1)). $$

Therefore, in the application of (10), we expect a faster convergence when X₀ is a stochastic matrix, rather than X₀ = 0. Indeed, numerical results shown in Section 5 exhibit a very rapid convergence profile when X₀ is stochastic, even better than the one predicted by ρ(H₁). This might be explained with the dependence of the asymptotic convergence rate on the second eigenvalue of the corresponding iteration matrices as reported in [12].

7 Adaptive strategies and efficiency analysis

The efficiency of fixed point iterations depends on both speed of convergence and complexity properties. Markov chains are generally defined in terms of sparse matrices. To take into account this feature we assume that γn², γ = γ(n), multiplications/divisions are sufficient to perform the following tasks:

• 1. to compute a matrix multiplication of the form A_i ⋅ W, where $A_{i}, W \in \mathbb R^{n\times n}$;

• 2. to solve a linear system of the form (I − A₀)Z = W, where $A_{0}, W \in \mathbb R^{n\times n}$.

We also suppose that the transition matrix P in (1) is banded, hence A_i = 0 for i > q. This is always the case in numerical computations where the matrix power series ${\sum }_{i=-1}^{\infty } A_{i} X_{k}^{i+1}$ has to be approximated by some finite partial sum ${\sum }_{i=-1}^{q} A_{i} X_{k}^{i+1}$. Under these assumptions, we obtain the following cost estimates per step:

• 1. the traditional fixed point iteration (6) requires qn³ + 2γn² + O(n²) multiplicative operations;

• 2. the U-based fixed point iteration (7) requires (q + 4/3)n³ + γn² + O(n²) multiplicative operations;

• 3. the staircase-based (S-based) fixed point iteration (10) requires (q + 1)n³ + 4γn² + O(n²) multiplicative operations.

Observe that the cost of the S-based fixed point iteration is comparable with the cost of the U-based iteration, which is the fastest among classical iterations [2]. Therefore, in the cases where the U/S-based fixed point iterative schemes require significantly less iterations to converge, these algorithms are more efficient than the traditional fixed point iteration.

Concerning the relaxed versions (11) of the S-based fixed point iteration for a given fixed choice of ω_k = ω, we get the same complexity of the unmodified scheme (10) obtained with ω_k = ω = 1. The adaptive selection of ω_k+ 1 exploited in Proposition 3 and Remark 1 with X₀ = 0 requires more care.

The strategy (14) is computationally unfeasible since it needs the additional computation of ${\sum }_{i=2}^{q} A_{i}Y_{k}^{i+1}$. To approximate this quantity, we recall that

$$ A_{i}(Y_{k}^{i+1} -X_{k}^{i+1})=A_{i}\sum\limits_{j=0}^{i} {Y_{k}^{j}} (Y_{k}-X_{k}) X_{k}^{i-j}\geq A_{i}\sum\limits_{j=0}^{i} {X_{k}^{j}} (Y_{k}-X_{k}) X_{k-1}^{i-j}. $$

Let 𝜃_k+ 1 be such that

$$ Y_{k}-X_{k} \geq \frac{X_{k}-X_{k-1}}{\theta_{k+1}}. $$

Then condition (14) can be replaced with

$$ \frac{\omega_{k+1}-1}{\omega_{k+1}} A_{1}(({Y_{k}^{2}}-{X_{k}^{2}})\leq (Y_{k}{\Gamma}_{k} + {\Gamma}_{k} Y_{k}) + (\hat \omega \theta_{k+1})^{-1} \sum\limits_{i=2}^{q} A_{i}(X_{k}^{i+1}-X_{k-1}^{i+1}). $$

(23)

The iterative scheme (11), complemented with the strategy based on (23) for the selection of the parameter ω_k+ 1, requires no more than (q + 3)n³ + 4γn² + O(n²) multiplicative operations. The efficiency of this scheme will be investigated experimentally in the next section.

8 Numerical results

In this section, we present the results of some numerical experiments which confirm the effectiveness of the proposed schemes. All the algorithms have been implemented in Matlab and tested on a PC i9-9900K CPU 3.60GHz with 8 cores. Our test suite includes:

• 1. Synthetic Examples:

  • (a) The block tridiagonal Markov chain of Remark 2. Observe that the drift of the Markov chain is exactly equal to − δ.

  • (b) A numerical example considered in [7, 16] for testing a suitable modification — named SSM — of the U-based fixed point iteration that avoids the matrix inversion at each step. The Markov chain of the M/G/1 type has blocks given by

    $$ A_{-1}=\frac{4(1-p)}{3} \left[\begin{array}{ccccc} 0.05 & 0.1 & 0.2 & 0.3 & 0.1\\ 0.2 & 0.05 & 0.1 & 0.1 & 0.3\\ 0.1 & 0.2 & 0.3 & 0.05 & 0.1\\ 0.1 & 0.05 & 0.2 & 0.1 & 0.3\\ 0.3 & 0.1 & 0.1 & 0.2 & 0.05 \end{array}\right], \quad A_{i}=p A_{i-1}, ~~i\geq 0. $$

    The Markov chain is positive recurrent, null recurrent or transient according as 0 < p < 0.5, p = 0.5, or p > 0.5, respectively. In our computations, we have chosen different values of p, in the range 0 < p < 0.6 and the matrices A_i are treated as zero matrix for i ≥ 51.

  • (c) Synthetic examples of M/G/1-type Markov chains described in [10]. These examples are constructed in such a way that the drift of the associated Markov chain is close to a given negative value. We do not describe in detail the construction, as it would take some space, but we refer the reader to [10, Sections 7.1].

• 2. Application Examples:

  • (a) Some examples of PH/PH/1 queues collected in [10, Sections 7.1] for testing purposes. The construction depends on a parameter ρ with 0 ≤ ρ ≤ 1. In this case the drift is η = 1 − ρ.

  • (b) The Markov chain of M/G/1 type associated with the infinitesimal generator matrix Q from the queuing model described in [17]. This is a complex queuing model, a BMAP/PHF/1/N model with retrial system with finite buffer of capacity N and non-persistent customers. For the construction of the matrix Q, we refer the reader to [17, Sections 4.3 and 4.5].

8.1 Synthetic examples

The first test concerns the validation of the analysis performed in the previous sections, regarding the convergence of fixed point iterations. In Table 1, we report the number of iterations required by different iterative schemes on Example 1.(a) with n = 100. Specifically, we compare the traditional fixed point iteration, the U-based fixed point iteration, the S-based fixed point iteration (10), and the relaxed fixed point iterations (11). For the latter case, we consider the S_ω-based iteration where ω_k+ 1 = ω is a priori fixed and the S$_{\omega _{k}}$-based iteration where the value of ω_k+ 1 is dynamically adjusted at any step according to the strategy (23), complemented with condition (13). The relaxed stationary iteration is applied for ω = 1.8,1.9,2. The relaxed adaptive iteration is applied with $\hat \omega =10$. The iterations are stopped when the residual error $\Vert X_{k}-{\sum }_{i=-1}^{q} A_{i} X_{k}^{i+1}\Vert _{\infty }$ is smaller than tol = 10^− 13.

Table 1 Number of iterations on Example 1.(a) for different values of δ

The first four columns of Table 1 confirm the theoretical comparison of asymptotic convergence rates of classical fixed point iterations applied to a block tridiagonal matrix. Specifically, the U-based and the S-based iterations are twice faster than the traditional iteration. Also, the relaxed stationary variants greatly improve the convergence speed. An additional remarkable improvement is obtained by adjusting dynamically the value of the relaxation parameter. Also notice that the S$_{\omega _{k}}$-based iteration is guaranteed to converge, differently from the stationary S_ω-based iteration.

The superiority of the adaptive implementation over the other fixed point iterations is confirmed by numerical results on Example 1.(b) In Table 2, for different values of p, we show the number of iterations required by different iterative schemes including also the successive-substitution Moser (SSM) method introduced in [7] and further analyzed in [16]. This algorithm avoids the explicit computation of the inverse matrix in the U-based iteration (7), by successively approximating it by the Moser formula. For a fair comparison with the results in [16], here we set tol = 10^− 8 in the stopping criterion, as in [16]. In [7], the same approach is also exploited to develop an inversion-free modification of the Newton iteration (Newton-Moser method — NM), applied for solving the nonlinear matrix (3). We have implemented the resulting iterative scheme. Although it is very fast and efficient for p ∈{0.3,0.48,0.55}, numerical difficulties occur when p is close to 0.5, due to the bad conditioning of the Jacobian matrix. In particular, for p = 0.5, our implementation fails to get the desired accuracy of tol = 10^− 8 and the iteration diverges.

Table 2 Number of iterations on Example 1.(b) for different values of p

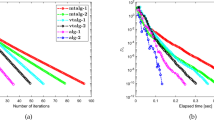
Finally, we compare the convergence speed of the traditional, U-based, S-based, and S$_{\omega _{k}}$-based fixed point iterations applied on the synthetic example 1.(c) of M/G/1-type Markov chains described in [10]. In Fig. 3, we report the semilogarithmic plot of the residual error in the infinity norm generated by the four fixed point iterations, for two different values of the drift η.

Fig. 3

Residual errors generated by the four fixed point iterations applied to the synthetic example 1.(c) with drift η = − 0.1 and η = − 0.005

Observe that the adaptive relaxed iteration is about twice faster than the traditional fixed point iteration. The observation is confirmed in in Table 3 where we indicate the speed-up in terms of CPU-time, with respect to the traditional fixed point iteration, for different values of the drift η.

Table 3 Speed-up, in terms of CPU-time, w.r.t. the traditional fixed point iteration for different values of the drift η

In Fig. 4, we repeat the set of experiments of Fig. 3 with a starting stochastic matrix $X_{0}= \boldsymbol {e}\boldsymbol {e}^{T}/n$. Here the adaptive strategy is basically the same as used before where we select ω_k+ 1 in the interval [0,ω_k] as the maximum value which maintains the nonnegativity of X_k+ 1.

Fig. 4

Residual errors generated by the four fixed point iterations applied to the synthetic example with drift η = − 0.1 and η = − 0.005

In this case the adaptive strategy seems to be quite effective in reducing the number of iterations. Other results are not so favorable and we believe that in the stochastic case, the design of a general efficient strategy for the choice of the relaxation parameter ω_k is still an open problem.

8.2 Application examples

The first set 2.(a) of examples from applications includes several cases of PH/PH/1 queues collected in [10]. The construction of the Markov chain depends on a parameter ρ, with 0 ≤ ρ ≤ 1, and two integers (i,j) which specify the PH distributions of the model. The Markov chain generated in this way is denoted as Example (i,j). Its drift is η = 1 − ρ. In Tables 4, 5, and 6, we compare the number of iterations for different values of ρ. Here and hereafter the relaxed stationary S_ω-based iteration is applied with ω = 2.

Table 4 Number of iterations for different values of ρ on Example (2,6)

Table 5 Number of iterations for different values of ρ on Example (8,3)

Table 6 Number of iterations for different values of ρ on Example (8,9)

In Table 7, we report the number of iterations on Example (8,3) of Table 5, starting with X₀ a stochastic matrix. We compare the traditional, U-based and S-based iterations. We observe a rapid convergence profile and the fact that the number of iterations is independent of the drift value.

Table 7 Number of iterations for different values of ρ on Example (8,3) with X₀ a stochastic matrix

For a more challenging example 2.(b) from applications, we consider the generator matrix Q from the queuing model described in [17]. The corresponding matrix H in (4), as well as the solution matrix G, is very sparse, so that this example is particularly suited for fixed point iterations. For N = 5, the nonzero blocks are 42 (i.e., q= 40), and have size 48 × 48. In Fig. 5, we show the Matlab spy plots of the leading principal submatrix of order 256 of H and of the solution matrix G.

Fig. 5

Matlab spy plots of H(1 : 256,1 : 256) and the solution matrix G for test 2.b with N = 5

In Table 8, we indicate the number of iterations for different values of the capacity N.

Table 8 Number of iterations for different values of N on Example 2.(b) described in [17]

Our implementation of the Newton method, incorporating the Moser iteration for computing the approximation of the inverse of the Jacobian matrix (NM method), again fails to get the desired accuracy of tol = 1.0e − 13 in all the cases. Finally, in Table 9, for N = 5 and different threshold values of accuracy, we report the timings of our proposed method compared with the cyclic reduction algorithm for M/G/1 type Markov chain implemented in the SMCSolver Matlab toolbox [18].

Table 9 Timings of our proposed method and the cyclic reduction (CR) algorithm in test 2.(b) with N = 5 and different values of the residual error

This table indicates that for a large and sparse Markov Chain in a multithread computing environment, the proposed approach can be a valid option.

9 Conclusions and future work

In this paper, we have introduced a novel fixed point iteration for solving M/G/1-type Markov chains. It is shown that this iteration complemented with suitable adaptive relaxation techniques is generally more efficient than other classical iterations. Incorporating relaxation techniques into other different inner-outer iterative schemes as the ones introduced in [10] is an ongoing research.