Solution of ill-posed problems with Chebfun

Abstract

The analysis of linear ill-posed problems often is carried out in function spaces using tools from functional analysis. However, the numerical solution of these problems typically is computed by first discretizing the problem and then applying tools from finite-dimensional linear algebra. The present paper explores the feasibility of applying the Chebfun package to solve ill-posed problems with a regularize-first approach numerically. This allows a user to work with functions instead of vectors and with integral operators instead of matrices. The solution process therefore is much closer to the analysis of ill-posed problems than standard linear algebra-based solution methods. Furthermore, the difficult process of explicitly choosing a suitable discretization is not required.

1 Introduction

We are interested in the solution of Fredholm integral equations of the first kind,

$${\int}_{{{\varOmega}}_{1}} \kappa(s,t) x(t) dt = g(s),\qquad s\in{{\varOmega}}_{2},$$

(1.1)

with a square integrable kernel κ. The Ω_i are subsets of ${\mathbb R}^{d_{i}}$ for i = 1,2, where d_i is a small positive integer. Such integral equations are common in numerous applications including remote sensing, computerized tomography, and image restoration.

Two major problems arise when solving (1.1): (i) The function space is of infinite dimensionality, and (ii) small changes in g may correspond to large changes in x as exemplified by

$$\begin{array}{@{}rcl@{}} \underset{s\in {{\varOmega}}_{2}}{\max} \vert{\int}_{{{\varOmega}}_{1}} \kappa(s,t)\cos(2\pi m t) dt\vert, \qquad {{\varOmega}}_{1}={{\varOmega}}_{2}=[0,1], \end{array}$$

where the maximum can be made tiny by choosing m large, despite the fact that the maximum of $\vert \cos \limits (2\pi \mathrm {m} \mathrm {t})\vert$ is one. This is a consequence of the Riemann–Lebesgue theorem; see, e.g., [7, 12] or below for discussions of this result. The second problem is particularly relevant when the available right-hand side g is a measured quantity subject to observational errors, as is the case in many applications.

Usually one deals with problem (i) by first discretizing the functions x(t) and g(s) in (1.1) using, for instance, n piece-wise constant, linear, or polynomial basis functions; see e.g., [11] or [13]. The kernel κ(s,t) is discretized analogously. This transforms the integral (1.1) into a linear system of algebraic equations. Problem (ii) causes the coefficient matrix of said system to be ill-conditioned when n is large. Straightforward solution of this linear system of equations generally is not meaningful because of severe error propagation. Therefore, the linear system has to be regularized. This can, for instance, be achieved by Tikhonov regularization or truncated singular value decomposition (TSVD). While the first dampens the influence of small singular values, the latter outright ignores them. One is then often faced with a trade-off between a small discretization error and a small error caused by the regularization; see, e.g., Natterer [18]. In fact, often the more basis functions are used for the discretization, the more ill-conditioned the resulting coefficient matrix becomes, and the larger the need of regularization.

In this paper, we first regularize and then discretize the problem. Regularization is achieved by modifying the singular value expansion (SVE) of the kernel. This expansion provides an excellent starting point for discretizing the problem. The discretized problem is a linear system of equations with a diagonal matrix. This system can be solved trivially. Furthermore, a user does not have to choose the number of discretization points. Regularizing first simplifies the discretization.

We will compute the SVE of the kernel using Chebfun [6], which is a software package that simulates working with functions in MATLAB. Chebfun approximates functions by piece-wise polynomials. The computed solution is a piece-wise polynomial approximation of the desired solution x(t) of (1.1). The advantage of using Chebfun is that the computed solution will feel and behave like a function. Therefore, our approach is arguably closer to directly solving (1.1) than to discretizing the integral equation before solution.

This paper is organized as follows. In the second section, we provide basic definitions, introduce our notation, and briefly discuss Chebfun and the singular value expansion. Section 3 discusses the truncated singular value expansion method (TSVE) for the solution of ill-posd problems, and the Tikhonov regularization method is described in Section 4. Numerical results that illustrate the performances of these methods are reported in Section 5. After we have established that this regularize-first approach works for linear ill-posed problems in one space-dimension, we will extend the ideas to problems in two space-dimensions in Section 6. Concluding remarks can be found in Section 7.

We note that other approaches to work with functions are described in the literature; see, e.g., Yarvin and Rokhlin [25]. We are not aware of discussions of this approach to the solution of linear ill-posed problems. The availability of Chebfun [6] makes the regularize-first technique easy to implement.

2 Basics

Let $L^{2}({{\varOmega }}_{i})$ for i = 1,2 be spaces of Lebesgue measurable square integrable functions with inner products

$$\langle a,b_{{{\varOmega}}_{i}} \rangle = {\int}_{{{\varOmega}}_{i}} {{\overline{a(t)}}} b(t) dt, \quad \text{ for } i=1,2,$$

(2.1)

where $\overline {a(t)}$ represents the complex conjugate of $a(t)\in {\mathbb C}$. Based on these inner products, we define the L²-norms

$$\begin{array}{@{}rcl@{}} {\left\Vert f \right\Vert}_{{{\varOmega}}_{i}}={\left\langle f,f \right\rangle}_{{{\varOmega}}_{i}}^{1/2}, \quad \text{ for } i=1,2. \end{array}$$

The spaces $L^{2}({{\varOmega }}_{i})$ for i ∈{1,2} equipped with the norms above are complete vector spaces, i.e., they are Hilbert space; see, e.g., [11]. A given kernel $\kappa (\cdot ,\cdot ) \in L^{2}({{\varOmega }}_{1} \times {{\varOmega }}_{2} )$ induces the bounded linear operator $A : L^{2}({{\varOmega }}_{1})\rightarrow L^{2}({{\varOmega }}_{2})$ defined by

$$(Ax)(s)={\int}_{{{\varOmega}}_{1}} \kappa(s,t)x(t) dt;$$

(2.2)

see, e.g., [11, Thm. 3.2.7]. The operator is sometimes called a Hilbert-Schmidt integral operator and the kernel κ a Hilbert-Schmidt kernel. We can write (1.1) as

$$Ax = g.$$

(2.3)

We assume here that g is in the range of A. If A has a nontrivial null space, then we are interested in the solution of (2.3) of minimal norm. We refer to this solution as x_exact.

In applications that arise in the sciences and engineering, the right-hand side g of (1.1) often is a measured quantity and therefore is subject to observational errors. We are therefore interested in the situation when the error-free function g is not available, and only an error-contaminated approximation $g^{\delta }\in L^{2}({{\varOmega }}_{2})$ of g is known. We assume that g^δ satisfies

$${\left\Vert g-g^{\delta}\right\Vert}_{{{\varOmega}}_{2}} \leq \delta,$$

with a known bound δ > 0. The solution of the equation

$$Ax=g^{\delta}, \quad \text{ with } x\in L^{2}({{\varOmega}}_{1}) \text{ and } g^{\delta} \in L^{2}({{\varOmega}}_{2}),$$

(2.4)

generally is not a meaningful approximation of the desired solution x_exact of (2.3), since A is not continuously invertible. In fact, (2.4) might not even have a solution.

The operator A depends on the kernel κ. We will now take a closer look at known theory about the kernel function κ. For any square integrable kernel κ, we define the singular value expansion (SVE) [21, §4] as

$$\kappa(s,t)=\sum\limits_{i=1}^{\infty} \sigma_{i} \phi_{i}(s)\psi_{i}(t)$$

(2.5)

with convergence in the L²-sense. The functions $\phi _{i}\in L^{2}({{\varOmega }}_{2})$ and $\psi _{i}\in L^{2}({{\varOmega }}_{1})$ are referred to as singular functions. These functions are orthonormal with respect to the appropriate inner product (2.1) [21, §5], i.e.,

$${\left\langle \psi_{i},\psi_{j} \right\rangle}_{{{\varOmega}}_{1}} = {\left\langle \phi_{i},\phi_{j} \right\rangle}_{{{\varOmega}}_{2}} = \delta_{ij}, \quad \text{ for } i,j=1,2,\dotsc~.$$

The quantities σ_i are known as singular values. They are nonnegative and we assume them to be ordered non-increasingly,

$$\sigma_{1} \geq \sigma_{2} \geq \sigma_{3} \geq \dotsb \geq 0.$$

It can be shown that the only limit point of the singular values for square integrable kernels is zero [21, §5].¹

Let the series (2.5) be uniformly convergent for s ∊ Ω₂ and t ∊ Ω₁. Then, as shown in [21, §8], the series converges point-wise. When the summation is finite, the kernel κ is said to be separable (or degenerate). Most applications do not have a separable kernel. However, square integrable kernels can be approximated well by such a kernel, which is obtained by truncating the number of terms in (2.5) to a suitable finite number ℓ. Let

$$\kappa_{\ell}(s,t)=\sum\limits_{i=1}^{\ell}\sigma_{i} \phi_{i}(s)\psi_{i}(t).$$

(2.6)

This is the closest kernel of rank at most ℓ to κ in the L²-norm [21, §18 Approximation Theorem]. We will use this result to justify the application of the truncated singular value expansion method (TSVE) discussed in Section 3.

We also will be using the Approximation Theorem to restrict our expansion to singular values that are larger than ε, where ε is a small enough cutoff, say 10^− 8 or 10^− 16. There is a trade-off between computing time and approximation accuracy. We try to choose ε far below the regularization error so that our choice does not have a significant effect on the accuracy. At the same time, a small ε means higher cost for computing the singular value expansion and forming the computed approximate solution.

In this paper, we will use two regularization methods, TSVE and Tikhonov regularization, to compute an approximate solution of (2.3). The right-hand side g is assumed not to be available; only a perturbed version g^δ is assumed to be known; cf. (2.4).

The TSVE method is based on the Approximation Theorem mentioned above. Thus, we approximate the kernel κ by κ_ℓ for some suitable ℓ ≥ 0. This results in an approximation A_ℓ to A. We are interested in computing the solution x_ℓ of minimal norm of the problem

$$\underset{x\in L^{2}({{\varOmega}}_{1})}{\min}{\left\Vert A_{\ell}x-g^{\delta}\right\Vert}_{{{\varOmega}}_{2}},$$

(2.7)

where

$$(A_{\ell}x)(s)={\int}_{{{\varOmega}}_{1}} \kappa_{\ell}(s,t) x(t) dt, \quad s\in{{\varOmega}}_{2}.$$

The parameter ℓ is a regularization parameter that determines how many singular values and basis functions of κ are used to compute the approximate solution x_ℓ of (2.4). The remaining singular values, which are smaller than or equal to σ_ℓ, are ignored.

Tikhonov regularization replaces the system (2.4) by the penalized least-squares problem

$$\underset{x\in L^{2}({{\varOmega}}_{1})}{\min}\left\{{\left\Vert Ax-g^{\delta}\right\Vert}_{{{\varOmega}}_{2}}^{2}+ \lambda^{2}{\left\Vert x\right\Vert}_{{{\varOmega}}_{1}}^{2}\right\},$$

(2.8)

which has a unique solution, denoted by x_λ, for any nonvanishing value of the regularization parameter λ. Substituting the SVE (2.5) into (2.8) shows that Tikhonov regularization dampens the contributions to x_λ of singular functions with large index i the most; increasing λ > 0 results in more damping. Since we cannot deal with an infinite series expansion, we will, in practice, first cutoff all singular values that are less than ε as explained above, and then apply Tikhonov regularization. This is sometimes referred to as a discretization by kernel approximation [11, Sect. 4.2].

The determination of suitable values of the regularization parameters, ℓ in (2.7) and λ in (2.8), is important for the quality of the computed approximate solution. Several methods have been described in the literature including the discrepancy principle, the L-curve criterion, and generalized cross validation; see [4, 8, 15, 16, 19, 20] for recent discussions on their properties and illustrations of their performance. Regularization methods typically require that regularized solutions for several values of the regularization parameter be computed and compared in order to determine a suitable approximate solution of (2.4).

2.1 Chebfun

We solve (1.1) by first regularizing followed by discretization. However, we still want to compute the solution numerically. Thus, we need a numerical library that can handle functions in an efficient way. Since a function t↦f(t) represents uncountable many pairs of {t,f(t)}, a computer only can handle approximations to functions numerically.²

We chose the MATLAB package Chebfun [6] for this purpose. Chebfun uses piece-wise polynomials anchored at Chebyshev points, so-called chebfuns, to approximate functions. All computations within Chebfun’s framework are done with these approximations of actual functions. This means that we project the functions in $L^{2}({{\varOmega }}_{2})$ onto a space of piece-wise Chebyshev polynomials over Ω₂. Thus, Chebfun simulates computation with functions that are approximated. One may argue that this is a discretization. However, Chebfun’s framework is significantly different from other discretizations in the sense that it gives a user the feeling of computing with functions. In particular, a user does not explicitly have to determine a discretization or where to split functions into polynomial pieces.

Chebfun’s functionality includes the computation of sums and products of functions and derivatives, inner products, norms, and integrals. Chebfun2/3, Chebfun’s extensions to functions of two and three variables, also can compute outer products and, most importantly for us here, the singular value expansion [23]. The algorithm behind the singular value expansion uses a continuous analogue of adaptive cross approximation: The approximation of κ(s,t) is computed by an iterative process. First, an approximation of a maximum point $(\hat {s},\hat {t})$ of κ(s,t) is determined. The exact computation of a maximum point is not important, and the maximum point is not required to be unique. The function is then approximated by

$$\begin{array}{@{}rcl@{}} \kappa_{1}(s,t) = \frac{\kappa(s,\hat{t}) \kappa(\hat{s},t)}{\kappa(\hat{s},\hat{t})}, \end{array}$$

where $s\mapsto \kappa (s,\hat {t})$ and $t\mapsto \kappa (\hat {s},t)$ are one-dimensional chebfuns in s and t, respectively. This process is then repeated for κ(s,t) − κ₁(s,t) to find a rank-1 approximation of the remainder. By recursion one obtains after k steps a rank-k approximation of the original kernel. As soon as the remainder is sufficiently small, the computed rank-k approximation is the sought approximation to κ(s,t). At the end we have κ(s,t) ≈ C(s)MR(t)^T, with C(s) and R(t) row vectors of functions, and M a dense matrix of size k × k.

Based on this approximation, it is easy to compute the singular value expansion. Chebfun’s continuous analogue of the QR factorization can be used to find orthogonal bases for C(s) and R(t),

$$C(s)=Q_{c}(s)R_{c},\qquad R(t)=Q_{r}(t)R_{r},$$

where the columns of Q_c and Q_r are orthonormal functions and the k × k matrices R_c and R_r are upper triangular. Let

$$\widetilde{M}=R_{c} M {R_{r}^{T}}$$

and compute the singular value decomposition $\widetilde {M}=U{\Sigma } V^{T}$. Then

$$\kappa(s,t)\approx Q_{c}(s)U{{\varSigma}} V^{T}Q_{r}(t)^{T}$$

is the desired singular value expansion of the approximation of the kernel. The singular functions are the columns of Q_c(s)U and Q_r(t)V; see [23] for further details. A very similar process, known as adaptive cross approximation [2, 3], was used in [17] for the discrete case of matrices and vectors.

Chebfun has some limitations. Currently only functions of at most three variables can be approximated by Chebfun. Hence, we are limited to ill-posed problems in one space-dimension and to problems in higher dimension with a special structure. We will in Section 6 discuss problems in two space-dimensions with special kernels that can be handled by the present version of Chebfun. In higher dimensions, Chebfun is limited to domains that are tensor products of intervals, disks, spheres, or solid spheres. In this paper, all domains are rectangles. Chebfun also needs multivariate functions to be of low rank for an efficient approximation, i.e., there has to exist a sufficiently accurate separable approximation. This is for instance not the case for the kernel $\kappa (s,t) = st - \min \limits (s,t)$ from the deriv2 example of the Regularization Tools package [13]. This limits the application of the methods described in this paper. However, the Chebfun package is still under development and some of the limitations mentioned might not apply to future releases.

3 The TSVE method

Assume that the kernel can be expressed as

$$\kappa(s,t)=\sum\limits_{i=1}^{\infty} \sigma_{i} \phi_{i}(s)\psi_{i}(t)$$

(3.1)

and is not separable, and that the solution of (1.1) can be written as

$$x(t)=\sum\limits_{j=1}^{\infty} \beta_{j} \psi_{j}(t).$$

(3.2)

The fact that κ is non-separable implies that all σ_i are positive, and the assumption that the solution is of the form (3.2) essentially states that the solution has no component in the null space of A. This assumption is justified since the null space of A is orthogonal to all the ψ_j and, thus, a component in the null space would increase the norm of the solution, but not help with the approximation of (1.1).

Substituting (3.1) and (3.2) into (1.1), and using the orthonormality of the basis functions yields

$$\begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{\infty} \sigma_{i}\beta_{i}\phi_{i}(s)=g(s). \end{array}$$

We further probe the equation with ϕ_k(s) for all k and use the orthonormality of the basis functions to obtain

$$\begin{array}{@{}rcl@{}} \sigma_{k}\beta_{k}={\int}_{{{\varOmega}}_{2}} \phi_{k}(s) g(s) ds,\qquad\text{for all } k. \end{array}$$

Thus, the exact solution of (2.3) is given by

$$x(t)=\sum\limits_{j=1}^{\infty} \beta_{j} \psi_{j}(t),\quad \text{ with } \beta_{j} = \frac{{\int}_{{{\varOmega}}_{2}} \phi_{j}(s) g(s) ds}{\sigma_{j}}.$$

(3.3)

Truncating this series after ℓ terms and using the error-contaminated right-hand side g^δ instead of g, we obtain the TSVE solution of (2.4),

$$x_{\ell}(t)=\sum\limits_{j=1}^{\ell} \beta^{\delta}_{j} \psi_{j}(t),\quad \text{ with } \beta^{\delta}_{j}= \frac{{\int}_{{{\varOmega}}_{2}} \phi_{j}(s) g^{\delta}(s) ds}{\sigma_{j}}.$$

(3.4)

The truncation parameter ℓ can be chosen as needed. Its choice will be discussed below.

The following lemma links the projection of the error onto the space spanned by the ϕ_i to the bound δ for the norm of the error in the data.

Lemma 3.1

Let n(s) = g(s) − g^δ(s) with ${\left \Vert n\right \Vert }_{{{\varOmega }}_{2}} \leq \delta$. Then,

$$\sum\limits_{i=1}^{\infty}\left({\int}_{{{\varOmega}}_{2}}\phi_{i}(s) n(s) ds\right)^{2}\leq \delta^{2},$$

(3.5)

where the ϕ_i are orthonormal basis functions determined by the SVE of the kernel κ.

Proof

Using the basis functions ϕ_i, the error n can be represented as

$$n(s)=\sum\limits_{j=1}^{\infty} \gamma_{j}\phi_{j}(s)+\phi^{\perp}(s)$$

for certain coefficients γ_j, where the function ϕ^⊥ is orthogonal to all the functions ϕ_j. It follows that

$${\int}_{{{\varOmega}}_{2}} \phi_{i}(s) n(s) ds={\int}_{{{\varOmega}}_{2}} \phi_{i}(s) \left(\sum\limits_{j=1}^{\infty} \gamma_{j}\phi_{j}(s)+\phi^{\perp}(s) \right) ds.\\$$

The orthogonality of the basis functions ϕ_j allows us to simplify the above expression to

$${\int}_{{{\varOmega}}_{2}}\phi_{i}(s) n(s) ds =\gamma_{i}.$$

The same argument can be used to show that

$$\sum\limits_{j=1}^{\infty} {\gamma_{j}^{2}} \leq {\left\Vert n\right\Vert}_{{{\varOmega}}_{2}}^{2} \leq \delta^{2}.$$

Combining these results shows (3.5). □

4 Tikhonov regularization

Instead of solving (2.3) exactly, we solve the minimization problem

$$\begin{array}{@{}rcl@{}} \underset{x \in L^{2}({{\varOmega}}_{1})}{\min}\left\{ {\left\Vert Ax-g^{\delta}\right\Vert}_{{{\varOmega}}_{2}}^{2}+ \lambda^{2}{\left\Vert x\right\Vert}_{{{\varOmega}}_{1}}^{2}\right\}, \end{array}$$

(4.1)

where the regularization parameter λ > 0 typically is determined during the solution process. This parameter balances the influence of the norm of the residual Ax − g^δ and the norm of the solution x. Using the definition of the L²-norm, (4.1) can be written as

$$\underset{x\in L^{2}({{\varOmega}}_{1})}{{\min}}\left\{{\int}_{{{\varOmega}}_{2}} {\left\vert Ax-g^{\delta}\right\vert}^{2} ds + \lambda^{2} {\int}_{{{\varOmega}}_{1}} {\vert x\vert}^{2} dt\right\}.$$

(4.2)

This minimization problem can be solved in a variety of ways. For instance, one could apply a continuous version of Golub–Kahan bidiagonalization to the operator A. Then A is reduced to (an infinite) bidiagonal matrix. The bidiagonalization process can be truncated as soon as a solution of the reduced problem that satisfies the discrepancy principle has been found; this approach is analogous to the computations described in [5] for discretized problems. A straightforward way to solve (4.2), though not necessarily the fastest, is to determine the minimizer by applying the SVE (2.5). We will use this approach in the computed examples. Thus, substituting (3.1) and (3.2) into (4.2), and using the orthonormality of the basis functions, we obtain

$$\begin{array}{@{}rcl@{}} \underset{x\in L^{2}({{\varOmega}}_{1})}{\min} \sum\limits_{i=1}^{\infty} \left({\sigma^{2}_{i}} {\beta^{2}_{i}} -2\sigma_{i} \beta_{i} {\int}_{{{\varOmega}}_{2}} {\phi_{i}(s)} g^{\delta}(s) ds + \lambda^{2}{\beta^{2}_{i}}\right) +{\int}_{{{\varOmega}}_{2}}{\vert g^{\delta}(s)\vert}^{2} ds. \end{array}$$

We now can compute the solution as

$$x_{\lambda}(t)=\sum\limits_{j=1}^{\infty} \beta^{(\lambda)}_{j} \psi_{j}(t),\quad \text{ with } \beta^{(\lambda)}_{j}= \frac{\sigma_{j}{\int}_{{{\varOmega}}_{2}} {\phi_{j}(s)} g^{\delta}(s) ds}{({\sigma^{2}_{j}} +\lambda^{2})}.$$

(4.3)

5 Numerical experiments

In this section, we illustrate the performance of the methods described in Sections 3 and 4 by reporting some numerical results. In particular, we compare the performance of the regularize-first approaches based on Chebfun discussed in this paper to more commonly used discretize-first approach. Both approaches have their advantages and the regularize-first approach can be expected to be slower due to the effort required to work with chebfuns. The examples of this section show this to be the case, but usually not by very much. This indicates that the regularize-first approach based on Chebfun is a practical solution method for many linear ill-posed problems.

We first consider five test problems in one space-dimension. These problems are from Regularization Tools by Hansen [13]. In the next section, we will follow up with two 2D problems, an image deblurring problem with Gaussian blur and a diffusion problem inspired by IR Tools [10]. All computations were carried out in MATLAB R2020b running on a computer with two CPUs: Intel(R) Xeon(R) E5-2683 v4@2.10 GHz processor with 512 GB of RAM. There are two MATLAB Live Scripts accompanying this paper that showcase the most important of the following numerical experiments.

The software used for the experiments in this section together with Matlab live scripts explaining the main idea of the paper are available as the na54 package.³

Table 1 1D examples used for the numerical experiments

Each test problem from Regularization Tools by Hansen [13] provides us with an integral equation of the form (1.1). These test problems are listed in Table 1. For two examples, Gravity and Shaw, the function g(s) is not explicitly given in the table, and is instead computed by evaluating the integral (1.1) with Chebfun. In example Wing, the expression $\textbf {1}_{[\frac {1}{3},\frac {2}{3}]}$ denotes the indicator function, which is 1 for all points in $[\frac {1}{3},\frac {2}{3}]$ and 0 otherwise. We compare the regularize-first approach using Chebfun-based computations with the discretize-first approach, where the discretizations are determined by MATLAB functions in Regularization Tools⁴ [13]. For the discretize-first approach, these problems are discretized by a Nyström method or a Galerkin method with orthogonal test and trial functions to give a linear system of equations $\tilde {A}\boldsymbol {x}=\boldsymbol {g}$, where $\tilde {A}\in {\mathbb {R}}^{n\times n}$ is the discretized integral operator, $\boldsymbol {x}\in {\mathbb {R}}^{n}$ is a discretization of the exact solution x_exact, and $\boldsymbol {g}\in {\mathbb {R}}^{n}$ is the corresponding error-free right-hand side vector. We generate the error-contaminated vector $\boldsymbol {g}^{\delta }\in \mathbb {R}^{n}$ according to

$$\begin{array}{@{}rcl@{}} \boldsymbol{g}^{\delta}=\boldsymbol{g}+\alpha\frac{{\left\Vert \boldsymbol{g}\right\Vert }_{2}}{\left\Vert \boldsymbol{e}\right\Vert}_{2}\boldsymbol{e}, \end{array}$$

where $\boldsymbol {e}\in {\mathbb {R}}^{n}$ is a random vector whose entries are from a normal distribution with mean zero and variance one. The parameter α > 0 is the noise level.

For the regularize-first approach, we use the MATLAB package Chebfun [6] to represent the kernel κ(s,t), the function g(s) that represents the error-free right-hand side, and the desired solution x(t). We define the error-contaminated function g^δ(s) by

$$\begin{array}{@{}rcl@{}} g^{\delta}(s)=g(s)+\alpha \frac{{\left\Vert g\right\Vert}_{{{\varOmega}}_{2}}}{{\left\Vert F\right\Vert}_{{{\varOmega}}_{2}}}F(s), \end{array}$$

where F(s) is a smooth Chebfun function, generated by the Chebfun command randnfun(𝜗,Ω₂), with maximum frequency about 2π/𝜗 and standard normal distribution N(0,1) at each point, and α > 0 is the noise level. The noise level is defined analogously as in the discretized problems to achieve comparability. In the computed examples, we let 𝜗 = 10^− 2. This gives Chebfun’s analogue of noise.

The discrepancy principle is used to determine the truncation parameter ℓ in (3.4) in the TSVE method, and the Tikhonov regularization parameter λ in (4.3). The discrepancy principle prescribes that the truncation index ℓ be chosen as small as possible so that the solution x_ℓ of (3.4) satisfies

$$\begin{array}{@{}rcl@{}} {\left\Vert{\int}_{{{\varOmega}}_{1}} \kappa(s,t) x_{\ell}(t) dt - g^{\delta}(s)\right\Vert}_{{{\varOmega}}_{2}} \leq \eta \delta, \end{array}$$

where η ≥ 1 is a user-supplied constant independent of δ. We let η = 1 in the examples. The discrepancy principle, when used with Tikhonov regularization, prescribes that the regularization parameter λ > 0 be chosen so that the solution x_λ of (4.1) satisfies

$$\begin{array}{@{}rcl@{}} {\left\Vert{\int}_{{{\varOmega}}_{1}} \kappa(s,t) x_{\lambda}(t) dt - g^{\delta}(s)\right\Vert}_{{{\varOmega}}_{2}} = \eta \delta. \end{array}$$

We use the MATLAB function fminbnd to find the λ-value.

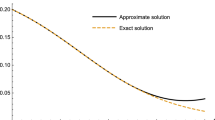
One of the five test problems that we are interested in solving is Baart. This example is a Fredholm integral equation of the first kind (1.1) with $\kappa (s, t) = \exp (s \cos \limits (t))$, $g(s) = 2 \sinh (s)/s$, and solution $x(t) = \sin \limits (t)$, where Ω₁ = [0,π] and Ω₂ = [0,π/2]. We compute approximate solutions by applying the TSVE and Tikhonov regularization with Chebfun. The approximate solutions, x_ℓ(t) and x_λ(t), respectively, can be determined by using the formulas (3.4) and (4.3). Figure 1(a) displays the kernel κ of the Baart example. The right-hand side function g(s) and the corresponding error-contaminated function g^δ(s) are illustrated in Fig. 1(b), where the noise level is 10^− 2. Figure 1(c) depicts the exact solution and the computed approximate solutions determined by TSVE and Tikhonov regularization with Chebfun. The latter figure shows that our methods give fairly accurate approximations of the exact solution.

Next, we apply the methods to several different examples and compare them to standard TSVD and Tikhonov regularization in a discretized setting. The quality of the computed approximate solutions is measured by the relative error norm

$$RE:=\frac{{\left\Vert x_{\text{method}}-x\right\Vert}_{*}}{{\left\Vert x\right\Vert}_{*}} ,$$

where ${\left \Vert \cdot \right \Vert }_{*}$ denotes the scaled Euclidean vector norm $(\frac {1}{n}{\sum }_{i=1}^{n}x_{i}^2)^{1/2}$ if $\boldsymbol {x}\in \mathbb {R}^{n}$ is a vector, or the L²-norm if x is a function.

Table 2 Comparison of TSVE with Chebfun and for the discretized problem

Table 3 Comparison of Tikhonov with Chebfun and for the discretized problem

Tables 2 and 3 compare the TSVE and Tikhonov regularization methods when used with Chebfun to standard methods for the test problems Baart, Fox-Goodwin, Gravity, Shaw, and Wing. These problems are discretized integral equations of the first kind and are described in [13].

Three noise levels α are considered. The number of discretization points, n, which is shown in the third column of the tables, is even and chosen between 2 and 2000, such that the smallest absolute difference between the relative error of the solution for the discretized problem and the relative error of the solution for the continuous problem is achieved. Thus, we choose the number of discretization points n so that the discretized problem gives an approximate solution of about the same accuracy as the approximate solution determined with Chebfun. This choice makes a comparison of the CPU times required by the methods meaningful. The computing time required for determining this choice of n is not included in the CPU time. We remark that the determination of a suitable value of n when solving a problem of the form (2.4) can be difficult: a too large value results in unnecessarily large CPU time, while a too small value gives a computed solution of unnecessarily poor resolution. Figure 2 shows the run time and accuracy for each n for the example Shaw. In the figure, we also annotate the different problems with the choice of the discretization. The regularize-first approach using Chebfun does not require a user to explicitly choose the discretization. This is one of the main advantages over the discretize-first approach.

The relative errors obtained by applying TSVD and Tikhonov regularization in the discretized setting are reported in the fourth column of Tables 2 and 3, respectively. The sixth column of the tables shows the relative errors obtained when applying TSVE and Tikhonov regularization with Chebfun. We also report the CPU times in seconds for each method in the fifth and seventh columns of the tables. The tables show the computed approximate solutions determined by the Chebfun-based regularize-first methods to give as accurate approximations of the exact solutions as the approximate solutions determined by discretize-first methods. Moreover, we observe that the methods based on Chebfun are competitive with respect to run time for some problems, while they are slower for most problems. The last column of Tables 2 and 3 shows that applying TSVE with Chebfun is faster than applying Tikhonov regularization with Chebfun. This is reasonable since the TSVE method does not require the use of a root-finder.

Fig. 1

Example—“Baart”: (a) kernel, (b) right-hand side, (c) solutions

Fig. 2

Example—“Shaw”, α = 1.00 e − 2

Fig. 3

Example—“Baart”, α = 1.00 e − 3

Fig. 4

Example—“Fox-Goodwin”, α = 1.00 e − 3

Fig. 5

Example—“Gravity”, α = 1.00 e − 3.

Fig. 6

Example—“Wing”, α = 1.00 e − 2.

Fig. 7

Example—“Blur2D”, α = 1.00 e − 2

The accuracy and run time for the discretize-first methods depend on the number of discretization points n; Chebfun-based regularize-first methods do not require a user to choose a discretization level n. Thus, in Figs. 2, 3, 4, 5, and 6, we show the relative accuracy on the vertical axis and the run time on the horizontal axis; being closer to the origin is better. The figures illustrate that the accuracy and computing time of the implementations with Chebfun are competitive.

6 Problems in two space-dimensions

Linear ill-posed problems based on integral equations in one space-dimension are arguably less challenging than ill-posed problems in two space-dimensions. We therefore also consider Fredholm integral equations of the first kind in two space-dimensions,

$${\int}_{{{\varOmega}}_{1}} \kappa(s_{1},s_{2},t_{1},t_{2}) x(t_{1},t_{2}) dt_{1}dt_{2} = g^{\delta}(s_{1},s_{2}),\qquad (s_{1},s_{2})\in{{\varOmega}}_{2}.$$

(6.1)

The obvious main difference from the situation discussed above is that κ is now a function of four variables. This poses a main obstacle, since Chebfun does not have a Chebfun4 version for the computation with functions of four variables. We will discuss two different examples, Gaussian blur and inverse diffusion, that illustrate how this limitation can be overcome. The solution methods for these problems differ, since blur has a kernel that can be written as a product and we will exploit this. Solving diffusion requires a more general, but also more expensive, approach.

6.1 Gaussian blur

The problem blur models Gaussian blur with a kernel that is based on a tensor product of 1D-blur kernels. It is given by

$$\kappa(s_{1},s_{2},t_{1},t_{2})=\kappa_{1}(s_{1},t_{1})\times\kappa_{2}(s_{2},t_{2})$$

(6.2)

with

$$\kappa_{i}(s_{i},t_{i})=\frac{1}{\sqrt{2\pi\sigma^{2}}}\exp\left(-\frac{\left(t_{i}-s_{i}\right)^{2}}{2\sigma^{2}}\right),\quad i=1,2,$$

where σ is the standard deviation of the Gaussian distribution. The exact solution x(t₁,t₂) is constructed as a continuous “image”⁵ that we blur and contaminate by noise, and then try to reconstruct. In our example, we let σ = 0.2 and construct the exact solution as

$$x(t_{1},t_{2})=\left\lbrace (t_{1},t_{2})\in {{\varOmega}} : -0.5\leq t_{1} \leq 0.2 \text{and} -0.6\leq t_{2} \leq -0.2 \right\rbrace,$$

which is shown in Fig. 7(a).⁶ The error-free right-hand side function is determined by

$$g(s_{1},s_{2}):={\int}_{{{\varOmega}}} \kappa(s_{1},s_{2},t_{1},t_{2}) x(t_{1},t_{2}) dt_{1}dt_{2}$$

and the error-contaminated function g^δ(s₁,s₂) in (6.1) is defined by

$$g^{\delta}(s_{1},s_{2})=g(s_{1},s_{2})+\alpha \frac{{\left\Vert g\right\Vert}_{{{\varOmega}}_{2}}}{{\left\Vert F\right\Vert}_{{{\varOmega}}_{2}}}F(s_{1},s_{2}),$$

where F(s₁,s₂) is a smooth Chebfun function in two space-dimensions with maximum frequency about 2π/𝜗 and standard normal distribution N(0,1) at each point; α is the noise level. In this problem, we let the noise level and 𝜗 equal 10^− 2. The error-free right-hand side is shown in Fig. 7(c), and Fig. 7(e) depicts the noise that we added to generate the error-contaminated function g^δ.

A kernel that can be separated into a product of two functions as in (6.2) can be handled by Chebfun. We first compute the singular value expansions of κ₁ and κ₂. They allow us to approximate κ as

$$\kappa(s_{1},s_{2},t_{1},t_{2})\approx \sum\limits_{i=1}^{r_{1}} \sigma_{i}\phi_{i}^{(1)}(s_{1})\psi_{i}^{(1)}(t_{1}) \sum\limits_{j=1}^{r_{2}} \mu_{j} \phi_{j}^{(2)}(s_{2})\psi_{j}^{(2)}(t_{2}),$$

(6.3)

where both the σ_i and μ_j denote singular values. We seek an approximate solution in the form

$$x(t_{1},t_{2})= \sum\limits_{k=1}^{r_{1}} \sum\limits_{\ell=1}^{r_{2}} \beta_{k \ell} \psi_{k}^{(1)}(t_{1})\psi_{\ell}^{(2)}(t_{2}).$$

(6.4)

By substituting (6.3) and (6.4) into (6.1), and using the orthonormality of the basis functions, we get

$$\sum\limits_{i=1}^{r_{1}}\sum\limits_{j=1}^{r_{2}} \sigma_{i} \mu_{j} \beta_{ij} \phi_{i}^{(1)}(s_{1}) \phi_{j}^{(2)}(s_{2}) =g^{\delta}(s_{1},s_{2}).$$

We probe this equation with $\phi _{p}^{(1)}(s_{1}) \phi _{q}^{(2)}(s_{2})$ for all p and q, and use the orthonormality of the basis functions, to obtain

$$\beta_{ij} =\frac{{\int}_{{{\varOmega}}_{2}} g^{\delta}(s_{1},s_{2}) \phi_{i}^{(1)}(s_{1})\phi_{j}^{(2)}(s_{2}) ds_{1} ds_{2}}{\sigma_{i} \mu_{j}}.$$

(6.5)

This allows us to implement the solution algorithm using functions of at most two variables and, thus, do not exceed the capabilities of Chebfun2. For the solution of the forward problem, that is for blurring the exact solution in the setup process of the example, we use Chebfun3 [14],

$$\begin{array}{@{}rcl@{}} g(s_{1},s_{2})&=&{\int}_{{{\varOmega}}_{1}} \kappa(s_{1},s_{2},t_{1},t_{2}) x(t_{1},t_{2}) dt_{1}dt_{2}\\ &=&{\int}_{{{\varOmega}}_{1,2}}{\int}_{{{\varOmega}}_{1,1}} \kappa_{1}(s_{1},t_{1}) x(t_{1},t_{2}) dt_{1} \kappa_{2}(s_{2},t_{2}) dt_{2}. \end{array}$$

The product κ₁(s₁,t₁)x(t₁,t₂) is a function of three variables, s₁, t₁, and t₂. The result of the inner integral is a function of s₁ and t₂. Thus, the product with κ₂(s₂,t₂) is another function of three variables.

Equation (6.3) provides a singular function expansion that also can be used for Tikhonov regularization. Instead of solving (6.1) exactly, we solve

$$\begin{array}{@{}rcl@{}} \underset{x\in L^{2}({{\varOmega}}_{1})}{\min}\bigg\{{\left\Vert{\int}_{{{\varOmega}}_{1}} \kappa(\cdot,\cdot,t_{1},t_{2})x(t_{1},t_{2}) dt_{1} dt_{2} - g^{\delta}\right\Vert}_{{{\varOmega}}_{2}}^{2} + \lambda^{2} {\left\Vert x\right\Vert}^{2}_{{{\varOmega}}_{1}}\bigg\}. \end{array}$$

(6.6)

Using the fact that the kernel is separable, substituting (6.3) and (6.4) into (6.6), and using the orthonormality of the basis functions, we get

$$\begin{array}{@{}rcl@{}} \underset{\beta_{ij}}{\min}\sum\limits_{i=1}^{r_{1}} \sum\limits_{j=1}^{r_{2}} &&\bigg(\beta^{2}_{ij} {\sigma^{2}_{i}} {\mu^{2}_{j}} -2 \beta_{ij}\sigma_{i} \mu_{j} {\int}_{{{\varOmega}}_{2}}\phi_{i}^{(1)}(s_{1})\phi_{j}^{(2)}(s_{2})\ g^{\delta}(s_{1},s_{2}) ds_{1} ds_{2} \\ &&+ \lambda^{2} \beta^{2}_{ij} \bigg) +{\int}_{{{\varOmega}}_{2}} {\vert g^{\delta}(s_{1},s_{2})\vert}^{2} ds_{1} ds_{2} \end{array}$$

(6.7)

and obtain the solution

$$\begin{array}{@{}rcl@{}} x_{\lambda}(t_{1},t_{2})&=& \sum\limits_{k=1}^{r_{1}} \sum\limits_{\ell=1}^{r_{2}} \beta_{k \ell} \psi_{k}^{(1)}(t_{1})\psi_{\ell}^{(2)}(t_{2}),\\ \text{ with } \beta_{k\ell}&=& \frac{\sigma_{k} \mu_{\ell}{\int}_{{{\varOmega}}_{2}}\phi_{k}^{(1)}(s_{1})\phi_{\ell}^{(2)}(s_{2})\ g^{\delta}(s_{1},s_{2}) ds_{1} ds_{2}}{{\sigma^{2}_{k}} \mu^{2}_{\ell} + \lambda^{2}} . \end{array}$$

(6.8)

This provides us with the tools to reconstruct the exact image x(t₁,t₂) from its blurred version. Similarly as for the problems in one space-dimension, the truncation parameter ℓ in (6.4) and the Tikhonov regularization parameter λ in (6.8) are determined with the aid of the discrepancy principle, where we set η to be 10 in our example. The reconstructed images obtained with Tikhonov and TSVE regularization with Chebfun are shown in Fig. 7(b) and (d), respectively. The two reconstructed images are seen to be of roughly the same quality, with the image determined by Tikhonov regularization being slightly less oscillatory. The computing times for both methods differ significantly: the TSVE with Chebfun required 411 s, while Tikhonov regularization with Chebfun took 1206 s.

6.2 Inverse diffusion

We next consider an integral equation with a non-separable kernel κ(s₁,s₂,t₁,t₂). In the following, we will first describe the example and then discuss a method to solve the problem. This example is a continuous version of the PRdiffusion example provided in IR Tools [10].

The partial differential equation

$$\dot{u} = u_{t_{1},t_{1}} + u_{t_{2},t_{2}},\qquad \text{for all}\ (t_{1},t_{2}) \in{\Omega}_{1},$$

describes a diffusion process, where u(t₁,t₂,τ) is the concentration at the point (t₁,t₂) in Ω₁ at time τ. The time derivative of u is denoted by $\dot {u}$, and $u_{t_{i},t_{i}}$ stands for the second derivative in direction t_i. We assume that u satisfies the initial condition

$$u(t_{1},t_{2},0) = u_{0}(t_{1},t_{2}),$$

for some given function u₀, and Neumann boundary conditions for all time τ ≥ 0,

$$u_{t_{1}}(t_{1},t_{2},\tau) =0,\qquad \text{for all}\ (t_{1},t_{2})\in\partial{\Omega}_{1},$$

where ∂Ω₁ denotes the boundary of Ω₁. After T seconds, the solution of the system is

$$u_{T}(t_{1},t_{2}) = u(t_{1},t_{2},T).$$

We assume that u_T or a noisy version of u_T are given, and our task is to recover u₀. In this example, we have Ω₁ = [0,1] × [0,1] and T = 0.01. The initial condition is

$$\begin{array}{@{}rcl@{}} u_{0}(t_{1},t_{2}) = 0.7\exp\left(-\left(\frac{t_{1}-0.4}{0.12}\right)^{2} - \left(\frac{t_{2}-0.5}{0.15}\right)^{2}\right) + \exp\left(-\left(\frac{t_{1}-0.7}{0.1}\right)^{2} - \left(\frac{t_{2}-0.4}{0.08}\right)^{2}\right). \end{array}$$

The fundamental solution of this problem is given by

$$\begin{array}{@{}rcl@{}} u(t_{1},t_{2},\tau) = {\int}_{0}^{1}{\int}_{0}^{1} \Big({\Gamma}(t_{1}-s_{1},\tau){\Gamma}(t_{2}-s_{2},\tau) +\\ {\Gamma}(t_{1}+s_{1},\tau){\Gamma}(t_{2}+s_{2},\tau)\Big) u_{0}(s_{1},s_{2}) ds_{1} ds_{2}, \end{array}$$

where

$$\begin{array}{@{}rcl@{}} {\Gamma}(x,\tau) = \frac{1}{\sqrt{4\pi \tau}} \exp\left(\frac{-\tau^{2}}{4t}\right). \end{array}$$

We have

$$\begin{array}{@{}rcl@{}} {\int}_{0}^{1}{\int}_{0}^{1} \kappa(s_{1},s_{2},t_{1},t_{2}) u_{0}(s_{1},s_{2}) ds_{1} ds_{2} = u_{T}(t_{1},t_{2}). \end{array}$$

The right-hand side is computed by solving the forward problem. As in the previous examples, we use Chebfun’s random function randnfun2 to generate two-dimensional noise; see Fig. 8(e). The kernel κ can be written as

$$\begin{array}{@{}rcl@{}} \kappa(s_{1},s_{2},t_{1},t_{2}) = \kappa_{1}(s_{1},t_{1})\kappa_2(s_{2},t_{2}) + \kappa_{3}(s_{1},t_{1}) \kappa_{4}(s_{2},t_{2}). \end{array}$$

(6.9)

This kernel has a special structure for which one could construct a specific method. Instead, we opted for implementing a more general method. As in the one-dimensional case, we use cross approximation followed by a singular value decomposition to compute the singular value expansion of κ. This method follows the description in Section 2.1 with the difference that s = (s₁,s₂) and t = (t₁,t₂) here. To find an approximation to the maximum κ in Ω₂ ×Ω₁, we use the MATLAB function fminsearch. We choose as pivot for the cross approximation the maximizer $(\hat {s}_{1},\hat {s}_{2},\hat {t}_{1},\hat {t}_{2})$. After computing the crosses $C_{1}(s) = \kappa (s_1,s_2,\hat {t}_{1},\hat {t}_{2})$ and $R_{1}(t)=\kappa (\hat {s}_{1},\hat {s}_{2},t_1,t_2)$, we update the remainder κ − C₁(s)M₁R₁(t)^T. We then repeat this process for the remainder so-obtained until the maximum is below a preset tolerance. The columns of C(s) and rows of R(t) determined by cross approximation are chebfun2 objects. Nevertheless, orthonormalization based on the Gram–Schmidt process is straightforward using Chebfun2. Thereby, one also obtains upper triangular matrices R_c and R_r, and the remaining computations are identical to those described in Section 2.1.

We developed a proof-of-concept implementation of this method. Our implementation lacks the run time optimization that a possible future Chebfun4 extension provided by the Chebfun developers would have.

Tikhonov regularization determines the solution f_λ, which is shown in Fig. 8(b); the exact solution is displayed in Fig. 8(a) for comparison. Since our implementation of Tikhonov regularization uses the singular value expansion, we can easily solve the problem using TSVE, too. The TSVE regularized solution is shown in Fig. 8(d) and is visually about the same as the solution determined by Tikhonov regularization, despite having a slightly higher relative norm-wise error. Figure 8(c) shows the exact right-hand side, Fig. 8(e) depicts the added noise, and the difference between the right-hand side computed from the TSVE regularized solution and the right-hand side with noise g^δ is shown in Fig. 8(f).

Our proof-of-concept implementation required about half an hour for the computations including about 20 min for the singular value expansion and about 10 min for determining λ using the discrepancy principle.

This method works for all kernel functions of four variables. However, the fact that κ can be written as in (6.9) ensures that the columns of C(s) and the rows of R(t) can each be represented by chebfun2 objects of rank 2. The ranks are relevant for the run time of the method. When applying the Gram–Schmidt process and when computing the singular functions, the ranks increase and are automatically truncated by Chebfun’s arithmetic. Nevertheless, the fact that the rank initially is 2 has a dampening effect on the computational complexity.

Fig. 8

Example—“Diffusion”, α = 1.00 e − 2

7 Conclusion

The computed results illustrate the feasibility of using Chebfun to solve linear discrete ill-posed problems and in this way carry out computations in a fashion that is close to the spirit of the analysis of ill-posed problems found, e.g., in [7]. The accuracy and timings of the implementations with Chebfun are competitive.

In the future, further extensions to Chebfun including the treatment of functions of four or six variables will allow the application of the Chebfun-based approach discussed in this paper to the solution of linear ill-posed problems in two and three space-dimensions. In the meantime, the two methods described in Section 6 can be used.