Effective numerical methods for simulating diffusion on a spherical surface in three dimensions

Abstract

In order to construct an algorithm for homogeneous diffusive motion that lives on a sphere, we consider the equivalent process of a randomly rotating spin vector of constant length. By introducing appropriate sets of random variables based on cross products, we construct families of methods with increasing efficacy that exactly preserve the spin modulus for every realisation. This is done by exponentiating an antisymmetric matrix whose entries are these random variables that are Gaussian in the simplest case.

1 Introduction and background

We take a non-standard approach to diffusion on the surface of a sphere, starting with an equation for a three-component spin vector written in Langevin form:

$$ \frac{\partial }{\partial t} S(t) =S(t) \times \eta, \quad \text{where} \quad S(t) = \left( \begin{array}{c} V(t) \\ Y(t) \\ Z(t) \end{array} \right), $$

(1)

where η is a vector of independent white noises with magnitude σ. Here × denotes the cross product—see Definition 1.

We understand (1) as an Itô stochastic differential equation for the vector-valued process

$$ S(t)=\left( V(t),Y(t),Z(t)\right)^{\mathrm{T}}. $$

Equation (1) can then be written as

$$ \mathrm{d} S(t) = - \sigma^{2} S(t) \mathrm{d} t + \sigma S(t) \times \mathrm{d} W(t) , $$

(2)

where $W(t)=\left (W_{1}(t),W_{2}(t),W_{3}(t)\right )^{\mathrm {T}}$ is a vector of independent Wiener processes. Given the definition of the cross product ×, this can be written as

$$ \begin{array}{@{}rcl@{}} \mathrm{d} V(t) = \sigma\left( Y(t) \mathrm{d} W_{3}(t) - Z(t) \mathrm{d} W_{2}(t) \right) - \sigma^{2} V(t) \mathrm{d} t\ \\ \mathrm{d} Y(t) = \sigma\left( Z(t) \mathrm{d} W_{1}(t) - V(t) \mathrm{d} W_{3}(t) \right) - \sigma^{2} Y(t) \mathrm{d} t\ \\ \mathrm{d} Z(t) = \sigma\left( V(t) \mathrm{d} W_{2}(t)- Y(t) \mathrm{d} W_{1}(t) \right) - \sigma^{2} Z(t)\mathrm{d} t. \end{array} $$

In matrix form, we can write this as the linear Itô SDE

$$ \mathrm{d} S(t) = -\sigma^{2} I S(t) \mathrm{d} t + \sigma \sum\limits_{i=1}^{3} A_{i} S(t) \mathrm{d} W_{i}(t), $$

(3)

where I is the 3×3 identity matrix and

$$ A_{1} = \left( \begin{array}{rrr} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0 \end{array} \right), \quad A_{2} = \left( \begin{array}{rrr} 0 & 0 & -1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{array} \right), \quad A_{3} = \left( \begin{array}{rrr} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right). $$

(4)

Another convenient representation of (3) is

$$ \mathrm{d} S = -\sigma^{2} S \mathrm{d} t + G(S) \mathrm{d} W(t) $$

(5)

where G(S) is the antisymmetric matrix

$$ G(S) = \sigma \left( \begin{array}{rrr} 0 & -S_{3} & S_{2} \\ S_{3} & 0 & -S_{1} \\ -S_{2} & S_{1} & 0 \end{array} \right) . $$

(6)

Based on (5), we can prove the following theorem.

Theorem 1

With S(t) the solution of (5) then

$$ u(t) := S^{\top} (t)S(t) = {S_{1}^{2}}(t) + {S_{2}^{2}}(t) + {S_{3}^{2}}(t) = S^{\top}(0) S(0), \quad \forall t.$$

Proof

The proof is by Itô’s Lemma—see for example Kloeden and Platen [1]. Consider the Itô SDE

$$ \mathrm{d} X = f(X) \mathrm{d} t + G(X) \mathrm{d} W(t), \quad X \in \mathbb{R}^{N}, \> W(t) \in \mathbb{R}^{d}, \> G(X) \in \mathbb{R}^{d \times d}, $$

where f and G are arbitrary functions satisfying appropriate integrability conditions—see [1] for details. Suppose $u = h(X) \in \mathbb {R}$, where h has continuous first- and second-order partial derivatives. Then Itô’s Lemma states

$$ \mathrm{d} u = \left( (\nabla h(X))^{\top} f(X) + \frac{1}{2} \text{Tr} (G(X) G^{\top}(X) \nabla[\nabla h(X)] \right) \mathrm{d} t + (\nabla h(X))^{\top} G(X) \mathrm{d} W(t),$$

where ∇[∇h(X)] is the matrix of second-order spatial derivatives of h. Now when N = d = 3

$$ \begin{array}{@{}rcl@{}} u(S) &=& {S_{1}^{2}} + {S_{2}^{2}} + {S_{3}^{2}}, \\ \nabla h(S) &=& 2 (S_{1}, \> S_{2}, \> S_{3})^{\top} \\ \nabla[\nabla h(S)] &=& 2I \end{array} $$

and G(S) is given by (6).

Hence, du = 0 and so u(t) = S^⊤(0)S(0).□

As a consequence of Theorem 1, the vector S(t) lives on the unit sphere of radius 1 for all time.

In this paper, we will construct different classes of numerical methods that preserve $|| S(t) ||_{2}^{2}$. The starting point is the Stratonovich form of (3) namely

$$ \mathrm{d} S = \sigma \sum\limits_{i=1}^{3} A_{i} S \mathrm{d} W_{i} , $$

(7)

where the A_i are as in (4). This equation is linear, but non-commutative, and we can write the solution as a Magnus expansion [2]:

$$ S(t) = e^{\Omega(t)} S_{0}, $$

(8)

in terms of iterated commutators of the A_i and stochastic Stratonovich integrals with respect to multiple Wiener processes.

Section 2 reviews the Magnus expansion in the general setting, but we also show that for (8) Ω(t) can be represented as an antisymmetric matrix

$$ {\Omega}(t) = \left( \begin{array}{ccc} 0 & \xi_{3}(\sigma t) & -\xi_{2}(\sigma t) \\ -\xi_{3}(\sigma t) & 0 & \xi_{1}(\sigma t) \\ \xi_{2}(\sigma t) & -\xi_{1}(\sigma t) & 0 \end{array} \right), $$

(9)

where the ξ_i(σt) are continuous random variables that are to be constructed. Given (9) then by (8)

$$ \begin{array}{@{}rcl@{}} || S(t) ||_{2}^{2} &=& S^{\top}_{0} e^{\Omega(t)^{\top}} e^{\Omega(t)} S_{0} \\ &=& S_{0}^{\top} e^{\Omega(t)^{\top} + {\Omega}(t)} S_{0} \\ &=& || S_{0} ||_{2}^{2}, \end{array} $$

and so this construction is norm-preserving. We also show in Section 3 that a stepwise implementation by, for example, the Euler-Maruyama method is not norm-preserving.

In Sections 3 and 4, we show how to construct the ξ_i(σt) based on an expansion of a weighted sum of increasing numbers of appropriate cross products. In Section 5, we estimate these weights based on the following idea: as a particle wanders randomly on the unit sphere, the steady-state distribution at $z = \cos \limits \theta$ is uniform as the curvature near the pole balances the girth near the equator. We can therefore write down an Itô SDE (2) for z(t) (= S₃(t)), namely

$$ \mathrm{d} z = -\sigma^{2} z \mathrm{d} t + \sigma \sqrt{1-z^{2}} \mathrm{d} W(t). $$

(10)

This satisfies

$$ E(z(t)) = -e^{-\sigma^{2} t} z_{0}, \quad E(z^{2}(t)) = \frac{1}{3} + e^{-3 \sigma^{2} t} ({z_{0}^{3}} - \frac{1}{3}). $$

(11)

We will use these weak forms to compare with S₃(t) derived from (8) and (9). In Section 6, we give some results and discussions, and in Section 7 give conclusions on the novelty of this work.

Finally, we note that the problem of a particle diffusing on a sphere has been studied in a number of settings. Yosida [3] in 1949 considered motion on a three-dimensional sphere by solving a certain parabolic partial differential equation in which the generating function of the right-hand side operator can be determined explicitly and is the Laplacian operator in polar co-ordinates. Brillinger [4] looked at this problem in terms of expected travel time to a cap. In a slightly different setting, a number of variants of walks on N-spheres have been constructed for solving the N-dimensional Dirichlet problem. Muller [5] constructed N-dimensional spherical processes through an iterative process extending the ideas of Kakutani [6] who used the exit locations of Brownian motion. Other approaches were introduced in [7, 8]. More recently, Yang et al. [9] showed how a constant-potential, time-independent Schrödinger equation can be solved by a classical walk-on-spheres approach.

2 The Magnus method

The form of the Magnus expansion of the solution for arbitrary matrices A₁,A₂, and A₃ was given in [2], as in Lemma 1.

Lemma 1

$$ \begin{array}{@{}rcl@{}} {\Omega}(t) &=& \sigma \sum\limits_{i=1}^{3} A_{i} J_{i}(t) + \frac{\sigma^{2}}{2} \sum\limits_{i=1}^{3} \sum\limits_{j=i+1}^{3} [A_{i},A_{j}] (J_{ji}(t)-J_{ij}(t)) \\ &+& \sigma^{3} \sum\limits_{i=1}^{3} \sum\limits_{k=1}^{3} \sum\limits_{j=k+1}^{3} [A_{i},[A_{j},A_{k}]] (\frac{1}{3}(J_{kji}(t)-J_{jki}(t)) + \\ && \quad \quad \quad \quad \quad \quad \quad \quad \frac{1}{12} J_{i}(t) (J_{jk}(t)-J_{kj}(t))) + O(\sigma^{4}), \end{array} $$

with Stratonovich integrals

$$ \begin{array}{@{}rcl@{}} J_{i}(t) &=& W_{i}(t) \\ J_{ij}(t) &=& {{\int}_{0}^{t}} {{\int}_{0}^{s}} dW_{i}(s_{1}) \> dW_{j}(s) \\ J_{ijk}(t) &=& {{\int}_{0}^{t}} {{\int}_{0}^{s}} {\int}_{0}^{s_{1}} dW_{i}(s_{2}) \> dW_{j}(s_{1}) \> dW_{k}(s). \end{array} $$

In fact for any positive integer p, the σ^p term in the expansion will include iterated commutators of order p that are summed over p summations and multiplied by complicated expressions involving Stratonovich integrals over p Wiener processes.

Theorem 2

With the A_i as in (4), then Ω(t) is the anti-symmetric matrix

$$ {\Omega}(t) = \sum\limits_{i=1}^{3} A_{i} \xi_{i}(\sigma t) = \left( \begin{array}{ccc} 0 & \xi_{3}(\sigma t) & -\xi_{2}(\sigma t) \\ -\xi_{3}(\sigma t) & 0 & \xi_{1}(\sigma t) \\ \xi_{2}(\sigma t) & -\xi_{1}(\sigma t) & 0 \end{array} \right). $$

(12)

Proof

Given (4), then

$$ \begin{array}{@{}rcl@{}} [A_{1}, A_{2}] = -A_{3}, \quad [A_{2}, A_{3}] &=& -A_{1}, \quad [A_{3}, A_{1}] = -A_{2} \\ \frac{1}{2} ({A_{1}^{2}} + {A_{2}^{2}} + {A_{3}^{2}}) &=& -I. \end{array} $$

(13)

This means that all high-order commutators of any order p will collapse down to one of A₁,A₂, or A₃. To illustrate this up to σ³, we apply (13) to the expansion in Lemma 1. This gives

$$ \begin{array}{@{}rcl@{}} A_{1} (\sigma J_{1} + \frac{\sigma^{2}}{2}(J_{23}-J_{32}) &+& \frac{\sigma^{3}}{12}(J_{2}(J_{12}-J_{21}) + J_{3}(J_{31}-J_{13})) \\ &+& \frac{\sigma^{3}}{3}(J_{212}-J_{122}+J_{133}-J_{313})) \\ + A_{2}(\sigma J_{2} + \frac{\sigma^{2}}{2}(J_{31}-J_{13}) &+& \frac{\sigma^{3}}{12}(J_{1} (J_{21}-J_{12}) + J_{3}(J_{23}-J_{32})) \\ &+& \frac{\sigma^{3}}{3}(J_{121}-J_{211}+J_{323}-J_{233})) \\ + A_{3}(\sigma J_{3} + \frac{\sigma^{2}}{2}(J_{12}-J_{21}) &+& \frac{\sigma^{3}}{12}(J_{1}(J_{31}-J_{13})+J_{2}(J_{32}-J_{23})) \\ &+& \frac{\sigma^{3}}{3}(J_{131}-J_{311} + J_{232} - J_{322})) + O(\sigma^{4}). \end{array} $$

Here, we have dropped the dependence on t for ease of notation. Clearly the form for Ω(t) is as in (12).□

Remarks

• The ξ_i(σt) are complicated expansions in σ of high-order Stratonovich integrals. However, these are extremely computationally intensive to simulate [1]. Instead, we will approximate them as continuous stochastic processes in some weak sense—see (26).

• Clearly, the simplest approximation to the ξ(σt) is to take

  $$ \xi(\sigma t) = (\xi_{1}(\sigma t),\xi_{2}(\sigma t),\xi_{3}(\sigma t))^{\top} = \sigma J(t) = \sigma W(t), $$

  (14)

  where W(t) is a three-vector of independent Wiener processes. This idea will be the basis of our first algorithm presented in Section 3.

3 Stepwise implementations

Before presenting our first method, we show that the Euler-Maruyama method is an inappropriate method in that it does not preserve $||S(t)||_{2}^{2}$, the spin norm. In fact, the mean drifts and the distribution of values grow rapidly wider with increasing time. An improved algorithm (without Itô correction) can narrow the distribution of values of the norm but will still have a mean that drifts. To see the behaviour of the EM method applied to (3), we have

$$ S_{k+1} = ((1-\sigma^{2} h)I + \sigma \sqrt{h} N_{k} ) \> S_{k}. $$

where, as before,

$$ N_{k} = \left( \begin{array}{ccc} 0 & N_{3k} & -N_{2k} \\ -N_{3k} & 0 & N_{1k} \\ N_{2k} & -N_{1k} & 0 \end{array} \right). $$

(15)

Hence, with $N_{k} + N_{k}^{\top } = 0$,

$$ ||S_{k+1}||^{2} = S_{k}^{\top} ((1 + \sigma^{4} h^{2} - 2 \sigma^{2} h ) \> I + \sigma^{2} h N_{k}^{\top} N_{k} ) \> S_{k}. $$

Note N_1k,N_2k,N_3k,k = 1,⋯ ,m are independent Normal random variables with mean 0 and variance 1. Now

$$ \begin{array}{@{}rcl@{}} N_{k}^{\top} N_{k} &=& -{N_{k}^{2}} \\ &=& \left( \begin{array}{ccc} N_{3k}^{2}+N_{2k}^{2} & -N_{1k}N_{2k} & -N_{1k}N_{3k} \\ -N_{2k}N_{1k} & N_{3k}^{2} + N_{1k}^{2} & -N_{2k}N_{3k} \\ -N_{3k}N_{1k} & -N_{3k}N_{2k} & N_{1k}^{2} + N_{2k}^{2} \end{array} \right) . \end{array} $$

Thus

$$ E(N_{k}^{\top} N_{k}) = 2I $$

and so

$$ E(||S_{k+1}||^{2} \> \vert \> ||S_{k}||^{2}) = (1 + \sigma^{4} h^{2})\> E(||S_{k}||^{2}). $$

Similarly,

$$ E(||S_{k+1}||^{4} \> \vert \> ||S_{k}||^{4}) = (1 + 6 \sigma^{4} h^{2})\> E(||S_{k}||^{4}). $$

Therefore, if (3) is solved on the time interval (0,T) with m steps h = T/m starting with ||S₀||² = 1 then, as $m\to \infty$ (h → 0), the value of ||S(t)||² obtained is a random variable with

$$ E(||S(t)||^{2}) = \exp\left( (\sigma^{4} h) t\right) = 1+\left( \sigma^{4} h \right) t + O(t^{2}) $$

and

$$ \left( E(||S(t)||^{4})-E(||S(t)||^{2}\right)^{{\textstyle{\frac12}}} = 2\sigma^{2}\left( h \right)^{{\textstyle{\frac12}}} \sqrt{t} +{\ldots} . $$

Thus, the spin modulus is not conserved and the mean error grows linearly with t. More importantly, the variance can be very large so that if the procedure described above is repeated numerous times, the standard deviation of the ensemble of values of ||S(T)||² obtained is proportional to $\sqrt {T}$. In fact, the probability density function of $\log (||S(t)||^{2})$ is Gaussian. This means that, while more than half of the values of ||S(t)||² obtained will be less than 1, rare large values of ||S(t)||² dominate the statistics.

In order to construct a simple method that preserves the spin norm, it will be based on (8), (9), and (14), which leads to

$$ S(t) = \exp(\sigma {\Omega}(t)) \> S_{0}, $$

(16)

with

$$ {\Omega}(t) = \left( \begin{array}{ccc} 0 & \hat{J}_{3}(t) & -\hat{J}_{2}(t) \\ -\hat{J}_{3}(t) & 0 & \hat{J}_{1}(t) \\ \hat{J}_{2}(t) & -\hat{J}_{1}(t) & 0 \end{array} \right) $$

(17)

where in the first instance we take $J(t) = (\hat {J}_{1}(t), \hat {J}_{2}(t), \hat {J}_{3}(t))^{\top } = (W_{1}(t), W_{2}(t), W_{3}(t))^{\top }$.

Our construction is based on Rodrigues’ formula [10]. Let

$$ A = \begin{pmatrix} 0&\ a_{3}&-a_{2}\\ -a_{3}&0&\ \ a_{1}\\ \ \ a_{2}&-a_{1}&0\\ \end{pmatrix} \text{and}~r = \sqrt{{a_{1}^{2}}+{a_{2}^{2}}+{a_{3}^{2}}}. $$

Then A³ = −r²A, so that

$$ \begin{array}{@{}rcl@{}} \exp\left( \sigma A\right) &=& I+A\left( \sigma-\frac16\sigma^{3}r^{2}+\ldots\right) +A^{2}\left( {\textstyle{\frac12}}\sigma^{2}-\frac1{24}\sigma^{4}r^{2} +\ldots\right) \\ &=&I+A \frac{\sin\left( \sigma r\right)}{r} + A^{2} \frac{1-\cos\left( \sigma r\right)}{r^{2}}. \end{array} $$

Hence from (16) and (17)

$$ \begin{array}{@{}rcl@{}} S(t) &=& (I + {\Omega}(t) \frac{\sin(\sigma r(t))}{r(t)} + {\Omega}^{2}(t) \frac{(1-\cos(\sigma r(t)))}{r^{2}(t)}) \> S_{0} \\ r(t) &=& ||J(t)||_{2}. \end{array} $$

(18)

Now let T = mh; then we can write

$$ \hat{J}_{i}(T) = \sqrt{h} \sum\limits_{k=1}^{m} N_{ik}. $$

This allows us to write a step-by-step method

$$ S_{k+1} = \exp (\sigma \sqrt{h} N_{k})\>S_{k}, $$

where N_k is given in (15),

and hence a step-by-step method is, from (18),

$$ \begin{array}{@{}rcl@{}} S_{k+1} &=& (I + f(h)\>N_{k} + g(h)\> {N_{k}^{2}})\>S_{k} \\ f(h) &=& \frac{\sin(\sigma \sqrt{h} r_{k})}{r_{k}}, \quad g(h) = \frac{1-\cos(\sigma \sqrt{h} r_{k})}{{r_{k}^{2}}} \\ r_{k} &=& \sqrt{N_{1k}^{2} + N_{2k}^{2} + N_{3k}^{2}}. \end{array} $$

Note that this step-by-step method will only be strong order 0.5.

4 A class of Magnus-type methods

A stepwise approach, as constructed previously, will not yield a method that has more than strong order 0.5 and weak order 1 so we will attempt to approximate the ξ_i(σt) to obtain a better weak order approximation. We will first consider the behaviour of the composition of the Magnus operator over two half steps and require this to be the same as the Magnus approximation over a full step up to some power of the stepsize h. This will give us a clue as to how to choose the ξ_j(t). In order to simplify the discussion, we will, wolog, take σ = 1.

Let $\bar {A}_{\xi }$ denote the matrix

$$ \bar{A}_{\xi} = \left( \begin{array}{ccc} 0 & \xi_{3} & -\xi_{2} \\ -\xi_{3} & 0 & \xi_{1} \\ \xi_{2} & -\xi_{1} & 0 \end{array} \right) $$

(19)

with ξ = (ξ₁, ξ₂, ξ₃)^⊤.

Suppose on the two half steps, we assume that the random variables behave as

$$ \begin{array}{@{}rcl@{}} \hat{\xi} &=& \sqrt{\frac{h}{2}}\>N_{1} + \frac{h}{2} \> P_{1} + O(h^{\frac{3}{2}}) \\ \tilde{\xi} &=& \sqrt{\frac{h}{2}}\>N_{2} + \frac{h}{2} \> P_{2} + O(h^{\frac{3}{2}}) \end{array} $$

and on the full step

$$ \xi = \sqrt{h}\>N + h\> P + O(h^{\frac{3}{2}}), $$

where N₁,N₂,N and P₁,P₂,P are 3 vectors of independent random variables that are to be determined in some manner. Furthermore, the matrices generated by these vectors through (19) will be denoted by $\bar {N}_{1}, \> \bar {N}_{2}, \> \bar {P}_{1}, \> \bar {P}_{2}$.

So from (12) and (16) and setting the composition over two half steps to be equal to the Magnus operator up to the h term implies

$$ \left( I + \sqrt{\frac{h}{2}} \bar{N}_{1} + \frac{h}{2} (\bar{P}_{1} + \frac{1}{2} \bar{N}_{1}^{2})\right) \left( I + \sqrt{\frac{h}{2}} \bar{N}_{2} + \frac{h}{2} (\bar{P}_{2} + \frac{1}{2} \bar{N}_{2}^{2})\right) $$

$$ = I + \sqrt{h} \bar{N} + h (\bar{P} + \frac{1}{2} \bar{N}^{2}) + O(h^{\frac{3}{2}}).$$

Hence

$$ \bar{N} = \frac{1}{\sqrt{2}} (\bar{N}_{1} + \bar{N}_{2}) $$

(20)

and

$$ \bar{P} + \frac{1}{2} \bar{N}^{2} = \frac{1}{2} (\bar{P}_{1} + \bar{P}_{2} + \frac{1}{2}(\bar{N}_{1}^{2} + \bar{N}_{2}^{2} + \bar{N}_{1} \bar{N}_{2})). $$

Hence from (20) and after some simple algebra

$$ \bar{P} = \frac{1}{2} (\bar{P}_{1} + \bar{P}_{2}) - \frac{1}{4} [\bar{N}_{2}, \bar{N}_{1}]. $$

(21)

Now with $\bar {N}_{1}$ and $\bar {N}_{2}$ generated by the vectors N₁ and N₂, via (19) it is easy to show that $[\bar {N}_{2},\bar {N}_{1}]$ generates a matrix of the form (19) in which the corresponding vector ξ that generates $\bar {A}_{\xi }$ is N₁ × N₂, where the cross product is given through the following definition.

Definition 1

Given vectors B = (B₁,B₂,B₃)^⊤, D = (D₁,D₂,D₃)^⊤ then

$$ B \times D = (B_{2}D_{3}-B_{3}D_{2}, \> B_{3}D_{1}-B_{1}D_{3}, \> B_{1}D_{2}-B_{2}D_{1})^{\top}.$$

Consequences of Definition 1 are the following well-known results:

Lemma 2

Given two three-vectors B and D, the following results on cross products hold.

$$ \begin{array}{@{}rcl@{}} B \times D + D \times B &=& 0 \\ B \times B &=& 0 \\ A \times (B \times C) &=& B (A^{\top} C) - C (A^{\top} B). \end{array} $$

Proof

Trivial use of Definition 1.□

Thus, in the vector setting, (20) and (21) and Lemma 2 give

$$ \begin{array}{@{}rcl@{}} N &=& \frac{1}{\sqrt{2}} (N_{1} + N_{2}) \end{array} $$

(22)

$$ \begin{array}{@{}rcl@{}} P &=& \frac{1}{2} (P_{1}+P_{2}) + \frac{1}{4} N_{1} \times N_{2}. \end{array} $$

(23)

Equation (22) suggests that we take N₁ and N₂ to be independent N(0,1) 3-vectors, so that N is also a 3-vector with independent N(0,1) components.

Furthermore, if we let u₁, u₂, v₁ and v₂ be independent N(0,1) 3-vectors and we take

$$ \begin{array}{@{}rcl@{}} N_{1} &=& \frac{1}{\sqrt{2}} (u_{1} + u_{2}), \quad \quad N_{2} = \frac{1}{\sqrt{2}} (v_{1} + v_{2}) \\ P_{1} &=& \frac{\sqrt{2}}{4} u_{1} \times \left( \frac{u_{2}+v_{2}}{\sqrt{2}}\right), \quad \quad P_{2} = \frac{\sqrt{2}}{4} v_{1} \times \left( \frac{u_{2}+v_{2}}{\sqrt{2}}\right) \end{array} $$

then from (23) and Lemma 2 we have

$$ \begin{array}{@{}rcl@{}} P &=& \frac{\sqrt{2}}{4} \l \left( \frac{u_{1} + v_{1}}{\sqrt{2}}\right) \times \left( \frac{u_{2} + v_{2}}{\sqrt{2}}\right) + \frac{1}{4} N_{1} \times (\sqrt{2} N - N_{1}) \\ &=& \frac{\sqrt{2}}{4} \left( \frac{u_{1} + v_{1}}{\sqrt{2}}\right) \times N - \frac{\sqrt{2}}{4} \left( \frac{u_{1} + u_{2}}{\sqrt{2}}\right) \times N \\ &=& \frac{\sqrt{2}}{4} \left( \frac{v_{1} - u_{2}}{\sqrt{2}}\right) \times N. \end{array} $$

Hence N,N₁, and N₂ have the same distributions as do P,P₁, and P₂, respectively.

Continuing this line of thought, this suggests that we base our choice of the ξ(t) on a cross product formulation. Thus, we will take for ξ(t) the expansion

$$ \xi(t) = \sum\limits_{j=1}^{r} d_{j} A_{j}(t), $$

(24)

where the d_j are chosen appropriately and

$$ \begin{array}{@{}rcl@{}} A_{j+1}(t) &=& J_{2}(t) \times A_{j}(t), \quad j = 1, 2, \cdots, r-1 \\ A_{1}(t) &=& J_{1}(t) \\ d_{1} &=& 1. \end{array} $$

(25)

We can choose any positive integer value for r in (24). But we will see in Section 5 when we attempt to estimate the d_j that they become overly sensitive for values of r > 5, and so we will take a specific value of r, namely r = 5.

This will lead to methods that we will denote by M(1,d₂,d₃,d₄,d₅). For clarity, we give the form of the ξ(t):

$$ \begin{array}{@{}rcl@{}} \xi(t)&=& J_{1}(t) + d_{2} J_{2}(t) \times J_{1}(t) + d_{3} J_{2}(t) \times (J_{2}(t) \times J_{1}(t)) \\ && + d_{4} J_{2}(t) \times (J_{2}(t) \times (J_{2}(t) \times J_{1}(t)) ) \\ && + d_{5} J_{2}(t) \times (J_{2}(t) \times (J_{2}(t) \times (J_{2}(t) \times J_{1}(t)))). \end{array} $$

(26)

We will show in Section 5 how to calibrate the parameters d₂,d₃,d₄,d₅ appropriately, in order to get good performance.

Note if we wish to simulate ξ(t) at some time point t = T, then we generate an equidistant time mesh with stepsize $h = \frac {T}{m}$. We then simulate two sequences of vectors of length m consisting of independent N(0,1)-3 vectors: G_1i,G_2i,i = 1,⋯ ,m. We then approximate

$$ \begin{array}{@{}rcl@{}} J_{1}(T) & \approx & \sqrt{h} \sum\limits_{i=1}^{m} G_{1i} \\ J_{2}(T) & \approx & \sqrt{h} \sum\limits_{i=1}^{m} G_{2i} \end{array} $$

and generate ξ(T) by using (26) and the definition of the cross product and related results in Lemma 1.

5 Model calibration

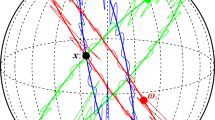
As a particle wanders randomly on a sphere, the steady-state distribution at latitude, $z = {\cos \limits } \theta$, is uniform as the curvature near the poles balances the greater girth near the equator (see also [4])—by symmetry, the same is true of x and y; see Fig. 1.

Fig. 1

Numerical distribution of x, y, and z

If we write the SDE for z alone, we find

$$ \mathrm{d} z(t) = -\sigma^{2} z(t) \mathrm{d} t + \sigma \sqrt{1-z(t)^{2}}\mathrm{d} W(t). $$

(27)

Hence, using the property of Itô SDEs

$$ E(z(t)) = e^{-\sigma^{2} t} z_{0}. $$

(28)

Furthermore, we can show via Itô’s Lemma that with u(t) = z²(t) then u satisfies

$$ du = \sigma^{2} (1-3u)\> dt + 2 \sigma \sqrt{u-u^{2}}\> dW(t). $$

Hence

$$ E(z^{2}(t)) = \frac{1}{3} + e^{-3 \sigma^{2} t} \left( {z_{0}^{2}} - \frac{1}{3}\right). $$

(29)

Now we saw that the solution S(t) to (2) is given in (18). Assume S₀ = (0, 0, 1)^⊤, σ = 1 and let z(t) be the third component of S(t); then

$$ \begin{array}{@{}rcl@{}} z(t) &=& \cos(r(t)) + \frac{1-\cos(r(t))}{r^{2}(t)} \> {\xi_{3}^{2}}(t) \\ &=& \sum\limits_{j=0}^{\infty} \frac{(-1)^{j}}{(2j)!} \> (r^{2j}(t) - {\xi_{3}^{2}}(t)r^{2j-2}(t)), \end{array} $$

where ξ(t) = (ξ₁(t),ξ₂(t),ξ₃(t))^⊤ is to be determined and

$$ r^{2}(t) = {\xi_{1}^{2}}(t) + {\xi_{2}^{2}}(t) + {\xi_{3}^{2}}(t). $$

Let $u^{2}(t) = {\xi _{1}^{2}}(t) + {\xi _{2}^{2}}(t)$, then

$$ z(t) = 1 + \sum\limits_{j=1}^{\infty} \frac{(-1)^{j}}{(2j)!} \left( \sum\limits_{k=0}^{j-1} \left( \begin{array}{c} j-1 \\ k \end{array} \right) \xi_{3}^{2(j-1-k)}(t)\> u^{2(k+1)}(t) \right). $$

Since u²(t) is independent from ξ₃(t) then with $\bar {z}(t) = E(z(t))$,

$$ \bar{z}(t) = 1 + \sum\limits_{j=1}^{\infty} \frac{(-1)^{j}}{(2j)!} \left( \sum\limits_{k=0}^{j-1} \left( \begin{array}{c} j-1 \\ k \end{array} \right) E(\xi_{3}^{2(j-1-k)}(t)) E(u^{2(k+1)}(t) ) \right). $$

(30)

We will compare $\bar {z}(t)$ with (28) in order to construct effective methods from the class M(1.d₂,d₃,d₄,d₅). To commence this, we now analyse the error for method M(1,0,0,0,0) (M₁), so that ξ(t) = J₁(t). Now for any of the 3 components of ξ(t), say ξ₁(t), we know, from the properties of the Normal distribution,

$$ \begin{array}{@{}rcl@{}} E(\xi_{1}^{2p}(t)) &=& (2p-1)(2p-3){\cdots} 1\> t^{p} \\ &=& \frac{(2p)!}{p!\>2^{p}}\> t^{p}. \end{array} $$

(31)

Substituting (31) into (30), we find after some manipulation

$$ \begin{array}{@{}rcl@{}} \bar{z}(t) &=& 1 + \sum\limits_{j=1}^{\infty} \frac{(-1)^{j} t^{j}}{(2j)!} \left( \frac{2}{3} \frac{(2j+1)!}{2^{j} j!} \right) \\ &=& 1 + \frac{2}{3} \sum\limits_{j=1}^{\infty} \frac{(-1)^{j} (\frac{t}{2})^{j}}{j!} (2j+1) \\ &=& \frac{1}{3} + \frac{2}{3} (1-t) e^{-t/2} \\ &=& 1 - t + \frac{1}{2}t^{2} - \frac{1}{12}t^{2} + O(t^{3}). \\ \end{array} $$

Hence

$$ \begin{array}{@{}rcl@{}} \bar{z}(t) - e^{-t} &=& -\frac{1}{12} t^{2} + O(t^{3}) \end{array} $$

(32)

$$ \begin{array}{@{}rcl@{}} &=& \frac{1}{3} (1+2(1-t)e^{-\frac{t}{2}} - 3 e^{-t}). \end{array} $$

(33)

A plot of this error in (33) is given in Fig. 2. We see that (32) is only accurate for modest values of time. So this is a word of caution in using a truncated error estimate for too large a value of t.

Fig. 2

Plots of the mean error (solid) and truncated mean error (dotted) for method M₁

We will now consider the behaviour of the general class of methods given by M(1,d₂,d₃,d₄,d₅) in terms of (30) where ξ(t) is given in (26). It will prove too difficult to get analytical results for the error in (33) so we will have to use a truncated error estimate. First, we will expand $\bar {z}(t)$ in (30) up to and including the t⁴ term. It can be shown with some simple expansions that

$$ \bar{z}(t) = -\frac{1}{2}G_{1} + \frac{1}{4!} G_{2} - \frac{1}{6!} G_{3} + \frac{1}{8!} G_{4} + \> \text{higher order terms} $$

where

$$ \begin{array}{@{}rcl@{}} G_{1} &=& E({\xi_{1}^{2}} + {\xi_{2}^{2}}) \\ G_{2} &=& E(u^{2} {\xi_{3}^{2}} + u^{4}) \\ G_{3} &=& E(u^{2} {\xi_{3}^{4}} + 2 u^{4} {\xi_{3}^{2}} + u^{6}) \\ G_{4} &=& E(u^{2} {\xi_{3}^{6}} + 3 u^{4} {\xi_{3}^{4}} + 3 u^{6} {\xi_{3}^{2}} + u^{8}) . \end{array} $$

In order to calculate these expectations, we note the following Lemma, where the product of vectors is considered component-wise.

Lemma 3

With the A_j(t) defined previously and ξ(t) given by (26)

$$ \begin{array}{@{}rcl@{}} E(A_{p}(t) \cdot A_{q}(t)) &=& 0, \quad p+q \> \> \text{odd} \\ E(A_{p}(t) \cdot A_{q}(t)) &=& C_{p,q} t^{\frac{p+q}{2}} e, \quad p + q \> \> \text{even} \\ e &=& (1, 1, 1)^{\top}. \end{array} $$

Proof

Without loss of generality we will assume p ≥ q = p − r and consider two cases: r = 2k + 1 and r = 2k, (k = 0,1,2,⋯ ). Let us consider the odd case first. Now

$$ \begin{array}{@{}rcl@{}} A_{p} \cdot A_{p-1} &=& (J_{2} \times A_{p-1}) \cdot A_{p-1} \\ A_{p} \cdot A_{p-3} &=& (J_{2} \times (J_{2} \times (J_{2} \times A_{p-3}))) \cdot A_{p-3} \\ &=& (J_{2} \times (J_{2} (J_{2}^{\top} A_{p-3}) \cdot A_{p-3}(J_{2}^{\top} J_{2}))) \cdot A_{p-3} \quad \text{(Lemma 2)} \\ &=& -(J_{2}^{\top} J_{2})((J_{2} \times A_{p-3}) \cdot A_{p-3}) \quad \text{(Lemma 2)} \\ A_{p} \cdot A_{p-5} &=& (J_{2} \times (J_{2} \times (J_{2} \times (J_{2} \times (J_{2} \times A_{p-5}))))) \cdot A_{p-5} \\ &=& -(J_{2}^{\top} J_{2}) (J_{2} \times (J_{2} \times (J_{2} \times A_{p-5})) \cdot A_{p-5}) \quad \text{from above} \\ &=& -(J_{2}^{\top} J_{2}) (J_{2} \times ((J_{2}^{\top} A_{p-5})J_{2} - (J_{2}^{\top} J_{2}) A_{p-5}) \cdot A_{p-5} ) \quad \text{(Lemma 2)} \\ &=& (J_{2}^{\top} J_{2})^{2} ((J_{2} \times A_{p-5}) \cdot A_{p-5}) \quad \text{(Lemma 2)}. \end{array} $$

It is easy to show by induction that

$$ A_{p} \cdot A_{p-(2k+1)} = (-1)^{k} (J_{2}^{\top} J_{2})^{k} ((J_{2} \times A_{p-(2k+1)}) \cdot A_{p-(2k+1)}). $$

(34)

Now, by definition of the cross product, the i^th component of J₂ × A_{p−(2k+ 1)} does not have a corresponding component from A_{p−(2k+ 1)} and since the powers of J₂ appearing in (34) are odd, then

$$ E(A_{p} \cdot A_{p-(2k+1)}) = 0, \quad \forall k = 0, 1, 2, {\cdots} . $$

(35)

Now let us consider the even case.

$$ \begin{array}{@{}rcl@{}} A_{p} \cdot A_{p-2} & = & (J_{2} \times (J_{2} \times A_{p-2})) \cdot A_{p-2} \\ & = & (J_{2}^{\top} A_{p-2}) (J_{2} \cdot A_{p-2}) - (J_{2}^{\top} J_{2})(A_{p-2} \cdot A_{p-2}) \quad \text{(Lemma 2)} \\ A_{p} \cdot A_{p-4} & = & (J_{2} \times (J_{2} \times (J_{2} \times (J_{2} \times A_{p-4})))) \cdot A_{p-4} \\ & = & (J_{2} \times (J_{2} \times ((J_{2}^{\top} A_{p-4}) J_{2} - (J_{2}^{\top} J_{2})A_{p-4}))) \cdot A_{p-4} \quad \text{from above} \\ & = & -(J_{2}^{\top} J_{2})((J_{2} \times (J_{2} \times A_{p-4})) \cdot A_{p-4}) \quad \text{(Lemma 2)} \\ & = & (J_{2}^{\top} J_{2})((J_{2}^{\top} J_{2})(A_{p-4} \cdot A_{p-4}) - (J_{2}^{\top} A_{p-4})(J_{2} \cdot A_{p-4})) \quad \text{from above}. \end{array} $$

Similarly to the odd case, then by induction, for k = 1,2,⋯

$$ A_{p} \cdot A_{p-2k} = (-1)^{k-1} (J_{2}^{\top} J_{2})^{k-1} ((J_{2}^{\top} A_{p-2k})(J_{2} \cdot A_{p-2k}) - (J_{2}^{\top} J_{2})(A_{p-2k} \cdot A_{p-2k})). $$

Clearly, in each of the 3 components of the vectors on the right-hand side, there will be terms that have even powers in J₂ and A_p− 2j and the power of t will behave as k + p − 2k = p − k. Furthermore, each of the 3 components will have the same form. Hence

$$ E(A_{p} \cdot A_{p-2k}) = C_{p,k} t^{p-k} e, \quad \text{as required.} $$

□

Some algebra and calculations of moments allow us to write

$$ \bar{z} = 1 - t + t^{2} (\frac{1}{2} + c_{2}) - t^{3} \left( \frac{1}{6} + c_{3}\right) + t^{4} \left( \frac{1}{24} + c_{4}\right) + O(t^{5}), $$

where c₂,c₃,c₄ can be considered to be the error terms when comparing $\bar {z}(t)$ to e^−t. It can be shown that

$$ \begin{array}{@{}rcl@{}} c_{2} &=& -2\left( {d_{2}^{2}} -2 d_{3} + \frac{1}{24}\right) \\ c_{3} &=& 10 {d_{3}^{2}} - \frac{5}{3} \left( {d_{2}^{2}} -2 d_{3} + \frac{1}{24}\right) \\ && - 2 d_{2} d_{4} E(A_{2}(t) \cdot A_{4}(t))_{i} - 2 d_{5} E(A_{1}(t) \cdot A_{5}(t))_{i} \\ c_{4} &=& \frac{10}{3} {d_{3}^{2}} + 2 {d_{2}^{4}} + \frac{2}{3} ({d_{2}^{2}} - 2 d_{3})^{2} - \frac{7}{12} (d_{2} - 2 d_{3}) - \frac{5}{192} \\ && - {d_{4}^{2}} E(A_{4}(t))^{2}_{i} - 2 d_{3} d_{5} E(A_{3}(t) \cdot A_{5}(t))_{i}. \end{array} $$

(36)

These results hold true for any component of ξ, i = 1,2, or 3. Some of the expectations in (36) have already been calculated, but we now show the analysis in Lemma 4 for some of the more complicated terms in (36).

Lemma 4

For any i = 1,2 or 3

• (i) E(A₂(t) ⋅ A₄(t))_i = 10t³

• (ii) E(A₁(t) ⋅ A₅(t))_i = 10t³

• (iii) E(A₄(t)²)_i = 70t⁴

• (iv) E(A₃(t) ⋅ A₅(t))_i = − 70t⁴.

Proof

We will drop the dependence on t for ease of notation.

• (i) As a consequence of Lemma 2 and (34),

  $$ \begin{array}{@{}rcl@{}} A_{2} \cdot A_{4} &=& (J_{2} \times J_{1}) \cdot (J_{2} \times (J_{2} \times (J_{2} \times J_{1}))) \\ &=& (J_{2} \times J_{1}) \cdot (J_{2} \times (J_{2} (J_{2}^{\top} J_{1}) - J_{1} (J_{2}^{\top} J_{2}))) \\ &=& -(J_{2} \times J_{1}) \cdot (J_{2} \times J_{1}) (J_{2}^{\top} J_{2}). \end{array} $$

  With J₂ = (B₁,B₂,B₃)^⊤, J₁ = (N₁,N₂,N₃)^⊤ then

  $$ J_{2} \times J_{1} = (B_{3} N_{2} -B_{2} N_{3}, \> B_{3} N_{1} - B_{1} N_{3}, \> B_{2} N_{1} - B_{1} N_{2})^{\top}.$$

  Take any component of the vectors, say the first component, then

  $$(A_{2} \cdot A_{4})_{1} = (B_{3}N_{2} - B_{2}N_{3})^{2} ({B_{1}^{2}} + {B_{2}^{2}} + {B_{3}^{2}}).$$

  Using results on expectation of normals

  $$E(A_{2} \cdot A_{4})_{1} = 1 + 1 + 1 + 3 + 3 + 1 = 10 t^{3}.$$

• (ii) From (34) and Lemma 2

  $$ \begin{array}{@{}rcl@{}} A_{1} \cdot A_{5} &=& J_{1} \cdot (J_{2} \times A_{4}) \\ &=& -J_{1} \cdot (J_{2} \times (J_{2} \times J_{1})) \> (J_{2}^{\top} J_{2}) \\ &=& -(J_{2}^{\top} J_{2}) J_{1} \cdot (J_{2} (J_{2}^{\top} J_{1}) - J_{1} (J_{2}^{\top} J_{2})). \end{array} $$

  Look at, say, the first component, then

  $$ \begin{array}{@{}rcl@{}} (A_{1} \cdot A_{5})_{1} &=& ({B_{1}^{2}} + {B_{2}^{2}} + {B_{3}^{2}})^{2} {N_{1}^{2}} - ({B_{1}^{2}}+{B_{2}^{2}}+{B_{3}^{2}})(B_{1}N_{1}\\ &&+B_{2}N_{2}+B_{3}N_{3})N_{1}B_{1} \\ E(A_{1} \cdot A_{5})_{1} &=& 3 + 3 + 3 + 2 + 2 + 2 - (3 + 1 + 1). \end{array} $$

  So E(A₁A₅)₁ = 10t³.

• (iii) From Lemma 2 and (34)

  $$ \begin{array}{@{}rcl@{}} {A_{4}^{2}} &=& (J_{2}^{\top} J_{2})^{2} ((J_{2} \times J_{1}) \cdot (J_{2} \times J_{1})) \\ ({A_{4}^{2}})_{1} &=& ({B_{1}^{2}}+{B_{2}^{2}}+{B_{3}^{2}})^{2} (B_{3} N_{2} - B_{2} N_{3})^{2} \\ E({A_{4}^{2}})_{1} &=& 70 t^{3}. \end{array} $$

• (iv) From (34) and Lemma 2

  $$ \begin{array}{@{}rcl@{}} A_{3} \cdot A_{5} &=& -(J_{2} \times (J_{2} \times J_{1})) \cdot (J_{2} (J_{2}^{\top} J_{1}) - J_{1} (J_{2}^{\top} J_{2})) (J_{2}^{\top} J_{2}) \\ &=& -(J_{2} (J_{2}^{\top} J_{1}) - J_{1} (J_{2}^{\top} J_{2}))^{2} (J_{2}^{\top} J_{2}). \end{array} $$

  Look at the first component say, then

  $$ \begin{array}{@{}rcl@{}} (A_{3} \cdot A_{5})_{1} &=& -{B_{1}^{2}} ({B_{1}^{2}}+{B_{2}^{2}}+{B_{3}^{2}})(B_{1}N_{1} + B_{2}N_{2} + B_{3} N_{3})^{2} \\ && -{N_{1}^{2}} ({B_{1}^{2}}+{B_{2}^{2}}+{B_{3}^{2}})^{3} \\ && + 2B_{1} N_{1}({B_{1}^{2}}+{B_{2}^{2}}+{B_{3}^{2}})^{2} (B_{1}N_{1} +B_{2}N_{2}+B_{3}N_{3}) \\ E(A_{3} \cdot A_{5})_{1} &=& -35 - 105 + 70 = -70. \end{array} $$

□

From Lemma 4 and (36)

$$ \begin{array}{@{}rcl@{}} c_{2} &=& -2\left( {d_{2}^{2}} -2 d_{3} + \frac{1}{24}\right) \\ c_{3} &=& 10 {d_{3}^{2}} -\frac{5}{3}\left( {d_{2}^{2}} -2d_{3} + \frac{1}{24}\right) - 20 d_{2} d_{4} - 20 d_{5} \\ c_{4} &=& \frac{10}{3} {d_{3}^{2}} + 2 {d_{2}^{4}} + \frac{2}{3}({d_{2}^{2}} -2d_{3})^{2} - \frac{7}{12}(d_{2}-2d_{3}) - \frac{5}{192} \\ && -70 {d_{4}^{2}} + 140 d_{3} d_{5}. \end{array} $$

(37)

We now consider the behaviour of the error constants as a function of the classes of methods.

Let M₂ denote M(1,d₂,0,0,0); then clearly c₂ and c₃ are minimised if d₂ = 0, and this reduces to M₁ : M(1,0,0,0,0). However, if we allow d₂ to be imaginary, then the most effective method within the class M₂ is when ${d_{2}^{2}} + \frac {1}{24} = 0$, that is $M(1,\frac {1}{\sqrt {24}} i, 0, 0, 0)$.

Let M₃ denote M(1,d₂,d₃,0,0); then

$$ c_{2} = 0 \iff {d_{2}^{2}} = 2\left( d_{3} - \frac{1}{48}\right) $$

(38)

in which case from (37)

$$ \begin{array}{@{}rcl@{}} c_{3} &=& 10 {d_{3}^{2}} \\ c_{4} &=& \frac{1}{3} \left( 34 {d_{3}^{2}} -d_{3} + \frac{15}{1728}\right) > 0 \quad \text{if}~d_{3}~\text{is real}. \end{array} $$

We now assume (38) holds and choose d₃ such that $c_{4} = \frac {1}{4} c_{3}$ (since the exponential solution for the mean has this property—and it turns out this ansatz is more effective than trying to make some of the error constants equal to zero). This leads to the quadratic

$$ 53 {d_{3}^{2}} - 2 d_{3} + \frac{5}{288} = 0$$

or

$$ d_{3} = \frac{1}{53}\left( 1 + \frac{1}{12} \sqrt{\frac{23}{2}}\right). $$

Thus, an effective method is $M_{3} = M(1,\sqrt {2d_{3}-\frac {1}{24}},\frac {1}{53}(1+\frac {1}{12}\sqrt {\frac {23}{2}}),0,0)$. That is,

$$M_{3} = M(1,\sqrt{\frac{1}{12} \left( \sqrt{46}-\frac{5}{106}\right)},\frac{1}{53}\left( 1+\frac{1}{12}\sqrt{\frac{23}{2}}\right),0,0).$$

For the class M₄ = M(1,d₂,d₃,d₄,0), then applying the same ansatz as for M₃, with $c_{4} = \frac {1}{4}c_{3}$ then (37) leads to

$$ 70 \left( d_{4} - \frac{1}{28}d_{2}\right)^{2} = \frac{53}{6}{d_{3}^{2}} - \frac{13}{84}d_{3} - \frac{5}{6048}.$$

Taking the negative square root of the right-hand side gives

$$ d_{4} = \frac{1}{28}d_{2} - \sqrt{\frac{1}{70}\left( \frac{53}{6}{d_{3}^{2}} - \frac{13}{84} d_{3} - \frac{5}{6048}\right)}, $$

(39)

where d₂ is determined from (38). Thus, d₃ is a free parameter, but with the caveat that the term under the square root in (39) must be positive, and from (38), $d_{3} > \frac {1}{48}$.

6 Results and discussion

We now present results for a set of methods, with just up to 4 terms—we do not consider M₅; see Remark 5. These methods are M₁(1,0,0,0), M₂(1,d₂,0,0) (d₂ > 0), $M_{2}^{*}(1,\frac {1}{\sqrt {24}}\>i,0,0)$, $M_{3}(1,\sqrt {\frac {1}{12}(\sqrt {46}-\frac {5}{106})},\frac {1}{53}(1+\frac {1}{12}\sqrt {\frac {23}{2}}))$, M₄(1,0.099716,0.025805, − 3.33310^− 4), $M_{4}^{*}(1,0.081984,0.024194,1.366 10^{-6})$. These last two methods were found after a parameter sweep over d₃—see Remark 4 below.

In all cases, we give the error in z (E₁) and the error in z² (E₂) at T = 1 with 500 steps and 400,000 (1st column) or 1,000,000 (second column) simulations (Table 1).

Table 1 Simulation results

We can make the following remarks.

• 1. Although we do not show the results, M₁ is always more accurate than the class M₂ for any real value of d₂ > 0.

• 2. If we choose $d_{2} = \frac {1}{\sqrt {24}} \> i$ then $M_{2}^{*}$ is much more accurate than M₁. However, in the case of $M_{2}^{*}$ the components of S are complex. Nevertheless they still satisfy ${S_{1}^{2}}(t) + {S_{2}^{2}}(t) + {S_{3}^{2}}(t) = 1,$ ∀t. Letting S_j = α_j + i β_j,j = 1,2,3 and writing

  $$ \alpha = (\alpha_{1},\alpha_{2},\alpha_{3})^{\top}, \quad \beta = (\beta_{1},\beta_{2},\beta_{3})^{\top},$$

  then this conservation property is equivalent to

  $$ ||\alpha||^{2} - ||\beta||^{2} = 1, \quad \alpha^{\top} \beta = 0. $$

  (40)

  Thus, rather than having a spherical-like structure, the solution to (2) is more akin to a hyperbolic structure.

• 3. Compared with M₁, method M₃ performs very well. The error, E₁, is approximately 50 times smaller than M₁ with 400,000 simulations and much less with 1,000,000 simulations. The errors are also considerably less for E₂ and we note that we did not attempt to optimise the parameters for the second moment. However, we do note that there is considerable variation between the results for 400,000 and 1,000,000 simulations.

• 4. The above remark brings us to the results for M₄ and $M_{4}^{*}$. In finding these results, we did a parameter sweep over the free parameter d₃ and we present the best results based on 400,000 and 1,000,000 simulations. M₄ is more accurate than M₃ with 400,000 simulations (but less accurate with 1,000,000 simulations), while $M_{4}^{*}$ behaves in the converse with respect to M₃. For both M₄ and $M_{4}^{*}$ the corresponding optimal d₄ is quite small and so these results are subject to the quality of the normal random number stream.

• 5. This last point explains why we do not go further and consider M₅. Some of the optimal parameters will likely be very small, as is already the case for the values of d₄, and the results will be even more sensitive to the normal random number stream.

7 Conclusions

It turns out that a Magnus method given by (16), where the antisymmetric matrix Ω(t) in (17) depends just on the three Wiener processes, guarantees that the solution stays on the surface of the sphere. However, this approach says nothing about the accuracy of the trajectories on the surface.

The novelty of this work is that we construct the continuous random variables ξ₁(t), ξ₂(t), and ξ₃(t) that guarantee that the trajectories lie on the surface but also give good accuracy in a weak sense. This is done by considering a one-dimensional model (27) in which we note that the steady-state distribution of the third variable at $z = {\cos \limits } \theta$ is uniform as the curvature near the pole balances the girth near the equator. From (27), we can get exact formulations for the first and second moments.

The additional novelty is that we now construct the ξ_j(t) in terms of a linear combination of iterated cross products (see (26)). We then find the weights d_j by comparing the Magnus solution with the above moments. This results in a family of methods with very small weak errors. We describe these methods to be effective in the sense of the above characterisation. This is important for making sure that the paths on the surface of the sphere are highly accurate. It turns out that method M₃ is the simplest and the most robust of the methods constructed. The final aspect of innovation is that these ideas can be extended to diffusion on higher dimensional spherical surfaces [11] and we hope to do this in a following paper.