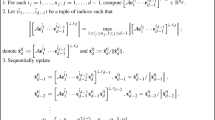Abstract
The paper is concerned with methods for computing the best low multilinear rank approximation of large and sparse tensors. Krylov-type methods have been used for this problem; here block versions are introduced. For the computation of partial eigenvalue and singular value decompositions of matrices the Krylov-Schur (restarted Arnoldi) method is used. A generalization of this method to tensors is described, for computing the best low multilinear rank approximation of large and sparse tensors. In analogy to the matrix case, the large tensor is only accessed in multiplications between the tensor and blocks of vectors, thus avoiding excessive memory usage. It is proved that if the starting approximation is good enough, then the tensor Krylov-Schur method is convergent. Numerical examples are given for synthetic tensors and sparse tensors from applications, which demonstrate that for most large problems the Krylov-Schur method converges faster and more robustly than higher order orthogonal iteration.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In many applications of today, large and sparse data sets are generated that are organized in more than two categories. Such multi-mode data can be represented by tensors. They arise in applications of data sciences, such as web link analysis, cross-language information retrieval and social network analysis (see, e.g., [32]). The effective analysis of tensor data requires the development of methods that can identify the inherent relations that exist in the data, and that scale to large data sets. Low rank approximation is one such method, and much research has been done in recent years in this area (for example, [2, 8, 16, 25, 30, 37, 42, 43, 53]). However, most of these methods are intended for small to medium size tensors. The objective of this paper is to develop an algorithm for best low-rank approximation of large and sparse tensors.
We consider the problem of approximating a 3-mode tensor \(\mathcal {A}\) by another tensor \({\mathscr{B}}\),
where the norm is the Frobenius norm, and \({\mathscr{B}}\) has low multilinear rank-(r1,r2,r3) (for definitions of the concepts used in this introduction, see Section 2). We will assume that \(\mathcal {A}\) is large and sparse. This problem can be written
where \(\mathcal {F} \in \mathbb {R}^{r_{1} \times r_{2} \times r_{3}}\) is a tensor of small dimensions, and \(\left (U,V,W \right )_{} \boldsymbol {\cdot } \mathcal {F}\) denotes matrix-tensor multiplication in all three modes. This is the best rank-(r1,r2,r3) approximation problem [8], and it is a special case of Tucker tensor approximation [50, 51]. It can be considered as a generalization of the problem of computing the Singular Value Decomposition (SVD) of a matrix [17]. In fact, a partial SVD solves the matrix approximation problem corresponding to (1) (see, e.g., [21, Chapter 2.4]). However, strictly speaking we can only expect to find a local optimum of (1), because the problem of finding a global solution is NP-hard [23], [34, p. 747].
In this paper, we develop a Block Krylov-Schur like (BKS) method for computing the best rank-(r1,r2,r3) approximation of large and sparse tensors. We are specially interested in small values of the rank, as in the two parallel papers [14, 15], where it is essential to use the best approximation rather than any Tucker approximation.
Krylov methods are routinely used to compute partial SVD’s (and eigenvalue decompositions) of large sparse matrices [33]. In [42], we introduced a generalization of Krylov methods to tensors. It was shown experimentally that tensor Krylov-type methods have similar approximation properties as the corresponding matrix Krylov methods. In this paper, we present block versions of Krylov-type methods for tensors, which are expected to be more efficient than the methods in [42]. Having problems in mind, where the tensor is symmetric with respect to two modes (e.g., sequences of adjacency matrices of graphs), we also formulate the block methods in terms of such tensors.
Even if matrix Krylov methods give low rank approximations, their convergence properties are usually not good enough, and, if used straightforwardly, they may require excessive memory and computer time. Therefore, they are accelerated using restart techniques [33], which are equivalent to the Krylov-Schur method [47]. We here present a tensor Krylov-Schur-like method, and show that it can be used to compute best multilinear low-rank approximations of large and sparse tensors.
The Krylov-Schur method is an inner-outer iteration. In the outer iteration we start from an approximate solution and generate new blocks of orthogonal vectors, using Krylov-type block methods. Thus, we use the large tensor only in tensor-matrix multiplications, where the matrix has few columns (this is analogous to the use of block Krylov methods for large matrices). Then, we project the problem (2) to a smaller problem of the same type, which we solve in the inner iterations, using a method for problems with a medium-size, dense tensor. The problem can be formulated as one on a product of Grassmann manifolds [16]. In our experiments, we use a Newton-Grassmann method. As a stopping criterion for the outer iteration we use the norm of the Grassmann gradient of the objective function. We show that this gradient can be computed efficiently in terms of the small projected problem.
We also prove that, if the starting approximation the Krylov-Schur method is good enough, the BKS method is convergent.
The literature on algorithms for best rank-(r1,r2,r3) approximation of large and sparse tensors is not extensive [22, 28, 31]. The main contributions are the following. (1) Block Krylov-type methods and an efficient way for computing gradients; (2) the Krylov-Schur approach and its convergence analysis; (3) the present paper is the first one that goes significantly beyond the Higher Order Orthogonal Iteration (HOOI) [8] (to the best of our knowledge). Our experiments indicate that the new method is more efficient and robust than HOOI for many large and sparse tensors.
The paper is organized as follows. Some tensor concepts are introduced in Section 2. The Krylov-Schur procedure for matrices is sketched in Section 3. In Section 4, block Krylov-type methods for tensors are described. The tensor Krylov-Schur method is presented and analyzed in Section 6. Some numerical examples are given in Section 7.2 that illustrate the accuracy and efficiency of the Krylov-Schur method. There we also discuss why some alternative methods are not well adapted to large and sparse tensors.
We are especially interested in tensors that are symmetric with respect to the first two modes (e.g., tensor consisting of a sequence of adjacency matrices of undirected graphs). However, most of the theory is formulated for the general case, and we also give one such numerical example.
The method presented in this paper is “like” a Krylov-Schur method for two reasons. The tensor Krylov-type method is not a Krylov method in a strict sense, as it does not build bases for Krylov subspaces [42]. The method is not a real Krylov-Schur method as it does not build and manipulate a Hessenberg matrix; instead, it uses a tensor, which is in some ways similar to Hessenberg. However, this structure is not utilized. For ease of presentation, we will sometimes omit “like” and “type.”
2 Tensor concepts and preliminaries
2.1 Notation
Throughout this paper, we use of the following notations. Vectors will be denoted by lower case roman letters, e.g., a and b, matrices by capital roman letters, e.g., A and B and tensors by calligraphic letters, e.g., \({\mathcal {A}}\) and \({{\mathscr{B}}}\).
Notice that sometimes we will not explicitly mention the dimensions of matrices and tensors, and assume that they are such that the operations are well-defined. Also, for simplicity of notation and presentation, we will restrict ourselves to tensors of order 3, which are defined in the next paragraph. The generalization to higher order tensors is straightforward. For more general definitions, we refer reader to [3].
Let \(\mathcal {A}\in \mathbb {R}^{l\times m\times n}\) be a 3-dimensional array of real numbers. With the definitions below and the approximation problem (2), \(\mathcal {A}\) is a coordinate representation of a Cartesian tensor (with some abuse of notation we will call \(\mathcal {A}\) a tensor for short) [34]. The order of a tensor is the number of dimensions, also called modes, e.g., a 3-dimensional array, is called a tensor of order 3 or 3-tensor. A fiber is a one-dimensional section of a tensor, obtained by fixing all indices except one; \({\mathcal {A}}(i,:,k)\) is referred to as a mode-2 fiber. A slice is a two-dimensional section of a tensor, obtained by fixing one index; \(\mathcal {A}(i,:,:)\) is a mode-1 slice or 1-slice. A particular element of a 3-tensor \(\mathcal {A}\) can be denoted in two different ways, i.e., “matlab-like” notation and standard subscripts with \(\mathcal {A}(i,j,k)\) and aijk, respectively.
Definition 1.
A 3-tensor \(\mathcal {A}\in \mathbb {R}^{m \times m \times n}\) is called (1,2)-symmetric if all its 3-slices are symmetric, i.e.,
Symmetry with respect to any two modes and for tensors of higher order than 3 can be defined analogously.
We use Ik for the identity matrix of dimension k.
2.2 Multilinear tensor-matrix multiplication
We first consider the multiplication of a tensor by a matrix. When a tensor is multiplied by a single matrix in mode i, say, we will call the operation the mode-i multilinear multiplication (or mode-i product) of a tensor by a matrix. For example, the mode-1 product of a tensor \(\mathcal {A}\in \mathbb {R}^{l\times m\times n}\) by a matrix \(U\in \mathbb {R}^{p\times l}\) is defined
This means that all mode-1 fibers in the 3-tensor \(\mathcal {A}\) are multiplied by the matrix U. The mode-2 and the mode-3 product are defined in a similar way. Let the matrices \(V\in \mathbb {R}^{q\times m}\) and \(W\in \mathbb {R}^{r\times n}\); multiplication along all three modes is defined
For multiplication with a transposed matrix \(X\in \mathbb {R}^{l\times s}\) it is convenient to introduce a separate notation,
In a similar way if \(x\in \mathbb {R}^{l}\) then
Thus, the tensor \({\mathscr{B}}\) is identified with a matrix B.
2.3 Inner product and norm, contractions
The inner product of two tensors \(\mathcal {A}\) and \({\mathscr{B}}\) of the same order and dimensions is denoted by \(\langle \mathcal {A},{\mathscr{B}}\rangle \) and is computed as a sum of element-wise products over all the indices, that is
The product allows us to define the Frobenius norm of a tensor \(\mathcal {A}\) as
As in the matrix case the Frobenius norm of a tensor is invariant under orthogonal transformations, i.e., \(\Vert A \Vert =\Vert {\left (U,V,W \right )_{} \boldsymbol {\cdot } \mathcal {A}}\Vert \), for orthogonal matrices U, V, and W. This follows immediately from the fact that mode-i multiplication by an orthogonal matrix does not change the Euclidean length of the mode-i fibers.
The inner product is a contraction. We also define partial contractions that involve less than three modes,
We use negative subscripts to denote partial contractions in all but one mode,
The result is a matrix of inner products between the mode-1 slices of the two tensors. For partial contractions only the contracted modes are required to be equal, so the result matrix may be rectangular.
2.4 Multilinear rank
Unlike the matrix case, there is no unique definition of the rank of a tensor. In this paper, we consider the concept of multilinear rank defined by Hitchcock [24]. Let A(i) denote the mode-i unfolding (matricization) of \(\mathcal {A}\) (using some ordering of the vectors),
where the columns of A(i) are all mode-i fibers [7]. Similarly, let i be the inverse of i. The multilinear rank of a third order tensor \({\mathcal {A}}\) is an integer triplet (p,q,r) such that
where rank(A(i)) is the matrix rank. In this paper we will deal only with multilinear rank, and we will use the notation rank-(p,q,r), and rank(A) = (p,q,r). For matrices the rank is obtained via the svd (see, e.g., [21, Chapter 2]). In exact arithmetic the multilinear rank can be computed using the higher order singular value decomposition (HOSVD) [7].
2.5 Best rank-(r 1,r 2,r 3) approximation
The problem (1) of approximating a given tensor \(\mathcal {A}\in \mathbb {R}^{l\times m\times n}\) by another tensor \({\mathscr{B}}\) of equal dimensions but of lower rank, occurs in many modern applications, e.g., machine learning [35], pattern classification [41], analytical and quantum chemistry [29, 44], and signal processing [6]. We assume that \(\text {rank}({\mathscr{B}})=(r_{1},r_{2},r_{3})\), which means that \({\mathscr{B}}\) can be written as a product of a core tensor \(\mathcal {F}\in \mathbb {R}^{r_{1}\times r_{2}\times r_{3}}\) and three matrices,
where \(U\in \mathbb {R}^{l\times r_{1}}\), \(V\in \mathbb {R}^{m\times r_{2}}\), and \(W\in \mathbb {R}^{n\times r_{3}}\) are full column rank matrices. Without loss a generality, we can suppose that U, V and W have orthonormal columns, as any nonorthogonality may be incorporatedFootnote 1 into \(\mathcal {F}\). Therefore, the best multilinear low rank problem (1) can be written as
There are a few major differences between the best low rank approximation of matrices and 3-mode tensors and higher. In the matrix case, the explicit solution of corresponding problem can be obtained from the SVD (see the Eckart-Young property in [21, Theorem 2.4.8]). A simple proof is given in [13, Theorem 6.7]. There is no known closed form solution for the minimization problem (4), but it can be shown that this is a well-defined problem in the sense that for any (r1,r2,r3) a solution exists [9, Corollary 4.5]. Several iterative methods for computing the low rank approximation for small and medium size tensors have been proposed (see [8, 16, 26, 43]). In [8], it is shown that (4) is equivalent to following maximization problem
where \({\Phi }(U,V,W)=\Vert \mathcal {A} \boldsymbol {\cdot } \left (U,V,W \right )_{} \Vert ^{2}\). Since the norm is invariant under orthogonal transformations, it holds that Φ(U,V,W) = Φ(UQ1,V Q2,WQ3) for any orthogonal matrices \(Q_{1}\in \mathbb {R}^{r_{1}\times r_{1}}\), \(Q_{2}\in \mathbb {R}^{r_{2}\times r_{2}}\) and \(Q_{3}\in \mathbb {R}^{r_{3}\times r_{3}}\). Hence, (5) is equivalent to a maximization problem over a product of Grassmann manifolds (for optimization on matrix manifolds, see [1, 12, 25, 26]).
Throughout this paper, we will assume that the multilinear rank of \(\mathcal {A}\) is larger (mode-wise) than (r1,r2,r3).
After computing the optimal U, V and W the optimal \(\mathcal {F}\) can be obtained by considering the minimization of (4) as a linear least squares problem with unknown \(\mathcal {F}\).
Lemma 2.1.
Let \(\mathcal {A}\in \mathbb {R}^{l\times \times m\times n}\) be given along with three matrices with orthonormal columns, \(U\in \mathbb {R}^{l\times r_{1}}\), \(V\in \mathbb {R}^{m\times r_{2}}\), and \(W\in \mathbb {R}^{n\times r_{3}}\), where r1 ≤ l, r2 ≤ m, and r3 ≤ n. Then, the least squares problem
has the unique solution
For a proof, see, e.g., [8, 42]. The tensor \(\mathcal {F}\) is a generalization of the matrix Rayleigh quotient.
2.6 Gradient on the product manifold
In [16] a Newton-Grassmann method is derived for computing the solution of maximization problem (5). The constraints on the unknown matrices U, V, and W are taken into account by formulating the problem as an optimization problem on a product of three Grassmann manifolds. In this paper, we will need the gradient of Φ in the tangent space of the product manifold for a stopping criterion. This gradient can be expressed in the ambient coordinate system, or in local coordinates. In the context of the new methods presented, it is practical and more efficient to use local coordinate representations (see Proposition 5.2). Let (UU⊥) denote the enlargement of U to a square orthogonal matrix, and use the analogous notation for V and W. Then, the Grassmann gradient at (U,V,W) can be written as
where \(\mathcal {F}^{1}_{\perp } = \mathcal {A} \boldsymbol {\cdot } \left (U_{\perp },V,W \right )_{}\), \(\mathcal {F}^{2}_{\perp } = \mathcal {A} \boldsymbol {\cdot } \left (U,V_{\perp },W \right )_{}\), and \(\mathcal {F}^{3}_{\perp } = \mathcal {A} \boldsymbol {\cdot } \left (U,V,W_{\perp } \right )_{}\). In the context of the HOOI (see Section 7.1), it is more efficient to use global coordinates. For instance, the first component of the gradient can be computed as
For more details on coordinate representations for this problem, see [16], [17, Section 3.2]. In the rest of this paper, the concept G-gradient will mean the Grassmann gradient in global or local coordinates.
2.7 Conditioning of the best approximation problem
The best rank-r approximation problem for a matrix A is not unique if the singular values satisfy σr(A) = σr+ 1(A). The problem is ill-conditioned if the gap is small, i.e., σr(A) > σr+ 1(A) but σr(A) ≈ σr+ 1(A) (see, e.g., [48, Chapter 3], [21, Chapter 8.6]). A similar situation exists for the tensor case [17, Corollary 4.5] (note that the perturbation theory for the SVD is a special case of that for the best rank-(r1,r2,r3) approximation of a tensor). Define
where the λ’s are eigenvalues, in descending order, of the symmetric matrices. We will refer to these quantities as S-values. Then, we can define three gaps, one for each mode,
(In the matrix case, there is only one set of \(s_{i}^{(k)}\), which are the singular values). It is shown in [17, Section 5.3] that the gaps can be taken as measures of the conditioning of the best approximation problem. If, for any k, \(s_{r_{k}}^{(k)}\) is considerably larger than \(s_{r_{k}+1}^{(k)}\) then the approximation problem is well-conditioned with respect to mode k. Conversely, if the gap is small, then the problem is ill-conditioned.
3 The Krylov-Schur method for matrices
Krylov subspace methods are the main class of algorithms for solving iteratively large and sparse matrix problems. Here we give a very brief introduction to Krylov-Schur methods, illustrating with the Arnoldi method for the eigenvalue problem. The method that we propose in Section 6 is analogous.
For a given square matrix \(A\in \mathbb {R}^{n\times n}\) and a nonzero vector \(u\in \mathbb {R}^{n}\) the subspace
is called the Krylov subspace of dimension k associated with A and u [21, Chapter 10]. Given a starting vector u = u1, the Arnoldi method computes successively w = Auj, and immediately orthogonalizes w against the previous u1,…,uj, thereby generating an orthogonal basis for the Krylov subspace (7)). The Arnoldi recursion is equivalent to the matrix equation
where Uk = [u1,…,uk] has orthonormal columns and \({H_{k}}\in \mathbb {R}^{k\times k}\) is a Hessenberg matrix with orthogonalization coefficients. Hk can be considered as the representative of A on the Krylov subspace, and its eigenvalues (the Ritz values) are approximations of those of A (see, e.g., [21, Chapter 10], [48, Chapter 5]).
Krylov methods are designed for computing the eigenvalues of large and sparse matrices. A problem with this approach is that when k grows the cost for orthogonalizing a newly generated vector against the columns of Uk increases. In addition, since Uk is dense, the memory requirements may increase too much. In order to save memory and work, an implicit restarting Arnoldi technique (IRA) was developed [46], and implemented in the highly successful ARPACK package [33]. In [47], Stewart proposed a Krylov-Schur method which is mathematically equivalent to IRA (see [48, Chapter 5]).
Assume that r < k eigenvalues are wanted, along with the corresponding eigenvectors. From Uk and the Schur decomposition of Hk, compute approximations of the wanted eigenvalues and eigenvectors. They satisfy a relation analogous to (8), but of dimension r. Starting a new recursion from this, expand the basis again to dimension k, and repeat the process. For a detailed description of this method, see [48, Chapter 5].
4 Krylov-type methods for tensors
Krylov-type methods that generalize the Arnoldi method to tensors are proposed in [42]. The methods are called Krylov-type methods, because the recursions are generalizations of matrix Krylov recursions, but no analogues of Krylov subspaces can be identified (to our knowledge). These methods are also inspired by Golub-Kahan bidiagonalization [20]. The bidiagonalization process generates two sequences of orthonormal basis vectors for certain Krylov subspaces. In the tensor case three sequences of orthogonal basis vectors are generated that are used to compute a core tensor corresponding to the matrix Hk in (8). For matrix Krylov methods, once an initial vector has been selected, the following vectors are determined uniquely; in the tensor case, one can choose different combinations of previously computed basis vectors. So there are different variants of tensor Krylov-type methods. We describe briefly two examples in the following.
For a given third order tensor \(\mathcal {A}\in \mathbb {R}^{l\times m\times n}\) and starting two vectors, \(u_{1}\in \mathbb {R}^{l}\) and \(v_{1}\in \mathbb {R}^{m}\), we can obtain a third mode vector by \(w_{1}=\mathcal {A} \boldsymbol {\cdot } \left (u_{1},v_{1} \right )_{1,2}\in \mathbb {R}^{n}\). Using the most recently obtained vectors, three sequences of vectors can be generated. Using the modified Gram-Schmidt process, a newly generated vector is immediately orthogonalized against all the previous ones in its mode. The minimal Krylov recursion [42, Algorithm 3], which can be seen as a generalization of the Golub-Kahan bidiagonalization method, is given in Algorithm 1. The function orthogonalizes \(\hat {u}\) against Ui, and normalizes it.

Using the three orthogonal matrices Uk, Vk, and Wk generated by Algorithm 1, we obtain a rank-k approximation of \(\mathcal {A}\) as
In the minimal Krylov recursion, a new vector ui+ 1 is generated based on the two most recently computed vi and wi (and correspondingly for the other modes). But we can choose any other available vj and wk that have not been combined before in an operation \(\mathcal {A} \boldsymbol {\cdot } \left (v_{j},w_{k} \right )_{2,3}\). If we decide to use all available combinations, then this is called the maximal Krylov recursion [42, Algorithm 5]. Given Vj and Wk, all combinations can be computed as
Next the mode-1 fibers of the tensor \(\hat U\) have to be orthogonalized. The number of basis vectors generated grows very quickly. In the following subsections, we will describe a few modifications of the maximal recursion that avoid computing many of the vectors in the maximal recursion, while maintaining as much as possible of the approximation performance.
5 Block-Krylov methods
For large and sparse tensors, it is convenient to use software that implements operations with tensors, in particular tensor-matrix multiplication. In our numerical experiments, we use the extension of the MATLAB tensor toolbox [3] to sparse tensors [4]; it is natural to base some algorithm design decisions on the use of such software. Other languages and implementations are likely to have similar properties.
There are two main reasons why we choose to use block-Krylov methods. Firstly, it is easier to design and describe modifications of the maximal Krylov recursion in terms of blocks. Secondly, the time required for the computation of sparse tensor-vector and tensor-matrix products is dominated by data movements [4, Sections 3.2.4-3.2.5], where the tensor is reorganized to a different format before the multiplication takes place. Therefore, it is better to reuse the reorganized tensor for several vectors, as is done in a tensor-matrix product (akin to the use of BLAS 3 operations in dense linear algebra). In our experiments with a few sparse tensors of moderate dimensions (approximately 500 × 500 × 500 and 3600 × 3600 × 60) and 6 vectors, the time for repeated tensor-vector multiplication was 3–9 times longer than for the corresponding tensor-matrix block multiplication. One should keep in mind, however, that such timings may also be highly problem-, software- and hardware-dependent.
Let \(\mathcal {A}\in \mathbb {R}^{l \times m \times n}\) be given, and assume that, starting from \(U_{0} \in \mathbb {R}^{l \times r_{1}}\), \(V_{0} \in \mathbb {R}^{m \times r_{2}}\) and \(W_{0} \in \mathbb {R}^{n \times r_{3}}\), three sequences of blocks of orthonormal basis vectors (referred to as ON-blocks) have been computed, \(\widehat {U}_{\lambda -1}=[U_{0} U_{1} {\cdots } U_{\lambda -1}]\), \(\widehat {V}_{\mu } = [V_{0} V_{1} {\cdots } V_{\mu }]\), and \(\widehat {W}_{\nu }=[W_{0} W_{1} {\cdots } W_{\nu }]\). Letting p be a block size, and \(\bar V \in \mathbb {R}^{m\times p}\) and \(\bar W \in \mathbb {R}^{n\times p}\) be blocks selected out of \(\widehat {V}_{\mu }\) and \(\widehat {W}_{\nu }\), we compute a new block \(U_{\lambda } \in \mathbb {R}^{l\times p^{2}}\) using Algorithm 2.

The algorithm is written in tensor form, in order to make the operations in steps (ii)–(iv) look like the Gram-Schmidt orthogonalization that it is. In our actual implementations we have avoided some tensor-matrix restructurings (see Appendix ??).
Clearly, after step (iii) we have \(\left (\widehat {U}_{\lambda -1}^{T} \right )_{1} \boldsymbol {\cdot } \widetilde {\mathcal {U}}^{(1)} =0\). In step (iv), the mode-1 vectors (fibers) of \(\widetilde {\mathcal {U}}^{(1)}\) are orthogonalized and organized in a matrix \(U_{\lambda } \in \mathbb {R}^{l \times p^{2}}\), i.e., a “thin” QR decomposition is computed,
where the matrix \(H_{\lambda }^{1}\) is upper triangular. The tensor \({\mathscr{H}}^{1}_{\lambda } = \mathtt {fold}_{1}(H_{\lambda }^{1}) \in \mathbb {R}^{p^{2} \times p \times p}\) contains the columns of \(H_{\lambda }^{1}\), and consequently it has a “quasi-triangular” structure.
The mode-1 step can be written
The mode-2 and mode-3 block-Krylov steps are analogous. Different variants of BK methods can be derived using different choices of \(\bar V\) and \(\bar W\), etc. However, we will always assume that the blocks U0, V0, and W0 are used to generate the blocks with subscript 1.
The recursion (9) and its mode-2 and mode-3 counterparts imply the following simple lemmaFootnote 2. It will be useful in the computation of gradients.
Lemma 5.1.
Assume that, starting from three ON-blocks U0, V0, and W0, Algorithm 2 and its mode-2 and mode-3 counterparts, have been used to generate ON-blocks \(\widehat {U}_{\lambda }=[U_{0} U_{1} {\cdots } U_{\lambda }]\), \(\widehat {V}_{\mu } = [V_{0} V_{1} {\cdots } V_{\mu }]\), and \(\widehat {W}_{\nu }=[W_{0} W_{1} \cdots W_{\nu }]\). Then,
The corresponding identities hold for modes 2 and 3.
Proof
Consider the identity (9) with \(\bar V = V_{0}\), and \(\bar W =W_{0}\), multiply by \({U_{j}^{T}}\) in the first mode, and use orthogonality and \(\left ({U_{j}^{T}} \right )_{1} \boldsymbol {\cdot } (\mathcal {A} \boldsymbol {\cdot } \left (V_{0},W_{0} \right )_{2,3})=\mathcal {A} \boldsymbol {\cdot } \left (U_{j},V_{0},W_{0} \right )_{ }\). □
Proposition 5.2.
Let (U0,V0,W0) with \(U_{0} \in \mathbb {R}^{l \times r_{1}}\), \(V_{0} \in \mathbb {R}^{m \times r_{2}}\), and \(W_{0} \in \mathbb {R}^{n \times r_{3}}\), have orthonormal columns. Let it be a starting point for one block-Krylov step in each mode with \(\mathcal {A} \in \mathbb {R}^{l \times m \times n} \), giving (U1,V1,W1) and tensors
Then, the norm of the G-gradient of (5) at (U0,V0,W0) is
Proof
The mode-1 gradient at (U0,V0,W0) is \(\langle \mathcal {F}, \mathcal {F}_{\perp }^{1} \rangle _{-1}\), where \(\mathcal {F} = {\mathscr{H}}_{0} = {\mathcal {A} \boldsymbol {\cdot } \left (U_{0},V_{0},W_{0} \right )_{}}\), and \(\mathcal {F}_{\perp }^{1} = \mathcal {A} \boldsymbol {\cdot } \left (U_{\perp },V_{0},W_{0} \right )_{}\), and (U0U⊥) is an orthogonal matrix. So we can write U⊥ = (U1U1⊥), where \(U_{1\perp }^{\textsf {T}} (U_{0} U_{1}) = 0.\) Since from Lemma 5.1
the mode-1 result follows. The proof for the other modes is analogous. □
Assume we have an algorithm based on block-Krylov steps in all three modes, and we want to compute the G-gradient to check if a point (U0,V0,W0) is approximately stationary. Then, by Proposition 5.2, we need only perform one block-Krylov step in each mode, starting from (U0,V0,W0), thereby avoiding the computation of U⊥, V⊥, and W⊥, which are usually large and dense. If the norm of the G-gradient is not small enough, then one would perform more block-Krylov steps. Thus, the gradient computation comes for free, essentially.
In many real applications, the tensors are (1,2)-symmetric. This is the case, for instance, if the mode-3 slices of the tensor represent undirected graphs. Here and in Sections 5.1–5.3, we will assume that \(\mathcal {A} \in \mathbb {R}^{m \times m \times n}\) is (1,2)-symmetric; in Section 5.4 we will come back to the general case. For the (1,2)-symmetric tensor, we will compute two sequences of blocks U1,U2,… and W1,W2,…, where the Uλ blocks contain basis vectors for modes 1 and 2, and the Wν for mode 3.
A new block Uλ is computed from given blocks \(\bar U\) and \(\bar W\) in the same way as in the nonsymmetric case, using Algorithm 2. To compute a new block Wν, we use two blocks \(\bar U\) and \(\bar {\bar U}\). If \(\bar {U} \neq \bar {\bar U}\), then we can use the analogue of Algorithm 2. In the case \(\bar {U} = \bar {\bar U}\), the product tensor \(\mathcal {A} \boldsymbol {\cdot } \left (\bar {U},\bar {U} \right )_{1,2}\) is (1,2)-symmetric, which means that almost half its 3-fibers are superfluous, and should be removed. Thus, letting \(\widetilde {\mathcal {W}}^{(3)}\) denote the tensor that is obtained in (iii) of Algorithm 2, we compute the “thin” QR decomposition,
where \(\mathtt {triunfold_{3}}(\mathcal {X})\) denotes the mode-3 unfolding of the (1,2)-upper triangular part of the tensor \(\mathcal {X}\). If \(\bar U \in \mathbb {R}^{m \times p}\), then \(W_{\nu } \in \mathbb {R}^{n \times p_{\nu }}\), where pν = p(p + 1)/2.
A careful examination of Lemma 5.1 for the case of (1,2)-symmetric tensors shows that the corresponding result holds also here. We omit the derivations in order not to make the paper too long.
5.1 Min-BK method for (1,2)-symmetric tensors
Our simplest block-Krylov method is the (1,2)-symmetric block version of the minimal Krylov recursion of Algorithm 1, which we refer to as the min-BK method. Here, instead of using only two vectors in the multiplication \(\hat u = \mathcal {A} \boldsymbol {\cdot } \left (u_{i},w_{i} \right )_{}\), we use the p first vectors from the previous blocks. Let \(\bar U = U(:,1:p)\), denote the first p vectors of a matrix block U. The parameter s in Algorithm 3 is the number of stages.

The min-BK method is further described in the two diagrams of Table 1. Note that to conform with Proposition 5.2, we always use \(\bar U_{0} = U_{0}\) and \(\bar W_{0} =W_{0}\). It is seen that the growth of the number of basis vectors, the ki parameters, is relatively slow. However, it will be seen in Section 7.2 that this method is not competitive.
5.2 Max-BK method for (1,2)-symmetric tensors
The max-BK method is maximal in the sense that in each stage we use all the available blocks to compute new blocks. The algorithm is defined by three diagrams (see Table 2). E.g., in stage 2, we use combinations of the whole blocks U0, U1, W0, and W1, to compute U2, U3, and U4 (U1 was computed already in stage 1).
The diagram for the Wi’s is triangular: due to the (1,2)-symmetry of \(\mathcal {A}\), the two tensor-matrix products \(\mathcal {A} \boldsymbol {\cdot } \left (U_{0}, U_{1} \right )_{ 1,2}\) and \(\mathcal {A} \boldsymbol {\cdot } \left (U_{1},U_{0} \right )_{1,2}\) generate the same mode-3 fibers.
It is clear that the fast growth of the number of basis vectors makes this variant impractical, except for small values of r and s, e.g. r = (2,2,2) and s = 2. In the same way as in the matrix Krylov-Schur method, we are not interested in too large values of k1 and k3, because we will project the original problem to one of dimension (k1,k1,k3), which will be solved by methods for dense tensors. Hence, we will in the next subsection introduce a compromise between the min-BK and the max-BK method.
5.3 BK method for (1,2)-symmetric tensors
The BK method is similar to min-BK in that it uses only the p first vectors of each block in the block-Krylov step. In each stage, more new blocks are computed than in min-BK, but not as many as in max-BK. Both these features are based on numerical tests, where we investigated the performance of the BK method in the block Krylov-Schur method to be described in Section 6. We found that if we omitted the diagonal blocks in the diagrams in Table 2, then the convergence of the Krylov-Schur method was only marginally impeded. The BK method is described in the two diagrams of Table 3.
It may happen that one of the dimensions of the tensor is considerably smaller than the other. Assume that m ≫ n. Then, after a few stages, the number of vectors in the third mode may be equal to n, and no more can be generated in that mode. Then, the procedure is modified in an obvious way (the right diagram is stopped being used) so that only vectors in the other modes (U blocks) are generated. The min-BK and max-BK methods can be modified analogously.
5.4 BK Method for general tensors
The block-Krylov methods for general tensor are analogous to those for (1,2)-symmetric tensors. In fact, they are simpler to describe, as one has no symmetry to take into account. Here we will only describe the BK method; the min-BK and max-BK variants are analogous. In Table 4, we give the diagram for computing the “U” blocks; the diagrams for the “V ” and “W ” blocks are similar.
6 A tensor Krylov-Schur-like method
When tensor Krylov-type methods are used for the computation of low multilinear rank approximations of large and sparse tensors, they suffer from the same weakness as Krylov methods for matrices: the computational burden for orthogonalizing the vectors as well as memory requirements may become prohibitive. Therefore, a restarting procedure should be tried. We will now describe a generalization of the matrix Krylov-Schur approach to a corresponding tensor method. Here, we assume that the tensor is non-symmetric.
Let \(\mathcal {A}\in \mathbb {R}^{l\times m\times n}\) be a given third order tensor, for which we want to compute the best rank-(r1,r2,r3) approximation. For reference, we restate the maximization problem,
Let k1, k2, and k3 be integers such that
and assume that we have computed, using a BK method, a rank-(k1,k2,k3) approximation
where \(X\in \mathbb {R}^{l\times k_{1}}\), \(Y\in \mathbb {R}^{m\times k_{2}}\), and \(Z\in \mathbb {R}^{n\times k_{3}}\) are matrices with orthonormal columns, and \(\mathcal {C}\in \mathbb {R}^{k_{1}\times k_{2}\times k_{3}}\) is a core tensor. With the assumption (12), we can use an algorithm for dense tensors, e.g., a Newton-Grassmann method [16, 26], to solve the projected maximization problem
From the solution of (14), we have the best rank-(r1,r2,r3) approximation of \(\mathcal {C}\),
where \(\mathcal {F} \in \mathbb {R}^{r_{1}\times r_{2}\times r_{3}}\) is the core tensor. This step is analogous to computing and truncating the Schur decomposition of the matrix Hk in the matrix case in Section 3. Combining (15) and (13), we can write
where \(U =X \hat U\in \mathbb {R}^{l\times r_{1}}\), \(V=Y\hat V\in \mathbb {R}^{m\times r_{2}}\), and \(W=Z \hat W\in \mathbb {R}^{n\times r_{3}}\), with orthonormal columns. Thus, (16) is a rank-(r1,r2,r3) approximation of \(\mathcal {A}\). Then, starting with U0 = U, V0 = V, and W0 = W, we can again expand (16), using a BK method, to a rank-(k1,k2,k3) approximation (13). A sketch of the tensor Krylov-Schur method is given in Algorithm 4.

The algorithm is an outer-inner iteration. In the outer iteration (11) is projected to the problem (14) using the bases (X,Y,Z). Step (i) of Algorithm 4 is the inner iteration, where we solve (14) using an algorithm for a small, dense tensor, e.g., the Newton algorithm on the Grassmann manifold [16, 26]. The Newton-Grassmann method is analogous to and has the same basic properties as the standard Newton method in a Euclidean space.
Notice that if \(\mathcal {A}\) is a (1,2)-symmetric tensor, then all aforementioned relations are satisfied with U = V and X = Y. So (16) transfers to
6.1 Convergence of the tensor Krylov-Schur algorithm
In the discussion below, we will assume that the G-Hessian for (11) at the stationary point is negative definite, i.e., the stationary point is a strict local maximum. This is equivalent to assuming that the objective function is strictly convex in a neighborhood of the stationary point. The situation when this is not the case is described in [17, Corollary 4.5] and Section 2.7.
Let (U0,V0,W0) be an approximate solution, and let the expanded bases of ON-blocks be \( X=[U_{0} U_{1}] \in \mathbb {R}^{l \times k_{1}}\), \(Y=[V_{0} V_{1}] \in \mathbb {R}^{m \times k_{2}}\), and \(Z=[W_{0} W_{1}] \in \mathbb {R}^{n \times k_{3}}\). For simplicity we here have included more than one block-Krylov steps in U1, V1, and W1. Let X⊥ be a matrix such that (XX⊥) is orthogonal, and make the analogous definitions for Y⊥ and Z⊥. We then make the change of variables
The tensor
is a subtensor of \({\mathscr{B}}\) (see Fig. 1).
In the discussion of convergence we can, without loss of generality, consider the equivalent maximization problem for \({\mathscr{B}}\),
Now, the approximate solution (U0,V0,W0) is represented by
and we have enlarged E0 by one or more block-Krylov steps to
In the inner iteration, we shall now compute the best rank-(r1,r2,r3) approximation for \(\mathcal {C}\),
using the Newton-Grassmann method (note that \(P \in \mathbb {R}^{k_{1} \times r_{1}}\), \(Q \in \mathbb {R}^{k_{2} \times r_{2}}\), and \(S \in \mathbb {R}^{k_{3} \times r_{3}}\)). Denote the core tensor after this computation by \(\widetilde {\mathcal {F}}\). Due to the fact that \(\mathcal {F}\) is a subtensor of \({\mathcal {C}}\), it follows that
and evidently the Krylov-Schur algorithm produces a non-decreasing sequence of objective function values that is bounded above (by \(\| \mathcal {A} \|\)).
If E0 is the local maximum point for (17), then the G-gradient \(\nabla _{{\mathscr{B}}}(E_{0})=0\), and, by Proposition 5.2, \(\nabla _{\mathcal {C}}(\bar E_{0})=0\), where \(\bar E_{0}\) corresponds to E0. Therefore, the Newton-Grassmann method for (14) will not advance, but give \( \widetilde {\mathcal {F}} = \mathcal {F}\).
On the other hand, if E0 is not the local maximum, then \(\nabla _{{\mathscr{B}}}(E_{0})\) and \(\nabla _{\mathcal {C}}(\bar E_{0})\) are nonzero. Assume that we are close to a local maximum so that the G-Hessian for (17) is negative definite. Then, the G-Hessian for (18) is also negative definite (see AppendixFootnote 3 ??) and the projected maximization problem (14) is locally convex. Therefore, the Newton-Grassmann method will converge to a solution that satisfies \( \| \widetilde {\mathcal {F}} \| > \| \mathcal {F} \|\) [18, Theorem 3.1.1].
Thus, we have the following result.
Theorem 6.1.
Assume that (U0,V0,W0) is close enough to a strict local maximum for (11). Then, Algorithm 4 will converge to that local maximum.
The G-gradient is zero at the local maximum; thus, the Krylov-Schur-like algorithm converges to a stationary point for the best rank-(r1,r2,r3) approximation problem.
7 Numerical experiments
In this section, we investigate the performance of Krylov-Schur methods applied to some large and sparse tensors. As a comparison we will use the HOOI method. We here give a brief description of HOOI, for details (see [8]).
7.1 Higher order orthogonal iteration and other methods
Consider first the nonsymmetric case (5). HOOI is an alternating iterative method [8], where in each iteration three maximization problems are solved. In the first maximization, we assume that V and W are given satisfying the constraints, and maximize
The solution of this problem is given by the first r1 left singular vectors of the mode-1 unfolding C(1) of \(\mathcal {C}_{1}\), and that is taken as the new approximation U. Then, in the second maximization, U and W are considered as given and V is determined.
The cost for computing the thin SVD is O(l(r2r3)2) (under the assumption (12)). As this computation is highly optimized, it is safe to assume that for large and sparse tensors the computational cost in HOOI is dominated by the tensor-matrix multiplications \(\mathcal {A} \boldsymbol {\cdot } \left (V,W \right )_{2,3}\) (and corresponding in the other modes), and the reshaping of the tensor necessary for the multiplication. In addition, the computation of the G-gradient involves extra tensor-matrix multiplications. Here, it is more efficient to use global coordinates (cf. Section 2.6). In our experiments, we computed the G-gradient only every ten iterations.
For a (1,2)-symmetric tensor, we use the HOOI method, where we have two maximizations in each step, one for U, with the previous value of U in \(\mathcal {C}_{1}\), and the other for W, with \(\mathcal {C}_{3}=\mathcal {A} \boldsymbol {\cdot } \left (U,U \right )_{1,2}\).
The HOOI iteration has linear convergence; its convergence properties are studied in [52]. In general, alternating methods are not guaranteed to converge to a local maximizer [39, 40]. For some tensors, HOOI needs quite a few iterations before the convergence is stabilized to a constant linear rate. On the other hand, HOOI has relatively fast convergence for several well-conditioned problems. In our tests the HOOI method is initialized with random matrices with orthonormal columns.
For large tensors, we use HOOI as a starting procedure for the inner Newton-Grassmann iterations to improve robustness. Note that here the tensor \(\mathcal {C}\) is much smaller of dimension (k1,k1,k3).
In the Introduction, we cite a few papers that deal with the computation of Tucker approximations. For instance, in [16, 25], the best approximation is computed using Riemannian Newton methods. However, the Hessian matrix is large and dense, and therefore such methods require too much memory and are unsuitable for large and sparse tensors. The same is true of the Quasi-Newton method in [43], unless the Hessian approximation is forced to be very sparse, say diagonal, which would impede the convergence rate seriously.
7.2 Numerical tests
To investigate the performance of Krylov-Schur methods, we first present results of experiments on a few (1,2)-symmetric tensors. In the outer iteration, the stopping criterion is the relative norm of the G-gradient \({\Vert \nabla \Vert }/{\Vert \mathcal {F}\Vert } \leq 10^{-13}\).
In the inner iteration (step (i) of Algorithm 4) the best rank-(r1,r1,r3) of the tensor \(\mathcal {C}\) is computed using the Newton-Grassmann algorithm [16], initialized by the HOSVD of \(\mathcal {C}\), truncated to rank (r1,r1,r3), followed by 5 HOOI iterations to improve robustness (recall that this problem is of dimension (k1,k1,k3)). The same stopping criterion as in the outer iteration was used. The typical iteration count for the inner Newton-Grassmann iteration was 4-5.
In the figures, the convergence history of the following four methods is illustrated, where the last three are named according to the block Krylov-type method used in the outer iterations:
-
1.
HOOI,
-
2.
max-BKS(s ; k1,k3),
-
3.
BKS(s,p; k1,k3),
-
4.
min-BKS(s,p; k1,k3).
Here, s denotes the stage, k1 and k3 the number of basis vectors in the X and Z basis, respectively, and p indicates that the first p vectors of each ON-block are used in BKS and min-BKS.
The convergence results are presented in figures, where the y-axis and x-axis represent the relative norm of G-gradient and the number of outer iterations, respectively. For the larger examples, we also plot the gradient against the execution time.
In the examples we used rather small values for (r1,r1,r3), like in some real world applications [36, 38]. In two forthcoming papers [14, 15] on tensor partitioning and data science applications we compute rank-(2,2,2) approximations.
The experiments were performed using MATLAB and the tensor toolbox [4] on a standard desktop computer with 8-GB RAM memory. In all test cases, the primary memory was sufficient.
7.3 Example 1. Synthetic signal-plus-noise tensor
For the first test, we generated synthetic (1,2)-symmetric tensors with specified low rank. Let \(\mathcal {A}=\mathcal {A}_{\text {signal}}+\rho \mathcal {A}_{\text {noise}}\), where \(\mathcal {A}_{\text {signal}}\) is a signal tensor with low multilinear rank, \(\mathcal {A}_{\text {noise}}\) is a noise tensor and ρ denotes the noise level. \(\mathcal {A}_{\text {signal}}\) was constructed as a tensor of dimension (r1,r1,r3) with normally distributed N(0,1) elements; this was placed at the top left corner of a zero tensor of size m × m × n. The elements of the noise tensor were chosen normally distributed N(0,1), and then the tensor was made (1,2)-symmetric. For testing purposes, we performed a random permutation such that the tensor remained (1,2)-symmetric. This tensor is dense. The purpose of this example is to demonstrate that the rate of convergence of all methods depends heavily on the conditioning of the approximation problem (cf. [17, Corollary 4.5] and the short statement in Section 6.1).
Figure 2 illustrates the convergence results for a 200 × 200 × 200 tensor approximated by one of rank-(2,2,2), which is the correct rank of the signal tensor. The problem with ρ = 10− 2 is more difficult than the other one, because the signal-to-noise ratio is smaller, making the approximation problem more ill-conditioned. This shows in the iteration count for all methods. See also Table 5, where the S-values are given. The HOOI was considerably more sensitive to the starting approximation than the other methods. For a few starting values it converged much more slowly than in the figure.
It is of some interest to see how good the result is as an approximation of the (noise free) signal tensor (see Table 6).
For this small problem, it is possible to compute the solution directly using HOOI and the Newton-Grassmann method, without the Krylov-Schur approach. We compared that solution with the one obtained using the max-BK method and they agreed to within less than the magnitude of the stopping criterion (the angles between the subspaces spanned by the solution matrices were computed).
For the small problems in this example, it is not meaningful to compare the computational efficiency of the BKS methods to that of HOOI: due to the simplicity of HOOI, it comes out as a winner in the cases when it converges.
7.4 Example 2. The Princeton tensor
The Princeton tensor is created using the Facebook data from Princeton [49]Footnote 4. We constructed it from a social network, using a student/faculty flag as third mode: the tensor element \(\mathcal {A}(\lambda ,\mu ,\nu )=1\), if students λ and μ are friends and one of them has flag ν. After zero slices in the third mode have been removed, this is a 6593 × 6593 × 29 tensor with 1.2 ⋅ 106 non zeros.
Figure 3 shows the convergence for the Princeton tensor approximated with a rank-(2,2,2) and a (4,4,4)-rank tensor. In both cases, the inner iterations were initialized with truncated HOSVD followed by 5 HOOI iterations.
The time measurements in Fig. 3 are based on the MATLAB functions tic and toc. A large proportion of the time in HOOI is the computation of the G-gradient (which was done every ten iterations).
In Table 7, we give the S-values. The mode-3 entries are a strong indication that the mode-3 multilinear rank of the tensor is equal to 3. Any attempt to compute, e.g., a rank-(4,4,4) approximation will suffer from the mode-3 ill-conditioning and is likely to give incorrect results. However, a rank-(4,4,3) can be computed easily using BKS. Here, the convergence of HOOI was very slow.
The number of iterations in the BKS method was rather insensitive to the choice of stage and block size parameters s and p. Thus, it did not pay off to use a larger inner subproblem. Similarly, the use of max-BKS(2;111,29) gave relatively fast convergence in terms of the number of iterations, but the extra information gained by using a large value of k1 was not so substantial that it made up for the heavier computations.
HOOI was sensitive to the choice of starting approximation. Often, the convergence rate was considerably slower than in Fig. 3.
7.5 Example 3. The Reuters tensor
The Reuters tensor is a sparse tensor of dimensions 13332 × 13332 × 66 with 486,894 nonzero elements. It is constructed from all stories released during 66 consecutive days by the news agency Reuters after the September 11, 2001, attack [5]. The vertices of the network are words. There is an edge between two words if they appear in the same text unit (sentence). The weight of an edge is its frequency.
Figure 4 shows the convergence results for the Reuters tensor, approximated with a rank-(2,2,2) and a rank-(6,6,6) tensor. In the second case, the inflexibility of the choice of k1 and k3 in max-BKS forced us to use stage 1, which led to slower convergence than with BKS and min-BKS.
Convergence for Example 3, the Reuters tensor with (m,m,n) = (13332,13332,66). Top plot: (r1,r2,r3) = (2,2,2). The methods min-BKS(3,4;34,25), BKS(2,4;20,13) and max-BKS(2;32,23) were used. Bottom plot: (r1,r2,r3) = (6,6,6). The methods min-BKS(2,4;58,37), BKS(1,6;42,27) and max-BKS(1;42,27) were used (the last two are identical for these parameters)
The S-values are given in Table 8. It is seen that none of the problems is particularly ill-conditioned.
It is argued in [15] that in cases when the 3-slices of a (1,2)-symmetric tensor are adjacency matrices of graphs, then one should normalize the slices so that the largest eigenvalue of each slice becomes equal to 1. In that context, a rank-(2,2,2) approximation is computed. We ran a test with the normalized tensor and the same parameter values as in Fig. 4. The results are shown in Fig. 5.
The S-values are given in Table 9. They indicate that this problem is slightly more ill-conditioned than the unscaled one.
7.6 Example 4. 1998DARPA tensor
The following description is taken from [14]. In [27] network traffic logs are analyzed in order to identify malicious attackers. The data are called the 1998 DARPA Intrusion Detection Evaluation Dataset and were first published by the Lincoln Laboratory at MITFootnote 5. We downloaded the data set from https://datalab.snu.ac.kr/haten2/ in October 2018. The records consist of (source IP, destination IP, port number, timestamp). In the data file there are about 22000 different IP addresses. We chose the subset of 8991 addresses that both sent and received messages. The time span for the data is from June 1, 1998, to July 18, and the number of observations is about 23 million. We merged the data in time by collecting every 63999 consecutive observations into one bin. Finally, we symmetrized the tensor \(\mathcal {A} \in \mathbb {R}^{m \times m \times n}\), where m = 8891 and n = 371, so that
In this example, we did not normalize the slices of the tensor: The 3-slices are extremely sparse, and normalization makes the rank-(2,2,2) problem so ill-conditioned that none of the algorithms converged. Instead we scaled the slices to have Frobenius norm equal to 1. The convergence history is shown in Fig. 6.
The HOOI method was sensitive to the (random) starting approximations. It did happen that the method converged rapidly, but in many cases convergence was extremely slow.
The S-values are given in Table 10. The problem is well-conditioned.
7.7 Example 5. Non-symmetric NeuroIPS tensor
Experiments with data from all the papers at the Neural Information Processing Systems Conferences 1987–2003 are described in [19]. We downloaded the data from http://frostt.io/ [45], and formed a sparse tensor of dimension 2862 × 14036 × 17, where the modes represent (author,terms,year), and the values are term counts. We performed a non-symmetric normalization of the 3-slices of the tensor [10], and computed approximations with (r1,r2,r3) = (2,2,2) and (r1,r2,r3) = (5,5,5). Convergence of BKS and HOOI is illustrated in Fig. 7.
The S-values are given in Table 11. It is seen that none of the problems is particularly ill-conditioned.
For larger values of (r1,r2,r3) the inner iterations of the BKS method became so heavy that the HOOI method was competitive in terms of execution time (recall that a relatively large portion of the work in HOOI is devoted to the computation of the gradient; the more seldom it is done, the more efficient becomes the method).
7.7.1 Discussion of experiments
Profiling tests of the BKS and HOOI methods for the Reuters example show that most of the computational work is done in the reshaping of tensors, and in tensor-matrix multiplications. For small values of the rank (r1,r1,r3), the number of stages and block size in the BKS methods, the time work for the dense tensor and matrix operations in the inner iterations in BKS and the SVD’s in HOOI is relatively small. A considerable proportion of the work in HOOI is the computation of the G-gradient; we reduced that by computing it only every ten iterations. The data shuffling and reshaping must be done irrespectively of which programming language is used. It is reasonable to assume that the implementation made in the sparse tensor toolbox [4] is efficient. Therefore, it is makes sense to measure efficiency by comparing the MATLAB execution times (by tic and toc) of the methods.
Our tests indicate that all methods considered here converge fast for very well-conditioned problems. However, the convergence behavior of HOOI was less predictable: sometimes it converged very slowly also for well-conditioned, large problems (see Example 4). Consistently, the min-BKS method converged much more slowly than the other two Krylov-Schur-like methods. The max-BKS method suffered from its inflexibility in the choice of k1 and k3, especially with r1 and r3 somewhat larger.
The design of BKS is to some extent based on heuristics and numerical experiments. A comparison of BKS and max-BKS shows that the choice of blocks of p vectors, for p rather small, in the Krylov steps, does not substantially impede the convergence rate. Using fewer blocks, in the sense of using only p vectors from the “diagonal” blocks in the diagram in Table 1, as in min-BKS, leads to slower convergence. Thus, BKS seems to be a reasonable compromise. Based on the experience presented in this paper and [14, 15] it seems clear that for large and sparse tensors the BKS method is in general more robust and efficient than HOOI. However, for large values of (r1,r2,r3), the inner problem in the BKS method becomes so large that it loses some of its competitive edge; for such problems HOOI may be preferred.
In the BKS method the parameters s and p (which give k1 and k3) could be chosen rather small, typically 2 and 4, respectively. Using larger values did not pay off.
8 Conclusions and future work
We have generalized block Krylov-Schur methods for matrices to tensors and demonstrated that the new method can be used for computing best rank-(r1,r2,r3) approximations of large and sparse tensors. The BKS method is shown to be flexible and has best convergence properties.
The purpose of this paper has been to show that the block-Krylov-Schur method is a viable approach. It may be possible to analyze BKS methods in depth, theoretically and by experiments, and optimize the method further, for instance with regard to the choice of blocks in the tables defining the method.
Since we are interested in very low rank approximation of (1,2)-symmetric tensors for applications such as those in [14, 15], the development of block Krylov-Schur type methods was done mainly with such applications in mind. More work is needed to investigate the application of BKS methods for nonsymmetric tensors.
The detailed implementation of block Krylov-Schur methods for matrices is rather technical (see, e.g., [54]). The generalization to tensors might improve the convergence properties for ill-conditioned problems. However, this is beyond the scope of the present paper, and may be a topic for future research.
It appears to be straightforward to generalize the results to tensors of order larger than 3. We are planning to do research in this direction in the future.
Notes
Assume that U = U0R0 is the thin QR decomposition of U. Then, \(\left ({U,V,W}\right )\cdot {\mathcal {F}} = ({U_{0} R_{0},V,W})\cdot {\mathcal {F}} = \left (U_{0},V,W \right )_{} \boldsymbol {\cdot } (({R_{0}})_{1}\cdot {\mathcal {F}}) =: \left ({U_{0},V,W}\right )\cdot {\mathcal {F}_{0}}\).
More general results can be obtained for \(\mathcal {A} \boldsymbol {\cdot } \left (U_{\lambda },V_{\mu },W_{\nu } \right )_{}\). Taken together, those results can be used to show the existence of a tensor structure that is analogous to the block Hessenberg structure obtained in a block-Arnoldi method for a matrix.
In the Appendix, we also take care of some Grassmann-technical details.
The data can be downloaded from https://archive.org/details/oxford-2005-facebook-matrix.
References
Absil, P.-A., Mahony, R., Sepulchre, R.: Optimization algorithms on matrix manifolds. Princeton University Press, Princeton (2007)
Andersson, C.A., Bro, R.: Improving the speed of multi-way algorithms: part i. Tucker3. Chemometrics and Intelligent Laboratory Systems 42, 93–103 (1998)
Bader, B.W., Kolda, T.G.: Algorithm 862: MATLAB tensor classes for fast algorithm prototyping. ACM Transactions on Mathematical Software (TOMS) 32, 635–653 (2006)
Bader, B.W., Kolda, T.G.: Efficient MATLAB computations with sparse and factored tensors. SIAM Journal on Scientific Computing 30, 205–231 (2007). https://doi.org/10.1137/060676489. http://link.aip.org/link/?SCE/30/205/1
Batagelj, V., Mrvar, A.: Density based approaches to network analysis. Analysis of Reuters Terror News Network. University of Ljubljana, Slovenia (2003). https://repozitorij.uni-lj.si/IzpisGradiva.php?id=33150&lang=eng
Comon, P., Mourrain, B.: Decomposition of quantics in sums of powers of linear forms. Signal Process. 53, 93–107 (1996)
De Lathauwer, L., De Moor, B., Vandewalle, J.: A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl. 21, 1253–1278 (2000)
De Lathauwer, L., De Moor, B., Vandewalle, J.: On the best rank-1 and rank-(r1,r2,...,rn) approximation of higher-order tensors. SIAM J. Matrix Anal. Appl. 21, 1324–1342 (2000)
De Silva, V., Lim, L.-H.: Tensor rank and the ill-posedness of the best low-rank approximation problem. SIAM J. Matrix Anal. Appl. 30, 1084–1127 (2008)
Dhillon, I.S.: Co-Clustering documents and words using bipartite spectral graph partitioning. In: Proc 7th ACM-SIGKDD Conference, pp 269–274 (2001)
Edelman, A., Arias, T., Smith, S.T.: The geometry of algorithms with orthogonality constraints. SIAM J. Matrix Anal. Appl. 20, 303–353 (1998)
Edelman, A., Arias, T.A., Smith, S.T.: The geometry of algorithms with orthogonality constraints. SIAM J. Matrix Anal. Appl. 20, 303–353 (1998)
Eldén, L.: Matrix methods in data mining and pattern recognition. SIAM (2007)
Eldén, L., Dehghan, M.: Analyzing large and sparse tensor data using spectral low-rank approximation, Tech. Report 2012.07754 arxiv,math.NA (2020)
Eldén, L., Dehghan, M.: Spectral partitioning of large and sparse tensors using low-rank tensor approximation. Numerical Linear Algebra Appl., https://doi.org/10.1002/nla.2435 (2022)
Eldén, L., Savas, B.: A Newton–Grassmann method for computing the best multilinear rank-(r1,r2,r3) approximation of a tensor. SIAM Journal on Matrix Analysis and applications 31, 248–271 (2009)
Eldén, L., Savas, B.: Perturbation theory and optimality conditions for the best multilinear rank approximation of a tensor. SIAM J. Matrix Anal. Appl. 32, 1422–1450 (2011)
Fletcher, R.: Practical Methods of Optimization, 2nd edn. Wiley, Hoboken (1987)
Globerson, A., Chechik, G., Pereira, F., Tishby, N.: Euclidean embedding of co-occurrence data. The Journal of Machine Learning Research 8, 2265–2295 (2007)
Golub, G., Kahan, W.: Calculating the singular values and pseudo-inverse of a matrix. Journal of the Society for Industrial and Applied Mathematics Series B: Numerical Analysis 2, 205–224 (1965)
Golub, G.H., Van Loan, C.F.: Matrix Computations, 4th edn. Johns Hopkins University Press, Baltimore (2013)
Goreinov, S., Oseledets, I.V., Savostyanov, D.V.: Wedderburn rank reduction and Krylov subspace method for tensor approximation. Part 1 Tucker case. SIAM Journal on Scientific Computing 34, A1–A27 (2012)
Hillar, C.J., Lim, L. -H.: Most tensor problems are NP-hard. J. ACM 60, 1–39 (2013)
Hitchcock, F.L.: Multiple invariants and generalized rank of a p-way matrix or tensor. Stud. Appl. Math. 7, 39–79 (1928)
Ishteva, M., Absil, P. -A., Van Huffel, S., De Lathauwer, L.: Best low multilinear rank approximation of higher-order tensors, based on the Riemannian trust-region scheme. SIAM J. Matrix Anal. Appl. 32, 115–135 (2011)
Ishteva, M., De Lathauwer, L., Absil, P.-A., Van Huffel, S.: Differential-geometric Newton method for the best rank-(r1,r2,r3) approximation of tensors. Numer. Algo. 51, 179–194 (2009)
Jeon, I., Papalexakis, E., Faloutsos, C., Sael, L., Kang, U.: Mining billion-scale tensors: algorithms and discoveries. The VLDB Journal 25, 519–544 (2016). https://doi.org/10.1007/s00778-016-0427-4
Kaya, O., Uçar, B.: High performance parallel algorithms for the Tucker decomposition of sparse tensors. In: 2016 45th International Conference on Parallel Processing (ICPP), pp 103–112 (2016), https://doi.org/10.1109/ICPP.2016.19
Khoromskij, B., Khoromskaia, V.: Low rank Tucker-type tensor approximation to classical potentials. Open Mathematics 5, 523–550 (2007)
Khoromskij, B.N., Khoromskaia, V.: Multigrid accelerated tensor approximation of function related multidimensional arrays. SIAM J. Sci. Comput. 31, 3002–3026 (2009)
Kolda, T., Sun, J.: Scalable tensor decompositions for multi-aspect data mining, in. Eighth IEEE International Conference on Data Mining 2008, 363–372 (2008)
Kolda, T.G., Bader, B.W., Kenny, J.P.: Higher-order web link analysis using multilinear algebra. In: Fifth IEEE International Conference on Data Mining, pp 27–30. IEEE (2005)
Lehoucq, R.B., Sorensen, D.C., Yang, C.: ARPACK Users’ guide: solution of large-scale eigenvalue problems with implicitly restarted Arnoldi methods. SIAM (1998)
Lim, L.-H.: Tensors in computations. Acta Numerica 30, 555–764 (2021). https://doi.org/10.1017/S0962492921000076
Lim, L. -H., Morton, J.: Cumulant component analysis: a simultaneous generalization of PCA and ICA. CASTA2008, 18 (2008)
Liu, X., Ji, S., Glänzel, W., De Moor, B.: Multiview partitioning via tensor methods. IEEE Trans. Knowl. Data Eng. 25, 1056–1069 (2013)
Oseledets, I.V., Savostianov, D., Tyrtyshnikov, E.E.: Tucker dimensionality reduction of three-dimensional arrays in linear time. SIAM J. Matrix Anal. Appl. 30, 939–956 (2008)
Persson, C., Bohlin, L., Edler, D., Rosvall, M.: Maps of sparse Markov chains efficiently reveal community structure in network flows with memory. arXiv:1606.08328 (2016)
Powell, M.J.: On search directions for minimization algorithms. Math. Program. 4, 193–201 (1973)
Ruhe, A., Åwedin, P.: Algorithms for separable nonlinear least squares problems. SIAM Rev. 22, 318–337 (1980)
Savas, B., Eldén, L.: Handwritten digit classification using higher order singular value decomposition. Pattern Recognit. 40, 993–1003 (2007)
Savas, B., Eldén, L.: Krylov-type methods for tensor computations I. Linear Algebra Appl. 438, 891–918 (2013)
Savas, B., Lim, L. -H.: Quasi-newton methods on Grassmannians and multilinear approximations of tensors. SIAM J. Sci. Comput. 32, 3352–3393 (2010)
Smilde, A., Bro, R., Geladi, P.: Multi-way analysis: applications in the chemical sciences. Wiley, Hoboken (2005)
Smith, S., Choi, J.W., Li, J., Vuduc, R., Park, J., Liu, X., Karypis, G.: FROSTT: The formidable repository of open sparse tensors and tools. http://frostt.io/ (2017)
Sorensen, D.C.: Implicit application of polynomial filters in a k-step Arnoldi method. SIAM J. Matrix Anal. Appl. 13, 357–385 (1992)
Stewart, G.W.: A Krylov–Schur algorithm for large eigenproblems. SIAM J. Matrix Anal. Appl. 23, 601–614 (2001)
Stewart, G.W.: Matrix Algorithms: Volume II: Eigensystems. SIAM (2001)
Traud, A.L., Kelsic, E.D., Mucha, P.J., Porter, M.A.: Comparing community structure to characteristics in online collegiate social networks. SIAM Rieview 53, 526–543 (2011)
Tucker, L.R.: The extension of factor analysis to three-dimensional matrices. In: Gulliksen, H., Frederiksen, N. (eds.) Contributions to mathematical psychology, pp 109–127. Holt, Rinehart and Winston, New York (1964)
Tucker, L.R.: Some mathematical notes on three-mode factor analysis. Psychometrika 31, 279–311 (1966)
Xu, Y.: On the Convergence of higher-order orthogonality Iteration, Tech. Report 1504.00538v2 arXiv [math.NA] (2015)
Zhang, T., Golub, G.H.: Rank-one approximation to higher order tensors. SIAM J. Matrix Anal. Appl. 23, 534–550 (2001)
Zhou, Y., Saad, Y.: Block Krylov-Schur method for large symmetric eigenvalue problems. Numer. Alg. 47, 341–359 (2008)
Acknowledgements
This work was done when the second author visited the Department of Mathematics, Linköping University. We thank the referees and the associate editor for constructive criticism and several suggestions that helped to improve the paper.
Funding
Open access funding provided by Linköping University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Availability of data and material
References to data repositories are given in the text.
Code availability
Codes are available from the web page of LE.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix : A: The Grassmann Hessian
Let \(X \in \mathbb {R}^{l \times r}\), be a matrix with orthonormal columns, XTX = Ir. We will let it represent an entire subspace, i.e., the equivalence class,
For convenience, we will say that X ∈Gr(l,r), the Grassmann manifold (of equivalence classes).
Define the product manifold
and, for given integers satisfying r1 < k1 < l, r2 < k2 < m, and r3 < k3 < n,
The following is a submanifold of Gr3:
Let \((X_{0},Y_{0},Z_{0}) \in \text {Gr}^{3}\), and let three matrices \(X_{1} \in \mathbb {R}^{l \times (k_{1}-r_{1})}\), \(Y_{1} \in \mathbb {R}^{m \times (k_{2}-r_{2})} \), and \(Z_{1} \in \mathbb {R}^{n \times (k_{3}-r_{3})}\) be given, such that
all have orthonormal columns.
For a given matrix P ∈Gr(l,r) we let P⊥∈Gr(l,l −r) be such that (PP⊥) is an orthogonal matrix. It can be shown [11, Section 2.5] that P⊥ is a matrix of basis vectors in the tangent space of Gr(l,r) at the point P.
In the maximization problem for \(\| \mathcal {A} \boldsymbol {\cdot } \left (X,Y,Z \right )_{}\|^{2}\) on the Grassmann product manifold Gr3, we now make a change of variables by defining
and further
Clearly \(\mathcal {C}\) is a leading subtensor of \({\mathscr{B}}\) (see Fig. 1). After this change of variables the point (X0,Y0,Z0) is represented by
and the bases for the tangent space of Gr3 at E0 are
The bases for the tangent space of the submanifold \({\text {Gr}_{s}^{3}}\) at E0 are given by
where the top zeros are in \(\mathbb {R}^{r_{i} \times r_{i}}\), i = 1, 2, 3, and the bottom in \(\mathbb {R}^{(l-k_{1}) \times (k_{1}-r_{1})}\), \(\mathbb {R}^{(m-k_{2}) \times (k_{2}-r_{2})}\), and \(\mathbb {R}^{(n-k_{3}) \times (k_{3}-r_{3})}\), respectively. Clearly, the tangent space of \({\text {Gr}^{3}_{s}}\) is a subspace of the tangent space of Gr3.
Define the functions
The subtensor property implies that for \((U,V,W) \in {\text {Gr}_{k}^{3}}\),
Proposition A.1.
Assume that the Grassmann Hessian of f is positive definite on the tangent space of Gr3 at E0. Then, the Grassmann Hessian of g is positive definite on the tangent space of \({\text {Gr}_{k}^{3}}\) at the point
Proof
As the tangent space in \({\text {Gr}^{3}_{s}}\) at E0 is a subspace of the tangent space in Gr3, the Hessian of f must be positive definite at E0 in \({\text {Gr}_{s}^{3}}\). Therefore, due to (21), the geometric properties of g are the same as those of f, and the Hessian of g is positive definite in \({\text {Gr}_{k}^{3}}\) at E0k. □
Appendix : B: Implementation of the block-Krylov step
Steps (ii)–(iv) in Algorithm 2 are written in tensor form to emphasize the equivalence to Gram-Schmidt orthogonalization. As we remarked in Section 5, the reorganization of data from tensor to matrix form before performing tensor-matrix multiplication is costly. Therefore, we keep the result of step (i) in matrix form and directly orthogonalize it to the previous vectors by performing a QR decomposition. Thereby we also avoid performing reorthogonalization, which might be necessary if we use the Gram-Schmidt method.
Rights and permissions
This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Eldén, L., Dehghan, M. A Krylov-Schur-like method for computing the best rank-(r1,r2,r3) approximation of large and sparse tensors. Numer Algor 91, 1315–1347 (2022). https://doi.org/10.1007/s11075-022-01303-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-022-01303-0