1 Introduction

The Golub and Welsch algorithm [12] is the classical way to compute the nodes λi and the weights ωi of an n-point Gaussian quadrature rule (GQR), commonly used to approximate integrals of the following kind,

$$ {\int}_{-\tau}^{\tau}f(x) \omega(x) dx \approx {\sum}_{i=1}^{n} f(\lambda_{i}) \omega_{i} $$

where ω(x) ≥ 0 is a positive weight function in the interval [−τ,τ], with τ > 0 and f(x) is a continuous function in the same interval. It computes the nodes, also called knots, as the eigenvalues of a symmetric tridiagonal matrix of order n, called the Jacobi matrix, while the corresponding weights are easily obtained from the first components of the associated eigenvectors (see [12] for more details). The nonzero entries of the Jacobi matrix are computed from the coefficients of the three-term recurrence relation of the orthogonal polynomials associated with the weight function ω(x).

The Matlab function gauss is a straightforward implementation of the Golub and Welsch algorithm [12], included in the package “OPQ: A Matlab suite of programs for generating orthogonal polynomials and related quadrature rules” by Walter Gautschi, and it is available at https://www.cs.purdue.edu/archives/2002/wxg/codes/OPQ.html.

In [19] it is shown that, when the weight function ω(x) is symmetric with respect to the origin, the positive nodes of the n-point GQR are the eigenvalues of a symmetric tridiagonal matrix, of order \( \frac {n}{2} \) if n is even and \( \frac {n+1}{2} \) if n is odd, obtained by eliminating half of the unknowns from the original eigenvalue problem. Moreover, the Cholesky factor of the latter tridiagonal matrix of reduced order is a nonnegative lower bidiagonal matrix of dimensions \( \frac {n}{2}\times \frac {n}{2}, \) if n is even, and \( \frac {n+1}{2} \times \frac {n-1}{2}, \) if n is odd, whose entries in its main diagonal and lower subdiagonal are respectively the odd and the even elements of the first subdiagonal of the original Jacobi matrix.

In the same paper, the authors propose modifications of the Golub and Welsch algorithm for computing the nodes and weights of a symmetric GQR (SGQR), by means of a three-term recurrence relation corresponding to the orthogonal polynomials associated with the modified weight function. This resulted in faster Matlab functions than gauss.

Inspired by [19], in this paper we propose to compute the positive nodes of the n-point SGQR as the singular values of a nonnegative bidiagonal matrix. These can be computed in \( \mathcal {O} (n^{2}) \) floating point operations and with high relative accuracy by the algorithm described in [5, 6]. Moreover, the weights of the SGQR can be obtained from the first row of the right singular vector matrix. The stability of the three-term recurrence relation arising in computing the weights of a nonsymmetric n-point GQR is also analyzed and a novel numerical method for computing the weights with high relative accuracy is proposed.

A different approach for computing nodes and weights of a GQR in \( \mathcal {O}(n)\) operations has been introduced in [10] and is implemented in the Matlab package Chebfun [15]. This method is based on approximations of the nodes and weights that appear to be relatively accurate in most nodes but no proof of such a result is given. For a very large number of nodes, this method is today the most efficient one [14, 25].

The paper is organized as follows. The basic notation and definitions used in the paper are listed in Section 2. In Section 3, the main features of the Golub and Welsch algorithm are described. In Section 4, the proposed algorithm for computing the nodes of an n-point SGQR as the singular values of a bidiagonal matrix is described. Different techniques for computing the weights of an n-point GQR are described in Section 5. In Section 6 we show the elementwise relative accuracy of the weights computed by our new method and in Section 7, we give a number of numerical examples confirming our stability results. We then end with a section of concluding remarks.

2 Notation and definitions

Matrices are denoted by upper-case letters X,Y,…,Λ,Θ,…; vectors with bold lower-case letters x,y,…,λ,𝜃,…; scalars with lower-case letters x,y,…,λ,𝜃,…. The element i,j of a matrix A is denoted by aij and the i th element of a vector x is denoted by xi.

Submatrices are denoted by the colon notation of Matlab: A(i : j,k : l) denotes the submatrix of A formed by the intersection of rows i to j and columns k to l, and A(i : j,:) and A(:,k : l) denote the rows of A from i to j and the columns of A and from k to l, respectively. Sometimes, A(i : j,k : l) is also denoted by Ai:j,k:l and x(i : j) by xi:j.

The identity matrix of order n is denoted by In, and its i th column, i = 1,…,n, i.e., the i th vector of the canonical basis of \( {\mathbb {R}}^{n}, \) is denoted by ei. The notation ⌊y⌋ stands for the largest integer not exceeding \( y \in \mathbb {R}_{+}.\)

Given a vector \(\boldsymbol {x} \in {\mathbb {R}}^{n}, \) then diag(x) is a diagonal matrix of order n, with the elements of vector x on the main diagonal. Given a matrix \( A \in {\mathbb {R}}^{m \times n},\) then diag(A) is a column vector of length \( i ={\min \limits } (m,n),\) whose entries are those of the main diagonal of A.

3 Computing the zeros of orthogonal polynomials

Let \(p_{\ell }(x) = k_{\ell }x^{\ell } + {\sum }_{j=0}^{\ell -1} c_{j} x^{j}, \ell =0, 1, \ldots , \) be the sequence of orthonormal polynomials with respect to a positive weight function ω(x) in the interval [−τ,τ],τ > 0, i.e.,

$$ {\int}_{-\tau}^{\tau}p_{i}(x) p_{j}(x) \omega(x) dx = \delta_{ij}, \quad \text{with}\quad \delta_{ij}= \left\{ \begin{array}{ll} 1, & \text{if } i=j, \\ 0, & \text{if } i\ne j, \end{array} \right. $$

where kℓ is chosen to be positive. The polynomials pℓ(x) satisfy the following three-term recurrence relation [23]

$$ \left\{ \begin{array}{l} p_{-1}(x)=0, \\ p_{0}(x)= k_{0}=\frac{\textstyle 1}{\sqrt{\textstyle \mu_{0}}},\\ \gamma_{\ell+1}p_{\ell+1}(x)=(x-\theta_{\ell}) p_{\ell}(x)-\gamma_{\ell}p_{\ell-1}(x), \ell \ge 0, \end{array} \right. $$
(1)

where

$$ \mu_{0} ={\int}_{-\tau}^{\tau}\omega(x) dx, $$

and

$$ \left\{ \begin{array}{l} \gamma_{0} = 0 \\ \\ \gamma_{\ell} = {k_{\ell}}/{k_{\ell-1}} > 0 \end{array} \right., \quad \theta_{\ell}= \frac{\displaystyle {\int}_{-\tau}^{\tau} x p^{2}_{\ell}(x) \omega(x) dx} {\displaystyle {\int}_{-\tau}^{\tau} p^{2}_{\ell}(x)\omega(x) dx}, \quad \ell=1,2,\ldots. $$

Using (1), we can write the n-step recurrence relation

$$ J \textbf{p}(x) = x \textbf{p}(x) - \gamma_{n} p_{n}(x)\textbf{e}_{n}, $$

where

$$ J= \left[ \begin{array}{ccccc} \theta_{0} & \gamma_{1} & & & \\ \gamma_{1} & \theta_{1} & \gamma_{2} & & \\ & \gamma_{2} & {\ddots} & {\ddots} & \\ & & {\ddots} & \theta_{n-2} & \gamma_{n-1} \\ & & & \gamma_{n-1} & \theta_{n-1} \end{array} \right], \quad \textbf{p}(x) = \left[ \begin{array}{c} p_{0}(x) \\ p_{1}(x) \\ {\vdots} \\ p_{n-2}(x) \\ p_{n-1}(x) \end{array} \right]. $$
(2)

The matrix J is called the Jacobi matrix [7]. The following theorem was shown in [7, Th. 1.31].

Theorem 1

Let J = QΛQT be the spectral decomposition of J, where \({\Lambda } \in {\mathbb {R}}^{n \times n} \) is a diagonal matrix and

$$ \boldsymbol{\lambda} := \text{diag}({\Lambda}) = \left[ \lambda_{1},\ldots, \lambda_{n}\right]^{T}, \quad \lambda_{1}< \lambda_{2} < {\cdots} <\lambda_{n}, $$

and \( Q \in {\mathbb {R}}^{n \times n} \) is an orthogonal matrix, i.e., QTQ = In. Then pn(λi) = 0,i = 1,…,n, and Q = V D, with

$$ V=\left[ \textbf{p}(\lambda_{1}), \textbf{p}(\lambda_{2}),\ldots, \textbf{p}(\lambda_{n})\right], D=\left[\begin{array}{cccc} \hat{\omega}_{1} & & & \\ & \hat{\omega}_{2} & & \\ & & {\ddots} & \\ & & & \hat{\omega}_{n} \end{array}\right], $$
(3)

and

$$ \hat{\omega}_{i}= \frac{1}{\left\|\textbf{p}(\lambda_{i} )\right\|_{2}} = \frac{1}{\sqrt{ {\sum}_{\ell=0}^{n-1} p_{\ell}^{2}(\lambda_{i}})}. $$

The eigenvalues λi are the nodes of the GQR and the corresponding weights ωi are defined as (see [23])

$$ \omega_{i} :=\omega_{i}(\lambda_{i})=\hat{\omega}_{i}^{2} =\frac{1}{{\sum}_{\ell=0}^{n-1}p_{\ell}^{2}(\lambda_{i})},\qquad i=1,\ldots,n. $$
(4)

Hence, the weights ωi of the GQR can be determined by (4), computing pℓ(λi),ℓ = 0,1,…,n − 1, i = 1,…,n, either by means of the three-term recurrence relation (1), as done in [19], or by computing the whole eigenvector matrix Q of J in (3). Both approaches will be described in Section 5, and their stability analysis will be provided as well.

As shown in [26], the weights can be also obtained by the first row of Q as

$$ \omega_{i}=\mu_{0} q_{1,i}^{2}, \qquad i=1,\ldots,n. $$
(5)

The Golub and Welsch algorithm [12], relying on a modification of the QR-method [4], yields the nodes and the weights of the GQR by computing only the eigenvalues of the Jacobi matrix and the first row of the associated eigenvector matrix.

3.1 Computing the zeros of orthogonal polynomials for a symmetric weight function

For a weight function ω(x), symmetric with respect to the origin, the diagonal elements 𝜃ℓ,ℓ = 1,…,n, in (2) become zero since, as shown in [7, Th. 1.17],

$$ {p}_{\ell}(-x)= (-1)^{\ell}{p}_{\ell}(x), \quad \ell=0,1,2,\ldots, $$
(6)

and, thus, \( x {p}^{2}_{\ell }(x) \) is an odd function in [−τ,τ]. Therefore, the Jacobi matrix in (2) becomes

$$ {J}= \left[ \begin{array}{ccccc} 0 & {\gamma}_{1} & & & \\ {\gamma}_{1} & 0 & {\gamma}_{2} & & \\ & {\gamma}_{2} & {\ddots} & {\ddots} & \\ & & {\ddots} & 0 & {\gamma}_{n-1} \\ & & & {\gamma}_{n-1} & 0 \end{array} \right]. $$
(7)

Furthermore, by (6), if λi,i = 1,…,n, is a zero of pℓ,ℓ ≥ 0, i.e., pℓ(λi) = 0, then λn−i+ 1 = −λi is also a zero of pℓ, since

$$ {p}_{\ell}({\lambda}_{n-i+1})= {p}_{\ell}(-{\lambda}_{i})=(-1)^{\ell}{p}_{\ell}({\lambda}_{i})= 0. $$

As a consequence,

$$ {\omega}_{i}= \frac{1}{{\sum}_{\ell=0}^{n-1}{p}_{\ell}^{2}({\lambda}_{i})}= \frac{1}{{\sum}_{\ell=0}^{n-1}{p}_{\ell}^{2}({\lambda}_{n-i+1})}={\omega}_{n-i+1},\qquad i=1,\ldots,n. $$

Therefore, for weight functions symmetric with respect to the origin, it is sufficient to compute only the positive nodes and the corresponding weights.

Without loss of generality, in the sequel we will consider the following reordering of λ,Λ and V, i.e.,

$$ {\boldsymbol{\lambda}}:={\boldsymbol{\lambda}}(\boldsymbol{j}), {\Lambda}:= {\Lambda}(\boldsymbol{j},\boldsymbol{j}), {V}:={V}(:,\boldsymbol{j}), $$

where j is the following permutation of the index set i = [1,…,n]

$$ \boldsymbol{j}=\left\{\begin{array}{ll} \left[\begin{array}{cccccccc}n, & n-1, & \ldots, & \frac{n}{2}+1, & 1, & 2, & \ldots, & \frac{n}{2} \end{array}\right], \text{if } n \text{even},\\ \\ \left[\begin{array}{ccccccccc}n, & n-1, & \ldots, & \frac{n+3}{2}, & 1, & 2, & \ldots, & \frac{n-1}{2}, & \frac{n+1}{2} \end{array}\right], \text{if } n \text{odd}. \end{array}\right. $$

Hence, the first \(\lfloor \frac {n}{2}\rfloor \) entries of λ are the strictly positive eigenvalues of J in a decreasing order, the second \(\lfloor \frac {n}{2}\rfloor \) entries of λ are the negative eigenvalues of J in an increasing order, and, if n is odd, the last entry of λ is the zero eigenvalue.

4 Computation of the nodes and the weights of a symmetric Gaussian quadrature rule

In this section we propose an alternative method to compute the positive nodes and corresponding weights of a SGQR. We will need the following Lemma [11].

Lemma 1

Let \( A \in {\mathbb {R}}^{m \times n}, m \le n,\) and

$$ S_{1}=A^{T} A, \quad S_{2} = A A^{T}. $$

Let A = UΣVT be the singular value decomposition of A, with \( U \in {\mathbb {R}}^{m \times m}, V \in {\mathbb {R}}^{n \times n} \) orthogonal, and

$${\Sigma} = \left[\begin{array}{cc} \text{diag}(\sigma_{1},\sigma_{2},\ldots,\sigma_{m}) & 0_{m,n-m} \end{array}\right] \in {\mathbb{R}}^{m \times n},$$

where σ1 ≥ σ2 ≥⋯ ≥ σm ≥ 0. Then

$$ A^{T} A= V \text{diag}({\sigma_{1}^{2}},{\sigma_{2}^{2}},\ldots,{\sigma_{m}^{2}}, \underbrace{0, \ldots,0}_{n-m})V^{T}, $$
$$ A A^{T}= U \text{diag}({\sigma_{1}^{2}},{\sigma_{2}^{2}},\ldots,{\sigma_{m}^{2}})U^{T}. $$

Moreover, if

$$ V = [\underbrace{V_{1}}_{m} \underbrace{ V_{2}}_{n-m}], $$

then

$$ \left[\begin{array} {cc} & A \\ A^{T} & \end{array}\right]= W {\Lambda} W^{T}, $$

with

$$ W= \frac{1}{\sqrt{2}} \left[\begin{array} {ccc} U & U & 0 \\ V_{1} & -V_{1} & \sqrt{2}V_{2} \end{array}\right] $$

and

$$ {\Lambda}= \text{diag}(\sigma_{1},\sigma_{2},\ldots,\sigma_{m},-\sigma_{1},-\sigma_{2},\ldots,-\sigma_{m}, \underbrace{0,\ldots,0}_{n-m}). $$

The following Corollary holds.

Corollary 1

Let Bn be the bidiagonal matrix

$$ B= \left\{ \begin{array}{ll} \left[ \begin{array}{@{}ccccc@{}} \gamma_{1} & \gamma_{2}& & & \\ [1mm] & \gamma_{3} & \gamma_{4} & & \\ & & \gamma_{5} & {\ddots} & \\ & & & {\ddots} & \gamma_{n-2} \\ & & & & \gamma_{n-1} \end{array} \right] \in {\mathbb{R}}^{\frac{n}{2} \times \frac{n}{2} } & \text{if} n \text{even},\\ \left[ \begin{array}{@{}cccccc@{}} \gamma_{1} & \gamma_{2}& & & \\ [1mm] & \gamma_{3} & \gamma_{4} & & \\ & & \gamma_{5} & {\ddots} & \\ & & & {\ddots} & \gamma_{n-3} \\ & & & & \gamma_{n-2} &\gamma_{n-1} \end{array} \right] \in {\mathbb{R}}^{\frac{n-1}{2} \times \frac{n+1}{2} }& \text{if} n \text{odd}, \end{array}\right. $$

with singular value decomposition

$$ {B} = {U} {\Sigma} {V}^{T}, $$

where U and V are orthogonal, \(\boldsymbol {\sigma }= \left [\begin {array}{cccc} \sigma _{1}, &\sigma _{2},& \ldots , &\sigma _{\lfloor \frac {n}{2}\rfloor } \end {array}\right ]^{T}\), and

$$ \left\{ \begin{array}{llll} U \in {\mathbb{R}}^{\frac{n}{2} \times \frac{n}{2}}, & {\Sigma}= \text{diag}(\boldsymbol{\sigma}) \in{\mathbb{R}}^{\frac{n}{2} \times \frac{n}{2}}, & V \in {\mathbb{R}}^{\frac{n}{2} \times \frac{n}{2}}, & \text{if} n \text{even},\\ U \in \mathbb{R}^{\frac{n-1}{2} \times \frac{n-1}{2}}, & {\Sigma} =\left[ \text{diag}(\boldsymbol{\sigma}), 0 \right] \in\mathbb{R}^{\frac{n-1}{2} \times \frac{n+1}{2}},& V \in\mathbb{R}^{\frac{n+1}{2} \times \frac{n+1}{2}}, &\text{if} n \text{odd}, \end{array} \right. $$

and, if n is odd, \(V=\left [\begin {array}{c|c} V_{1} &\boldsymbol {v}_{2} \end {array}\right ], V_{1} \in {\mathbb {R}}^{\frac {n+1}{2} \times \frac {n-1}{2}}, \boldsymbol {v}_{2} \in {\mathbb {R}}^{\frac {n+1}{2}}.\) Then

$$ \begin{array}{@{}rcl@{}} {J} & = & {Q} {\Lambda} {Q}^{T} \\ & =& \left\{ \begin{array}{ll} \frac{1}{2} P^{T} \left[\begin{array} {cc} U & U \\ V & -V \end{array}\right] \hat{\Lambda} \left[\begin{array} {cc} U & U \\ V & -V \end{array}\right]^{T} P, &\text{if} n \text{even},\\ \frac{1}{2} P^{T} \left[\begin{array} {ccc} U & U & \\ V_{1} & -V_{1} & \sqrt{2} \boldsymbol{v}_{2} \end{array}\right] \hat{\Lambda} \left[\begin{array} {ccc} U & U & \boldsymbol{0} \\ V_{1} & -V_{1} & \sqrt{2} \boldsymbol{v}_{2} \end{array}\right]^{T} P, &\text{if} n \text{odd}, \end{array} \right. \end{array} $$
(8)

and \(\hat {\Lambda } \) is the square diagonal matrix

$$ \hat{\Lambda} = \left\{\begin{array}{ll} \text{diag}\left( [\boldsymbol{\sigma};-\boldsymbol{\sigma}]\right) &\text{if} n \text{even},\\ \text{diag}\left( [\boldsymbol{\sigma};-\boldsymbol{\sigma};0]\right), &\text{if} n \text{odd}, \end{array}\right. $$

where \(P:= I_{n}(\tilde {\boldsymbol {\jmath }},:)\) is the even-odd permutation matrix corresponding to the even-odd permutation of the index set i = [1,…,n], i.e.,

$$ \tilde{\boldsymbol{\jmath}}= \left\{ \begin{array}{ll} \left[\begin{array}{c}2,4,\ldots,n-2,n,1,3,\ldots, n-3,n-1 \end{array}\right]^{T} &\text{if} n \text{even},\\ \left[\begin{array}{c}2,4,\ldots,n-3,n-1,1,3,\ldots, n-2,n \end{array}\right]^{T} &\text{if} n \text{odd}. \end{array}\right. $$

Proof

Obviously, we have

and (8) follows then straightforwardly from Lemma 1. □

Taking the even-odd structure of P into account, we have \(\textbf {e}_{1}^{T} P^{T}=\textbf {e}_{\lfloor \frac {n}{2}\rfloor +1}^{T}\) and thus the first row of Q is given by

$$ \textbf{e}_{1}^{T}Q = \left\{ \begin{array}{l} \frac{1}{\sqrt{2}} \textbf{e}_{1}^{T} P^{T} \left[\begin{array} {ll} U & U \\ V & -V \end{array}\right]=\frac{1}{\sqrt{2}}\left[\begin{array} {cc} V(1,:) & -V(1,:) \end{array}\right], \text{if} n \text{even},\\ \\ \frac{1}{\sqrt{2}} \textbf{e}_{1}^{T} P^{T} \left[\begin{array} {ccc} U & U & \boldsymbol{0} \\ V_{1} & -V_{1} & \sqrt{2} \boldsymbol{v}_{2} \end{array}\right] = \left[\begin{array}{ccc} \frac{V_{1}(1,:)}{\sqrt{2}}, & -\frac{V_{1}(1,:)}{\sqrt{2}}, &\boldsymbol{v}_{2}(1) \end{array}\right], \text{if} n \text{odd}, \end{array} \right. $$

and, hence, by (4) and (5), the weights ωi are given by

$$ \left\{ \begin{array}{ll} \omega_{i}= \frac{\displaystyle \mu_{0} }{2}[V(1,i)]^{2}, \qquad i=1,\ldots, \lfloor \frac{n}{2}\rfloor, \\ \omega_{n-i+1} =\omega_{i}, \end{array} \right. $$

and, for n odd,

$$ \omega_{\frac{n+1}{2}}=\frac{ \mu_{0} }{2}\left[V\left( 1,\frac{n+1}{2}\right)\right]^{2}. $$

Remark 1

Transforming the problem of computing the eigenvalues of J into the problem of computing the singular values of the nonnegative bidiagonal matrix B, allows us to compute the nodes of a SGQR with high relative accuracy by using the algorithm described in [5, 6] and implemented in LAPACK (subroutine dlasq1.f) [1]. Note that dlasq1.f computes the singular values of square bidiagonal matrices and for the n-point SGQR with odd n, the bidiagonal matrix B is rectangular of size \(\lfloor \frac {n}{2}\rfloor \times \lfloor \frac {n+1}{2}\rfloor . \) But one step of the QR iteration with zero shift, implemented as described in [5], is sufficient to transform B to \( \left [\begin {array}{c|c} \hat {B} & \textbf {0} \end {array} \right ], \) with \( \hat {B}\) square bidiagonal of order \(\lfloor \frac {n}{2}\rfloor \) to high relative accuracy.

On the other hand, the componentwise stability of computing ωi,i = 1,…,n, from the first row of either Q or V, is not ensured if these matrices are computed by the QR algorithm. Indeed, these orthogonal matrices are computed in a normwise backward stable manner but not necessarily in a componentwise stable manner [27, p. 236], [16]. In Section 7, we show in the example of Fig. 2 that using the eigenvalue decomposition of J for computing the sequence (10), the computation of the small weights is not elementwise stable even though the eigenvectors are computed in a normwise backward stable manner [16]. For the sake of completeness, it is worth mentioning that a similar behavior is not observed for other classes of orthogonal polynomials, such as the Jacobi ones, since the weights do not have such a large range of values and, thus, the computation of GQR for such weights with the function gauss is as accurate as the method proposed in this paper.

5 Computation of the weights of the Gaussian quadrature rules

In this section we consider different techniques for computing the weights ωi,i = 1,…,n, of an n-point GQR, relying only on the knowledge of the corresponding nodes λi for nonsymmetric weight functions. At the end of the section we will shortly describe how these techniques can be adapted to symmetric weight functions. As pointed out in Section 3, the nodes and the weights of the n-point Gaussian rule associated with a weight function ω(x), are the zeros λi,i = 1,…,n, of the orthogonal polynomial pn(x) of degree n and the corresponding weights are

$$ \omega_{i}= \frac{1}{{\sum}_{\ell=0}^{n-1}p_{\ell}^{2}(\lambda_{i})}, \quad i=1,\ldots, n. $$
(9)

The following methods have been proposed in the literature for computing the sequence

$$ p_{\ell}(\lambda_{i}), \ell=0,1,\ldots,n-1, $$
(10)
  1. 1.

    the eigenvalue decomposition [11];

  2. 2.

    the forward three-term recurrence relation (FTTR) [8];

  3. 3.

    the backward three-term recurrence relation (BTTR) [20, 24].

The computation of the weights by means of the FTTR was considered in [19] without providing any stability analysis.

Given \(\tilde {p}_{0}(\bar {\lambda })\) and a zero \( \bar {\lambda }\) of pn(λ), we denote by \(\tilde {p}_{1}(\bar {\lambda }), \) \( \tilde {p}_{2}(\bar {\lambda }), \) \( \ldots , \tilde {p}_{n-1}(\bar {\lambda }),\) the sequence computed by means of (1) in a forward manner, i.e., by FTTR. Analogously, since \({p}_{n}(\bar {\lambda })=0,\) we can set an arbitrary value for \(\hat {p}_{n-1}(\bar {\lambda }), \) and denote by \(\hat {p}_{n-2}(\bar {\lambda }), \hat {p}_{n-2}(\bar {\lambda }), {\ldots } , \hat {p}_{1}(\bar {\lambda }), \hat {p}_{0}(\bar {\lambda }), \) the sequence computed using (1) in a backward fashion, i.e., by BTTR. The latter procedure is often referred to as the Miller’s backward recurrence algorithm [3, 8, 20] in the literature. It was originally proposed by J.C.P. Miller for the computation of tables of the modified Bessel function [3, page xvii].

The stability of the generic FTTR and BTTR, i.e., sequences generated by three-term recurrence relations not linked to orthogonal polynomials, was analyzed in [8, 20, 24], and in these papers the preference went to the BTTR for stability purposes.

For the weight functions depending on the parameters α and β listed in Table 1, we carried out extensive tests, choosing many different values of α and β, for computing the sequences pj(λi),j = 0,1,…,n − 1, by means of FTTR and BTTR. FTTR works in an accurate way for some classes of weights and BTTR works in an accurate way for other classes of weights.

Table 1 Success (“Ok”) and failure results obtained by FTTR and BTTR when computing the sequence of orthogonal polynomials associated to the weight ω, considering many different values of α and β
Full size table

The results of these experiments are displayed in Table 1 in which we mention “Ok” if the method computes the sequence in an accurate way for all the considered values of α and β, and “ ” if the method fails to compute the sequence in an accurate way for some values of α and β. In Fig. 1 (left) we show on a logarithmic scale, the results obtained for the Hermite polynomials of degree j, j = 0,1,…,127, in the largest zero of the Hermite polynomial of degree 128, with FTTR in extended precision (128 digits), with FTTR in double precision and with BTTR in double precision. While the Hermite polynomials are accurately computed with FTTR, the results obtained by BTTR after some steps diverge from the actual values. In this case we report an “Ok” in column FTTR and a “ ” in column BTTR in Table 1. In Fig. 1 (right) we show the results for the Hahn polynomials of degree j = 0,1,2,...,127, evaluated in the fourth smallest zero of the Hahn polynomial of degree 128, computed in double precision with FTTR and BTTR, for α = β = −.5. In this case, FTTR does not compute the sequence of Hahn polynomials in an accurate way, while BTTR does. We thus report a “ ” in column FTTR and an “Ok” in column BTTR in Table 1.

Fig. 1
figure 1

Left: plot of the absolute values of the Hermite polynomials of degree j, j = 0,1,…,127, evaluated in the largest zero of the Hermite polynomial of degree 128, and computed by FTTR in double precision (denoted by “ ”), by BTTR in double precision (denoted by “ ”) and by gauss with extended precision (128 digits) (denoted by “∘”). Right: plot of the absolute values of the Hahn polynomials of degree j, j = 0,1,…,127, evaluated in the fourth smallest zero of the Hahn polynomial of degree 128, and computed by FTTR in double precision (denoted by “ ”), by BTTR in double precision (denoted by “ ”) and by gauss with extended precision (128 digits) (denoted by “∘”)

Full size image

The Hahn polynomials in Table 1 are discrete orthogonal polynomials on the discrete set of n points {0,1,2,...,n − 1} with respect to the weight \(\binom {\alpha +k}{k} \binom { \beta +n-1-k}{ n-1-k}, \alpha , \beta >-1, k=0,1,2,...,n-1.\)

Hence, since experimentally it is not clear which of FTTR and BTTR can be chosen, we describe an algorithm, called LMV, that combines the FTTR and the BTTR methods in order to compute the sequence (10) with high relative accuracy.

Let \(\bar {\lambda }\) be a zero of pn(x) and let us denote by \(\tilde {\textbf {p}}\) and by \(\hat {\textbf {p}}\) the following vectors, computed by FTTR and BTTR, respectively:

$$ \tilde{\textbf{p}}= \frac{1}{\sqrt{\mu_{0}}} \frac{1}{\tilde{p}_{0}(\bar{\lambda}) } \left[ \begin{array}{c} \tilde{p}_{0}(\bar{\lambda}) \\ \tilde{p}_{1}(\bar{\lambda}) \\ {\vdots} \\ \tilde{p}_{n-2}(\bar{\lambda}) \\ \tilde{p}_{n-1}(\bar{\lambda}) \end{array} \right], \hat{\textbf{p}}= \frac{1}{\sqrt{\mu_{0}}} \frac{1}{\hat{p}_{0}(\bar{\lambda})} \left[ \begin{array}{c} \hat{p}_{0}(\bar{\lambda}) \\ \hat{p}_{1}(\bar{\lambda}) \\ {\vdots} \\ \hat{p}_{n-2}(\bar{\lambda}) \\ \hat{p}_{n-1}(\bar{\lambda}) \end{array} \right]. $$

The following theorem emphasizes the relationship between the sequence \( \tilde {p}_{j}(\bar {\lambda }), \) j = 1,…,n − 1, computed by (1) and the columns of the \(\tilde Q\) factor of the QR factorization of \(J - \bar {\lambda }I_{n}. \)

Theorem 2

Let \( \bar {\lambda } \) be a zero of pn(x), and let \( \tilde G_{1}, \tilde G_{2}, \ldots , \tilde G_{n-1} \) be the sequence of Givens rotations

$$ \tilde G_{i} = \left[ \begin{array}{cccc} I_{i-1} & & & \\ & \tilde c_{i} & \tilde s_{i} & \\ &-\tilde s_{i} & \tilde c_{i} & \\ & & & I_{n-i-1} \end{array} \right],\quad i=1,\ldots, n-1, $$
(11)

such that

$$ \tilde G_{n-1} \tilde G_{n-2} {\cdots} \tilde G_{2} \tilde G_{1} (J - \bar{\lambda}I_{n}) = R, $$

with \( R \in {\mathbb {R}}^{n\times n}\) upper triangular. Let \( \tilde {p}_{0}(\bar {\lambda }), \tilde {p}_{1}(\bar {\lambda }), \ldots , \tilde {p}_{n-2}(\bar {\lambda }), \tilde {p}_{n-1}(\bar {\lambda }) \) be the sequence of orthogonal polynomials evaluated in \( \bar {\lambda }\) by means of the three-term recurrence relation (1). Then

$$ \tilde {G_{1}^{T}} \tilde {G_{2}^{T}} {\cdots} \tilde {G_{i}^{T}} \textbf{e}_{i+1} = \tilde{\nu}_{i} \left[\begin{array}{c} \tilde{p}_{0}(\bar{\lambda})\\ \tilde{p}_{1}(\bar{\lambda})\\ {\vdots} \\ \tilde{p}_{i}(\bar{\lambda})\\ \textbf{o}_{n-i-1} \end{array} \right],\quad i=1,\ldots, n-1, $$
(12)

with \(\tilde {\nu }_{i} \in {\mathbb {R}}, \tilde {\nu }_{i} \ne 0.\)

Proof

We prove (12) by induction. Let \( \tilde {p}_{0}(\bar {\lambda })= 1/\sqrt {\mu _{0}}. \) Then, by (1),

$$ \tilde{p}_{1}(\bar{\lambda})= \frac{\bar{\lambda} \tilde{p}_{0}(\bar{\lambda})}{\gamma_{1}}= \frac{1}{\sqrt{\mu_{0}}}\frac{\bar{\lambda} }{\gamma_{1}}. $$

On the other hand,

$$ \tilde c_{1}= \frac{-\bar{\lambda}}{\sqrt{\bar{\lambda}^{2} +{\gamma_{1}^{2}}}}, \tilde s_{1}= \frac{\gamma_{1}}{\sqrt{\bar{\lambda}^{2} +{\gamma_{1}^{2}}}}. $$

Therefore,

$$ \tilde {G_{1}^{T}} \textbf{e}_{2} = \left[\begin{array}{c} -\tilde s_{1} \\ \tilde c_{1} \\ \textbf{o}_{n-2} \end{array} \right]= \frac{1}{\sqrt{\bar{\lambda}^{2} +{\gamma_{1}^{2}}}} \left[\begin{array}{c} -\gamma_{1} \\-\bar{\lambda} \\ \textbf{o}_{n-2} \end{array} \right]= \tilde{\nu}_{1} \left[\begin{array}{c} \tilde{p}_{0}(\bar{\lambda}) \\ \tilde{p}_{1}(\bar{\lambda}) \\ \textbf{o}_{n-2} \end{array} \right], $$

with

$$ \tilde{\nu}_{1}=-\frac{\gamma_{1} \sqrt{\mu_{0}}}{\sqrt{\bar{\lambda}^{2} +{\gamma_{1}^{2}}}}. $$

Let us suppose that (12) holds for i, 1 ≤ i < n and let us prove (12) for i + 1.

Observe that

$$ \tilde G_{i} {\cdots} \tilde G_{2} \tilde G_{1} (J - \bar{\lambda}I_{n})= \left[ \begin{array}{ccccccc} \times & \times & \times & & & & \\ & {\ddots} & {\ddots} & {\ddots} & & & \\ & & \times & \times & \times & & \\ & & & \upsilon_{i} & \tilde c_{i} \gamma_{i+1} & & \\ & & & \gamma_{i+1} &\theta_{i+2} -\bar{\lambda} & {\ddots} &\\ & & & & {\ddots} & {\ddots} & \gamma_{n-1} \\ & & & & & \gamma_{n-1} & \theta_{n} -\bar{\lambda} \end{array} \right], $$
(13)

with \(\upsilon _{i}= -\tilde s_{i} \tilde c_{i-1}\gamma _{i} +\tilde c_{i} (\theta _{i+1} \bar {\lambda }).\) Moreover, by the induction hypothesis (12),

$$ \tilde {G_{1}^{T}} {\cdots} \tilde G_{i-1}^{T} \tilde {G_{i}^{T}} \textbf{e}_{i+1} = \left[\begin{array}{c} (-1)^{i} {\prod}_{j=1}^{i} \tilde s_{j} \\ (-1)^{i-1} \tilde c_{1}{\prod}_{j=2}^{i} \tilde s_{j} \\ (-1)^{i-2} \tilde c_{2}{\prod}_{j=3}^{i} \tilde s_{j} \\ {\vdots} \\ \tilde c_{i-2} \tilde s_{i-1} \tilde s_{i} \\ -\tilde c_{i-1} \tilde s_{i} \\ \tilde c_{i} \\ \textbf{o}_{n-i-1} \end{array} \right] = \tilde{\nu}_{i} \left[\begin{array}{c} \tilde{p}_{0}(\bar{\lambda})\\ \tilde{p}_{1}(\bar{\lambda})\\ {\vdots} \\ \tilde{p}_{i}(\bar{\lambda})\\ \textbf{o}_{n-i-1} \end{array} \right], \quad i=1,\ldots, n-1. $$

By (1) and the induction hypothesis (12),

$$ \tilde{p}_{i+1}(\bar{\lambda})=\frac{\bar{\lambda}\tilde{p}_{i}(\bar{\lambda})- \gamma_{i} \tilde{p}_{i-1}(\bar{\lambda}) }{\gamma_{i+1}} =\frac{\bar{\lambda} \tilde c_{i} + \gamma_{i} \tilde c_{i-1}\tilde s_{i} }{\tilde{\nu}_{i}\gamma_{i+1}}. $$

On the other hand, from (13),

$$ \tilde c_{i+1}= \frac{ \upsilon_{i}}{\xi_{i+1}}= \frac{ -\tilde s_{i} \tilde c_{i-1}\gamma_{i} - \tilde c_{i} \bar{\lambda}}{\xi_{i+1}} \text{and} \tilde s_{i+1}=\frac{ \gamma_{i+1}}{\xi_{i+1}}, $$

with \(\xi _{i+1}=\sqrt { (-\tilde s_{i} \tilde c_{i-1}\gamma _{i} - \tilde c_{i} \bar {\lambda })^{2}+\gamma _{i+1}^{2}}.\) Hence,

$$ \tilde{p}_{i+1}(\bar{\lambda})=-\frac{ 1 }{\tilde{\nu}_{i} }\frac{ \tilde c_{i+1} }{\tilde s_{i+1}}. $$

Therefore,

$$ \begin{array}{@{}rcl@{}} \tilde {G_{1}^{T}} {\cdots} \tilde {G_{i}^{T}} \tilde G_{i+1}^{T} \textbf{e}_{i+2} & = & \left[\begin{array}{@{}c@{}} {\displaystyle(-1)^{i+1} {\prod}_{j=1}^{i+1} \tilde s_{j} }\\ {\displaystyle (-1)^{i} \tilde c_{1}{\prod}_{j=2}^{i+1} \tilde s_{j}} \\ {\displaystyle (-1)^{i-1} \tilde c_{2}{\prod}_{j=3}^{i+1} \tilde s_{j} } \\ {\vdots} \\ \tilde c_{i-1} \tilde s_{i} \tilde s_{i+1} \\ -\tilde c_{i} \tilde s_{i+1} \\ \tilde c_{i+1} \\ \textbf{o}_{n-i-2} \end{array} \right] = -\tilde s_{i+1} \left[\begin{array}{@{}c@{}} {\displaystyle (-1)^{i} {\prod}_{j=1}^{i} \tilde s_{j} }\\ {\displaystyle (-1)^{i-1} \tilde c_{1}{\prod}_{j=2}^{i} \tilde s_{j} } \\ {\displaystyle (-1)^{i-2} \tilde c_{2}{\prod}_{j=3}^{i-1} \tilde s_{j} }\\ {\vdots} \\ -\tilde c_{i-1} \tilde s_{i} \\ \tilde c_{i} \\ -\frac{ \displaystyle \tilde c_{i+1}}{\displaystyle \tilde s_{i+1}} \\ \textbf{o}_{n-i-2} \end{array} \right] \\ & = & \tilde{\nu}_{i+1} \left[\begin{array}{@{}c@{}} \tilde{p}_{0}(\bar{\lambda})\\ \tilde{p}_{1}(\bar{\lambda})\\ {\vdots} \\ \tilde{p}_{i}(\bar{\lambda})\\ \tilde{p}_{i+1}(\bar{\lambda})\\ \textbf{o}_{n-i-2} \end{array} \right], \end{array} $$

with \( \tilde {\nu }_{i+1}=-\tilde s_{i+1} \tilde {\nu }_{i}. \)□

Remark 2

The matrix \(\tilde Q=\tilde {G_{1}^{T}} {\cdots } \tilde G_{n-2}^{T} \tilde G_{n-1}^{T} \) is the orthogonal upper Hessenberg matrix

$$ \tilde Q= \left[ \begin{array}{c@{}c@{}c@{}c@{}c@{}c} {\tilde c}_{1} & -{\tilde s}_{1} {\tilde c}_{2} & {\tilde s}_{1} {\tilde s}_{2} {\tilde c}_{3} & {\ddots} &(-1)^{n-2} {\tilde c}_{n-1} {\displaystyle {\prod}_{i=1}^{n-2}} {\tilde s}_{i} & (-1)^{n-1} {\displaystyle {\prod}_{i=1}^{n-1}} {\tilde s}_{i} \\ {\tilde s}_{1} & {\tilde c}_{1} {\tilde c}_{2} &-{\tilde c}_{1} {\tilde s}_{2} {\tilde c}_{3} & {\ddots} &(-1)^{n-3} {\tilde c}_{1} {\tilde c}_{n-1} {\displaystyle {\prod}_{i=2}^{n-2}} {\tilde s}_{i} & (-1)^{n-2} {\tilde c}_{1} {\displaystyle {\prod}_{i=2}^{n-1}} {\tilde s}_{i} \\ & {\tilde s}_{2} & {\tilde c}_{2} {\tilde c}_{3} & {\ddots} & {\ddots} & {\vdots} \\ & & {\ddots} & {\ddots} & -{\tilde c}_{n-3}{\tilde s}_{n-2} {\tilde c}_{n-1} & {\tilde c}_{n-3}{\tilde s}_{n-2} {\tilde s}_{n-1} \\ & & & {\tilde s}_{n-2}& {\tilde c}_{n-2} {\tilde c}_{n-1} & -{\tilde c}_{n-2}{\tilde s}_{n-1} \\ & & & & {\tilde s}_{n-1} & {\tilde c}_{n-1} \end{array} \right]. $$

since \(J - \bar {\lambda }I_{n} \) is a tridiagonal matrix. Therefore, by Theorem 2, the subvector made by the first i entries of \(\textbf {p} (\bar {\lambda })\) is parallel to the vectors made by the first i entries of the columns j of \(\tilde Q,\) with j ≥ i.

Theorem 3 shows the relationship between the sequence \( \{ \hat {p}_{j}(\bar {\lambda })\}_{j=0}^{n-1}\) and the columns of the factor \( \hat {Q}\) of the QL factorization of \( J - \bar {\lambda } I_{n}. \) For the sake of brevity, we omit the proof since it is very similar to the one of Theorem 2.

Theorem 3

Let \( \bar {\lambda } \) be a zero of pn(x), and let \( \hat {G}_{1}, \hat {G}_{2}, \ldots , \hat {G}_{n-1} \) be the sequence of Givens rotations

$$ \hat{G}_{i} = \left[ \begin{array}{cccc} I_{n-i-1} & & & \\ & \hat{c}_{i} & \hat{s}_{i} & \\ &- \hat{s}_{i} & \hat{c}_{i} & \\ & & & I_{i-1} \end{array} \right],\quad i=1,\ldots, n-1, $$
(14)

such that

$$ \hat{G}_{n-1}^{T} \hat{G}_{n-2}^{T} {\cdots} \hat{G}_{2}^{T}\hat{G}_{1}^{T} (J - \bar{\lambda}I_{n}) = L, $$

with \( L \in {\mathbb {R}}^{n\times n}\) lower triangular. Let \( \hat {p}_{n-1}(\bar {\lambda }), \hat {p}_{n-2}(\bar {\lambda }), {\ldots } , \hat {p}_{1}(\bar {\lambda }), \hat {p}_{0}(\bar {\lambda }), \) be the sequence evaluated in \( \bar {\lambda }\) by the three-term recurrence relation (1) in a backward fashion, with \(\hat {p}_{n-1}(\bar {\lambda }) \) fixed. Then

$$ \hat{G}_{1} \hat{G}_{2} {\cdots} \hat{G}_{i} \textbf{e}_{n-i} = \left[\begin{array}{c} \textbf{o}_{n-i-1}\\ \hat{c}_{i} \\ -\hat{c}_{i-1} \hat{s}_{i} \\ \hat{c}_{i-2} \hat{s}_{i-1} \hat{s}_{i} \\ {\vdots} \\ (-1)^{i-2} \hat{c}_{2}{\prod}_{j=3}^{i} \hat{s}_{j} \\ (-1)^{i-1} \hat{c}_{1}{\prod}_{j=2}^{i} \hat{s}_{j} \\ (-1)^{i} {\prod}_{j=1}^{i} \hat{s}_{j} \end{array} \right] = \hat{\nu}_{i} \left[\begin{array}{c} \textbf{o}_{n-i-1} \\ \hat{p}_{n-i-1}(\bar{\lambda})\\ \hat{p}_{n-i-2}(\bar{\lambda})\\ {\vdots} \\ \hat{p}_{n-2}(\bar{\lambda})\\ \hat{p}_{n-1}(\bar{\lambda}) \end{array} \right],\quad i=1,\ldots, n-1, $$
(15)

with \(\hat {\nu }_{i} \in {\mathbb {R}}, \hat {\nu }_{i} \ne 0.\)

Theorem 2 shows that the vector \( \tilde {\textbf {p}}, \) computed using FTTR, can also be obtained by applying either one step of the implicit QR algorithm with shift \( \bar {\lambda } \) to J or computing the QR factorization of \( J - \bar {\lambda } I_{n}, \) since the orthogonal matrices generated by both methods are the same. The last column of the orthogonal matrices generated by both methods will be parallel to \( \tilde {\textbf {p}}. \) Therefore, forward instability can occur in the computation of \( \tilde {\textbf {p}} \) if premature convergence occurs in one step of the forward implicit QR (FIQR) method with shift \( \bar {\lambda } \) to J [17, 21].

On the other hand, Theorem 3 shows that the vector \( \hat {\textbf {p}}, \) computed applying BTTR, can also be obtained applying either one step of the backward implicit QR algorithm with shift \( \bar {\lambda } \) to J or computing the QL factorization of \( J - \bar {\lambda } I_{n}. \) The first column of the orthogonal matrices generated by both methods will be parallel to \( \hat {\textbf {p}}. \) Therefore, forward instability can occur in the computation of \( \hat {\textbf {p}} \) if premature convergence occurs in one step of the backward implicit QL (BIQL) method with shift \( \bar {\lambda } \) to J [17, 21].

The premature convergence of the implicit QR method with shift \(\bar {\lambda } \) depends on the distance between the eigenvalues of the consecutive matrices J1:i,1:i and J1:i+ 1,1:i+ 1,i = 1,2,…,n − 1. Hence, if \( \lambda _{j}^{(i)}, j=1,\ldots ,i,\) and \( \lambda _{j}^{(i+1)}, j=1,\ldots ,i+1,\) are the eigenvalues of J1:i,1:i and J1:i+ 1,1:i+ 1, respectively, then, by the Cauchy interlacing Theorem [22],

$$ \lambda_{1}^{(i+1)}< \lambda_{1}^{(i)}< \lambda_{2}^{(i+1)}< \lambda_{2}^{(i)}< {\cdots} < \lambda_{i}^{(i+1)}< \lambda_{i}^{(i)}< \lambda_{i+1}^{(i+1)}. $$

If \( \mid \lambda _{j}^{(i+1)}- \lambda _{j}^{(i)}\mid \) and \(\mid \lambda _{j}^{(i)}- \lambda _{j+1}^{(i+1)}\mid \), j = 1,…,i,i = 1,…,n − 1, are sufficiently large, then premature convergence does not occur in one step of the implicit forward QR algorithm with shift \( \bar {\lambda } \) and, hence, FTTR computes the sequence (10) accurately. This is the reason why FTTR computes the sequence (10) accurately for the Chebyshev polynomials Tj(x) of the first kind, i.e., Jacobi polynomials associated with the weight \(\frac {1}{\sqrt {1-x^{2}}} \) in the interval [− 1,1], since the distance of the zeros of two consecutive polynomials Tj(x) an Tj+ 1(x) is of order \( \mathcal {O} \left (\frac {1}{j^{2}}\right )\) at least.

In [17, 18], an algorithm combining one step of FIQR and one step of BIQL with shift \(\bar {\lambda } \) is described in order to compute the corresponding eigenvector. Therefore, the eigenvector associated with \(\bar {\lambda } \) is computed combining the first \( \bar {\jmath }-1\) Givens rotations of FIQR with shift \(\bar {\lambda } \) and the first \(n-\bar {\jmath } \) rotations of BIQL with shift \(\bar {\lambda }.\) It is proven that each eigenvector is computed accurately with \(\mathcal {O} (n) \) floating point operations. Once the eigenvector is computed, the weights are obtained by applying (9).

Following [17, 18], we now describe a recursive procedure to determine an interval in which the index \(\bar {\jmath } \) lies. Let us consider the sequence of Givens rotations \( \tilde G_{i} \in {\mathbb {R}}^{n \times n}, i=1,\ldots ,n-1, \) defined in (11). It turns out that

$$ \tilde G_{1} \tilde G_{2} {\cdots} \tilde G_{i} \tilde{\textbf{p}} =\frac{1}{\sqrt{\mu_{0}}} \frac{1}{\tilde{p}_{0}(\bar{\lambda}) } \left[ \begin{array}{c} 0 \\ {\vdots} \\ 0 \\ \sqrt{{\sum}_{\ell=1}^{i}\tilde{p}^{2}_{i}(\bar{\lambda})}\\ \tilde{p}_{i+1}(\bar{\lambda}) \\ {\vdots} \\ \tilde{p}_{n-1}(\bar{\lambda}) \end{array} \right]. $$

Then we compute the sequence of normalized vectors \( \tilde {\textbf {v}}_{i} \in {\mathbb {R}}^{i}, i=1,\ldots ,n, \) in the following way,

$$ \left\{ \begin{array}{lll} \tilde{\textbf{v}}_{i} =1, && i=1, \\ \textbf{w}_{i} =\tilde {G_{1}^{T}} \tilde {G_{2}^{T}} {\cdots} \tilde G_{i-1}^{T} \textbf{e}_{i}, & \tilde{\textbf{v}}_{i}= \textbf{w}_{i}(1:i)= \left[\begin{array}{c}\tilde s_{i-1}\tilde{\textbf{v}}_{i-1} \\ \tilde c_{i-1} \end{array} \right],& i=2,\ldots, n, \end{array} \right. $$

and the Rayleigh quotients \(\tilde {\lambda }^{(i)}=\tilde {\textbf {v}}_{i}^{T} J_{1:i,1:i} \tilde {\textbf {v}}_{i}, \) for i = 2,…,n, as follows,

with \( \tilde c_{0}=1, \tilde {\lambda }^{(1)}=\theta _{1}.\)

If premature convergence occurs at step \(\tilde {\jmath }\) of FIQR with shift \(\bar {\lambda }, \) then \( \tilde {\textbf {v}}_{\tilde {\jmath }} \) is the eigenvector of \(J_{1:\tilde {\jmath }}\) associated with the eigenvalue \(\bar {\lambda } \approx \tilde {\lambda }^{(\tilde {\jmath })}=\tilde {\textbf {v}}_{\tilde {\jmath }}^{T} J_{1:\tilde {\jmath },1:\tilde {\jmath }} \tilde {\textbf {v}}_{\tilde {\jmath }}.\) It then follows that \(\bar {\jmath } \le \tilde {\jmath } \) (see [17, 18]).

Similarly, let \(\hat {G}_{i} \in {\mathbb {R}}^{n \times n}, i=1,\ldots , n \) be the sequence of Givens rotations defined in (11). Then

$$ \hat{G}_{1}^{T} \hat{G}_{2}^{T} {\cdots} \hat{G}_{i}^{T} = \frac{1}{\sqrt{\mu_{0}}} \frac{1}{\hat{p}_{0}(\bar{\lambda}) } \left[\begin{array}{c} \hat{p}_{0}(\bar{\lambda})\\ {\vdots} \\ \hat{p}_{n-i-2}(\bar{\lambda})\\ \sqrt{{\sum}_{\ell=1}^{i+1}\hat{p}^{2}_{n-i}(\bar{\lambda})}\\ 0\\ {\vdots} \\ 0 \end{array} \right],\quad i=1,\ldots, n-1. $$

We construct the sequence of vectors \( \hat {\textbf {v}}_{i} \in {\mathbb {R}}^{i}, i=1,\ldots , n, \) as follows,

$$ \hat{\textbf{v}}_{i}= \hat{\textbf{w}}_{i}(n-i+1:n)= \left[\begin{array}{c}\hat{c}_{i-1} \\ \hat{s}_{i-1}\hat{\textbf{v}}_{i-1} \end{array} \right], \quad i=2,\ldots, n, $$

where \(\hat {\textbf {w}}_{i} =\hat {G}_{1} \hat {G}_{2} {\cdots } \hat {G}_{i-1} \textbf {e}_{n-i+1},\) and \(\hat {\textbf {v}}_{1}\equiv 1, \) and the Rayleigh quotients \(\hat {\lambda }^{(i)}=\hat {\textbf {v}}_{i}^{T} J_{n-i+1:n,n-i+1:n} \hat {\textbf {v}}_{i}, \) as,

with \( \hat {\lambda }^{(1)}=\theta _{n} \) and \( \hat {c}_{0}=1. \)

It turns out that if premature convergence occurs at step \( \hat {\jmath }, 1\le \hat {\jmath } \le n-1, \) in IBIQL with shift \( \bar {\lambda },\) then \( \hat {\textbf {v}}_{\tilde {\jmath }} \) is the eigenvector of \( J_{n-\tilde {\jmath }:n,n-\tilde {\jmath }:n} \) associated with the eigenvalue \(\bar {\lambda } \approx \tilde {\lambda }^{(\tilde {\jmath })}=\tilde {\textbf {v}}_{\tilde {\jmath }}^{T} J_{1:\tilde {\jmath }} \tilde {\textbf {v}}_{\tilde {\jmath }}.\)

Since J is an irreducible tridiagonal matrix, it was shown in [17, 18, 21] that if premature converge occurs at step \(\tilde {\jmath }\) of FIQR with shift \( \bar {\lambda }\), with \( 1 \le \hat {\jmath } \le n-1,\) then premature convergence can only occur at the step \( \hat {\jmath }\) of BIQL with shift \( \bar {\lambda }\), with \(1 \le \hat {\jmath }\le \tilde {\jmath }. \)

This suggests the Algorithm 1, written in a Matlab-style, to compute the interval \( [\hat {\jmath }, \tilde {\jmath }]\) in which \( \bar {\jmath } \) lies.

figure m

Once the interval \( [\hat {\jmath }, \tilde {\jmath }] \) is determined, the index \( \bar {\jmath } \) is chosen as the index with the maximum element in absolute value in the subvector \( \tilde {\textbf {p}}_{\hat {\jmath }: \tilde {\jmath }} \) [17, 18].

Remark 3

Given \(\bar {\lambda } \), a similar recursion holds for estimating if premature convergence occurs in a singular value of the bidiagonal matrix B.

Remark 4

We have described in Section 4 that the sequence pℓ(λi),ℓ = 0,1,…,n − 1, can be retrieved from the eigenvector of J associated with λi. Since the eigenvalue decomposition of J can be obtained from the singular value decomposition of B, then, the eigenvector sequences can be retrieved in a similar way from the left and right singular vectors associated with the singular value λi of the corresponding bidiagonal matrix. For the sake of brevity, we omit the details.

6 Stability of the eigenvectors and weights

In this section we analyze the sensitivity of the calculation of the eigenvector of the tridiagonal matrix J and the sensitivity of the corresponding weight of the GQR, for a particular eigenvalue λj. Let us define the shifted matrix as T := J − λjIn, where T is tridiagonal and unreduced, let p be the corresponding vector of orthogonal polynomials evaluated at λj, i.e., Tp = 0, and let ω be the corresponding weight, i.e., ω := 1/(pTp). Let us now consider any nonzero element pi≠ 0 of p. We then partition the rows of the matrix T as follows:

$$ T=\left[ \begin{array}{c} T_{1:i-1,:} \\ \textbf{t}_{i} \\ T_{i+1:n,:} \end{array}\right], $$

implying that T1:0 and Tn+ 1:n,: are void matrices. Then the equation pTT = 0 and the fact that pi≠ 0, implies that the row vector ti is in the row space of the remaining rows of T. If we then construct the matrix

$$ T_{(i)}:= \left[ \begin{array}{c} T_{1:i-1,:} \\ 0 \\ T_{i+1:n,:} \end{array}\right] = (I_{n}-\textbf{e}_{i}{\textbf{e}_{i}^{T}})T. $$

then the two systems of equations Tp = 0 and T(i)p = 0 have the same one dimensional set of solutions, i.e., their kernels are the same:

$$ \ker T= \ker T_{(i)} = \text{Im} \textbf{p}. $$

We now compare their sensitivities with respect to perturbations of the data. Let us denote the normalized vector p/∥p∥2 by q, which is thus the normalized eigenvector of J. It follows that qi≠ 0 and

$$ M \left[ \begin{array}{c} T_{1:i-1,:} \\ \textbf{t}_{i} \\ T_{i+1:n,:} \end{array}\right] = \left[ \begin{array}{c} T_{1:i-1,:} \\ 0 \\ T_{i+1:n,:} \end{array}\right], \text{with} \left[ \begin{array}{c} \textbf{q}_{1:i-1} \\ q_{i} \\ \textbf{q}_{i+1:n} \end{array}\right]:= \textbf{q}, M:=\left[ \begin{array}{ccc} I_{i-1} & 0 & 0 \\ \textbf{q}_{1:i-1}^{T} & q_{i} & \textbf{q}_{i+1:n}^{T} \\ 0 & 0 & I_{n-1} \end{array}\right]. $$

This then yields the following theorem.

Theorem 4

Let

$$ T_{(i)}:= (I_{n}-\textbf{e}_{i}{\textbf{e}_{i}^{T}})T, \quad \text{and} \quad \hat{\textbf{q}}:= (I_{n}-\textbf{e}_{i}{\textbf{e}_{i}^{T}})\textbf{q} = \left[ \begin{array}{c} \textbf{q}_{1;i-1} \\ 0 \\ \textbf{q}_{i+1:n} \end{array}\right], $$

then for any qi≠ 0, we have

$$ \sigma_{n-1}(T)\mid q_{i}\mid /\sqrt{2} < \sigma_{n-1}(T_{(i)}) \le \sigma_{n-1}(T) $$
(16)

and for any \(\mid q_{i}\mid =\| \textbf {q} \|_{\infty }\), or, equivalently, \(\mid p_{i}\mid =\| \textbf {p} \|_{\infty }\), we have

$$ \sigma_{n-1}(T)/\sqrt{2n} < \sigma_{n-1}(T_{(i)}) \le \sigma_{n-1}(T). $$
(17)

Proof

The Cauchy inequalities for singular values yields σn− 1(T(i)) ≤ σn− 1(T) since we deleted one row of the matrix T to obtain T(i). Let \(Q \in \mathbb {R}^{n\times (n-1)}\) be the orthogonal complement of q, i.e., QTQ = In− 1 and QTq = 0. Then

$$ MTQ = T_{(i)}Q, \quad \sigma_{n-1}(T)=\sigma_{\min}(TQ), \quad \sigma_{n-1}(T_{(i)})=\sigma_{\min}(T_{(i)}Q). $$

Let \(\textbf {v}\in {\mathbb {R}}^{n-1}\) be such that ∥v∥2 = 1, and \(\|MTQ\textbf {v}\|_{2}=\sigma _{\min \limits }(MTQ)=\sigma _{\min \limits }(T_{(i)}Q)\). We then have \(\|MTQ\textbf {v}\|_{2}\ge \sigma _{\min \limits }(M) \|TQv\|_{2} \ge \sigma _{\min \limits }(M)\sigma _{\min \limits }(TQ)\), which implies

$$ \sigma_{\min}(M) . \sigma_{\min}(TQ) \le \sigma_{\min}(T_{(i)}Q).$$

Moreover,

$$ MM^{T}= I + \textbf{e}_{i} \hat{\textbf{q}}^{T} + \hat{\textbf{q}} {\textbf{e}_{i}^{T}}, $$

and it has been shown in [2, Thm 3.6] that

$$\sigma_{\min}(M)=\sqrt{1-\|\hat{\textbf{q}} \|_{2}}=\mid q_{i}\mid /\sqrt{1+\|\hat{\textbf{q}} \|_{2}}>\mid q_{i}\mid /\sqrt{2}.$$

Putting this together yields (16). The inequalities (17) for \(\mid ~q_{i}\mid =\| \textbf {q} \|_{\infty }\) then follow from \(\mid q_{i}\mid \ge 1/\sqrt {n}\). □

Let us denote by pfl the approximation of the vector p computed by LMV, and let us look at how pfl is constructed from the matrix equation T(i)p = 0 and show that it is backward stable in the sense that there exists a perturbation Δ such that the computed vector pfl satisfies exactly the equation

$$ (T_{(i)}+{\Delta})\textbf{p}_{fl}=0, \quad \|{\Delta}\|_{2} \le \mathcal{O}(\epsilon_{M}) \|T_{(i)}\|_{2}, $$
(18)

where 𝜖M is the machine precision of the computer used. Once the index i has been chosen, the LMV method computes the vector shared by the kernels of T1:i− 1,: and Ti+ 1:n. Basis vectors for these kernels are respectively given by

$$ \alpha\left[ \begin{array}{c} \tilde{\textbf{p}}_{1:i-1} \\ \tilde{p}_{i} \\ \tilde{\textbf{x}} \end{array}\right] \quad \text{and} \quad \beta \left[ \begin{array}{c} \hat{\textbf{x}} \\ \hat{p}_{i} \\ \hat{\textbf{p}}_{i+1:n} \end{array}\right], $$

where \(\tilde {\textbf {x}}\) and \(\hat {\textbf {x}}\) are arbitrary. In order to construct a common vector in the two kernels, we impose \(\beta = \alpha \tilde p_{i}/\hat {p}_{i} \), and then choose α such that the common vector corresponds to the initialization \(\tilde p_{0}(\lambda _{j})=1/\sqrt {\mu _{0}}\). The subvectors

$$ \alpha \left[ \begin{array}{c} \tilde{\textbf{p}}_{1:i-1} \\ \tilde p_{i} \end{array}\right] \quad \text{and} \quad \beta\left[ \begin{array}{c} \hat{p}_{i} \\ \hat{\textbf{p}}_{i+1:n} \end{array}\right], $$

are computed by a forward and backward recurrence using the three-term recurrence of the tridiagonal matrix T. After fixing the starting values in these recurrences, they each can be interpreted as a back substitution of a triangular system of equations. This was analyzed in depth in [16, Ch. 8], from which it follows that the computed vectors satisfy exactly

$$ (\tilde T_{1:i-1,:} +\tilde {\Delta}) \left[ \begin{array}{c} \alpha \tilde{\textbf{p}}_{1:i-1} \\ \alpha \tilde p_{i} \\ 0 \end{array}\right] =0, \quad \text{and} \quad (\hat T_{i+1:n,:} +\hat {\Delta}) \left[ \begin{array}{c} 0 \\ \beta \hat{p}_{i}\\ \beta \hat{\textbf{p}}_{i+1:n} \end{array}\right]=0 , $$

where ζn := nu/(1 − nu)Footnote 1 and \(\tilde {\Delta }\) and \(\hat {\Delta }\) satisfy the elementwise bounds

$$ \mid \tilde {\Delta} \mid \le \zeta_{2} \mid \tilde T_{1:i-1,:} \mid \quad \text{and} \quad \mid \hat {\Delta} \mid \le \zeta_{2} \mid \hat T_{i+1:n,:} \mid . $$

Moreover, the above bounds are independent of the scaling factors α and β. Putting this together shows that the proposed method constructs the computed vector pfl that satisfies exactly the perturbed system of equations

$$ \left( T_{(i)} + {\Delta} \right) \textbf{p}_{fl}=0, \text{where} \textbf{p}_{fl}:= \left[ \begin{array}{c} \tilde{\textbf{p}}_{1:i-1} \\ \tilde p_{i} \\ \hat{\textbf{p}}_{i+1:n} \end{array}\right] , {\Delta} :=\left[ \begin{array}{c} \tilde {\Delta} \\ 0 \\ \hat {\Delta} \end{array}\right], \mid \! {\Delta} \! \mid \le \zeta_{2} \mid \! T_{(i)} \! \mid. $$
(19)

This finally leads to the following theorem.

Theorem 5

The computed quantities pfl and \(\omega _{fl}:=fl(1/\textbf {p}_{fl}^{T}\textbf {p}_{fl})\), obtained by the LMV algorithm with \(\mid p_{i}\mid =\|\textbf {p}\|_{\infty }\), satisfy the bounds

$$\|\textbf{p}_{fl}-\textbf{p}\|_{2}/\|\textbf{p}_{fl}\|_{2} \le \mathcal{O}(\epsilon_{M})\frac{\max_{i}\mid\lambda_{i}\mid}{\min_{i,i\neq j}(\mid \lambda_{i}-\lambda_{j}\mid)}, $$

and

$$\mid\omega_{fl}-\omega\mid/ \mid\omega\mid \le \mathcal{O}(\epsilon_{M})\frac{\max_{i}\mid\lambda_{i}\mid}{\min_{i,i\neq j}(\mid \lambda_{i}-\lambda_{j}\mid)} , $$

which implies normwise forward stability for p and forward stability for the corresponding weight ω.

Proof

It follows from the compatible equations T(i)p = 0 and (T(i) + Δ)pfl = 0 that

$$\|\textbf{p}_{fl}-\textbf{p}\|_{2}\le \| {\Delta} \|_{2}\|\textbf{p}_{fl}\|_{2}/\sigma_{n-1}(T_{(i)}). $$

Since Δ is tridiagonal and elementwise bounded by ζ2∥T∥2 it follows that ∥Δ∥2 ≤ 3ζ2∥T∥2. Using this and the bound (17) then implies that

$$ \|\textbf{p}-\textbf{p}_{fl}\|_{2}/\|\textbf{p}_{fl}\|_{2}\le 3\zeta_{2}\sqrt{2n}\| T \|_{2}/\sigma_{n-1}(T)=\mathcal{ O}(\epsilon_{M})\frac{\max_{i}\mid\lambda_{i}\mid}{\min_{i,i\neq j}(\mid \lambda_{i}-\lambda_{j}\mid)}. $$
(20)

For bounding the relative error in ω, we make use of the relative perturbation theory of norms and inverses, as developed in [16, Chap 3]:

$$ \mid fl(\textbf{p}^{T}\textbf{p})-\textbf{p}^{T}\textbf{p}\mid< \zeta_{n} \mid \textbf{p}^{T}\textbf{p} \mid, \quad \mid fl(1/a)-1/a\mid< \zeta_{1} \mid 1/a \mid, $$

which shows that both functions are forward stable in a relative sense. Combining this with the bound (20) yields a similar bound for ω. □

We point out that the stability result for the eigenvector is similar to what one has for the eigendecomposition of the matrix J, since it is inversely proportional to the smallest nonzero singular value of T, i.e., to the smallest gap between λj and the remaining eigenvalues. The sensitivity of each weight has this same inverse factor, but it has, except for this factor, a forward error that is stable in a relative sense. This is a strong property that is not shared by the eigenvalue method.

7 Numerical examples

In this section we compare the computation of the nodes and weights of n-point GQRs obtained by the proposed method, called LMV, to gauss, the Matlab function available in [9] and to the methods proposed in [19]. All the experiments were performed in Matlab ver. R2020b. In [19], the authors show that the positive nodes and the corresponding weights of a GQR associated with a symmetric weight function can be retrieved from the eigendecomposition of a tridiagonal matrix \( J_{\lfloor \frac {n}{2} \rfloor }\) of order \(\lfloor \frac {n}{2} \rfloor \), providing the Matlab functions displayed in Table 2.

Table 2 Numerical methods for computing the nodes and the weights of GQRs associated with symmetric weight functions proposed in [19]
Full size table

In the first and second example these methods are used to compute n-point GQRs corresponding to the Chebyshev weights of first and second kind, respectively, since their nodes and weights are known. In the third example the proposed method is compared to the function gauss in computing an integral on the whole real line.

Example 1

The nodes of the n-point GQR associated with the Chebyshev weight of the first kind,

$$ w(x)= \frac{1}{\sqrt{1-x^{2}}},$$

are \(x_{j}= \cos \limits (\frac {(2j-1)\pi }{2n}), j=1,\ldots , n, \) the zeros of \( \mathcal {T}_{n}(x)\), the Chebyshev polynomial of the first kind of degree n. Moreover, the weights are wj = π/n,j = 1,…,n. The maxima of the relative errors of the nodes computed by the considered numerical methods

$$ \max_{j} \frac{\mid \lambda_{j} - {x}_{j}\mid }{\mid{x}_{j}\mid } $$

are reported in Table 3, while the maxima of the relative errors of the computed nodes

$$ \max_{j} \frac{ \mid w_{j} - \omega_{j} \mid}{\mid w_{j} \mid} $$

are reported in Table 4.

Table 3 Maxima of the relative errors of the computed nodes for n-point GQRs associated with the Chebyshev weight of the first kind w(x) = (1 − x2)− 1/2. For each n, the smallest error is displayed in boldface
Full size table
Table 4 Maxima of the relative errors of the computed weights for n-point GQRs associated with the Chebyshev weight of the first kind w(x) = (1 − x2)− 1/2. For each n, the smallest error is displayed in boldface
Full size table

In all the cases, the relative errors of the nodes and weights computed by the proposed method are comparable to those of the results yielded by the algorithms proposed in [19].

Example 2

The nodes of the n-point GQR associated with the Chebyshev weight of the second kind,

$$ w(x)= {\sqrt{1-x^{2}}},$$

are \(x_{j}= \cos \limits (\frac {\pi }{n+1}), j=1,\ldots , n, \) the zeros of \( \mathcal {U}_{n}(x)\), the Chebyshev polynomial of the second kind of degree n. Moreover, the weights are \(w_{j} = (1-{x_{j}^{2}})\frac {\pi }{n+1}, j=1,\ldots , n.\) The maxima of the relative errors of the nodes computed by the considered numerical methods are reported in Table 5 while the maxima of the relative errors of the computed nodes are reported in Table 6.

Table 5 Maxima of the relative errors of the computed nodes for n-point GQRs associated with the Chebyshev weight of second kind w(x) = (1 − x2)1/2. For each n, the smallest error is displayed in boldface
Full size table
Table 6 Maxima of the relative errors of the computed weights for n-point GQRs associated with the Chebyshev weight of second kind w(x) = (1 − x2)1/2. For each n, the smallest error is displayed in boldface
Full size table

In all the cases, the relative errors of the nodes and weights computed by the proposed method are smaller than those of the results yielded by the algorithms proposed in [19].

Example 3

In this example we consider a GQR for integrals on the whole real line with the Hermite weight \( \omega (x)= e^{-x^{2}} \)

$$ {\int}_{-\infty}^{\infty} \omega(x) f(x) dx = {\sum}_{j=1}^{n} \omega_{j} f(\lambda_{j}) + E_{n}(f). $$

We computed the Hermite weights, for different values of n, with the following three different methods:

  • the function gauss [9], computed in double precision.

  • the function gauss [9], computed in variable precision with 128 digits; these values can therefore be considered as exact values for the weights.

  • the proposed method, called LMV.

In Fig. 2 (top) we plotted on a logarithmic scale the absolute values of the Hermite polynomials of degree j = 0,1,…,127, evaluated in the largest zeros of the Hermite polynomial of degree 128, computed by the function gauss in double and extended precision (128 digits) and by the proposed method in double precision. In Fig. 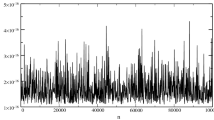2 (bottom), we show the componentwise relative errors of each weight \(e_{rel}({\omega _{j}^{g}}):=\frac {\mid {\omega _{j}^{g}}-\omega _{j}^{ex}\mid }{\mid \omega _{j}^{ex}\mid }\), computed with gauss (in “ ”), and \(e_{rel}(\omega ^{LMV}_{j}):=\frac {\mid \omega _{j}^{LMV}-\omega _{j}^{ex}\mid }{\mid \omega _{j}^{ex}\mid }\), computed with the new method LMV (in “ ”). We also show the corresponding relative error estimate of each weight \(e_{est}(\omega _{j}^{LMV}):=\frac {\epsilon _{M}\max \limits _{i}\mid \lambda _{i}\mid }{\min \limits _{i, i\neq j}\mid \lambda _{i}-\lambda _{j}\mid }\) (in “∘”). We observe that the Hermite weights corresponding to large nodes are very tiny and gauss, which is based on the QR method, computes them with only normwise backward accuracy, but their elementwise relative forward error can be quite bad. On the other hand, LMV computes them with a relative forward error that is componentwise of the order of the machine precision, as predicted by our analysis in Section 6, and the estimated bounds of Theorem 5 are quite accurate.

Fig. 2
figure 2

Top: Plot of the Hermite weights for n = 128, computed with the function gauss in double precision (denoted by “ ”) and in extended precision with 128 digits (denoted by “∘”), and computed by the function LMV (denoted by “ ”). Bottom: Plot of the componentwise relative errors of each weight \(e_{rel}({\omega _{j}^{g}})\), computed with gauss (in “ ”), and \(e_{rel}(\omega _{j}^{LMV})\), computed with the new method LMV (in “ ”). The corresponding relative error estimate \(e_{est}(\omega _{j}^{LMV})\) for each weight computed with the method LMV is also given in “∘”

Full size image

Hence, integrals can not be approximated accurately with the nodes and weights provided by gauss if \( f(x) \sim e^{cx^{2}}, 1-\varepsilon \le c <1\), with ε > 0, small enough.

Let us now consider the integral [13]

$$ \mathcal{I}(a,b)={\int}_{-\infty}^{\infty} e^{-(1+a)x^{2} -\frac{b}{x^{2}}} dx =\sqrt{\frac{\pi}{1+a}} e^{-2\sqrt{(1+a)b}}, a> -1, b>0, $$
(21)

that can be rewritten as

$$ \mathcal{I}(a,b)={\int}_{-\infty}^{\infty} e^{-x^{2}} e^{-ax^{2} -\frac{b}{x^{2}}} dx={\int}_{-\infty}^{\infty} \omega(x) e^{-ax^{2} -\frac{b}{x^{2}}} dx. $$

If a is close to − 1, then the n-point GQR computed with gauss blows up as n increases. In Table 7 the approximation of the integral with GQR computed with the proposed method and with the function gauss are reported, for a = − 0.8 and b = 20. The correct digits are highlighted in boldface.

Table 7 Approximation of the integral (21) obtained by an n-point GQR computed with the proposed method (second column) and with the function gauss (third column), for different values of n
Full size table

8 Conclusions

The nodes and the weights of n-point Gaussian quadrature rules are computed from the eigenvalue decomposition of a tridiagonal matrix of order n by the Golub and Welsch algorithm. In case the weight function is symmetric, Meurant and Sommariva showed that the same information can be fetched from a tridiagonal matrix of order \(\lfloor \frac {n}{2}\rfloor , \) proposing different algorithms.

In this paper it is shown that, for symmetric weight functions, the positive nodes and the corresponding weights can be computed from a bidiagonal matrix with positive entries of size \(\lfloor \frac {n}{2}\rfloor \times \lfloor \frac {n+1}{2}\rfloor . \) Therefore the nodes can be computed with high relative accuracy by an algorithm proposed by Demmel and Kahan. Moreover, the stability of different methods for computing the weights is analyzed, proposing an algorithm for computing them with relative accuracy of the order of the machine precision. The numerical experiments confirm the effectiveness of the proposed approach.