Deviation maximization for rank-revealing QR factorizations

Abstract

In this paper, we introduce a new column selection strategy, named here “Deviation Maximization”, and apply it to compute rank-revealing QR factorizations as an alternative to the well-known block version of the QR factorization with the column pivoting method, called QP3 and currently implemented in LAPACK’s xgeqp3 routine. We show that the resulting algorithm, named QRDM, has similar rank-revealing properties of QP3 and better execution times. We present experimental results on a wide data set of numerically singular matrices, which has become a reference in the recent literature.

1 Introduction

The Rank-Revealing QR (RRQR) factorization was introduced by [16] and it is nowadays a classic topic in numerical linear algebra; for example, [17] introduce RRQR factorization for least squares problems where the matrix has not full column rank: in such a case, a plain QR computation may lead to an R factor in which the number of nonzeros on the diagonal does not equal the rank and the matrix Q does not reveal the range nor the null space of the original matrix. Here, the SVD decomposition is the safest and most expensive solution method, while approaches based on a modified QR factorization can be seen as cheaper alternatives. Since the QR factorization is essentially unique once the column ordering is fixed, these techniques all amount to finding an appropriate column permutation. The first algorithm was proposed in [7] and it is referred as QR factorization with column pivoting (QRP). It should be noticed that, if the matrix of the least squares problem has not full column rank, then there is an infinite number of solutions and we must resort to rank-revealing techniques which identify a particular solution as “special”. QR with column pivoting identify a particular basic solution (with at most r nonzero entries, where r is the rank of the matrix), while biorthogonalization methods [17], identify the minimum ℓ₂ solution. Rank-revealing decompositions can be used in a number of other applications [20]. The QR factorization with column pivoting works pretty well in practice, even if there are some examples in which it fails, see, e.g., the Kahan matrix [23]. However, further improvements are possible, see, e.g., [8] and [15]: the idea here is to identify and remove small singular values one by one. Gu and Eisenstat [19] introduced the strong RRQR factorization, a stable algorithm for computing a RRQR factorization with a good approximation of the null space, which is not guaranteed by QR factorization with column pivoting. Both can be used as optional improvements to the QR factorization with column pivoting. Rank-revealing QR factorizations were also treated in [9, 18, 22].

Column pivoting makes it more difficult to achieve high performances in QR computation, see [3,4,5,6, 27]. The state-of-the-art algorithm for computing RRQR, named QP3, is a block version [27] of the standard column pivoting and it is currently implemented in LAPACK [1]. Other recent high-performance approaches are tournament pivoting [10] and randomized pivoting [14, 25, 31]. In this paper we present a technique based on correlation analysis we call “Deviation Maximization”, that selects a subset of sufficiently linearly independent columns. The deviation maximization may be adopted as a block pivoting strategy in more complex applications that require subset selection. We successfully apply the deviation maximization to the problem of finding a rank-revealing QR decomposition, but, e.g., the authors experimented also a preliminary version of this procedure in the context of active set methods, see [11, 12]. The rest of this paper is organized as follows. In Section 2 we motivate and describe this novel column selection technique. In Section 3 we define the rank-revealing factorization, we review the QRP algorithm and then we introduce a block algorithm for RRQR by means of deviation maximization; furthermore, we give theoretical worst case bounds for the smallest singular value of the R factor of the RRQR factorizations obtained with these two methods. In Section 4 we discuss the algorithm QRDM and some fundamental issues regarding its implementation. Section 5 compares QP3 and QRDM against a relevant database of singular matrices, and finally, the paper concludes with Section 6.

1.1 Notation

For any matrix A of size m × n, we denote by [A]_I,J the submatrix of A obtained considering the entries with row and columns indices ranging in the sets I and J, respectively. We make use of the so-called colon notation, that is we denote by [A]_k:l,p:q the submatrix of A obtained considering the entries with row indices k ≤ i ≤ l and column indices p ≤ j ≤ q. When using colon notation, we write [A]_:,p:q ([A]_k:l,:) as a shorthand for [A]_1:m,p:q ([A]_k:l,1:n). We also denote the (i,j)-th entry as a_ij or [A]_ij. The singular values of a matrix A are denoted as

$$ \sigma_{\max}(A) = \sigma_{1}(A) \geq \sigma_{2}(A) \geq {\dots} \geq \sigma_{\min}(A) = \sigma_{\min(m,n)}(A) \geq 0. $$

Given the vector norm $\Vert x \Vert _{p} = (|x_{1}|^{p} + {\dots } |x_{n}|^{p})^{1/p}$, p ≥ 1, we denote the family of p-norms as

$$ \Vert A \Vert_{p} = \sup_{\Vert x\Vert_{p} = 1} \Vert Ax \Vert_{p}. $$

We denote the operator norm by $\Vert A \Vert _{2} = \sigma _{\max \limits }(A)$. When the context allows it, we drop the subscript on the 2-norm. With a little abuse of notation, we define the max-norm of A as $\Vert A \Vert _{\max \limits } = \max \limits _{i,j} |a_{ij}|$. Recall that the max-norm is not a matrix norm (it is not submultiplicative), and it should not be confused with the $\infty$-norm $\Vert A \Vert _{\infty } = \max \limits _{i} {\sum }_{j} |a_{ij}|$.

2 Column selection by deviation maximization

Consider an m × n matrix A which has not full column rank, that is rank(A) = r < n, and consider the problem of finding a subset of well-conditioned columns of A. Before presenting a strategy to solve this problem, let us recall that for an m × k matrix $C = (\mathbf {c}_{1}\ {\dots } \ \mathbf {c}_{k})$ whose columns c_j are non-null, the correlation matrix Θ has entries

$$ \theta_{ij} = \frac{\mathbf{c}_{i}^{T} \mathbf{c}_{j}}{\Vert \mathbf{c}_{i} \Vert\Vert \mathbf{c}_{j} \Vert}, \quad 1 \leq i,j \leq k. $$

(1)

In particular, we have ${\varTheta } = \left (C D^{-1} \right )^{T} C D^{-1} = D^{-1} C^{T} C D^{-1}$, where D is the diagonal matrix with entries d_i = ∥c_i∥ , 1 ≤ i ≤ k. It is immediate to see that Θ is symmetric positive semidefinite, it has only ones on the diagonal, and its entries range from − 1 to 1. Notice that 𝜃_ij is the cosine of α_ij = α(c_i,c_j) ∈ [0,π), the angle (modulo π) between c_i and c_j. In order to emphasize this geometric interpretation, from now on we refer to Θ as the cosine matrix.

Let us first recall a few definitions taken from [2]. A squared matrix A = Δ + N, where Δ is diagonal and N has a zero diagonal, is said to be τ-diagonally dominant with respect to a norm ∥⋅∥ if $\Vert N \Vert \leq \tau \min \limits _{i} |{\varDelta }_{ii}|$ for some 0 ≤ τ < 1. A matrix A = D₁(Δ + N)D₂, where Δ,D₁,D₂ are diagonal and N has a zero diagonal, is said to be τ-scaled diagonally dominant with respect to a norm ∥⋅∥ if Δ + N is τ-diagonally dominant with respect to same norm, for some 0 ≤ τ < 1. If A is symmetric, then Δ + N is symmetric and we have D := D₁ = D₂, with diagonal entries d_i = |A_ii|^1/2. The main idea behind the deviation maximization is based on the following result.

Lemma 1

Let $C = (\mathbf {c}_{1} \ {\dots } \ \mathbf {c}_{k})$ be an m × k matrix such that $\Vert \mathbf {c}_{1}\Vert = \max \limits _{j} \Vert \mathbf {c}_{j}\Vert >0$. Suppose there exists 1 > τ > 0 such that ∥c_j∥≥ τ∥c₁∥ for all j, and that C^TC is τ-scaled diagonally dominant matrix with respect to the ${\infty }$-norm. Then

$$ \begin{array}{@{}rcl@{}} &&\sigma_{\min}(C) \geq \Vert\mathbf{c}_{1}\Vert \sqrt{\tau(\tau-\Vert N \Vert_{\infty})}, \end{array} $$

(2)

$$ \begin{array}{@{}rcl@{}} &&\sigma_{\min}(C) \geq \Vert\mathbf{c}_{1}\Vert \tau \sqrt{1- \tau}. \end{array} $$

(3)

Proof

Let us write A = C^TC = DΘD, where D = diag(d_j), with d_j = ∥c_j∥, and the cosine matrix Θ decomposes as Θ = (I + N).

We first prove (2). Let us show that A is diagonally dominant in the classic sense, that is for i we have

$$ \vert a_{ii}\vert -\underset{j\neq i}{\sum} \vert a_{ij}\vert = {d_{i}^{2}} -\underset{j\neq i}{\sum} \vert d_{i} d_{j} \theta_{ij}\vert >0. $$

For all 1 ≤ i ≤ k, we have

$$ \underset{j\neq i}{\sum} |d_{i}d_{j} \theta_{ij}| = |d_{i}| \underset{j\neq i}{\sum} |d_{j} \theta_{ij}| \leq |d_{i}| \max_{j} |d_{j}| \underset{j\neq i}{\sum} |\theta_{ij}| = |d_{i}| \Vert \mathbf{c}_{1} \Vert \underset{j\neq i}{\sum} |\theta_{ij}|, $$

and hence

$$ {d_{i}^{2}} - \underset{j\neq i}{\sum} | d_{i}d_{j} \theta_{ij}| \geq |di| \Vert \mathbf{c}_{1} \Vert \tau - |d_{i}| \Vert \mathbf{c}_{1} \Vert \underset{j\neq i}{\sum} |\theta_{ij}| =|di| \Vert \mathbf{c}_{1} \Vert \left( \tau - \underset{j\neq i}{\sum} |\theta_{ij}| \right). $$

Since |d_i| > 0 for all i, and ∥c₁∥ > 0, the right-hand side is positive if and only if

$$ \tau > \max_{i} {\underset{j\neq i}{\sum} |\theta_{ij}|} = \Vert N \Vert_{\infty}, $$

that is true by assumption since the cosine matrix Θ is τ-diagonally dominant with respect to the ${\infty }$-norm. Moreover, we have

$$ \begin{array}{@{}rcl@{}} \min_{i}\left\{ {d_{i}^{2}} - \underset{j\neq i}{\sum} | d_{i}d_{j} \theta_{ij}| \right\} &\geq& \tau \Vert \mathbf{c}_{1} \Vert^{2} \left( \tau - \max_{i} \underset{j\neq i}{\sum} |\theta_{ij}| \right) = \tau \Vert \mathbf{c}_{1} \Vert^{2} \left( \tau - \Vert N \Vert_{\infty} \right) \\ & =& \tau \Vert \mathbf{c}_{1} \Vert^{2} \left( \tau - \Vert N \Vert_{\infty} \right). \end{array} $$

For any strictly diagonally dominant matrix A with $\alpha = \min \limits _{i}\left \{ |a_{ii}| - \underset {j\neq i}{\sum } | a_{ij}| \right \}>0$, we have (see [30])

$$ \Vert A^{-1} \Vert < \frac{1}{\alpha} \quad \Rightarrow \quad \Vert A^{-1} \Vert^{-1} = \sigma_{\min}(A) > \alpha. $$

Then

$$ \sigma_{\min}(C^{T}C) \geq \tau \Vert\mathbf{c}_{1}\Vert^{2} \left( \tau - \Vert N \Vert_{\infty} \right) \quad \Rightarrow \quad \sigma_{\min}(C) \geq \Vert\mathbf{c}_{1}\Vert \sqrt{\tau \left( \tau - \Vert N \Vert_{\infty} \right) } . $$

Let us now prove (3). First notice that the cosine matrix Θ = I + N is symmetric, hence $\Vert N \Vert _{\infty } = \Vert N \Vert _{1}$. In particular, Θ is τ-diagonally dominant also with respect to the 2-norm, since by Hölder’s inequality we get

$$ \Vert N \Vert_{2} \leq \left( \Vert N \Vert_{1} \Vert N \Vert_{\infty}\right)^{1/2} = \Vert N \Vert_{\infty} < \tau. $$

Moreover, assume without loss of generality that $d_{1}\geq d_{2} \geq {\dots } \geq d_{k}$, where d_i = ∥c_i∥. Recall the variational characterization (Courant-Fischer Theorem) of the eigenvalues $\lambda _{1} \geq {\dots } \geq \lambda _{k}$ of a symmetric matrix A of order k

$$ \lambda_{i} = \underset{\underset{\dim(S)=i-1}{S \subseteq \mathbb{R}^{n}}}{\min} \quad \underset{\underset{\Vert \mathbf{x}\Vert = 1}{\mathbf{x} \in S^{\perp}}}{\max} \mathbf{x}^{T} A \mathbf{x}. $$

Let $S_{i-1} \subseteq \mathbb {R}^{k}$ be the subspace spanned by the first i − 1 elements of the canonical basis. Its orthogonal complement $S_{i-1}^{\perp }$ is then the subspace spanned by the last k − i + 1 elements of the canonical basis. We have

$$ \lambda_{i} \leq \underset{\underset{\Vert \mathbf{x}\Vert = 1}{\mathbf{x} \in S_{i-1}^{\perp}}}{\max} \mathbf{x}^{T} A \mathbf{x} = \max_{\Vert \hat{\mathbf{x}}\Vert = 1} \hat{\mathbf{x}}^{T} A_{i-1} \hat{\mathbf{x}}, $$

where $\hat {\mathbf {x}} \in \mathbb {R}^{k-i+1}$ is the vector obtained by deleting the first i − 1 entries of x and A_i− 1 is the square submatrix of order k − i + 1 obtained by deleting the first i − 1 rows and columns of A. Consider the eigenvalues λ_i of the symmetric matrix A = C^TC. Take $\mathbf {x}\in S_{i-1}^{\perp }$ with ∥x∥ = 1, then by Cauchy-Schwarz inequality

$$ \begin{array}{@{}rcl@{}} \hat{\mathbf{x}}^{T} A_{i-1} \hat{\mathbf{x}} \!&=& \hat{\mathbf{x}}^{T} D_{i-1} {\varTheta}_{i-1} D_{i-1} \hat{\mathbf{x}} = \hat{\mathbf{x}}^{T} D_{i-1} (I+N_{i-1}) D_{i-1} \hat{\mathbf{x}} \\ &=&\Vert D_{i-1} \hat{\mathbf{x}} \Vert^{2} + (D_{i-1} \hat{\mathbf{x}})^{T} N_{i-1} D_{i-1} \hat{\mathbf{x}} \!\leq\! \Vert D_{i-1} \hat{\mathbf{x}} \Vert^{2} + \Vert N_{i-1} D_{i-1} \hat{\mathbf{x}} \Vert \Vert D_{i-1} \hat{\mathbf{x}} \Vert \\ & \leq& \Vert D_{i-1} \hat{\mathbf{x}} \Vert^{2} + \tau \Vert D_{i-1} \hat{\mathbf{x}} \Vert^{2} \leq (1+\tau) \Vert D_{i-1} \Vert^{2} \\ & =& (1+\tau) \max_{i \leq j \leq k}\Vert \mathbf{c}_{j} \Vert^{2} = (1+\tau) \Vert \mathbf{c}_{i} \Vert^{2}, \end{array} $$

and thus $\lambda _{i} \leq (1+\tau ) \Vert \mathbf {c}_{i} \Vert ^{2} \leq (1+\tau ) \Vert \mathbf {c}_{1} \Vert ^{2}$. Considering − A instead, we get

$$ \begin{array}{@{}rcl@{}} \hat{\mathbf{x}}^{T} (-A_{i-1} ) \hat{\mathbf{x}}&=& \hat{\mathbf{x}}^{T} D_{i-1} (-I - N_{i-1} ) D_{i-1} \hat{\mathbf{x}} = -\Vert D_{i-1} \hat{\mathbf{x}} \Vert^{2} - (D_{i-1} \hat{\mathbf{x}})^{T} N_{i-1} D_{i-1} \hat{\mathbf{x}} \\ &\leq& (-1+\tau) \Vert D_{i-1} \hat{\mathbf{x}} \Vert^{2} \\ &\leq& (-1+\tau) \Vert \mathbf{c}_{i} \Vert^{2}, \end{array} $$

and thus λ_i ≥ (1 − τ)∥c_i∥². Since $\lambda _{i} = {\sigma _{i}^{2}}$, we have

$$ \sigma_{i} \geq \Vert \mathbf{c}_{1} \Vert \tau \sqrt{1-\tau} . $$

□

The proof of the bound (3) is mainly based on results contained in [2]. Inequalities (2)–(3) show quite clearly that the bound on the smallest singular value of C depends on the norms of the column vectors and on the angles between each pair of such columns. This suggests to choose k columns of A, namely those with indices ${J} = \left \{ j_{1},\dots ,j_{k} \right \}$, k ≤ r, such that the submatrix C = [A]_:,J has columns with large euclidean norms, i.e., larger than the length defined by a parameter τ > 0, and with large deviations, meaning that each pair of columns form an angle whose cosine in absolute value is bounded by a parameter δ ≥ 0. For these reasons, the overall procedure is called deviation maximization and it is presented in Algorithm 1.

Let us detail the above procedure. Define the vector u containing the column norms of A, namely u = (u_i) = (∥a_i∥), for $i=1,\dots ,n$. The set J of column indices is initialized at step 1 with a column index corresponding to the maximum column norm, namely

$$ {J} = \left\{j : j \in \arg\max \mathbf{u} \right\}. $$

At step 2, a set of “candidate” column indices I to be added in J is identified by selecting those columns with a large norm with respect to the parameter τ, that is

$$ {I} = \left\{i\ :\ u_{i} \geq \tau \max \mathbf{u},\ i\neq j \right\}, $$

(4)

and then the cosine matrix associated to the corresponding submatrix Θ, i.e., the cosine matrix of [A]_:,I, is computed at step 4. With a loop over the indices of the candidate set I, an index i ∈ I is inserted in J only if the i-th column has a large deviation from the columns whose index is already in J. In formulae, we ask

$$ |\theta_{ij}| < \delta, \qquad \text{for all }j \in {J}, $$

i.e., the columns a_i and a_j are orthogonal up to the factor δ. At the end of the iterations, we have ${J} = \left \{j_{1},\dots ,j_{k} \right \}$, with 1 ≤ k ≤ k_max, where $k_{\max \limits }$ is the cardinality of the candidate set I, and we set C = [A]_:,J. The following static choice of the parameter δ, namely

$$ \delta = \frac{\tau}{k_{\max}-1}, $$

(5)

yields a submatrix C = [A]_:,J that satisfies the hypotheses of Lemma 1 for a fixed choice of parameters δ and τ. Indeed, for every j ∈ J, this choice ensures

$$ \underset{\underset{i\neq j}{i\in{J}}}{\sum} |\theta_{ij}| < (k-1) \delta = (k-1)\frac{\tau}{k_{\max}-1} \leq (k_{\max}-1) \frac{\tau}{k_{\max}-1} =\tau, $$

and hence the cosine matrix Θ is τ-diagonally dominant. Other strategies are possible: for example, at each iteration, an index i can be added to J if

$$ |\theta_{ij}| < \tau - \underset{\underset{l\neq j}{l\in{J} }}{\sum}|\theta_{lj}|, $$

for all j ∈ J, suggesting that the value δ can be updated dynamically as follows

$$ \delta = \tau - \max_{j \in J}\underset{\underset{l\neq j}{l\in{J}}}{\sum}|\theta_{lj}|. $$

(6)

In both (5) and (6), we have 0 ≤ δ < τ < 1. In practice, the value of δ can be chosen independently from τ, as we detail in Section 4, and this is why it is kept as an input parameter.

2.1 Computing the cosine matrix

Let us focus on some details of the implementation of the deviation maximization presented in Algorithm 1. First, the candidate set I defined in (4) can be computed with a fast sorting algorithm, e.g., quicksort, applied to the array of column norms. The most expensive operation in Algorithm 1 is the computation of the cosine matrix Θ in step 4. The cosine matrix of the columns indexed in the candidate set I is given by

$$ {\varTheta} = D^{-1} [A]^{T}_{:,{I}} [A]_{:,{I}} D^{-1}, $$

(7)

where D = diag(∥a_j∥), with j ∈ I. The matrix Θ is symmetric, thus we only need its upper (lower) triangular part. This can be computed as

$$ {\varTheta} = {U_{1}^{T}} U_{1}, \qquad U_{1} = [A]_{:,{I}} D^{-1}, $$

(8)

or

$$ {\varTheta} = D^{-1} U_{2} D^{-1}, \qquad U_{2} = [A]^{T}_{:,{I}} [A]_{:,{I}}. $$

(9)

The former approach requires m × n additional memory to store U₁ and it requires $m^{2}k_{\max \limits }^{2}$ flops to compute U₁ and $(2m-1)k_{\max \limits }(k_{\max \limits }-1)/2$ flops for the upper triangular part of ${U_{1}^{T}} U_{1}$, while the latter does not require additional memory since the matrix U₂ can be stored in the same memory space used for the cosine matrix Θ, and it requires $(2m-1)k_{\max \limits }(k_{\max \limits }-1)/2$ flops the upper triangular part of U₂ and $k_{\max \limits }(k_{\max \limits }-1)$ flops for the upper triangular part of D^− 1U₂D^− 1. The cheapest strategy is to compute Θ according to (9), even if it requires to write an ad hoc low level routine which is not implemented in the BLAS library. It should be noted that both (8) and involve a symmetric matrix–matrix multiplication, which can be efficiently computed with the BLAS subroutine xsyrk.

In order to limit the cost and the amount of additional memory of Algorithm 1, we propose a restricted version of the deviation maximization pivoting. If the candidate is given by ${I} = \{j_{l}: l = 1,{\dots } , {k_{\max \limits }}\}$, we limit its cardinality to be smaller or equal to a machine dependent parameter k_DM, that is

$$ {I} = \{j_{l} : l = 1,{\dots} , \min({k_{\max}},{k_{DM}})\}. $$

(10)

We refer to the value k_DM as block size, and we discuss its value in terms of achieved performances in Section 5.

3 Rank-revealing QR decompositions

In exact arithmetic, we say that an m × n matrix A is rank-deficient if 0 = σ_r+ 1(A) < σ_r(A), where $r < \min \limits (m,n)$ is its rank. However, rank determination is nontrivial in presence of errors in the matrix elements. Golub and Van Loan [17] define ε-rank of a matrix A as

$$ \text{rank}(A,\varepsilon) = \min_{\Vert A-B\Vert < \varepsilon } \text{rank}(B), $$

(11)

for some small ε > 0. Thus, if the input data have an initial uncertainty of a known order η, then it has sense to look at rank(A,η). Similarly, for a floating point matrix A it is reasonable to regard A as numerically rank-deficient if $\text {rank}(A,\varepsilon ) < \min \limits (m,n)$, where ε = u∥A∥ and u is the unit roundoff. This issue is discussed more in detail in Section 3.4.

Let us now introduce the mathematical formulation for the problem of finding a rank-revealing decomposition of a matrix A of size m × n with numerical rank r, defined up to a certain tolerance ε as discussed above. Let π denote a permutation matrix of size n, then we can compute

$$ A{\varPi} = QR = \left( Q_{1}\ Q_{2} \right) \left( \begin{array}{cc} R_{11} & R_{12} \\ 0 & R_{22} \end{array} \right), $$

(12)

where Q is an orthogonal matrix of order m, Q₁ ∈ m × r and Q₂ ∈ m × (m − r), R₁₁ is upper triangular of order r, R₁₂ ∈ r × (n − r) and R₂₂ ∈ (m − r) × (n − r). The QR factorization above is called rank-revealing if

$$ \sigma_{\min}(R_{11}) = \sigma_{r}(R_{11}) \approx \sigma_{r}(A), $$

or

$$ \sigma_{\max}(R_{22}) = \sigma_{1}(R_{22}) \approx \sigma_{r+1}(A), $$

or both conditions hold. Notice that if $\sigma _{\min \limits }(R_{11})\gg \varepsilon$ and ∥R₂₂∥ is small, then the matrix A has numerical rank r, but the converse is not true. In other words, even if A has $(\min \limits (m,n)-r)$ small singular values, it does not follow that any permutation π yields a small ∥R₂₂∥, even if there exist strategies that ensure a small value of ∥R₂₂∥ by identifying and removing small singular values, see, e.g., [8, 15]. It is easy to show that for any factorization like (12) the following relations hold

$$ \begin{array}{@{}rcl@{}} && \sigma_{\min}(R_{11}) \leq \sigma_{r}(A), \end{array} $$

(13)

$$ \begin{array}{@{}rcl@{}} && \sigma_{\max}(R_{22}) \geq \sigma_{r+1}(A). \end{array} $$

(14)

The proof is an easy application of the interlacing inequalities for singular values [29], namely

$$ \sigma_{k}(A) \geq \sigma_{k} (B) \geq \sigma_{k+r+s}(A), \quad k \geq 1, $$

which hold for any (m − s) × (n − r) submatrix B of A. In fact we have

$$ \begin{array}{@{}rcl@{}} && \sigma_{\min}(R_{11}) = \sigma_{\min}\left( \begin{array}{c} R_{11} \\ 0 \end{array}\right) = \sigma_{r}([Q^{T}A{\varPi}]_{1:m,1:r}) \leq \sigma_{r}(Q^{T}A{\varPi}) = \sigma_{r}(A), \\ && \sigma_{\max}(R_{22}) = \sigma_{\max}(0\ R_{22}) = \sigma_{1}([Q^{T}A{\varPi}]_{r+1:m,1:n}) \geq \sigma_{r+1}(Q^{T}A{\varPi}) = \sigma_{r+1}(A). \end{array} $$

Ideally, the best rank-revealing QR decomposition is obtained by the column permutation π which solves

$$ \max_{{\varPi}} \sigma_{\min} (R_{11}), $$

(15)

for a fixed rank r. Recall that the volume of a rectangular real matrix A is defined as $\sqrt {\det (A^{T}A)}$ or $\sqrt {\det (AA^{T})}$ depending on the shape of A [26], that is the volume of A equals the square root of the product of the singular values of A. It is not difficult to show that problem (15) is equivalent to the problem of selecting r columns such that the volume of the corresponding submatrix [πA]_:,1:r is maximal. Problem (15) clearly has a combinatorial nature, thus algorithms that compute RRQR usually provide (see, e.g., [9, 22]) at least one of the following bounds

$$ \begin{array}{@{}rcl@{}} \sigma_{\min}(R_{11}) &\geq& \frac{\sigma_{r}(A)}{p(n)}, \end{array} $$

(16)

$$ \begin{array}{@{}rcl@{}} \sigma_{\max}(R_{22}) &\leq& \sigma_{r+1}(A){q(n)}, \end{array} $$

(17)

where p(n) and q(n) are low degree polynomials in n. These are worst case bounds and are usually not sharp. We provide a bound of type (16) in Section 3.3.

3.1 The standard column pivoting

Let us introduce the QR factorization with column pivoting proposed by [7], which can be labeled as a greedy approach in order to cope with the combinatorial optimization problem (15). Suppose at the s-th algorithmic step we have already selected s < r well-conditioned columns of A, which are moved to the leading positions by the permutation matrix π^(s) as follows

$$ A {\varPi}^{(s)} = Q^{(s)} R^{(s)} = Q^{(s)} \left( \begin{array}{cc} R_{11}^{(s)} & R_{12}^{(s)} \\ & R_{22}^{(s)} \end{array} \right), $$

(18)

where $R_{11}^{(s)}$ is an upper triangular block of order s, and the blocks $R_{12}^{(s)}$ and $R_{22}^{(s)}$ have size s × (n − s) and (m − s) × (n − s), respectively. The block $R_{22}^{(s)}$ is what is left to be processed, and it is often called the “trailing matrix”. Let us introduce the following column partitions for $R_{12}^{(s)}$, $R_{22}^{(s)}$ respectively

$$ \begin{array}{@{}rcl@{}} R_{12}^{(s)} &=& \left( \mathbf{b}_{1} {\dots} \mathbf{b}_{n-s} \right), \\ R_{22}^{(s)} &=& \left( \mathbf{c}_{1} {\dots} \mathbf{c}_{n-s} \right). \end{array} $$

We aim at selecting, within the n − s remaining columns, that column such that the condition number of the next block $R_{11}^{(s+1)}$ is kept the largest possible. Formally, we would like to solve

$$ \sigma_{\min}\left( R_{11}^{(s+1)}\right) = \sigma_{\min}\left( \begin{array}{cc} R_{11}^{(s)} & \mathbf{b}_{j} \\ & \mathbf{c}_{j} \end{array} \right) = \max_{1 \leq i \leq n-s} \sigma_{\min}\left( \begin{array}{cc} R_{11}^{(s)} & \mathbf{b}_{i} \\ & \mathbf{c}_{i} \end{array} \right). $$

(19)

Using the following fact

$$ \sigma_{\min}\left( \begin{array}{cc} R_{11}^{(s)} & \mathbf{b}_{j} \\ & \mathbf{c}_{j} \end{array} \right) = \sigma_{\min}\left( \begin{array}{cc} R_{11}^{(s)} & \mathbf{b}_{j} \\ & \Vert \mathbf{c}_{j} \Vert \end{array} \right), $$

which is a simple consequence of the invariance of singular values under left multiplication by orthogonal matrices and the insertion of null rows, and using the bound

$$ \sigma_{\min}(A) \leq \min_{i} (\Vert \mathbf{e}_{i}^{T} A^{-1} \Vert^{-1}_{2}) \leq \sqrt{n} \sigma_{\min}(A), $$

(20)

which holds for any nonsingular matrix A, we can approximate up to a factor $\sqrt {s+1}$ the smallest singular value as

$$ \sigma_{\min}\left( \begin{array}{cc} R_{11}^{(s)} & \mathbf{b}_{j} \\ & \mathbf{c}_{j} \end{array} \right) \approx \min_{h} \left\Vert \mathbf{e}_{h}^{T} \left( \begin{array}{cc} R_{11}^{(s)} & \mathbf{b}_{j} \\ & \Vert \mathbf{c}_{j} \Vert \end{array} \right)^{-1} \right\Vert^{-1} , $$

where e_h is the h-th element of the canonical basis of $\mathbb {R}^{s+1}$. Using this result, as argued in [9], the maximization problem (19) can be solved approximately by solving

$$ j = \arg\max_{1 \leq i \leq n-n_{s}} \Vert \mathbf{c}_{j} \Vert \approx \arg\max_{1 \leq i \leq n-n_{s}} \sigma_{\min}\left( \begin{array}{cc} R_{11}^{(s)} & \mathbf{b}_{i} \\ & \mathbf{c}_{i} \end{array} \right) . $$

The resulting procedure is referred as QR factorization with column pivoting, and it is presented in Algorithm 2. This algorithm can be efficiently implemented since the column norms of the trailing matrix can be updated at each iteration instead of being recomputed from scratch. This can be done [17] by exploiting the following property

$$ Q \mathbf{a} = \begin{array}{cc} \left( \begin{array}{c} \beta \\ \mathbf{c} \end{array}\right) & \begin{array}{c} 1 \\ m-1 \end{array} \end{array} \Rightarrow \Vert \mathbf{a} \Vert^{2} = \Vert Q \mathbf{a} \Vert^{2} = \beta^{2} + \Vert \mathbf{c} \Vert^{2}, $$

which holds for any orthogonal matrix Q and any vector a of order m. Therefore, once defined the vector u^(s) whose entry $u^{(s)}_{j}$ is the j-th partial column norm of Aπ^(s), that is the norm of the subcolumn with row indices ranging fromm − n_s to m, and initialized $u^{(1)}_{j} = \Vert \mathbf {a}_{j} \Vert ^{2}$, with 1 ≤ j ≤ n, we can perform the following update

$$ u^{(s+1)}_{j} = \begin{cases} \sqrt{\left( u^{(s)}_{j}\right)^{2} - r_{sj}^{2}}, & s+1 \leq j \leq n, \quad 2 \leq s \leq n, \\ 0, & j < s+1, \end{cases} $$

(21)

where r_ij is the entry of indices (i,j) in R^(s), 1 ≤ i ≤ m, 1 ≤ j ≤ n. The partial column norm update allows to reduce the operation count from ${\mathscr{O}}(mn^{2})$ to ${\mathscr{O}}(mn)$. Actually, the formula (21) cannot be applied as it is because of numerical cancellation, and it needs to modified, see, e.g., [13] for a robust implementation. The pivoting strategy just presented produces a factor R that satisfies [21]

$$ |r_{kk}|^{2} \geq \sum\limits_{i=k}^{j} |r_{ij}|^{2}, \qquad k\leq j \leq n,\ 1\leq k\leq n, $$

(22)

and, in particular,

$$ \begin{array}{@{}rcl@{}} |r_{11}| &\geq& |r_{22}| \geq {\dots} \geq |r_{nn}|, \end{array} $$

(23)

$$ \begin{array}{@{}rcl@{}} |r_{kk}| &\geq& |r_{kj}|, \quad k\leq j \leq n,\ 1\leq k\leq n. \end{array} $$

(24)

A block version of Algorithm 2 has been proposed [27], and it is currently implemented in LAPACK’s xgeqp3 routine, that we will use in the numerical section for comparison.

Remark 1

Geometric interpretation: Introduce the following block column partitioning R^(s) = (R₁ R₂) and Q^(s) = (Q₁ Q₂), where R₁ and Q₁ have s columns. By the properties of the QR decomposition, we have

$$ \mathscr{R}\left( Q_{1}\right) =\mathscr{R}\left( R_{1}\right) \quad \mathscr{R}\left( Q_{2}\right) =\mathscr{R}\left( R_{1}\right)^{\perp}. $$

where ${\mathscr{R}}(B)$ denotes the subspace spanned by the columns of a matrix B. Every unprocessed column of A rewrites as

$$ \mathbf{a}_{j} = Q_{1}\mathbf{b}_{j-s} + Q_{2}\mathbf{c}_{j-s}, $$

where Q₁b_j−s and Q₂c_j−s are the orthogonal projection of a_j on the subspace ${\mathscr{R}}\left (Q_{1}\right )$ and on its orthogonal complement ${\mathscr{R}}\left (Q_{2}\right )$, respectively. The most linearly independent column a_i from the columns in R₁ can be seen as the one with the largest orthogonal projection of the complement on the subspace spanned by such columns, namely

$$ \max_{i\geq s} \left\Vert \mathscr{P}_{\mathscr{R}\left( Q_{2} \right)} \mathbf{a}_{i}\right\Vert = \max_{i\geq 1} \left\Vert Q_{2}\mathbf{c}_{i}\right\Vert. $$

However, the matrix Q^(s) is never directly available unless it is explicitly computed. We then settle for the index j such that

$$ \Vert \mathbf{c}_{j-s}\Vert = \max_{i\geq 1} \Vert \mathbf{c}_{i}\Vert. $$

3.2 The deviation maximization pivoting

Consider the partial factorization in (18), and now suppose at the s-th algorithmic step we have already selected n_s, with s ≤ n_s < r, well-conditioned columns of A, so that $R_{11}^{(s)}$ has size n_s × n_s, while blocks $R_{12}^{(s)}$ and $R_{22}^{(s)}$ have size n_s × (n − n_s) and (m − n_s) × (n − n_s) respectively. The idea is to pick k_s, with n_s+ 1 = n_s + k_s ≤ r, linearly independent and well-conditioned columns from the remaining n − n_s columns of A, which are also sufficiently linearly independent from the n_s columns already selected, in order to keep the smallest singular value of the R₁₁ block as large as possible. We aim at selecting those columns with indices $j_{1}, \dots , j_{k_{s}}$ that solve

$$ \sigma_{\min}\left( \begin{array}{cccc} R_{11}^{(s)} & \mathbf{b}_{j_{1}} & {\dots} & \mathbf{b}_{j_{k_{s}}}\\ & \mathbf{c}_{j_{1}} & \dots& \mathbf{c}_{j_{k_{s}}} \end{array} \right) = \max_{1 \leq i_{1},\dots,i_{k_{s}} \leq n-n_{s}} \sigma_{\min}\left( \begin{array}{cccc} R_{11}^{(s)} & \mathbf{b}_{i_{1}} & {\dots} & \mathbf{b}_{i_{k_{s}}}\\ & \mathbf{c}_{i_{1}} & \dots& \mathbf{c}_{i_{k_{s}}} \end{array} \right). $$

(25)

Of course, this maximization problem has the same combinatorial nature as problem (15), so we rather solve it approximately. We propose to approximate the indices $\left \{ {j_{1}}, \dots , {j_{k_{s}}} \right \}$ that solves problem (25) with the indices selected by means of the deviation maximization procedure presented in Algorithm 1 applied to the trailing matrix $R_{22}^{(s)}$. For the moment, let τ > 0 and δ be fixed accordingly to (5) or (6). More efficient choices will be widely discussed in Section 5. For sake of brevity, we will denote by $B = (\mathbf {b}_{j_{1}} \dots \mathbf {b}_{j_{k_{s}}})$ and $C = (\mathbf {c}_{j_{1}} {\dots } \mathbf {c}_{j_{k_{s}}})$ the matrices made up of the columns selected, and by $\bar {B}$ and $\bar {C}$ the matrices made up by the remaining columns. The rest of the block update, which we detail below, proceeds in a way similar to the recursive block QR. Let $\tilde {Q}^{(s+1)}$ be an orthogonal matrix of order (m − n_s) such that

$$ \left( \tilde{Q}^{(s)}\right)^{T} C = \left( \begin{array}{c} T \\ 0 \end{array}\right) \in \mathbb{R}^{(m-n_{s})\times k_{s}}, $$

(26)

where T is an upper triangular matrix of order k_s. The matrix $\tilde {Q}^{(s+1)}$ is obtained as a product of k_s Householder reflectors, that we represent by mean of the so-called compact WY form [28] as

$$ \tilde{Q}^{(s)} = I - Y^{(s)} W^{(s)} (Y^{(s)})^{T}, $$

where Y^(s) is lower trapezoidal with k_s columns and W^(s) is upper triangular of order k_s. This allows us to carry out the update of the rest of trailing matrix, that is

$$ \left( \tilde{Q}^{(s)}\right)^{T} \bar{C} = \left( \begin{array}{c} \bar{T} \\ R_{22}^{(s+1)} \end{array}\right) \in \mathbb{R}^{(m-n_{s})\times (n-n_{s}-k_{s})}, $$

(27)

by means of BLAS-3 kernels, for performance efficiency. Denoting by $\tilde {{\varPi }}^{(s)}$ a permutation matrix that moves columns with indices $j_{1},\dots ,j_{k_{s}}$ to the current leading positions, we set ${\varPi }^{(s+1)} = {\varPi }^{(s)}\tilde {{\varPi }}^{(s)}$ and

$$ Q^{(s+1)} = Q^{(s)} \left( \begin{array}{cc} I & \\ & \tilde{Q}^{(s)} \end{array}\right) \in \mathbb{R}^{m\times m}, $$

then the overall factorization of Aπ^(s+ 1) takes the form

$$ Q^{(s)} \left( \begin{array}{ccc} R_{11}^{(s)} & B & \bar{B} \\ & C & \bar{C} \end{array} \right)= Q^{(s+1)} \left( \begin{array}{ccc} R_{11}^{(s)} & B & \bar{B} \\ & T & \bar{T} \\ & & R_{22}^{(s+1)} \end{array} \right), $$

(28)

where, for the successive iteration, we set

$$ \begin{aligned} & R_{11}^{(s+1)} = \left( \begin{array}{cc} R_{11}^{(s)} & B \\ & T \end{array} \right) \in \mathbb{R}^{n_{s+1}\times n_{s+1}}, \\ & R_{12}^{(s+1)} = \left( \begin{array}{c} \bar{B} \\ \bar{T} \end{array} \right) \in \mathbb{R}^{n_{s+1}\times(n-n_{s+1})}, \end{aligned} $$

with n_s+ 1 = n_s + k_s. The resulting procedure is presented in Algorithm 3. Last, we point out that the partial column norms can be updated at each iteration also in this case with some straightforward changes of (21), namely

$$ u^{(s+1)}_{j} = \begin{cases} \sqrt{\left( u^{(s)}_{j}\right)^{2} - \displaystyle {\sum}_{l=n_{s}}^{n_{s+1}} r_{lj}^{2}}, & n_{s+1} < j \leq n, \quad n_{s+1} \leq n, \\ 0, & j \leq n_{s+1}. \end{cases} $$

(29)

The above formula cannot be applied as it is because of numerical cancellation, like (21). Thus, we apply safety switch from [13] for a robust implementation.

Algorithm 2 has the particular feature that the diagonal elements of the final upper triangular factor R are monotonically non-increasing in modulus, i.e., they satisfy (23). This is because we have (22), that also implies that the diagonal element is larger than any other extra diagonal entry in modulus, see (24). For what concerns Algorithm 3, an analogous of (22) cannot hold in general. Suppose that Algorithm 3 terminates in S ≥ 1 steps for a given matrix A and parameters τ, δ, and the dimension of the $R_{11}^{(s)}$ factor at the s-th algorithmic step is n_s, so that $0=n_{0}<n_{1}<\dots <n_{S}=n$. It is easy to show that a weaker version of (22) holds, namely we have

$$ |r_{n_{s}+1,n_{s}+1}|^{2} \geq {\sum}_{i=n_{s}+1}^{j} |r_{ij}|^{2}, \qquad n_{s}+1 < j \leq n,\ 0\leq s<S, $$

(30)

which essentially establishes that we have diagonally dominance only for the first pivot of each block, while the standard pivoting ensures it for all pivots (22). In particular, we can only ensure that

$$ \begin{array}{@{}rcl@{}} |r_{n_{s},n_{s}}|&\geq |r_{n_{s}+j,n_{s}+j}|, &1 \leq j \leq n_{s+1}-n_{s},\ 1 \leq s < S \end{array} $$

(31)

$$ \begin{array}{@{}rcl@{}} |r_{n_{s},n_{s}}|&\geq |r_{n_{s},n_{s}+j}|, &1 \leq j \leq n_{s+1}-n_{s},\ 1 \leq s < S . \end{array} $$

(32)

Thus Algorithm 3 does not ensure that the factor R will have a monotonically decreasing diagonal, as it is not the case for other recently proposed pivoting strategies [10].

Remark 2

Geometric interpretation: We pointed out in Remark 1 that the standard pivoting can be seen as an approximate procedure to compute at each iteration the most linearly independent column from the columns already processed. Following this line, Algorithm 3 is an approximate procedure to compute at each iteration a set of linearly independent columns which are the most linearly independent from the columns already processed. In fact, the first task is achieved by selecting vector columns $\{\mathbf {c}_{j_{1}}, \dots , \mathbf {c}_{j_{k}}\}$ which are pairwise orthogonal up to a factor δ, i.e.,

$$ \left|\frac{\mathbf{c}_{j_{i}}^{T}\mathbf{c}_{j_{l}}}{\Vert\mathbf{c}_{j_{i}}\Vert\Vert\mathbf{c}_{j_{l}}\Vert}\right| < \delta, $$

for all 1 ≤ i,l ≤ k, i≠l. The second task is achieved by selecting columns with the largest norm up to a factor τ, i.e.,

$$ \Vert \mathbf{c}_{j_{l}}\Vert \geq \tau \max_{i} \Vert \mathbf{c}_{i}\Vert, $$

for all 1 ≤ l ≤ k.

3.3 Worst-case bound on the smallest singular value

Let us denote by $\bar {\sigma }^{(s)}$ the smallest singular value of the computed $R_{11}^{(s)}$ block at step s, that is

$$ \bar{\sigma}^{(s)} = \sigma_{\min}\left( R_{11}^{(s)} \right). $$

Let us first report from [9] an estimate of $\bar {\sigma }^{(s+1)}$ for QRP.

Theorem 1

Let $R_{11}^{(s)}$ be the upper triangular factor of order s computed by Algorithm 2. We have

$$ \bar{\sigma}^{(s+1)} \geq \sigma_{s+1}(A) \frac{\bar{\sigma}^{(s)}}{\sigma_{1}(A)}\frac{1}{\sqrt{2(n-s)(s+1)}}. $$

Before coming to the main result, we introduce the following auxiliary Lemma.

Lemma 2

With reference to the notation used for introducing the block partition in (28), we have

$$ \sigma_{\min}(T) \geq \frac{\tau \sqrt{1-\tau}}{\sqrt{n-n_{s+1}+1}} \sigma_{n_{s+1}}(A). $$

(33)

Proof

Consider following column partitions $T = (\mathbf {t}_{1} {\dots } \mathbf {t}_{k})$, $\bar {T} = (\mathbf {t}_{k+1} {\dots } \mathbf {t}_{n-n_{s}})$, $R_{22}^{(s+1)} = (\mathbf {r}_{k+1}\dots \mathbf {r}_{n-n_{s}})$, and set r_j = 0, for 1 ≤ j ≤ k. Moreover, let T = (t_i,j), with 1 ≤ i ≤ j ≤ k, and $\bar {T}=(t_{i,j})$ with 1 ≤ i ≤ k,1 ≤ j ≤ n − n_s. First, notice that by (14) we have

$$ \left\Vert \begin{array}{cc} t_{k,k} & t_{k,k+1}, \dots,t_{k,n-n_{s}} \\ 0 & R_{22}^{(s+1)} \end{array} \right\Vert \geq \sigma_{n_{s+1}}(A). $$

We have

$$ \left\Vert \begin{array}{cc} t_{k,k} & t_{k,k+1}, \dots,t_{k,n-n_{s}} \\ 0 & R_{22}^{(s+1)} \end{array} \right\Vert^{2} \leq (n-n_{s+1}+1) \max\left\{t_{k,k}^{2}, \max_{j\geq k+1}\left( \Vert \mathbf{r}_{j}\Vert^{2} + t_{k,j}^{2}\right)\right\}. $$

Since $t_{k,j}^{2} \leq \Vert \mathbf {t}_{j} \Vert ^{2}$, for all 1 ≤ j ≤ n − n_s, and computing the maximum on a larger set of indices we have

$$ \begin{array}{@{}rcl@{}} \max\left\{t_{k,k}^{2}, \max_{j\geq k+1}\left( \Vert \mathbf{r}_{j}\Vert^{2} + t_{k,j}^{2}\right)\right\} &\leq& \max\left\{\Vert \mathbf{t}_{k} \Vert^{2}, \max_{j\geq k+1}\left( \Vert \mathbf{r}_{j}\Vert^{2} + \Vert \mathbf{t}_{j} \Vert^{2} \right)\right\} \\ &\leq& \max_{j\geq 1}\left( \Vert \mathbf{r}_{j}\Vert^{2} + \Vert \mathbf{t}_{j}\Vert^{2}\right). \end{array} $$

From equations (26–27), for all 1 ≤ j ≤ n − n_s, we have

$$ \Vert \mathbf{c}_{j}\Vert^{2} = \Vert \mathbf{r}_{j}\Vert^{2} + \Vert \mathbf{t}_{j}\Vert^{2}, $$

and, finally, since $\Vert \mathbf {t}_{1}\Vert ^{2} = \Vert \mathbf {c}_{1}\Vert ^{2} = \max \limits _{j} \Vert \mathbf {c}_{j}\Vert ^{2}$ and by using Lemma 1, we get

$$ \left\Vert \begin{array}{cc} t_{k,k} & t_{k,k+1}, \dots,t_{k,n-n_{s}} \\ 0 & R_{22}^{(s+1)} \end{array} \right\Vert^{2} \leq (n-n_{s+1}+1) \Vert \mathbf{c}_{1}\Vert^{2} \leq \frac{n-n_{s+1}+1}{\tau^{2}(1- \tau)} \sigma_{\min}^{2}(C). $$

We can conclude by noticing that $\sigma _{\min \limits }(T)=\sigma _{\min \limits }(C)$, since the two matrices differ by a left multiplication by an orthogonal matrix. □

By the interlacing property of singular values, we have

$$ \bar{\sigma}^{(s+1)} \leq \min \left\{ \bar{\sigma}^{(s)},\sigma_{\min} \left( \begin{array}{c} B \\ T \end{array}\right) \right\}, $$

thus the bounds on $\bar {\sigma }^{(s)}$ and $\sigma _{\min \limits }(T)$ are, by themselves, not a sufficient condition. Let us introduce the following result, which provides a bound of type (16) for Algorithm 3.

Theorem 2

Let $R_{11}^{(s)}$ be the upper triangular factor of order n_s computed by Algorithm 3. We have

$$ \bar{\sigma}^{(s+1)} \geq \sigma_{n_{s+1}}(A) \frac{\bar{\sigma}^{(s)}}{\sigma_{1}(A)} \frac{1}{\sqrt{2(n-n_{s+1})n_{s+1}}} \frac{\tau \sqrt{1-\tau}}{k^{2} n_{s}}. $$

Proof

Let us drop the subscript and the superscript on the inverse of $R_{11}^{(s)}$ and its inverse $\left (R_{11}^{(s)}\right )^{-1}$, which will be denoted as R and R^− 1 respectively. Then, the inverse of matrix $R_{11}^{(s+1)}$ is given by

$$ \left( R_{11}^{(s+1)}\right)^{-1} = \left( \begin{array}{cc} R^{-1} & -R^{-1}BT^{-1} \\ & T^{-1} \end{array} \right). $$

Let us introduce the following partitions into rows

$$ F = R^{-1}BT^{-1} = \left( \begin{array}{c}\mathbf{f}_{1}^{T}\\ \vdots\\ \mathbf{f}_{n_{s}}^{T} \end{array}\right),\quad R^{-1} = \left( \begin{array}{c}\mathbf{g}_{1}^{T}\\ \vdots\\ \mathbf{g}_{n_{s}}^{T} \end{array}\right), \quad T^{-1} = \left( \begin{array}{c}\mathbf{h}_{1}^{T}\\ \vdots\\ \mathbf{h}_{k}^{T} \end{array}\right). $$

The idea is to use (20), that is

$$ \bar{\sigma}^{(s+1)} \leq \min_{h} \left\Vert \mathbf{e}_{h}^{T}\left( \begin{array}{cc} R^{-1} & F \\ & T^{-1} \end{array} \right) \right\Vert^{-1} \leq \sqrt{n_{s+1}}\sigma_{\min}\bar{\sigma}^{(s+1)} , $$

to estimate the minimum singular value up to a factor $\sqrt {n_{s+1}}$. For 1 ≤ h ≤ n_s+ 1 we have

$$ \left\Vert \mathbf{e}_{h}^{T}\left( \begin{array}{cc} R^{-1} & F \\ & T^{-1} \end{array} \right) \right\Vert^{2} = \begin{cases} \Vert \mathbf{g}_{h}\Vert^{2} + \Vert \mathbf{f}_{h}\Vert^{2}, & h\leq n_{s},\\ \Vert \mathbf{h}_{h-n_{s}}\Vert^{2}, & h> n_{s}. \end{cases} $$

We can bound ∥g_h∥ using (20) again, which gives

$$ \bar{\sigma}^{(s)} \leq \min_{h} \left( \left\Vert \mathbf{g}_{h} \right\Vert^{-1} \right) \leq \sqrt{n_{s}} \bar{\sigma}^{(s)} . $$

In particular, for every 1 ≤ h ≤ n_s, we get

$$ \bar{\sigma}^{(s)} \leq \min_{h} \left( \left\Vert \mathbf{g}_{h} \right\Vert^{-1} \right) \leq \left\Vert \mathbf{g}_{h} \right\Vert^{-1}, $$

and thus we have

$$ \left\Vert \mathbf{g}_{h} \right\Vert \leq \frac{1}{\bar{\sigma}^{(s)} } = \frac{1}{\sigma_{\min}(R)} = \sigma_{\max}(R^{-1}) = \Vert R^{-1} \Vert. $$

Similarly, we can bound $\Vert \mathbf {h}_{h-n_{s}}\Vert$ by ∥T^− 1∥. Let us now concentrate on bounding ∥f_h∥. We have

$$ \begin{aligned} \Vert \mathbf{f}_{h}\Vert_{2} &\leq \Vert \mathbf{f}_{h}\Vert_{1} = {\sum}_{l=1}^{k} \left| f_{hl} \right| = {\sum}_{l=1}^{k} \left| {\sum}_{i=1}^{k} [R^{-1}B]_{hi}[T^{-1}]_{il} \right| \\ &= {\sum}_{l=1}^{k} \left| {\sum}_{i=1}^{k} {\sum}_{j=1}^{n_{s}} [R^{-1}]_{hj}[B]_{ji}[T^{-1}]_{il} \right| \\ &\leq {\sum}_{l=1}^{k} {\sum}_{i=1}^{k} {\sum}_{j=1}^{n_{s}} \left| [R^{-1}]_{hj} \right|\ \left| [B]_{ji} \right|\ \left| [T^{-1}]_{il} \right| \\ &\leq {\sum}_{l=1}^{k} {\sum}_{i=1}^{k} {\sum}_{j=1}^{n_{s}} \left\Vert R^{-1} \right\Vert_{\max} \left\Vert B \right\Vert_{\max} \left\Vert T^{-1} \right\Vert_{\max} \\ &= k^{2} n_{s} \left\Vert R^{-1} \right\Vert_{\max} \left\Vert B \right\Vert_{\max} \left\Vert T^{-1} \right\Vert_{\max} \\ & \leq k^{2} n_{s} \left\Vert R^{-1} \right\Vert \left\Vert B \right\Vert \left\Vert T^{-1} \right\Vert \\ &= \frac{k^{2} n_{s}}{\bar{\sigma}^{(s)}} \left\Vert B \right\Vert \left\Vert T^{-1} \right\Vert, \end{aligned} $$

where we use the following well-known inequalities ∥x∥₂ ≤∥x∥₁, $\left \Vert A \right \Vert _{\max \limits } \leq \left \Vert A \right \Vert$. Moreover, we can write

$$ \begin{array}{@{}rcl@{}} &&\Vert \mathbf{g}_{h}\Vert^{2} + \Vert \mathbf{f}_{h}\Vert^{2} \leq \frac{1}{(\bar{\sigma}^{(s)})^{2}} + \frac{k^{4} {n_{s}^{2}}}{(\bar{\sigma}^{(s)})^{2}} \left\Vert B \right\Vert^{2} \left\Vert T^{-1} \right\Vert^{2} \\ &=& \frac{\sigma_{\min}^{2}(T) + k^{4} {n_{s}^{2}} \left\Vert B \right\Vert^{2} }{(\bar{\sigma}^{(s)}\sigma_{\min}(T))^{2}} \leq \frac{\Vert T\Vert^{2} + k^{4} {n_{s}^{2}} \left\Vert B \right\Vert^{2} }{(\bar{\sigma}^{(s)}\sigma_{\min}(T))^{2}} \\ & \leq& \frac{ 2k^{4} {n_{s}^{2}} }{(\bar{\sigma}^{(s)}\sigma_{\min}(T))^{2}} \max\left\{ \Vert T\Vert^{2}, \Vert B\Vert^{2}\right\} \leq \frac{2 k^{4} {n_{s}^{2}} }{(\bar{\sigma}^{(s)}\sigma_{\min}(T))^{2}} \Vert A\Vert^{2}, \end{array} $$

where, in the last inequality, we used the interlacing property and the invariance under matrix transposition of the singular values. In fact

$$ \sigma_{1}(A) \geq \sigma_{1}\left( \begin{array}{c} B \\ T \end{array} \right) = \sigma_{1}\left( B^{T}\ T^{T} \right) \geq \max\left\{\sigma_{1}(B), \sigma_{1}(T)\right\}. $$

Hence, we get

$$ \begin{aligned} \frac{1}{\sqrt{\Vert \mathbf{g}_{h}\Vert^{2} + \Vert \mathbf{f}_{h}\Vert^{2}}} \geq \frac{\bar{\sigma}^{(s)}\sigma_{\min}(T)}{\sqrt{2} k^{2} n_{s} \sigma_{1}(A)}. \end{aligned} $$

If $\bar {\sigma }^{(s)}$ is a good approximation of $\sigma _{n_{s}}(A)$, we can suppose that $\bar {\sigma }^{(s)}/\sigma _{n_{s}}(A) \approx 1$, and we can write

$$ \begin{aligned} \sqrt{n_{s+1}} \bar{\sigma}^{(s+1)} &\geq \min \left\{ \min_{h} \Vert \mathbf{h}_{h}\Vert^{-1}, \min_{h} \frac{1}{\sqrt{\Vert \mathbf{g}_{h}\Vert^{2} + \Vert \mathbf{f}_{h}\Vert^{2}}} \right\} \\ &\geq \min \left\{ 1, \frac{\bar{\sigma}^{(s)}}{\sqrt{2} k^{2} n_{s} \sigma_{1}(A)} \right\}\sigma_{\min}(T) \\ & = \frac{\bar{\sigma}^{(s)}}{\sqrt{2} k^{2} n_{s} \sigma_{1}(A)} \sigma_{\min}(T). \end{aligned} $$

Finally, using Lemma 2, we get

$$ \bar{\sigma}^{(s+1)} \geq \sigma_{n_{s+1}}(A) \frac{\bar{\sigma}^{(s)}}{\sigma_{1}(A)} \frac{1}{\sqrt{2(n-n_{s+1})n_{s+1}}} \frac{\tau \sqrt{1-\tau}}{k^{2} n_{s}}, $$

which is the desired bound. □

This shows that even if the leading n_s columns have been carefully selected, so that $\bar {\sigma }^{(s)}$ is an accurate approximation of $\sigma _{n_{s}}(A)$, there could be a potentially dramatic loss of accuracy in the estimation of the successive block of singular values, namely $\sigma _{n_{s}+1}(A),\dots ,\sigma _{n_{s+1}}(A)$, just like for the standard column pivoting. In fact, it is well known that failure of QRP algorithm may occur (one such example is the Kahan matrix [23]), as well as for other greedy algorithms, but it is very unlikely in practice.

3.4 Termination criteria

In principle, both Algorithms 2 and 3 reveal the rank of a matrix. In finite arithmetic we have

$$ \left( \begin{array}{cc} \hat{R}_{11}^{(s)} & \hat{R}_{12}^{(s)} \\ & \hat{R}_{22}^{(s)} \end{array} \right), $$

(34)

where $\hat {R}^{(s)}_{ij}$ is the block $R^{(s)}_{ij}$ computed in finite representation, for i = 1,2,j = 2. If the block $\hat {R}^{(s)}_{22}$ is small in norm, then it is reasonable to say that the matrix A has rank n_s, where n_s is the order of the upper triangular block $\hat {R}_{11}^{(s)}$. [17] propose the following termination criterion

$$ \left\Vert \hat{R}^{(s)}_{22} \right\Vert \leq f(n)\varepsilon \left\Vert A \right\Vert, $$

(35)

where ε is the machine precision and f(n) is a modestly growing function of the number n of columns. Notice that even if a block $\hat {R}_{22}^{(s)}$ with small norm implies numerical rank-deficiency, the converse is not true in general: an example is the Kahan matrix [23], discussed in Section 5.1. Let us write the column partition $\hat {R}^{(s)}_{22} = (\hat {\mathbf {c}}_{1}\ {\dots } \ \hat {\mathbf {c}}_{n-n_{s}})$. We have

$$ \left\Vert \hat{R}^{(s)}_{22} \right\Vert \leq \sqrt{n-n_{s}} \max_{i} \left\Vert \hat{\mathbf{c}}_{i} \right\Vert, \quad \max_{i} \left\Vert \mathbf{a}_{i} \right\Vert \leq \left\Vert A \right\Vert. $$

Therefore, the stopping criterion (35) holds if

$$ \sqrt{n-n_{s}} \max_{i} \left\Vert \hat{\mathbf{c}}_{i} \right\Vert \leq f(n)\varepsilon \max_{i} \left\Vert \mathbf{a}_{i} \right\Vert, $$

(36)

but the converse is not true in general. Suppose now to have input data with an initial uncertainty of a known order η in A. In this case, the numerical rank may be defined up to a perturbation of order η, see (11), and the stopping criterion (36) is replaced as follows

$$ \sqrt{n-n_{s}} \max_{i} \left\Vert \hat{\mathbf{c}}_{i} \right\Vert \leq \eta \max_{i} \left\Vert \mathbf{a}_{i} \right\Vert, $$

(37)

where η is a user defined input parameter. We do not investigate this case, however it is left as an option in the software. In Section 5 we test the practical stopping criterion (36) and discuss the following two choices:

$$ \begin{array}{@{}rcl@{}} f(n) &=& n, \end{array} $$

(38)

$$ \begin{array}{@{}rcl@{}} f(n) &=& \sqrt{n}. \end{array} $$

(39)

4 The QR with deviation maximization algorithm

In this section we introduce the QR with deviation maximization (QRDM) algorithm and discuss some crucial aspects related to its implementation.

The deviation maximization procedure exploits diagonal dominance in order to ensure linear independence. Diagonal dominance is sufficient but obviously not necessary and it often turns out to be a too strong condition to be satisfied in practice. Let us briefly comment the choice of the parameter τ: on the one hand, its value should be small in order to get a large candidate set I; on the other hand, a small value of τ implies a small value of δ < τ if (5) or (6) are applied, likely yielding fewer selected columns. Notice that when the value of δ is close to zero, only pairwise nearly orthogonal columns are selected, and it is unlikely to find such matrices in real world problems. However, the value of δ can be chosen independently from τ, as we now detail. Suppose to give up the constraint δ < τ and to settle for any value of τ and δ in the interval (0,1). Then the deviation maximization may identify a set of numerically linearly dependent columns. In order to overcome this issue, we incorporate a filtering procedure in the Householder triangularization. The selected columns $\left \{ j_{1},\dots ,j_{k_{s}} \right \}$ at the s-th algorithmic step satisfy

$$ \Vert [A]_{n_{s}:m,n_{s}+j} \Vert \geq \varepsilon_{s} := \tau\ \max_{i > n_{s}} \Vert [A]_{n_{s}:m,i} \Vert, \quad j = j_{1},\dots,j_{k_{s}}, $$

(40)

before being reduced to triangular form. If a partial column norm becomes too small during the Householder triangularization, then that column is not sufficiently linearly independent from the columns already processed and the procedure is interrupted. In general, the converse is not true. For instance, we demand that the partial column norms $\Vert [A]_{n_{s}+l:m,n_{s}+l} \Vert$ do not become smaller than the parameter ε_s defined above in order to compute the related Householder reflectors.

The QR computation obtained in this way is called QRDM and it is presented in Algorithm 4, where the filtering procedure on the partial column norms appears at step 9. Other values of ε_s are possible, e.g., a small and constant threshold. However, numerical tests show that the choice (40) works well in practice. In this case, the Householder reduction to triangular form terminates withl < k Householder reflectors, and the algorithm continues with the computation and the application of the compact WY representation of these l reflectors. At the next iteration, the pivoting strategy moves the rejected column away from the leading position, if necessary. As we show in Section 5, this break mechanism enables us to independently set values for τ andδ, and thus to obtain the best results in execution times.

4.1 Minimizing memory communication

The performance of an algorithm is highly impacted by the amount of communication performed during its execution, as explicitly pointed out in the literature, see, e.g., [10], where communication refers to data movement within a memory hierarchy of a processor or even between different processors of a parallel computer. In this context, the goal of this section is to design a pivoting strategy that is effective in revealing the rank of a matrix but also minimizes communication. Each time step 5 in Algorithm 3 is reached, the deviation maximization selects k_s columns $\left \{ j_{1}, \dots , j_{k_{s}}\right \}$ to be moved to the leading positions $\left \{ n_{s}+1, \dots , n_{s}+{k_{s}}\right \}$. However, if one of more columns are already situated within the leading position indices then it is not necessary to move them from their current positions: in this case, since the columns $\left \{ j_{1}, \dots , j_{k_{s}}\right \}$ are placed in the leading positions with a different ordering, the smallest singular value $\bar {\sigma }^{(s)}$ of the $R_{11}^{(s)}$ factor is unchanged, i.e., Theorem 2 still holds. This change on the pivoting strategy allows a huge memory saving in terms of data movement without affecting the rank-revealing properties of the resulting decomposition. This result does not come for free, namely we lose any monotonically decreasing trend in the magnitude of the diagonal elements of the R₁₁ factor and the weak diagonally dominance established in (30)–(32) does not hold anymore. Let us briefly describe the structure of the permutations employed. For every $i = 1,\dots ,k_{s}$, the column j_i is not moved if it is within the k_s leading positions. Otherwise, it is moved in place of the first free spot within the k_s leading positions, namely we swap the columns j_i and n_s + l, where l is the minimum integer 1 ≤ l ≤ k_s such that $n_{s}+l \notin \left \{ j_{1},\dots , j_{k_{s}} \right \}$. In this way, the memory communication is minimized and the pivoting strategy requires only m additional memory slots. Let us stress that this communication avoiding pivoting strategy if possible only when multiple columns are selected at once, and hence it cannot be extended to the QR decomposition with standard column pivoting.

5 Numerical experiments

In this section we discuss the numerical accuracy of QRDM against the SVD decomposition and the block QRP algorithm, briefly called QP3 [27]. We report experimental results comparing the double precision codes dgeqrf and dgeqp3 from LAPACK, and dgeqrdm, a double precision C implementation of our block algorithm QRDM available online at the URL: https://github.com/mdessole/qrdm. All tests are carried out on a computer with an Intel(R) Core(TM) i7-2700K processor and a 8 GB system memory, employing CBLAS and LAPACKE, the C reference interfaces to BLAS and LAPACK implementations on Netlib, respectively. All codes have been compiled through a GNU Compiler Collection or a GNU Fortran compiler on a Linux system. The libraries BLAS and LAPACK have been installed from the package libatlas-base-dev for Linux Ubuntu, derived from the well-known ATLAS project (Automatically Tuned Linear Algebra Software), http://math-atlas.sourceforge.net/. It must be pointed out that the absolute timings of the algorithms here discussed are sensitive to the particular optimization adopted for the BLAS library, but it does not change the significance of the results here presented. Actually, a better optimization of the BLAS means more efficient BLAS-3 operations and QRDM increases the speedup with respect to QP3.

Particular importance is given to the values on the diagonal of the upper triangular factor R of the RRQR factorization, which are compared with the singular values of the R₁₁ block and with the singular values of the input matrix A. The tests are carried out on several instances of the Kahan matrix [23] and on a subset of matrices from the San Jose State University Singular matrix database, which were used in other previous papers on the topic, see, e.g., [10, 19].

5.1 Kahan matrix

We first discuss the Kahan matrix [24, p. 31], that is defined as follows

$$ K(n,\varphi) = \text{diag}\left( 1,{\varsigma},\dots,{\varsigma}^{n-1}\right) \left( \begin{array}{cccc} 1 & -\varphi & {\dots} & -\varphi\\ & 1 & {\ddots} & {\vdots} \\ & & {\ddots} & -\varphi \\ & & & 1 \end{array}\right), $$

(41)

where ς² + φ² = 1, and, in general we have

$$ K(n,\varphi) = \left( \begin{array}{cccc} 1 & -\varphi & \dots& -\varphi \\ 0 & \multicolumn{3}{c}{{\varsigma} K(n-1,\varphi)} \end{array} \right), \qquad \varphi = \cos(\alpha),\ {\varsigma} = \sin(\alpha). $$

(42)

For φ = 0, the singular values are all equal to one. An increasing gap between the last two singular values is obtained when the value of φ is increased. The QRP algorithm does not perform any pivoting, producing a RRQR factorization in which the Q factor is the identity matrix and thus leaving these matrices unchanged [17]. This implies that $\left \Vert R_{22}^{(s)}\right \Vert \geq {\varsigma }^{n-1}$, for 1 ≤ s ≤ n − 1. For example, the matrix K(300,0.99) has no particular small trailing matrix though, since ς²⁹⁹ ≈ 0.5. In such case $\sigma _{\min \limits }(R_{11}^{(n-1)})$ can be much smaller than σ_n− 1(K(n,φ)) [19]. It is not difficult to see that the QRDM algorithm does not perform any pivoting on these matrices too. Let us show this fact by induction on the algorithmic step s. Let $(\mathbf {k}_{1} {\dots } \mathbf {k}_{n})$ be the column partition of K(n,φ). It is easy to see that all columns of the Kahan matrix have unit norm. Moreover, take i < j and we have

$$ \begin{aligned} \theta_{ij} &= \mathbf{k}_{i}^{T}\mathbf{k}_{j} = {\sum}_{l=1}^{n} k_{li}k_{lj} = {\sum}_{l=1}^{i} k_{li}k_{lj} = \varphi^{2} {\sum}_{l=1}^{i-1} {\varsigma}^{2(l-1)} + \left( -\varphi {\varsigma}^{i-1} \right){\varsigma}^{i-1} \\ &= 1 - {\varsigma}^{2(i-1)} (1+\varphi), \end{aligned} $$

that is the cosine of the angle α_ij ∈ [0,π) between k_i and k_j does not depend on j. In other words, the column k_i forms the same angle (modulo π) with all columns k_j, with j > i, thus no column permutations are necessary in the first iteration of QRDM. Suppose no permutations are necessary in the first s iterations, then (42) allows to write

$$ K(n,\varphi) = \left( \begin{array}{cccc} K(n_{s},\varphi) & \mathbf{b}_{1} & {\dots} & \mathbf{b}_{n-n_{s}}\\ & \mathbf{c}_{1} & \dots& \mathbf{c}_{n-n_{s}} \end{array} \right) = \left( \begin{array}{cccc} K(n_{s},\varphi) & \mathbf{b}_{1} & {\dots} & \mathbf{b}_{n-n_{s}}\\ & \multicolumn{3}{c}{{\varsigma}^{n_{s}} K(n-n_{s},\varphi)} \end{array} \right). $$

At the s-th algorithmic step the trailing matrix is then $R_{22}^{(s)} = {\varsigma }^{n_{s}} K(n-n_{s},\varphi )$, whose columns all have the same norm equal to ${\varsigma }^{n_{s}}$. Moreover, the column c_i forms the same angle (modulo π) with all other columns c_j, for 1 ≤ i < j ≤ (n − n_s), hence no permutations are necessary. However, the matrix K(n,φ) may not be in rank-revealed form. In this case, QRDM shows poor rank-reveling properties, similarly to QRP. It is well known that rounding errors due to finite precision may cause nontrivial permutation and the QRP algorithm may reveal the rank. Following [10], in order to avoid this issue we consider instead the matrix

$$ \hat{K}(n,\varphi,\xi) = K(n,\varphi) \left( \begin{array}{cccc} (1- \xi) & & & \\ & (1- \xi)^{2} & & \\ & & {\ddots} & \\ & & & (1-\xi)^{n} \end{array} \right), $$

(43)

where 1 > ξ > 0. In other words, the j-th column of the matrix $\hat {K}(n,\varphi ,\xi )$ is the j-th column of K(n,φ) scaled by (1 − ξ)^j, for $j=1,\dots ,n$. Tables 1 and 2 show results for scaled Kahan matrices $\hat {K}(n,\varphi ,\xi )$, with size n = 128, for several values of φ. For each test case, we show the last two singular values σ_n− 1, σ_n and the last two diagonal entries k_{n− 1,n− 1}, k_n,n of the current instance of $\hat {K}(n,\varphi ,\xi )$. For both algorithms QRP and QRDM, we report the (n − 1)-th singular value $\bar {\sigma }_{n-1}$ of the R₁₁ block of order n − 1 and the absolute value of the last two diagonal entries d_n− 1, d_n of the factor R. The singular values here presented computed with the xgejsv subroutine of LAPACK. Here, we use the following setting for the hyperparameters τ = 0.15 and δ = 0.9, whose choice is motivated in the next section. When ξ is small (see Table 1), e.g., ξ = 10^− 15, both algorithms reveal the rank for some values of φ. However, when the parameter ξ is increased (see Table 2), e.g., ξ = 10^− 7, the algorithms do not perform any pivoting for any value of φ, thus resulting in poor rank revealing, according to results in [10]. This fact can be deduced by comparing the diagonal values d_n− 1,d_n of the R factor with the corresponding singular values σ_n− 1,σ_n, and the singular value $\bar {\sigma }_{n-1}$ of the computed R₁₁ block with the corresponding singular value σ_n− 1.

Table 1 Numerical tests on scaled Kahan matrices $\hat {K}(n,\varphi ,\xi )$, where n = 128 and ξ = 10^− 15

Table 2 Numerical tests on scaled Kahan matrices $\hat {K}(n,\varphi ,\xi )$, where n = 128 and ξ = 10^− 7

5.2 SJSU matrices

We now discuss results coming from two subsets of the San Jose State University Singular matrix database, that we call:

• 1. “small matrices”: it consists of the 261 matrices with m ≤ 1024, 32 < n ≤ 2048, sorted in ascending order with respect to the number of columns n;

• 2. “big matrices”: it consists of the first 247 matrices with m > 1024, n > 2048, sorted in ascending order with respect to the number of columns n.

These datasets consist of “fat” (m > n), “tall” (m < n) and square matrices, the results presented hereafter do not depend on this characteristic. For each matrix A, we denote by σ_i the i-th singular value of A computed with the xgejsv subroutine of LAPACK, and by r the numerical rank computed with the option JOBA=‘A': in this case, small singular values are comparable with roundoff noise and the matrix is treated as numerically rank deficient. Deviation maximization does not guarantee that the diagonal values of the factor R are monotonically decreasing in modulus, therefore we do not sort the diagonal entries and we denote by d_i the i-th diagonal entry with positive sign. As an example, we show in Fig. 1 the singular values σ_i and diagonal values d_i computed with both QP3 and QRDM for the instance n. 3 of the set “small matrices”. Figure 1a shows that the diagonal values d_i computed with QP3 are monotonically decreasing, while the diagonal values d_i computed with QRDM are not ordered. However, as it is highlighted in Fig. 1b, the order of magnitude of σ_i is well approximated by that of the corresponding d_i for both methods.

Fig. 1

Singular values σ_i (⋅) and diagonal values d_i computed with QP3 (×) and QRDM (+ ) for the 3rd instance of the set “small matrices”, natural (a) and logarithmic (b) scale

Let us first discuss results provided by QP3. Figure 2 compares the positive diagonal entry d_i and the correspoding singular value σ_i for each matrix in the two collections, by taking into account the maximum and minimum value of the ratios d_i/σ_i. Results show that the positive diagonal value d_i approximates the corresponding singular value σ_i up to a factor 10, for $i = 1,\dots ,r$. Moreover, Fig. 3 compares σ_i(R₁₁), that is the i-th singular value of R₁₁ = [R]_1:r,1:r computed by LAPACK’s xgejsv, with σ_i for each matrix in the two collections, by taking into account the ratios σ_i(R₁₁)/σ_i. These results confirm that QP3 provides an approximation of the singular value σ_r up to a factor 10.

Fig. 2

Ratio d_i/σ_i, minimum and maximum values for QP3 on the dataset “small matrices” (a) and “big matrices” (b)

Fig. 3

Ratio σ_i(R₁₁)/σ_i, minimum and maximum values for QP3 on the dataset “small matrices” (a) and “big matrices” (b)

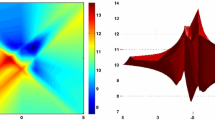
Before providing similar results for QRDM, let us discuss the sensitivity of parameters τ and δ to the rank-revealing property (16). To this aim, we set a grid ${\mathscr{G}}$ of values ${\mathscr{G}}(i,j) = (\delta _{i},\tau _{j}) = (0.05\ i,0.05\ j)$, with $i,j=0,\dots ,20$, and we consider the R factor obtained by QRDM. Figure 4a shows the order of magnitude of

$$ \min_{A} \min_{1\leq i\leq r} \frac{d_{i}}{\sigma_{i}(A)}, $$

where A ranges in the collection “small matrices”, for each grid point (δ_i,τ_j). We see that the positive diagonal elements provide an approximation up to a factor 10 of the singular values for a wide range of parameters, corresponding to the light gray region of the grid that we call stability region. In practice, any choice of 1 ≥ τ > 0 and 1 > δ ≥ 0 leads to a rank-revealing QR decomposition.

Fig. 4

Order of magnitude of the minimum $\min \limits (r_{i}/\sigma _{i})$ over all matrices (a) and cumulative execution times for QRDM (b) in function of the parameters τ and δ on the “small matrices” data set

Therefore, for an optimal parameters’ choice, we look at execution times. Figure 4b shows the cumulative execution times (in seconds) ${\sum }_{A} t_{QRDM}(A)$ where A ranges in the “small matrices” collection and where t_QRDM(A) is the execution time of QRDM, for each grid point (δ_i,τ_j) in the stability region. It is evident that best performances are obtained toward the right-bottom corner, in correspondence of the dark gray region. Hence, we set τ = 0.15 and δ = 0.9, which are the optimal values for the validation set here considered.

We can now analyze the quality of the RRQR factorization obtained by QRDM with the choice of parameters just discussed. Figure 5 shows that the positive diagonal entries approximate the singular values up to a factor 10, and Fig. 6 shows that the singular values of R₁₁ provide an approximation up to a factor 10², loosing an order of approximation with respect to QP3 in very few cases.

Fig. 5

Ratio d_i/σ_i, minimum and maximum values for QRDM on the dataset “small matrices” (a) and “big matrices” (b)

Fig. 6

Ratio σ_i(R₁₁)/σ_i, minimum and maximum values for QRDM on the dataset “small matrices” (a) and “big matrices” (b)

Let us now consider QRDM with a stopping criterion. We show the accuracy in the determination of the numerical rank, and the benefits in terms of execution times, when the matrix rank is much smaller than its number of columns. We consider the stopping criterion in (36)–(38): the numerical rank is this case is given by the number of columns processed by QRDM and we denote it by $\tilde {r}$. The matrix

$$ A_{\tilde{r}} = Q\left( \begin{array}{cc} R_{11} & R_{12} \\ 0 & 0 \end{array}\right){\varPi}^{T} $$

denotes the corresponding rank-$\tilde {r}$ approximation of A. Figure 7 shows the ratios $\sigma _{\tilde {r}+1}/\Vert A\Vert$ (in red) and $\Vert A - A_{\tilde {r}}\Vert /\Vert A\Vert$ (in blue), for all matrices in the “small matrices” (Fig. 7a) and “big matrices” (Fig. 7b) collections. Whenever the i-th matrix has full rank, i.e., it has rank $\tilde {r}$, the singular value $\sigma _{\tilde {r}+1}$ does not exist and we replaced its value with ε = 10^− 16. We also considered the stopping criterion in (36) with the choice (39), which turned out to be less accurate and for this reason we omit the results.

Fig. 7

Relative error on the computed numerical rank $\tilde {r}$ for QRDM expressed as the ratios $\sigma _{\tilde {r}+1}/\Vert A\Vert$ (+ ) and $\Vert A - A_{\tilde {r}}\Vert /\Vert A\Vert$ (⋅), on the set “small matrices” (a) and “big matrices” (b)

Finally, we compare the execution times of QR computations for the matrices of the set “big matrices”. Here, the instances have been ordered accordingly to the total number of entries nm. Figure 8 shows the speedup of QRDM (Fig. 8a) and QRDM with stopping criterion (Fig. 8b) over QP3, namely the ratio t_QP3/t_QRDM, where t_QP3 and t_QRDM are the execution times (in seconds) of QP3 and QRDM respectively. The algorithm QRDM achieves an average speedup of 2.1 ×, as a consequence of the lower amount of memory communication employed to carry out the pivoting, as detailed in Section 4.1. In a stopping criterion is adopted, the average speedup reached is 2.5 ×. It may also be interesting to consider a comparison with an implementation of QP3 with a termination criterion, but this is beyond the scope of the present work.

Fig. 8

Speedup of QRDM (a) and QRDM with stopping criterion (b) over QP3

Figure 9 compares QP3 and QRDM with the QR without pivoting, briefly called QR, implemented by the dgeqrf subroutine of LAPACK. We display the ratios t_QRDM/t_QR and t_QP3/t_QR, where t_QR is the array of execution times (in seconds) of QR. The standard QR is indeed faster, since it does not involve any column permutation, and it is in average 3 × faster than QP3 while it is only 1.3 × faster than QRDM. This result is obtained thanks to the permutation strategy described in Section 4.1.

Fig. 9

Overhead of QRDM (+ ) and QP3 (⋅) over the QR without pivoting

Last, let us discuss briefly the effect of the block size k_DM introduced to limit the cardinality of the candidate set in (10). This parameter depends on the specific architecture, mainly in terms of cache-memory size, and typical values are k_DM = 32,64,128. We observed that there is an optimal value of k_DM, in sense that it gives the smallest for a fixed experimental setting, and its computation is similar to the well-known computation practice of the BLAS block size, which is out of scope of this paper. For sake of clarity we say that in our test environment we observed the optimal value k_DM = 64, but other choices exhibit a similar behavior, e.g., k_DM = 32.

6 Conclusions

In this work we have presented a new subset selection strategy we called “Deviation Maximization”. Our method relies on correlation analysis in order to select a subset of sufficiently linearly independent vectors. Despite this strategy is not sufficient by itself to identify a maximal subset of linearly independent columns for a given numerically rank deficient matrix, it can be adopted as a column pivoting strategy. We introduced the rank-revealing QR factorization with Deviation Maximization pivoting, briefly called QRDM, and we compared it with the rank-revealing QR factorization with standard column pivoting, briefly QRP. We have provided a theoretical worst case bound on the smallest singular value for QRDM and we have shown it is similar to available results for QRP. Extensive numerical experiments confirmed that QRDM reveals the rank similarly to QRP and provides a good approximation of the singular values obtained with LAPACK’s xgejsv routine. Moreover, we have shown that QRDM has better execution times than those of QP3 implemented in LAPACK’s double precision dgeqp3 routine for a large number of test cases, thanks to the lower amount of memory communication involved. The software implementation of QRDM used in this article is available at the URL: https://github.com/mdessole/qrdm.

Our future work will focus on applying deviation maximization as pivoting strategy to other problems which require column selection, e.g., constrained optimization problems, on which the authors successfully experimented a preliminary version in the context of active set methods for NonNegative Least Squares problems, see [11, 12].