Abstract
The aim of this paper is to visually investigate the dynamics and stability of the process in which the classic derivative is replaced by the fractional Riemann–Liouville or Caputo derivatives in the standard Newton root-finding method. Additionally, instead of the standard Picard iteration, the Mann, Khan, Ishikawa and S iterations are used. This process when applied to polynomials on complex plane produces images showing basins of attractions for polynomial zeros or images representing the number of iterations required to achieve any polynomial root. The images are called polynomiographs. In this paper, we use the colouring according to the number of iterations which reveals the speed of convergence and dynamic properties of processes visualised by polynomiographs. Moreover, to investigate the stability of the methods, we use basins of attraction. To compare numerically the modified root-finding methods among them, we demonstrate their action for polynomial z3 − 1 on a complex plane.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Polynomiographs and the problem of finding their roots are interesting both for mathematicians and engineers. In the seventeenth century, Newton proposed a method for calculating polynomial’s zeros approximately. In 1879, Cayley, when solving simple equation z3 − 1 = 0 in the complex plane, discovered a strange and chaotic behaviour of the solution process that he could not explain. Investigations of the Cayley’s problem led Julia in 1919 to the discovery of the famous Julia sets. Then, Julia sets inspired, in 1970s, the great Mandelbrot’s discoveries—the Mandelbrot set and fractals [28]. The next interesting contribution to the polynomial root-finding problem was made by Kalantari [26], who introduced to science the so-called polynomiography. Following Kalantari [25, 26], polynomiography is both the art and science based on visualisation of root-finding iteration processes of polynomials in the complex plane. In order to generate polynomiographs, any root-finding method can be applied starting from the well-known Newton method, the methods from the Basic or the Euler-Schröder families of iterations or many other known modifications of the Newton method. For example, in [17], Gdawiec and Kotarski and, in [18], Gdawiec et al. presented a survey of some modifications of Kalantari’s results related to the classic Newton method, the higher-order Newton-like root-finding methods and the pseudo-methods for polynomials in the complex plane. By using different kinds of iterations instead of the standard Picard one, various convergence criteria and different colouring methods of a great variety of polynomiographs were obtained in [18]. It is also worth mentioning that in [4, 11, 12] the methods of polynomiography were used to visually analyse the behaviour of various root-finding methods, whereas in [4, 12, 15] the root-finding methods were investigated by using different numerical measures, e.g. the average number of iterations or the convergence area index.
Recently, Brambila-Paz et al. in [7, 8] proposed some modification of the classical Newton–Raphson method in \(\mathbb {R}\) for root-finding of polynomial equations. Instead of the classical derivative, the fractional ν-order Riemann–Liouville derivative was used. The modified root-finding method is able to find a root with complex part, if it exists, when starting from an initial point lying on reals. By changing the ν-order of the derivative and the starting point on reals, the new root-finding method finds all polynomial zeros. Inspired by this new idea, Gdawiec et al. in [19] carried out a qualitative analysis of the fractional Newton (FN) method with standard Picard iteration and Riemann–Liouville or Caputo derivatives. Visual analysis of the convergence of the FN method was performed for several complex polynomials basing on their polynomiographs. A more precise result concerning convergence of FN method shows that for ν = 1, the FN method converges quadratically and for ν≠ 1 it converges at least linearly for polynomials having roots of multiplicity 1 [19]. In [3], Akgül et al. introduced a damping factor in fractional Newton’s method obtaining in this way the 2ν th-order of convergence, where ν is the order of the fractional derivative. Recently, in [14], Cordero et al. studied the use of fractional derivative in a variant of Chebyshev’s method. They proved that this type of method has the 3ν th-order of convergence. The fractional derivatives were also applied to the damped Traub’s method [10]. In this case, the method has the (2ν + 1)th-order of convergence. To summarise, in Table 1, we gathered the orders of convergence of the root-finding methods with fractional derivatives and the original methods with the classical derivative that were the base for the fractional ones.
In this paper, we visually investigate the dynamics and stability of the process in which the classic derivative is replaced by the fractional Riemann–Liouville or Caputo derivatives in the standard Newton root-finding method. Additionally, instead of the standard Picard iteration, the Mann, Khan, Ishikawa and S iterations are used.
This paper is organised as follows. In Section 2, some basic information about fractional derivatives is presented and the two basic fractional derivatives (Riemann–Liouville and Caputo) are defined. In Section 3, Mann, Khan, Ishikawa and S iterations are introduced. Section 4 presents formulas for Newton’s method with fractional order derivatives. In Section 5, some modifications of the fractional Newton method obtained by using various iterations in place of the standard Picard iteration are given. In Section 6, some examples of polynomiographs and the results of numerical experiments are presented. Section 7 concludes the paper and shows the future directions.
2 Fractional derivatives
Integer-order derivatives and integrals have clear physical interpretation and are used to describe many concepts in classical physics, e.g. velocity and area. In 1695, Leibnitz in his letter to L’Hospital mentioned about fractional derivatives at first. The concept of fractional derivatives was investigated by mathematicians Liouville, Riemann and Caputo who have done major work in fractional calculus. The first practical application of \(\frac {1}{2}\)-order derivative can be found in tautochrone problem [1], in which the aim was to determine the shape of the curve such that the time of descent of a frictionless point mass sliding along the curve under gravity force is independent of the starting point.
Fractional calculus in the last 30 years became a popular mathematical tool for applied sciences used e.g. in modelling processes with memory and hereditary effects [36]. Fractional-order models can describe reality more accurately in comparison with the classical integer-order models [36]. Many applications in physics, chemistry, biology, economics, signal and image processing and aerodynamics are described in a survey paper [35] and references therein. Fractional calculus and its applications are presented in many books and papers [21, 22, 31, 34].
Integer-order derivative and integral are uniquely determined in the classical analysis. The same is for fractional integral. But the situation for fractional-order derivatives is more complicated. There are many different definitions of them. We will use the two most known ones: Riemann–Liouville and Caputo derivatives. We recall their definitions and basic properties following the works [24, 34].
We need the special Gamma Function Γ that is a generalisation of the factorial function n!, i.e. Γ(n) = (n − 1)! for \(n \in \mathbb {N}\). For the complex arguments \(z \in \mathbb {C}\) such that Re(z) > 0 the Γ function is defined as:
By analytical continuation, the function can be extended to the whole complex plane except the points 0,− 1,− 2,− 3,…, where it has single poles. Some of the most important properties of Γ are the following:
-
Γ(1) = Γ(2) = 1,
-
Γ(z + 1) = zΓ(z),
-
Γ(n) = (n − 1)! for \(n \in \mathbb {N}\),
-
\({\varGamma }(1 / 2) = \sqrt {\pi }\).
The Riemann–Liouville derivative (RL derivative) of order ν ∈ (n − 1,n], \(n \in \mathbb {N}\) of a real-valued function f is defined as:
The Riemann–Liouville fractional derivative operation is linear and has the interpolation property, that means that:
and for a constant function f(t) = c = const and ν≠ 1 it is not 0 and equals:
For the power functions, their Riemann–Liouville ν–fractional-order derivatives are defined as follows:
where ν ∈ (n − 1,n), \(n \in \mathbb {N}\) and \(m \in \mathbb {R}\) is such that m > n − 1.
The Caputo derivative (C-derivative) of order ν ∈ (n − 1,n], \(n \in \mathbb {N}\) of a real-valued function f is defined as:
The Caputo fractional derivative operation is linear and has the interpolation property, that means that:
and for a constant function it is equal to 0. For the power functions, their Caputo ν–fractional-order derivatives are defined as follows:
where ν ∈ (n − 1,n), \(n \in \mathbb {N}\) and \(m \in \mathbb {R}\).
Let us see some examples of the C-derivative for various values of m in tm:
From (6) and (10), we see that \(D^{\nu }_{C} t^{m} = {D}_{RL}^{\nu } t^{m}\) if m > n − 1. In general, fractional RL- and C-derivatives do not coincide, i.e. \({D}_{RL}^{\nu } f(t) \ne D^{\nu }_{C} f(t)\). They are equal to each other if the function f is such that f(s)(0) = 0, for all s ∈{0,1,2,…,n − 1}.
Up to now in this section, we discussed fractional derivatives of functions defined on \(\mathbb {R}\). But further we need such functions defined on \(\mathbb {C}\). Because analysis in \(\mathbb {C}\) is more complicated than in \(\mathbb {R}\), we cannot replace the real variable x by a complex variable z directly under integrals in (2) and (7). The difficulty is related to multi-valuedness of expressions that are under integrals in RL- and C-fractional derivatives. Fortunately, following [30, 32, 34], it is known that for analytic functions (e.g. polynomials, exponentials) fractional RL- and C-derivatives can be generalised in a natural way to the complex plane. So then, we can define RL-derivative of ν-order for a monomial as:
where \(z \in \mathbb {C} \setminus \{ c \in \mathbb {C} : Im(c) = 0 \wedge Re(c) < 0 \}\), m≠ − 1,− 2,− 3,… and ν ∈ (n − 1,n) for some \(n \in \mathbb {N}\).
It is easily seen that:
where c = const and ν ∈ (n − 1,n) for some \(n \in \mathbb {N}\). To obtain \(D_{RL}^{\nu }p(z)\) for any complex polynomial p, one needs to apply formula (11), term by term.
Further, to define C-derivative of ν-order we need the additional postulate:
where c = const. It is easy to see that \(D_{C}^{\nu }p(z) = D_{RL}^{\nu }p(z)\) if and only if p has the constant term equal to zero. Formula (11) is well defined because the branch cuts procedure removed multi-valuedness in it. Here, it is worth to add that the branch cuts procedure has been implemented in many Computer Algebra Systems (CAS) (Maple, Matlab) and programming languages (Python, Java).
3 Iterations
The problem of finding a fixed point of a given mapping is well known and there exist many theorems and methods that allow one to find such points. In fixed-point theory, one of the popular techniques is an iterative approximation of the fixed points. In this technique, we use various kinds of iteration processes. Let us recall some of them, i.e. the ones that will be used in this paper.
Let \(w: X \rightarrow X\) be a mapping on a metric space (X,d), where d is a metric. Furthermore, let u0 ∈ X be a starting point.
-
The Picard iteration (introduced in 1890) [33]:
$$ u_{k+1} = w(u_{k}), \quad k = 0, 1, 2, \ldots, $$(14) -
The Mann iteration (defined in 1953) [29]:
$$ u_{k+1} = \alpha_{k} w(u_{k}) + (1 - \alpha_{k}) u_{k}, \quad k = 0, 1, 2, \ldots, $$(15)where αk ∈ (0,1].
-
The Khan iteration (defined in 2013) [27]:
$$ \begin{array}{ll} u_{k+1} &= w(v_{k}),\\ v_{k}& = \alpha_{k} w(u_{k}) + (1 - \alpha_{k}) u_{k}, \quad k = 0, 1, 2, \ldots, \end{array} $$(16)where αk ∈ (0,1].
-
The Ishikawa iteration (introduced in 1974) [23]:
$$ \begin{array}{ll} u_{k+1} &= \alpha_{k} w(v_{k}) + (1 - \alpha_{k}) u_{k},\\ v_{k} &= \beta_{k} w(u_{k}) + (1 - \beta_{k}) u_{k}, \quad k=0, 1, 2, \ldots, \end{array} $$(17)where αk ∈ (0,1] and βk ∈ [0,1].
-
The S iteration (defined in 2007) [2]:
$$ \begin{array}{ll} u_{k+1} &= \alpha_{k} w(v_{k}) + (1 - \alpha_{k}) w(u_{k}),\\ v_{k} &= \beta_{k} w(u_{k}) + (1 - \beta_{k}) u_{k}, \quad k=0, 1, 2, \ldots, \end{array} $$(18)where αk ∈ (0,1] and βk ∈ [0,1].
The presented iterations for particular values of the parameters (α for the one-parameter iterations, and α, β for the two-parameter iterations) can be reduced to other iterations, i.e.:
-
The Mann iteration for αn = 0 is the Picard iteration,
-
The Ishikawa iteration for βn = 0 is the Mann iteration, and for βn = 0 and αn = 1 is the Picard iteration,
-
The S iteration for αn = 1 and βn≠ 0 is the Khan iteration, and for αn = 1 and βn = 0 is the Picard iteration.
Only the Khan iteration does not reduce to any other iteration considered in this paper.
The considered iterations have one and two parameters. In the literature, there exist also iterations with more than two parameters. Some reviews of 18 iteration processes and their dependencies can be found in [17].
Our further considerations will be conducted in the space \(X = \mathbb {C}\) with a standard modulus metric. We take \(u_{0} \in \mathbb {C}\) and αk = α, βk = β, such that α ∈ (0,1] and β ∈ [0,1].
4 Newton’s method with fractional derivatives
Let us denote any polynomial by p. The Newton iteration is defined as:
with a starting point z0. This iteration is used to solve the equation p(z) = 0 both in real and complex domains.
By replacing the classical first derivative \(p^{\prime }(z)\) in (19) by the RL- or C-derivative of fractional order ν, both denoted as Dνp(z), we get:
with a starting point z0. Such defined methods are called fractional Newton methods. Some visual and numerical studies related to these methods were presented in [19].
After introducing the ν-fractional Newton operator:
formula (20) takes the following simple form:
with a starting point z0. It is easily seen that in formula (22) the standard Picard iteration (14) is used.
5 Fractional Newton method with different iterations
To find a root of the equation p(z) = 0 one can transform this problem to a problem of finding a fixed point of some operator T [9]. Then, the fixed point of T will be the root of p. In the case of fractional Newton’s method, the operator T is simply the Nν operator defined in (21).
As we mentioned in Section 3, in fixed-point theory, we use various iteration processes to find the fixed points. Therefore, let us replace the standard Picard iteration in formula (22) by one of the iterations introduced in Section 3, i.e. Mann (15), Khan (16), Ishikawa (17) and S (18) iterations. Then, we get the following modified ν-fractional Newton processes:
-
Fractional Newton’s method with the Mann iteration:
$$ z_{k+1} = (1 - \alpha) z_{k} + \alpha N_{\nu}(z_{k}), \quad k = 0, 1, 2, \ldots, $$(23)where α ∈ (0,1].
-
Fractional Newton’s method with the Khan iteration:
$$ \left\{\begin{array}{ll} z_{k+1} = N_{\nu}(v_{k}), \\ v_{k} = (1 - \alpha) z_{k} + \alpha N_{\nu}(z_{k}), \quad k = 0, 1, 2, \ldots, \end{array}\right. $$(24)where α ∈ (0,1].
-
Fractional Newton’s method with the Ishikawa iteration:
$$ \left\{\begin{array}{ll} z_{k+1} = (1 - \alpha) z_{k} + \alpha N_{\nu}(v_{k}), \\ v_{k} = (1 - \beta) z_{k} + \beta N_{\nu}(z_{k}), \quad k = 0, 1, 2, \ldots, \end{array}\right. $$(25)where α ∈ (0,1] and β ∈ [0,1].
-
Fractional Newton’s method with the S iteration:
$$ \left\{\begin{array}{ll} z_{k+1} = (1 - \alpha) N_{\nu}(z_{k}) + \alpha N_{\nu}(v_{k}), \\ v_{k} = (1 - \beta) z_{k} + \beta N_{\nu}(z_{k}), \quad k = 0, 1, 2, \ldots, \end{array}\right. $$(26)where α ∈ (0,1] and β ∈ [0,1].
We are interested in the convergence of sequence \(\{z_{k}\}_{k=0}^{\infty }\) (or orbit of the point z0) to a root of p. If the sequence converges to a root z∗ then we say that z0 is attracted to z∗. The set of all starting points z0 for which \(\{z_{k}\}_{k=0}^{\infty }\) converges to z∗ is called the basin of attraction of z∗.
6 Numerical and graphical results
In this section, the numerical and graphical results are presented. They were performed for all the fractional methods introduced in Section 5.
The graphical examples were obtained by applying the methods of polynomiography. The algorithm for generation of a polynomiograph is presented in Algorithm 1.

In this algorithm, any kind of iteration iν can be used, for instance Mann (23), Khan (24), Ishikawa (25) and S (26). Moreover, the convergenceTest (zk+ 1,zk,ε,p) returns TRUE if the method has converged to the root, and FALSE otherwise. The two most widely used convergence tests are the following:
Finally, in the last step of the algorithm, the point is coloured according to the selected colouring method. There are two standard methods of colouring, namely iteration colouring and basins of attraction. In the first method, the starting point is coloured by linearly mapping the number of performed iterations on the colour in the colour map. In the basins of attraction colouring, each root has a distinct colour (other than black). Then, if the method has converged to some root (the number of performed iterations is less than M), then for the last point zk+ 1 we search for the closest root and colour z0 accordingly to the colour of the root. If the method has not converged (the number of performed iterations is equal to M), then z0 gets the black colour.
In the subsequent sections, the detailed results of polynomiograph generation and the corresponding numerical measures for the different iterations with different derivatives are presented.
6.1 Stability
The root-finding methods are usually investigated not only with respect to their convergence but also with respect to their stability. We say that a method is stable when, independently on the small perturbations of the starting point, this method finds the same root. For the methods with parameters, their stability can be investigated under fixed or variable parameters. In the second case, stability is dependent not only on perturbations of the starting point but also on the parameters of the method.
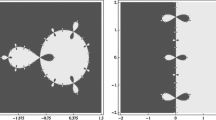
To study the stability of fractional Newton method, Akgül et al. in [3] used a visual method that is based on Cayley’s quadratic test [6]. The Cayley test relies on the interpretation of the polynomiographs showing basins of attraction for z2 − 1 depending on ν-order. The reference polynomiograph for the classical Newton method shows two basins separated by imaginary axis on the complex plane (see Fig. 1—the basin of attraction for − 1 is coloured with the green colour, whereas for 1 with the red colour). This case is considered as the most stable. Any other root-finding methods are visually compared with it.
In our study on the stability, we used the same visual method as in [3]. To generate the needed basins of attraction, we used the following parameters: p(z) = z2 − 1, area A = [− 2,2] × [− 2,2], resolution of images 600 × 600 pixels, M = 40, ε = 0.001, and the convergence test in (27). The colours for the basins of attraction are the same as the ones used in Fig. 1. Moreover, the black colour is used to mark the points that do not converge to any root in the given number of iterations, i.e. M = 40.
In Figs. 2 and 3, the examples of basins of attraction for the Newton method with the Picard iteration and the RL- and C-derivatives are presented, respectively. A detailed discussion on this case can be found in [19]. These basins of attraction will serve, among others, as a reference for the basins generated for the iterations considered in this paper.
6.1.1 Mann iteration
We start our discussion about stability with Mann iteration. In Fig. 4, one can see the sample basins of attraction for this iteration with classical derivative with different values of parameter α. As one can see, there is nearly no convergence for α = 0.1. For α = 0.2, we can observe the nearly perfect stability except corners and the points lying on the imaginary axis where there is no convergence. For α > 0.2, we obtain the most stable case.
In Figs. 5 and 6, the basins of attraction for the considered iteration with RL- and C-derivatives, respectively, for different values of order ν are presented. We presented these results for α = 0.5 since this kind of results is the common one in the case of Mann iteration (as discussed above). From these images, one can observe the following. The decrease of the value of order ν degrades the stability of this method. The vertical border becomes more rough and wraps up to the right tending to total non-convergence for one of the roots (namely − 1, represented by green colour). On the other hand, the increase of the value of ν just rather changes the shape of the border which is sharp and wraps up to the left tending to the total convergence for one of the roots, namely 1. Additionally, in the very most cases, the change of ν causes that any initial point which goes in the reference method (for ν = 1) to the red basin goes for different values of ν to the same basin or nowhere and the initial point which goes in the reference method to the green basin goes for different values of ν everywhere (green basin, red basin, nowhere).
6.1.2 Khan iteration
Similarly, as in the previous section, we present in Fig. 7 the basins of attraction for Khan iteration with classical derivative. In this case for all values of parameter α, we obtain the most stable case, shown in this image.
In order to discuss the stability of Khan iteration in Figs. 8 and 9, the basins of attraction for the considered iteration with RL- and C-derivatives, respectively, for different values of order ν are presented. In this case, α = 0.5 was fixed as the one giving the most representative images. In images in Figs. 8 and 9, one can see that for ν ≤ 0.4 and ν ≥ 1.6, only red and black colours are visible which means that fractional processes with Khan iteration both for RL- and C-derivatives lose the convergence to one of the roots and the basins are far away from the ones presented in Fig. 7. Moreover, we see that for the C-derivative case for ν = 1.6, the method finds only one of the roots for all the points in the considered area. The processes considered here are more and more stable for ν-order increasing from 0.8 to 1.0 when the stability is the best one. Further increase of ν-order up to 1.3 worsens the stability in comparison with the most stable case (Fig. 7).
6.1.3 Ishikawa iteration
In Fig. 10, one can see the sample basins of attraction for Ishikawa iteration with classical derivative with different values of parameters α and β. As one can see, there is nearly no convergence for α = 0.1 and β = 0.8, similarly as in the case of Mann iteration. In fact, this is true for α = 0.1 and all values of β. For α = 0.2 and β = 0.3, we can observe the nearly perfect stability except the small points lying on the imaginary axis where there is no convergence. This holds for α = 0.2 and all values of β. For α > 0.2 and all values of β, we obtain the most stable cases.
In Figs. 11 and 12, the basins of attraction for Ishikawa iteration for different values of order ν are presented. Differently, so far, we have shown not the typical basins (as they are for α > 0.2 and all values of β) but the more rare case for α = 0.2 and β = 0.3. The reason is twofold. Firstly, the typical case is very similar to Picard and Khan cases, so we avoid repeating the discussion. Secondly, it seems to be interesting to see something different than that so far. So, by analysing these images, one can see that both decreasing and increasing the value of ν lead to vanishing of convergence for all roots, but this is done faster for − 1 (green colour). Additionally, for the values of ν slightly below 1, the stability becomes to be worse along the border, especially in the RL-derivative case.
6.1.4 S iteration
In Fig. 13, the basins of attraction for S iteration with classical derivative are presented as the reference. They are shown for α = 0.5 and β = 0.5, but this stable case holds for all values of these parameters.
In Figs. 14 and 15, the basins of attraction for S iteration with RL- and C-derivatives, respectively, for different values of order ν are presented. They are shown for α = 0.5 and β = 0.2. This case was chosen as the most different from the previous ones, to avoid repetition and show the different character of this method. When we look at the RL-derivative case, we see that the perfect stability is lost for all values of ν. The further away we move from the classical case (ν = 1), the less the basins remind the basins presented in Fig. 1. For values ν < 1, the border between the basins bends in the right direction and we lose convergence to the root marked by green colour, i.e. − 1, whereas for values ν > 1 the basin for − 1 shrinks and forms a star-like shape and again we lose convergence to the − 1 root. If we compare the basins for the RL-derivative (Fig. 14) and the C-derivative (Fig. 15), we see that the stability is very similar, but the C-derivative is more stable. Moreover, we see that very interesting flower-like patterns emerged. Now, if we look at the Picard iteration case (Figs. 2 and 3) and compare it with S iteration, we can observe that the overall behaviour for both iterations is similar. Only the shapes of basins’ boundaries are different, which shows that the use of other iteration has impact on the stability of the method.
6.2 Dynamics
To visually present the dynamics of the proposed methods, we use polynomiographs coloured with the use of the iteration colouring. All the experiments were conducted for p(z) = z3 − 1. This polynomial has the following roots: \(\left \{ -\frac {1}{2} - \frac {\sqrt {3}}{2}i, -\frac {1}{2} + \frac {\sqrt {3}}{2}i, 1\right \}\).
To generate the polynomiographs, the following parameters were used: area A = [− 2,2] × [− 2,2], resolution of images 600 × 600 pixels, M = 40, ε = 0.001 and the convergence test in (27). The colour map used in the experiments is presented in Fig. 16. The blue colour means a small number of iterations (fast convergence), whereas the red one means the large number of iterations (low convergence).
6.2.1 Mann iteration
We start the examples with showing some polynomiographs generated by the Mann iteration and the classical derivative. These polynomiographs will serve as a reference for the ones obtained with the fractional derivatives. Figure 17 presents polynomiographs obtained for the following values of parameter α in Mann iteration: (a) 0.30, (b) 0.50, (c) 0.60, (d) 0.70 and (e) 0.90. From the images, we see that parameter α has a great impact on the shape of the polynomiographs and the convergence of Newton’s method. The more detailed discussion on this fact for the classical derivative can be found in [18].
In the first example with the fractional derivatives used in Newton’s method, we will see how for a fixed order of the derivative the shape of polynomiographs changes with the change of α in Mann iteration. In Figs. 18 and 19, the polynomiographs for ν = 0.80 in the RL- and C-derivative are presented, respectively. In both figures, the same values of parameter α were used, namely (a) 0.30, (b) 0.50, (c) 0.70 and (d) 0.90. By looking at the images from Fig. 18, we see that, like for the images obtained with the classical derivative (Fig. 17), the value of α has a great impact on polynomiograph’s shape. The larger the value of α, the more noticeable change occurs, especially in the braids. They have a very complicated structure, but for low values of α, the braids are losing their complexity and become almost uniform (see Fig. 18a). The colours in the polynomiographs also change. We see that the smaller the value of α, the more points have red colour, which means that the points do not converge to any of the roots (the maximum number of iterations has been performed). By comparing the polynomiographs for the RL-derivative with those obtained for the classical derivative, we see that the most noticeable changes are visible at the braids. For the classical derivative, the braids are rather small, whereas for the RL-derivative we see many branches and the braid that is located near the negative real axis is spreading towards two directions, i.e. in the direction of the positive and negative infinity on the imaginary axis. In the C-derivative case (Fig. 19), the overall behaviour of the Newton method is very similar to the one that was observed for the RL-derivative case, i.e. the shape of the polynomiographs changes with the change of α parameter and the smaller the value of α the more points lose their convergence. The biggest visible differences are in the braids. In the C-derivative case, the braids have a simpler structure. We also see many small red areas in the braids. Moreover, by looking at the colours in the polynomiographs, we see that in the C-derivative case, the convergence is faster than that in the RL-derivative case; this is especially visible for α = 0.30.
In the second example, we fix the value of parameter α in Mann iteration and change the order values of the fractional derivatives. The value of α was fixed to 0.60 and the values of ν were the following: (a) 0.50, (b) 0.76, (c) 1.24, (d) 1.50. The obtained polynomiographs for the RL-derivative are presented in Fig. 20, whereas for the C-derivative in Fig. 21. By comparing the polynomiographs for the RL-derivative with the one obtained for the classical derivative (Fig. 17c), we see that the order of the derivative has a great impact on the polynomiographs. The obtained shapes are very different from the shape visible in the classical derivative case. When we take the values of ν less than 1 (classical derivative case), the braids become bigger and they are bending in the right direction (Fig. 20b), and then they disappear and most of the polynomiograph’s area becomes uniform (Fig. 20a). Moreover, we see that the red colour becomes more dominant in the polynomiograph with the decrease of ν, which means that more points do not converge to any root. If we change the value of ν above 1, the shape of polynomiographs changes in some other way. At the beginning (Fig. 20c), one of the braids disappear, namely the one located at the negative real axis. The other two braids are smaller and they are bending in the left direction. Then, the area on the left from the braids becomes almost red (Fig. 20d); there are only some small areas with other colours. From all the polynomiographs presented in Fig. 20, we see that for ν > 1 we obtain a faster speed of convergence than in the case ν < 1. Now, when we look at the case of the C-derivative (Fig. 21), we see a very similar behaviour to the one for the case of the RL-derivative. The most visible difference is that for the C-derivative, we have fewer points with red colour, and the points with a colour distinct from red have colour located more to the left in the colour map than the corresponding points for the RL-derivative. All these means that for the C-derivative we obtain faster speed of convergence.
The two presented examples were obtained for particular values of α and ν parameters, but the overall observed behaviour is very similar for the other values of these two parameters. The only difference is in the threshold values, i.e. some of the values are smaller and others are larger.
6.2.2 Khan iteration
The images in this section present several polynomiographs depending on ν-order and parameter α obtained via RL- and C-Newton method with the Khan iteration process. For ν-order smaller than 0.50 and arbitrary α ∈ [0,1], mostly uniform brown colour polynomiographs are generated. They are not presented here, as they are not interesting. The reference set of polynomiographs obtained via Khan iteration for the case of ν = 1 and parameter α taking the following values: 0.30, 0.50, 0.70 and 0.90 is shown in Fig. 22. All the images in Fig. 22 are mostly blue in colour which means that the convergence to the three well-visible zeros of z3 − 1 is very high. With increasing α, we can observe three enlarging dark blue areas surrounding zeros and three symmetric narrow bright blue subtle braids consisting of small loops. In general, these images differ slightly only in shapes, whereas in colours rather not.
Figures 23 and 24 show changes in polynomiographs generated in the case of Khan iteration with the RL- and C-derivatives for fixed ν = 0.70 and parameter α with the following values: 0.30, 0.50, 0.70 and 0.90. In all these images, except of the polynomiograph in Fig. 23d, three yellowish very wide fuzzy braids covered by dark blue and bright blue spots for the RL-derivative case are visible and more subtle, regular, aesthetic blueish braids with small brown areas on them are seen for the C-derivative case. Wide braids determine areas of chaos and instability of visualised iteration process. The polynomiograph in Fig. 23d differs dramatically. In the left part of the image dominates brown colour and two intriguing yellowish shapes appeared, whereas in the right the blue area is seen. Summing up, in the general case, the C-derivative has faster convergence than the RL-derivative. It is easily seen that the images from Figs. 23 and 24 are completely different compared with those in the reference set (Fig. 22).
Next, Figs. 25 and 26 demonstrate how the polynomiographs for Khan iteration process with fixed α = 0.60 are modified by changing the ν-order taking the following values: 0.50, 0.76, 1.24 and 1.50 in the case of the RL- and C-derivatives. With the increase of the v-order in the RL-derivative case, we observe the following sequence of polynomiographs: brown colour-dominated image (Fig. 25a), three fuzzy wide blue braids (Fig. 25b), two narrow bright blue braids and one short one (Fig. 25c) and yellow shape with well-visible two adjoint complex zeros in blue in the left side, and the right blue part covering the real zero (see Fig. 25d). Changes in polynomiographs for the C-derivative case are more distinct: in the left red/blue pattern appears (Fig. 26a), three subtle braids are visible (Fig. 26b), one of the three braids in the left side almost disappeared (see Fig. 26c) and the image (Fig. 26d) is similar to Fig. 25d. Figures 25 and 26 for specific parameters ν and α deliver new kinds of polynomiographs.
The polynomiographs shown in this section present typical shapes and colours that can be found by changing ν and α parameters in Newton’s method with Khan iteration for the RL- and C-derivative cases.
6.2.3 Ishikawa iteration
A quite different situation than that for Mann and Khan iterations is for Ishikawa iteration since we deal with one more parameter. Due to this fact, the presentation of the results is more complicated. Anyway, in Fig. 27, presented there are the polynomiographs for Ishikawa iteration with classical derivative for a fixed parameter α and varying parameter β. Similarly, in Fig. 28, there is presented the opposite situation (with fixed β and varying α). As one can see, the dynamics of convergence are quite different depending whether we change the value of parameter α or β. In this case by changing β values for α = 0.40, we can see that the braids are quite similar and the dark blue blobs slightly change their shapes for different values of β. But the change of α for β = 0.40 leads to more dramatic change of convergence. In more detail, the larger the value of α the faster the convergence (more dark blue colour) for the whole polynomiograph.
Since we are interested in fractional derivatives in this paper, in Figs. 29 and 30 there are polynomiographs presented for Ishikawa iteration with the RL-derivative for ν = 0.70, and fixed and varying parameters α and β appropriately. Let us recall that in the case of the classical derivative the change of the value of β parameter has low impact on the polynomiograph’s convergence. But in the case of the RL-derivative, we can observe that impact is larger. Indeed, the larger the value of β the faster the convergence. However, the change of the value of α causes that the convergence is more faster for larger α.
Similarly, in Figs. 31 and 32, there are some polynomiographs presented for Ishikawa iteration with the C-derivative for ν = 0.70, and fixed and varying parameters α and β accordingly. In comparison with the RL-derivative, one can see that the overall shapes of the polynomiographs are quite similar but the speed of convergence for the C-derivative is different. Indeed, the less amount of dark red colour means that the latter method converges faster.
In Figs. 33 and 34, there are polynomiographs presented for Ishikawa iteration with the RL- and C-derivatives, respectively, for fixed α = 0.18 and β = 0.8 and for varying order ν. Unlike as in the previous examples, the convergence of these polynomiographs is low. The dark red colour defines the areas of points which are non-convergent. However, the overall tendency can be observed from these images as well. Namely, the change of the value of order ν has a great impact on the polynomiograph’s shape. For the classical derivative, the braids are symmetrical, whereas for ν < 1 the braids turn to the right and the quite new area arises on the left. A different situation is for ν > 1. In such a case, one of the braids is getting shorter and the other two turn on the left. And once more, we can observe that the C-derivative produces polynomiographs in which the converge is faster than that for the RL-derivative.
6.2.4 S iteration
Similarly, as in the Ishikawa case, in S iteration we deal with two parameters (α and β). So, the presentation will be performed in a similar way as in the previous section. In Figs. 35 and 36, there are polynomiographs obtained for the classical derivative with fixed and varying parameters α and β. In both situations, we can observe that enlarging the values of α or β causes the change of polynomiographs’ shapes in the same degree. Indeed, α and β lead to the same changes of images in the same way. The presence of much blue colour means that the points converge fast.
In Figs. 37 and 38, there are the same sets of images as above but this time for the RL-derivative with order ν = 1.30. From these images, we can observe that parameters α and β influence the change of polynomiographs’ shapes in the same manner. Namely, by enlarging either α or β, more dark blue colour appears in the same way.
For comparison purposes, in Figs. 39 and 40, the polynomiographs for the C-derivative with changing α or β parameters are presented. Relative to the RL-derivative, these polynomiographs are a little bit lower convergent (more light blue colour appears). Additionally, we can observe that the boundary between the regions is more ragged.
In Figs. 41 and 42 are presented images for fixed α = 0.20 and β = 0.20 and varying order ν for the RL- and C-derivative, respectively. As one can see the closer the value of ν to 1 the more similar the polynomiograph is to the one with the classical derivative. For ν < 1, the gravity of the the image goes to the right and the braids turn to the right as well. The left side becomes non-convergent. For ν > 1, we observe the vanishing of the left braid and something like the collapse of the two right braids which are going to the left. In the case of the C-derivative, the overall convergence is faster for ν = 0.70 (more yellow colour). And, in general, the braids are in lighter blue which means that they converge slower.
6.3 Numerical results
To numerically compare the methods, we performed a series of experiments for the same parameters as in the case of the dynamics. Therefore, the polynomiographs were generated for p(z) = z3 − 1 and the following parameters: area A = [− 2,2] × [− 2,2], resolution of images 600 × 600 pixels, M = 40, ε = 0.001 and the convergence test in (27). All the experiments were performed on the computer with the Intel Core i5-2520M processor, 4 GB RAM, Windows 10 (64-bit). The software for polynomiograph’s generation has been implemented in Processing, a programming language based on Java.
In the experiments, three different measures were used to compare the use of RL- and C- derivatives. These measures are as follows: ANI (the average number of iterations) [4], CAI (the convergence area index) [5] and generation time [15]. All these measures are computed from the polynomiographs.
The ANI is computed from the polynomiograph in the way that each point in this polynomiograph corresponds to the number of iterations needed to find a root. In the case in which the root-finding method has not converged to any root, the value is fixed as the maximal number of iterations. The ANI measure is computed as the mean number of iterations in the given polynomiograph.
The CAI is computed from the polynomiograph obtained by using the iteration colouring. By using the polynomiograph, the number of converging points Nc is counted, i.e. the points whose value in the polynomiograph is less than the maximum number of iterations. Then, Nc is divided by the total number of points N in the polynomiograph, i.e.:
The value of CAI is between 0 and 1 and tells us how much of the polynomiograph’s area has converged to roots. The higher the value, the larger the area converged (0, no point has converged; 1, all points have converged).
Generation time is the time it takes to generate the polynomiograph. This time gives us information about the real time of computations, as distinct from the ANI, where we obtain information about the number of iterations without taking into account the cost of computations in a single iteration.
6.3.1 Mann iteration
The numerical results obtained for Mann iteration with fractional derivatives are presented in Figs. 43, 44, and 45. In Fig. 43, we see the results for ANI. From the plots, we see that for both fractional derivatives the dependency of ANI on the derivative order and parameter α in Mann iteration is very similar and it is a non-linear dependency. The best values of ANI, i.e. the lowest values, are visible for high values of α and near ν = 1 which corresponds to the classical derivative. The minimal value for the RL-derivative equal to 4.918 is attained at ν = 1.02 and α = 1.0, whereas for the C-derivative the minimal value equal to 5.056 is attained at ν = 1.0 and α = 1.0, i.e. for the classical derivative and Picard iteration. If we omit the classical derivative and take into consideration only fractional orders for the C-derivative, then the minimal value is attained at ν = 1.02 and α = 1.0 and it is equal to 5.093. So, the difference in value is 0.037 in favour of the classical derivative. We can also observe that the minimal value for the RL-derivative is smaller than the best results for the classical derivative. Moreover, by looking at the two plots, we see that in general the values of ANI for the C-derivative are lower than in the case of RL-derivative.
The numerical results for CAI in the parameters’ space are presented in Fig. 44. At first sight, we see that both plots look very similar to the plots for ANI. The highest values of CAI, i.e. 1.0, are obtained for points located in the neighbourhood of ν = 1, but the neighbourhood is much bigger than in the case of ANI. This means that for the fractional derivatives, we are able to obtain convergence of all points in the considered area. For instance, the maximal values are attained at ν = 0.84 and α = 0.72 for the RL-derivative, and at ν = 0.96 and α = 0.9 for the C-derivative. From the plots, we also see that the use of fractional derivatives and Mann iteration can cause that the root-finding method is not convergent to any root, i.e. the value of CAI is equal to 0.0. In the case of both fractional derivatives, we see many such points, e.g. for ν = 0.2 and α = 0.04 for the RL-derivative, and for ν = 0.02 and α = 0.02 for the C-derivative. In general, the lowest values of CAI are attained at the low values of α parameter in the Mann iteration and at the low values of the fractional order in both fractional derivatives. Moreover, similar to the ANI case, we can observe that the C-derivative obtains better CAI values than the RL-derivative.
Figure 45 presents the results for the last numerical measure, namely the polynomiograph’s generation time (in seconds). In the case of this measure, the colours are not assigned in the same way for both derivatives because the range of obtained values was different. For the RL-derivative, the range was [0.741,16.990], whereas for the C-derivative [0.741,10.501]. Thus, we see that the worst generation time for the C-derivative (attained at ν = 0.04 and α = 0.24) is smaller than the worst time for the RL-derivative (attained at ν = 1.12 and α = 0.2). In both plots, the best time (0.741 s) was obtained for ν = 1 and α = 0.98 which corresponds to the classical derivative with Mann iteration. The shortest times for the fractional derivatives equal to 1.797 s (RL-derivative) and 1.164 s (C-derivative) were attained at ν = 1.02 and α = 1.0. Moreover, we can observe that the overall shape of both plots is very similar to the plots obtained for ANI (Fig. 43), but with the one difference, namely we see a discontinuity at ν = 1 which is not present in the plots for ANI. This discontinuity is a consequence of the fact that the computational cost for classical derivative is lower than that for the fractional derivatives considered in this paper.
6.3.2 Khan iteration
Information regarding the ANI, CAI and time for Newton’s method with Khan iteration for the RL- and C-derivative are presented in Figs. 46, 47, and 48, respectively. In Fig. 46, colour-coded ANI values versus (α,ν) parameters are presented. From this plot, it is easily seen that in the RL- and C-derivative cases, distribution of brown and blue colours is similar. It means that, in general, low values of ANI occur for ν ∈ (0.70,2.0) excluding a small strip covering ν = 1.50. The minimal ANI values are the following: ANI = 2.232 attained at ν = 1.02, α = 1.0 for the RL-derivative case and ANI = 2.281 attained at ν = 1.0, α = 1.0 for the C-derivative case. In Fig. 47, showing colour-coded CAI values versus (α,ν) parameters for the RL- and C-derivative cases, the distribution of brown and blue colours is similar. It means that, in general, high values of CAI occur for ν ∈ (0.70,2.0), whereas low values of CAI occur for ν ∈ (0.0,0.60). Brown colour means the convergence of more points, whereas blue means that a low number of points has converged. Generation times (in seconds) for the RL- and C-derivative case are presented in Fig. 48. It should be pointed out that the colour maps are spanned on different lengths of time interval: shorter [1.123,13.907] for the C-derivative and longer [1.733,24.156] for the RL-derivative. Time boundaries for the shorter interval were obtained for ν = 1.02, α = 0.96 and ν = 0.2,α = 0.22, respectively, whereas, for the longer one for ν = 1.02,α = 1.0 and ν = 0.02,α = 0.82, respectively. From Fig. 48, it is easily seen that, in general, the generation time is shorter for the C-derivative compared with the RL-derivative. The next striking fact is that the distribution of brown and blue colours for the ANI plots (Fig. 46) and the generation time plots (Fig. 48) are very similar. In Fig. 48, it is clearly seen a dark blue line for ν = 1. This means that the generation time is the shortest for the classical Newton method with Khan iteration. Moreover, generation time remains relatively short for ν ∈ (0.70,2.0) excluding a small strip covering ν = 1.50.
6.3.3 Ishikawa iteration
In order to observe the tendencies in the parameter’s space, we show the plots of ANI, CAI and time generation, as in the previous sections. However, since we deal with three varying parameters, we present a sequence of plots for a fixed space of parameters, unlike in the previous sections.
In Fig. 49, there are the sequences of plots of the average number of iterations for the RL- (the left column) and C-derivatives (the right column), respectively. Taking into account the influence of parameters α and β, one can see that, as follows from the above presented examples, parameter α has very low impact on the change of convergence speed, especially for the values of ν close to 1. With the increase or decrease of ν, the impact becomes greater (especially for lower values of ν). On the other hand, the impact of parameter β is substantial, but mainly in the range [0.14,0.4] (depending on ν value). For the small values of ν, there is no convergence at all.
In Fig. 50, presented are the sequences of plots of the convergence area index for the RL- (the left column) and C-derivatives (the right column), respectively. These images lead to the same conclusions as the plots of ANI. In short, the influence of α is small and the influence of β are substantial, mainly in the range [0.14,0.4]. Since for small values of β, there were no convergent points; these areas are dark blue on the plots of CAI which means that the number of convergent points equals zero for such images. On the other hand, for large values of β (the dark red regions), all points are convergent.
In Fig. 51, there are the sequences of plots of the generation time (in seconds) for the RL- (the left column) and C-derivatives (the right column), respectively. These plots are very similar in shapes to the ones of ANI or CAI. It follows from the fact that the more convergent points in the polynomiograph, the shorter the generation time. So, for small values of β, we observed non-convergent polynomiographs; therefore, the generation time is large. On the other hand, for large values of β, the number of convergent points was quite large, so the generation time is short.
6.3.4 S iteration
In Fig. 52, the two sequences of plots of the average number of iterations are presented for the RL- (the left column) and C-derivatives (the right column), respectively. From these plots, it is easily seen that, as follows from the previously presented examples, the changes of α and β influence the convergence in the same degree. Moreover, for ν close to 1, the convergence is very fast and uniform. For large values of ν, the change of convergence is negligible, whereas for small values of ν it changes dramatically. Especially, we can see that for ν = 0.70 the smaller the values of α and β the lower the convergence, for the RL-derivative even more than for the C-derivative.
In Fig. 53, the two sequences of plots of the convergence area index are presented for the RL- (the left column) and C-derivatives (the right column), respectively. In some sense, these plots resemble the ones from Fig. 52. In this case, we deal with nearly completely convergence (the dark red colour) for appropriately large values of ν. For smaller values of ν (for ν = 0.70 in this case) for small α and β, we observe a lower number of convergent points in the polynomiographs.
In Fig. 54, the two sequences of plots of the generation time (in seconds) are presented for the RL- (the left column) and C-derivatives (the right column), respectively. From these plots, we can conclude that, in general, the larger the values of α and β the faster the time of polynomiograph generation. It followed also from the ANI plots. Indeed, in those plots, we have observed that for larger α and β there were lesser numbers of iterations in average. So, that is why the generation time is faster. From these plots, it also follows clearly that the influence of α and β parameters is equal.
6.4 Comments
From the experiments performed on the base of the polynomiographs, ANI, CAI, time generation plots and dependencies among the presented iterations, the following conclusions can be drawn:
-
The stability of the considered methods and iterations highly depends on the order of the fractional derivative and less on the parameters of the iterations. The overall behaviour for all the methods is similar. For ν < 1, the vertical border between the basins of attraction wraps up to the right and it becomes more rough. For ν > 1, the basin for − 1 shrinks and forms a closed shape that depends on the iteration. The best stability compared with the most stable case presented in Fig. 1 is obtained near ν = 1, which corresponds to the classical derivative.
-
For ν-order approaching to 1.0 from above or from below, the fractional Newton method is equivalent to the classical Newton root-finding method modified by α or α and β parameters in the used iterations. For the classical Newton method with various iterations, one can observe symmetric polynomiographs having three braids separating cube roots of unity. The width of those braids depends on the kind of iteration used and its parameters. A more detailed discussion on that case can be found in [18].
-
With ν decreasing below 1.0 or ν increasing above 1.0, one can observe that the polynomiographs lose their rotational symmetry, but they still possess an axial symmetry with only one axis of symmetry located on the real axis. Moreover, their shapes are changing quickly, especially in their left parts, where areas of chaos and non-convergence are getting larger and are more visible. Fractional Newton’s method gradually loses possibility of finding complex cube roots of unity, but the real root (1) is still found.
-
The use of various iterations in fractional Newton’s method has influence on the convergence of the processes (measured by ANI and CAI). Namely, Khan assures better convergence than Mann. Unfortunately, both Mann and Khan are worse in comparison with Picard iteration for most of the parameters’ values. In the neighbourhood of α = 1, Khan iteration obtains better (lower) values of ANI in comparison with the Picard iteration. Similarly, S iteration is better than Ishikawa, but both are worse in comparison with Picard iteration for most of the parameters’ values. The S iteration obtains lower values of ANI than Picard iteration for values in the neighbourhood of the (1,1) point in the parameters’ space. In each case, the size of the neighbourhood depends on the value of the derivative order ν used in Newton’s method. Moreover, the dependency of the two measures (ANI, CAI) on the parameters of the methods (derivative order and the iteration parameters) is a highly nonlinear one. The minimal and maximal values of the ANI and CAI for the considered methods and iterations are gathered in Table 2.
-
For each of the considered iterations (Picard, Mann, Khan, Ishikawa and S), one can observe that the obtained generation times of polynomiographs are much longer than those in the case of the classical derivative. This is an obvious observation when one looks at the complexity of computations needed in each case. To compute fractional derivative, we need more computations and in consequence one iteration of Newton’s method has greater computational complexity. Moreover, from the generation time plots, we can observe that the dependency of this measure on the parameters (derivative order and the iteration parameters) is a nonlinear one. The minimal and maximal values of the time (in seconds) for the considered methods and iterations are gathered in Table 2.
-
In general, C-derivative assures better behaviour of the considered root-finding processes in comparison with RL-derivatives.
-
Two-parameter iterations allow obtaining more ample collection of different images in comparison with those generated with the help of one-parameter iterations.
7 Conclusions and future work
In this paper, some modifications of fractional Newton’s method with Riemann–Liouville or Caputo derivatives were investigated via polynomiographs. The standard Picard iteration was replaced by the one of the four iteration processes: Mann, Khan, Ishikawa and S iterations. For polynomial z3 − 1, polynomiographs coloured with respect to the number of iterations together with the plots showing the dependence of the ν-order and iteration parameters α,β, when applicable, on the three different measures (ANI, CAI and the generation time) were presented. Obtained polynomiographs and measures allowed to compare properties of the considered root-finding processes.
Further modifications of the fractional Newton’s method are possible in several directions by the use of the other known multi-parameter iterations, various convergence criteria or different-coloured maps, as e.g. in [18] and with the help of higher-order methods based on the Basic or the Euler–Schröder families of iterations [26] with non-standard iteration processes. Then, it would be interesting to check experimentally how the considered root-finding processes behave when using complex parameters instead of real ones in multi-parameter iterations. Another direction for future work could be the investigation of switching processes similarly in [16]. One could use switching of the fractional orders of the RL- and C-derivatives or the various fractional derivatives.
Finally, it is worth to mention that fractional derivatives can be directly calculated also for the exponential functions with complex variable [34] and therefore for other functions related to them as e.g. \(\sin \limits \), \(\cos \limits \). The fractional Newton method when applied to these functions produces images that could be also investigated.
References
Abel, N.: Opløsning af et par opgaver ved hjælp af bestemte integraler. Magazin for Naturvidenskaberne 2, 205–215 (1823)
Agarwal, R., O’Regan, D., Sahu, D. R.: Iterative construction of fixed points of nearly asymptotically nonexpansive mappings. J. Nonlinear Convex A. 8 (1), 61–79 (2007)
Akgül, A., Cordero, A., Torregrosa, J.: A fractional Newton method with 2α th-order of convergence and its stability. Appl. Math. Lett. 98, 344–351 (2019). https://doi.org/10.1016/j.aml.2019.06.028
Ardelean, G., Balog, L.: A qualitative study of Agarwal others. iteration procedure for fixed points approximation. Creative Math. Inf. 25(2), 135–139 (2016)
Ardelean, G., Cosma, O., Balog, L.: A comparison of some fixed point iteration procedures by using the basins of attraction. Carpathian J. Math. 32(3), 277–284 (2016)
Babajee, D., Cordero, A., Torregrosa, J.: Study of iterative methods through the Cayley quadratic test. J. Comput. Appl. Math. 291, 358–369 (2016). https://doi.org/10.1016/j.cam.2014.09.020
Brambila-Paz, F., Torres-Hernandez, A.: Fractional newton–Raphson method. arXiv:1710.07634 (2017)
Brambila-Paz, F., Torres-Hernandez, A., Iturrarán-Viveros, U.: Caballero-cruz: Fractional newton-Raphson method accelerated with Aitken’s method. arXiv:1804.08445 (2018)
Burden, R., Faires, J.: Numer. Analysis, 9th edn. Brooks–Cole, Boston (2011)
Candelario, G., Cordero, A., Torregrosa, J.: A fractional Traub method with (2α + 1)th-order of convergence and its stability. arXiv:1909.09076v1 (2019)
Chun, C., Neta, B.: Comparison of several families of optimal eighth order methods. Appl. Math. Comput. 274, 762–773 (2016). https://doi.org/10.1016/j.amc.2015.10.092
Chun, C., Neta, B.: On the new family of optimal eighth order methods developed by Lotfi others. Numer. Algorithms 72(2), 636–376 (2016). https://doi.org/10.1007/s11075-015-0048-9
Cordero, A., Ferrero, A., Torregrosa, J.: Damped Traub’s method: Convergence and stability. Math. Comput. Simul. 119, 57–68 (2016). https://doi.org/10.1016/j.matcom.2015.08.012
Cordero, A., Girona, I., Torregrosa, J.: A variant of Chebyshev’s method with 3α th-order of convergence by using fractional derivatives. Symmetry 11(8), Article 1017 (2019). https://doi.org/10.3390/sym11081017
Gdawiec, K.: Fractal patterns from the dynamics of combined polynomial root finding methods. Nonlinear Dyn. 90(4), 2457–2479 (2017). https://doi.org/10.1007/s11071-017-3813-6
Gdawiec, K.: Switching processes in polynomiography. Nonlinear Dyn. 87(4), 2235–2249 (2017). https://doi.org/10.1007/s11071-016-3186-2
Gdawiec, K., Kotarski, W.: Polynomiography for the polynomial infinity norm via Kalantari’s formula and nonstandard iterations. Appl. Math. Comput. 307, 17–30 (2017). https://doi.org/10.1016/j.amc.2017.02.038
Gdawiec, K., Kotarski, W., Lisowska, A.: Polynomiography based on the non-standard Newton-like root finding methods. Abstract and Applied Analysis 2015, Article ID 797, 594 (2015). https://doi.org/10.1155/2015/797594
Gdawiec, K., Kotarski, W., Lisowska, A.: Visual analysis of the Newton’s method with fractional order derivatives. Symmetry 11(9), Article ID 1143 (2019). https://doi.org/10.3390/sym11091143
Gilbert, W.: Generalizations of Newton’s method. Fractals 9(3), 251–262 (2001). https://doi.org/10.1142/S0218348X01000737
Herrmann, R.: Fractional Calculus: an Introduction for Physicists, 2nd edn. World Scientific, Singapore (2014)
Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)
Ishikawa, S.: Fixed points by a new iteration method. Proc. Am. Math. Soc. 44(1), 147–150 (1974). https://doi.org/10.1090/S0002-9939-1974-0336469-5
Ishteva, M.: Properties and Applications of the Fractional Caputo Operator. Master’s Thesis, Department of Mathematics, Universität Karlsruhe (2005)
Kalantari, B.: Polynomiography: from the fundamental theorem of algebra to art. Leonardo 38(3), 233–238 (2005). https://doi.org/10.1162/0024094054029010
Kalantari, B.: Polynomial Root-Finding and Polynomiography, World Scientific, Singapore (2009)
Khan, S.: A picard-Mann hybrid iterative process. Fixed Point Theory Appl. 2013, Article 69 (2013). https://doi.org/10.1186/1687-1812-2013-69
Mandelbrot, B.: The Fractal Geometry of Nature. W.H. Freeman and Company, New York (1983)
Mann, W.: Mean value methods in iteration. Proc. Am. Math. Soc. 4(3), 506–510 (1953). https://doi.org/10.1090/S0002-9939-1953-0054846-3
Munkhammar, J.: Fractional calculus and the taylor-Riemann series. Ros-Hulman Undergraduate Math. J. 6(1), Article 6 (2005)
Oldham, K., Spanier, J.: The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order Mathematics in Science and Engineering, vol. 111. Academic Press, San Diego (1974)
Ortigueira, M., Rodríguez-Germá, L., Trujillo, J.: Complex grünwald-Letnikov, Liouville, riemann-Liouville, and Caputo derivatives for analytic functions. Commun. Nonlinear Sci. Numer. Simul. 16(11), 4174–4182 (2011). 10.1016/j.cnsns.2011.02.022
Picard, E.: Mémoire sur la théorie des équations aux dérivées partielles et la méthode des approximations successives. J Math. Pure. Appl. 6(4), 145–210 (1890)
Samko, S., Kilbas, A., Marichev, O.: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach Science Publishers, Amsterdam (1993)
Sun, H., Zhang, Y., Baleanu, D., Chen, W., Chen, Y.: A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 64, 213–231 (2018). https://doi.org/10.1016/j.cnsns.2018.04.019
Vázquez, L.: From Newton’s equation to fractional diffusion and wave equations. Adv Differ Equ 169, Article ID 169,421 (2011). https://doi.org/10.1155/2011/169421
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gdawiec, K., Kotarski, W. & Lisowska, A. Newton’s method with fractional derivatives and various iteration processes via visual analysis. Numer Algor 86, 953–1010 (2021). https://doi.org/10.1007/s11075-020-00919-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-020-00919-4