Simple digital quantum algorithm for symmetric first-order linear hyperbolic systems

Abstract

This paper is devoted to the derivation of a digital quantum algorithm for the Cauchy problem for symmetric first-order linear hyperbolic systems, thanks to the reservoir technique. The reservoir technique is a method designed to avoid artificial diffusion generated by first-order finite volume methods approximating hyperbolic systems of conservation laws. For some class of hyperbolic systems, namely, those with constant matrices in several dimensions, we show that the combination of (i) the reservoir method and (ii) the alternate direction iteration operator splitting approximation allows for the derivation of algorithms only based on simple unitary transformations, thus being perfectly suitable for an implementation on a quantum computer. The same approach can also be adapted to scalar one-dimensional systems with non-constant velocity by combining with a non-uniform mesh. The asymptotic computational complexity for the time evolution is determined and it is demonstrated that the quantum algorithm is more efficient than the classical version. However, in the quantum case, the solution is encoded in probability amplitudes of the quantum register. As a consequence, as with other similar quantum algorithms, a post-processing mechanism has to be used to obtain general properties of the solution because a direct reading cannot be performed as efficiently as the time evolution.

Appendices

Appendix A: Numerical example for the reservoir method with diagonal system

We now illustrate this approach with a simple classical diagonal two-dimensional test, with $\lambda _{1}^{(1)}= 1,\lambda _{2}^{(1)}= 4,\lambda _{3}^{(1)}= 8$ and $\lambda _{1}^{(2)}= 1,\lambda _{2}^{(2)}= 2,\lambda _{3}^{(2)}= 4$. The computational domain is [0, 10]², and T = 0.75, m = 3, d = 2, Δx₁ = Δx₂ = 0.1. The time step is given by Δt_n = 0.012488 for all n ≤ n_T = 60. The initial data is U_0;1(x₁,x₂) = exp (− 2 ((x₁ − 5/2)² + (x₂ − 5/2)²)), U_0;2(x₁,x₂) = exp (− 4 ((x₁ − 5/2)² + (x₂ − 5/2)²)), U_0;3(x₁,x₂) = exp (− 8 ((x₁ − 5/2)² + (x₂ − 5/2)²)). The reservoir solution components are represented in Fig. ?? (2nd column), showing no numerical diffusion whatsoever, unlike the “CFL= 1” solutions also represented in Fig. ?? (3rd column).

Fig. 9

Solution components (rows 1 to 3): initial data (1st column), CFL=1 solution (2nd column), and reservoir method solution (3rd column), at final time T = 0.75

Appendix B: Example for a rotation operator

A simple explicit example for a rotation operator can easily be constructed, inspired from [27]. We consider for d = 3, m = 2², the following system:

$$\begin{array}{@{}rcl@{}} \left\{ \begin{array}{lcl} \partial_{t}u + A^{(\mathrm{x})}\partial_{x}u + A^{(\mathrm{y})}\partial_{y}u +A^{(\mathrm{z})}\partial_{z}u& = & 0, \qquad (x,y,z,t) \in {\mathbb{R}}^{3}\times (0,T),\\ u(\cdot,0) & = & u_{0}, \qquad (x,y,z) \in \mathbb{R}^{3} \end{array} \right. \end{array} $$

(19)

with A^(x) = S^(x)Λ^(x)S^(xT) (resp. A^(y) = S^(y)Λ^(y)S^(y)T, A^(z) = S^(z)Λ^(z)S^(z)T), where S^(γ) with γ = x,y,z, are defined by

$$\begin{array}{@{}rcl@{}} \left. \begin{array}{clc} S^{(\gamma)} & = & \cfrac{1}{\sqrt{2}} \left( \begin{array}{cc} \mathrm{I}_{2} & \sigma_{\gamma}\\ \sigma_{\gamma} & -\mathrm{I}_{2} \end{array} \right) \end{array} \right. \end{array} $$

(20)

and where {σ_γ}_{γ = x,y,z} are the Pauli matrices. From a quantum algorithm point of view, these rotations operators can be decomposed [27] as:

$$\begin{array}{@{}rcl@{}} S[\gamma] = \mathrm{C}(\sigma_{\gamma})\mathrm{H}\otimes \mathrm{I}_{2} \mathrm{C}(\sigma_{\gamma}) \end{array} $$

where C(σ_γ) (resp. H) is σ_γ-controlled (resp. Hadamard) gate (see Fig. 1 in [27]). In this case, the construction of the quantum circuit can directly be deduced from [27], thanks to a simple decomposition in elementary quantum gates of S^(γ). More elaborated cases corresponding to more complex S^(γ) can be considered as discussed above, but then necessitate more complex quantum circuits.

Appendix C: Determining minimal resource requirements of the quantum algorithm with Quipper

Quipper is a Haskell-based embedded functional language whose purpose is to emulate the implementation of quantum algorithms on realistic quantum computers by providing explicit gate decompositions of quantum algorithms [31, 32]. In particular, functions for transforming complex quantum circuits into elementary gates (Hadamard, CNOT, Clifford...) are included in Quipper, along with many other functionalities allowing for circuit assembly and for resource requirement diagnosis. In this section, we will implement some of the algorithms presented above.

Throughout, it is assumed that all logical operations are implemented without error. In a real quantum device, the quantum system interacts with its environment, generating some noise and error in each operation. In this sense, the gate counts given below represent a lower bound estimates for the “true” algorithm, which may require error-correcting steps.

The algorithm for the solution of hyperbolic systems was formulated in the abstract Hilbert space of the quantum register. Therefore, it is independent of the computer architecture and thus is amenable to any digital quantum devices. For example, quantum computers based on superconducting circuits [10, 11, 39], trapped ions [41], and cavity quantum electrodynamics [50] have been used with some success for other problems and could be used in principle to implement our algorithm. The main limitations however are (i) the number of available qubits in the current register and (ii) the coherence time of these devices that restricts the number of logic quantum gates. State-of-the-art quantum computations on actual digital computers reach ≈ 1000 quantum logic gates on ≈ 9 qubits [11].

In all the examples considered in the following, minimal requirements are studied in order to assess the feasibility of simulations on these real quantum devices. In particular, we count the number of quantum gates (circuit depth) and the total number of qubits (circuit width) required to evolve the initial condition data to a given final time. Due to physical limitations in terms of the number of qubits and the coherence time, only systems with overly small meshes are investigated. As emphasized in [27], this may be enough for proof-of-principle calculations but is far from outperforming classical computations. Nevertheless, given the amount of effort and resources devoted to the development of these quantum devices, these numbers will likely be improved in the future.

1.1 C.1 One-dimensional hyperbolic system

We consider a one-dimensional system with a computational domain as [0, 1] × [0,T]:

$$\begin{array}{@{}rcl@{}} \partial_{t} u + {\Lambda} \partial_{x} u = 0, \qquad (x,t) \in [0,1] \times [0,T] \end{array} $$

where A = Λ is a diagonal matrix in $M_{2}({\mathbb {R}})$, with eigenvalues λ₁ = 1,λ₂ = − 3. If A were not diagonal, it would be necessary to add a transition operator at the beginning and the end of the circuit. For T = 10^− 1 and n_T = 40, we can determine the sets:

$$\begin{array}{@{}rcl@{}} \mathcal{I}^{n_{T}} & =& (2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 1, \\ && 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 1 ) , \\ \mathcal{S}^{n_{T}} & =& (-, -, -, +, -, -, -, +, -, -, -, +, -, -, -, +, -, -, -, +, -, -, -, +, \\ && -, -, -, +, -, -, -, +, -, -, -, +, -, -, -, +, ) . \end{array} $$

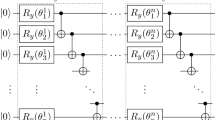
We then implement the quantum algorithm described in Section ??, with Quipper. In this case, it is only necessary to implement the decrement and increment operators, thanks to the preliminarily established list $\mathcal {I}^{n_{T}}$ of characteristics to be updated. Following Table I from [27], we report the minimal requirements for simulating the one-dimensional system described above, for proof-of-principle calculations. More specifically using Quipper, we can evaluate precisely the number of elementary gates necessary to implement the quantum algorithm. Say for respectively n_x = 2, n_x = 4, and n_x = 8, the circuit depth computed by Quipper is 780, 5520, and 27960, and the circuit width is respectively 3, 7, and 15. For instance for n_x = 4 that is N_x = 16, the respective number of Hadamard, Clifford, Toffoli, and CNOT gates is found to be 540, 1890, 1350, and 1560. We report in Fig. 10 the quantum circuit for the first 4 iterations with N_x = 16. This quantum circuit has a width equal to 5, that is 4 qubits for labeling the coordinate space positions, and 1 qubit for the labeling of the component. The circuits which are represented correspond to the first 4 time iterations. We notice that the circuit for the first component (top) has 4 times the same pattern (elementary circuit), corresponding to 4 translations from the left to the right, while the circuit for the second component (bottom) corresponds to only 1 iteration from the right to the left, for the same lapse of time. This is due to the fact that λ₂ = − 3 × λ₁, so that after 4 iterations, 4 translations to the right are applied to the first component, while the second component is only translated once to the left. The quantum circuit for 1 iteration is generated by Quipper.

Fig. 10

Circuit diagram with N_x = 16. a First 4 iterations of the quantum reservoir method and first component. b Second component

As an illustration for the same test, but with N_x = 4, we also report in Fig. 11 the quantum circuit for the corresponding gate decomposition and which is still generated by Quipper. This time we only have 3 qubits, 1 for the component index, and 2 for the positions.

Fig. 11

Circuit diagram obtained from the gate decomposition with N_x = 4 in 1-D for one iteration

The case with the smallest circuit depth, for the lower number of lattice points (n_x = 2,N_x = 4), could possibly be implemented on actual device for a proof-of-principle calculation, as long as the initialization phase requires less than approximately 300 gates. However, the results obtained from the gate decomposition demonstrate that it would be a challenging task to perform quantum simulations of hyperbolic systems on actual quantum device with larger lattice size. Moreover, performing a relevant quantum simulation outperforming classical computation demands much improvement from both the coherence time and the number of qubits.

1.2 C.2 Three-dimensional hyperbolic system

In this subsection, we implement with Quipper the quantum version of the reservoir method for a three-dimensional linear hyperbolic system (1) with $\lambda _{1}^{(\mathrm {x})}=\lambda _{2}^{(\mathrm {x})}=-1$, $\lambda _{3}^{(\mathrm {x})}=\lambda _{4}^{(\mathrm {x})}=\sqrt {2}$, $\lambda _{1}^{(\mathrm {y})}=\lambda _{2}^{(\mathrm {y})}=-2$, $\lambda _{3}^{(\mathrm {y})}=\lambda _{4}^{(\mathrm {y})}= 2\sqrt {2}$, $\lambda _{1}^{(\mathrm {z})}=\lambda _{2}^{(\mathrm {z})}=-4$, $\lambda _{3}^{(\mathrm {z})}=\lambda _{4}^{(\mathrm {z})}= 4\sqrt {2}$. Notice that we have associated the following upper indices: (x) ⇔ (1), (y) ⇔ (2), (z) ⇔ (3). We then select S^(γ) as in (2), where we recall that Pauli’s matrices are defined by:

$$\begin{array}{@{}rcl@{}} \sigma_{x} = \left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right] \text{,} \sigma_{y} = \left[\begin{array}{ll} 0 & -{\tt i} \\ {\tt i} & 0 \end{array}\right] \text{and} \sigma_{z} = \left[\begin{array}{ll} 1 & 0 \\ 0 & -1 \end{array}\right] . \end{array} $$

(21)

The motivation for considering such “simple” transition matrices is to design simple quantum circuit portion for diagonalization. As mentioned in Section ??, more complex transition unitary matrices could be considered, but would then require additional work for decomposing in elementary quantum gates. The quantum algorithm is applied from time 0 to 10^− 2, with Δx = 10^− 2, corresponding to n_T = 30 iterations. In addition, $\mathcal {I}^{n_{T}}$ and $\mathcal {S}^{n_{T}}$ are such that:

$$\begin{array}{@{}rcl@{}} \mathcal{I}^{n_{T}} & =& ((3,3), (4,3), (1,3), (2,3), (3,2), (3,3), (4,2), (4,3), (1,2), (1,3), \\ && (2,2), (2,3), (3,3),(4,3),(3,1),(3,2), (3,3),(4,1),(4,2), (4,3), \\ && (1,3),(2,3),(3,3),(4,3),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3) ) \\ \mathcal{S}^{n_{T}} & =& (+, +, -, -, +, +, +, +, -, -, \\ && -, -, +,+,+,+, +,+,+, +, \\ && -,-,+,+,-,-,-,-,-,- ) \end{array} $$

The corresponding time steps take the value 0.0177, 0.0073, 0.0104, 0.0030, 0.0177, 0.0043⋯. We then encode $\mathcal {I}^{n_{T}}$ in the quantum algorithm in order to implement the quantum reservoir method. This list provides the directional characteristic field to update. Say for respectively n_x = n_y = n_z = 2, n_x = n_y = n_z = 4, and n_x = n_y = n_z = 8, the circuit depth computed by Quipper is 672, 3042, and 14262, and the circuit width is respectively 8, 16, and 32. For instance for n_x = n_y = n_z = 4 that is N_x = N_y = N_z = 16, the respective numbers of Hadamard, Clifford, Toffoli, and CNOT gates are found to be 400, 1037, 675, and 840. We report in Fig. 12 the quantum circuit for the first iteration with N_x = N_y = N_z = 4, and a circuit width equal to 8. The quantum circuit which is generated by Quipper is much more complex (Toffoli, Hadamard, Clifford quantum gates, etc.), as it also includes the changes of basis (rotations) and the translations.

Fig. 12

Circuit diagram obtained from the gate decomposition with N_x = 16 in 3-D for the first iteration

The same conclusion as in the 1-D case can be reached from these results, i.e., a proof-of-principle calculation could possibly be performed with the smaller systems, but relevant calculations would require improvements in quantum technologies.