Skip to main content
SpringerLink
Log in

Ginzburg-Landau system of complex modulation equations for distributed nonlinear dissipative transmission lines

  • Published:
Nonlinear Oscillations

Abstract

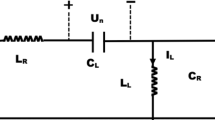
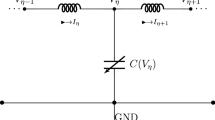
The envelope modulation of a monoinductance transmission line is reduced to generalized coupled Ginzburg-Landau equations, from which a single cubic-quintic Ginzburg-Landau equation containing derivatives with respect to the space variable in the cubic terms is deduced. We investigate the modulational instability of the space wave solutions of both the system and the single equation. For the generalized coupled Ginzburg-Landau system, we consider only the zero wave numbers of the perturbations whose modulational instability conditions depend only on the coefficients of the system and the wave numbers of the carriers. In this case, a modulational instability criterion is established, which depends on both the perturbation wave numbers and the carrier. We also study the coherent structures of the generalized coupled Ginzburg-Landau system and present some numerical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. C. Scott, Active and Nonlinear Wave Propagation in Electronics, Wiley, New York (1970).

    Google Scholar 

  2. E. Kengne, “Envelope modulational instability in a nonlinear dissipative transmission line,” Nonlin. Oscillations, 5, No. 1, 20–29 (2002).

    Article  Google Scholar 

  3. A. C. Hicks, A. K. Common, and M. I. Sobhy, “Approximations to large amplitude solitary waves on nonlinear electrical lattice,” Physica D, 95, 167–186 (1996).

    Article  MATH  Google Scholar 

  4. E. Kengne, “Ginzburg-Landau system of complex modulation equations for a distributed nonlinear-dispersive transmission line,” J. Phys. A: Math. Gen., 37, 6053–6066 (2004).

    Article  MATH  Google Scholar 

  5. M. C. Cross and P. C. Hohenberg, “Pattern formation outside of equilibrium,” Rev. Mod. Phys., 65, 851–1112 (1993).

    Article  Google Scholar 

  6. M. van Hecke and W. van Saarloos, “Convection in rotating annuli: Ginzburg-Landau equations with tunable coefficients,” Phys. Rev. E, 55, 1259–1262 (1997).

    Article  Google Scholar 

  7. M. van Hecke, C. Storm, and W. van Saarloos, “Sources, sinks and wavenumber selection in coupled CGL equations and experimental implications for counter-propagating wave systems,” Physica D, 134, 1–47 (1999).

    Article  MATH  Google Scholar 

  8. A. Doelman, Ph.D. Thesis, Utrecht (1990).

  9. E. Kengne, S. T. Chui, and W. M. Liu, “Modulational instability criteria for coupled nonlinear transmission lines with dispersive elements,” Phys. Rev. E, 74, 036614-1–036614-10 (2006).

    Article  Google Scholar 

  10. R. J. Deissler and H. R. Brand, “The effect of nonlinear gradient terms on localized states near a weakly inverted bifurcation,” Phys. Lett. A, 146, 252–255 (1990).

    Article  Google Scholar 

  11. W. van Saarloos and P. C. Hohenberg, “Fronts, pulses, sources and sinks in generalized complex Ginzburg-Landau equations,” Physica D, 56, 303–367 (1992).

    Article  MATH  Google Scholar 

  12. A. Doelman and W. Eckhaus, “Periodic and quasi-periodic solutions of degenerate modulation equations,” Physica D, 53, 249–266 (1991).

    Article  MATH  Google Scholar 

  13. P. Holmes, “Structure of time-periodic solution of the Ginzburg-Landau equation,” Physica D, 23, 84–90 (1986).

    Article  MATH  Google Scholar 

  14. E. Kengne, “Modified Ginzburg-Landau equation and Benjamin-Feir instability,” Nonlin. Oscillations, 6, No. 3, 346–356 (2003).

    MATH  Google Scholar 

  15. E. Kengne and W.M. Liu, “Exact solutions of the derivative nonlinear Schrödinger equation for a nonlinear transmission line,” Phys. Rev. E, 73, 026603-1–026603-8 (2006).

    Article  Google Scholar 

  16. O. Thual and S. Fauve, “Localized structures generated by subcritical instabilities,” J. Phys. France, 49, 1829–1833 (1988).

    Article  Google Scholar 

  17. S. Fauve and O. Thual, “Solitary waves generated by subcritical instabilities in dissipative systems,” Phys. Rev. Lett., 64, 282–284 (1990).

    Article  Google Scholar 

  18. A. A. Kolyshkin, R. Vaillancourt, and I. Volodko, “Complex Ginzburg-Landau equation for suddenly blocked unsteady channel,” Cent. Rech. Math. Univ. Montréal, CRM-3194 (2005).

  19. A. A. Kolyshkin, R. Vaillancourt, and I. Volodko, “Weakly nonlinear analysis of rapidly decelerated channel flow,” IASME Trans., 2, No. 7, 1157–1165 (2005).

    Google Scholar 

  20. C. K. R. T. Jones, T. Kapitula, and J. Powell, “Nearly real fronts in a Ginzburg-Landau equation, ” Proc. Roy. Soc. Edin. A, 116, 193–206 (1990).

    Google Scholar 

  21. M. van Hecke, “Building blocks of spatiotemporal intermittency,” Phys. Rev. Lett., 80, 1896–1899 (1998).

    Article  Google Scholar 

  22. W. van Saarloos and P. C. Hohenberg, “Fronts, pulses, sources and sinks in generalized complex Ginzburg-Landau equations,” Physica D, 56, 303–367 (1992).

    Article  MATH  Google Scholar 

  23. W. van Saarloos and P. C. Hohenberg, “Fronts, pulses, sources and sinks in generalized complex Ginzburg-Landau equations. Erratum,” Physica D, 69, 209 (1993).

    Article  MATH  Google Scholar 

  24. N. Bekki and K. Nozaki, “Formations of spatial patterns and holes in the generalized Ginzburg-Landau equation,” Phys. Lett. A, 110, 133–135 (1985).

    Article  Google Scholar 

  25. R. Conte and M. Musette, “Linearity inside nonlinearity: exact solutions to the complex Ginzburg-Landau equation,” Physica D, 69, 1–17 (1993).

    Article  MATH  Google Scholar 

  26. P. Marcq, H. Chaté, and R. Conte, “Exact solutions of the one-dimensional quintic complex Ginzburg-Landau equation,” Physica D, 73, 305–317 (1994).

    Article  MATH  Google Scholar 

  27. S. Popp, O. Stiller, I. Aranson, A. Weber, and L. Kramer, “Localized hole solutions and spatiotemporal chaos in the 1D complex Ginzburg-Landau equation,” Phys. Rev. Lett., 70, 3880–3883 (1993).

    Article  Google Scholar 

  28. A. Doelman, “Breaking the hidden symmetry in the Ginzburg-Landau equation,” Physica D, 97, 398–428 (1996).

    Article  Google Scholar 

  29. J. M. Soto-Crespo, N. Akhmediev, and G. Town, “Interrelation between various branches of stable solitons in dissipative systems. Conjecture for stability criterion,” Opt. Commun., 199, 283–293 (2001).

    Article  Google Scholar 

  30. E. Kengne and C.N. Bame, “Wave modulation in nonlinear dissipative and dispersive transmission line, ” Far East J. Appl. Math., 16, No. 2, 213–232 (2004).

    MATH  Google Scholar 

  31. V. I. Arnold, Mathematical Methods of Classical Mechanics, Springer, New York (1978).

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Dschang, Dschang, Cameroon

    E. Kengne

  2. University of Ottawa, Ottawa, Canada

    E. Kengne & R. Vaillancourt

Authors
  1. E. Kengne
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. Vaillancourt
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Published in Neliniini Kolyvannya, Vol. 9, No. 4, pp. 451–489, October–December, 2006.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kengne, E., Vaillancourt, R. Ginzburg-Landau system of complex modulation equations for distributed nonlinear dissipative transmission lines. Nonlinear Oscill 9, 438–477 (2006). https://doi.org/10.1007/s11072-006-0055-9

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11072-006-0055-9

Keywords

Search

Navigation