Skip to main content
SpringerLink
Log in

Homogenization of a Boundary-Value Problem with Varying type of Boundary Conditions in a Thick Two-Level Junction

  • Published:
Nonlinear Oscillations

Abstract

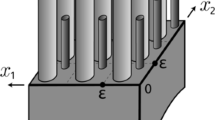
We consider a mixed boundary-value problem for the Poisson equation in a plane two-level junction Ω ɛ that is the union of a domain Ω0 and a large number 2N of thin rods with thickness of order ɛ = \(\mathcal{O}\) (N −1). Depending on their lengths, the thin rods are divided into two levels. In addition, the rods from each level are ɛ-periodically alternated. Inhomogeneous Neumann boundary conditions are given on the vertical sides of the thin rods of the first level, and homogeneous Dirichlet boundary conditions are given on the vertical sides of the rods of the second level. We investigate the asymptotic behavior of a solution of this problem as ɛ → 0 and prove a convergence theorem and the convergence of the energy integral.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. N. S. Bakhvalov and G. P. Panasenko, Homogenization of Processes in Periodic Media [in Russian], Nauka, Moscow (1984).

    Google Scholar 

  2. A. Bensoussan, J.-L. Lions, and G. Papanicolau, Asymptotic Analysis for Periodic Structures, North Holland, Amsterdam (1978).

    MATH  Google Scholar 

  3. P. G. Ciarlet, Plates and Junctions in Elastic Multi-Structures, Masson, Paris (1990).

    MATH  Google Scholar 

  4. D. Cioranescu and J. Saint Jean Paulin, Homogenization of Reticulated Structures, Springer, New York (1999).

    MATH  Google Scholar 

  5. V. V. Jikov, S. M. Kozlov, and O. A. Oleinik, Homogenization of Differential Operators and Integral Functionals, Springer, Berlin-Heidelberg (1994).

    Google Scholar 

  6. A. A. Kovalevskii, “Averaging of the Neumann problems for nonlinear elliptic equations in domains with accumulators,” Ukr. Mat. Zh., 47, No.2, 194–212 (1995).

    Article  MATH  MathSciNet  Google Scholar 

  7. V. A. Kozlov, V. G. Maz'ya, and A. B. Movchan, “Asymptotic representation of an elastic field in a multi-structure,” Asymptot. Analysis, 11, 343–415 (1995).

    MathSciNet  MATH  Google Scholar 

  8. M. Lobo and E. Perez, “Asymptotic behaviour of an elastic body with a surface having small stuck regions,” Math. Models Meth. Appl. Sci., 22, No.4, 609–624 (1988).

    MathSciNet  MATH  Google Scholar 

  9. M. Lobo and E. Perez, “Asymptotic behaviour of the vibrations of a body having many concentrated masses near the boundary,” C. R. Acad. Sci., Ser. II, 314, 13–18 (1992).

    MATH  Google Scholar 

  10. V. A. Marchenko and E. Ya. Khruslov, Boundary-Value Problems in Domains with Fine-Grained Boundary [in Russian], Naukova Dumka, Kiev (1974).

    MATH  Google Scholar 

  11. S. A. Nazarov, Asymptotic Analysis of Thin Plates and Rods. Vol. 1._Reduction of Dimension and Integral Estimates [in Russian], Nauchnaya Kniga, Novosibirsk (2002).

    Google Scholar 

  12. O. A. Oleinik, G. A. Iosif'yan, and A. S. Shamaev, Mathematical Problems in the Theory of Strongly Inhomogeneous Elastic Media [in Russian], Moscow University, Moscow (1990).

    Google Scholar 

  13. J. Sanchez-Hubert and E. Sanchez-Palencia, Vibration and Coupling of Continuous Systems, Springer, Berlin (1989).

    MATH  Google Scholar 

  14. I. V. Skrypnik, Methods for Investigation of Nonlinear Elliptic Boundary-Value Problems [in Russian], Nauka, Moscow (1990).

    MATH  Google Scholar 

  15. F. Fleury and E. Sanchez-Palencia, “Asymptotic and spectral properties of the acoustic vibrations of body perforated by narrow channels,” Bull. Sci. Math., 2, No.110, 149–176 (1986).

    MathSciNet  Google Scholar 

  16. V. P. Kotlyarov and E. Ya. Khruslov, “On the limit boundary condition for one Neumann problem,” Teor. Funkts. Funkts. Anal. Prilozhen., No. 10, 83–96 (1970).

  17. G. V. Suzikov and E. Ya. Khruslov, “On the passage of sound waves through thin channels in a reflecting layer,” Teor. Funkts. Funkts. Anal. Prilozhen., No. 5, 35–49 (1976).

  18. E. Ya. Khruslov, “On resonance phenomena in a diffraction problem,” Teor. Funkts. Funkts. Anal. Prilozhen., No. 10, 113–120 (1968).

  19. T. A. Mel'nyk and S. A. Nazarov, “Asymptotic structure of the spectrum of the Neumann problem in a thin comb-like domain,” C. R. Acad. Sci., Ser. I, 319, 1343–1348 (1994).

    MathSciNet  MATH  Google Scholar 

  20. T. A. Mel'nyk and S. A. Nazarov, “Asymptotics of eigenvalues of a Neumann problem in a domain of the ‘thick-comb’ type,” Dokl. Ros. Akad. Nauk, 342, No.1, 23–25 (1995).

    MathSciNet  Google Scholar 

  21. T. A. Mel'nyk and S. A. Nazarov, “Asymptotics of a solution of a spectral Neumann problem in a domain of the ‘thick-comb’ type,” Tr. Sem. Im. Petrovskogo, 19, 138–174 (1996); English translation: J. Math. Sci., 85, No. 6, 2326–2346 (1997).

    Google Scholar 

  22. T. A. Mel'nyk, “Homogenization of the Poisson equation in a thick periodic junction,” Z. Anal. Anwendungen., 18, No.4, 953–975 (1999).

    MATH  MathSciNet  Google Scholar 

  23. T. A. Mel'nyk, “Asymptotic analysis of a spectral problem in a periodic thick junction of type 3:2:1,” Math. Meth. Appl. Sci., 23, No.4, 321–346 (2000).

    Article  MATH  MathSciNet  Google Scholar 

  24. T. A. Mel'nyk and S. A. Nazarov, “Asymptotic analysis of a Neumann problem on a junction of a body with thin heavy rods,” Alg. Analiz, 12, No.2, 188–238 (2000); English translation: St.Petersburg Math. J., 12, No. 2, 317–351 (2001).

    MathSciNet  Google Scholar 

  25. T. A. Mel'nyk, “Homogenization of a singularly perturbed parabolic problem in a thick periodic junction of the type 3:2:1,” Ukr. Mat. Zh., 52, No.11, 1524–1533 (2000); English translation: Ukr. Math. J., 52, No. 11, 1737–1748 (2000).

    MATH  MathSciNet  Google Scholar 

  26. T. A. Mel'nyk, “Asymptotic behavior of eigenvalues and eigenfunctions of the Steklov problem in a thick periodic junction,” Nonlin. Oscillations, 4, No.1, 91–105 (2001).

    MATH  MathSciNet  Google Scholar 

  27. T. A. Mel'nyk, “Asymptotics of the spectrum of a Fourier problem in a thick junction of the type 2:1:1,” Visn. Kyiv Univ., Ser. Fiz.-Mat. Nauk, 1, 143–153 (2001).

    MATH  MathSciNet  Google Scholar 

  28. T. A. Mel'nyk, “Asymptotic behavior of eigenvalues and eigenfunctions of a Fourier problem in a thick junction of the type 3:2:1,” in: Group and Analytic Methods in Mathematical Physics [in Ukrainian], Institute of Mathematics, Ukrainian Academy of Sciences, Kyiv (2001), pp. 187–196.

    Google Scholar 

  29. T. A. Mel'nyk, “Vibrations of a thick periodic junction with concentrated masses,” Math. Models Meth. Appl. Sci., 11, No.6, 1001–1029 (2001).

    Article  MATH  MathSciNet  Google Scholar 

  30. S. A. Nazarov, “Junctions of singularly degenerating domains of different limit dimensions. I, II,” Tr. Sem. Im. Petrovskogo, 18, 1–78 (1995); 20, 155–196 (2000).

    Google Scholar 

  31. T. A. Mel'nyk, “Eigenmodes and pseudo-eigenmodes of thick multi-level junctions,” in: Proceedings of the International Conference “Days on Diffraction 2004” (2004), pp. 51–52.

  32. U. De Maio, T. A. Mel'nyk, and C. Perugia, “Homogenization of the Robin problem in a thick multilevel junction,” Nelin. Kolyvannya, 7, No.3, 336–356 (2004).

    MATH  Google Scholar 

  33. U. De Maio, T. Durante, and T. A. Mel'nyk, “Asymptotic approximation for the solution to the Robin problem in a thick multi-level junction,” Math. Models Meth. Appl. Sci., 15, No.12 (2005).

    Google Scholar 

  34. A. Damlamian and Li Ta-Tsien, “Boundary homogenization for elliptic problems,” J. Math. Pures Appl., 66, 351–361 (1987).

    MathSciNet  MATH  Google Scholar 

  35. G. A. Chechkin, “Homogenization of boundary-value problems with singular perturbations of boundary conditions,” Mat. Sb., 184, No.6, 99–105 (1993).

    MATH  MathSciNet  Google Scholar 

  36. G. A. Chechkin, “Asymptotic expansion of a solution of a boundary-value problem with rapidly varying type of boundary conditions,” Tr. Sem. Im. Petrovskogo, 19, 323–338 (1996).

    MATH  Google Scholar 

  37. R. Brizzi and J. P. Chalot, “Boundary homogenization and Neumann boundary value problem,” Ric. Mat., 46, 341–387 (1997).

    MathSciNet  MATH  Google Scholar 

  38. T. A. Mel'nyk, “Homogenization of elliptic equations that describe processes in strongly inhomogeneous thin perforated domains with rapidly varying thickness,” Dopov. Nats. Akad. Nauk. Ukr., No. 10, 15–19 (1991).

Download references

Author information

Authors and Affiliations

  1. Taras Shevchenko National University of Kyiv, Kyiv, Ukraine

    T. A. Mel'nyk & P. S. Vashchuk

Authors
  1. T. A. Mel'nyk
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. P. S. Vashchuk
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

__________

Translated from Neliniini Kolyvannya, Vol. 8, No. 2, pp. 241–257, April–June, 2005.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mel'nyk, T.A., Vashchuk, P.S. Homogenization of a Boundary-Value Problem with Varying type of Boundary Conditions in a Thick Two-Level Junction. Nonlinear Oscill 8, 240–255 (2005). https://doi.org/10.1007/s11072-005-0053-3

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11072-005-0053-3

Keywords

Search

Navigation