Parameterization of nonlinear aeroelastic reduced order models via direct interpolation of Taylor partial derivatives

Abstract

The identification of optimally sparse Taylor partial derivatives presents a new opportunity in efficient nonlinear model reduction for complex aeroelastic systems. Unfortunately, for this class of reduced order model (ROM), the robustness that is observed in the linear regime to parameters including; dynamic pressure, control hinge linear stiffness, or even freeplay, can be quickly compromised in the nonlinear regime. In this paper, the nonlinear sensitivity of selected critical parameters is addressed by interpolating a library of nonlinear unsteady aerodynamic ROMs across a compact subspace in dynamic pressure and freeplay magnitude. The ROM, based on Lagrange interpolation of sparse higher-order Taylor partial derivatives, demonstrates excellent precision in modelling high amplitude transonic limit cycle oscillations for an all-movable wing with freeplay, capturing the LCO region (up to 96% of the linear flutter boundary), and for a range of freeplay values.

1 Introduction

One of the challenges in modeling aeroelastic systems with discrete structural nonlinearities such as, freeplay, in the transonic flow regime, is the potential for nonlinear aerodynamic loads that coexist with the structural nonlinearity [1, 2]. While linearization of the nonlinear structural model is common practice in aeroelastic problems involving freeplay (employing techniques such as fictitious masses [3] or residual vectors [4]), the assumption of aerodynamic linearization may, for some transonic systems, be invalid even for small parameter changes [5]. In such cases, to avoid the exhaustive computational burden associated with using a computational fluid dynamics (CFD) code to resolve the forces at each time-step, a vast range of nonlinear unsteady aerodynamic reduced order models (ROMs) have been proposed [6,7,8,9,10,11].

Considering that in the field of nonlinear aeroelasticity the nonlinear unsteady aerodynamic forces on the elastic structure are typically reduced to integrated quantities, the functional series approach (multi-variable Taylor series expansion or Volterra series) is well suited, describing the generalized nonlinear aerodynamic forces acting on the structure as a nonlinear dynamic function of the generalized structural displacements. The merits of this class of ROM are that i) it is relatively simplistic to implement with minimal modification to standard CFD software, ii) it intrinsically captures nonlinearity in its functional form, and iii) the online computational savings are typically several order of magnitude compared to full-order aeroelastic simulations. Two primary drawbacks include the curse of dimensionality that is associated with identifying higher-order systems - traditionally limiting it from being applied to complex 3D aeroelastic systems, and a reduced ability to generalize for systems with strong nonlinearity.

In recent work by the authors [2], limitations related to the curse-of-dimensionality are addressed using sparsity promoting algorithms to significantly reduce the amount of training data required to identify the higher-order polynomial terms. The study demonstrates that through Orthogonal Matching Pursuit, it is possible to efficiently identify the optimized s-sparse nonlinear unsteady aerodynamic ROMs, exemplified through application to a three-dimensional aeroelastic stabilator model experiencing high amplitude freeplay-induced limit cycles. The comparison shows excellent agreement between the ROM and the full-order model (FOM), demonstrating the feasibility of applying accurate, higher-order polynomial-based ROMs to complex nonlinear aeroelastic problems without incurring significant computational burdens.

In terms of the second limitation related to increased sensitivity and reduced ability to generalize, first one must consider the importance of generalization and what a reasonable expectation is for a given ROM to generalize. For example, consider the linear definition of functional series-based ROMs, i.e., the aerodynamic impulse response which, within the linear unsteady aerodynamic regime, is quite robust to certain parameter changes. These include: dynamic pressure (the generalized forces scale linearly for a fixed Mach number and angle-of-attack (AoA)), structural stiffness and damping parameters (e.g., related to control surfaces or pylon linkages), and even nonlinear structural parameters, such as, freeplay magnitude. As a result of this insensitivity, it is common practice to generate a linear ROM at a fixed Mach number and AoA (noting high sensitivity to these two parameters), and to then use the linearized ROM freely for the desired application. Unfortunately, in the nonlinear regime (e.g., high amplitude limit cycles and/or high-AoA maneuvers in transonic flow), there is no guarantee of such generalizability given the structural amplitude (or velocity) dependency of the nonlinear aerodynamic loading on the structure. Specifically, as the nonlinearity strength increases, the ROM can become sensitive to said parameters, hereby leading to a reduction in the ability of the ROM to generalize. To this end, the aim is to develop a unified nonlinear reduced order model that performs effectively across the specified parametric sub-spaces – this forms the core objective of this research.

This paper proposes that using Lagrange polynomials, it is possible to interpolate a library of linear and sparse nonlinear unsteady aerodynamic ROMs (in the form of Taylor partial derivatives), across a subspace defined in dynamic pressure and freeplay. The library contains unsteady aerodynamic ROMs computed for a three-dimensional aeroelastic stabilator model that are tuned for optimal aeroelastic performance for various combinations of freeplay and dynamic pressure, referred to as sampled ROMs from now on. The interpolation scheme allows the sampled ROMs to be generated with disparity in polynomial-order, sparsity, and cardinality, i.e., the shape and sparsity of the derivative tensors to be interpolated are unimportant. The interpolated nonlinear unsteady aerodynamic ROM is applied to the model with freeplay undergoing high amplitude LCO at high transonic Mach numbers, demonstrating excellent precision with respect to the full-order aeroelastic model.

The remainder of the paper is organized as follows; in Sect. 2 the ROM identification procedure and interpolation scheme are defined. The nonlinear aeroelastic system is described in Sect. 3 including practical details pertaining to the implementation of the nonlinear unsteady aerodynamic ROM library and interpolation scheme. The results are presented and discussed in Sect. 4, then final discussion and concluding remarks are offered in Sect. 5.

2 Generation and interpolation of the unsteady aerodynamic ROM library

2.1 Unsteady aerodynamic ROMs based on functional series

The earliest works in nonlinear aeroelasticity consider the identification of Volterra kernels by applying unit-impulse/step functions (or variations of these) to excite the structural system within a full-order aerodynamic solver, and recording the “exact” linear / nonlinear aerodynamic impulse response [12,13,14,15,16,17,18,19]. More recently, it has been shown that identification of the nonlinear kernels using impulses can be overly rigid and comes with a range of limitations, in particular for CFD-based identification [20]. An alternative approach is to randomly excite the full-order system and record the unsteady aerodynamic response. Then using any form of linear regression, the linear and nonlinear kernels can be derived. Examples include; time-delay neural networks [21], least squares (LS) [20, 22], or sparsity promoting LS algorithms [2], where the limitations described above can be largely overcome. To this effect, Balajewicz and Dowell [20] introduce the sparse Volterra series for efficient generation of higher-order order transonic aeroelastic ROMs, which was recently extended by the authors [2] using sparsity promoting algorithms to drastically reduce the amount of training data needed to identify the higher-order system. Brown [23] presents a multi-input Volterra based approach for a 3-DOF aeroelastic system. A blended step is used as excitation and $\ell _1$-regularized least-squares is used to derive the kernels which are expressed in terms of Laguerre polynomials to reduce the number of coefficients to be identified. The performance is generally very good, however, it is noted that out-of-sample performance in terms of reduced velocity is challenging in the nonlinear regime, as to be expected.

2.2 Multi-variable taylor series expansion of the unsteady aerodynamic forces

Assuming that the unsteady aerodynamic forces on a structure can be described in discrete as a dynamic function of structural displacement by

$$\begin{aligned} Q_n = f(\varvec{u}) \end{aligned}$$

(1)

where the subscripts denotes the discrete time interval, ${Q_n}$ represents the generalized aerodynamic force at the current time interval n, $\varvec{u} = \{u_n, u_{n-1}, u_{n-2}, \ldots u_{n-k}\}^\textrm{T}$ is a vector of generalized displacements, k defines the number of time lags and f() is an unknown nonlinear dynamic function. Then, provided that the system is mildly nonlinear and memory fading $f(\varvec{u})$ can be approximated using a multi-variable Taylor series expansion according to

$$\begin{aligned} f(\varvec{u}) \approx T(\varvec{u}) \end{aligned}$$

(2)

which is evaluated at a reference location $\varvec{u} = \varvec{a}$ according to

$$\begin{aligned} \begin{aligned} T(\varvec{u})&= f(\varvec{a}) + \sum ^{n-k}_{j_1=n}\frac{\partial f(\varvec{a})}{\partial u_{j_1}}(u_{j_1} - a_{j_1}) \\&\quad + \frac{1}{2!}\sum ^{n-k}_{j_1=n} \sum ^{n-k}_{j_2=n}\frac{\partial ^2 f(\varvec{a})}{\partial u_{j_1} \partial u_{j_2}}\\&(u_{j_1}-a_{j_1})(u_{j_2}-a_{j_2}) + \ldots \\&+ \frac{1}{p!}\sum ^{n-k}_{j_1=n}\sum ^{n-k}_{j_2=n} \ldots \sum ^{n-k}_{j_p=n} \frac{\partial ^p f(\varvec{a})}{\partial u_{j_1} \partial u_{j_2} \ldots \partial u_{j_p}}\\&(u_{j_1}-a_{j_1})(u_{j_2}-a_{j_2}) \ldots (u_{j_p}-a_{j_p}) \end{aligned} \end{aligned}$$

(3)

where p is the order of the Taylor expansion [24]. This can be reduced to multi-index form and written as

$$\begin{aligned} T(\varvec{u}) = f(\varvec{a}) + \sum _{p_i=1}^p \frac{1}{{p_i}!}(\varvec{u} - \varvec{a})^{p_i}\varvec{D}^{p_i} \end{aligned}$$

(4)

where $\varvec{D}^{p_i} = (\partial ^{p_i} f)(\varvec{a})$ is a tensor of partial derivatives of $f(\varvec{a})$ of order $p_i$. Specifically, $\varvec{D}^1$ is the gradient of $f(\varvec{a})$, $\varvec{D}^2$ is the Hessian matrix, and so on. Given that $f(\varvec{a})$ is not known a priori, the coefficients of $\varvec{D}^{p_i}$ are estimated from input–output training data, i.e., the coefficients are identified to minimize the error between the Taylor approximation and the true values by $min||Q_n - T(\varvec{u})||$.

2.3 Identification of the Taylor partial derivatives

The procedure for identifying the unsteady unsteady aerodynamic ROMs is now described. This definition is for a single-input single-output system. The reader is referred to [20] for identification using a multi-input approach.

2.3.1 Band limited random excitation

The first step in creating any unsteady aerodynamic ROM is to perturb the structural modes using a full order aerodynamic solver and to record the aerodynamic responses. In this approach, the structural model is excited using band limited random noise within a commercial finite volume CFD solver. Using the SISO identification procedure, each mode is excited in isolation (i.e., nonlinear interactions between structural modes are neglected). The amplitude and frequency band of the excitation functions are chosen by estimating the LCO amplitudes and frequencies in the aeroelastic response.

An important consideration is to observe a smooth transition from the undeformed structure and converged steady-state fluid forces. The reason being that any discontinuity (i.e., a step-like change in structural displacement) will cause spurious aerodynamic response information and inaccuracies in the ROM identification process. A hyperbolic tangent (Fig. 1) is applied to the raw signal $\varvec{u}_{j,r}$, ensuring a smooth transition to the modal excitation over the first 50 time intervals, given for n total input samples by

$$\begin{aligned}{} & {} \varvec{S_F} = 0.5\tanh {\left( \frac{n-20}{6}\right) +1} \end{aligned}$$

(5)

$$\begin{aligned}{} & {} \varvec{u}_j = \varvec{S_F}\varvec{u}_{j,r} \end{aligned}$$

(6)

where $\varvec{u}_j$ is the band limited random signal used to excite the $j^{th}$ structural mode.

Fig. 1

Hyperbolic tangent smoothing function

2.3.2 Input and output matrices

Considering a total of m structural modes, the vector of outputs is constructed by exciting each $j^{th}$ structural mode individually using $\varvec{u}_j \in \mathbb {R}^n, j = 1,\ldots , m$ (Eq. 6) and the resultant full-order aerodynamic forces are projected onto each $i^{th}$ structural mode to give:

$$\begin{aligned} \varvec{Q}^{ij}= & {} \{Q_1^{ij}, Q_2^{ij}, \ldots , Q_n^{ij}\}^\textrm{T} \in \mathbb {R}^n, \nonumber \\{} & {} i = 1,\ldots , m, j = 1,\ldots , m \end{aligned}$$

(7)

where n is the total number of samples and $\varvec{Q}^{ij}$ represents the generalized aerodynamic forces in mode i due to perturbation of mode j. To construct the matrix of inputs, first a lower left triangular circulant matrix is constructed from $\varvec{u}_j$ (truncated for k time lags) to give:

$$\begin{aligned} \varvec{L}^j = \begin{bmatrix} u_{j,1} &{} 0 &{} \ldots &{} 0\\ u_{j,2} &{} u_{j,1} &{} \ldots &{} 0\\ \vdots &{} \vdots &{} \ddots &{} 0\\ u_{j,n} &{} u_{j,n-1} &{} \ldots &{} u_{j,n-k}\\ \end{bmatrix} \in \mathbb {R}^{n \times k}, j = 1,\ldots , m \end{aligned}$$

(8)

and the $p^{th}$-order polynomial expansion of the rows gives:

$$\begin{aligned} \varvec{\mathcal {M}}^j =&\begin{bmatrix} u_{j,1} &{} 0 &{} \ldots &{} 0 &{} u_{j,1}^{2} &{} 0 &{} \ldots &{}0 \\ u_{j,2} &{} u_{j1} &{} \ldots &{} 0&{} u_{j,2}^{2} &{} u_{j,2}u_{j,1} &{} \ldots &{}0\\ &{} &{} &{} &{} \vdots &{} &{} \ddots \\ u_{j,n} &{} u_{j,n-1} &{} \ldots &{} u_{j,n-k} &{} u_{j,n}^2&{} \ldots &{} &{} u_{j,n-k}^p\\ \end{bmatrix} \nonumber \\&\in \mathbb {R}^{n \times \kappa }, j = 1,\ldots , m \end{aligned}$$

(9)

where $\kappa = \sum _{l = 1}^p\left( {\begin{array}{c}k+(l-1)\\ l\end{array}}\right)$.

2.3.3 Identification of the reduced order model using Pseudo-inverses

Identifying the coefficients of the partial derivatives is a linear problem [25], given for the system inputs and outputs by

$$\begin{aligned} \varvec{Q}^{ij} = \varvec{\mathcal {M}}^j\varvec{d}^{ij} \end{aligned}$$

(10)

where $\varvec{d}^{ij} = \{d_1^{ij}, d_2^{ij}, \ldots , d_\kappa ^{ij} \}^\textrm{T} \in \mathbb {R}^{\kappa }, i = 1,\ldots , m, j = 1,\ldots , m$ contains the flattened tensors of partial derivatives corresponding to the generalised aerodynamic forces for $\varvec{Q}_i(\varvec{u}_j)$ which is an unknown. The full set of partial derivatives (no sparsity) can be identified by solving the inverse linear problem using pseudo-inverses:

$$\begin{aligned} \varvec{d}^{ij} = \varvec{\mathcal {M}}^{j+}\varvec{Q}^{ij} \end{aligned}$$

(11)

where $^+$ is the Moore-Penrose Pseudo-Inverse. Finally, iterating through each structural mode, all instances of $\varvec{d}^{ij}$ are stored in a three-dimensional array $\varvec{\bar{D}} \in \mathbb {R}^{m \times m \times \kappa }$.

2.3.4 Identification of the reduced order model using orthogonal matching pursuit

Initially, the OMP algorithm is explicitly defined. [26] Considering the linear problem for $\varvec{A} \in \mathbb {R}^{n_b\times n_x}$ ($n_x \gg n_b$) inputs and $\varvec{b} \in \mathbb {R}^{n_b}$ output observations, which is given by

$$\begin{aligned} \varvec{Ax} = \varvec{b} \end{aligned}$$

(12)

then the objective is to recover a sparse representation of $\varvec{x} \in \mathbb {R}^{n_x}$ by solving the $\ell _0$-minimization problem

$$\begin{aligned} \underset{\varvec{x}}{{\text {argmin}}} ||\varvec{x}||_0 \quad \text {subject to} \quad \varvec{Ax} = \varvec{b} \end{aligned}$$

where $||\varvec{x}||_0$ is the $\ell _0$ pseudo-norm, which is the number of non-zero elements in $\varvec{x}$. Assuming that $\varvec{x}$ is s-sparse ($s_x \ge ||\varvec{x}||_0$), it can be recovered exactly by OMP if $\varvec{A}$ and $\varvec{x}$ satisfy following inequality:

$$\begin{aligned} \mu _A < \frac{1}{2s_x - 1} \end{aligned}$$

(13)

where $\mu _M$ is the mutual coherence of the columns of $\varvec{A}$ and $s_x$ is the sparsity of $\varvec{x}$. From Eq. 13, $\varvec{x}$ can be at most $\frac{1}{2\mu }$-sparse. The OMP algorithm is as follows

Algorithm 1

OMP ($\varvec{A}$, $\varvec{b}$)

To construct the Optimal Sparsity ROM (OS-ROM), the $\ell _0$-minimization problem is written in terms of $\varvec{\mathcal {M}}^j$ and $\varvec{Q}^{ij}$ as

$$\begin{aligned} \underset{\varvec{d_s}^{{ij}}}{{\text {argmin}}} ||\varvec{d_s}^{{ij}}||_0 \quad \text {subject to} \quad \varvec{\mathcal {M}}^{j}\varvec{d_s}^{{ij}} = \varvec{Q}^{ij} \end{aligned}$$

where $\varvec{d_s}^{{ij}} \in \mathbb {R}^{\kappa }$ contains the optimal sparse partial derivatives corresponding to the generalised aerodynamic forces for $\varvec{Q}_i(\varvec{u}_j)$. Equation 2.3.4 can be solved directly using the OMP Algorithm 1 according to

$$\begin{aligned} \varvec{d_s}^{ij} = \textrm{OMP}(\varvec{\mathcal {M}}^j,\varvec{Q}^{ij}) \end{aligned}$$

(14)

Finally, iterating through each structural mode, all instances of $\varvec{d_s}^{ij}$ are stored in a three-dimensional array $\varvec{\bar{D}_s} \in \mathbb {R}^{m \times m \times \kappa }$. Practically speaking, $\varvec{\bar{D}_s}$ contains the optimal set of s-sparse coefficients of the $p^{th}$-order unsteady aerodynamic ROM, satisfying the linear problem in Eq. 10. This can be used in a time-marching aerodynamic or aeroelastic simulation to obtain the aerodynamic forces on the structure at each time interval.

2.4 Scheme for direct interpolation of the ROM library

This inability of the nonlinear ROM identified at a single set of operating conditions to generalize to new operating conditions is a limitation that is addressed by interpolating a library of ROMs (Taylor partial derivatives). The objective is to minimize the number of sampled ROMs that need to identified (given the associated computational cost), while ensuring that the two-dimensional subspace can be resolved with sufficient accuracy.

For an $\mathcal {N}$-dimensional parameter space, containing the parameters $\chi _{1}, \chi _{2}, \ldots , \chi _{\mathcal {N}}$, for $N_R > 1$ sampled ROMs $\varvec{\bar{D}_{T}}^{i} \in \mathbb {R}^{m\times m \times \kappa }, i=1,\ldots ,N_R$ that are constructed at operating points $\varvec{X}_i = \{\chi _{1i}, \chi _{2i}, \ldots , \chi _{{\mathcal {N}}_i}\}$, then the set of operating points of these ROMs $\varvec{\varLambda }$ is given by

$$\begin{aligned} \varvec{\varLambda } = \{\varvec{X}_1, \varvec{X}_2, \ldots \varvec{X}_{N_R}\} \end{aligned}$$

(15)

Then the objective is to interpolate the basis of ROMs to construct a new ROM at the operating point $\varvec{X}_{N_R + 1} \notin \varvec{X}$.

Given that each sampled ROM $\varvec{\bar{D}_{T}}^{i}$ can be generated with a different polynomial order and a different number of lag terms, disparity in the index location of the terms in each ROM in the basis must be accounted for. Figure 2a gives an example of three vectors with disparity in the number of linear and nonlinear terms (first-order terms are black, second-order terms are red and third-order terms are blue). $\varvec{d}^1$ contains four first-order terms only, $\varvec{d}^2$ contains three first-order terms and six second-order terms, and $\varvec{d}^3$ contains two first-order terms, three second-order terms and four third-order terms. Direct interpolation of these vectors is not possible using the scheme proposed in this paper. Therefore a base vector $\varvec{{d}_{T_{I0}}}$ is created by identifying the ROM with the maximum number of terms for each derivative order separately, given by

$$\begin{aligned} \varvec{{d}_{T_{I0}}} = \{0, 0, \ldots , 0\} \in \mathbb {R}^{\kappa _I} \end{aligned}$$

(16)

where $\kappa _I = \left( {\begin{array}{c}k_{m1}\\ 1\end{array}}\right) + \left( {\begin{array}{c}k_{m2}+1\\ 2\end{array}}\right) + \cdots + \left( {\begin{array}{c}k_{mp}+(p-1)\\ p\end{array}}\right)$, $k_{mp}$ is the number of lag terms used to generate the largest $p^{th}$-order tensor in the basis, and therefore, $\varvec{{d}_{T_{I0}}}$ contains the index of every coefficient in the basis. Returning to the example problem, the base vector $\varvec{{d}_{T_{I0}}}$ is pre-initialized with allocations for four linear terms, six second-order terms and four third-order terms. The indices of the original vectors are then re-allocated to the locations in the base vector (Fig. 2b) and direct interpolation is possible.

Fig. 2

a Example vectors with inconsistent linear and nonlinear terms, and b the reallocation of the indices using a consistent base vector

Lagrange polynomials are used to interpolate the ROM basis which, considering that each parameter can be defined by an interpolation scheme of different order $p_{\mathcal {L}1}, p_{\mathcal {L}2}, \ldots , p_{\mathcal {L}{\mathcal {N}}}$, are given for the new operating conditions $\varvec{X}_I$ by

$$\begin{aligned} \textrm{ROM}:= & {} \varvec{\bar{D}_{T_I}} = \sum _{R_1=1}^{p_{\mathcal {L}1}+1} \sum _{R_2=1}^{p_{\mathcal {L}2}+1} \ldots \sum _{R_{\mathcal {N}}=1}^{p_{\mathcal {L}\mathcal {N}}+1} \mathcal {L}_{R_{1},\ldots , R_{\mathcal {N}}}\nonumber \\{} & {} (\varvec{X}_{I})\varvec{\bar{D}_T}^{R_{1},\ldots , R_{\mathcal {N}}} \end{aligned}$$

(17)

where

$$\begin{aligned} \mathcal {L}_{R_{1},\ldots , R_{\mathcal {N}}}(\varvec{X}_I)= & {} \prod _{\genfrac{}{}{0.0pt}{}{0 \le k_1 \le p_{\mathcal {L}1}}{k_1 \ne {R_1}}} \frac{\chi _{1I} - \chi _{1{k_1}}}{\chi _{1{R_1}} - \chi _{1{k_1}}} \nonumber \\{} & {} \ldots \prod _{\genfrac{}{}{0.0pt}{}{0 \le k_{\mathcal {N}} \le p_{\mathcal {L}\mathcal {N}}}{k_\mathcal {N} \ne {R_{\mathcal {N}}}}} \frac{\chi _{\mathcal {N}I} - \chi _{{\mathcal {N}}{k_{\mathcal {N}}}}}{\chi _{{\mathcal {N}}R_{{\mathcal {N}}}} - \chi _{{\mathcal {N}} k_{\mathcal {N}}}} \end{aligned}$$

(18)

where $\chi _{{\mathcal {N}}k_{{\mathcal {N}}}}$ and $\chi _{{\mathcal {N}} R_\mathcal {N}}$ are the operating conditions for parameter $\mathcal {N}$ at sampling locations $k_\mathcal {N}$ and $R_\mathcal {N}$, and $\chi _{\mathcal {N}I}$ is the interpolated location of parameter $\mathcal {N}$.

3 Nonlinear aeroelastic framework

3.1 Modified AGARD 445.6 wing

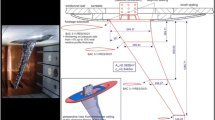
The AGARD 445.6 wing is a well known transonic benchmark case, with experiments conducted in the NASA transonic dynamic wind tunnel. The model consists of a tapered swept wing (see Fig. 3a) with a NACA 65A004 airfoil section and sweep angle of 45 [$^\circ$]. The material properties considered here are those of the weakened model (No. 3) [27]. For a comprehensive validation of the AGARD benchmark model using aerodynamic impulse responses, see recent work by the authors [28, 29].

Fig. 3

a Modified AGARD 445.6 wing geometry specifications and b hinge stiffness as a function of rotation

In this paper, the wing is modified to represent an all-movable control surface (first presented by Carrese et al. [30]), with a torsional spring added to a centered node at the root, which is free to rotate about the pitch axis. The torsional spring contains a zero-stiffness dead-zone and a nominal stiffness of $k_{\delta } = 500$ Nm/rad otherwise, as depicted in Fig. 3b.

3.2 Nonlinear aeroelastic equations-of-motion

The equation-of-motion for an aeroelastic system with concentrated structural nonlinearity in discrete (nodal) coordinates is given as

$$\begin{aligned}{} & {} \varvec{M_v}\ddot{\varvec{v}} + \varvec{R}(\delta ) + \varvec{F_v} = 0 \end{aligned}$$

(19)

$$\begin{aligned}{} & {} \varvec{R}(\delta ) = \varvec{K_v}\varvec{v} + \varvec{F_c}(\delta ) \end{aligned}$$

(20)

where $\varvec{M_v}$ and $\varvec{K_v}$ are the structural mass and stiffness matrices, $\varvec{v} = \{v_1,\ v_2,\ \ldots ,\ v_N\}^\textrm{T}$ is the displacement vector of N degrees-of-freedom, and $\dot{\varvec{v}}$ is the time derivative of $\varvec{v}$. $\varvec{F_v} = \{F_{v1},\ F_{v2},\ \ldots ,\ F_{vN}\}^\textrm{T}$ is the aerodynamic force vector in nodal coordinates. The freeplay loads are given by $\varvec{F_c}(\delta )$ which is only non-zero at the node which contains freeplay, taking the form

$$\begin{aligned} \varvec{F_c}(\delta ) = \left\{ \begin{array}{lll} k_{\delta }(\delta -\delta _s) &{} &{}\quad \delta > \delta _s \\ 0, &{}\quad \text {if}&{}\quad -\delta _s< \delta< \delta _s \\ -k_{\delta }(\delta -\delta _s) &{} &{}\quad \delta < -\delta _s \end{array} \right. \end{aligned}$$

(21)

where $\delta$ is the rotational displacement of the root about the freeplay hinge axis and $2\delta _s$ is the total rotational freeplay magnitude. The system described by Eq. (19) can be reduced by considering modal coordinates, such that the structural motion is approximated as the linear superposition of a subset of m normal modes $\varvec{\varPhi }_{v}$ due to generalised displacement $\varvec{\xi }$. Given the freeplay nonlinearity, the mode shapes in $\varvec{\varPhi }_{v}$ cannot properly account for localized displacements in the region of the nonlinear hinge. In this work, the fictitious masses (FM) method proposed by Karpel and Newman [3] is used to improve the representation of these local deformations in the set of low frequency modes. A large fictitious mass is added to the mode of the mass matrix where the discrepancy in localized displacements occurs, then the normal mode shapes are obtained from free vibration analysis and used in the aeroelastic simulation. The baseline FM modes $\varvec{\varPhi }_B$ are derived using ANSYS MAPDL, yielding the generalised system in baseline fictitious mass coordinates

$$\begin{aligned} \varvec{M}_B\varvec{\ddot{\xi }} + \varvec{R}_B(\delta ) + \varvec{Q} = 0 \end{aligned}$$

(22)

where $\varvec{M}_B = \varvec{\varPhi }_{B}^\textrm{T}\varvec{M_v}\varvec{\varPhi }_{B}$, $\varvec{R}_B(\delta ) = \varvec{\varPhi }_{B}^\textrm{T}\varvec{K_v}\varvec{\varPhi }_{B}\varvec{\xi } + \varvec{\varPhi }_{B}^\textrm{T}\varvec{F_c}(\delta )$, and $\varvec{Q} = \varvec{\varPhi }_{B}^\textrm{T}\varvec{F_v}$ is the generalized aerodynamic force vector. The first four FM modes are provided in Fig. 4. The first eight eigenvalues of the baseline FM modes and normal modes are given in Table 1 where excellent agreement with the results of Carrese et al. [30] can be observed. The poor matching of mode 8 is an artifact of the fictitious masses method which accounts primarily for local deformations. For comprehensive numerical validation and derivation of the FM model, see Hale et al. [31].

Fig. 4

First four fictitious mass modes with zero stiffness at the root with a mode 1 (0 Hz), b mode 2 (28.24 Hz), c mode 3 (39.52 Hz) and d mode 4 (84.33 Hz)

Table 1 Natural frequencies for the root stiff and free cases calculated directly and with fictitious masses

At this point it is important to note that in the general definition of the Taylor series expansion of the unsteady aerodynamic forces, the structural displacements defined by $\varvec{u}$ (Eq. 1) are equivalent to $\varvec{\xi }$ and will be referred to as such from now on.

3.3 Computational fluid dynamics model

For the FOM, the generalized aerodynamic force vector $\varvec{Q}$ is obtained using the commercial finite-volume Navier–Stokes solver ANSYS Fluent 2023 R1. The Euler equations for transient flowfields are solved via a coupled pressure-based solver with implicit second-order spatial and first-order temporal discretization of the flowfields with Rhie-Chow: distance-based flux interpolation. The convergence criteria are set to $1\times 10^{-4}$ for the scaled residuals at each time-step. The investigation is conducted on a structured grid of $70\times 10^{3}$ elements, with a minimum orthogonal quality of 0.032. It is important to note that this numerical mesh is validated against experimental campaign [27] via linear stability analysis [28, 29] for the unmodified AGARD wing. Grid deformation is facilitated using a diffusion-based approach. The Modal Projection and force Reconstruction (MPR) method [32] is used to project the structural mode shapes onto the fluid grid. MPR includes a robust interpolation scheme that accounts for disparity in the grid topologies, and conserves forces and moments.

3.4 Unsteady aerodynamic ROM library and interpolation scheme

3.4.1 Generalized aerodynamic forces

The ROMs are generate with knowledge of the modal LCO response. Three separate sets of generalized aerodynamic forces are generated; using generalized displacements that are based on the natural frequencies and modal LCO amplitudes for (i) the lowest dynamic pressure $q_\infty =3768$ [Pa] ($\varvec{\bar{\xi }_A}$), (ii) the highest dynamic pressure of $q_\infty = 4012$ [Pa] with $\delta _s = 0.5^\circ$ ($\varvec{\bar{\xi }_B}$), and (iii) the highest dynamic pressure with $\delta _s = 1^\circ$ ($\varvec{\bar{\xi }_C}$). Table 2 summarizes the frequencies and maximum amplitudes of the random excitation of the generalized displacements for each mode. Four modes are used in the identification procedure which is the minimum number required for the basis to provide a good representation of the full-order structural model [31]. Figure 5a presents an example of the band limited random excitation of mode 2 $\varvec{{\xi }_{2,C}}$ for a total of $n = 400$ samples. Figure 5b presents the total generalized aerodynamic forces in mode 1 and mode 2, comparing $\varvec{Q_{FOM}}$, the linear $\varvec{Q_{ROM}}$ and the third-order $\varvec{Q_{OS-ROM}^{42}}$. Although the forces in mode 1 are well captured by the linear model, the third-order ROM demonstrates a more than $2\times$ reduction in error. In mode 2 it is clear that the third-order OS-ROM provides superior performance with a 3–4$\times$ reduction in error compared to the linear ROM, nearly perfectly overlaying the FOM aerodynamic response.

Table 2 Parameters of the band limited random excitation

Fig. 5

Cross validation data; a band limited random excitation of mode 2, and b comparison between the FOM and ROM generalized aerodynamic forces for $\varvec{Q_4}(\varvec{\xi _2})$

3.4.2 Parametric subspace

The parameter space is discretized according to nine separate sampled ROM locations $\varvec{\bar{D}_{T}^{ij}}$ (Fig. 6). The ROMs are specifically targeted at freeplay values $0.5^\circ \le \delta _s \le 1^\circ$, and dynamic pressures $3768~ [\text {Pa}] \le q_\infty \le 4102 [\text {Pa}]$, capturing the nonlinear instability region up to 96% of the flutter boundary.

Fig. 6

Two-dimensional subspace and locations of the sampled ROMs

3.4.3 Hyperparameter optimization

Hyperparameter optimization is conducted for each sampled ROM, i.e., tuning the ROM to optimize aeroelastic performance at the discrete location of the subspace. For the lowest dynamic pressure linear models are generated using pseudo-inverses where $\varvec{\bar{\xi }_A}$ is used to generate the generalized forces. For the highest dynamic pressure, OS-ROMs are generated using $\varvec{\bar{\xi }_B}$ for $\delta _s = 0.5^\circ$ and, $\varvec{\bar{\xi }_C}$ for $\delta _s = 0.75^\circ$ and $\delta _s = 1^\circ$. To reduce the computational burden associated with ROM generation, the ROMs for the mid-point dynamic pressures are simply defined as some ratio between the ROM generated for the maximum and minimum dynamic pressures, according to

$$\begin{aligned} \varvec{\bar{D_{T}}}^{i2} = C_1 \varvec{\bar{D_{T}}}^{i1} + C_3 \varvec{\bar{D_{T}}}^{i3} \end{aligned}$$

(23)

The aeroelastic optimization problem uses the objective $\text {argmin}||\delta _{FOM}(t) - \delta _{ROM}(t)||$ which is quantified according to

$$\begin{aligned} nrmsd_{\delta } = nrmsd(\delta _{FOM}(t),\delta _{ROM}(t)) \end{aligned}$$

(24)

where $\delta$ is the rotational aeroelastic response at the root hinge node. The hyperparameters of the aeroelastic optimization are summarized in Table 3.

Table 3 Hyperparameter space for the aeroelastic optimization

3.4.4 Direct interpolation scheme

The discretization and interpolation schemes for the subspace are as follows; (i) $2 \times 2$ discretization of the subspace with bilinear interpolation ($\mathrm {ROM_{4}^{1}}$), and (ii) $3 \times 3$ discretization of the subspace with biquadratic interpolation($\mathrm {ROM_{9}^{2}}$).

Given that both linear and third-order ROMs are used, and that the second-order and third-order partial derivatives are identified using the same number of lag terms, then the base vector (Eq. 27) is created using

$$\begin{aligned} \kappa _I = \left( {\begin{array}{c}k_{m,lin}\\ 1\end{array}}\right) + \left( {\begin{array}{c}k_{m,nl}+1\\ 2\end{array}}\right) + \left( {\begin{array}{c}k_{m,nl}+2\\ 3\end{array}}\right) \end{aligned}$$

(25)

The interpolated ROM is then derived for the new freeplay $\delta _{s_I}$ and dynamic pressure $q_{\infty _I}$ from Eq. 17, for interpolation scheme of order $p_{\mathcal {L}}$ by

$$\begin{aligned}{} & {} \mathrm {ROM_{(p_{\mathcal {L}}+1)^2}^{p_{\mathcal {L}}}} :=\varvec{\bar{D}_{T_I}} = \sum _{i=1}^{p_{\mathcal {L}}+1} \sum _{j=1}^{p_{\mathcal {L}}+1} \mathcal {L}_{ij}(\delta _{s_I}, q_{\infty _I})\varvec{\bar{D}}_T^{ij}\nonumber \\{} & {} \textrm{where} \quad i \ne 2, j\ne 2 \quad \textrm{if} \quad p_{\mathcal {L}} < 2 \end{aligned}$$

(26)

where

$$\begin{aligned}{} & {} \mathcal {L}_{ij}(\delta _{s_I},q_{\infty _I})\nonumber \\{} & {} \quad = \prod _{\genfrac{}{}{0.0pt}{}{0\le k_\delta \le p_\mathcal {L}}{k_\delta \ne i}} \frac{\delta _{sI} - \delta _{sk_\delta }}{\delta _{si} - \delta _{sk_\delta }} \prod _{\genfrac{}{}{0.0pt}{}{0 \le k_q \le p_\mathcal {L}}{k_q \ne j}} \frac{q_{\infty _I} - q_{\infty k_q}}{q_{\infty j} - q_{\infty k_q}} \end{aligned}$$

(27)

3.5 Aeroelastic time integration

The aeroelastic system is solved using the RMIT in-house Fluid–Structure Interaction code PyFSI. Full-order aeroelastic solutions are achieved by marching Eq. 22 forward in time, where the wing transient structural motion is solved using Newmark-$\beta$ time-integration. Newton–Raphson iterations are used to converge the state-dependent freeplay load within each time-step by minimizing error in the stiffness matrix. The nonlinear fluid loads $\varvec{Q}$ are resolved at every time-step using the CFD model described above.

For nonlinear unsteady aerodynamic ROM solutions, substituting Eqs. 10 into 22, the aeroelastic equation-of-motion becomes

$$\begin{aligned} \varvec{M}_B\varvec{\ddot{\xi }} + \varvec{R}_B(\delta ) + q_\infty \varvec{\mathcal {M}_B}\varvec{\bar{D}_{T_I}} = 0 \end{aligned}$$

(28)

where $\varvec{\mathcal {M}_B}$ contains the aeroelastic response in FM coordinates, updated at every time-step by marching the system of equations forward in time using the approach described above. The linear scaling of the generalized aerodynamic forces with dynamic pressure is entirely valid for the interpolated ROM. A numerical time-step of $\varDelta t = 0.001$ s is used in all simulations.

4 Results and discussion

In this section the results of the aeroelastic ROM are presented and discussed. All simulations are conducted at $M_\infty = 0.96$ and $\alpha _0 = 0^\circ$ with varying dynamic pressure and freeplay values.

4.1 Structural modal basis

Both the FOM and ROM consider a reduced structural modal basis and therefore this work is concerned only with the ROM being able to reproduce the CFD-based nonlinear aerodynamics. Provided that the number of modes is consistent between the FOM and ROM, the number of modes selected is less important than in studies concerned with nonlinear structural model reduction. That being said, it is important to ensure that the modal basis is sufficient to reasonably represent the nonlinear dynamics (LCO). A convergence study is conducted where each iteration computes the change in time response as additional modes are added to the basis using according to the nrmsd. A target of 2% is considered reasonable for this research given the offline computational resources associated with computing the nonlinear ROMs. Figure 7 presents the convergence study conducted for $\delta _s = 1$ [$^\circ$] and $q_\infty = 4102$ [Pa] where it can be seen that the addition of the fourth mode to the basis produces a change of less than 2% in the time response.

Fig. 7

Change in time response with increasing size of the modal basis for $\delta _s = 1$ [$^\circ$] and $q_\infty = 4102$ [Pa]

4.2 Sampled ROMs and performance without interpolation

4.2.1 Identification and sparsity promoting method

To justify the use of a higher-order system identification strategy with OMP as the sparsity inducing technique to solve the LS problem, the approach is now compared to other methods. These include; the linearized aerodynamic impulse response function (IRF) which was proposed originally by Silva [12] where the system is identified by directly impulsing the FOM and recording the aerodynamic response, diagonal sparsity (D-ROM) proposed by Balajewicz and Dowell [20] where a pre-selected sparsity pattern is embedded in $\varvec{\mathcal {M}}$ before solving for $\varvec{D_s}$ (the main diagonal terms), and the OMP-based approach originally proposed by the authors in [2] (OS-ROM). A rigorous hyperparameter grid search is performed for both sparsity inducing methods to ensure consistency. For a more detailed summary of the study performed in this section and the methods used see [12, 31, 33]. Figure 8 compares the phase portraits as predicted by the FOM and ROMs identified using different approaches. The case considered here is the highest amplitude LCO considered in this paper at $\delta _s = 1$ [$^\circ$] and $q_\infty = 4102$ [Pa]. It can be seen that the ROM identified using OMP outperforms that identified using the linearized aerodynamic impulse response. Both the diagonal sparsity technique and OMP perform well, although the ROM identified using OMP clearly outperforms. Furthermore, in [33] it is shown that the ROM identified using OMP is superior in terms of generalization.

Fig. 8

Phase portraits of the root rotational axis LCO comparing the FOM and ROMs identified using methods from the literature with $\delta _s = 1$ [$^\circ$] and $q_\infty = 4102$ [Pa]

4.2.2 Aeroelastic hyperparameter optimization

Table 4 summarizes the results of the aeroelastic hyperparameter grid search. For the linear ROMs the optimal number of lag terms is relatively consistent, as to be expected. For the OS-ROMs, the optimal number of lag terms increases as the freeplay magnitude increases, i.e., as the strength of the nonlinearity increases the memory fading nature of the system implies that more lags (or components in terms of Volterra kernels) are required. It is quite remarkable that high-precision ROMs can be identified with less than 15 total coefficients, where the full model is defined by hundreds. Figure 9 presents the phase portraits of the aeroelastic response at the freeplay hinge at the locations of the sampled ROMs. Excellent precision at these discrete locations can be observed, as to be expected. It should be noted that at $\delta _s = 0.5$ [$^\circ$], $q_\infty = 3768$ [Pa], the system is actually marginally stable - captured by the FOM and ROM $\varvec{\bar{D}_{T}}^{11}$.

Table 4 Hyperparameter optimization results (* are used in both ROM$_4^1$ and ROM$_9^2$)

Fig. 9

Comparison between FOM and ROM limit cycles at the sampled ROM locations

4.2.3 Out-of-sample performance

To demonstrate the ROM out-of-sample performance without interpolation the linear ROM $\varvec{\bar{D}_T}^{31}$ and third-order OS-ROM $\varvec{\bar{D}_T}^{33}$ are considered and the dynamic pressure and freeplay magnitude are varied. Figure 10a [2] presents the LCO amplitude at the hinge rotational axis as a function of dynamic pressure with a freeplay of $\delta _s = 1^\circ$. It can be seen that, as expected, the third-order OS-ROM does not scale particularly well with dynamic pressure, certainly not as well as what would be expected for an aeroelastic problem that is characterized by linear unsteady aerodynamics. That being said, considering the complexity and nonlinearity in the system, the result is reasonable and in line with the recent findings of Brown et al. [23]. The linear ROM that has been tuned for aeroelastic performance at the lowest dynamic pressure of interest performs very poorly when scaled with dynamic pressure.

Figure 10b presents the LCO amplitude as a function of freeplay magnitude, dynamic pressure remains constant at the exact values that the linear ROM $\varvec{\bar{D}_T}^{31}$ and third-order OS-ROM $\varvec{\bar{D}_T}^{33}$ were calibrated to. The third-order OS-ROM generalizes quite well, aside from an over prediction of the amplitude of the LCO for the lowest freeplay value of $\delta _s = 0.5^\circ$. The linear ROM also performs very well, however, is unable to capture the stable response at $\delta _s = 0.5^\circ$. Despite generally good performance in terms of new freeplay values, the over prediction at the lowest freeplay value means that in order to derive a nonlinear ROM that is highly accurate across the entire parameter space, interpolation is necessary.

Fig. 10

LCO amplitude at the hinge rotational axis using the linear ROM $\varvec{\bar{D}_T^{31}}$ third-order OS-ROM $\varvec{\bar{D}_T^{33}}$ without interpolation as a function of a dynamic pressure with $\delta _s = 1$ [$^\circ$], and b freeplay magnitude with $q_\infty = 3768$ [Pa] $q_\infty = 4102$ [Pa] [2]

4.3 Interpolated ROM performance

4.3.1 Limit cycle amplitude

The out-of-sample performance of the two interpolated ROMs is first investigated in terms of the ability to capture the transonic limit cycle amplitudes.

In Fig. 11 the contours demonstrate that the biquadratic ROM$_9^2$ is able to capture the entire parameter space with excellent precision while the bilinear ROM$_4^1$ is less accurate. The discrepancies are larger in regions of the space that are furthest from the sampled ROM$_1^4$ locations. The direction of the contours indicates that the LCO amplitude is more sensitive to dynamic pressure than to freeplay amplitude.

Figure 12 presents the LCO amplitude predictions for the entire parameter space. As mentioned previously, at the lowest dynamic pressure and freeplay the system is found to be stable and the sampled ROM is tuned to capture this. Although this was not by design, it is an excellent finding that the inclusion of this ROM in the library allows robust identification of the nonlinear flutter point. Figure 15b demonstrates that at $\delta _s = 0.5^\circ$ the bilinear ROM$_4^1$ captures the LCO amplitudes at the root rotational axis with very good precision and reasonable precision for $\delta _s = 0.625^\circ$. However, for freeplay values above this, discrepancies can be observed through under prediction of the LCO amplitude as the dynamic pressure increases beyond $q_\infty = 3846$ [Pa]. Figure 12b presents the LCO amplitudes modeled using the biquadratic ROM$_9^2$. Excellent agreement can be observed between the FOM and ROM solutions - demonstrating that the nonlinear parameter space can indeed be captured with excellent precision using a biquadratic interpolation scheme. Although not presented here, almost identical trends are observed for the tip response using ROM$_4^1$ and ROM$_9^2$.

Fig. 11

Contours of the LCO amplitude in the 2D parameter space at a the hinge rotational axis ($\pm \delta$ [$^\circ$]) and b the wing tip ($\pm u$ [m])

Fig. 12

LCO amplitude as a function of dynamic pressure at the root rotational axis comparing a FOM to ROM$_4^1$ and b FOM to ROM$_9^2$

4.3.2 Limit cycles at the parametric centroids

Figure 13 presents phase portraits at the centroids of biquadratic parameter space, i.e., at the furthest distances from the sampled ROMs. At the lower dynamic pressure region $q_\infty = 3846$ [Pa], the bilinear ROM$_4^1$ and biquadratic ROM$_9^2$ both capture the LCO with excellent precision for $\delta _s = 0.625^\circ$. With a freeplay of $\delta _s = 0.875^\circ$ the biquadratic ROM$_9^2$ is generally in very good agreement with the FOM, however, slightly over predicts the amplitude, making it more conservative. The bilinear ROM$_4^1$ slightly under predicts the amplitude and over predicts the depth of the inflections at the rotational velocity maxima.

For the higher dynamic pressure of $q_\infty = 4012$ [Pa] the biquadratic ROM$_9^2$ captures the limit cycle with excellent precision for freeplay of $\delta _s = 0.625^\circ$, while the bilinear ROM$_4^1$ under predicts the amplitude and over predicts the inflection points (at the maximum velocity regions of the cycle). With freeplay of $\delta _s = 0.875^\circ$, the bilinear ROM$_4^1$ severely under predicts the amplitude and also does not capture the sharpness of the inflection points. The biquadratic ROM$_9^2$ performs well, however, still slightly under predicts the velocity magnitude.

Figure 14 presents the nrmsd error at the parametric centroids for different numbers of sampled locations in the ROM basis. One sampled location (where the error is highest) considers only the ROM $\varvec{D_T^{33}}$ with no interpolation, four sampled locations is the ROM$_4^1$ and 9 sampled locations is the ROM$_9^2$. To achieve an nrmsd error of less than 2% for all locations, the ROM$_9^2$ is required, although at a significantly higher offline computational cost as is discussed in Sect. 4.5.

Fig. 13

Phase portraits of the root rotational axis LCO at the centroids of the biquadratic parameter space

Fig. 14

Error versus number of sampled locations in the ROM basis for the root rotational axis LCO

4.3.3 Limit cycles in generalized coordinates

To probe the ROM performance further, the generalized displacements are now investigated comparing the FOM to the biquadratic ROM$_9^2$ solutions. Figure 15 presents bifurcation diagrams for each mode with freeplay $\delta _s = 0.875^\circ$, i.e., plotting the maxima and minima of the generalized displacements at the five dynamic pressure validation locations. It can be seen that mode 1 is captured with excellent precision. Modes 2 and 3 are also captured well, however, some asymmetry can be observed at the highest dynamic pressure in the ROM which leads to a slight over prediction and there is a general under prediction at the lowest dynamic pressure. The dynamics of mode 4 present more interesting quasi-periodic behavior. It is quite impressive that the biquadratic ROM$_9^2$ is able to capture these dynamics quite well, including bifurcations that appear to occur between $q_\infty = 3846$ [Pa] and $q_\infty = 4012$ [Pa], i.e., the transition from a five period to three-period response. The lowest dynamic pressures present more error for mode 4, which is likely due to the low amplitude at this speed making it difficult to resolve. These discrepancies to not impact the global response in nodal coordinates.

Phase portraits of the generalized displacements are presented in Fig. 16 for the dynamic pressure $q_\infty = 4012$ [Pa]. For the lower freeplay $\delta _s = 0.625^\circ$ the biquadratic ROM$_9^2$ performance is very good for all modes. For the larger freeplay $\delta _s = 0.875^\circ$ mode 1 is captured with excellent precision while mode 2 and mode 3 demonstrate small discrepancies - not surprising given that this is at the centroid the most nonlinear quadrant of the parameter space. For mode 4 the five-period response is captured, however, asymmetry and associated discrepancies in amplitude can be observed. From these findings it is clear that the discrepancies that are observed for this case in Fig. 13 are the result of error in modes 2–4. The accuracy of the ROM could be potentially be improved using a multi-input identification framework, or certainly by optimizing the ROM in generalized coordinates, rather than for a single location in nodal coordinates.

Fig. 15

Bifurcation diagrams in generalized coordinates comparing FOM to ROM$_9^2$ solutions displaying a maxima of the LCO, and b minima of the LCO (logarithmic scale)

Fig. 16

Limit cycles in generalized coordinates at $q_\infty$ = 4012 [Pa] comparing the FOM to ROM$_9^2$ solutions

4.4 Extrapolation

The ability of the ROM to extrapolate to values outside the sampling range is investigated for the upper-right portion of the parameter space, i.e., increasing freeplay $\delta _s > 1^\circ$ for $q_\infty = 4102$ [Pa] and increasing $q_\infty > 4102$ [Pa] with $\delta _s = 1^\circ$. Figure 17 demonstrates that the ROM performs well in terms of extrapolating to new freeplay values as is expected from the preliminary analysis performed in Sect. 4.2.3. The change in amplitude and therefore the change in the structure of the nonlinear aerodynamic forces is relatively insignificant. Figure 18 presents the prediction of the LCO when the ROM is extrapolated to a new dynamic pressure of $q_\infty = 4205$ [Pa] which is the linear flutter boundary. The ability of the ROM to extrapolate to this new dynamic pressure is poor, with the ROM predicting an asymmetrical limit cycle and failing to capture the general form. This is not surprising and therefore a strong recommendation for highly nonlinear problems such as the one presented in this paper to ensure that the sampling locations encapsulate the entire parametric sub-region of interest.

Fig. 17

Phase portraits of the root rotational axis LCO at extrapolated freeplay values comparing the FOM and ROM$_9^2$

Fig. 18

Phase portraits of the root rotational axis LCO at extrapolated dynamic pressure of $q_\infty = 4205$ [Pa] comparing the FOM and ROM$_9^2$

4.5 Computational savings

To ensure a stable limit cycle is achieved, 3000 numerical time-steps are required. Any CFD-based aerodynamic solutions are run on an Intel Xeon Gold 6152 CPU using 16 cores, while any ROM solutions on a single core (i.e., insignificant resources). Table 5 presents the computational cost associated with the various solution strategies presented in this paper. In terms of simulation time, the ROM solutions are three orders of magnitude faster. However, the time taken to generate the ROM must also be taken into account. The ROM$_4^1$ takes approximately 350 CPU-h to generate, while the ROM$_9^2$ takes approximately 675 CPU-h to generate.

Table 5 Computational cost for the FOM and ROM solutions

5 Summary and conclusion

Non-parametric nonlinear model reduction methods, such as, those based on polynomial functionals, can suffer from reduced ability to generalize. For complex nonlinear problems this means that convenient relations that are observed in the linear regime, such as the linear relationship between generalized force and dynamic pressure, or insensitivity to linear/nonlinear control stiffness properties, are invalid. In this paper an approach for parameterizing nonlinear non-parametric unsteady aerodynamic ROMs is presented, for application to complex nonlinear aeroelastic systems. The approach considers direct interpolation (using Lagrange polynomials) of a an aeroelastic-tuned polynomial-based unsteady aerodynamic ROM library, consisting of a combination of linear and optimally sparse nonlinear tensors of Taylor partial derivatives, equivalent to Volterra kernels. The primary features of the framework and interpolation scheme are as follows:

• 1. Through OMP it is possible to efficiently generate a library of nonlinear ROMs.

• 2. Each ROM in the library can be of different order, sparsity (or lack-of), sparsity pattern, and cardinality.

• 3. The ROM library can be relatively sparse and the interpolation scheme is simple.

• 4. A completely new ROM is generated for each new set of operating conditions and thus the interpolation is only done once, before running the simulation.

The example given considers a 3D aeroelastic stabilator model with freeplay undergoing high amplitude LCO, where the nonlinear unsteady aerodynamic ROM is parameterized in dynamic pressure and freeplay magnitude. A bilinear interpolation of the subspace performs very well for low freeplay values and dynamic pressures, while to model the entire subspace with high accuracy a biquadratic scheme is necessary. The online computational savings are more than three orders of magnitude. The time taken to generate the ROM is also of significance. It is estimated that it takes 8–16 times longer to generate the nonlinear ROM library, than generating the linearized aerodynamic impulse responses for this same system.

In conclusion, this work demonstrates that it is possible to generate a highly accurate nonlinear unsteady aerodynamic ROM that is as robust to parameter changes as a linearized ROM within the linear regime, albeit with a larger but reasonable offline computational cost. Generating the same ROM without sparsity promotion would be computationally prohibitive.