1 Introduction

In general, the dynamics of structures and systems exhibit nonlinear behaviour. Yet, in most macro-scale applications in mechanical and civil engineering, a linear analysis is sufficient given their design and operating ranges. Modelling and investigating dynamical behaviour using linear techniques has therefore been the expected standard for an engineer performing experimental investigation and validation. However, for nonlinearly behaving structures and systems, such standard engineering tools are no longer applicable.

For example, they fail to identify solutions that are either unstable, or stable but with a very narrow basin of attraction. Other phenomena that linear analysis tools struggle with are identifying sudden changes of stability at bifurcation points, jumps due to hysteric behaviours, self-excitation, parametric resonance, period doubling, and chaotic dynamics.

Numerical continuation algorithms, developed back in the 1970’s, encompass a family of methods for numerically determining solutions of nonlinear differential equations over varying parameters [1, 2]. A popular continuation scheme is the pseudo-arclength method, which enables path-following of solutions past and in between fold bifurcations in a smooth, continuous manner. However, not all physical systems can be described or modelled mathematically, especially those whose physics are determined by multiple field interactions (when including e.g. sensor and actuator influences, fluid–structure interactions and/or filter and controller properties). Incorporating experimental techniques into mathematical approaches becomes vitally important in describing their dynamic behaviour. Hence, using model-free experimental methods is an ongoing field of research, which enables investigation directly on a physical system to probe its dynamical landscape. One such method that has shown promising results is control-based continuation (CBC).

The concept of CBC, or experimental continuation, was first introduced by Sieber et al. [3, 4] and demonstrated with an experiment that explored the nonlinear dynamics of a vertically forced pendulum. The underlying idea is to turn widely used numerical continuation algorithms into an equivalent experimental methodology to find and then track or continue (steady-state or periodic) responses of the experiment itself, without requiring a model of the system. CBC is a tool to investigate the system dynamics continuously as a control parameter is changed. In particular, it can follow steady-state and periodic solutions through fold bifurcations, thereby smoothly transitioning between stable and unstable branches. The use of a suitable control law enables tracking of unstable solutions. It is crucial that the implementation of the controller does not interfere with or modify the inherent dynamics of the system. Hence, the control must “nudge” the system to the target solution with small perturbations that are effectively zero when the target is reached; this is known as non-invasive control [4,5,6].

Mechanical oscillators subject to harmonic forcing, specifically beams or cantilevers, make up a large subset of control-based continuation experiments. Schilder et al. [7,8,9] considered a downwards cantilever beam with a nonlinearity induced by hitting side-stops. The authors track the associated hysteresis loop as a function of the forcing frequencies and strength. Kleyman et al. [10] investigated the effects of nonlinear damping and shaker-structure interactions with CBC to construct frequency response functions (FRF) for a beam clamped on both ends. Multiple authors [11,12,13,14] have used an arched beam with an inherent curvature, which resulted in a softening-hardening effect. In their study, CBC is compared to phase locked loops (PLL) in parallel, which allowed a discussion on similarities between the two methods. A separate study by Kerschen et al. in [6, 15] used a cantilevered beam. As the beam configuration exhibits linear behaviour, the nonlinearity was superimposed artificially through the actuator. Cantilevered beams were also utilised by Barton et al. in several experiments [16,17,18,19,20,21]. Their cantilevers required an iron mass interacting with a magnetic field to harvest energy, which induces the nonlinearity. They presented a nonlinear response surface as a function of forcing frequency and amplitude. Barton et al. also demonstrated CBC for a nonlinear system with discrete spring and mass components [22, 23], which is quite different from the cantilever systems they probed in other studies. Additionally, CBC has been applied to self-excited systems, including an aerofoil [24, 25] and a driven tyre [26, 27]. Moreover, it has been adapted to quasi-static examples exhibiting hysteric behaviour, such as the Zeeman catastrophe machine [28] and in the force-displacement response of a shallow arch [29]. In summary, these aforementioned systems share the common characteristic of exhibiting nonlinear behaviours that result in a fold bifurcation. These experiments have been designed such that their geometries and constraints allow the nonlinearity to be a prominent feature within the range of available actuation strengths; as such, they constitute academic demonstrations where the resulting phenomena are somewhat exaggerated.

Fig. 1
figure 1

a Schematic sketch and b experimental realisation of the test-rig used for experimental validation. (i) main beam; (ii) thin beam; (iii) electrodynamic shaker; (iv) dSpace controller; (v) accelerometers; (vi) impedance head; (vii) sensor amplifier; (viii) actuator amplifier

Full size image

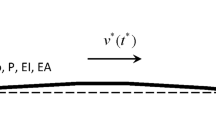
In this study we apply CBC to investigate the dynamics of a dual-beam system comprised of a primary beam clamped to a second, thin and flexible beam with fixed-fixed end conditions. Figure 1 shows our dual-beam setup and technical details are given in Sect. 2.1. The mechanical properties of the system are adjustable, and therefore the nonlinearity can be customised by specifying the properties of the secondary beam, such as its length, stiffness and damping. This dual-beam structure is different from other systems probed with CBC in the literature because its nonlinearity is intrinsic to its mechanical structure, without the use of additional element(s) that introduce, influence, or accentuate its nonlinear response. More specifically, the motion of the primary beam causes mid-plane stretching within the thin, secondary beam because its stress–strain relationship becomes nonlinear at the operating point [30,31,32], best described by the dominating cubic stiffness. Our study pertaining to CBC in mechanical oscillators is motivated by ongoing research to employ CBC to enable experimental bifurcation analysis of micro-electromechanical systems (MEMS) [33]. While the time-scales involved in M/NEMS are, in general, much faster (kHz range in low-frequency applications, up-to MHz-GHz range for high-switching applications [34, 35]), the microbeam and macro dual-beam share similar nonlinear characteristics given by the geometric nonlinearity.

Table 1 Physical properties of the beam system
Full size table

This paper is organised as follows. Section 2 presents the physical experimental setup, with the associated instrumentation and equipment; here we also present open-loop results for sweeps in both excitation frequency and amplitude, which are used a-priori for eventual CBC implementation. Section 3 then introduces a simple conceptual model in the form of a harmonically forced Duffing oscillator, which we then use to describe methodology and setup of the CBC implementation for the actual experiment. In Sect. 4 we present results obtained by tracking periodic solutions of the closed-loop experiment with CBC. More specifically, we present a solution surface over the plane of excitation frequency and amplitude, rendered from continuations of solution branches for selected fixed values of the excitation frequency while the excitation amplitude is varied. Via suitable post-processing, we identify fold curves that meet at a point of cusp bifurcation; they bound the parameter region where hysteresis is observed. The concluding Sect. 5 discusses and summarises our findings and points towards future research.

2 Experimental setup

Our experiment is inspired by a benchmark system in [36], for which structural/mechanical hardening and softening system behaviour is expected and results are available and known. It has been investigated, for example, with the conditioned reverse path method [37], proper orthogonal decomposition [38], identification of nonlinear normal modes (NNM) [39, 40] and developing the backbone curve by using PLL [41, 42]. Hence the experiment illustrated in Fig. 1 constitutes a good test-case example for applying CBC to a purely mechanical system with strong nonlinearity in the operating range of the excitation. This section describes the experimental setup consisting of the mechanical structure and the associated instrumentation required to implement CBC. This is followed by open-loop measurements showing that our dual-beam system indeed exhibits bistability and hysteresis.

2.1 Mechanical design

In the experimental system depicted in Fig. 1, the nonlinear mechanical oscillator under investigation is an ‘overall beam’ with piecewise continuous geometry. It consists of a primary beam (i), manufactured out of mild steel, and a thin secondary beam (ii), made from steel sheet metal. The primary beam measures \({700\,\textrm{mm}}\) in length and has a square cross-section of \({16\,\textrm{mm}} \times {16\,\textrm{mm}}\), which is a slight modification from the original ECL benchmark. This was chosen for the convenience of standard sizes available, and does not affect the governing dynamics being investigated. The thin beam, with a nominal thickness of \({0.5\,\textrm{mm}}\), is clamped to the primary beam with two bolts and an additional cut-out of mild steel. The centerlines of the two beams along their lengths are aligned. Physical properties of the mechanical system are given in Table 1. With a sufficiently large oscillation amplitude, a geometric nonlinearity will arise through large deflections induced within the thin beam.

This dual-beam setup is subject to fixed-fixed boundary conditions. On both ends are a pair of right-angle aluminium brackets, which are used to hold up the beam structure to a desirable height. A custom-designed breadboard made of mild steel is used to clamp the beam to the brackets. The right-angle brackets are then bolted to the surface of a vibration isolation table.

Finally, a pre-tensioning bracket on the thin beam side produces an axial force which determines the linear and nonlinear characteristics of the structure [36]. Based on studies conducted by Thouverez [36] and Kerschen [37], a hardening cubic stiffness is expected. The pre-tension is adjusted with the aid of a bolt.

2.2 Actuation and instrumentation

The dual-beam is actuated by an LDS-V408 \({100\,\textrm{N}}\) electrodynamic shaker (iii), which is complimented with a PA100E power amplifier (vii) to provide the required current. The actuator is responsible for providing the periodic forcing signal. The shaker is placed \({200\,\textrm{mm}}\) from the edge of the left-hand clamp. A stinger ensures that the excitation signal is isolated to the lateral motion direction only. A magnetic mounting base provides a connection between the actuator and the oscillator. Generally, the shaker structure is considered to be included within the dynamics of what is referred to as the “system” where imperfections can cause distortion in the forcing signal [43]. Preliminary vibration testing showed that the distortion was minimal and of negligible effect. A proportional-integral controller is used to achieve force-level control of the shaker action through measuring the amplitude of the force sensor.

The lateral deflections of the beam are measured by using two 352C03 ICP accelerometers (v). The first accelerometer is located 650 mm from the left end on the primary beam, where the largest dynamic deflection is produced (in the first mode). The second accelerometer is placed adjacent to the electrodynamic shaker. Additionally, a 228D01 ICP impedance head (vi) was chosen to measure the force at the end of the electrodynamic shaker (henceforth referred to as the force sensor). As these sensors are charge-based, the M72A3 IEPE signal conditioner (vii) is used to provide constant current and it integrates the acceleration signal into velocity and displacement. The signal conditioner amplifies, filters, and integrates the incoming IEPE signals as required to acquire the desired signals.

Finally, the dSpace DS1104 controller board (iv) is responsible for signal acquisition and real-time control of the nonlinear system. The software packages Simulink and ControlDesk are used to measure experimental data, implement the underlying CBC algorithm (see Sect. 3) and, hence, generate the required control input to the shaker.

2.3 Open-loop characterisation

Experimental modal analysis (EMA) with the software package ModalView was employed to determine the system’s experimental vibration modes and damping properties. EMA is achieved by exciting the structure with a modal impact hammer (PCB Piezoelectronics 086C03 ICP) in order to measure the impulse response, and, hence, its frequency response. Table 2 compares the experimentally measured natural frequencies with theoretically expected finite-element simulations, conducted in SolidWorks. An increase in pre-tension results in a linearly increasing natural frequency (see Table 3). This study considers only the first mode with a pre-tension of 20 \(\upmu \)m / m, chosen to enhance the effects of the geometric nonlinearity. This level of pre-tension was consistently achieved by winding the pre-tensioning bracket to its physical limit.

Table 2 Comparison of computational and experimental modes
Full size table
Table 3 First mode frequency as a function of the pre-tension
Full size table

Subsequently, sine sweeps (chirps) were conducted to identify hysteric behaviour and the associated bistable region experimentally — for both constant amplitude with varying frequency (see Fig. 2), and for constant frequency with varying amplitude (see Fig. 3). In both cases, the sweeps are produced by conducting a linear parameter increment given by:

$$\begin{aligned} p(t) = p_0 + \frac{p_1 - p_0}{T}t \qquad t\in \{0,\ldots ,T\}, \end{aligned}$$
(1)

where T is the length of the sweep, and \(p_0\) and \(p_1\) are the start and end values of the parameter, which is either frequency or forcing amplitude for our purposes.

The recorded timeseries are post-processed by using an RMS envelope and applied through a smoothing low-pass filter. Markers \(\circ \) and \(\times \) differentiate parameter sweeps in the upward- and downward-directions, respectively. Variance near the hysteric region where the response jumps from one branch to another can be attributed to remainders of the transient parts of the measured response. Increasing the sweep duration improves this variance and leads to higher accuracy of the hysteresis behaviour (see Fig. 6). The sweeps we performed are satisfactory in that they allow us to identify relevant operating region(s) where CBC should be performed.

Fig. 2
figure 2

Open-loop frequency response for constant-amplitude sine sweeps. Colours depict constant forcing amplitudes. Markers denote sweep direction. Bistable region depicted as shaded area

Full size image

Figure 2 depicts the open-loop frequency response from 41 to 44 Hz for forcing amplitudes of \({0.25\,\textrm{N}}\), \({0.50\,\textrm{N}}\), and \({1.00\,\textrm{N}}\), for both an up- and down-sweep of the frequency. This reveals the hardening nonlinearity near the first primary frequency, and the expected hysteric effect; the shading indicates the respective bistable frequency range, within which the unstable solution branch would be expected.

Fig. 3
figure 3

Open-loop amplitude response conducted with traditional sine sweeps. Colours depict constant forcing frequencies. Markers denote sweep directions. Bistable region depicted as shaded area

Full size image

Figure 3 depicts the open-loop amplitude response for 42.1 Hz, 42.2 Hz, and 42.3 Hz, with up- and down-sweeps over the range between 0.1 and 1.0 N. This illustrates that an amplitude range of bistability (shaded region) emerges for frequencies slightly above 42.1 Hz.

3 Framework and implementation of CBC

We are motivated to further develop CBC in becoming one of the standard engineering tools to investigate and understand the dynamical landscape of a nonlinear system. Indeed, finding and tracking open-loop unstable solution(s) is impractical, as such intentions would require infinite precision, the absence of noise or perturbation, and an initial condition exactly on the unstable trajectory.

The approach CBC takes to track even unstable solutions is two-fold: firstly, CBC employs a local control law with associated control gains, with which to stabilize the unstable solution (see Sect. 3.1); secondly, a zero-problem is solved to obtain a point in the sequence along the solution branch (see Sect. 3.2). The first point requires a suitable choice of gains to ensure the continued operation of the experiment at each new parameter step throughout the considered continuation regime. Further, the solution to the zero-problem ensures that a given closed-loop response agrees with the open-loop response up to an acceptable measurement/experimental tolerance.

We describe our experimental method by using a suitable mathematical model, which is also done for Sieber et al.’s experimental system [3, 4]. Note, that the model is chosen to adequately describe the dominating dynamics to an accuracy of a reasonable degree, which acts as a proxy to be replaced by the actual experiment. For this purpose, the harmonically forced Duffing oscillator is used here, wherein the second-order differential equation

$$\begin{aligned} \ddot{x}\left( t\right) + 2\zeta \dot{x}\left( t\right) + x\left( t\right) + \mu x^3\left( t\right) = u\left( t\right) \, \end{aligned}$$
(2)

describes (in this case) the dynamics of the first bending mode x(t) of the considered dual-beam. Parameters and variables in (2) are: \(\zeta \) is the damping ratio, \(\mu \) is the strength of the cubic stiffness, and derivatives are taken with respect to the time t. Note, that we present the equation in nondimensionalised, scaled form.

The time-dependent input \(u\left( t\right) \) takes on one of two forms:

$$\begin{aligned} u\left( t\right) = {\left\{ \begin{array}{ll} u_{OL}(t) = \hat{u}\cos \left( \eta t\right) &{} \text {if open-loop},\\ u_{CL}(t) = g\left( \textbf{e}(t)\right) &{} \text {if closed-loop}. \end{array}\right. } \end{aligned}$$
(3)

Here \(\hat{u}\) is the open-loop forcing amplitude and \(\eta \) the forcing frequency (as a ratio of physical excitation and the natural frequency of the oscillator). Additionally, a locally stabilising controller, \(g\left( \textbf{e}(t)\right) \), is defined for the closed-loop feedback actuation, where \(\textbf{e}(t)\) is a measurable error signal. The error signal dictates the forced response of the closed-loop system.

3.1 Controller choice

The natural dynamics of the uncontrolled system can be preserved by ensuring that the controller algorithm is non-invasive [5]. Any type of non-invasive controller can be used for this purpose [16, 44]. The controller described here, from the class of proportional plus derivative (PD) controllers, can be made non-invasive by choosing an appropriate reference solution r(t), and takes the form:

$$\begin{aligned} \begin{aligned} u_{CL}(t)&= g\left( \textbf{e}(t)\right) \\&= K_p \big (r(t) - x(t)\big ) + K_d \big (\dot{r}(t) - \dot{x}(t)\big ). \end{aligned} \end{aligned}$$
(4)

The control action depends on the differences between the measured state x(t) and a desired reference solution r(t), their derivatives, and by associated user-set control gains \(K_p\) and \(K_d\), which determine the strength of the overall feedback control. For now, we assume that r(t) is chosen such that \(u_{CL}(t)\) is non-invasive; see Sect. 3.2 for details on the form of r(t). Thus, for this controller, gain design is decoupled from the choice of r(t) to ensure non-invasiveness.

Figure 4 demonstrates the effects of taking only the proportional and only the derivative component of the PD controller, respectively, for the example of a bistable frequency response of (2) as computed with the software package MatCont. Blue and red curves in Fig. 4 represent the open-loop and closed-loop frequency responses, respectively. Here, we fix \(\zeta = 0.01\) and \(\mu = 0.375\) as suitable values to represent our actual experiment. Furthermore, we consider an operating frequency of \(\eta =1.1\). The reference trajectory r(t) (which is constructed in Sect. 3.2) has the amplitude \(\hat{r}_1\) at the operating frequency.

The proportional component of the controller, determined by \(K_p\), shifts the bistable region away from the operating frequency of interest. Figure 4a demonstrates this shift for \(K_p = 1\) and \(\hat{r}_1 = 0.6672\). We observe that the closed-loop response is mono-stable at this particular excitation frequency \(\eta =1.1\), and the measured response is equivalent to the unstable solution branch of the open-loop. The derivative component, determined by \(K_d\), attenuates the response near the resonance peak. An example with \(K_d = 0.1\) is shown in Fig. 4b. To achieve the same open-loop amplitude we use \(\hat{r}_1 = 0.9570\). Once again, the closed-loop response is mono-stable at this frequency and is equivalent to the open-loop response. Generally, a combination of controller gains \(\textbf{K} = \left[ K_p, K_d\right] \) is chosen to stabilise any open-loop unstable solutions with the closed-loop control law (4).

Fig. 4
figure 4

Effect of the control gains on a bistable frequency response of (2) with \(\zeta = 0.01\) and \(\mu = 0.375\), where blue curves represent open-loop dynamics (\(\hat{u}=0.05\)) and red curves closed-loop dynamics. a proportional-only controller (\(K_p = 1\), \(K_d = 0\), \(\hat{r}_1 = 0.6672\)); b derivative-only controller (\(K_p = 0\), \(K_d=0.1\), \(\hat{r}_1=0.9570\))

Full size image

There is no standard or “one-fits-all” method to choose control gains that would ensure a successful experimental continuation for a nonlinear system. Unlike gain design as known from linear control theory, each CBC methodology is case-specific to each experiment, including structure, actuation mechanism and controller algorithm. However, standard experimental techniques, such as the modal and linear frequency sweeps to reveal properties including modal frequencies and damping ratios, can inform the task of determining a suitable parameter range of controller gains vital for a successful CBC analysis.

The control gains must be sufficiently large to ensure successful local stabilisation during all experimental conditions. However, larger gains are usually undesirable in an experimental setting due to the physical limitation of the experimental equipment, and the need to avoid exceeding supply restrictions in electrical and mechatronics equipment. For a thorough analysis of gain choice, see the study by Tatzko et al. [45] who derive an approximate relationship between the controller gains and system parameters for a similar, Duffing-like system. Recently, Dankowicz et al. [46] proposed noninvasive adaptive control strategies for CBC that achieve similar performance and a level of robustness to disturbances and time delays, without the need for manual tuning of the control gains.

3.2 Reference trajectory and non-invasivenessness

The reference trajectory r(t) is intentionally constructed and ensures the controller is non-invasive. We achieve this by prescribing a closed-loop steady-state actuation which is equivalent to the open-loop forcing, thus, preserving the natural dynamics of the open-loop system. For the “physical” beam system, here described by (2), the open-loop actuation \(u_{OL}(t)\) in (3) is harmonic. Therefore, the closed-loop controller must match that of the open-loop actuation, in actuation strength and frequency. Furthermore, any higher harmonics of the nonlinear system must be eliminated. A suitable choice of r(t) must therefore satisfy the following condition:

$$\begin{aligned} u_{CL, ss}(t)&= K_P \left( r(t) - x_{ss}(t)\right) + K_D \left( \dot{r}(t) - \dot{x}_{ss}(t)\right) \nonumber \\&= a \cos {(\eta t)} + b \sin {(\eta t)} \,. \end{aligned}$$
(5)

Determining the mathematical expression of r(t) in-silico is achieved by studying the mathematical model (such as (2)) with numerical simulation or analytical approximation techniques. However, we emphasise that this computational problem of constructing r(t) must be achieved on a physical test-rig with little-to-no knowledge of the underlying parameters that govern the dynamics.

A suitable approach is to define r(t) as a periodic function. Since the response, x(t), follows the reference, it is also periodic and, therefore, can be reconstructed as a periodic signal by taking experimental observations of the steady-state behaviour. Thus, the signal x(t) can be represented by using a Fourier series. Due to real-life, practical limitations, the Fourier series is truncated to the first N modes through a discrete Fourier transform or similar,

$$\begin{aligned} x\left( t\right) = A^x_0 + \sum _{n=1}^{N-1} \Bigl ( A^x_n \cos (n\eta t) + B^x_n \sin (n\eta t) \Bigr ) \end{aligned}$$
(6)

and

$$\begin{aligned} r\left( t\right) = A^r_0 + \sum _{n=1}^{N-1} \Bigl ( A^r_n \cos (n\eta t) + B^r_n \sin (n\eta t) \Bigr ). \end{aligned}$$
(7)

Fourier coefficients in (6) and (7) can be concisely bundled into the following vectors

$$\begin{aligned} \begin{aligned} \textbf{X}(\eta )&= \left[ A^x_0, A^x_1, B^x_1, A^x_2, B^x_2, ... , A^x_{N-1}, B^x_{N-1}\right] ^T\\&=\left[ A^x_0, \left( A^x_n, B^x_n\right) _{n=1}^{N-1}\right] ^T \end{aligned} \end{aligned}$$
(8)

and

$$\begin{aligned} \begin{aligned} \textbf{R}(\eta )&= \left[ A^r_0, A^r_1, B^r_1, A^r_2, B^r_2, ... , A^r_{N-1}, B^r_{N-1}\right] ^T\\&=\left[ A^r_0, \left( A^r_n, B^r_n\right) _{n=1}^{N-1}\right] ^T \end{aligned} \end{aligned}$$
(9)

The Fourier coefficients \(A^r_n\) and \(B^r_n\) in (7) are determined by a simple fixed-point iteration such that (4) is harmonic and fulfills the non-invasivity condition (5). Considering the beam system, represented here by the Duffing oscillator (2), one can set the amplitudes in (9) to be the corresponding measured amplitudes of (8) for all elements, excluding the fundamental frequency; this achieves the necessary cancellation effect of any higher-order harmonics. The first Fourier mode of \(\textbf{R}\left( \eta \right) \) is then used as a continuation parameter, and it has a fixed value at any given point along the continued curve. The fixed-point iteration is expressed as

$$\begin{aligned} \begin{aligned} A^r_i&:= A^x_i \qquad \forall \quad i \subseteq [0 ... N-1], i\ne 1\,, \\ B^r_i&:= B^x_i \qquad \forall \quad i \subseteq [2 ... N-1] \,. \end{aligned} \end{aligned}$$
(10)

Equation (10) is applied in an iterative process (see Fig. 5) until the prescribed steady-state actuation is harmonic.

Fig. 5
figure 5

The iterative process behind the fixed-point iteration scheme for CBC. The real-time control loop is shown in black, and the asynchronous fixed-point iteration in red. See also Algorithm 1 for more details

Full size image

To ensure that the controller has become non-invasive we require that an error criterion is satisfied, whose definition is based on all non-harmonic Fourier coefficients:

$$\begin{aligned} \begin{aligned} \text {err} = \left\| (A_i^r, B_i^r) - (A_i^x, B_i^x) \right\| < \text {tol} \\ \qquad \qquad \forall \quad i \subseteq [0... N-1], i\ne 1. \end{aligned} \end{aligned}$$
(11)

Once this error is below the pre-specified tolerance \(\text {tol}\), the final Fourier coefficients \(\textbf{X}_{k}(\eta ), \textbf{R}_{k}(\eta ), \textbf{U}_{k}(\eta )\) are recorded; here subscripts denote the kth discrete point along the solution curve, and \(\textbf{U}_{k}(\eta )\) are the corresponding Fourier coefficients of the control as computed from (4), similarly to (8)-(9). The associated fundamental frequency coefficient is then used to identify the equivalent forcing amplitude, as given by

$$\begin{aligned} \hat{u}_1:= \sqrt{ A^u_1 + B_1^u} = \sqrt{a^2 + b^2}, \end{aligned}$$
(12)

where \(A^u_1, B_1^u\) are the respective coefficients of \(\textbf{U}_{k}(\eta )\); see (5).

3.3 Prediction of successive points

Once a trajectory has been stabilised and recorded, the next point along the solution curve can be determined. This is analogous to the prediction step of a numerical continuation scheme. Thus, the prediction by the CBC algorithm uses the Fourier coefficients of the two prior points,

$$\begin{aligned} \Delta \textbf{R}_{k}:= \frac{\textbf{R}_{k} - \textbf{R}_{(k-1)}}{\left\| \textbf{R}_{k} - \textbf{R}_{(k-1)} \right\| }. \end{aligned}$$
(13)

The previous Fourier coefficients are then incremented (or decremented) based on the secant difference

$$\begin{aligned} \textbf{R}_{(k+1)}:= \textbf{R}_{k} + h \Delta \textbf{R}_{k}, \end{aligned}$$
(14)

where h represents the step-size.

Obtaining an initial prediction to initialise the continuation algorithm requires two points, \(R_{(-1)}\) and \(R_{(-2)}\). Typically, they are chosen close to one another to yield nearby points on a known stable branch. In this way, an initial validation in comparison to the open-loop dynamics can be conducted.

3.4 Summary and outline of CBC algorithm

A summary of the CBC algorithm proceeds as outlined in Algorithm 1 by computing a sequence of points indexed k along a branch, starting with \(k=0\). Steps 4–12 describe the correction algorithm that satisfies the non-invasivity condition. Furthermore, Steps 14–15 are the prediction for the identification the next point in the sequence along the solution path.

The process of initializing and then computing a solution curve over a desired range is repeated for fixed values of a second parameter, here \(\eta \), for a suitable number of iterations until an overall two-parameter bifurcation diagram is identified.

Algorithm 1
figure a

CBC algorithm

Full size image

4 Experimental application of CBC

We perform CBC on the aforementioned dual-beam with hardening resonance behaviour to identify co-existing solution branches. All default experimental settings are tabulated in Table 4, unless stated otherwise.

Note that there are some differences between the theoretical framework presented above and the actual experimental investigations in this section. The dynamical system described in (2) is replaced with the physical dual-beam system and the actuation term u(t) in (3) is implemented by means of an electrodynamic shaker. We represent the truncated Fourier series (6), (7) by using a DC-offset and the first three harmonics, \(N_{harm} = 3\), having confirmed that any higher-order harmonics (\(N_{harm} > 3\)) are of negligible influence. An adaptive filter (see [6, 15]) is used to compute the Fourier amplitudes. The fixed-point iterations are asynchronous (offline), that is, they are performed independently of updating the filter coefficients. Furthermore, the physical experiment uses an explicit forcing frequency (f, measured in Hz) rather than the tuning ratio (\(\eta \), from (3)). Finally, response amplitudes described in this section are taken at the excitation frequency, noting again that higher-order harmonic contributions are of negligible effect. We use the uniform control gains \(\textbf{K} = \begin{bmatrix} 1,&0.001 \end{bmatrix}\), tolerance \(\text {tol}=1\times 10^{-4}\) and step-size \(h = 0.02\). These values were determined empirically through observation, as the ones best suited for the entire operational range. To determine whether the transient response has decayed, we take the logarithmic moving variance (200 samples) of the fundamental Fourier coefficient. Once the variance is below a chosen threshold for a sufficient period (1 s), the continuation algorithm evaluates the (non)-harmonicity by (11). If non-invasive convergence is achieved, the continuation algorithm will record a point and perform a prediction (14); otherwise, it will perform an iteration (10).

Table 4 Typical CBC parameters and associated values
Full size table

4.1 Amplitude response via CBC

Figure 6 compares the open-loop sweeps up and down with the closed-loop CBC solution for a forcing frequency of \(f = {40\,\textrm{Hz}}\). Amplitude envelopes of the open-loop response were taken as the average over two sweeps each. An extended sweep duration of \(T={500\,\textrm{s}}\) was used here to improve the accuracy of results by further reducing transient effects. The closed-loop CBC markers denote the confirmed solution response by the CBC algorithm as the mean of six consecutive experiments. A coarser step size of \(h = 0.1\) was used to speed up the process of continuation. The CBC method successfully identifies all stable and unstable solution branches. A comparison between open- and closed-loop results shows excellent qualitative and even quantitative agreement, which indicates successful non-invasive tracking of the inherent dynamics.

Fig. 6
figure 6

Experimental comparison of open-loop (OL) sine-sweep tests (solid lines) and closed-loop (CL) CBC sweeps (crosses). Dashed lines indicate operating points shown in the time-series in Fig. 7

Full size image
Fig. 7
figure 7

Experimental time response; comparison between open-loop (sweep up and down) and closed-loop (CBC method). a Lower, stable branch \(\hat{u} = {0.3\,\textrm{N}}\), b bistable region of three co-existing solutions, \(\hat{u} = {0.45\,\textrm{N}}\), c Upper, stable branch \(\hat{u} = {0.70\,\textrm{N}}\)

Full size image

The corresponding time-series data is compared in Fig. 7 for the three operating regions (indicated by the dashed lines in Fig. 6): (a) before; (b) inside, and (c) after the bistable region. For sake of comparison, maxima of signals have been aligned in the time series of Fig. 7, hence, disregarding any phase information. The mono-stable solutions outside the bistable region are identified by both the open-loop sweeps and the closed-loop CBC, and they agree to good accuracy (Fig. 7 (a) for \(\hat{u}={0.3\,\textrm{N}}\), (c) for \(\hat{u}={0.7\,\textrm{N}}\)). However, the open-loop sweeps only capture the respective stable solution in the bistable region, whereas CBC additionally identifies the unstable branch, corresponding to a middle-amplitude response (Fig. 7 (b) for \(\hat{u}={0.45\,\textrm{N}}\)).

To ensure that the response is harmonic (to an acceptable experimental degree), we monitor the Fourier coefficients over the experiment. As described in Sect. 3.2, the first Fourier coefficient \(A^r_1\) is used as a continuation parameter, \(B^r_1\) is set to zero, and all other coefficients are updated according to (10); we report that this iteration converges throughout. Figure 8 illustrates the harmonicity of the response with a sample CBC run: the higher harmonics \(\hat{r}_2\) and \(\hat{r}_3\) are consistently three orders of magnitude smaller than the first harmonic \(\hat{r}_1\).

4.2 Experimental bifurcation analysis

We repeat the CBC process for various constant forcing frequencies by way of gaining insight into the dynamical landscape of the dual-beam system. Figure 9 shows the result of the experimental continuation of curves of solutions for the stated four values of the forcing frequency, where the forcing amplitude is again the continuation parameter. Here we used a fine step size of \(h = 0.02\); moreover, we interpolate the computed points by a smoothed spline [47] with relaxation parameter of \(p=0.999\) to mitigate any experimental imperfections caused by sensor noise, variance in non-invasive cancellation, and deformations caused by the thin beam.

Fig. 8
figure 8

The harmonics \(\hat{r}_1\), \(\hat{r}_2\) and \(\hat{r}_3\), shown on a logarithmic scale, of the experimentally determined Fourier coefficients \(\textbf{R}\) (9), as set by fixed-point iterations (10) where \(A^r_1\) is used as the bifurcation parameter

Full size image
Fig. 9
figure 9

Selected closed-loop response found with CBC. The curves are obtained by smoothed spline interpolation from the experimental data, and their colours indicate the constant forcing frequencies shown

Full size image
Fig. 10
figure 10

CBC data (circles and crosses), with identification of fold bifurcation points by: method A, polynomial curvefit; method B, smoothed spline

Full size image
Fig. 11
figure 11

Response surface of the clamped dual-beam system, constructed from the shown constant-frequency curves obtained as smoothed splines (method B) from the CBC data. The fold curves (red: method A; blue: method B) divides the surface into parts of stable (light grey) and unstable (dark grey) solutions. a The 3D view of the response surface represented by the response amplitude, \(\hat{x}\), as a function of forcing frequency, f, and forcing amplitude, \(\hat{u}\); 2D projections onto b the \((f, \hat{u})\)-plane, c the \((f, \hat{x})\)-plane, and d the \((\hat{u}, \hat{x})\)-plane

Full size image

The four curves depicted in Fig. 9 are selected examples, and experimental continuations have been performed for more values of the forcing frequency, as is shown in Figs. 10 and 11. For each chosen value of the forcing frequency f, Fig. 10 shows the actual points that were found by the CBC algorithm during an up-sweep followed by a down-sweep. This not only gives an impression of the actual experimental output of CBC, but also allows us to discuss issues regarding identifying from the data the fold bifurcation points that bound the region of bistability. The main issue here is that there is mechanical drift during the performance of successive experimental continuations, and this is represented in Fig. 10 by the visible differences between the up- and down-sweeps. Additional CBC continuation runs (not shown here) confirm that the overall parameter drift is on the order of the differences between the respective pairs of curves shown in Fig. 10. Note that, not unexpectedly, the differences are most pronounces along the intermediate branches of unstable solutions.

Since CBC does not detect bifurcations during a continuation run, the fold points need to be found by post-processing the CBC data for each curve offline. Note from Fig. 9 and the unprocessed data in Fig. 10 that each curve of solutions can be seen as a graph of the forcing amplitude as a function of the response amplitude. Hence, the fold points are the maxima and minima of the different graphs. For each pair of up- and down-sweeps we compute from the data points a single smooth curve, which is then used to identify the two fold points (if they exist for the given forcing frequency). We now present and compare in Fig. 10 two methods, A and B, for identifying the folds in this way, which differ in the type of interpolation used:

  1. (A)

    employs a fifth-order polynomial least-squares curve-fit of all data points; the thus computed fold points shown as asterisks in Fig. 10.

  2. (B)

    uses the smoothed spline with relaxation parameter \(p = 0.9995\) to interpolate all data points, as in Fig. 9; the corresponding fold points are shown as plus symbols.

Figure 10 demonstrates that each of these methods is equally proficient in finding the fold bifurcation points from the data. However, there are clearly some differences, which tend to be more pronounced in the vertical direction of the response amplitude the closer the two fold points are to each other. Indeed, it is a difficult task to detect minima and maxima reliably from experimental data when their difference is rather small. After all, this means that the bistable region is very narrow, near where the two fold points come together in a cusp bifurcation, so that resolution and accuracy of the experimental data play a significant role.

Methods A and B generate a set of smooth curves of solutions from the computed CBC data, from which the response surface of the beam system can be generated. More specifically, a sufficient number of constant-frequency curves is generated over a range of interest. Each (generally S-shaped) curve is segmented into three segments at the fold points (where appropriate), which correspond to the different branches. Each segment or branch is represented by a fixed number of points that are chosen to lie at (approximately) equal arclength distance (i.e., measured along the curve) from each other. The surface is then constructed via triangulation between these sets of points on neighbouring curves. Figure 11 shows the response surface rendered in this way from smoothed splines obtained with method B — in the space of response amplitude \(\hat{x}\) as a function of forcing frequency f and forcing amplitude \(\hat{u}\), as well as in three two-dimensional projections. The curves used to generate the surface are also shown, where colour again indicates the associated fixed frequency; compare with Fig. 9.

Also shown in Fig. 11 are two curves of fold points, generated from the bifurcation coordinates identified with methods A and B, respectively; here the colour of the curve corresponds to the fold points identified in Fig. 10. Generating such a fold curve requires some manual processing: the respective fold points must be reordered to lie sequentially along the the fold curve. Specifically, we generate a single array of fold points, starting with descending frequency along the top branch, and then ascending frequency along the bottom branch (the choice of direction is arbitrary). A smoothed spline with relaxation parameter/weighting of \(p = 0.99\) was used to generate the fold curve, and the cusp bifurcation is then found as its turning point. The cusp is identified at \((f^*, \hat{u}^*, \hat{x}^*) = (41.89, 0.246, 0.281)\) with the polynomial curve-fit (method A), whereas smoothed splines (method B) give \((f^*, \hat{u}^*, \hat{x}^*) = (41.89, 0.252, 0.286)\) as the location of the cusp.

The agreement between these two estimates for the cusp is quite good, but there are of course some slight differences as would be expected. Both methods estimate the cusp point near the frequency of \({41.9\,\textrm{Hz}}\), which we attribute to the chosen frequency spacing of \(\Delta f = {0.05\,\textrm{Hz}}\). Particularly, we expect the gap between the left-most pairs of bifurcation points in Fig. 10 to converge as the cusp is approached. Clearly, both approaches to locating the cusp point are hindered by a limited sampling resolution, and could be improved with finer frequency spacing near the cusp bifurcation.

5 Discussion

In this section, we discuss new findings from our dual-beam experiment by focusing on four different aspects: sensor variance in measurements; drifts induced by nonlinear operation; invasive cancellation; and cusp identification.

5.1 Sensor variance

Repeated measurements alongside post-processing is a vital component in determining trends sought by using the CBC algorithm. An example of variance in measurements is illustrated by the dots shown in Fig. 10, which each represent an accepted point during an experimental continuation with the CBC algorithm. The use of averaging (see Fig. 6) or curve-fitting (see Fig. 9) is a vital aspect of identifying the trends associated with the bifurcation curves we have presented.

Figure 12 quantifies the sensor variance associated with the accelerometer and force sensor, respectively. The error bars represent the uncertainty half-range of the average over six closed-loop experiments shown in Fig. 6. We note that observed discrepancies are mainly associated with the input channel, the choice of actuation by means of the electro-magnetic shaker. As such, the variance observed in the force sensor is larger than that of the accelerometer (see Fig. 12). Therefore, variances observed in the CBC-continued curves are directly associated with the identified variances of the actuation. The methodology as described in Sect. 3 delivers satisfying results. To further improve the accuracy of the method would mean to reduce the variance of the actuation signal by possibly considering another actuation principle or method.

Fig. 12
figure 12

Uncertainty halfrange over six CBC runs computed from force sensor (left range, undulating data points); accelerometer (integrated twice) (right range, monotonically increasing data points)

Full size image

5.2 Mechanical drifts

We re-emphasise that the dynamics of the presented dual-beam are dominated by the geometric nonlinearity through the properties of the secondary beam. Compared to similar studies, we distinguish our experimental system by a purely mechanically induced nonlinearity (not including equipment for instrumentation). Therefore, it does not rely on additional, external nonlinear sources such as an electromagnetic field [16,17,18,19,20,21], mechanical stops [7,8,9], or artificially through the forcing [6, 15].

We acknowledge that the presented results may vary between experiments for different operating conditions. Such variation can be seen in Fig. 10, where the shown successive up- and down-sweeps with CBC are distinct, particularly in the vicinity of the unstable solution branch. Further experimental continuation runs (not shown) confirm the existence of drifts at the shown level and, moreover, indicate that the observed differences are not consistently biased or ordered from run to run at constant forcing frequency. Hence, we speculate that the observed drift is not generated by the continuation algorithm itself.

Our experiment relies on the midplane stretching effect in the nonlinear operation, where the thin beam approaches its yielding point. We conjecture that repeated loading could lead to fatigue in the material, resulting in drift of experimental parameters such as the natural frequency (as seen in Table 3) and strength of nonlinear hardening. Such drifts could originate from e.g. strain hardening induced by large deflections within the thin beam, altering the elastic properties of the system. Further investigations in the future would need to validate our conjecture. For the presented work, we are satisfied with the proof of principle this benchmark study presents, where the dynamics identified are consistent. As such, calibration of the physical beam (especially near the fixed ends) requires careful attention, particular on the thin-beam end. We achieve consistency and repeatability of experiments in two ways: first, by turning the tensioning screw to its physical limit, which had the added by-product of a more pronounced nonlinear hardening effect; second, by clamping symmetrically across the mid-section of the dual-beams; third, by mass-manufacturing a set of replacement thin-beams from a single sheet of material using a water-jet cutter for consistent material properties.

5.3 Invasiveness cancellation

We emphasise the difficulty in eliminating the invasiveness of the control signal in a physical experiment. This phenomenon is well known in the CBC community [16, 19, 45]. Experimental imperfections such as limitations on instrumentation, measurement noise, or manufacturing defects/faults can induce variance/invasiveness in the controller. Reducing shaker-structure interactions is a research area of future interest; whilst invasiveness cancellation occurs in the control signal u(t), the true forcing F(t) may be induced with further distortion.

Furthermore, whilst the first mode and its integer-multiple harmonics dominate the response, other bending modes can interfere with the feedback signal. Future experiments should consider this through observability checks (in smart sensor placement) and/or sampling frequency to ensure aliasing is not a concern.

The effect of instrumentation and signal processing can be vital in the implementation of CBC. The various band-pass filtering stages aid in signal acquisition, yet they may induce filter delay and overall lag to the control loop. Whilst this can be neglected for this experiment, increased phase delays could play a significant role in other experiments.

5.4 Cusp identification

Experimental identification of the cusp bifurcation remains an open challenge. In this study, offline/post analysis via curve-fitting techniques is deemed adequate in approximating the parameter region in which a cusp bifurcation appears. As such, these insights are sufficient in an engineering design context, wherein operating regions can be specifically chosen based on the bifurcation landscape. For an engineer, understanding the region(s) where a cusp bifurcation is expected should be automatic or unambiguous. Therefore, developing online methods which can experimentally identify bifurcation behaviour is an interesting open challenge. Whilst this is addressed in [20], current curve-fitting methods are much simpler and sufficient for practical implementation.

6 Conclusion

In this paper, we have demonstrated the existence of bistable behaviour of the dynamics of a nonlinear dual-beam mechanism with fixed boundary conditions. We employed CBC to identify solution branches of the dual-beam system experimentally as a function of excitation amplitude, at various levels of constant forcing frequencies. CBC enabled the smooth, continuous transition between stable and unstable solutions that exist in between a pair of fold bifurcation points. The open-loop behaviour of the system is also revealed in its closed-loop CBC response, and agrees with fixed-amplitude tests (Fig. 6).

Upon constructing the solution surface (Fig. 11), an experimental bifurcation analysis using suitable post-processed curve-fitting techniques estimated the fold bifurcations and, hence the cusp bifurcation. Through polynomial-curvefit-based method and a smoothed-spline-based method, the cusp point was approximated to be located at \((f^*, \hat{u}^*, \hat{x}^*) = (41.89, 0.246, 0.281)\) and \((f^*, \hat{u}^*\), \(\hat{x}^*) = (41.89, 0.252, 0.286)\), respectively.

Future work in this area is vast and extensive. It is important to acknowledge that physical experiments and their associated implementations are subject to limitations. In particular, practical considerations of hardware/instrumentation requirements, signal processing/sampling times, the sensitivity of measurement devices, and cost-effectiveness of computation and implementation should be considered. Further analysis on the effects of signal processing and filter lag can be of concern, especially for practical implementation in fast timescale applications. Whilst the various band-pass filtering stages aid in the signal acquisition of the experiment, the associated delays or lags may be non-negligible for other avenues of research.

We reiterate and emphasise that the motivation for this study lies in a larger body of work concerned with analysing novel dynamics in an active micro-cantilever through experimental validation. Hence, the benchmark fixed-fixed dual-beam system acts as a proof-of-concept towards implementation and testing for the micro device. We hope to extend CBC to broader and wider audiences and applications, including but not limited to structural dynamics and health monitoring, as a viable alternative to existing linear modal testing methods. The methods presented can be used as scalable tools for the wider experimental and applied dynamics community.