On the simplification of the internal nonlinear robot models for the MPC-based visual servoing

Abstract

Visual servoing enables tracking and grasping of static and moving objects and locating regions of interest. Its implementation requires the coordination of low-level control tasks with high-level supervision and planning. The use of the PID-based manipulation control addresses only the dynamical response and requires the use of optimization-based techniques at the supervisory level. On the contrary, model predictive control (MPC) simplifies the design as it combines both tasks within a single algorithm. However, successful MPC implementation depends on the quality of the internal model utilized by the algorithm. Robots are intrinsically and significantly nonlinear control objects, so their models are inherently complex. This leads to computational problems. Standard solutions are to shorten the MPC horizons or to parallelize calculations. The approach suggested here returns to the problem roots, i.e. to the model. This study proposes simplified models that allow the use of the MPC. General Hammerstein–Wiener-like model is applied to an arm, which is further simplified into the linear dynamics used as the predictive supervisory control over the torque control. The head uses linear dynamics used by the supervisory MPC working with the base servomotors. It is shown that they are computationally efficient and sufficiently accurate. It is shown that the linear MPC controllers, which use the suggested simplified dynamic robot models, can successfully support visual servoing with accurate control. They are compared with standard PID-based structures and show their superiority. The proposed approach is successfully validated using Matlab and Gazebo robot simulator and is ultimately confirmed by experiments on a real robot.

1 Introduction

The modeling phase is the focal point of the majority of modern control engineering analyses. Robot control is not an exception. There are dozens of different model types and modeling approaches used in robotics [51]. Due to various robot types and possible model simplifications, there are many different variants. The robot model is generally highly nonlinear with coupled dynamics, hard to handle, and even harder to identify. Therefore, practitioners often use dedicated simulation software such as Gazebo [37], Webots [43], or CoppeliaSim [47]. Implementation of the feedback control paradigm is often performed using those simulators. Position, impedance and admittance control [9, 27] follows this path. On the contrary, predictive control requires an accurate and computationally undemanding internal model. The model presented here satisfies this requirement. The novelty is in the use of static nonlinear kinematics [40] accompanied by simple linear time-invariant (LTI) dynamics [34]. This approach stems from the Wiener-Hammerstein models and is motivated by the considered robot structure.

Control of robots executing complex service tasks usually relies on camera-based feedback measurements; thus, visual servos are studied intensively [7]. One can find several definitions, for instance, the one proposed by François Chaumette: “Visual servoing refers to the use of computer vision data as input of real-time closed-loop control schemes to control the motion of a dynamic system, a robot typically” [7]. Thus, if we integrate a visual sensor, image processing and visual recognition with a module utilizing the results provided by control theory, we obtain a visual servoing system. One iteration of the standard visual servoing algorithm is composed of several steps: image acquisition, tracking object feature extraction, evaluation of object properties (e.g., location in the image or 3D space), computation of the error between the end-effector’s current location and the desired one associated with the current location of the object (this is the control error), and finally the generation control commands according to the employed control rule. This sequence of steps does not require an explicit use of the internal dynamics model of the robot within the used control algorithm. However, the knowledge provided by the robot’s model and the tracked object’s behaviour can significantly improve the control quality. The use of predictive control modifies the mentioned sequence by embedding the model of the robot into the calculations. Model Predictive Control uses an internal model iteratively during each optimization step [53], and the modeling phase cannot be skipped. MPC performance significantly depends on the internal model quality [17]. The introduction of the predictive control paradigm into robot control creates challenges. Computation time is crucial. Robotic applications require a fast response; thus, the control rule must be often evaluated within a few milliseconds. Therefore, the predictive rule must be calculated very fast. Predictive control can be realized in two ways [39], i.e., using either analytical or nonlinear optimization formulation.

The general formulation requires the utilization of an online optimization routine to evaluate new controller output during each iteration. Such online MPC uses multiple model evaluations to find a feasible solution of some cost function over the receding horizon. Unfortunately, applying a complex nonlinear model and optimization constraints will immediately cause numerical problems. On the contrary, explicit (analytical) MPC formulation enables the exclusion of the optimization step executed iteratively. The control rule is precomputed offline once, using some simplifications generally associated with the model and the cost function. The model should be generally linear, while the cost function quadratic. Therefore, time is spared at the cost of model/optimization simplicity. Both approaches have been implemented successfully. Nevertheless, one should always keep in mind the advantages and disadvantages brought about by each of those approaches.

Present research considers predictive visual servoing applied to the KUKA LWR 4+ robot. This work focuses on the efficient implementation of nonlinear modeling required for the MPC-based control of a robot manipulator. The model has to take into account both the non-linearity and the dynamics to capture enough of the system complexity to support the MPC strategy. Moreover, the selected model must perform satisfactorily over the selected long horizons and must simultaneously meet computational constraints to execute the calculations within the sampling period. The majority of reported visual servoing systems are limited to their kinematic relations, while our solution adds the dynamics into the control system. Moreover, it is not just any theoretical definition but such a formulation that is simple enough to be efficiently handled by the industrial implementation of the predictive control system.

Robustness is another essential requirement. MPC has to operate inside the visual servoing framework. The tasks of image acquisition, feature extraction, and evaluation of the selected object properties are time-consuming. Though the used algorithms are efficient and optimized towards their calculation time, they are not deterministic. It may always happen that the image processing time overruns the sampling period. In such a situation, the information is not provided on time. However, the controller still has to perform appropriately. Therefore, the applied MPC strategy should be able to operate despite such situations. Initial investigation of similar issues in the process industry shows that the predictive structure is more resistant to lost samples than PID-based algorithms [48].

The considered application uses position-based servoing with two camera-based visual servos: (1) visually tracking the object by the pan-tilt head and (2) approaching the object by the robot arm using visual feedback. Thus, two separate MPC instances are designed. The arm manipulation MPC (arm-MPC) controls the operation of the 7-DOF arm and the robot column (torso). In contrast, the head tracking (head-MPC) controls the robot head (pan-tilt neck, also influenced by the robot column motions) equipped with an RGB-D camera. Both MPC controllers are coupled through the robot column. The arm-MPC can generate the column motion, constituting a head-MPC disturbance.

Each predictive control instance operates with a different MPC setup. The arm-MPC acts as the supervisory control over the basic torque arm control. It has to be noted that two versions are considered: the full version that uses the fully nonlinear model, and the simplified one using its linear version. The head-MPC operates as a classical position-based servo controller. Therefore, two unique dynamical models are developed, analyzed, and presented. This paper focuses on the model configuration, identification, and performance. Control quality aspects are treated as additional features, although model quality cannot be validated without the ultimate MPC strategy. The analysis is performed using Matlab and Gazebo simulations.

Proper predictive control application to visual servoing improves its operation and combines joint control and trajectory tracking in operational space. Successful real-time predictive control application requires the satisfaction of sampling time constraints and simultaneous assurance of the quality of the internal model. The presented research proposes a simple and efficient approach to addressing this issue. Formulating the task in this way provides a new perspective to visual servoing.

The proposed approach inherits all the advantages of MPC control over the classical reactive algorithms, such as the PID: the ability to use knowledge of the process embedded in the process model, the anticipation of future system behavior over an assumed control horizon, multidimensionality and applicability to nonlinear objects. The visual servoing template allows the use of yet another aspect of predictive control that practically remains both underestimated and unnoticed, i.e. the use of setpoint prediction.

Using knowledge of the setpoint’s future (over the horizon) behavior enables the full exploitation of the advantages of predictive control and even further improves its tracking performance. Moreover, the vision component of the visual servoing system enables extrapolation of the behavior of the tracked object, similarly to the one provided by an Extended Kalman Filter (EKF). This very rarely used element of the proposed solution makes it possible to obtain and maintain high tracking quality, superior to the other solutions, and moreover accounts for its uniqueness.

The proposed approach can be applied to any mechanical systems which are characterized by complex kinematics entangled with dynamics. If a computationally simple and effective direct modeling solution is not available, the proposed Wiener-Hammerstein approach can be useful as it decouples linear dynamics from the nonlinear static element. Its applicability might be increased by the fact that such models are convenient and easy to use within the predictive control templates as their internal models. If anybody needs to design predictive control for a complex mechanical device, the proposed approach can be taken into account as a potential solution.

The paper starts with the presentation of methods used in this research. Section 2 presents relevant predictive visual servoing problems focusing on the modeling issues. The main contribution in the form of the nonlinear dynamics models tailored to the role of the MPC internal model is described in Sect. 3. The developed models are validated using Matlab and Gazebo simulations (Sect. 4). The final confirmation of the modeling concept is obtained through the observation of the MPC’s performance using these models in real robot control. Section 5 summarizes the results of the work, draws conclusions, and presents the identified open issues for further research.

2 Model predictive control and visual servoing

The introduction of a camera, which is used to observe the robot’s environment, closes the external feedback loop, enabling the reactions to changes occurring in that environment, thus broadening the range of possible robot applications. Generally, this concept is known under the name of visual servoing. First applications used the so-called look-and-go scheme. In such cases, the vision system establishes object’s location, and the manipulator follows the precomputed trajectory to reach that location without further visual feedback. Nowadays, continuous visual tracking in a closed-loop configuration is possible.

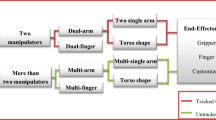
Visual servos can be classified using diverse criteria [8, 52]. Figure 1 presents sample classification. Initially, control law was based on the computation of the error using the current image, sometimes supplemented with previous ones. However, currently, the future predicted behavior of the manipulator and the tracked object can also be taken into account. This enables the application of MPC as the main controller.

Fig. 1

Visual servo classifications based on diverse criteria

In this paper, a supervisory PB-SAC-EOL-MPC servo with an RGB-D camera is used. This setup has been chosen because it resembles the one prominent in humans, i.e., stereo vision system with two cameras situated in a head, which is mounted on a neck attached to the torso composed of a rotating column and two arms attached to both of its sides. Coordination between the visual system located in the head and the manipulator control is implemented by integrating robot regulatory control with online real-time manipulator optimal path planning in a single control task. Despite its high calculation complexity, MPC can be successfully applied to the task of visual servoing. Its promises, i.e., integrating real-time operational planning, outweigh deficiencies, especially the need for a nonlinear model resulting in high computational load. One may distinguish three different types of MPC utilized in robots (see Fig. 2). The use of Internal Model Control (IMC) [33] enables the most straightforward incorporation of the predictive feature and internal model into the control strategy. IMC uses a single one-point ahead comparison between model output and future desired value with a simple linear model. Its applications are occasional, although IMC is computationally undemanding. Recent works report fractional-order versions of IMC strategy applied to parallel robots [56].

Fig. 2

Types of MPC used in robotics

Model Predictive Control strategy can be realized in two ways: using the simplified analytical version of the algorithm or employing a complex model and numerical MPC. Each approach attains a compromise between the exactness of the internal model and the calculation time. It can be noticed that the application of the analytical MPC to image-based visual servoing follows a path laid out by the process industry. This approach uses simplified linear modeling theory accompanied by a quadratic performance index. Therefore, classical linear versions of the MPC may be used. Dynamic matrix control (DMC) formulation uses the model in the form of step responses [12]. The approach originated in the ’70s and is still very popular and widely used in the process industry. Its application to visual servoing is limited due to the restriction imposed by the method. The model must be linear and identified in the form of a step response. Its initial applications [5] have not been followed by more profound research.

Generalized Predictive Control (GPC) strategy [10] relies on the transfer function model formulation. However, this approach uses a linear model [21] to obtain a fast response without deeper considerations of the visual servoing specifics. This research was followed in [13, 28]. The GPC-based approach is still limited to the small neighborhood of an operating point and requires controller switching for larger movements.

Both approaches (DMC and GPC) share similar limitations. The internal model is linear. Thus, the control strategy is valid only in the relatively small neighborhood of the selected operating point. Further research heads towards overcoming this obstacle. One may find two approaches: multi-regional controllers [16, 42], called linear time-varying (LTV), or nonlinear MPC with trajectory linearization. LTV MPC was initially proposed for path following by autonomous vehicles [18] and is still successfully applied in similar applications. Recently, this concept has been applied to visual servoing [19]. The Linear Lime-Varying approach uses the model with varying parameters to approximate the nonlinear system, similarly to the gain scheduling, adaptive approach [4]. In some applications, a similar method uses a different name: Linear Parameter-Varying (LPV) [55]. This method is relatively easy to implement. Another approach is to build a neural network model of the robot and use it as an internal MPC model [58].

The MPC algorithm with Nonlinear Prediction and Linearization Along the Predicted Trajectory (MPC-NPLPT) is frequently recommended to reduce the computational effort [53]. It enables the use of a nonlinear plant model, which should be beneficial for visual servoing, mainly because it may be efficiently applied to variable trajectories [44].

The numerical MPC strategy enables any nonlinear formulation of the internal model; however, the optimization routine uses it in every iteration. Moreover, such a formulation can impose various constraints or utilize any internal performance index formulation. This flexibility significantly increases the computational load of the controller. There are different ways to overcome this problem. One approach is to use efficient code optimization to speed up calculations [35]. Another solution is to utilize stronger processing units, mainly parallel computations executed on a Graphics Processing Unit (GPU) [30]. Parallelization supports the use of other predictive control concepts, such as, for instance, Evolutionary MPC [29], which enables the use of global optimization algorithms.

An interesting approach is to apply MPC-predicted trajectory parametrization. It minimizes the search space for the optimization algorithm and thereby reduces the computational load. The parametrization may be done in different ways, e.g. using polynomials, trigonometric functions, Laguerre functions [54] or piece-wise linear models [31].

Finally, horizon shortening is used to diminish the optimization search space. This approach imposes a substantial limitation on the achievable solution. Short horizons minimize the calculation time [3]. Thus, in some cases, the control horizon is reduced even to 1 [49], which is an extreme limitation.

In most cases, predictive control applied in the image-based visual servoing uses MPC as a direct controller. However, by analogy with process control, predictive control may be applied at a supervisory level too [20]. In such a situation, it is reasonable to differentiate the time sampling of the two layers, as the lower level dynamic control should work with higher frequencies. Supervision of the lower-level controller can be done at lower frequencies. Such an approach relaxes time limitations for the MPC and offers an interesting alternative. This approach has been exploited in [36] and shows interesting properties. As an alternative to direct and supervisory configurations, an interesting possibility is the use of MPC to generate a real-time trajectory for robot arm [2], however, with the use of a linear model. An interesting predictive control scheme using disturbance observers was proposed in [41] and further continued in [46].

For Eye in Hand setups using image-based visual servoing, different robust model predictive control approaches have been used [25]. Some of them, by formulating adequate constraints, can keep the desired object in the camera field of view, avoid the Jacobian singularity and have a fast convergence rate. An input mapping technique, which uses past output-input servo data to supplement the original feedback control, reduces the negative effects of model inaccuracy and improves system performance without resorting to system identification [26]. However, the system model is based on kinematics and does not consider the robot dynamics.

The research presented herein pertains to the task of a robot gripping an object handed to it by a human. For that purpose, two visual servos are used (see Fig. 3). They form a position-based (PB) visual servoing system.

Fig. 3

Visual servoing block diagram

One drives the head in such a way that the tracked object is always in the centre of the image. The other servo guides the gripper of the manipulator to the object. Thus, two instances of predictive control are employed. The head-MPC controller operates in a direct mode with a high sampling frequency of 500 Hz. Its direct operation means that it directly controls the joint angles. Its setpoint is generated by the vision system, which acquires the image of the target. Visual object pose estimation operates with a longer sampling rate of 20 Hz. Therefore, the dynamic pan-tilt controller has enough time to realize each setpoint signal. Moreover, there is some time left for setpoint signal shaping and smoothing. However, this aspect is not addressed in the presented research.

The arm-MPC works in the supervisory configuration, exerting influence over a torque controller. It delivers joint angles, which form setpoint signals (inputs) for low-level control. The arm-MPC operates with a 20 Hz sampling rate, while the lower-level torque controllers use a 500 Hz frequency. Moreover, the arm-MPC does not directly control the arm joints but generates a trajectory that the arm should follow to approach the target point. Differences between the supervisory and the direct structures are shown in Fig. 4.

Fig. 4

MPC structures: supervisory as applied to the arm control and direct used for the head control

Thus, the following issues need to be addressed: the adopted nonlinear MPC formulation and possible MPC internal models.

2.1 Nonlinear model predictive control problem formulation

MPC algorithms generate control signals considering the predicted future behavior of the control plant outputs many sampling instants ahead. The prediction is obtained using the internal plant model. Values of manipulated variables (controller outputs) are usually calculated by solving the following optimization problem [53]:

$$\begin{aligned}&\min _{\Delta {\varvec{u}}}\left\{ J_{\textrm{MPC}}=\sum _{p=1}^{n_y} \sum _{r=1}^{N}\kappa _p\left( {{\overline{y}}}_{k+r|k}^p-y_{k+r|k}^p\right) ^2\right. \nonumber \\&\quad +\sum _{m=1}^{n_u}\sum _{r=0}^{N_u-1}\lambda _m\left( \Delta u_{k+r|k}^m\right) ^2\nonumber \\&\quad \left. +\sum _{m=1}^{n_u}\sum _{r=0}^{N_u-1}\mu _m\left( u_{k+r|k}^m\right) ^2\right\} \end{aligned}$$

(1)

subject to:

$$\begin{aligned} \Delta {\varvec{u}}_{\min }\le & {} \Delta {\varvec{u}} \le \Delta {\varvec{u}}_{\max } , \end{aligned}$$

(2)

$$\begin{aligned} {\varvec{u}}_{\min }\le & {} {\varvec{u}} \le {\varvec{u}}_{\max }, \end{aligned}$$

(3)

$$\begin{aligned} {\varvec{y}}_{\min }\le & {} {\varvec{y}} \le {\varvec{y}}_{\max }, \end{aligned}$$

(4)

$$\begin{aligned} {\varvec{y}}_{\min }^c\le & {} {\varvec{y}}^c \le {\varvec{y}}_{\max }^c, \end{aligned}$$

(5)

$$\begin{aligned}= & {} f_{\textrm{model}}(\cdot )+{\varvec{d}}, \end{aligned}$$

(6)

where $y_{k+r|k}^p$ is the value of the pth output for the $(k+r)$th sampling instant predicted at the kth sampling instant using the control plant model, ${{\overline{y}}}_{k+r|k}^p$ are elements of a reference trajectory for the pth output, $\Delta u_{k+r|k}^m$ are future changes in manipulated variables, $u_{k+r|k}^m$ are future values of manipulated variables, $\kappa _p\ge 0$ are the weighting coefficients for the predicted control errors of the pth output, $\lambda _m\ge 0$ are the weighting coefficients for the changes of the mth manipulated variable, and $\mu _m\ge 0$ are the weighting coefficients for the values of the mth manipulated variable (often it is assumed that $\mu _m=0$), N and $N_u$ denote prediction and control horizons, respectively; $n_y$, $n_{yc}$, $n_u$ denote number of controlled output variables, only constrained output variables and manipulated variables, respectively;

$$\begin{aligned} {\varvec{y}}= & {} \left[ {\varvec{y}}^{1},\ldots ,{\varvec{y}}^{n_y}\right] ^T,\;{\varvec{y}}^{p}=\left[ y_{k+1|k}^{p},\ldots ,y_{k+N|k}^{p}\right] , \end{aligned}$$

(7)

$$\begin{aligned} {\varvec{y}}^c= & {} \left[ {\varvec{y}}^{c,1},\ldots ,{\varvec{y}}^{c,n_{yc}}\right] ^T,\nonumber \\ {\varvec{y}}^{c,p}= & {} \left[ y_{k+1|k}^{c,p},\ldots ,y_{k+N|k}^{c,p}\right] ,\end{aligned}$$

(8)

$$\begin{aligned} \Delta {\varvec{u}}= & {} \left[ \Delta {\varvec{u}}^{1},\ldots ,\Delta {\varvec{u}}^{n_u}\right] ^T,\nonumber \\ \Delta {\varvec{u}}^{m}= & {} \left[ \Delta u_{k|k}^{m},\ldots ,\Delta u_{k+N_u-1|k}^{m}\right] ,\end{aligned}$$

(9)

$$\begin{aligned} {\varvec{u}}= & {} \left[ {\varvec{u}}^{1},\ldots ,{\varvec{u}}^{n_u}\right] ^T,\nonumber \\ {\varvec{u}}^{m}= & {} \left[ u_{k|k}^{m},\ldots ,u_{k+N_u-1|k}^{m}\right] , \end{aligned}$$

(10)

$$\begin{aligned} {\varvec{d}}= & {} \left[ {\varvec{d}}^{1},\ldots ,{\varvec{d}}^{n_y}\right] ^T,\;{\varvec{d}}^{p}=\left[ d_{k}^{p},\ldots ,d_{k}^{p}\right] ^T, \end{aligned}$$

(11)

${\varvec{y}}^c$ is the vector containing outputs that are not controlled, but constrained; this mechanism is used in Sect. 4.1.1 to constrain joint angles (36), which are not included in the performance function of the optimization problem.

$\Delta {\varvec{u}}_{\min }$, $\Delta {\varvec{u}}_{\max }$, ${\varvec{u}}_{\min }$, ${\varvec{u}}_{\max }$, ${\varvec{y}}_{\min }$, ${\varvec{y}}_{\max }$, ${\varvec{y}}_{\min }^c$, ${\varvec{y}}_{\max }^c$ are vectors of lower and upper bounds of changes and values of the control signals and the values of output variables controlled and constrained or only constrained, respectively. In the last constraint, $f_\textrm{model}$ is a function of the inputs of the model and $d_k^{p}$ describes the modeling error. The formulation of the MPC optimization problem presented above is a general one. However, the constraints can be taken into consideration if needed, i.e., not all or none of them can be used. In the latter case, when a linear model is used for prediction, the generation of the control signals can be simplified (a control law is obtained).

As a solution to the optimization problem (1–4), the optimal vector of changes in the manipulated variables ${\Delta {\varvec{u}}}$ is obtained in each iteration. The predicted values of output variables $y_{k+r|k}^p$ are derived using the dynamic control plant model. A simplified arm model is a nonlinear, structured (consisting of nonlinear static and linear dynamic block) model. Therefore, the optimization problem (1–4) solved in each iteration of the MPC algorithm is a nonlinear optimization problem. Finding the solution to such an optimization problem is a non-trivial and important issue. Fortunately, the numerically efficient methods were developed. One can use, e.g., iterative linear quadratic regulator (iLQR) algorithm [32], sequential quadratic programming (SQP) approach [15], or real-time iteration (RTI) scheme [23] to obtain the future values of the manipulated variables generated by the NMPC algorithm in a reasonable time.

2.2 Linear model predictive control problem formulation

A pan-1tilt head model used in the MPC algorithm is a linear model. In such a case, the optimization problem can be simplified, because the vector of predicted output values ${\varvec{y}}$, after application of the superposition principle, can be formulated as:

$$\begin{aligned} {\varvec{y}}&=\varvec{{{\widetilde{y}}}}+{\varvec{A}}\cdot \Delta {\varvec{u}}\hspace{5.0pt}, \end{aligned}$$

(12)

$$\begin{aligned} \varvec{{{\widetilde{y}}}}&=\left[ \varvec{{{\widetilde{y}}}}^{1},\ldots ,\varvec{{{\widetilde{y}}}}^{n_y}\right] ^T,\varvec{{{\widetilde{y}}}}^{p}=\left[ {{{\widetilde{y}}}}_{k+1|k}^{p},\ldots ,{{{\widetilde{y}}}}_{k+N|k}^{p}\right] \hspace{5.0pt}, \end{aligned}$$

(13)

where $\varvec{{{\widetilde{y}}}}$ is called a free response of the plant (it contains future values of output variables calculated assuming that the control signal does not change in the prediction horizon),

$$\begin{aligned} {\varvec{A}}&=\left[ \begin{array}{cccc} {\varvec{A}}^{11} &{} {\varvec{A}}^{12} &{} \ldots &{} {\varvec{A}}^{1n_u} \\ {\varvec{A}}^{21} &{} {\varvec{A}}^{22} &{} \ldots &{} {\varvec{A}}^{2n_u} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {\varvec{A}}^{n_y1} &{} {\varvec{A}}^{n_y2} &{} \ldots &{} {\varvec{A}}^{n_yn_u} \\ \end{array} \right] , \nonumber \\ {\varvec{A}}^{p,m}&=\left[ \begin{array}{ccccc} a_1^{p,m} &{} 0 &{} \ldots &{} 0 &{} 0 \\ a_2^{p,m} &{} a_1^{p,m} &{} \ldots &{} 0 &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ a_p^{p,m} &{} a_{N-1}^{p,m} &{} \ldots &{} a_{N-N_u+2}^{p,m} &{} a_{N-N_u+1}^{p,m} \end{array} \right] \end{aligned}$$

(14)

is a matrix, called the dynamic matrix, composed of the plant step response coefficients $a_i^{p,m}$ describing the influence of the mth input on the pth output.

The following vectors are introduced:

$$\begin{aligned} \varvec{{{\overline{y}}}}&=\left[ \varvec{{{\overline{y}}}}^{1},\ldots ,\varvec{{{\overline{y}}}}^{n_y}\right] ^T,\nonumber \\ \varvec{{{\overline{y}}}}^{j}&=\left[ {{{\overline{y}}}}_{k+1|k}^{j},\ldots ,{{{\overline{y}}}}_{k+N|k}^{j}\right] . \end{aligned}$$

(15)

After assuming $\mu _m=0\, (m=1,\ldots ,n_u)$, the performance function in (1) can be rewritten as:

$$\begin{aligned} J_{MPC}&=(\varvec{{{\overline{y}}}}-{\varvec{y}})^T\cdot \varvec{\kappa } \cdot (\varvec{{{\overline{y}}}}-{\varvec{y}})+\Delta {\varvec{u}}^T\cdot \varvec{{\lambda }}\cdot \Delta {\varvec{u}} , \end{aligned}$$

(16)

where $\varvec{\kappa }=\left[ \varvec{\kappa }_1,\ldots ,\varvec{\kappa }_{n_y} \right] \cdot {\varvec{I}}$; $\varvec{\kappa }_r=\left[ \kappa _r, \ldots , \kappa _r \right]$ have N elements, $\varvec{\lambda }=\left[ \varvec{\lambda }_1,\ldots ,\varvec{\lambda }_{n_u} \right] \cdot {\varvec{I}}$; $\varvec{\lambda }_r=\left[ \lambda _r, \ldots , \lambda _r\right]$ have $N_u$ elements; ${\varvec{I}}$ denotes the identity matrix of the appropriate dimension. After applying the prediction (12) in the performance function (16) one obtains:

$$\begin{aligned} J_{{\textit{LMPC}}}&=(\varvec{{{\overline{y}}}}-\varvec{{{\widetilde{y}}}}-{\varvec{A}}\cdot \Delta {\varvec{u}})^T\cdot \varvec{\kappa } \cdot (\varvec{{{\overline{y}}}}-\varvec{{{\widetilde{y}}}}-{\varvec{A}}\cdot \Delta {\varvec{u}})\nonumber \\&\quad +\Delta {\varvec{u}}^T\cdot \varvec{\lambda }\cdot \Delta {\varvec{u}}. \end{aligned}$$

(17)

Performance function (17) depends quadratically on decision variables $\Delta {\varvec{u}}$. If the constraints are not taken into account during optimization, then the control signals can be generated using the following formula:

$$\begin{aligned} \Delta {\varvec{u}} = \left( {\varvec{A}}^T\cdot \varvec{\kappa }\cdot {\varvec{A}} + \varvec{\lambda }\right) ^{-1}\cdot {\varvec{A}}^T\cdot \varvec{\kappa }\cdot \left( \varvec{{{\overline{y}}}}-\varvec{{{\widetilde{y}}}}\right) . \end{aligned}$$

(18)

The paper deals with appropriate MPC internal model selection, which ultimately leads to efficient robot predictive control. Classical MPC design requires the derivation of a proper model of the controlled plant first. If the model is not accurate enough, MPC fails. There are two solutions to this issue: to improve the model accuracy or to change the applied control strategy. If the model improvement helps, we do not have to change the control algorithm (tube or robust MPC). Thus, once the model works, other MPC parameters, such as the control horizon $N_u$ and prediction horizon N as well as the performance index weighting coefficients ${\varvec{\lambda }}$ and ${\varvec{\kappa }}$ can be selected.

Tuning of both the model and the controller can be done using simulations, usually by taking into account the minimization of some performance indices, such as mean square error or integral absolute error. As the paper focuses on the MPC internal model selection, the models are identified according to the mentioned above mean square error index MSE. Once the model is appropriate, it is inserted into the MPC structure, and the controller is cross-checked to determine whether it meets the time constraints. Finally, the MPC controller is fine-tuned, which ultimately validates the model selection.

3 The proposed internal MPC models for visual servoing

The robot modeling subject, especially the one focusing on the visual servoing, has existed in the literature for a long time with a comprehensive reference discussed in [8]. Following this approach, the detailed model of the robot used has been already developed and published [22]. Moreover, the kinematics and dynamics investigation for exactly the same robot can be found in [57]. Such models are useful from the design perspective; however they are not suitable for the control purpose, especially as the internal models of the predictive control. Internal model used by the predictive strategy must be simple enough to be executed on industrial control hardware, which often is not highly sophisticated.

The MPC internal model derivation differs significantly from conventional plant modeling. The internal model of the predictive strategy operates in a very specific real-time environment. The controller works with a certain sampling period, considered a hard constraint that cannot be violated. Any approach that exceeds the sampling interval is unacceptable, even if it is very accurate. The same applies to the MPC. Its internal model has to be run many times within the sampling period, and thus it needs to be fast.

Concluding, the internal model has to maintain the compromise between the accuracy and the calculation time, and the model is not validated by its behavior but by the MPC performance. Conventional first principle models are characterized by high accuracy, but they need much time and resources for calculation. This work aims at deriving a simple enough model that allows for good performance of the MPC controller.

Fig. 5

Structure of the simplified arm dynamics model

In arm-MPC and head-MPC we use simplified models. General Hammerstein–Wiener-like model is applied to an arm, which is further simplified into the linear dynamics used as the predictive supervisory control over the torque control. The head uses linear dynamics used by the supervisory MPC working with the base servomotors.

3.1 Arm-MPC internal model

The 7DOF arm model of the KUKA LWR 4+ robot mounted on a rotating torso (column) is designed for the MPC algorithm. Two model configurations are addressed in the research: the nonlinear model and its linear simplification. The first one may be used in the direct MPC control, while the second one is incorporated in the hierarchical structure with the supervisory MPC over base torque controllers.

3.1.1 Arm-MPC nonlinear model

The model uses the Hammerstein–Wiener structure, depicted in Fig. 5, in which two static nonlinear blocks surround the LTI dynamic block. Hammerstein–Wiener modeling can be used when it is possible to decompose the system model into the part describing the inertial dynamics of the motors and the nonlinear part describing the kinematics. The examples of Hammerstein–Wiener–like models used in robotic systems can be found in the literature. In [45], a Hammerstein–Wiener model is used to describe a SCARA robot. In [24], such a model is used to model the leg of the Quadruped with Parallel Actuation Leg (QPAL) robot. A Hammerstein model applied to describe a flexible robot manipulator is described in [38]. A three-axis gimbal system mounted on UAV, modeled with a Hammerstein model, used in an MPC, is described in [1]. A Hammerstein–Wiener model applied in the altitude control of the VTOL aerial robot is described in [14].

The Hammerstein–Wiener model here differs from the previous model’s structure, consisting of standard but complex inverse kinematics (static part) and simple but effective first-order dynamics, incorporating dynamical behaviour into the model. This dynamics is further utilized in the MPC control to generate dynamical predictions. Moreover, the validation takes into account the MPC performance, not the internal model itself.

Static model #2 The static model #2 calculates forward kinematics for the end-effector [11]:

$$\begin{aligned} ^{0}_{8}{\mathcal {T}} = ^{0}_{1}{\mathcal {T}} \, ^{1}_{2}{\mathcal {T}} \ldots ^{7}_{8}{\mathcal {T}} = \prod _{i=1}^{8} \, ^{i-1}_{i}{\mathcal {T}}, \end{aligned}$$

(19)

where frame 0 is the base coordinate frame fixed to the ground, 1 is the column frame, and the following frames are affixed to the consecutive links of the manipulator. Frame 8 is affixed to the last link and treated as the end-effector. Each matrix $\, ^{i-1}_{i}{\mathcal {T}}$ is a homogeneous transformation matrix from frame $i-1$ to frame i. Frames $0,\ldots , 8$ are attached to the consecutive links forming the kinematic chain, from the base to the end-effector. The result $^{0}_{8}{\mathcal {T}}$ is the pose of the end-effector expressed in the base frame as a homogenous transformation matrix, and it is transformed into the form: $\left[ x_{ce} \quad y_{ce} \quad z_{ce} \quad \varphi _{ce.1} \quad \varphi _{ce.2} \quad \varphi _{ce.3}\right] ^T$, where $\varphi _{ce.1}$, $\varphi _{ce.2}$, $\varphi _{ce.3}$ are the Roll, Pitch and Yaw angles of rotations about the fixed x, y, z axes of the base frame.

Static model #1 Calculation of gravity forces is realized by the static model #1. Center of mass of a link i of the kinematic chain is represented by a frame $C_{i}$ connected to it (its origin is at the center of mass, Fig. 6) [11]. The base frame 0 is inertial; however, frames $C_{i}$ are not.

Fig. 6

A single link annotated with symbols: $C_{i}$—center of mass of link i, $_{i}F$—force exerted by link $i-1$ on link i, $_{C_{i}}F$ – inertial force acting at c.o.m. of link i, $_{i}N$—torque exerted by link $i-1$ on link i, $_{C_{i}}N$—inertial torque acting at c.o.m. of link i

Inertial forces acting on link i are:

$$\begin{aligned} ^{i}_{C_{i}}F = M_{i} \, ^{i}(\,^{0}_{C_{i}}{\mathcal {A}}), \end{aligned}$$

(20)

where $M_{i}$ is the mass of the link, and $^{0}_{C_{i}}{\mathcal {A}}$ is the acceleration of link center of mass (c.o.m.) with respect to (w.r.t.) the base coordinate frame. In the present case, we assume that the accelerations and velocities equal to zero, what implies that $\,^{0}_{C_{i}}{\mathcal {A}} = {\mathcal {O}}$ and $^{i}_{C_{i}}F = {\mathcal {O}}$, where ${\mathcal {O}}$ denotes the vector containing zeros. As the result, this part of the model can be assumed static. Dynamics is introduced in the form of linear transfer functions, which are introduced after this static part.

Inertial torque acting at c.o.m. of link i:

$$\begin{aligned} ^{i}_{C_{i}}N = \, ^{i}(\, ^{0}_{C_{i}}\omega ) \times \Big ( ^{C_{i}}I_{i} \, ^{i}(\, ^{0}_{C_{i}}\omega ) \Big ) + ^{C_{i}}I_{i} \, ^{i}(\, ^{0}_{C_{i}}{\mathcal {E}}), \end{aligned}$$

(21)

in the static model is ${\mathcal {O}}$, because rotational velocity $\, ^{0}_{C_{i}}\omega = {\mathcal {O}}$ and rotational acceleration $\, ^{0}_{C_{i}}{\mathcal {E}} = {\mathcal {O}}$. Thus $^{i}_{C_{i}}N = {\mathcal {O}}$. $^{C_{i}}I_{i}$ is the inertia matrix w.r.t. c.o.m. frame, and $^{i}()$ is the instantaneous projection onto the link i coordinate frame.

Torques that compensate gravity forces are calculated by iterating from the end-effector to the base ($i = n \rightarrow 1$); in our case $n=8$ (the column plus 7 d.o.f. of the LWR arm):

• For $i=n+1$: $^{n+1}_{n+1}F = {\mathcal {O}}$, $^{n+1}_{C_{n+1}}F = {\mathcal {O}}$

• Inter-link interaction forces:

  $$\begin{aligned} ^{i}_{i}F = \, ^{i}_{C_{i}}F + \, ^{i}_{i+1}{\mathcal {R}} \, ^{i+1}_{i+1}F - M_{i} \, ^{i}\!g, \end{aligned}$$

  (22)

  where $^{i}_{i+1}{\mathcal {R}}$ is the orientation of link $i+1$ frame w.r.t. link i frame, and $^{i}_{C_{i}}F = {\mathcal {O}}$ for the static model.

• Inter-link interaction torques:

  $$\begin{aligned} ^{i}_{i}N&= \, ^{i}_{C_{i}}N + \, ^{i}_{i+1}{\mathcal {R}} \, ^{i+1}_{i+1}N + \, ^{i}_{C_{i}}{\mathcal {P}} \times \, ^{i}_{i}F\nonumber \\&\quad + (\, ^{i}_{i+1}{\mathcal {P}} - \, ^{i}_{C_{i}}{\mathcal {P}} ) \times \, ( \, ^{i}_{i+1}{\mathcal {R}}\, ^{i+1}_{i+1}F), \end{aligned}$$

  (23)

  where $^{i}_{C_{i}}N = {\mathcal {O}}$ for the static model, and $^{i}_{C_{i}}{\mathcal {P}}$ and $^{i}_{i+1}{\mathcal {P}}$ are the positions of origins of link i c.o.m. and link $i+1$ frame w.r.t. link i frame, respectively.

• Torque to be developed in the revolute joint:

  $$\begin{aligned} \tau _{i} = \, ^{i}_{i}N^{T} \, ^{i}_{i}z, \end{aligned}$$

  (24)

  where z is axis of the joint. Other than z components are canceled out by reaction forces/torques.

Finally, the model calculates

$$\begin{aligned} \tau _{g.i} = \tau _{c.i} - \tau _i \end{aligned}$$

(25)

for $i \in \left\{ 1,\ldots ,8 \right\}$.

Dynamics model It is assumed that the dynamics model consists of inertias followed by integrators. Thus, the transfer function between each joint torque residual after gravity removal $\tau _{g,i}\, (i= col,2,\ldots , 8)$, and each joint angle $q_i$ is as follows:

$$\begin{aligned} G_i(s)=\frac{K_i}{s(T_is+1)}, \end{aligned}$$

(26)

where s is the complex variable and the gains are as follows:

$$\begin{aligned} K_{{\textit{col}}}&=10, \quad K_2=K_3=K_4\nonumber \\&=K_5=K_6=K_7=K_8=1. \end{aligned}$$

(27)

Time constants $T_i$ are identified based on the responses of the arm, collected from the Gazebo simulator. The applied procedure is as follows:

• 1. Four responses are obtained for different arm configurations (minimally extended and maximally extended) and without or with a load of 6 kg.

• 2. Next, these responses are averaged (as it is often done in process control).

• 3. Time constants are obtained using the optimization routine, minimizing the difference between the response of the simplified model and the responses acquired from the Gazebo simulator, defined as a Sum of Squared Errors (the Levenberg-Marquardt optimization algorithm was used). The obtained values (in seconds) are as follows:

  $$\begin{aligned} \begin{array}{llll} T_2=3.6056 &{}\; T_3=3.8827&{}\; T_4=2.1347&{}\; T_5=2.6108\,\\ T_6=1.5404 &{}\; T_7=1.5832&{}\; T_8=1.5687 &{}\; T_{{\textit{col}}}=1.4382. \end{array} \end{aligned}$$

  (28)

• 4. Finally, a preliminary validation is done, checking if the obtained model can generate a correct prediction on the demanded horizon of 10-time steps (0.5 [s]). Examples of responses are presented in Fig. 7, which depicts the three components of the end-effector’s position obtained using the simplified model. They are compared with the ones obtained using the Gazebo simulator. Both responses are very close to each other; in the exact figure, a portion of the x component is magnified; one can observe that the simplified model generates the response sufficiently close to the response of the Gazebo simulator. For the example data set, also the MSE and MAE indexes were calculated (errors on all three components of the position of the end-effector were taken into account and summed up); they attained relatively small values:

  $$\begin{aligned} \text {MSE}=1.5308e\!-\!04,\quad \text {MAE}=0.0121. \end{aligned}$$

  (29)

Fig. 7

Responses of the simplified model (red, dashed lines) and real responses of the Gazebo simulator (blue lines); components of the position of the end-effector, with a portion of the x component magnified. (Color figure online)

The last step proved that the obtained simplified model properly generates the prediction. The Hammerstein–Wiener-like robot model consists of nonlinear static elements and linear dynamics. As is shown, the nonlinear elements can be derived analytically with the support of the Gazebo simulator. Once they are ready, the dynamics can be identified. It is done empirically using an optimization approach. Robot data are collected, and the dynamics are fitted to them. However, its ultimate validation can be done in the control system with the MPC based on the designed model, generating the setpoint trajectory for the lower-level controllers described in the next section.

3.1.2 Arm-MPC simplified linear model

The simplified model and thus the MPC control structure assumes that the input of the predictive algorithm is defined as the current position of the arm in the joint space (${q_2,\ldots ,q_8,q_{col}}$). Thus, the control algorithm generates the control signal in the form of changes of the target joint positions for the torque control—clear indirect supervisory control as in Fig. 4a. The above is very similar to the one used in the head-MPC. The difference in solution comes from the type of the lower level control (in the case of the arm, it is the torque controller, while the head uses a servomotor). As the motion of the arm is characterized by dynamics comparable to the sampling period of 50 ms, the process model for each joint can be described by dynamical transfer functions. It is suggested that, similarly to the full version of the dynamics, use the first order dynamics as in Fig. 8.

Fig. 8

Simplified model structure for the arm-MPC

The assumed model configuration includes the process dynamics from the robot arm and embedded torque control. The model is used as an input target joint position by the torque controller, while the current position changes from the model output. Optimization of model parameters was performed with the Levenberg–Marquardt algorithm to minimize the error between the data obtained from the simulation and the results yielded by the model. The reference data were obtained from the Gazebo simulator, where we introduced small step changes in each input signal, obtaining overall eight-step responses—one for each joint. We have experimented with various operating points (starting points) to obtain the step responses, as those change based on the starting configuration of the robot. We have then minimized the SSE between all of those responses and the one from the model as a function of model parameters, achieving a result that was, on average, the best for all reference data. Parameters of the resulting model are presented in Table 1. It is worth mentioning that the model of the column is ignored, as it is assumed that it is not moving because it is both slow and has minimal impact on the overall position of the arm end-effector.

Table 1 Parameters of the simplified model

Due to the fact that the arm-MPC utilizes the simplified model, the information about the current position in joint space is transferred to the MPC. The MPC algorithm output, i.e. the generated joint target position (again, in joint space), is passed to the torque controller.

Setpoint information originates from the vision system and is defined in Cartesian space. To convert the position of the tracked target, i.e. the setpoint, it is required to determine the desired arm position in the joint space. The solver of the inverse kinematics is used to achieve this goal. The path from the current position to the setpoint is determined to obtain a relatively smooth trajectory of the approach. A set of positions on that path is determined using the predefined maximum velocity in the Cartesian space. Next, those points are converted to the corresponding joint positions. From that moment onward, all the calculations are conducted in the joint space, with the assumption that reaching the setpoint in the joint space means that the setpoint position in Cartesian space is reached as well.

The proposed multivariate model consists of 8 independent linear transfer functions. As we assume the use of linear models and also no cross-dependencies between those, we can use a fast analytical MPC template, such as the DMC (Dynamic Matrix Control), to make sure we do not violate the sampling period time constraint.

3.2 Head-MPC internal model

A continuous-time model of the considered robot head is proposed using second-order transfer functions for pan and tilt joints, respectively:

$$\begin{aligned} G^{{\textit{pan}}}(s)&=\frac{K^{{\textit{pan}}}(T_{1}^{{\textit{pan}}}s+1)}{(T_{2}^{{\textit{pan}}}s+1)(T_{3}^{{\textit{pan}}}s+1)}, \end{aligned}$$

(30)

$$\begin{aligned} G^{{\textit{tilt}}}(s)&=\frac{K^{{\textit{tilt}}}(T_{1}^{{\textit{tilt}}}s+1)}{(T_{2}^{{\textit{tilt}}}s+1)(T_{3}^{{\textit{tilt}}}s+1)}, \end{aligned}$$

(31)

where $K^{{\textit{pan}}}$ and $K^{{\textit{tilt}}}$ are respective gains, while $T_{1}^{{\textit{pan}}}$, $T_{2}^{{\textit{pan}}}$, $T_{3}^{{\textit{pan}}}$ and $T_{1}^{{\textit{tilt}}}$, $T_{2}^{{\textit{tilt}}}$, $T_{3}^{{\textit{tilt}}}$ are the time constants. The model’s inputs are the pan and tilt joint positions, denoted as q, measured at the current moment of simulation j, while the outputs are the target positions estimated for pan and tilt, denoted as $\Theta$.

This model has been considered to check whether a simple, linear model is sufficient to recreate the dynamics of the robot pan and tilt joints. A graphical representation of the simplified head dynamics model is presented in Fig. 9. To implement the model in any MPC algorithm, it is discretized and rewritten in the form of the following difference equations:

$$\begin{aligned} \Theta ^{\mathrm {{{pan}}}}(j)&=-a^{\mathrm {{{pan}}}}_{1}\cdot \Theta ^{\textrm{pan}}(j-1) -a^{\textrm{pan}}_2\cdot \Theta ^{\textrm{pan}}(j-2)\nonumber \\&\quad +b^{\textrm{pan}}_1\cdot q^{\textrm{pan}}(j-1), \end{aligned}$$

(32)

$$\begin{aligned} \Theta ^{\textrm{tilt}}(j)&=-a^{\textrm{tilt}}_1\cdot \Theta ^{\textrm{tilt}}(j-1) -a^{\textrm{tilt}}_2\cdot \Theta ^{\textrm{tilt}}(j-2)\nonumber \\&\quad +b^{\textrm{tilt}}_1\cdot q^{\textrm{tilt}}(j-1), \end{aligned}$$

(33)

where j is the time instant and $a_{1}$, $a_{2}$, $b_{1}$ are constant coefficients for pan and tilt joints, respectively.

Fig. 9

Structure of the head simplified dynamics model

4 Model validation within the predictive servoing framework

The experiments were done using the Gazebo simulator and Matlab. The robot model simulated in Gazebo was used as the control plant for the designed algorithms. The control signals were generated by the MPC algorithms implemented in Matlab.

4.1 Arm model

Arm model validation is divided into two steps. At first, the MPC controller is validated using the Gazebo simulator, followed by the real robot operation. The simplified model, described in Sect. 3.1, is used together with the NMPC described in Sect. 2.1.

4.1.1 Simulated robot arm-MPC validation

Simulations allow the validation of the full nonlinear model. The NMPC algorithm generates the setpoint trajectory for the torque controller. It is assumed that control inputs are the joint torque residuals expressed in [Nm], after gravity removal $\tau _{g,i}\, (i= 1,\ldots ,8)$ and $(1 \equiv {\textit{col}})$; thus eight control inputs are taken into consideration, and:

$$\begin{aligned} {\varvec{u}}^{i}&=\left[ \tau _{g,i,k|k},\ldots ,\tau _{g,i,k+N_u-1|k}\right] \quad (i=2,\ldots , 8), \nonumber \\ {\varvec{u}}^{ {\textit{col}}}&=\left[ \tau _{g,col,k|k},\ldots ,\tau _{g,{\textit{col}},k+N_u-1|k}\right] . \end{aligned}$$

(34)

There are 6 controlled outputs, which are 3 components of the position of the end-effector and 3 components of the orientation of the end-effector, thus:

$$\begin{aligned} {\varvec{y}}^{1}&=\left[ x_{ce,k+1|k},\ldots ,x_{ce,k+N|k}\right] ,\nonumber \\ {\varvec{y}}^{2}&=\left[ y_{ce,k+1|k},\ldots ,y_{ce,k+N|k}\right] ,\nonumber \\ {\varvec{y}}^{3}&=\left[ z_{ce,k+1|k},\ldots ,z_{ce,k+N|k}\right] ,\nonumber \\ {\varvec{y}}^{4}&=\left[ \varphi _{ce.1,k+1|k},\ldots ,\varphi _{ce.1,k+N|k}\right] ,\nonumber \\ {\varvec{y}}^{5}&=\left[ \varphi _{ce.2,k+1|k},\ldots ,\varphi _{ce.2,k+N|k}\right] ,\nonumber \\ {\varvec{y}}^{6}&=\left[ \varphi _{ce.3,k+1|k},\ldots ,\varphi _{ce.3,k+N|k}\right] . \end{aligned}$$

(35)

It is assumed that only joint angles expressed in degrees are constrained, thus

$$\begin{aligned} {\varvec{y}}^{c,i}&=\left[ q_{i,k+1|k},\ldots ,q_{i,k+N|k}\right] \quad (i=2,\ldots , 8),\nonumber \\ {\varvec{y}}^{c, {\textit{col}}}&=\left[ q_{{\textit{col}},k+1|k},\ldots ,q_{{\textit{col}},k+N|k}\right] . \end{aligned}$$

(36)

The NMPC problem solved in each time step minimizes the following performance function:

$$\begin{aligned}&\min _{{\varvec{u}}}\left\{ J_{\textrm{MPC}}=\sum _{j=1}^{6}\kappa _j\cdot \left( \varvec{{{\overline{y}}}}^j-{\varvec{y}}^j\right) \cdot \left( \varvec{{{\overline{y}}}}^j-{\varvec{y}}^j\right) ^T\right. \nonumber \\&\left. \quad +\sum _{m=1}^{8}\mu _m\cdot {\varvec{u}}^m\cdot \left( {\varvec{u}}^m\right) ^T\right\} \end{aligned}$$

(37)

subject to the constraints imposed on the values of manipulated variables and joint angles and equality constraint resulted from using the process model to obtain the prediction:

$$\begin{aligned} {\varvec{u}}_{\min }&\le {\varvec{u}} \le {\varvec{u}}_{\max }, \end{aligned}$$

(38)

$$\begin{aligned} {\varvec{y}}_{\min }^c&\le {\varvec{y}}^c \le {\varvec{y}}_{\max }^c, \end{aligned}$$

(39)

$$\begin{aligned}&=f_{\textrm{model}}({\varvec{u}})+{\varvec{d}}, \end{aligned}$$

(40)

where

$$\begin{aligned}{} & {} \begin{array}{ll} {\varvec{u}}_{\min }=\left[ {\varvec{u}}^{1}_{\min },\ldots ,{\varvec{u}}^{8}_{\min }\right] ^T, &{}\; {\varvec{u}}_{\max }=\left[ {\varvec{u}}^{1}_{\max },\ldots ,{\varvec{u}}^{8}_{\max }\right] ^T,\\ {\varvec{u}}^{1}_{\min }=\left[ -50,\ldots ,-50\right] ,&{}\; {\varvec{u}}^{1}_{\max }=\left[ 50,\ldots ,50\right] ,\\ {\varvec{u}}^{2}_{\min }=\left[ -15,\ldots ,-15\right] ,&{}\; {\varvec{u}}^{2}_{\max }=\left[ 15,\ldots ,15\right] ,\\ {\varvec{u}}^{3}_{\min }=\left[ -15,\ldots ,-15\right] ,&{}\; {\varvec{u}}^{3}_{\max }=\left[ 15,\ldots ,15\right] ,\\ {\varvec{u}}^{4}_{\min }=\left[ -15,\ldots ,-15\right] ,&{}\; {\varvec{u}}^{4}_{\max }=\left[ 15,\ldots ,15\right] ,\\ {\varvec{u}}^{5}_{\min }=\left[ -15,\ldots ,-15\right] ,&{}\; {\varvec{u}}^{5}_{\max }=\left[ 15,\ldots ,15\right] ,\\ {\varvec{u}}^{6}_{\min }=\left[ -15,\ldots ,-15\right] ,&{}\; {\varvec{u}}^{6}_{\max }=\left[ 15,\ldots ,15\right] ,\\ {\varvec{u}}^{7}_{\min }=\left[ -15,\ldots ,-15\right] ,&{}\; {\varvec{u}}^{7}_{\max }=\left[ 15,\ldots ,15\right] ,\\ {\varvec{u}}^{8}_{\min }=\left[ -50,\ldots ,-50\right] ,&{}\; {\varvec{u}}^{8}_{\max }=\left[ 50,\ldots ,50\right] , \end{array}\\{} & {} \begin{array}{ll} {\varvec{y}}_{\min }^c=\left[ {\varvec{y}}_{\min }^{c,1},\ldots ,{\varvec{y}}_{\min }^{c,8}\right] ^T, &{}\; {\varvec{y}}_{\max }^c=\left[ {\varvec{y}}_{\max }^{c,1},\ldots ,{\varvec{y}}_{\max }^{c,8}\right] ^T,\\ {\varvec{y}}_{\min }^{c,1}=\left[ -154,\ldots ,-154\right] ,&{}\; {\varvec{y}}_{\max }^{c,1}=\left[ 154,\ldots ,154\right] ,\\ {\varvec{y}}_{\min }^{c,2}=\left[ -104,\ldots ,-104\right] ,&{}\; {\varvec{y}}_{\max }^{c,2}=\left[ -26,\ldots ,-26\right] ,\\ {\varvec{y}}_{\min }^{c,3}=\left[ -154,\ldots ,-154\right] ,&{}\; {\varvec{y}}_{\max }^{c,3}=\left[ 154,\ldots ,154\right] ,\\ {\varvec{y}}_{\min }^{c,4}=\left[ 26,\ldots ,26\right] ,&{}\; {\varvec{y}}_{\max }^{c,4}=\left[ 104,\ldots ,104\right] ,\\ {\varvec{y}}_{\min }^{c,5}=\left[ -154,\ldots ,-154\right] ,&{}\; {\varvec{y}}_{\max }^{c,5}=\left[ 154,\ldots ,154\right] ,\\ {\varvec{y}}_{\min }^{c,6}=\left[ -104,\ldots ,-104\right] ,&{}\; {\varvec{y}}_{\max }^{c,6}=\left[ -26,\ldots ,-26\right] ,\\ {\varvec{y}}_{\min }^{c,7}=\left[ -154,\ldots ,-154\right] ,&{}\; {\varvec{y}}_{\max }^{c,7}=\left[ 154,\ldots ,154\right] ,\\ {\varvec{y}}_{\min }^{c,8}=\left[ -75,\ldots ,-75\right] ,&{}\; {\varvec{y}}_{\max }^{c,8}=\left[ 75,\ldots ,75\right] \end{array} \end{aligned}$$

and the model used in (40) is the one detailed in Sect. 3.1.1 (Fig. 10).

The constraints are taken into consideration using the exterior penalty function. It represents the need to move the arm as little as possible to achieve the goal. This also helps to provide a smooth motion of the arm, as the solver will not select control signals that change the configuration of the arm in a significant way—it will always return the one that is easiest to achieve. Target trajectory recorded by the real robot camera beforehand was used during the experiments. The following values of the tuning parameters were assumed: prediction horizon $N=4$, control horizon $N_u=4$, $\kappa _j=1,\, (j=1,\ldots ,6)$, $\mu _m=1, \, (m=1,\ldots ,8)$. The obtained results are presented in Figs. 11 and 12; the target’s trajectory is drawn using dashed lines. The result is satisfactory; the end-effector grasped the target after around 2.5s, even though the MPC algorithm used the simplified model.

Fig. 10

WUT Velma robot

Fig. 11

Components of trajectories of the end-effector ($x_{ce}$, $y_{ce}$, $z_{ce}$; solid lines), the target ($x_{trgt}$, $y_{trgt}$, $z_{trgt}$; dashed lines), and the setpoint for torque controller ($x_{sp}$, $y_{sp}$, $z_{sp}$; dotted lines)

Fig. 12

Trajectories of the target (dashed red line) and the end-effector (blue solid line). (Color figure online)ss

The calculation of the prediction in the optimization problem (37) is implemented as an iterative routine, which uses the fact that elements of this prediction are functions of the decision variables, i.e., of future control values. Due to the use of the simplified model of the process, calculation of the prediction, and, in consequence, finding the solution to the optimization problem (37) is much less time-consuming than when the full nonlinear model is used. In another experiment, the computation times of the simplified and full models were compared. The results are summarized in Table 2, showing that the simplified model is over 100 times faster than the full-scale one.

4.1.2 Real robot arm-MPC validation

The validation on the real robot is performed using the simplified model. The reason is that the calculation time required to execute the MPC calculations is much higher in the full version due to the embedded kinematics non-linearities. However, it should be noted that from the perspective of the MPC operation, the information about the dynamics is crucial to satisfy proper transient time responses. The results show reasonable arm operation.

Table 2 Comparison of calculation times of single iteration for simplified and full model

Fig. 13

Output (q) and control (${\hat{q}}$) signals of the MPC implemented for each arm joint, where object moves in circles—data from the real robot

In Fig. 13, the control process of each MPC controller is presented. The object, followed by the arm’s end-effector, moves in circles in the Y and Z plane, i.e. stays at a constant distance from the robot. As the object moves, its position is transformed into a setpoint for each MPC algorithm using inverse kinematics, and the results are visible in Fig. 13. MSE values were calculated for each joint controller (Table 3). Best results were obtained with the value of the parameter $\lambda$, describing the penalty imposed on the control increments, assigned by taking into account how far the joint is located from the column, i.e. $\lambda = 100, 50, 40, 30, 20, 10, 1$, consecutively for joints $2,\ldots ,8$. This enabled faster movements of joints with lower mass attached to them, thus introducing lower disturbances. It is visible that the quality of control is satisfactory while maintaining smooth control signal trajectories.

Figure 14 depicts the same experiment, but only the Cartesian space position and orientation of the end-effector and the target object are considered. It is worth noting that position and orientation of the end-effector result from the controllers operating in the joint space. In such a case, the end-effector setpoint values form the ultimate goal for the arm-MPC control, contrary to the specific joint setpoint signals. Table 4 shows the MSE for the position and orientation of the end-effector in reference to the target object. Tracking the target object’s position is more than satisfactory, as the position is accurate with a mean error of approximately 0.5 mm. At the same time, the orientation of the end-effector is constantly rejecting disturbances introduced by the tracking movement of the arm, resulting in the MSE of the same order.

Fig. 14

Position and orientation of the end-effector and the object (setpoint) in Cartesian space, where object moves in circles—data from the real robot

Table 3 Mean squared error for each joint control loop $i=2,\ldots ,8$, target object moving in circles—data from the real robot

Table 4 Mean squared error for the end-effector position $E^\textrm{pos}_\textrm{MSE}$ and orientation $E^\textrm{ori}_\textrm{MSE}$ relative to the target object moving in circles—data from the real robot

4.2 Pan-tilt head model

Similarly to the previous section, the description is divided into paragraphs considering the robot simulations (in Matlab and Gazebo simulator) and the robot natural environment operation.

4.2.1 Robot head-MPC validation in Matlab

First, the head model validation is performed using the Matlab environment. However, the experiments use the target observations data obtained from the real experiment, in which the head of the KUKA robot has been moving according to sample set positions. The data contain current pan and tilt joint positions for each time instant.

The identification procedure of the transfer function parameters consisted of three steps. In the first step, the transfer functions have arbitrary values of parameters. Secondly, responses are obtained for the same input data as in the performed real experiments and are compared to the real data. Furthermore, the value of MSE indicator for each joint is noted. Thirdly, one of the parameters of the transfer functions is changed and the second step is repeated for the new simulated responses. The third step is repeated many times until the lowest MSE indicator is obtained for both joints. This procedure is a simple trial and error method, but it proves to be very effective in this case due to the uncomplicated dynamics of the robot’s head. As a result, good parameters can be obtained quite fast. The best results out of several conducted experiments are obtained for the following set of model parameters:

• $K^{{\textit{pan}}}=K^{{\textit{tilt}}}=1$, $T_1^{{\textit{pan}}}=T_1^{{\textit{tilt}}}=0$ [s],

• $T_2^{{\textit{pan}}}=T_2^{{\textit{tilt}}}=0.1$ [s],

• $T_3^{{\textit{pan}}}=T_3^{{\textit{tilt}}}=0$ [s].

Figure 15 presents the respective simulation results. The values of the MSE performance measure for both joints are: $E_{\textrm{MSE}}^{\textrm{pan}}=1.9867\cdot 10^{-3}$, $E_{\textrm{MSE}}^{\textrm{tilt}}=2.2413\cdot 10^{-3}$. However, it is confirmed that the LMPC controller using this internal model does not work efficiently. It is tested using the Gazebo model. It becomes evident that the control quality can still be improved. Thus, the internal model is modified using a fine-tuning method. The fine-tuning uses the implemented LMPC algorithm and the Gazebo model. The best parameters of the continuous-time model for both pan and tilt joints are:

• $K=1.0452$, $T_1=0.97752$ [ms],

• $T_2=26.2$ [ms],

• $T_3=33.2$ [ms].

The above parameters reduce the differential equations of the model to the following form:

$$\begin{aligned} \Theta ^{\textrm{pan}}(j)&=1.868\cdot \Theta ^{\textrm{pan}}(j-1)\nonumber \\&\quad -0.872\cdot \Theta ^{\textrm{pan}}(j-2)+0.005\cdot q^{\textrm{pan}}(j-1), \end{aligned}$$

(41)

$$\begin{aligned} \Theta ^{\textrm{tilt}}(j)&=1.868\cdot \Theta ^{\textrm{tilt}}(j-1)\nonumber \\&\quad -0.872\cdot \Theta ^{\textrm{tilt}}(j-2)+0.005\cdot q^{\textrm{tilt}}(j-1). \end{aligned}$$

(42)

Above discrete-time model is obtained for the sampling period $T_{\textrm{s}}=2$ [ms]. The results for this model parameters are presented in Fig. 16. The MSE indicators after fine-tuning for the respective joints were as follows: $E_{\textrm{MSE}}^{\textrm{pan}}=1.3054\cdot 10^{-3}$, $E_{\textrm{MSE}}^{\textrm{tilt}}=1.4669\cdot 10^{-3}$.

Fig. 15

Initial validation of the simplified pan-tilt head model ($\Theta$ is expressed in radians)

Fig. 16

Validation of the fine-tuned pan-tilt head model ($\Theta$ is expressed in radians)

Considered linear model works satisfactory, and the fine-tuning process has improved the performance measured with the MSE index significantly.

4.2.2 Robot head-MPC validation in Gazebo

Next, the pan–tilt head model is validated using dedicated robot simulation environment – Gazebo. Two scenarios are considered:

• 1. custom generated sample set-trajectory of the joints,

• 2. real trajectory obtained in the robot experiments with the camera.

The results for the first scenario are shown in Fig. 17. The response from the model tracks the setpoint accurately, with a sudden significant change in the set trajectory of the joints (time instant $k=800$). It increases the modeling error, but later it is quickly reduced. The values of the MSE estimators for this scenario are: $E_{\textrm{MSE}}^{\textrm{pan}}=5.8118\cdot 10^{-4}$, $E_{\textrm{MSE}}^{\textrm{tilt}}=6.0325\cdot 10^{-4}$.

Fig. 17

Validation of the simplified pan-tilt head model, with the use of custom set-trajectory of the joints, against the data obtained from the Gazebo simulation model ($\Theta$ is expressed in radians)

Results for the second scenario (real tracked trajectory) are shown in Fig. 18. Similarly to the previous experiment, modeling errors are present during simulation. The values of the MSE estimators for the second scenario are: $E_{\textrm{MSE}}^{\textrm{pan}}=6.6624\cdot 10^{-4}$, $E_{\textrm{MSE}}^{\textrm{tilt}}=5.3477\cdot 10^{-4}$.

Fig. 18

Validation of the simplified pan-tilt head model, with the use of set trajectory of the joints, interpreted from a gesture shown in front of the robot’s camera, against the data obtained from the Gazebo simulation model ($\Theta$ is expressed in radians)

The MPC controller uses LMPC version, which is described in Sect. 2.2. The general optimization problem (1) with the cost function (17) is rewritten specifically for the head as:

$$\begin{aligned}&\min \limits _{\triangle {\varvec{u}}(j)} \Bigg \{ J_{\textrm{LMPC}}(j)={\displaystyle \sum _{p=1}^{N}} \left\| {\overline{\Theta }}(j+p|j)-{\hat{\Theta }}(j+p|j) \right\| ^{2}_{\varvec{\kappa }_p}\nonumber \\&\quad +{\displaystyle \sum _{p=0}^{N_{\textrm{u}}-1}} \left\| \triangle {\hat{q}}(j+p|j)\right\| ^{2}_{\varvec{\lambda }_p}\Bigg \} \nonumber \\&\text {subject to}\nonumber \\&{\hat{q}}^{\min } \le {\hat{q}}(j+p|j)\le {\hat{q}}^{\max },\quad p=0,\ldots ,N_{\textrm{u}}-1 , \end{aligned}$$

(43)

where ${\hat{q}}^{\min }=-1.5708$ and ${\hat{q}}^{\max }=1.5708$ are the limits imposed on the movement range of both joints expressed in radians, i.e. $\pm 90^{\circ }$.

Many simulations have been performed, and ultimately, the following satisfactory parameters are chosen: $N=20$, $N_\textrm{u}=5$, $\lambda _1=3$, $\lambda _2=3$, $\kappa _1=1$ and $\kappa _2=1$. Figure 19 shows the simulation results of this case with the use of the desired set trajectory $q_\textrm{d}$ for the joints and the use of the Gazebo simulation environment. The outputs of the predictive LMPC are ${\hat{q}}^\textrm{pan}$ and ${\hat{q}}^\textrm{tilt}$, which are the pan and tilt joint angles calculated for the next time instant of the simulation.

Fig. 19

Simulation results of the pan-tilt head control system with the applied LMPC controller; the use of the desired set-trajectory $q_\textrm{d}$ of the joints interpreted from a gesture shown in front of the real robot’s camera and the use of Gazebo simulation environment ($\Theta$ is expressed in radians)

It should be noted that the column position can be measured and taken into account as a disturbance. It is shown that the column effect is insignificant, even during the first time instants, when the column introduces a sudden change. As a result, no column position measures are considered and the results are obtained, when the robot’s column does not move.

4.2.3 Head-MPC validation with the WUT (Warsaw University of Technology) Velma robot

The same MPC, in the DMC formulation, with the same parameters set is implemented on the WUT Velma robot [50] (Fig. 10). Figure 20 presents the sample results from that experiment. The following values of the performance MSE are obtained: $E^{\textrm{pan}}_{\textrm{MSE}}=1.70\times 10^{-4}$ and $E^{\textrm{tilt}}_{\textrm{MSE}}=6.19\times 10^{-3}$. These MSE values are quite close to the ones calculated in the Gazebo simulation case. The setpoint is tracked accurately. The results confirm that the proposed model is appropriate for the predictive pan-tilt robot head control.

Fig. 20

Experimental results for the pan-tilt control ($\Theta$ is expressed in radians)

5 Conclusions and future research

This paper presents a method for producing and validating models that can be used for MPC, i.e. they are computationally efficient yet accurate enough. The work was motivated by the need to implement a visual servoing system on a real robot. However, the control task might be hampered by the time limitations required for real-time implementation of the model predictive control technology. As MPC control requires iterative optimization evaluation during each sampling period, the plant model must be simple enough to enable fitting into tight time constraints. A review of the subject literature shows that the subject is relatively rarely addressed. This research fills that gap.

The presented models are motivated by the need to implement a predictive visual servoing system for a real WUT Velma robot. Efficient implementation of the visual servoing system in the PB-SAC-EOL-MPC configuration requires two MPC instances: one to control the arm and enable it to grasp the tracked object (arm-MPC) and the second to control the head pan-tilt system (head-MPC) to allow efficient target tracking. Both models have been successfully validated. The arm-MPC model is a Wiener-Hammerstein-type nonlinear model. Its accuracy was verified using Matlab, the Gazebo simulations, and the real KUKA LWR 4+ robot. The head-MPC model has been evaluated using real robot pan-tilt system data, and further, it has been validated similarly to the arm-MPC model.

To a greater extent, this research has been motivated by practical implementation issues rather than theoretical considerations. Primarily, predictive visual servoing has to work according to the design specification. In particular, it must not violate time constraints associated with the system sampling intervals. These time limitations must be maintained, and simultaneously, the best available control quality has to be guaranteed. It uses the MPC strategy as the core element and adds prediction to the standard regulatory control.

The proposed predictive capability of the control system enables the integration of torque joint control with the predictive strategy. Besides dynamic control over a specific trajectory, it also takes into account different types of constraints resulting from the kinematic and dynamic structure of the robot. However, one must realize that the internal model must harmoniously work within the system. Thus, the model must be a compromise between accuracy, simplicity, and relatively low computational complexity. Moreover, incorporating knowledge about future setpoint behavior (available due to the vision element), rarely used in practice, makes a significant change allowing high-tracking performance.

The proposed approach solves this problem. The model using Wiener-Hammerstein assumptions is, on the one hand, simple enough and, on the other hand, able to represent the robot accurately enough so that the visual servoing system is able to work as intended.

The proposed solution is an essential element of a service robot accompanying humans. Precise tracking of moving objects or humans facilitates adequate interaction with the robot’s environment. For instance, programming by demonstration [6] requires the robot to track the actions of the human instructor; thus, servoing onto a region of interest becomes essential. Predictive control of the pan-tilt head and the manipulators will provide accurate and efficient manoeuvring capability, enabling in the future the execution of elaborate complex tasks.

Finally, these models were integrated into the MPC control in Gazebo simulations and on the real robot. They confirmed their applicability. Time constraints were met, allowing MPC operation. The next steps of the research aim at utilisation of the thus-produced visual servos in real robots executing complex tasks, e.g. getting hold of moving objects or acquiring objects from a cluttered environment, which requires active sensing.

The main contribution of this study was to show that computationally efficient simplified dynamics models are accurate enough and allow the use of MPC in the visual control of robots. General Hammerstein–Wiener-like model fulfils both requirements, i.e. computational efficiency and accuracy, and thus is suitable for visual robot control.