1 Introduction

To support the controller synthesis for the plant which is hard to be described because there exist nonlinearities, the Takagi-Sugeno (T-S) fuzzy-model-based (FMB) technique is viewed as a powerful alternative [1]. The T-S fuzzy model combining multiple sub-systems through a weighted sum can be used to depict the nonlinear plant [2]. To implement feedback control, the fuzzy controller which combines multiple sub-controllers through a weighted sum is applied [3, 4]. When the T-S FMB technique is applied, the stability could be investigated via the linear-matrix-inequality (LMI) method.

Recently, the polynomial fuzzy-model-based (PFMB) technique extended from the T-S FMB technique has been extensively utilized to support the controller synthesis [5, 6]. The polynomial fuzzy model is regarded to possess better description capability. For the stability investigation where polynomials are involved, [5, 6] leveraged the sum-of-squares (SOS) method.

The discussion of fuzzy sets is very important for fuzzy control. Type-1 fuzzy sets are popular for handling nonlinearities, but their capability of directly capturing uncertainties is far from enough [7]. To tackle nonlinearities as well as uncertainties, type-2 fuzzy sets were employed [8]. Through the footprint of uncertainty (FOU), the information of uncertainties is able to be seized. Despite the superior capability of capturing uncertainties, the increasing computational complexity is still a problem. Thanks to the appearance of interval type-2 (IT2) fuzzy sets, not only can the information of nonlinearities and uncertainties be seized, but also the computational burden can be reduced at the same time [8, 9]. In [10], an IT2FMB control system was put forward. [11] then further proposed an IT2PMFB control system.

The alleviation of the conservativeness of stability conditions is a key target in the design. To realize it, the parallel distributed compensation (PDC) approach was used [4]. However, the PDC approach requires the membership functions (MFs) and the number of rules of the fuzzy controller to be consistent with those of the fuzzy model, which results in weak design flexibility [12]. Given this, the following works were done. In [13], the membership-function-dependent (MFD) approach was used for alleviating the conservativeness. [14] put forward an imperfect premise matching (IPM) concept. Under the IPM concept, it can be flexible in determining the MFs and the number of rules of the fuzzy controller. Then, large amounts of works adopting the MFD approach as well as the IPM concept were proposed [7, 15,16,17]. In some papers, the switching control is also regarded as a great option to relax the stability conditions. For example, in [18], a switching sampled-data (SD) control approach was applied to relax results. In [19], a switching polynomial fuzzy controller accompanying a switching polynomial Lyapunov function was put forward for relaxation.

Along with the rapid advancements in digital technology as well as other related technologies, the SD control strategy has found extensive applications [20,21,22]. In the SD control strategy, the control input is in staircase form, which makes the stability analysis extremely difficult [23]. For the facilitation of the stability analysis, many techniques were applied, like the looped-functional-based technique, the input delay technique, etc. [24,25,26,27,28]. Till now, there have been many excellent achievements regarding the SD control strategy. [29] applied the aperiodic SD control strategy to the networked control systems taking into account time-varying delays. In [30], the mode-dependent aperiodic SD control strategy was proposed for delayed error stochastic Markovian jump neural networks. [31] analyzed the stability of the Itô stochastic systems incorporating time-delays under the aperiodic SD control strategy. However, the IT2PFMB control system that adopts both the SD control strategy and switching control scheme has not been considered.

This study implements the stability investigation of an interval type-2 sampled-data polynomial fuzzy-model-based (IT2SDPFMB) control system with a switching control scheme. In the study, a switching control scheme with a variable sampling period is carried out. The modeling domain consists of some sub-domains. If the system is within a sub-domain and does not transit from the sub-domain to another sub-domain, the sampler will sample every interval \(h_s\), and a corresponding local IT2SD polynomial fuzzy controller will be chosen; if the system transits from one sub-domain to another sub-domain, the sampler will sample immediately, and a local IT2SD polynomial fuzzy controller corresponding to the new sub-domain will be chosen to generate the new control input. These local IT2SD polynomial fuzzy controllers compose the switching IT2SD polynomial fuzzy controller. A looped-functional-based technique is applied to the analysis, and then the information between \(t_k\) and t can be used. Due to the mismatch dilemma caused by the SD control strategy and uncertainties, the PDC approach cannot be implemented. Given this situation, the IPM concept as well as the MFD approach are applied. For relaxing the stability conditions, the information of IT2 MFs is utilized. For further relaxation, the state information is also considered [23]. In addition, the stability conditions have the potential to be more relaxed by the switching control scheme.

Listed below are the primary contributions:

  1. (1)

    The stability of an IT2SDPFMB control system with a switching control scheme is investigated for the first time.

  2. (2)

    The IPM concept is employed to promote flexibility by freely determining the MFs and the number of rules of the switching IT2SD polynomial fuzzy controller. In addition, the implementation cost can be reduced by granting the simpler shape of MFs and the smaller number of rules to the switching IT2SD polynomial fuzzy controller.

  3. (3)

    An MFD switching IT2SD polynomial fuzzy controller design considering the information between \(t_k\) and t, the state information, the information of IT2 MFs and the switching control scheme with a variable sampling period is proposed, which can achieve less conservative results.

  4. (4)

    The SOS-based conditions presented in this paper are first developed to guarantee the stability of the IT2SDPFMB control system where a switching control scheme with a variable sampling period is considered.

Below is an outline of the remaining sections in this paper. Section 2 introduces the preliminary knowledge. Section 3 presents the main results. Section 4 reveals the efficacy of the proposed method through the simulation outcomes. A conclusion has been drawn in Section 5.

Notations: The monomial in \(\zeta (t)=\left[ \varsigma _1(t)\text { }\varsigma _2(t)\text { } \cdots \right. \)\(\left. \text { }\varsigma _n(t)\right] ^T\) is considered to be \(\varsigma _1^{o_1}(t)\varsigma _2^{o_2}(t)\cdots \varsigma _n^{o_n}(t)\) in which \(o_i\ge 0\), \(i=1\), 2, \(\cdots \) n, denotes the integer. \(\mathfrak {o}=\sum _{i=1}^n o_i\) represents the degree of a monomial. A polynomial \(e\left( \zeta (t)\right) \) denotes an SOS when \(e\left( \zeta (t)\right) =\sum _{j=1}^m f_j^2\left( \zeta (t)\right) \) where \(f_j\left( \zeta (t)\right) \) is the polynomial, \(m>0\) denotes an integer. Clearly, \(e\left( \zeta (t)\right) \ge 0\) when \(e\left( \zeta (t)\right) \) denotes an SOS. Superscript “T” represents the transposition of a matrix and superscript “\(-1\)” signifies the inverse of a matrix, “\({\textbf {0}}_{m\times n}\)” signifies the \(m \times n\) zero matrix and “\({\textbf {I}}_{m}\)” represents the \(m \times m\) identity matrix. “\(Sym\left\{ {\textbf {C}}\right\} \)” is equivalent to \({\textbf {C}}+{\textbf {C}}^T\).

2 Preliminaries

2.1 IT2 polynomial fuzzy model

The \(i_{th}\) rule of the IT2 polynomial fuzzy model with p rules is shown below [7, 19]:

$$\begin{aligned}&\text {Rule}\quad i: \text {IF }f{_1}(\zeta (t)) \text { is } \tilde{M}_1^i\text { AND }\dots \text { AND }f{_\varPsi }(\zeta (t)) \text { is } \tilde{M}_\varPsi ^i, \nonumber \\&\text {THEN } \dot{\zeta }(t)={\textbf {A}}_i\left( \zeta (t)\right) \check{\zeta }\left( \zeta (t)\right) +{\textbf {B}}_i\left( \zeta (t)\right) {\textbf {u}}(t) \end{aligned}$$
(1)

in which \(\tilde{M}_\alpha ^i\) represents the \(i_{th}\) rule’s IT2 fuzzy term that corresponds to the function \(f{_\alpha }(\zeta (t))\), where i is from 1 to p and \(\alpha \) is from 1 to \(\varPsi \), \(p>0\) and \(\varPsi >0\) are integers; \(\zeta (t)=\left[ \varsigma _1(t)\text { }\varsigma _2(t)\text { } \cdots \text { }\varsigma _n(t)\right] ^T\) represents the state vector; \(\check{\zeta }\left( \zeta (t)\right) =\left[ \check{\varsigma }_1\left( \zeta (t)\right) \text { }\check{\varsigma }_2\left( \zeta (t)\right) \text { } \cdots \text { }\check{\varsigma }_N\left( \zeta (t)\right) \right] ^T\) represents the vector of the monomials in \(\zeta (t)\); \({\textbf {u}}(t)=\left[ \mathfrak {u}_1(t)\text { }\mathfrak {u}_2(t)\text { } \cdots \text { }\mathfrak {u}_m(t)\right] ^T\) represents the input vector; \({\textbf {A}}_i\left( \zeta (t)\right) \in \mathfrak {R}^{n\times N}\) that represents the polynomial system matrix and \({\textbf {B}}_i\left( \zeta (t)\right) \in \mathfrak {R}^{n\times m}\) that represents the polynomial input matrix have been given. Through the proper selection of \(\check{\zeta }\left( \zeta (t)\right) \), the condition \(\check{\zeta }\left( \zeta (t)\right) ={\textbf {0}}\) if and only if \(\zeta (t)={\textbf {0}}\) is considered. The \(i_{th}\) rule’s firing strength is shown below:

$$\begin{aligned} \breve{\mathscr {W}}_i\left( \zeta (t)\right) = \left[ \underline{w}_i\left( \zeta (t)\right) ,\text { } \overline{w}_i\left( \zeta (t)\right) \right] , \text { } i \text { is from }1\text { to }p \end{aligned}$$
(2)

in which \(\underline{w}_i\left( \zeta (t)\right) \) that signifies the lower grade of membership equals \(\prod _{\alpha =1}^\varPsi \underline{\mu }_{\tilde{M}_\alpha ^i}\left( f{_\alpha }\left( \zeta (t)\right) \right) \), \(\underline{\mu }_{\tilde{M}_\alpha ^i}\left( f{_\alpha }\left( \zeta (t)\right) \right) \) signifies the lower MF; \(\overline{w}_i\left( \zeta (t)\right) \) that signifies the upper grade of membership equals \(\prod _{\alpha =1}^\varPsi \) \(\overline{\mu }_{\tilde{M}_\alpha ^i}\left( f{_\alpha }\left( \zeta (t)\right) \right) \), \(\overline{\mu }_{\tilde{M}_\alpha ^i}\left( f{_\alpha }\left( \zeta (t)\right) \right) \) signifies the upper MF; \(\underline{\mu }_{\tilde{M}_\alpha ^i}\left( f{_\alpha }\left( \zeta (t)\right) \right) \) and \(\overline{\mu }_{\tilde{M}_\alpha ^i}\left( f{_\alpha }\left( \zeta (t)\right) \right) \) satisfy \(0\le \underline{\mu }_{\tilde{M}_\alpha ^i}\left( f{_\alpha }\left( \zeta (t)\right) \right) \) \(\le \overline{\mu }_{\tilde{M}_\alpha ^i}\left( f{_\alpha }\left( \zeta (t)\right) \right) \le 1\), then we have \(0\le \underline{w}_i\left( \zeta (t)\right) \le \overline{w}_i\left( \zeta (t)\right) \le 1\).

Finally, we have

$$\begin{aligned}&\dot{\zeta }(t)=\sum _{i=1}^p\tilde{w}_i\left( \zeta (t)\right) \Big ({\textbf {A}}_i\left( \zeta (t)\right) \check{\zeta }\left( \zeta (t)\right) +{\textbf {B}}_i\left( \zeta (t)\right) {\textbf {u}}(t)\Big ) \end{aligned}$$
(3)

where

$$\begin{aligned} \tilde{w}_i\left( \zeta (t)\right) =\underline{\lambda }_i\left( \zeta (t)\right) \underline{w}_i\left( \zeta (t)\right) +\overline{\lambda }_i\left( \zeta (t)\right) \overline{w}_i\left( \zeta (t)\right) , \end{aligned}$$
(4)

in which \(\tilde{w}_i\left( \zeta (t)\right) \) is nonnegative, \(\sum _{i=1}^p\tilde{w}_i\left( \zeta (t)\right) =1\), \(\underline{\lambda }_i\left( \zeta (t)\right) \) and \(\overline{\lambda }_i\left( \zeta (t)\right) \) both lie between zero (inclusive) and one (inclusive), the sum of \(\underline{\lambda }_i\left( \zeta (t)\right) \) and \(\overline{\lambda }_i\left( \zeta (t)\right) \) is one, for \(\forall i\), functions \(\underline{\lambda }_i\left( \zeta (t)\right) \) and \(\overline{\lambda }_i\left( \zeta (t)\right) \) are not demanded to be given.

2.2 Switching IT2SD polynomial fuzzy controller

A switching control scheme with a variable sampling period is considered in this work. Suppose the modeling domain \(\varUpsilon \) includes \(\hat{L}\) sub-domains, in other words, \(\varUpsilon =\bigcup ^{\hat{L}}_{l=1}\varUpsilon _l\), where \(\hat{L}>0\) denotes an integer. A corresponding local IT2SD polynomial fuzzy controller will be chosen if the system is within the sub-domain \(\varUpsilon _l\).

The \(j_{th}\) rule of the switching IT2SD polynomial fuzzy controller with c rules is shown below [7, 19]:

$$\begin{aligned}&\text {Rule }j: \text {IF }g{_1}\left( \zeta (t_k)\right) \text { is } \tilde{N}_1^j\text { AND }\dots \text { AND }g{_\varOmega }\left( \zeta (t_k)\right) \text { is } \tilde{N}_\varOmega ^j,\nonumber \\&\text {THEN } {\textbf {u}}(t)={\textbf {G}}_{jl}\check{\zeta }\left( \zeta (t_k)\right) , \text { for }\zeta (t)\in \varUpsilon _l \end{aligned}$$
(5)

in which \(\tilde{N}_\beta ^j\) represents the \(j_{th}\) rule’s IT2 fuzzy term that corresponds to the function \(g{_\beta }\left( \zeta (t_k)\right) \), where j is from 1 to c, l is from 1 to \(\hat{L}\) and \(\beta \) is from 1 to \(\varOmega \), \(c>0\) and \(\varOmega >0\) are integers, \(k =\) 0,..., \(\infty \). \({\textbf {G}}_{jl} \in \mathfrak {R}^{m\times N}\) represents the feedback gain matrix which will be obtained. The \(j_{th}\) rule’s firing strength is below:

$$\begin{aligned} \breve{\mathscr {M}}_j\left( \zeta (t_k)\right) = \left[ \underline{m}_j\left( \zeta (t_k)\right) ,\text { } \overline{m}_j\left( \zeta (t_k)\right) \right] , \text { } j \text { is from }1\text { to }c \end{aligned}$$
(6)

in which \(\underline{m}_j\left( \zeta (t_k)\right) \) that signifies the lower grade of membership equals \(\prod _{\beta =1}^\varOmega \underline{\mu }_{\tilde{N}_\beta ^j}\left( g{_\beta }\left( \zeta (t_k)\right) \right) \), \(\underline{\mu }_{\tilde{N}_\beta ^j}\left( g{_\beta }\left( \zeta (t_k)\right) \right) \) signifies the lower MF; \(\overline{m}_j\left( \zeta (t_k)\right) \) that signifies the upper grade of membership equals \(\prod _{\beta =1}^\varOmega \) \(\overline{\mu }_{\tilde{N}_\beta ^j}\left( g{_\beta }\left( \zeta (t_k)\right) \right) \), \(\overline{\mu }_{\tilde{N}_\beta ^j}\left( g{_\beta }\left( \zeta (t_k)\right) \right) \) signifies the upper MF; \(\underline{\mu }_{\tilde{N}_\beta ^j}\left( g{_\beta }\left( \zeta (t_k)\right) \right) \) and \(\overline{\mu }_{\tilde{N}_\beta ^j}\left( g{_\beta }\left( \zeta (t_k)\right) \right) \) satisfy \(0\le \underline{\mu }_{\tilde{N}_\beta ^j}\left( g{_\beta }\left( \zeta (t_k)\right) \right) \) \(\le \overline{\mu }_{\tilde{N}_\beta ^j}\left( g{_\beta }\left( \zeta (t_k)\right) \right) \) \(\le 1\), then we have \(0\le \underline{m}_j\left( \zeta (t_k)\right) \le \overline{m}_j\left( \zeta (t_k)\right) \) \(\le 1\).

Finally, we have

$$\begin{aligned}&{\textbf {u}}(t)=\sum ^{c}_{j=1}\tilde{m}_j\left( \zeta (t_k)\right) {\textbf {G}}_{jl}\check{\zeta }\left( \zeta (t_k)\right) , \nonumber \\&\text { for }\zeta (t)\in \varUpsilon _l, \text { } l \text { is from }1\text { to } \hat{L},\nonumber \\&t_k\le t<t_{k+1} \end{aligned}$$
(7)

where

$$\begin{aligned}&\tilde{m}_j\left( \zeta (t_k)\right) \nonumber \\&\quad {=}\frac{\underline{\kappa }_j\left( \zeta (t_k)\right) \underline{m}_j\left( \zeta (t_k)\right) +\overline{\kappa }_j\left( \zeta (t_k)\right) \overline{m}_j\left( \zeta (t_k)\right) }{\sum _{f=1}^c\left( \underline{\kappa }_f\left( \zeta (t_k)\right) \underline{m}_f\left( \zeta (t_k)\right) {+}\overline{\kappa }_f\left( \zeta (t_k)\right) \overline{m}_f\left( \zeta (t_k)\!\right) \!\right) }, \end{aligned}$$
(8)

in which \(\tilde{m}_j\left( \zeta (t_k)\right) \) is nonnegative, \(\sum _{j=1}^c\tilde{m}_j\left( \zeta (t_k)\right) =1\), \(\underline{\kappa }_j\left( \zeta (t_k)\right) \) and \(\overline{\kappa }_j\left( \zeta (t_k)\right) \) both lie between zero (inclusive) and one (inclusive), the sum of \(\underline{\kappa }_j\left( \zeta (t_k)\right) \) and \(\overline{\kappa }_j\left( \zeta (t_k)\right) \) is one, for \(\forall j\), \(\underline{\kappa }_j\left( \zeta (t_k)\right) \) and \(\overline{\kappa }_j\left( \zeta (t_k)\right) \) are functions to be provided. \(h_s\ge h_k=t_{k+1}- t_k>0\) and \(h_s\) signifies the largest sampling interval.

Lemma 1

[32] Let z: \([l,\text { }u]\rightarrow \mathfrak {R}^{n}\) be a vector function, where l and u are both scalars and \(l<u\). For a vector \(\xi \in \mathfrak {R}^{m}\), matrix \({\textbf {K}} \in \mathfrak {R}^{m\times n}\) and positive definite matrix \({\textbf {J}}={\textbf {J}}^T \in \mathfrak {R}^{n\times n}\), then

$$\begin{aligned}&-\int ^u_l{\textbf {z}}^T(s){\textbf {J}}{} {\textbf {z}}(s)ds \le (u-l)\xi ^T{\textbf {K}}{} {\textbf {J}}^{-1}{} {\textbf {K}}^T\xi \nonumber \\&+2\xi ^T{\textbf {K}}\int ^u_l{\textbf {z}}(s)ds. \end{aligned}$$
(9)

3 Main results

The IT2SDPFMB control system with a switching control scheme shown as below can be obtained based on (3), (7), and \(\sum _{i=1}^p\tilde{w}_i\left( \zeta (t)\right) =\sum _{j=1}^c\tilde{m}_j\left( \zeta (t_k)\right) =\sum _{i=1}^p\sum _{j=1}^c\tilde{w}_i\left( \zeta (t)\right) \) \(\times \tilde{m}_j\left( \zeta (t_k)\right) =1\),

$$\begin{aligned} \dot{\zeta }(t)&=\sum _{i=1}^p\tilde{w}_i\left( \zeta (t)\right) \Big ({\textbf {A}}_i\left( \zeta (t)\right) \check{\zeta }\left( \zeta (t)\right) \nonumber \\&\quad +{\textbf {B}}_i\left( \zeta (t)\right) \sum ^{c}_{j=1}\tilde{m}_j\left( \zeta (t_k)\right) {\textbf {G}}_{jl}\check{\zeta }\left( \zeta (t_k)\right) \Big ) \nonumber \\&=\sum _{i=1}^p\sum ^{c}_{j=1}\tilde{w}_i\left( \zeta (t)\right) \tilde{m}_j\left( \zeta (t_k)\right) \Big ({\textbf {A}}_i\left( \zeta (t)\right) \check{\zeta }\left( \zeta (t)\right) \nonumber \\&\quad +{\textbf {B}}_i\left( \zeta (t)\right) {\textbf {G}}_{jl}\check{\zeta }\left( \zeta (t_k)\right) \Big ), \nonumber \\&\quad \text { for }\zeta (t)\in \varUpsilon _l,\text { } l = 1,\text { }\dots ,\text { }\hat{L}. \end{aligned}$$
(10)

Consider \(\dot{\check{\zeta }}\left( \zeta (t)\right) \) as below:

$$\begin{aligned}&\dot{\check{\zeta }}\left( \zeta (t)\right) =\frac{\partial \check{\zeta }\left( \zeta (t)\right) }{\partial \zeta (t)}\frac{d \zeta (t)}{dt}={\textbf {U}}\left( \zeta (t)\right) \dot{\zeta }(t) \end{aligned}$$
(11)

in which \({\textbf {U}}\left( \zeta (t)\right) \in \mathfrak {R}^{N\times n}\) whose \(\alpha \beta _{th}\) element is shown below:

$$\begin{aligned}&U_{\alpha \beta }\left( \zeta (t)\right) =\frac{\partial \check{\varsigma }_{\alpha }\left( \zeta (t)\right) }{\partial {\varsigma }_{\beta }(t)}, \text { } \alpha = 1,\text { }\dots ,\text { }N; \nonumber \\&\text { } \beta = 1,\text { }\dots ,\text { }n. \end{aligned}$$
(12)

To be further, we have

$$\begin{aligned}&\dot{\check{\zeta }}\left( \zeta (t)\right) \nonumber \\&\quad =\sum _{i=1}^p\sum ^{c}_{j=1}\tilde{w}_i\left( \zeta (t)\right) \tilde{m}_j\left( \zeta (t_k)\right) \Big (\acute{{\textbf {A}}}_i\left( \zeta (t)\right) \check{\zeta }\left( \zeta (t)\right) \nonumber \\&\quad +\acute{{\textbf {B}}}_i\left( \zeta (t)\right) {\textbf {G}}_{jl}\check{\zeta }\left( \zeta (t_k)\right) \Big ), \text { for }\zeta (t)\in \varUpsilon _l,\text { } \nonumber \\&\quad l = 1,\text { }\dots ,\text { }\hat{L} \end{aligned}$$
(13)

where \(\acute{{\textbf {A}}}_i\left( \zeta (t)\right) ={\textbf {U}}\left( \zeta (t)\right) {\textbf {A}}_i\left( \zeta (t)\right) \) and \(\acute{{\textbf {B}}}_i\left( \zeta (t)\right) ={\textbf {U}}\left( \zeta (t)\right) \) \({\textbf {B}}_i\left( \zeta (t)\right) \).

To simplify representations, define \(\varvec{\varpi }=\)\( \left[ {\begin{array}{*{20}{c}} \check{\zeta }^T\left( \zeta (t)\right)&\dot{\check{\zeta }}^T\left( \zeta (t)\right)&\check{\zeta }^T\left( \zeta (t_k)\right) \end{array}} \right] ^T\), \({\textbf {E}}_1= \left[ {\begin{array}{*{20}{c}} {\textbf {I}}_{N}&{\textbf {0}}_{N\times 2N } \end{array}} \right] \), \({\textbf {E}}_2=\left[ {\begin{array}{*{20}{c}} {\textbf {0}}_{N\times N}&{\textbf {I}}_{N}&{\textbf {0}}_{N\times N } \end{array}} \right] \), \({\textbf {E}}_3=\left[ {\begin{array}{*{20}{c}} {\textbf {0}}_{N\times 2N}&{\textbf {I}}_{N} \end{array}} \right] \).

3.1 MFI stability analysis and controller design

Theorem 1

Suppose \({\textbf {G}}_{jl}\) in (7) is known beforehand. The IT2SDPFMB control system with a switching control scheme formed by an uncertain nonlinear plant depicted via the IT2 polynomial fuzzy model (3) as well as the switching IT2SD polynomial fuzzy controller (7) composed of several local IT2SD polynomial fuzzy controllers can be deemed asymptotically stable, when there exist matrices \({\textbf {P}}={\textbf {P}}^{T} \in \mathfrak {R}^{N\times N}\), \({\textbf {S}}={\textbf {S}}^{T} \in \mathfrak {R}^{N\times N} \), \({\textbf {R}}_1={\textbf {R}}_1^T \in \mathfrak {R}^{N\times N} \), \({\textbf {R}}_2 \in \mathfrak {R}^{N\times N} \), \({\textbf {M}}={\textbf {M}}^T \in \mathfrak {R}^{N\times N}\), \({\textbf {Q}} \in \mathfrak {R}^{3N\times N} \) and \(\tilde{{\textbf {X}}} \in \mathfrak {R}^{N\times N}\) satisfying the SOS-based conditions below for \(i = 1,\text { }\dots ,\text { } p;\) \(j=1,\text { }\dots ,\text { }c;\) \(l=1,\text { }\dots ,\text { }\hat{L}\):

$$\begin{aligned}&\varrho _1^T\left( {\textbf {P}}-\epsilon _1{\textbf {I}}_{N}\right) \varrho _1\text { is SOS}; \end{aligned}$$
(14)
$$\begin{aligned}&\varrho _1^T\left( {\textbf {M}}-\epsilon _2{\textbf {I}}_{N}\right) \varrho _1\text { is SOS}; \end{aligned}$$
(15)
$$\begin{aligned}&-\varrho _2^T\left( \varTheta _{1,ijl}\left( \zeta (t)\right) +\epsilon _3\left( \zeta (t)\right) {\textbf {I}}_{3N}\right) \varrho _2 \text { is SOS}, \text { }\forall i,\text { } j,\text { } l; \end{aligned}$$
(16)
$$\begin{aligned}&-\varrho _2^T\left( \varTheta _{1,ijl}\left( \zeta (t)\right) +h_s\varTheta _2+\epsilon _4\left( \zeta (t)\right) {\textbf {I}}_{3N}\right) \varrho _2 \text { is SOS},\nonumber \\&\quad \forall i,\text { } j,\text { } l; \end{aligned}$$
(17)
$$\begin{aligned}&-\varrho _3^T\Bigg (\left[ {\begin{array}{*{20}{c}} \varTheta _{1,ijl}\left( \zeta (t)\right) +h_s\varTheta _3 &{} h_s{\textbf {Q}}\\ h_s{\textbf {Q}}^T &{} -h_s{\textbf {M}}\end{array}} \right] +\epsilon _5\left( \zeta (t)\right) {\textbf {I}}_{4N}\Bigg )\varrho _3 \nonumber \\&\text {is SOS}, \text { }\forall i,\text { } j,\text { } l; \end{aligned}$$
(18)

in which \(\varrho _1 \in \mathfrak {R}^{N}\), \(\varrho _2 \in \mathfrak {R}^{3N}\) as well as \(\varrho _3 \in \mathfrak {R}^{4N}\) represent arbitrary vectors not dependent of \(\zeta (t)\); user-defined \(\epsilon _1>0\), \(\epsilon _2>0\), \(\epsilon _{\hat{f}}\left( \zeta (t)\right) >0\), \({\hat{f}}\) is from 3 to 5; scalars \(h_s\), \(\varkappa _{1}\), \(\varkappa _{2}\) and \(\varkappa _{3}\) are predetermined; \(\acute{{\textbf {A}}}_i\left( \zeta (t)\right) ={\textbf {U}}\left( \zeta (t)\right) {\textbf {A}}_i\left( \zeta (t)\right) \), \(\acute{{\textbf {B}}}_i\left( \zeta (t)\right) ={\textbf {U}}\left( \zeta (t)\right) {\textbf {B}}_i\left( \zeta (t)\right) \), \({\textbf {U}}\left( \zeta (t)\right) \in \mathfrak {R}^{N\times n}\) in which \(U_{\alpha \beta }\left( \zeta (t)\right) =\frac{\partial \check{\varsigma }_{\alpha }\left( \zeta (t)\right) }{\partial {\varsigma }_{\beta }(t)}\), \(\alpha \) is from 1 to N and \(\beta \) is from 1 to n; furthermore,

$$\begin{aligned}&\varTheta _{1,ijl}\left( \zeta (t)\right) =\varLambda _{1}+\varLambda _{3,1}+\varLambda _{4,3}+\varLambda _{5,ijl}\left( \zeta (t)\right) ,&\\&\varTheta _{2}=\varLambda _{2,1}+\varLambda _{3,2}+\varLambda _{4,1},&\\&\varTheta _{3}=\varLambda _{2,2},&\\&\varLambda _{1}=Sym\left\{ {\textbf {E}}_2^T{\textbf {P}}{} {\textbf {E}}_1\right\} ,&\\&\varLambda _{2,1}= {\textbf {E}}_3^T{\textbf {S}}{} {\textbf {E}}_3,&\\&\varLambda _{2,2}=-{\textbf {E}}_3^T{\textbf {S}}{} {\textbf {E}}_3,&\\&\varLambda _{3,1}= -\left( {\textbf {E}}_1^T-{\textbf {E}}_3^T\right) {\textbf {R}}_1\left( {\textbf {E}}_1-{\textbf {E}}_3\right) -Sym \\&\quad \left\{ \left( {\textbf {E}}_1^T-{\textbf {E}}_3^T\right) {\textbf {R}}_2{\textbf {E}}_3 \right\} ,&\\&\varLambda _{3,2}=Sym\left\{ \left( {\textbf {E}}_1^T-{\textbf {E}}_3^T\right) {\textbf {R}}_1 {\textbf {E}}_2+{\textbf {E}}_2^T{\textbf {R}}_2{\textbf {E}}_3 \right\} ,&\\&\varLambda _{4,1}={\textbf {E}}_2^T{\textbf {M}}{} {\textbf {E}}_2,&\\&\varLambda _{4,3}=Sym\left\{ {\textbf {Q}} \left( {\textbf {E}}_1-{\textbf {E}}_3\right) \right\} ,&\\&\varLambda _{5,ijl}\left( \zeta (t)\right) \\&\quad =Sym\bigg \{\mathfrak {F}\Big (\acute{{\textbf {A}}}_i\left( \zeta (t)\right) {\textbf {E}}_1+\acute{{\textbf {B}}}_i\left( \zeta (t)\right) {\textbf {G}}_{jl}{} {\textbf {E}}_3-{\textbf {E}}_2\Big )\bigg \},&\\&\mathfrak {F}=\varkappa _1{\textbf {E}}_1^T\tilde{{\textbf {X}}}^T+\varkappa _2{\textbf {E}}_2^T\tilde{{\textbf {X}}}^T+\varkappa _3{\textbf {E}}_3^T\tilde{{\textbf {X}}}^T.&\end{aligned}$$

Proof

Please see Appendix A.

Theorem 2 as below is derived based on Theorem 1 to get the switching IT2SD polynomial fuzzy controller. \(\square \)

Theorem 2

The IT2SDPFMB control system with a switching control scheme formed by an uncertain nonlinear plant depicted via the IT2 polynomial fuzzy model (3) as well as the switching IT2SD polynomial fuzzy controller (7) composed of several local IT2SD polynomial fuzzy controllers can be deemed asymptotically stable, when there exist matrices \({\textbf {X}} \in \mathfrak {R}^{N\times N}\), \(\grave{{\textbf {P}}}=\grave{{\textbf {P}}}^{T} \in \mathfrak {R}^{N\times N}\), \(\grave{{\textbf {S}}}=\grave{{\textbf {S}}}^{T} \in \mathfrak {R}^{N\times N} \), \(\grave{{\textbf {R}}}_1=\grave{{\textbf {R}}}_1^T \in \mathfrak {R}^{N\times N} \), \(\grave{{\textbf {R}}}_2 \in \mathfrak {R}^{N\times N} \), \(\grave{{\textbf {M}}}=\grave{{\textbf {M}}}^T \in \mathfrak {R}^{N\times N}\), \(\grave{{\textbf {Q}}} \in \mathfrak {R}^{3N\times N} \) and \({\textbf {N}}_{jl} \in \mathfrak {R}^{m\times N}\) satisfying the SOS-based conditions below for \(i = 1,\text { }\dots ,\text { } p;\) \(j=1,\text { }\dots ,\text { }c;\) \(l=1,\text { }\dots ,\text { }\hat{L}\):

$$\begin{aligned}&\varrho _1^T\left( \grave{{\textbf {P}}}-\epsilon _1{\textbf {I}}_{N}\right) \varrho _1\text { is SOS}; \end{aligned}$$
(19)
$$\begin{aligned}&\varrho _1^T\left( \grave{{\textbf {M}}}-\epsilon _2{\textbf {I}}_{N}\right) \varrho _1\text { is SOS}; \end{aligned}$$
(20)
$$\begin{aligned}&-\varrho _2^T\left( \grave{\varTheta }_{1,ijl}\left( \zeta (t)\right) +\epsilon _3\left( \zeta (t)\right) {\textbf {I}}_{3N}\right) \varrho _2 \text { is SOS}, \text { }\forall i,\text { } j,\text { } l; \end{aligned}$$
(21)
$$\begin{aligned}&-\varrho _2^T\left( \grave{\varTheta }_{1,ijl}\left( \zeta (t)\right) +h_s\grave{\varTheta }_2+\epsilon _4\left( \zeta (t)\right) {\textbf {I}}_{3N}\right) \varrho _2 \text { is SOS},\nonumber \\&\quad \forall i,\text { } j,\text { } l; \end{aligned}$$
(22)
$$\begin{aligned}&-\varrho _3^T\Bigg (\left[ {\begin{array}{*{20}{c}} \grave{\varTheta }_{1,ijl}\left( \zeta (t)\right) +h_s\grave{\varTheta }_3 &{} h_s\grave{{\textbf {Q}}}\\ h_s\grave{{\textbf {Q}}}^T &{} -h_s\grave{{\textbf {M}}}\end{array}} \right] +\epsilon _5\left( \zeta (t)\right) {\textbf {I}}_{4N}\Bigg )\varrho _3 \nonumber \\&\text {is SOS}, \text { }\forall i,\text { } j,\text { } l; \end{aligned}$$
(23)

in which \(\varrho _1 \in \mathfrak {R}^{N}\), \(\varrho _2 \in \mathfrak {R}^{3N}\) as well as \(\varrho _3 \in \mathfrak {R}^{4N}\) represent arbitrary vectors not dependent of \(\zeta (t)\); user-defined \(\epsilon _1>0\), \(\epsilon _2>0\), \(\epsilon _{\hat{f}}\left( \zeta (t)\right) >0\), \({\hat{f}}\) is from 3 to 5; scalars \(h_s\), \(\varkappa _{1}\), \(\varkappa _{2}\) and \(\varkappa _{3}\) are predetermined; \(\acute{{\textbf {A}}}_i\left( \zeta (t)\right) ={\textbf {U}}\left( \zeta (t)\right) {\textbf {A}}_i\left( \zeta (t)\right) \), \(\acute{{\textbf {B}}}_i\left( \zeta (t)\right) ={\textbf {U}}\left( \zeta (t)\right) {\textbf {B}}_i\left( \zeta (t)\right) \), \({\textbf {U}}\left( \zeta (t)\right) \in \mathfrak {R}^{N\times n}\) in which \(U_{\alpha \beta }\left( \zeta (t)\right) =\frac{\partial \check{\varsigma }_{\alpha }\left( \zeta (t)\right) }{\partial {\varsigma }_{\beta }(t)}\), \(\alpha \) is from 1 to N and \(\beta \) is from 1 to n; furthermore,

$$\begin{aligned}&\grave{\varTheta }_{1,ijl}\left( \zeta (t)\right) =\grave{\varLambda }_{1}+\grave{\varLambda }_{3,1}+\grave{\varLambda }_{4,3}+\grave{\varLambda }_{5,ijl}\left( \zeta (t)\right) ,&\\&\grave{\varTheta }_{2}=\grave{\varLambda }_{2,1}+\grave{\varLambda }_{3,2}+\grave{\varLambda }_{4,1},&\\&\grave{\varTheta }_{3}=\grave{\varLambda }_{2,2},&\\&\grave{\varLambda }_{1}=Sym\left\{ {\textbf {E}}_2^T\grave{{\textbf {P}}}{} {\textbf {E}}_1\right\} ,&\\&\grave{\varLambda }_{2,1}= {\textbf {E}}_3^T\grave{{\textbf {S}}}{} {\textbf {E}}_3,&\\&\grave{\varLambda }_{2,2}=-{\textbf {E}}_3^T\grave{{\textbf {S}}}{} {\textbf {E}}_3,&\\&\grave{\varLambda }_{3,1}= -\left( {\textbf {E}}_1^T-{\textbf {E}}_3^T\right) \grave{{\textbf {R}}}_1\left( {\textbf {E}}_1-{\textbf {E}}_3\right) -Sym\\&\quad \left\{ \left( {\textbf {E}}_1^T-{\textbf {E}}_3^T\right) \grave{{\textbf {R}}}_2{\textbf {E}}_3 \right\} ,&\\&\grave{\varLambda }_{3,2}=Sym\left\{ \left( {\textbf {E}}_1^T-{\textbf {E}}_3^T\right) \grave{{\textbf {R}}}_1 {\textbf {E}}_2+{\textbf {E}}_2^T\grave{{\textbf {R}}}_2{\textbf {E}}_3 \right\} ,&\\&\grave{\varLambda }_{4,1}={\textbf {E}}_2^T\grave{{\textbf {M}}}{} {\textbf {E}}_2,&\\&\grave{\varLambda }_{4,3}=Sym\left\{ \grave{{\textbf {Q}}}\left( {\textbf {E}}_1-{\textbf {E}}_3\right) \right\} ,&\\&\grave{\varLambda }_{5,ijl}\left( \zeta (t)\right) =Sym \\&\quad \bigg \{\grave{\mathfrak {F}}\Big (\acute{{\textbf {A}}}_i\left( \zeta (t)\right) \mathbb {X}_1{\textbf {E}}_1+\acute{{\textbf {B}}}_i\left( \zeta (t)\right) {\textbf {N}}_{jl}{} {\textbf {E}}_3&\\ {}&\quad \quad \quad \quad \hspace{5.0pt} -\mathbb {X}_1{\textbf {E}}_2\Big )\bigg \},&\\&\grave{\mathfrak {F}}=\varkappa _1{\textbf {E}}_1^T+\varkappa _2{\textbf {E}}_2^T+\varkappa _3{\textbf {E}}_3^T.&\end{aligned}$$

\({\textbf {G}}_{jl}\) is given by:

$$\begin{aligned}&{\textbf {G}}_{jl}={\textbf {N}}_{jl}{} {\textbf {X}}^{-1}, \text { for }\zeta (t)\in \varUpsilon _l. \end{aligned}$$
(24)

Proof

Please see Appendix B. \(\square \)

3.2 MFD stability analysis and controller design

Theorem 3

Suppose \({\textbf {G}}_{jl}\) in (7) is known beforehand. The IT2SDPFMB control system with a switching control scheme formed by an uncertain nonlinear plant depicted via the IT2 polynomial fuzzy model (3) as well as the switching IT2SD polynomial fuzzy controller (7) composed of several local IT2SD polynomial fuzzy controllers can be deemed asymptotically stable, when there exist matrices \({\textbf {P}}={\textbf {P}}^{T} \in \mathfrak {R}^{N\times N}\), \({\textbf {S}}={\textbf {S}}^{T} \in \mathfrak {R}^{N\times N} \), \({\textbf {R}}_1={\textbf {R}}_1^T \in \mathfrak {R}^{N\times N} \), \({\textbf {R}}_2 \in \mathfrak {R}^{N\times N} \), \({\textbf {M}}={\textbf {M}}^T \in \mathfrak {R}^{N\times N}\), \({\textbf {Q}} \in \mathfrak {R}^{3N\times N}\), \(\tilde{{\textbf {X}}} \in \mathfrak {R}^{N\times N}\), \( \underline{{\textbf {H}}}_{ijl}\left( \zeta (t)\right) =\underline{{\textbf {H}}}^T_{ijl}\left( \zeta (t)\right) \in \mathfrak {R}^{3N\times 3N}\), \( \overline{{\textbf {H}}}_{ijl}\left( \zeta (t)\right) =\overline{{\textbf {H}}}^T_{ijl}\left( \zeta (t)\right) \in \mathfrak {R}^{3N\times 3N}\) and \( {\textbf {Y}}_l\left( \zeta (t)\right) ={\textbf {Y}}_l^T\left( \zeta (t)\right) \) \( \in \mathfrak {R}^{3N\times 3N}\) satisfying the SOS-based conditions below for \(i = 1,\text { }\dots ,\) p;  \(j=1,\text { }\dots ,\text { }c;\) \(l=1,\text { }\dots ,\) \(\hat{L}\):

$$\begin{aligned}&\varrho _1^T\left( {\textbf {P}}-\epsilon _1{\textbf {I}}_{N}\right) \varrho _1\text { is SOS}; \end{aligned}$$
(25)
$$\begin{aligned}&\varrho _1^T\left( {\textbf {M}}-\epsilon _2{\textbf {I}}_{N}\right) \varrho _1\text { is SOS}; \end{aligned}$$
(26)
$$\begin{aligned}&\varrho _2^T\left( \underline{{\textbf {H}}}_{ijl}\left( \zeta (t)\right) -\epsilon _3\left( \zeta (t)\right) {\textbf {I}}_{3N}\right) \varrho _2 \text { is SOS}, \text { }\forall i,\text { } j,\text { } l; \end{aligned}$$
(27)
$$\begin{aligned}&\varrho _2^T\left( \overline{{\textbf {H}}}_{ijl}\left( \zeta (t)\right) -\epsilon _4\left( \zeta (t)\right) {\textbf {I}}_{3N}\right) \varrho _2 \text { is SOS}, \text { }\forall i,\text { } j,\text { } l; \end{aligned}$$
(28)
$$\begin{aligned}&\varrho _2^T\left( {\textbf {Y}}_l\left( \zeta (t)\right) -\epsilon _5\left( \zeta (t)\right) {\textbf {I}}_{3N}\right) \varrho _2 \text { is SOS}, \text { }\forall l; \end{aligned}$$
(29)
$$\begin{aligned}&-\varrho _2^T\left( \varPhi _{1,ijl}\left( \zeta (t)\right) +\epsilon _6\left( \zeta (t)\right) {\textbf {I}}_{3N}\right) \varrho _2 \text { is SOS}, \text { }\forall i,\text { } j,\text { } l; \end{aligned}$$
(30)
$$\begin{aligned}&-\varrho _2^T\left( \varPhi _{1,ijl}\left( \zeta (t)\right) +h_s\varTheta _2+\epsilon _7\left( \zeta (t)\right) {\textbf {I}}_{3N}\right) \varrho _2 \text { is SOS}, \nonumber \\&\forall i,\text { } j,\text { } l; \end{aligned}$$
(31)
$$\begin{aligned}&-\varrho _3^T\Bigg (\left[ {\begin{array}{*{20}{c}} \varPhi _{1,ijl}\left( \zeta (t)\right) +h_s\varTheta _3 &{} h_s{\textbf {Q}}\\ h_s{\textbf {Q}}^T &{} -h_s{\textbf {M}}\end{array}} \right] +\epsilon _8\left( \zeta (t)\right) {\textbf {I}}_{4N}\Bigg )\varrho _3 \nonumber \\&\text {is SOS}, \text { }\forall i,\text { } j,\text { } l; \end{aligned}$$
(32)

in which \(\varrho _1 \in \mathfrak {R}^{N}\), \(\varrho _2 \in \mathfrak {R}^{3N}\) as well as \(\varrho _3 \in \mathfrak {R}^{4N}\) represent arbitrary vectors not dependent of \(\zeta (t)\); user-defined \(\epsilon _1>0\), \(\epsilon _2>0\), \(\epsilon _{\hat{f}}\left( \zeta (t)\right) \ge 0\), \({\hat{f}}\) is from 3 to 5, \(\epsilon _{\hat{r}}\left( \zeta (t)\right) >0\), \({\hat{r}}\) is from 6 to 8; \(\underline{\delta }_{ijl}=\underline{w}_{il}\underline{m}_{jl}\), \(\overline{\delta }_{ijl}=\overline{w}_{il}\overline{m}_{jl}\); scalars \(h_s\), \(\varkappa _{1}\), \(\varkappa _{2}\), \(\varkappa _{3}\), \(\underline{w}_{il}\), \(\overline{w}_{il}\), \(\underline{m}_{jl}\), \(\overline{m}_{jl}\), vectors \(\underline{\zeta }_l \in \mathfrak {R}^{n}\), \(\overline{\zeta }_l \in \mathfrak {R}^{n}\) and the diagonal matrix \({\textbf {T}} \in \mathfrak {R}^{n\times n}\) are predetermined; \(\acute{{\textbf {A}}}_i\left( \zeta (t)\right) ={\textbf {U}}\left( \zeta (t)\right) {\textbf {A}}_i\left( \zeta (t)\right) \), \(\acute{{\textbf {B}}}_i\left( \zeta (t)\right) ={\textbf {U}}\left( \zeta (t)\right) {\textbf {B}}_i\left( \zeta (t)\right) \), \({\textbf {U}}\left( \zeta (t)\right) \in \mathfrak {R}^{N\times n}\) in which \(U_{\alpha \beta }\left( \zeta (t)\right) =\frac{\partial \check{\varsigma }_{\alpha }\left( \zeta (t)\right) }{\partial {\varsigma }_{\beta }(t)}\), \(\alpha \) is from 1 to N and \(\beta \) is from 1 to n; furthermore,

$$\begin{aligned}&\varPhi _{1,ijl}\left( \zeta (t)\right) =\varLambda _{1}\\&\quad +\varLambda _{3,1}+\varLambda _{4,3}+\varLambda _{5,ijl}\left( \zeta (t)\right) +\underline{{\textbf {H}}}_{ijl}\left( \zeta (t)\right) \\&\quad \negthickspace -\overline{{\textbf {H}}}_{ijl}\left( \zeta (t)\right) +\sum ^p_{r=1}\sum ^{c}_{s=1}\Big (-\underline{\delta }_{rsl}\underline{{\textbf {H}}}_{rsl}\left( \zeta (t)\right) \\&\quad \negthickspace +\overline{\delta }_{rsl}\overline{{\textbf {H}}}_{rsl}\left( \zeta (t)\right) \Big ) +\bigg (\left( \zeta (t)-\underline{\zeta }_l\right) ^T{\textbf {T}}\\&\quad \negthickspace \times \left( \overline{\zeta }_l-\zeta (t)\right) \bigg ){\textbf {Y}}_l\left( \zeta (t)\right) ,\\&\varTheta _{2}=\varLambda _{2,1}+\varLambda _{3,2}+\varLambda _{4,1},\\&\varTheta _{3}=\varLambda _{2,2},\\&\varLambda _{1}=Sym\left\{ {\textbf {E}}_2^T{\textbf {P}}{} {\textbf {E}}_1\right\} ,\\&\varLambda _{2,1}= {\textbf {E}}_3^T{\textbf {S}}{} {\textbf {E}}_3,\\&\varLambda _{2,2}=-{\textbf {E}}_3^T{\textbf {S}}{} {\textbf {E}}_3,\\&\varLambda _{3,1}= -\left( {\textbf {E}}_1^T-{\textbf {E}}_3^T\right) {\textbf {R}}_1\left( {\textbf {E}}_1-{\textbf {E}}_3\right) -Sym \\&\quad \left\{ \left( {\textbf {E}}_1^T-{\textbf {E}}_3^T\right) {\textbf {R}}_2{\textbf {E}}_3 \right\} ,\\&\varLambda _{3,2}=Sym\left\{ \left( {\textbf {E}}_1^T-{\textbf {E}}_3^T\right) {\textbf {R}}_1 {\textbf {E}}_2+{\textbf {E}}_2^T{\textbf {R}}_2{\textbf {E}}_3 \right\} ,\\&\varLambda _{4,1}={\textbf {E}}_2^T{\textbf {M}}{} {\textbf {E}}_2,\\&\varLambda _{4,3}=Sym\left\{ {\textbf {Q}} \left( {\textbf {E}}_1-{\textbf {E}}_3\right) \right\} ,\\&\varLambda _{5,ijl}\left( \zeta (t)\right) =Sym \\&\quad \bigg \{\mathfrak {F}\Big (\acute{{\textbf {A}}}_i\left( \zeta (t)\right) {\textbf {E}}_1+\acute{{\textbf {B}}}_i\left( \zeta (t)\right) {\textbf {G}}_{jl}{} {\textbf {E}}_3-{\textbf {E}}_2\Big )\bigg \},\\&\mathfrak {F}=\varkappa _1{\textbf {E}}_1^T\tilde{{\textbf {X}}}^T+\varkappa _2{\textbf {E}}_2^T\tilde{{\textbf {X}}}^T+\varkappa _3{\textbf {E}}_3^T\tilde{{\textbf {X}}}^T. \end{aligned}$$

Proof

Please see Appendix C.\(\square \)

Theorem 4 as below is derived based on Theorem 3 to get the switching IT2SD polynomial fuzzy controller.

Theorem 4

The IT2SDPFMB control system with a switching control scheme formed by an uncertain nonlinear plant depicted via the IT2 polynomial fuzzy model (3) as well as the switching IT2SD polynomial fuzzy controller (7) composed of several local IT2SD polynomial fuzzy controllers can be deemed asymptotically stable, when there exist matrices \({\textbf {X}} \in \mathfrak {R}^{N\times N}\), \(\grave{{\textbf {P}}}=\grave{{\textbf {P}}}^{T} \in \mathfrak {R}^{N\times N}\), \(\grave{{\textbf {S}}}=\grave{{\textbf {S}}}^{T} \in \mathfrak {R}^{N\times N} \), \(\grave{{\textbf {R}}}_1=\grave{{\textbf {R}}}_1^T \in \mathfrak {R}^{N\times N} \), \(\grave{{\textbf {R}}}_2 \in \mathfrak {R}^{N\times N} \), \(\grave{{\textbf {M}}}=\grave{{\textbf {M}}}^T \in \mathfrak {R}^{N\times N}\), \(\grave{{\textbf {Q}}} \in \mathfrak {R}^{3N\times N} \), \( \grave{\underline{{\textbf {H}}}}_{ijl}\left( \zeta (t)\right) =\grave{\underline{{\textbf {H}}}}^T_{ijl}\left( \zeta (t)\right) \in \mathfrak {R}^{3N\times 3N}\), \( \grave{\overline{{\textbf {H}}}}_{ijl}\left( \zeta (t)\right) =\grave{\overline{{\textbf {H}}}}^T_{ijl}\left( \zeta (t)\right) \in \mathfrak {R}^{3N\times 3N}\), \( \grave{{\textbf {Y}}}_l\left( \zeta (t)\right) =\grave{{\textbf {Y}}}_l^T\left( \zeta (t)\right) \in \mathfrak {R}^{3N\times 3N}\) and \({\textbf {N}}_{jl} \in \mathfrak {R}^{m\times N}\) satisfying the SOS-based conditions below for \(i = 1,\text { }\dots ,\text { } p;\) \(j=1,\text { }\dots ,\text { }c;\text { }l=1,\text { }\dots ,\text { }\hat{L}\):

$$\begin{aligned}&\varrho _1^T\left( \grave{{\textbf {P}}}-\epsilon _1{\textbf {I}}_{N}\right) \varrho _1\text { is SOS}; \end{aligned}$$
(33)
$$\begin{aligned}&\varrho _1^T\left( \grave{{\textbf {M}}}-\epsilon _2{\textbf {I}}_{N}\right) \varrho _1\text { is SOS}; \end{aligned}$$
(34)
$$\begin{aligned}&\varrho _2^T\left( \grave{\underline{{\textbf {H}}}}_{ijl}\left( \zeta (t)\right) -\epsilon _3\left( \zeta (t)\right) {\textbf {I}}_{3N}\right) \varrho _2 \text { is SOS}, \text { }\forall i,\text { } j,\text { } l; \end{aligned}$$
(35)
$$\begin{aligned}&\varrho _2^T\left( \grave{\overline{{\textbf {H}}}}_{ijl}\left( \zeta (t)\right) -\epsilon _4\left( \zeta (t)\right) {\textbf {I}}_{3N}\right) \varrho _2 \text { is SOS}, \text { }\forall i,\text { } j,\text { } l; \end{aligned}$$
(36)
$$\begin{aligned}&\varrho _2^T\left( \grave{{\textbf {Y}}}_l\left( \zeta (t)\right) -\epsilon _5\left( \zeta (t)\right) {\textbf {I}}_{3N}\right) \varrho _2 \text { is SOS}, \text { }\forall l; \end{aligned}$$
(37)
$$\begin{aligned}&-\varrho _2^T\left( \grave{\varPhi }_{1,ijl}\left( \zeta (t)\right) +\epsilon _6\left( \zeta (t)\right) {\textbf {I}}_{3N}\right) \varrho _2 \text { is SOS}, \text { }\forall i,\text { } j,\text { } l; \end{aligned}$$
(38)
$$\begin{aligned}&-\varrho _2^T\left( \grave{\varPhi }_{1,ijl}\left( \zeta (t)\right) +h_s\grave{\varTheta }_2+\epsilon _7\left( \zeta (t)\right) {\textbf {I}}_{3N}\right) \varrho _2 \text { is SOS},\nonumber \\&\forall i,\text { } j,\text { } l; \end{aligned}$$
(39)
$$\begin{aligned}&-\varrho _3^T\Bigg (\left[ {\begin{array}{*{20}{c}} \grave{\varPhi }_{1,ijl}\left( \zeta (t)\right) +h_s\grave{\varTheta }_3 &{} h_s\grave{{\textbf {Q}}}\\ h_s\grave{{\textbf {Q}}}^T &{} -h_s\grave{{\textbf {M}}}\end{array}} \right] +\epsilon _8\left( \zeta (t)\right) {\textbf {I}}_{4N}\Bigg )\varrho _3 \nonumber \\&\text {is SOS}, \text { }\forall i,\text { } j,\text { } l; \end{aligned}$$
(40)

in which \(\varrho _1 \in \mathfrak {R}^{N}\), \(\varrho _2 \in \mathfrak {R}^{3N}\) as well as \(\varrho _3 \in \mathfrak {R}^{4N}\) represent arbitrary vectors not dependent of \(\zeta (t)\); user-defined \(\epsilon _1>0\), \(\epsilon _2>0\), \(\epsilon _{\hat{f}}\left( \zeta (t)\right) \ge 0\), \({\hat{f}}\) is from 3 to 5, \(\epsilon _{\hat{r}}\left( \zeta (t)\right) >0\), \({\hat{r}}\) is from 6 to 8; \(\underline{\delta }_{ijl}=\underline{w}_{il}\underline{m}_{jl}\), \(\overline{\delta }_{ijl}=\overline{w}_{il}\overline{m}_{jl}\); scalars \(h_s\), \(\varkappa _{1}\), \(\varkappa _{2}\), \(\varkappa _{3}\), \(\underline{w}_{il}\), \(\overline{w}_{il}\), \(\underline{m}_{jl}\), \(\overline{m}_{jl}\), vectors \(\underline{\zeta }_l \in \mathfrak {R}^{n}\), \(\overline{\zeta }_l \in \mathfrak {R}^{n}\) and the diagonal matrix \({\textbf {T}} \in \mathfrak {R}^{n\times n}\) are predetermined; \(\acute{{\textbf {A}}}_i\left( \zeta (t)\right) ={\textbf {U}}\left( \zeta (t)\right) {\textbf {A}}_i\left( \zeta (t)\right) \), \(\acute{{\textbf {B}}}_i\left( \zeta (t)\right) ={\textbf {U}}\left( \zeta (t)\right) {\textbf {B}}_i\left( \zeta (t)\right) \), \({\textbf {U}}\left( \zeta (t)\right) \in \mathfrak {R}^{N\times n}\) in which \(U_{\alpha \beta }\left( \zeta (t)\right) =\frac{\partial \check{\varsigma }_{\alpha }\left( \zeta (t)\right) }{\partial {\varsigma }_{\beta }(t)}\), \(\alpha \) is from 1 to N and \(\beta \) is from 1 to n; furthermore,

$$\begin{aligned}&\grave{\varPhi }_{1,ijl}\left( \zeta (t)\right) =\grave{\varLambda }_{1}+\grave{\varLambda }_{3,1}\\&\quad +\grave{\varLambda }_{4,3}+\grave{\varLambda }_{5,ijl}\left( \zeta (t)\right) +\grave{\underline{{\textbf {H}}}}_{ijl}\left( \zeta (t)\right)&\\&\quad \negthickspace -\grave{\overline{{\textbf {H}}}}_{ijl}\left( \zeta (t)\right) +\sum ^p_{r=1}\sum ^{c}_{s=1}\Big (-\underline{\delta }_{rsl}\grave{\underline{{\textbf {H}}}}_{rsl}\left( \zeta (t)\right)&\\&\quad \negthickspace +\overline{\delta }_{rsl}\grave{\overline{{\textbf {H}}}}_{rsl}\left( \zeta (t)\right) \Big )+\bigg (\left( \zeta (t)-\underline{\zeta }_l\right) ^T{\textbf {T}}&\\&\quad \negthickspace \times \left( \overline{\zeta }_l-\zeta (t)\right) \bigg )\grave{{\textbf {Y}}}_l\left( \zeta (t)\right) ,&\\&\grave{\varTheta }_{2}=\grave{\varLambda }_{2,1}+\grave{\varLambda }_{3,2}+\grave{\varLambda }_{4,1},&\\&\grave{\varTheta }_{3}=\grave{\varLambda }_{2,2},&\\&\grave{\varLambda }_{1}=Sym\left\{ {\textbf {E}}_2^T\grave{{\textbf {P}}}{} {\textbf {E}}_1\right\} ,&\\&\grave{\varLambda }_{2,1}= {\textbf {E}}_3^T\grave{{\textbf {S}}}{} {\textbf {E}}_3,&\\&\grave{\varLambda }_{2,2}=-{\textbf {E}}_3^T\grave{{\textbf {S}}}{} {\textbf {E}}_3,&\\&\grave{\varLambda }_{3,1}= -\left( {\textbf {E}}_1^T-{\textbf {E}}_3^T\right) \grave{{\textbf {R}}}_1\left( {\textbf {E}}_1-{\textbf {E}}_3\right) -Sym \\&\quad \left\{ \left( {\textbf {E}}_1^T-{\textbf {E}}_3^T\right) \grave{{\textbf {R}}}_2{\textbf {E}}_3 \right\} ,&\\&\grave{\varLambda }_{3,2}=Sym\left\{ \left( {\textbf {E}}_1^T-{\textbf {E}}_3^T\right) \grave{{\textbf {R}}}_1 {\textbf {E}}_2+{\textbf {E}}_2^T\grave{{\textbf {R}}}_2{\textbf {E}}_3 \right\} ,&\\&\grave{\varLambda }_{4,1}={\textbf {E}}_2^T\grave{{\textbf {M}}}{} {\textbf {E}}_2,&\\&\grave{\varLambda }_{4,3}=Sym\left\{ \grave{{\textbf {Q}}}\left( {\textbf {E}}_1-{\textbf {E}}_3\right) \right\} ,&\\&\grave{\varLambda }_{5,ijl}\left( \zeta (t)\right) \\&\quad =Sym\bigg \{\grave{\mathfrak {F}}\Big (\acute{{\textbf {A}}}_i\left( \zeta (t)\right) \mathbb {X}_1{\textbf {E}}_1+\acute{{\textbf {B}}}_i\left( \zeta (t)\right) {\textbf {N}}_{jl}{} {\textbf {E}}_3&\\&\quad \hspace{5.0pt} -\mathbb {X}_1{\textbf {E}}_2\Big )\bigg \},&\\&\grave{\mathfrak {F}}=\varkappa _1{\textbf {E}}_1^T+\varkappa _2{\textbf {E}}_2^T+\varkappa _3{\textbf {E}}_3^T.&\end{aligned}$$
Table 1 Sub-domains
Full size table

\({\textbf {G}}_{jl}\) is given by:

$$\begin{aligned}&{\textbf {G}}_{jl}={\textbf {N}}_{jl}{} {\textbf {X}}^{-1}, \text { for }\zeta (t)\in \varUpsilon _l. \end{aligned}$$
(41)

Proof

Please see Appendix D. \(\square \)

4 Simulation example

For the demonstration of the efficacy of the proposed method, the simulation outcomes are presented below.

Take into account the IT2 polynomial fuzzy model below for depicting an uncertain nonlinear plant,

$$\begin{aligned}&\check{\zeta }\left( \zeta (t)\right) =\zeta (t) = \left[ {\begin{array}{*{20}{c}} {\varsigma _1}(t) \\ {\varsigma _2}(t) \end{array}}\right] ,\\&{\textbf {A}}_1\left( {\varsigma _1}(t)\right) =\left[ {\begin{array}{*{20}{c}} 0.59-0.03{\varsigma _1^2}(t) &{} -1.29+0.21{\varsigma _1}(t) \\ 0.02 &{} -2.85 \end{array}}\right] ,\\&{\textbf {A}}_2\left( {\varsigma _1}(t)\right) =\left[ {\begin{array}{*{20}{c}} 0.02-0.15{\varsigma _1^2}(t) &{} -2.64+0.03{\varsigma _1}(t) \\ 0.35 &{} -1.86 \end{array}}\right] , \\&{\textbf {A}}_3\left( {\varsigma _1}(t)\right) =\left[ {\begin{array}{*{20}{c}} a+0.73 &{} 2.45+ 0.05{\varsigma _1}(t) \\ 0.26 &{} -1.54 \end{array}}\right] , \\&{\textbf {B}}_1\left( {\varsigma _1}(t)\right) =\left[ {\begin{array}{*{20}{c}} 2.12+0.03{\varsigma _1^2}(t) \\ 0 \end{array}}\right] , \\&{\textbf {B}}_2\left( {\varsigma _1}(t)\right) =\left[ {\begin{array}{*{20}{c}} 7.89+0.25{\varsigma _1}(t) \\ 0 \end{array}}\right] , \\&{\textbf {B}}_3\left( {\varsigma _1}(t)\right) =\left[ {\begin{array}{*{20}{c}} b+0.21+0.12{\varsigma _1^2}(t) \\ 0.8 \end{array}}\right] , \end{aligned}$$

where the IT2 MFs are defined as [33]: \(\underline{w}_1({\varsigma _1}(t))=\underline{\mu }_{\tilde{M}_1^1}({\varsigma _1}(t))\) \(=1-\frac{1}{1+e^{-{\varsigma _1}(t)-3.5}}\), \(\underline{w}_3({\varsigma _1}(t))=\)\(\underline{\mu }_{\tilde{M}_1^3}({\varsigma _1}(t)) =\frac{1}{1+e^{-{\varsigma _1}(t)+3.5}}\) and \(\overline{w}_2({\varsigma _1}(t))=\overline{\mu }_{\tilde{M}_1^2}({\varsigma _1}(t)) =1-\underline{\mu }_{\tilde{M}_1^1}({\varsigma _1}(t))-\underline{\mu }_{\tilde{M}_1^3}({\varsigma _1}(t))\); \(\overline{w}_1({\varsigma _1}(t))=\overline{\mu }_{\tilde{M}_1^1}({\varsigma _1}(t))\) \(=1-\frac{1}{1+e^{-{\varsigma _1}(t)-2.5}}\), \(\overline{w}_3({\varsigma _1}(t))= \) \(\overline{\mu }_{\tilde{M}_1^3}({\varsigma _1}(t))=\frac{1}{1+e^{-{\varsigma _1}(t)+2.5}}\) and \(\underline{w}_2({\varsigma _1}(t))=\underline{\mu }_{\tilde{M}_1^2}({\varsigma _1}(t))=1-\overline{\mu }_{\tilde{M}_1^1}({\varsigma _1}(t))-\overline{\mu }_{\tilde{M}_1^3}({\varsigma _1}(t))\). In addition, the modeling domain of \({\varsigma _1}(t)\) is \([-10\text {, } 10]\).

Take into account a 2-rule switching IT2SD polynomial fuzzy controller for control. Select its IT2 MFs to be [33]: \(\underline{m}_1(\varsigma _1(t_k))\) \(=\underline{\mu }_{\tilde{N}_1^1}(\varsigma _1(t_k))=\{1\) for \(\varsigma _1(t_k) < -5.5\); \(\frac{-\varsigma _1(t_k)+4.5}{10}\) for \(-5.5 \le \varsigma _1(t_k) \le 4.5\); 0 for \(\varsigma _1(t_k) > 4.5\}\), and \(\overline{m}_2(\varsigma _1(t_k))=\overline{\mu }_{\tilde{N}_1^2}(\varsigma _1(t_k))\) \(=1-\underline{\mu }_{\tilde{N}_1^1}(\varsigma _1(t_k))\); \(\overline{m}_1(\varsigma _1(t_k))=\overline{\mu }_{\tilde{N}_1^1}(\varsigma _1(t_k))=\{1\) for \(\varsigma _1(t_k) < -4.5\); \(\frac{-\varsigma _1(t_k)+5.5}{10}\) for \(-4.5 \le \varsigma _1(t_k) \le 5.5\); 0 for \(\varsigma _1(t_k) > 5.5\}\), \(\underline{m}_2(\varsigma _1(t_k))=\underline{\mu }_{\tilde{N}_1^2}(\varsigma _1(t_k))=1-\overline{\mu }_{\tilde{N}_1^1}(\varsigma _1(t_k))\).

Choose \(h_s=0.001\)s; \(\epsilon _1=\epsilon _2=\epsilon _3\left( \zeta (t)\right) =\epsilon _4\left( \zeta (t)\right) =\epsilon _5\left( \zeta (t)\right) =\epsilon _6\left( \zeta (t)\right) =\epsilon _7\left( \zeta (t)\right) =\epsilon _8\left( \zeta (t)\right) =0.0001\); \(\varkappa _{1}=1\), \(\varkappa _{2}=0.1\) and \(\varkappa _{3}=1\); \({\textbf {T}}=\left[ {\begin{array}{*{20}{c}} 1 &{} 0\\ 0 &{} 0 \end{array}} \right] \); the degrees of \( \grave{\underline{{\textbf {H}}}}_{ijl}\left( \zeta (t)\right) \), \(\grave{\overline{{\textbf {H}}}}_{ijl}\left( \zeta (t)\right) \) and \(\grave{{\textbf {Y}}}_l\left( \zeta (t)\right) \) are all 0.

In this example, the three cases are employed to study how \(\hat{L}\) influences the stability regions for \(0 \le a \le 90\), \(0 \le b \le 5\) (the spacing of a is 10 and the spacing of b is 1). The detailed information of the three cases can be found in Table 1. Firstly, Theorem 2 is applied to acquire the solutions for the three cases for different a and b, but all solutions are infeasible. Then, Theorem 4 is applied to acquire the solutions. The stability regions for \(\hat{L}=1\), \(\hat{L}=3\) and \(\hat{L}=5\) with Theorem 4 can be found in Fig. 1. It is obvious that the region for \(\hat{L}=1\) where feasible solutions can be sought out is the smallest, while the region for \(\hat{L}=5\) where feasible solutions can be sought out is the broadest.

Fig. 1
figure 1

The stability regions for Case 1 \((\times )\), Case 2 \((\square )\) and Case 3 \((\bigcirc )\) with Theorem 4

Full size image
Table 2 \({\textbf {G}}_{jl}\) got through Theorem 4 for Case 1 for \(a = 0\) and \(b = 0\)
Full size table
Table 3 \({\textbf {G}}_{jl}\) got through Theorem 4 for Case 2 for \(a = 30\) and \(b = 3\)
Full size table
Table 4 \({\textbf {G}}_{jl}\) got through Theorem 4 for Case 3 for \(a = 90\) and \(b = 5\)
Full size table

To conduct simulations, the following settings are considered: \(\underline{\lambda }_1({\varsigma _1}(t))=\frac{\sin {(5{\varsigma _1}(t))}+1}{2}\) and \(\overline{\lambda }_1({\varsigma _1}(t))=1-\underline{\lambda }_1({\varsigma _1}(t))\), \(\underline{\lambda }_3({\varsigma _1}(t))=\frac{\cos {(5{\varsigma _1}(t))}+1}{2}\) and \(\overline{\lambda }_3({\varsigma _1}(t))=1-\underline{\lambda }_3({\varsigma _1}(t))\), the explicit definitions of \(\underline{\lambda }_2({\varsigma _1}(t))\) and \(\overline{\lambda }_2({\varsigma _1}(t))\) are no need to be given because \(\tilde{w}_1({\varsigma _1}(t))=\underline{\lambda }_1({\varsigma _1}(t))\underline{w}_1({\varsigma _1}(t))+\overline{\lambda }_1({\varsigma _1}(t))\) \(\overline{w}_1({\varsigma _1}(t))\), \(\tilde{w}_3({\varsigma _1}(t))=\underline{\lambda }_3({\varsigma _1}(t))\underline{w}_3({\varsigma _1}(t))+\overline{\lambda }_3({\varsigma _1}(t))\) \(\overline{w}_3({\varsigma _1}(t))\) as well as \(\tilde{w}_2({\varsigma _1}(t))=1-\tilde{w}_1({\varsigma _1}(t))-\tilde{w}_3({\varsigma _1}(t))\); \(\underline{\kappa }_j(\varsigma _1(t_k))\) and \(\overline{\kappa }_j(\varsigma _1(t_k))\) are both 0.5, for \(j=1\), 2.

Fig. 2
figure 2

Phase plots of \({\varsigma _1}(t)\) and \({\varsigma _2}(t)\) with Theorem 4. (Red curves: phase flows. Black circles: initial states. The black dot: the origin). (Color figure online)

Full size image
Fig. 3
figure 3

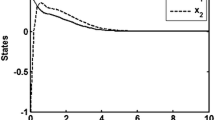
Time responses for Case 1 for \(a = 0\) and \(b = 0\) with Theorem 4

Full size image
Fig. 4
figure 4

Time responses for Case 2 for \(a = 30\) and \(b = 3\) with Theorem 4

Full size image
Fig. 5
figure 5

Time responses for Case 3 for \(a = 90\) and \(b = 5\) with Theorem 4

Full size image

Some stable points in Fig. 1 are chosen for further verification. For Case 1, \(a = 0\) and \(b = 0\) are chosen; through Theorem 4, we can obtain feedback gain matrices shown in Table 2. For Case 2, \(a = 30\) and \(b = 3\) are chosen; through Theorem 4, we can obtain feedback gain matrices shown in Table 3. For Case 3, \(a = 90\) and \(b = 5\) are chosen; through Theorem 4, we can obtain feedback gain matrices shown in Table 4. The phase plots of \({\varsigma _1}(t)\) and \({\varsigma _2}(t)\) for the three cases for specific a and b with Theorem 4 are shown in Fig. 2. As seen from Fig. 2, the curves for the three cases for specific a and b originating from 4 different initial states which are \(\left[ {\begin{array}{*{20}{c}} 10&10 \end{array}}\right] ^T\), \(\left[ {\begin{array}{*{20}{c}} -5&6 \end{array}}\right] ^T\), \(\left[ {\begin{array}{*{20}{c}} -8&-4 \end{array}}\right] ^T\) and \(\left[ {\begin{array}{*{20}{c}} 9&-7 \end{array}}\right] ^T\), all approach the origin. In addition, the time responses for the three cases for specific a and b with Theorem 4 are provided, where the initial states are \(\left[ {\begin{array}{*{20}{c}} 5.5&0 \end{array}}\right] ^T\). It can be found that the sampling intervals in Fig. 3b are the same, which is because there is only one domain for Case 1. Then, from Figs. 4b and 5b, the variation in sampling intervals can be intuitively viewed. Note that the sampling intervals between 0 and 0.02s are given in figures because the switching for Case 2 for \(a = 30\) and \(b = 3\), and the switching for Case 3 for \(a = 90\) and \(b = 5\), both happen in 0.02s.

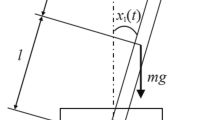
As seen from the simulation outcomes, the proposed method can be used to realize the control of the uncertain nonlinear plant depicted by the IT2 polynomial fuzzy model. It is well known that the most practical examples, such as the inverted pendulum [17], can be considered to be uncertain nonlinear plants, so the proposed method can be widely applied to practical examples, and achieve relaxed results.

5 Conclusion

The stability of an IT2SDPFMB control system with a switching control scheme has been studied. A switching IT2SD polynomial fuzzy controller consisting of several local IT2SD polynomial fuzzy controllers has been synthesized for control. For the support of the stability analysis, a looped-functional-based technique has been adopted. For solving the mismatch dilemma and improving design flexibility, the IPM concept has been leveraged. The state information, the information of IT2 MFs, as well as the switching control scheme, have been considered, resulting in relaxed stability conditions. The simulation outcomes have confirmed the efficacy of the proposed method.

In the future, the optimization of MFs will be considered based on the proposed method for the improvement of control performance.