Bifurcation analysis of bistable oscillator dynamics for human hair-cell bundle structures by mapping the Floquet multipliers

Abstract

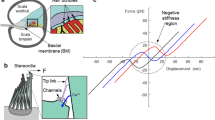
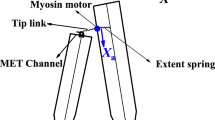
This study presents an initial study on the bifurcation analysis of bistable oscillator dynamics for human hair-cell bundle structures. The hair-cell bundles within the human cochlea possess highly nonlinear stiffness while sound transmission. To better understand this bistable oscillator dynamics, this study focused on the bifurcation phenomena using the Floquet theory. To define the bifurcations associated with super- and sub-harmonic resonances, the harmonic balance method (HBM) was first utilized with Hill’s method, for determining the dynamics stability conditions. In addition, the Floquet multipliers were mapped to examine their relationship with the bifurcation characteristics. To examine the bifurcation characteristics, only the Floquet multipliers associated with unstable conditions were selected because those associated with stable conditions were decaying terms. Then, the complex values of the Floquet multipliers at specific frequency locations were compared with the bifurcations’ characteristics. When numerically calculated bifurcations were compared with the results obtained using the HBM, mapping the Floquet multipliers was sufficient for predicting the bifurcations of a biomimetic system inspired by the hair-cell bundle structure. This study suggests practical techniques for employing the HBM with Hill’s method by mapping the Floquet multipliers to investigate complex nonlinearities that occur in bistable-stiffness systems.

Appendix A

Derivations of the Hill’s method.

Using Taylor’s expansion, the nonlinear terms can be simplified, as follows:

$$ \underline {{\bf{F}}_{\bf{S}} } \left( {\underline {{\bf{x}}_{{\bf{bs}}} } \left( t \right) + \underline {\bf{\xi }} \left( t \right)} \right) \cong \underline {{\bf{F}}_{\bf{S}} } \left( {\underline {{\bf{x}}_{{\bf{bs}}} } \left( t \right)} \right) + \left. {\frac{{\partial \underline {{\bf{F}}_{\bf{S}} } }}{{\partial \underline {\bf{x}} }}} \right|_{\underline {\bf{x}} = \underline {{\bf{x}}_{{\bf{bs}}} } } \underline {\bf{\xi }} \left( t \right) $$

(11)

By substituting Eq. (11) into Eq. (10), the overall equation can be summarized, as follows:

$$ \left[ {m\underline {\ddot{x}_{bs} } \left( t \right) + c\underline {\dot{x}_{bs} } \left( t \right) + \underline {F_S } \left( {\underline {x_{bs} } \left( t \right)} \right)} \right] - \underline {F_b } \left( t \right) + \left[ {m\underline {\ddot{\xi }} \left( t \right) + c\underline {\dot{\xi }} \left( t \right) + \left. {\frac{{\partial \underline {F_S } }}{{\partial \underline x }}} \right|_{\underline x = \underline {x_{bs} } } \underline \xi \left( t \right)} \right] = \underline 0 $$

(12)

In the above, the first term is $\left[ {m\underline {{\bf{\ddot{x}}}_{{\bf{bs}}} } \left( t \right) + c\underline {{\bf{\dot{x}}}_{{\bf{bs}}} } \left( t \right) + \underline {{\bf{F}}_{\bf{S}} } \left( {\underline {{\bf{x}}_{{\bf{bs}}} } \left( t \right)} \right)} \right] - \underline {{\bf{F}}_{\bf{b}} } \left( t \right) = \underline {\bf{0}}$, because it is the exact solution after the perturbation decays completely. The second term in Eq. (12) should be satisfied and the first and second derivatives of the perturbation $\underline {\bf{\xi }} \left( {\bf{t}} \right) = \underline {\bf{p}} \left( {\bf{t}} \right)e^{\lambda t}$ are obtained as $\underline{\dot{\xi }} \left( t \right) = \underline{\dot{p}} \left( t \right)e^{\lambda t} + \lambda \underline{p} \left( t \right)e^{\lambda t} t$ and $\underline {\ddot{\xi }} \left( t \right) = \underline {\ddot{p}} \left( t \right)e^{\lambda t} + 2\lambda \underline {\dot{p}} \left( t \right)e^{\lambda t} + \lambda ^2 \underline p \left( t \right)e^{\lambda t}$ respectively, and are substituted into the perturbation terms of Eq. (12), as follows:

$$ m\left[ {\underline {\ddot{p}} \left( t \right) + 2\lambda \underline {\dot{p}} \left( t \right) + \lambda ^2 \underline p \left( t \right)} \right]e^{\lambda t} + c\left[ {\underline {\dot{p}} \left( t \right) + \lambda \underline p \left( t \right)} \right]e^{\lambda t} + \left. {\frac{{\partial \underline {F_S } }}{{\partial \underline x }}} \right|_{\underline x = \underline {x_{bs} } } \underline p \left( t \right)e^{\lambda t} = \underline 0 $$

(13)

Based on Eqs. (4) and (5), $\underline {\bf{p}} \left( {\bf{t}} \right)$ can be expressed using the Galerkin scheme, by means of the Fourier transformation. Thus, let the series of the time history of $\underline {\bf{p}} \left( {\bf{t}} \right)$ be $\underline {\bf{p}} \left( {\bf{t}} \right) = \underline{\underline {\bf{\mathfrak{I}}}} \underline {{\bf{p}}_{\bf{c}} }$, $\underline {{\bf{\dot{p}}}} \left( {\bf{t}} \right) = \varpi \underline{\underline {\bf{\mathfrak{I}}}} \underline{\underline {\bf{D}}}^{\prime} \underline {{\bf{p}}_{\bf{c}} }$, and $\left. {\frac{{\partial \underline {F_S } }}{{\partial \underline x \left( {t_i } \right)}}} \right|$. Here, $\left. {\frac{{\partial \underline {{\bf{F}}_{\bf{S}} } }}{{\partial \underline {\bf{x}} }}} \right|_{\underline {\bf{x}} = \underline {{\bf{x}}_{{\bf{bs}}} } }$ is determined from the predictor and corrector concepts for each iteration using $\left. {\frac{{\partial \underline {{\bf{F}}_{\bf{S}} } }}{{\partial \underline {\bf{x}} \left( {t_i } \right)}}} \right|$(i = 0,1,···, j-2, j-1). Thus, Eq. (13) is organized with respect to λ by ignoring the common factor $\underline {{\bf{p}}_{\bf{c}} }$, as follows:

$$ \underline{\underline {\bf{\mathfrak{I}}}} \left[ {\lambda^2 m\underline{\underline {\bf{I}}} + \lambda \left( {2\varpi m\underline{\underline {\bf{D}}}^{\prime} + c\underline{\underline {\bf{I}}} } \right)} \right]{\bf{ + }}\underline{\underline {\bf{\mathfrak{I}}}} \left( { - \varpi^2 m\underline{\underline {\bf{D}}}^{{\prime} {\prime} } + \varpi c\underline{\underline {\bf{D}}}^{\prime} + \underline{\underline {\bf{\mathfrak{I}}}}^+ \frac{{\partial \underline {{\bf{F}}_{\bf{S}} } \left( {\bf{x}} \right)}}{{\partial \underline {\bf{x}} \left( t \right)}}\underline{\underline {\bf{\mathfrak{I}}}} } \right){\bf{ = }}\underline {\bf{0}} $$

(14)

Here, the pseudo-inverse matrix $\underline{\underline {\bf{\mathfrak{I}}}}^+$ is defined as . Because $\underline{\underline {\bf{\mathfrak{I}}}} \ne \underline{\underline {\bf{0}}}$, the eigenvalues λ_i are estimated using Eq. (14), as follows:

(15a,b)