Modeling and vibration analyzing of a double-beam system with a coupling nonlinear energy sink

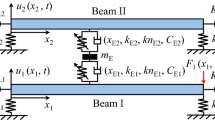
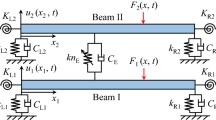
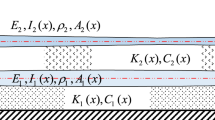
Abstract

Elastic beams are applied to various complex engineering structures in engineering fields. Unwanted vibration of elastic beams may cause some serious vibration problems for complex structures. The current studies mainly focus on the vibration control of the single-beam system by employing nonlinear energy sinks. Little literature combines the NES with nonlinear couplers, limiting the vibration control of the coupling beam system by employing nonlinearities. Motivated by the limitations of current studies, a type of coupling nonlinear energy sink (CNES) is proposed and the vibration prediction model of the double-beam system (DBS) with a coupling nonlinear energy sink (CNES) is established theoretically. After ensuring the correctness of numerical results, vibration responses of DBS with a CNES are deeply studied. According to the numerical analysis and discussion, it can be found that suitable parameters of CNES can effectively reduce the vibration of DBS without changing the vibration characteristics of DBS. Unsuitable parameters of CNES not only motivate complicated responses but also worsen the vibration reduction rate of DBS. Under complicated responses, the vibration kinetic energy of DBS and CNES presents the targeted energy transfer phenomenon at some time intervals. Furthermore, choosing suitable parameters of CNES to change within a certain range greatly influences the magnitude-frequency responses of DBS. Overall, the vibration of suB-beams can be simultaneously controlled by employing the CNES, presenting that installing CNES on DBS provides a feasible way to control the vibration of DBS.

Appendices

Appendix A

Vibration governing equations of the DBS with a CNES can be obtained by putting Eqs. (A-1) to (A-3) into Eq. (11).

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta T_{{{\text{System}}}} {\text{d}}t} = - \sum\limits_{i = 1}^{2} {\int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{i} }} {\rho_{i} S_{i} \frac{{\partial^{2} w_{i} }}{{\partial t^{2} }}{\text{d}}x_{i} \delta w_{i} } } {\text{d}}t} - \int_{{t_{1} }}^{{t_{2} }} {m_{{\text{N}}} \frac{{{\text{d}}^{2} u_{{\text{N}}} }}{{{\text{d}}t^{2} }}\delta u_{{\text{N}}} {\text{d}}t} $$

(A-1)

$$ \begin{gathered} \int_{{t_{1} }}^{{t_{2} }} {\delta V_{{{\text{System}}}} {\text{d}}t} = \sum\limits_{i = 1}^{2} {\int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{i} }} {E_{i} I_{i} } \frac{{\partial^{4} w_{i} }}{{\partial x_{i}^{4} }}\delta w_{i} {\text{d}}x_{i} {\text{d}}t} } \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array} + \sum\limits_{i = 1}^{2} {\int_{{t_{1} }}^{{t_{2} }} {\left[ \begin{gathered} - E_{i} I_{i} \frac{{\partial^{2} w_{i} \left( {0,t} \right)}}{{\partial x_{i}^{2} }}\delta \left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right) + E_{i} I_{i} \frac{{\partial^{3} w_{i} \left( {0,t} \right)}}{{\partial x_{i}^{3} }} \hfill \\ + E_{i} I_{i} \frac{{\partial^{2} w_{i} \left( {L_{i} ,t} \right)}}{{\partial x_{i}^{2} }}\delta \left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right) - E_{i} I_{i} \frac{{\partial^{3} w_{i} \left( {L_{i} ,t} \right)}}{{\partial x_{i}^{3} }} \hfill \\ \end{gathered} \right]{\text{d}}t} } \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array} + \sum\limits_{i = 1}^{2} {\int_{{t_{1} }}^{{t_{2} }} {\left[ \begin{gathered} k_{Li} w_{i} \left( {0,t} \right)\delta w_{i} + K_{Li} \frac{{\partial w_{i} \left( {0,t} \right)}}{{\partial x_{i} }}\delta \left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right) \hfill \\ + k_{{{\text{R}}i}} w_{i} \left( {L_{i} ,t} \right)\delta w_{i} + K_{{{\text{R}}i}} \frac{{\partial w_{i} \left( {L_{1} ,t} \right)}}{{\partial x_{i} }}\delta \left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right) \hfill \\ \end{gathered} \right]{\text{d}}t} } \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array} + \sum\limits_{n = 1}^{4} {\int_{{t_{1} }}^{{t_{2} }} {k_{{\text{E}}} \left[ {w_{1} \left( {x_{1n} ,t} \right) - w_{2} \left( {x_{2n} ,t} \right)} \right]\delta \left( {w_{1} - w_{2} } \right){\text{d}}t} } \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array} + \int_{{t_{1} }}^{{t_{2} }} {k_{{\text{N}}} \left[ {u_{{\text{N}}} - w_{1} \left( {x_{{{\text{1N}}}} ,t} \right)} \right]^{3} \delta w_{1} {\text{d}}t} + \int_{{t_{1} }}^{{t_{2} }} {k_{{\text{N}}} \left[ {u_{{\text{N}}} - w_{2} \left( {x_{{{\text{2N}}}} ,t} \right)} \right]^{3} } \delta w_{2} {\text{d}}t \hfill \\ \end{gathered} $$

(A-2)

$$ \begin{gathered} \int_{{t_{1} }}^{{t_{2} }} {\delta W_{{{\text{System}}}} {\text{d}}t} = \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{1} }} {G\left( {x_{1} - L_{1} } \right)F_{{0}} \sin \left( {\omega t} \right)\delta w_{1} } {\text{d}}x_{1} } {\text{d}}t - \sum\limits_{i = 1}^{2} {\int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{i} }} {C_{i} \frac{{\partial w_{i} }}{\partial t}} {\text{d}}x_{i} \delta w_{i} {\text{d}}t} } \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array} - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{1} }} {C_{{\text{N}}} \left[ {\frac{{{\text{d}}u_{{\text{N}}} }}{{{\text{d}}t}} - G\left( {x_{1} - x_{{{\text{1N}}}} } \right)\frac{{\partial w_{1} }}{\partial t}} \right]\delta \left( {u_{{\text{N}}} - w_{1} } \right)} {\text{d}}x_{1} {\text{d}}t} \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array} - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{2} }} {C_{{\text{N}}} \left[ {\frac{{{\text{d}}u_{{\text{N}}} }}{{{\text{d}}t}} - G\left( {x_{2} - x_{{{\text{2N}}}} } \right)\frac{{\partial w_{2} }}{\partial t}} \right]\delta \left( {u_{{\text{N}}} - w_{2} } \right)} {\text{d}}x_{2} {\text{d}}t} \hfill \\ \end{gathered} $$

(A-3)

Appendix B

For HBM, the aimed equations and flexible displacements are the same as those of the GTM. The unknown time terms are set as,

$$ q_{1z} \left( t \right) = C_{{1{\text{z}}}} \sin \left( {\omega t} \right) + C_{{2{\text{z}}}} \cos \left( {\omega t} \right) + C_{{3{\text{z}}}} \sin \left( {3\omega t} \right) + C_{{4{\text{z}}}} \cos \left( {3\omega t} \right) $$

(B-1)

$$ q_{2m} \left( t \right) = D_{1m} \sin \left( {\omega t} \right) + D_{2m} \cos \left( {\omega t} \right) + D_{3m} \sin \left( {3\omega t} \right) + D_{4m} \cos \left( {3\omega t} \right) $$

(B-2)

and

$$ u_{{\text{N}}} \left( t \right) = X_{1} \sin \left( {\omega t} \right) + X_{2} \cos \left( {\omega t} \right) + X_{3} \sin \left( {3\omega t} \right) + X_{4} \cos \left( {3\omega t} \right) $$

(B-3)

where C_1z, C_2z, C_3z, C_4z, D_1m, D_2m, D_3m, D_4m, X₁, X₂, X₃, and X₄ are the unknown coefficients. Putting Eqs. (B-1), (B-2), (B-3) into Eq. (17), the equations related to the unknown coefficients are established. The unknown coefficients can be obtained by using the arc-length method to solve the corresponding equations. After obtaining the unknown coefficients, and putting them into Eq. (15), the vibration responses of DBS with a CNES can be obtained.

For LM, according to the energy expressions derived in Sect. 2.2, the Lagrange term of DBS with a CNES is derived as,

$$ L = T_{{{\text{System}}}} - V_{{{\text{System}}}} $$

(B-4)

The virtual external work (δW_System) acting on the vibration system is derived as,

$$ \delta{W}_{{{\text{System}}}} = \delta{W}_{{\text{V}}} + \delta{W}_{{{\text{DBS}}}} + \delta{W}_{{{\text{CNES}}}} $$

(B-5)

Then, the flexible vibration displacements of DBS are reformed into the following forms

$$ w_{1} \left( {x_{1} ,t} \right) = {\mathbf{\varphi }}_{1} \cdot {\mathbf{q}}_{1} $$

(B-9)

and

$$ w_{2} \left( {x_{2} ,t} \right) = {\mathbf{\varphi }}_{2} \cdot {\mathbf{q}}_{2} $$

(B-7)

where each term is shown in Eqs. (B-6) and (B-7) are listed in the following,

$$ {\mathbf{\varphi }}_{1} = \left[ {\begin{array}{*{20}c} {\varphi_{11} } & {...} & {\varphi_{1z} } & {...} & {\varphi_{{{\text{1Z}}}} } \\ \end{array} } \right] $$

(B-8)

$$ {\mathbf{\varphi }}_{2} = \left[ {\begin{array}{*{20}c} {\varphi_{21} } & {...} & {\varphi_{2m} } & {...} & {\varphi_{{{\text{2M}}}} } \\ \end{array} } \right] $$

(B-9)

$$ {\mathbf{q}}_{1} = \left[ {\begin{array}{*{20}c} {q_{11} } & {...} & {q_{1z} } & {...} & {q_{{{\text{1Z}}}} } \\ \end{array} } \right]^{{\text{T}}} $$

(B-10)

and

$$ {\mathbf{q}}_{2} = \left[ {\begin{array}{*{20}c} {q_{21} } & {...} & {q_{2m} } & {...} & {q_{{{\text{2M}}}} } \\ \end{array} } \right]^{{\text{T}}} $$

(B-11)

To unified describe the displacement of the vibration system, the motion displacement of CNES is rewritten as,

$$ {\mathbf{q}}_{3} = \left[ {u_{{\text{N}}} } \right]^{{\text{T}}} $$

(B-12)

After substituting Eqs. (B-6) and (B-7) into Eqs. (B-4) and (B-5), using the next step, the Lagrange function of DBS with a CNES can be established.

$$ \frac{\partial }{\partial t}\left( {\frac{{\partial L_{{{\text{System}}}} }}{{\partial {\dot{\mathbf{q}}}_{i} }}} \right) - \frac{{\partial L_{{{\text{System}}}} }}{{\partial {\mathbf{q}}_{i} }} = {\mathbf{Q}}_{i} $$

(B-13)

where Q_i is the generalized force column vector. By solving the corresponding Lagrange function, unknown time coefficients of displacements belonging to DBS with a CNES can be obtained. Putting the obtained time coefficients into Eq. (15), vibration responses of DBS with a CNES are obtained.