1 Introduction

Cobweb models belong to the oldest and most studied contributions to the theory of mathematical economic dynamics. In general, these models describe a dynamic price adjustment process on a competitive market for a single nonstorable commodity with a supply response lag of one period, requiring firms to form price expectations. Classical cobweb models such as Ricci [29], Tinbergen [34] and Schultz [31] assume that firms have naïve price expectations, i.e. they expect the commodity price to remain constant. As a result, the dynamics of classical cobweb models is due to one-dimensional maps. Leontief [22] demonstrates that the stability of the fixed point of such types of cobweb models depends on the slopes of their supply and demand schedules. In particular, he shows that their ratio, defined as parameter s in our paper, has to be smaller than one in modulus at the fixed point. When the fixed point is stable, the negative expectations feedback structure of cobweb models implies that commodity prices approach their fixed point in a zigzag pattern. When the fixed point loses its stability via a flip bifurcation – the dominant bifurcation scenario in nonlinear cobweb models – the resulting period-two commodity price cycle again describes a zigzag pattern. Moreover, chaotic commodity price dynamics may then arise via a cascade of period doubling bifurcations.

Against this background, Goodwin ([16], pp. 191–192) concludes that “The producer in a market with a commodity cycle is always tending to get the worst of it; he has little to sell when prices are high and much when they are low (naturally, since that is what makes them low). For these and other reasons producers may cease to take current prices as expected prices, especially if the duration of the cycle is short”. Moreover, he continues with the observation that “Expectations present a difficult task for economic analysis because there are so many possibilities and little information about their actual behavior. Both expediency and realism suggest the investigation of a very simple type”. Therefore, in his paper he introduces a contrarian expectation rule according to which firms expect the price of the commodity to reverse its current direction, stressing that this is “sensible since it fits the nature of cycles”.

While our cobweb model rests on Goodwin’s [16] main hypothesis, we consider that firms rely on a more sophisticated contrarian-type expectation rule, albeit leading to a very simple model. The key elements of our cobweb model may be sketched as follows. Since the commodity is nonstorable, its price adjusts such that consumers’ demand for the commodity is equal to firms’ supply of the commodity. Consumers’ demand function is linear and depends negatively on the current commodity price. Firms’ supply function is also linear but depends positively on the firms’ commodity price expectations. In this paper, we assume that firms use a regime-switching expectation rule that combines contrarian and naïve elements. As long as the commodity price is relatively stable, firms believe that the commodity price will remain constant. However, firms expect the commodity price to fall by a certain amount if the commodity price rises sharply and to rise by a certain amount if the commodity price falls sharply. Consequently, the dynamics of our cobweb model is driven by a two-dimensional piecewise linear discontinuous map. Since the study of such maps is relatively new – despite their ability to generate intriguing dynamics – the main goal of our paper is to contribute to this line of research.

The peculiarity of our map is that it is described by three different functions with the same Jacobian matrix, having one negative eigenvalue, given by \(-s\), and one eigenvalue equal to 0. This kind of map has \(\omega -\)limit sets that belong to critical lines. Sometimes this simplifies the analysis, since it may be possible to define a one-dimensional map, obtained as a first return on some critical set, that represents the dynamics of the system. The main role in the study of the possible bifurcations leading to different dynamics is related to bifurcations involving the discontinuity lines of the map. The existence of coexisting attracting cycles, in the stable regime (\(0<s<1\)), is determined via border collision bifurcationsFootnote 1 (BCB for short), which occur when a periodic point of a cycle has a contact with a discontinuity point on a critical line. We shall prove that when the attracting basic fixed point is not globally attracting, at most three different attracting cycles can coexist with it. At \(s=1\), the degenerate flip bifurcation of the fixed point leads to a drastic change, from a few coexisting attracting cycles to only saddle cycles and chaotic attractors consisting of intervals. In the unstable regime of the fixed point (\(s>1\)) a chaotic attractor must involve at least one discontinuity point, and this property leads to acyclic chaotic intervals (i.e. a chaotic attractor consisting of k disjoint intervals is not invariant for the \(k-th\) iterate of the map). Moreover, the boundaries of the chaotic intervals belonging to a chaotic attractor are critical points obtained from the images of the involved discontinuity points, via the functions defined on the two sides of the discontinuity line to which they belong. As a consequence, the merging bifurcations of chaotic attractors always involve some critical points.

Since our paper is related to the study of cobweb models and the analysis of piecewise linear maps, let us briefly discuss some related works. Cobweb models have served as a workhorse to investigate a number of crucial economic ideas over the last 100 years. For instance, Goodwin [16], Nerlove [27] and Muth [26] introduced the concepts of extrapolative, adaptive and rational expectation rules, respectively, starting a revolution in economic theory. With the advent of chaos theory, e.g. Lorenz [24], Li and Yorke [23] and May [25], papers by Artstein [2], Jensen and Urban [20], Chiarella [5] and [18] showed that nonlinear cobweb models may give rise to quite irregular commodity price dynamics. Within the cobweb model by Brock and Hommes [4], firms switching between naïve and rational expectation rules may yield chaotic commodity price dynamics. Further papers that investigate learning in cobweb models include Goeree and Hommes [15], Lasselle et al. [21] and Schmitt and Westerhoff [30]. Dieci and Westerhoff [6] explore the behavior of interacting cobweb markets, while Dieci et al. [7] consider that firms may face larger production lags. See Ezekiel [9], Waugh [35], Gandolfo [10] and Hommes [19] for surveys.

Our system is piecewise linear and discontinuous. It is worth mentioning that the study of the dynamics and bifurcations occurring in two-dimensional piecewise smooth and piecewise linear discontinuous maps is a fairly new research topic, and only a few papers have been published on the subject. We have recently published some works, Gardini et al. [11,12,13], where we study economic models that, like our cobweb model, correspond to this class of maps. However, in these papers we focus on positive expectations feedback systems, while our current cobweb model is a negative expectations feedback system. In fact, the governing systems are different and lead to different kinds of dynamics and bifurcations. Besides these works, we can mention Dutta et al. [8], Gu and Guo [17], Simpson [32] and Anufriev et al. [1]. In these works, the discontinuity line in the \(\left( x,y\right) \) phase plane is at \(x=0.\) It is worth noting that the systems there investigated have dynamic properties that are quite different from those of the discontinuous maps resulting from the mentioned economic applications, and also differ from the one here investigated, where the discontinuity line or lines are parallel to the line \(x=y\). These two classes of maps are not topologically conjugate.

We continue as follows. In Sec. 2, we propose a novel cobweb model represented by a two-dimensional piecewise linear discontinuous map. In Sec. 3, we present some preliminary properties of our system, showing that after one iteration the trajectories belong to at most three critical lines. The dynamics occurring in the regular domain where the basic fixed point is locally stable (\(0<s<1\)) are described in Sec. 4, where we detect all the BCBs related to attracting cycles coexisting with the basic fixed point. We determine when the fixed point is globally attracting and when its basin of attraction consists of a simple quadrilateral region. In this section, we also analytically describe a few one-dimensional first return maps, which are useful in the analysis of the dynamic behaviors performed in Sec. 5 and Sec. 6. The dynamics at the bifurcation value \(s=1\) are considered in Sec. 5. We prove that there are segments filled with 2-cycles and 4-cycles with different symbolic sequences, and that any point outside such segments is mapped into a periodic point of one of these cycles in a finite number of iterations. Sec. 6 addresses the chaotic domain, where the basic fixed point is unstable (\(s>1\)). We highlight the particular role of a saddle 2-cycle, whose stable set bounds the region of points having divergent trajectories. When the saddle 2-cycle is not homoclinic, chaotic attractors consisting of acyclic segments exist - one unique or two symmetric. Moreover, the transition from chaotic attractors to chaotic repellors can occur via four different kinds of homoclinic bifurcations of the saddle 2-cycle, all of which are analytically determined in this section. Some conclusions are drawn in Sec. 7.

2 A piecewise linear cobweb model

Cobweb models describe the price dynamics of a nonstorable commodity on a competitive market that to produce takes time. Due to the supply response lag, firms must form price expectations. We assume a supply response lag of one period. Hence, in period \(t-1\), firms have to predict the commodity price for the market that operates in period t. We express firms’ commodity supply as

$$\begin{aligned} S_{t} = c P_{t}^{e} \end{aligned}$$
(1)

Since c is a positive supply parameter, firms’ commodity supply depends positively on their one-period-ahead price expectations, denoted by \(P_{t}^{e}\). Consumers’ commodity demand reads as

$$\begin{aligned} D_{t}=a-bP_{t} \end{aligned}$$
(2)

where a and b are two positive demand parameters. Accordingly, consumers’ commodity demand depends negatively on the current commodity price \(P_{t}\). The market clearing condition

$$\begin{aligned} D_{t}=S_{t} \end{aligned}$$
(3)

yields

$$\begin{aligned} P_{t}=\left( a-cP_{t}^{e}\right) /b \end{aligned}$$
(4)

Note that the commodity price hinges negatively on firms’ commodity price expectations, which is why cobweb models are negative expectations feedback systems.

Motivated by Goodwin [16], we assume that firms rely on a contrarian-type of expectation rule. In this paper, we assume that firms’ commodity price predictions result from the regime-switching expectation rule

$$\begin{aligned} P_{t}^{e}=\left\{ \begin{array}{lll} P_{t-1}-d &{} \quad \text {if} \quad &{} P_{t-1}-P_{t-2}>h\\ P_{t-1} &{} \quad \text {if} \quad &{} -h\le P_{t-1}-P_{t-2}\le h\\ P_{t-1}+d &{} \quad \text {if} \quad &{} P_{t-1}-P_{t-2}<-h \end{array} \right. \end{aligned}$$
(5)

which includes a no-change regime, or persistence regime, dependent on the value of parameter \(h>0\). That is, as long as the commodity price is relatively stable, firms have naïve expectations. However, firms expect the commodity price to decrease by a certain amount when the current commodity price trend exceeds parameter h, while they expect the commodity price to increase by a certain amount when the current commodity price trend falls short of threshold \(-h\). Clearly, firms only expect a price reversal in the presence of strong commodity price changes. In contrast to Goodwin [16], the expected price change is not proportional to the past price change, but determined by parameter \(d>0\). Moreover, Goodwin [16] considers a simple linear expectation rule, while we consider a more sophisticated regime-switching expectation rule.

Combining (4) and (5) reveals that the commodity price obeys

$$\begin{aligned} P_{t}=\left\{ \begin{array}{lll} -\frac{c}{b}P_{t-1}+\frac{a+cd}{b} &{} \quad \text {if} \quad &{} P_{t-1}-P_{t-2}>h \\ -\frac{c}{b}P_{t-1}+\frac{a}{b} &{} \quad \text {if} \quad &{} -h\le P_{t-1}-P_{t-2}\le h \\ -\frac{c}{b}P_{t-1}+\frac{a-cd}{b} &{} \quad \text {if} \quad &{} P_{t-1}-P_{t-2}<-h \end{array} \right. \nonumber \\ \end{aligned}$$
(6)

Before we continue, it is instructive to consider a well-known benchmark scenario. Classical cobweb models assume that firms always have naïve price expectations, i.e. \(P_{t}^{e}=P_{t-1}\). Then, from (4), the commodity price evolves according to:

$$\begin{aligned} P_{t}=\frac{a-cP_{t-1}}{b} \end{aligned}$$
(7)

Note that (7) is equivalent to the inner branch of (6). As already pointed out by Leontief [22], the stability of the fixed point

$$\begin{aligned} P^{*}=\frac{a}{b+c} \end{aligned}$$
(8)

of the classical (linear) cobweb model depends on the relationship between the slopes of firms’ supply and consumers’ demand schedules. Obviously, there are two generic scenarios. For \(s=c/b<1\), the commodity price approaches \(P^{*}\) in a zigzag manner. For \(s=c/b>1\), the commodity price describes a zigzag explosion path.

For our purpose, it is convenient to formulate our cobweb model in deviations from the fixed point of the classical (linear) cobweb model. Since parameters c and b are only involved in their ratio, it is convenient to use the aggregate parameter \(s=c/b\). Hence, defining

$$\begin{aligned} x_{t}=P_{t}-P^{*}\text {,}\quad s=\frac{c}{b} \end{aligned}$$
(9)

our cobweb model becomes

$$\begin{aligned} x_{t}=\left\{ \begin{array}{lll} -sx_{t-1}+sd &{} \quad \text {if} \quad &{} x_{t-1}-x_{t-2}>h \\ -sx_{t-1} &{} \quad \text {if} \quad &{} -h\le x_{t-1}-x_{t-2}\le h\\ -sx_{t-1}-sd &{} \quad \text {if} \quad &{} x_{t-1}-x_{t-2}<-h \end{array} \right. \nonumber \\ \end{aligned}$$
(10)

where the fixed point of the classical cobweb model is set to \(x_{t}=P_{t}-P^{*}=0\). Furthermore, introducing the auxiliary variable \(y_{t-1}=x_{t-2}\), we obtain a two-dimensional piecewise linear discontinuous map T, governing the dynamics of our cobweb model:

$$\begin{aligned} \left\{ \begin{array}{lll} x_{t} &{} = &{} \left\{ \begin{array}{lll} -sx_{t-1}+sd &{} \quad \text {if} \quad &{} x_{t-1}-y_{t-1}>h \\ -sx_{t-1} &{} \quad \text {if} \quad &{} -h\le x_{t-1}-y_{t-1}\le h \\ -sx_{t-1}-sd &{} \quad \text {if} \quad &{} x_{t-1}-y_{t-1}<-h \end{array} \right. \\ y_{t} &{} = &{} x_{t-1} \end{array} \right. \nonumber \\ \end{aligned}$$
(11)

Here, \(x_{t}\) linearly depends on \(x_{t-1}\) with negative slope (\(-s\)), and there are different offsets, depending on the difference \(\left( x_{t-1}-x_{t-2}\right) =\left( x_{t-1}-y_{t-1}\right) \). In the phase plane \(\left( x,y\right) \), we can introduce the unit time advancement operator \(\left( x^{\prime },y^{\prime }\right) =T\left( x,y\right) \), stating

$$\begin{aligned} T:\left\{ \begin{array}{lll} x^{\prime } &{} = &{} \left\{ \begin{array}{lllll} f_{L}\left( x\right) &{} = &{} -sx+sd &{} \quad \text {if} \quad &{} y<x-h \\ f_{M}\left( x\right) &{} = &{} -sx &{} \quad \text {if} \quad &{} x-h\le y\le x+h\\ f_{U}\left( x\right) &{} = &{} -sx-sd &{} \quad \text {if} \quad &{} y>x+h \end{array} \right. \\ y^{\prime } &{} = &{} x \end{array} \right. \nonumber \\ \end{aligned}$$
(12)

We define three different partitions of the \(\left( x,y\right) \) plane for map T as regions \(D_{L}\), \(D_{M}\) and \(D_{U}\), where the definition of map T is different. We label the lower function \(T_{L}\) because it acts below the straight line \(y=x-h\), and the upper function \(T_{U}\) because it acts above the straight line \(y=x+h\). Function \(T_{M}\), representing the classical (linear) cobweb model, with the equilibrium point in the origin, acts in the middle partition. Hence, map T is given by

$$\begin{aligned} T\left( x,y\right) =\left\{ \begin{array}{lllll} T_{L}\left( x,y\right) &{} = &{} \left( -sx+sd,x\right) &{} \quad \text {if} \quad &{} \left( x,y\right) \in D_{L}=\left\{ \left( x,y\right) |\ y<x-h\right\} \\ T_{M}\left( x,y\right) &{} = &{} \left( -sx,x\right) &{} \quad \text {if} \quad &{} \left( x,y\right) \in D_{M}=\left\{ \left( x,y\right) |\ x-h\le y\le x+h\right\} \\ T_{U}\left( x,y\right) &{} = &{} \left( -sx-sd,x\right) &{} \quad \text {if} \quad &{} \left( x,y\right) \in D_{U}=\left\{ \left( x,y\right) |\ y>x+h\right\} \end{array} \right. \end{aligned}$$
(13)

3 Preliminary properties and remarks

The three parameters of map T in (13) - s, d and h - are positive. Moreover, one of the two parameters d and h can be considered as a scaling factor. For example, defining \(x:=\frac{x}{h}\), \(y:=\frac{y}{h}\), \(d:=\frac{d}{h}\), we can set \(h=1\). However, to better interpret the results in the applied context, we prefer to explicitly include the two parameters in the formulas, although we use \(h=1\) in the numerics.

The fixed point in the middle partition,Footnote 2 denoted by \(O=\left( 0,0\right) \), is the only real fixed point of map T, since the two additional fixed points of the linear functions \(T_{L/U}\), which are applied in the lower and upper partitions, \(L^{*}=\left( P_{L}^{*},P_{L}^{*}\right) =\left( \frac{ds}{1+s},\frac{ds}{1+s}\right) \) and \(U^{*}=\left( P_{U}^{*},P_{U}^{*}\right) =\left( -\frac{ds}{1+s},-\frac{ds}{1+s}\right) \), belong to the main diagonal in the middle partition, and are always virtual.Footnote 3 Since in the middle partition \(D_{M}\) the map is defined by \(T_{M}\), the virtual fixed points cannot be reached by a trajectory applying the functions \(T_{L/U}\).

The Jacobian matrix

$$\begin{aligned} J=\left( \begin{array}{cc} -s &{} 0\\ 1 &{} 0 \end{array} \right) \end{aligned}$$
(14)

is the same in all points of the phase plane \(\left( x,y\right) \), except for the two discontinuity lines \(y=x-h\), denoted \(LC_{(-1)L}\), and \(y=x+h\), denoted \(LC_{(-1)U}\). The eigenvalues of J are always real and are given by 0 and \(-s\).

Due to the eigenvalue 0, each partition is mapped to a single line in one iteration. In fact, any point \(\left( x_{0},y\right) \) of a vertical segment of the lower partition \(D_{L}\) is mapped to the point \(\left( -sx_{0}-sd,x_{0}\right) \) that does not depend on y, belonging to the critical line \(LC_{L}\) of equation \(y=-\frac{1}{s}x+d\). Similarly, any point \(\left( x_{0},y\right) \) of a vertical segment of the upper partition \(D_{U}\) is mapped to the point \(\left( -sx_{0}+sd,x_{0}\right) \) belonging to the critical line \(LC_{U}\) of equation \(y=-\frac{1}{s}x-d\). The region in the middle partition of the \(\left( x,y\right) \) phase plane is mapped to the critical line \(LC_{M}\) of equation \(y=-\frac{1}{s}x\), since any point \(\left( x_{0},y\right) \) of a vertical segment of \(D_{M}\) is mapped to the point \(\left( -sx_{0},x_{0}\right) \).

The two straight lines \(LC_{(-1)L/U}\) (\(y=x\mp h\)), where the map is discontinuous, are responsible for border collision bifurcations, leading to the appearance/disappearance of cycles. Moreover, the three lines \(LC_{U}\), \(LC_{M}\) and \(LC_{L}\) identified above, i.e.

$$\begin{aligned} \begin{array}{lll} LC_{L}: \ \ y &{} = &{} -\frac{1}{s}x+d\\ \\ LC_{M}: \ \ y &{} = &{} -\frac{1}{s}x\\ \\ LC_{U}: \ \ y &{} = &{} -\frac{1}{s}x-d\\ \end{array} \end{aligned}$$
(15)

include each a real or virtual fixed point, and all have the same direction of the eigenvector of the matrix J corresponding to the eigenvalue \(-s\), and include the images of the three partitions after one iteration of map T. This implies that the asymptotic states (\(\omega -\)limit sets) of the map must belong to the three lines \(LC_{U}\), \(LC_{M}\) and \(LC_{L}\). In particular, it follows that all periodic points, as well as any other invariant set,Footnote 4 must belong to these three lines, and the border collision bifurcations must be associated with the discontinuity points belonging to the critical lines in (15).

As it is usual in the study of piecewise smooth and piecewise linear maps, the symbolic sequence of a trajectory, and in particular of a cycle, may be defined via the symbols L, M, U, which represent the three different partitions to which a point belongs. That is, the trajectory of a point may be represented by a sequence of symbols \(\sigma _{0}\sigma _{1}\sigma _{2}\sigma _{3}\sigma _{4}...\), where \(\sigma _{i}\in \left\{ L,M,U\right\} \) is determined depending on the partition to which the point belongs.

It is easy to see that map T in (12)-(13) satisfies \(T\left( -x,-y\right) =-T\left( x,y\right) \), implying that the dynamics of the map are symmetric with respect to the origin. Hence, an invariant set \(\mathcal {A}\) is either symmetric with respect to the fixed point O, or the symmetric one with respect to O, say \(\mathcal {A}^{\prime }\), also exists.

When the fixed point O coexists with other attracting cycles, the related basins of attraction are bounded by segments of the discontinuity lines, as well as segments of vertical lines issuing from the preimages of the discontinuity points on the critical lines (i.e. the intersection points of the critical lines with the discontinuity lines). This is a consequence of the fact that the map is piecewise linear, and that one eigenvalue is 0. Similarly, the stable set of a saddle cycle consists of segments belonging to the vertical lines issuing from the \(x-\)coordinates of the points of the cycle and \(x-\)coordinates of the related preimages.

As we will see, for \(0<s<1\), all existing cycles are stable nodes, and the attracting fixed point O may coexist with other attracting cycles (at most with three cycles). For \(s=1\), all points that differ from O are mapped into a point of a 2-cycle or (for \(d>h\)) into a point of a 4-cycle, stable but not attracting, which may have different symbolic sequences. For \(s>1\), all existing cycles are saddles. In particular, a saddle 2-cycle appears at the bifurcation occurring at \(s=1\), and chaotic attractors consisting of acyclical intervals may exist if and only if the saddle 2-cycle is not homoclinic, while the region of divergent trajectories is bounded by the stable set of the saddle 2-cycle. The saddle 2-cycle does not always exist for \(s>1\); we will see that it disappears via a BCB.

The three different regimes that depend on the eigenvalue \(-s\) are described in detail in the next three sections.

We close the present section by noting that the limiting case \(h=0\) is considered in Gardini et al. [14]. Assuming \(h=0\), map T in (12)-(13) is essentially defined in two partitions only, since the middle partition reduces to the main diagonal. As a result, also the real fixed point is never attracting, nor are the other two virtual fixed points. The following main differences can be remarked. For \(0<s<1\), the model with \(h=0\) has only a globally attracting 4-cycle, while for \(h>0\), the middle partition always has an attracting fixed point that may be globally attracting, or coexisting with at most three different attracting cycles, as described in the next section. For \(s>1\), chaotic dynamics may occur in both models, although the chaotic sets of the model with \(h>0\) seem more interesting. This is because trajectories may jump very close to the real fixed point O and then depart in oscillating dynamic behaviors. From the dynamical point of view, while for \(h=0\) the homoclinic bifurcation of the saddle 2-cycle is of one type only, now the saddle 2-cycle may not exist or, when it does exist, it may become homoclinic with four different types of bifurcations, as shown in Sec. 6.

4 Stability regime \(\mathbf {0<s<1}\)

According to Leontief [22], the fixed point of classical nonlinear (linear) cobweb models is locally (globally) stable when parameter s belongs to the range \(\left( 0,1\right) \). For our cobweb model, however, all three linear maps are contractions and, in particular, the real fixed point \(O=\left( 0,0\right) \), is either globally attracting or coexisting with other attracting cycles. Examples are shown in Fig. 1. This figure shows that when there are coexisting attracting cycles, the related basins of attraction are separated by segments of the discontinuity lines \(y=x\pm h\) and vertical segments associated with the preimages of the discontinuity points on the critical lines.

Fig. 1
figure 1

Attracting cycles and related basins of attraction in the \(\left( x,y\right) \) phase plane. In yellow the basin of the fixed point O, in green the basin of the 4-cycle MLMU,  in azure the basin of the 4-cycle LLUU, in pink the basin of the 6-cycle MLLMUU. Parameter setting: \(h=1\), \(d=3.5\) and in a \(s=0.3\), in b \(s=0.9\), in c \(s=0.75\)

Full size image

When the fixed point O is globally attracting, then its basin is the whole \(\left( x,y\right) \) phase plane. When some attracting cycles coexist with the fixed point O, the vertical segments of the basin boundaries of O are related to the points of the discontinuity lines that intersect the critical line \(LC_{M}\). The two discontinuity lines \(y=x\pm h\) intersect the critical line \(LC_{M}\) at two symmetric points \(C_{\pm }\) at \(x=\mp \frac{hs}{1+s}\) (that is, \(C_{\pm }=\left( \mp \frac{hs}{1+s},\pm \frac{h}{1+s}\right) \)), whose rank-1 preimages by map \(T_{M}^{-1}\) lead to the vertical segments at \(x=\pm \frac{h}{1+s}\). It follows that if the basin of the origin consists only of a quadrilateral region (as in Fig. 1b,c), then the lateral boundaries are given by the vertical segments in the middle partition \(D_{M}\) at \(x=\pm \frac{h}{1+s}\). If the basin of the fixed point O is larger, these two segments still belong to the boundary, i.e. the rectangular region in the middle partition belongs to the basin of O, and other rectangles also exist belonging to the three partitions issuing from values of x obtained from further preimages (as in Fig. 1a).

Note that when the critical lines \(LC_{U/L}\) do not have points converging to the fixed point O (as in Fig. 1b,c), the dynamics of the map related to trajectories not convergent to O may also be investigated via the first return map on one of the critical lines \(LC_{U/L}\). The expression and shape of the first return map generally depend on the parameters. We shall return to this aspect below, since it is useful for the analysis of some bifurcations.

Let us define points A and B as the intersections of line \(LC_{L}\) with the discontinuity lines \(y=x+h\) and \(y=x-h\), respectively. These points have \(x-\)coordinates \(x_{A}=\frac{s\left( d-h\right) }{1+s}\) and \(x_{B}=\frac{s\left( d+h\right) }{1+s}\), so that

$$\begin{aligned} A= & {} \left( x_{A},y_{A}\right) =\left( \frac{s\left( d-h\right) }{1+s},-\frac{\left( d-h\right) }{1+s}+d\right) ,\nonumber \\ B= & {} \left( x_{B},y_{B}\right) =\left( \frac{s\left( d+h\right) }{1+s},-\frac{\left( d+h\right) }{1+s}+d\right) \end{aligned}$$
(16)

The two points that are symmetric to A and B with respect to the origin, say \(B^{\prime }=\left( -x_{B},-y_{B}\right) \) and \(A^{\prime }=\left( -x_{A},-y_{A}\right) \), are the intersections of line \(LC_{U}\) with the discontinuity lines \(y=x+h\) and \(y=x-h\), respectively. Let us now prove the following.

Proposition 1

Let \(0<s<1\), then

  1. (i)

    for \(d\ge \frac{h\left( 1+s\right) }{s}\), the total basin of the fixed point O is the parallelogram in the middle partition with vertical segments in the points with \(x=\pm \frac{h}{1+s}\);

  2. (ii)

    at most three different attracting cycles coexist with the attracting fixed point O. These cycles have symbolic sequences LLUU, MLMU and MLLMUU;

  3. (iii)

    for \(0<d\le h\), the fixed point O is globally attracting.

Proof of Proposition 1

(i) The vertical segment in the middle partition at \(x=\frac{h}{1+s}\) (bounding the immediate basin of the fixed point O on its right side) may be on the left side of the vertical line with \(x=x_{A}\) or on its right side. For \(\frac{h}{1+s}>\frac{s(d-h)}{1+s}\) (which occurs for \(d<\frac{h(1+s)}{s}\)), the vertical segment bounding the immediate basin of the fixed point O also has points at the right side of the critical line \(LC_{L}\). Therefore, there exist other preimages (via the inverse \(T_{L}^{-1}\)) of such points, leading to regions belonging to the basin of O, and further preimages may also exist. Differently, when \(d\ge \frac{h(1+s)}{s}\), the basin of the fixed point O has no other points outside the parallelogram in the middle partition \(D_{M}\) bounded by segments with \(x=\pm \frac{h}{1+s}\).

(ii) In order to see how many cycles can coexist with the fixed point O, let us remark that all possible existing cycles must have one or two points on the critical lines \(LC_{U/L}\). Thus, due to the symmetry, it is enough to consider just one line, say \(LC_{U}\). There are two discontinuity points on that line, \(B^{\prime }\) and \(A^{\prime }\), which bound the interval to which map \(T_{M}\) is applied; and a cycle with M in the symbolic sequence must have at least one point in that segment. Since the border collisions must occur with \(B^{\prime }\) or \(A^{\prime }\), it follows that at most two cycles can coexist with this type of symbolic sequence.

If a cycle does not have M in the symbolic sequence, then at least two letters UL must exist in the symbolic sequence. Considering the preimage of \(A^{\prime }\) with \(T_{U}^{-1}\left( A^{\prime }\right) \), we have the \(x-\)coordinate \(x_{a}=-\frac{h+ds}{1+s}<-x_{B}=-\frac{s(d+h)}{1+s}\) (since the eigenvalue is \(-s\) with \(0<s<1\)). When a periodic point belongs to the upper part of \(LC_{U}\), in \(D_{U}\), it is necessarily mapped on \(LC_{U}\) into the lower one, in \(D_{L}\), closer to the border \(A^{\prime }\) of the region, and its BCB can occur only via point \(A^{\prime }\) (put differently, a periodic point from the upper region \(D_{U}\) of \(LC_{U}\) approaching the border \(B^{\prime }\) is necessarily mapped into the middle partition \(D_{M}\)). It follows that only one attracting cycle with the symbolic sequence UL can exist, and at least two periodic points belong to \(LC_{U}\). Now let us consider a periodic point on \(LC_{U}\cap D_{U}\) that is mapped by \(T_{U}\) into a periodic point on \(LC_{U}\cap D_{L}\). Map \(T_{L}\) must be applied to this point and since \(s<1\) it necessarily leads to a point on \(LC_{L}\) in the lower partition closer to the border (since for the considered cycle it cannot be mapped in \(D_{M}\)). This means that the application of \(T_{L}\) follows, leading to a point on \(LC_{L}\cap D_{U}\) (closer to the virtual fixed point). Thus, at least we have the symbolic sequence ULLU. But that is all, because a cycle cannot have three consecutive symbols UUU in its symbolic sequence. It must therefore be a 4-cycle.

Reasoning in a similar way, considering a periodic point on \(LC_{U}\cap D_{M}\), it is possible to show that for \(s<1\), the symbolic sequence of the other possible coexisting cycles is MLMU and MLLMUU.

(iii) The proof that for \(0<d\le h\) the fixed point O is globally attracting results from the fact that all other possible cycles do not exist. This is because the bifurcation curves associated with their existence, determined in the next subsection, belong to the region \(d>h\). Thus, the proof of this statement ends with the bifurcation conditions given below.\(\square \)

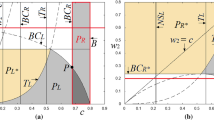
As illustrated in Fig. 1, there are regions of existence of cycles of period 4 with different symbolic sequences, LLUU and MLMU (denoted by cycle 4 and cycle \(4_{M}\), respectively) and a region associated with the existence of a cycle of period 6 with the symbolic sequence MLLMUU. Attracting cycles other than the three mentioned here cannot exist. The related existence regions may overlap, leading to the coexistence of different attracting cycles. That is, the fixed point O may coexist with one, two or three attracting cycles (as shown in Fig. 1). Figure 2 shows the different existence regions for \(0<s<1\), and their overlapping parts. The related borders (all associated with BCBs) are determined in the following subsection.

Fig. 2
figure 2

Existence regions of periodic and chaotic attarctors in the \(\left( s,d\right) \) parameter plane at \(h=1\). For \(0<s<1\), attracting cycles coexisting with the fixed point O. For \(s>1\), the dynamics are either convergent to a chaotic attractor or divergent

Full size image

For parameters above the red curve in Fig. 2b, the basin of the fixed point O has the simplest structure, as commented in Proposition 1(i). Note that the existence region of a 6-cycle is completely above that curve. For \(0<s<1\) and for parameters below the lower boundary of the existence region of the 4-cycle LLUU, the fixed point O is globally attracting.

4.1 BCB curves related to attracting cycles

In this section, we derive the BCB curves related to the cycles that can coexist with fixed point O. Unlike with the 6-cycle, we will see that two cycles of period 4 also exist in the region of instability.

4.1.1 4-cycle LLUU

Let \(\left( x_{1},y_{1}\right) \) be the periodic point of the 4-cycle LLUU belonging to \(LC_{U}\) (i.e. with \(y_{1}=-x_{1}/s-d\)) in the lower partition. Then this point of the 4-cycle satisfies

$$\begin{aligned} T_{L}\circ T_{L}\left( x_{1},y_{1}\right) =\left( -x_{1},-y_{1}\right) \end{aligned}$$
(17)

leading to

$$\begin{aligned} \left( x_{1},y_{1}\right) =\left( \frac{s\left( s-1\right) d}{1+s^{2}},-\frac{\left( s-1\right) d}{1+s^{2}}-d\right) \end{aligned}$$
(18)

The BCB occurs when \(\left( x_{1},y_{1}\right) \in LC_{U}\), that is \(x_{1}=-x_{A}\). The 4-cycle exists for \(x_{1}>-x_{A}\), where \(x_{1}\) is given in (18), leading to \(d>h\frac{1+s^{2}}{2s^{2}}\) and the bifurcation curve is

$$\begin{aligned} BCB_{4}:\ \ d=h\frac{1+s^{2}}{2s^{2}} \end{aligned}$$
(19)

4.1.2 4-cycle MLMU

Let \(\left( x_{1},y_{1}\right) \) be the periodic point of the 4-cycle MLMU in the middle partition belonging to \(LC_{U}\) (i.e. with \(y_{1}=-x_{1}/s-d\)). Then this point of the 4-cycle satisfies

$$\begin{aligned} T_{L}\circ T_{M}\left( x_{1},y_{1}\right) =\left( -x_{1},-y_{1}\right) \end{aligned}$$
(20)

leading to

$$\begin{aligned} \left( x_{1},y_{1}\right) =\left( \frac{-sd}{1+s^{2}},\frac{d}{1+s^{2}}-d\right) \end{aligned}$$
(21)

The existence of this 4-cycle is related to two conditions. First, this point \(\left( x_{1},y_{1}\right) \) must be inside the middle partition, that is, \(x_{1}>-x_{B}\), where \(x_{1}\) is given in (21). Second, its image \(T_{M}\left( x_{1},y_{1}\right) =\left( -sx_{1},x_{1}\right) \) (belonging to \(LC_{M}\)) must belong to the lower partition (with \(y<x-h\)), that is, \(x_{1}<\left( -sx_{1}-h\right) \). The first condition leads to

$$\begin{aligned} d\frac{s-s^{2}}{1+s^{2}}<h \end{aligned}$$
(22)

so that for \(s<1\), the condition becomes \(d<h\frac{1+s^{2}}{s-s^{2}}\), while for \(s>1\), the inequality in (22) is satisfied. The BCB curve is

$$\begin{aligned} BCB_{4_{M}}^{1}:\ \ d=h\frac{1+s^{2}}{s-s^{2}} \end{aligned}$$
(23)

The second condition leads to \(d>h\frac{1+s^{2}}{s+s^{2}}\) and the BCB curve is given by

$$\begin{aligned} BCB_{4_{M}}^{2}:\ \ d=h\frac{1+s^{2}}{s+s^{2}} \end{aligned}$$
(24)

4.1.3 6-cycle MLLMUU

Let \(\left( x_{1},y_{1}\right) \) be the periodic point of the 6-cycle MLLMUU in the middle partition belonging to \(LC_{U}\) (i.e. with \(y_{1}=-x_{1}/s-d\)). Then this point of the 6-cycle satisfies

$$\begin{aligned} T_{L}\circ T_{L}\circ T_{M}\left( x_{1},y_{1}\right) =\left( -x_{1},-y_{1}\right) \end{aligned}$$
(25)

leading to

$$\begin{aligned} \left( x_{1},y_{1}\right) =\left( \frac{-sd}{1+s+s^{2}},\frac{d}{1+s+s^{2}}-d\right) \end{aligned}$$
(26)

The existence of the 6-cycle is also related to two conditions. First, it must be \(x_{1}<-x_{A}\), where \(x_{1}\) is given in (26), and second, it must be \(x_{3}>x_{B}\), where \(\left( x_{3},y_{3}\right) =T_{L}\circ T_{M}\left( x_{1},y_{1}\right) \), so that \(x_{3}=s^{2}x_{1}+sd\).

From the first condition we obtain \(d<h\frac{1+s+s^{2}}{s^{2}}\) and the BCB

$$\begin{aligned} BCB_{6}^{1}:\ \ d=h\frac{1+s+s^{2}}{s^{2}} \end{aligned}$$
(27)

while from the second condition we have \(d>h\frac{1+s+s^{2}}{s}\) and the BCB

$$\begin{aligned} BCB_{6}^{2}:\ \ \frac{1+s+s^{2}}{s} \end{aligned}$$
(28)

4.1.4 Discussion

It is immediate to verify that the two BCB curves, bounding the existence region of the 6-cycle, intersect at \(s=1\) and \(d=3h\), and that the 6-cycle does not exist for \(s>1\). Differently, the two 4-cycles also exist for \(s>1\), but they are saddles.

In Fig. 3 are depicted the existence regions of the cycles LLUU, MLMU and MLLMUU. For \(0<s<1\), all cycles are stable nodes. For \(s>1\), LLUU and MLMU are saddles, while the 6-cycle does not exist.

Fig. 3
figure 3

Existence regions of cycles in the \(\left( s,d\right) \) parameter plane at \(h=1\). In yellow the region in which the fixed point O is globally attracting. a Existence region of the 4-cycle LLUU, attracting for \(s<1\) and a saddle for \(s>1\). b Existence region of the 4-cycle MLMU, attracting for \(s<1\) and a saddle for \(s>1\). c Existence region of the 6-cycle MLLMUU, existing and attracting only for \(s<1\). The boundaries are the BCB curves determined in this section

Full size image

The overlapping of the three regions related to the coexistence of the cycles is evidenced in Fig. 2, by using different colors in the overlapped parts. Note that for \(0<s<1\) the fixed point O is also attracting.

Remark. As can be seen from (19), (24) and (28), for \(0<s<1\), the existence regions of the three different cycles identified above belong to the region \(d>h\), which completes the proof of statement (iii) in Proposition 1.

4.2 First return map

As already mentioned, when the critical line \(LC_{U}\) does not intersect the basin of the fixed point O, we can describe some properties of the two-dimensional map by using the first return map on that critical line. Consider a point \(\left( x,y\right) \) belonging to \(LC_{U}\), its iterates, and the first point that is mapped again on \(LC_{U}\), say \(\left( x_{p},y_{p}\right) \). Then, the one-dimensional map \(x^{\prime }=g\left( x\right) \) that to each point x associates the first return \(x_{p}\) is denoted first-return map. This map is piecewise linear, with many discontinuity points, and its shape depends on the parameters, especially when \(0<s<1\). This first-return map is particularly useful in the case \(s\ge 1\). However, let us use an example to show that the first return map can also be useful in the stability regime (that is, when \(0<s<1\)), for \(d>h\).

Fig. 4
figure 4

a The \(\left( x,y\right) \) phase plane from Fig. 1c at \(h=1\), \(d=3.5\) and \(s=0.75\). b The related one-dimensional first return map on the critical line \(LC_{U}\), \(x^{\prime }=g\left( x\right) \) given in (29)

Full size image

Consider the discontinuity points on the critical line \(LC_{U}\), \(B^{\prime }=\left( -x_{B},-y_{B}\right) \) and \(A^{\prime }=\left( -x_{A},-y_{A}\right) \), with \(-x_{B}=-\frac{s\left( d+h\right) }{1+s}\) and \(-x_{A}=-\frac{s\left( d-h\right) }{1+s}\). Consider also

  • the solution of the equation \(f_{L}\circ f_{M}\left( x\right) =x_{B}\), \(\xi =\frac{h-ds}{s\left( 1+s\right) }\);

  • the solution of the equation \(f_{L}\circ f_{L}\left( x\right) =x_{A}\), \(\eta _{1}=\frac{s^{2}d-h}{s\left( 1+s\right) }\);

  • the solution of the equation \(f_{L}\left( x\right) =x_{B}\), \(\eta _{2}=\frac{sd-h}{1+s}\);

  • the solution of the equation \(f_{L}\left( x\right) =x_{A}\), \(\eta _{3}=\frac{sd+h}{1+s}\).

Then the one-dimensional map \(x^{\prime }=g\left( x\right) \) shown in Fig. 4b is defined as follows:

$$\begin{aligned} g\left( x\right) =\left\{ \begin{array}{lll} g_{1}\left( x\right) =f_{U} \left( x\right) =-sx-sd &{} \quad \text {if} \quad &{} x<-x_{B} \\ g_{2}\left( x\right) =f_{U}\circ f_{M}\circ f_{L}\circ f_{M}\left( x\right) =s^{4}x+s^{3} d-sd &{} \quad \text {if} \quad &{} -x_{B}<x<\xi \\ g_{3}\left( x\right) =f_{U}\circ f_{M}\circ f_{L}^{2}\circ f_{M}\left( x\right) =-s^{5}x-s^{4}d+s^{3}d-sd &{} \quad \text {if} \quad &{} \xi<x<-x_{A} \\ g_{4}\left( x\right) =f_{U}\circ f_{L}^{2}\left( x\right) =-s^{3}x+s^{3}d-s^{2}d-sd &{} \quad \text {if} \quad &{} -x_{A}<x<\eta _{1}\\ g_{5}\left( x\right) =f_{U}\circ f_{M}\circ f_{L}^{2}\left( x\right) =s^{4}x-s^{4}d+s^{3}d-sd &{} \quad \text {if} \quad &{} \eta _{1}<x<\eta _{2} \\ g_{6}\left( x\right) =f_{U}\circ f_{M}\circ f_{L}\left( x\right) =-s^{3}x+s^{3}d-sd &{} \quad \text {if} \quad &{} \eta _{2}<x<\eta _{3} \\ g_{7}\left( x\right) =f_{U}\circ f_{L}\left( x\right) =s^{2}x-s^{2}d-sd &{} \quad \text {if} \quad &{} x>\eta _{3} \end{array} \right. \end{aligned}$$
(29)

For \(0<s<1\), the slopes of the first return map on the critical line \(LC_{U}\) are smaller than 1 in modulus. The basins of the attractors are bounded by the discontinuity points and their preimages. Figure 4b shows the periodic points inside the absorbing interval. The fixed point in green corresponds to the point of the 4-cycle MLMU belonging to the critical line \(LC_{U}\); the 2-cycle of \(g\left( x\right) \) with points in blue corresponds to the two points of the 4-cycle LLUU belonging to the critical line \(LC_{U}\); and the 2-cycle of \(g\left( x\right) \) with points in red corresponds to the two points of the 6-cycle MLLMUU belonging to the critical line \(LC_{U}\).

For \(s=1\), we can use the definition in (29), and we have \(-x_{B}=-\frac{\left( d+h\right) }{2}\), \(-x_{A}=-\frac{\left( d-h\right) }{2}=\xi \), \(\eta _{1}=\eta _{2}=x_{A}\), \(\eta _{3}=x_{B}\) so that the first return map, say \(x^{\prime }=g_{s1}\left( x\right) \), to be used in Sec. 5, does not have the branches related to the functions \(g_{3}\left( x\right) \) and \(g_{5}\left( x\right) \), and it results to be defined as follows:

$$\begin{aligned} g_{s1}\left( x\right) =\left\{ \begin{array}{lll} g_{1}\left( x\right) =f_{U}\left( x\right) =-x-d &{} \quad \text {if} \quad &{} x<-x_{B} \\ g_{2}\left( x\right) =f_{U}\circ f_{M}\circ f_{L}\circ f_{M}\left( x\right) =x+d-d=x &{} \quad \text {if} \quad &{} -x_{B}<x<-x_{A}\\ g_{4}\left( x\right) =f_{U}\circ f_{L}^{2}\left( x\right) =-x-d=g_{1}\left( x\right) &{} \quad \text {if} \quad &{} -x_{A}<x<x_{A} \\ g_{6}\left( x\right) =f_{U}\circ f_{M}\circ f_{L}\left( x\right) =-x+d-d=-x &{} \quad \text {if} \quad &{} x_{A}<x<x_{B} \\ g_{7}\left( x\right) =f_{U}\circ f_{L}\left( x\right) =x-2d &{} \quad \text {if} \quad &{} x>x_{B} \end{array} \right. \end{aligned}$$
(30)

Differently, for \(s>1\) the points of the critical line \(LC_{U}\) with \(x>-x_{A}\) are mapped directly by \(T_{L}\) in the upper partition. So, by defining the solution of the equation \(f_{L}\circ f_{M}\left( x\right) =x_{A}\) as \(\widetilde{\xi }=-\frac{h+ds}{s\left( 1+s\right) }\), the first return map, say \(x^{\prime }=g_{s}\left( x\right) \), to be used in Sec. 6, is defined as follows:

$$\begin{aligned} g_{s}\left( x\right) =\left\{ \begin{array}{lll} g_{1}\left( x\right) =f_{U}\left( x\right) =-sx-sd &{} \quad \text {if} \quad &{} x<-x_{B} \\ \widetilde{g}_{2}\left( x\right) = f_{U}\circ f_{L}\circ f_{M}\left( x\right) =s^{4}x+s^{3}d-sd &{} \quad \text {if} \quad &{} -x_{B}<x<\widetilde{\xi } \\ g_{2}\left( x\right) = f_{U}\circ f_{M}\circ f_{L}\circ f_{M}\left( x\right) =s^{4}x+s^{3}d-sd &{} \quad \text {if} \quad &{} \widetilde{\xi }<x<-x_{A} \\ g_{4}\left( x\right) =f_{U}\circ f_{L}^{2}\left( x\right) =-s^{3}x+s^{3}d-s^{2}d-sd &{} \quad \text {if} \quad &{} -x_{A}<x<\eta _{2}\\ g_{6}\left( x\right) =f_{U}\circ f_{M}\circ f_{L}\left( x\right) =-s^{3}x+s^{3}d-sd &{} \quad \text {if} \quad &{} \eta _{2}<x<\eta _{3} \\ g_{7}\left( x\right) =f_{U}\circ f_{L}\left( x\right) =s^{2}x-s^{2}d-sd &{} \quad \text {if} \quad &{} x>\eta _{3} \end{array} \right. \end{aligned}$$
(31)

5 Bifurcation value \(s=1\)

At \(s=1\), the fixed point O undergoes a degenerate flip bifurcation, with eigenvalue \(-1\) (Sushko and Gardini [33]), and the segment of its eigenvector \(LC_{M}\left( y=-x\right) \) inside the middle partition, for \(x\in \left( -\frac{h}{2},+\frac{h}{2}\right) \), is filled with cycles of period 2. They are stable but not attracting. There exists a stable set for such 2-cycles. In fact, all points in the quadrilateral region bounded by two segments of the discontinuity lines and the two vertical segments with \(x=\pm \frac{h}{2}\) inside the middle partition (see the yellow region in Fig. 5) are mapped into one of the 2-cycles filling the segment of \(LC_{M}\). That is, any point \(\left( x_{0},y_{0}\right) \) in that quadrilateral region is mapped by \(T_{M}\) in the point \(\left( -x_{0},x_{0}\right) \) belonging to \(LC_{M}\), leading to a 2-cycle.

For \(d\le h\), no other cycle exists, and that segment of \(LC_{M}\) filled with 2-cycles attracts all other points of the \(\left( x,y\right) \) phase plane. That is, any initial condition is mapped in one of these 2-cycles in a finite number of iterations.

Fig. 5
figure 5

a The \(\left( x,y\right) \) phase plane at \(h=1\), \(s=1\) and \(d=3.5\). b The related one-dimensional first return map on the critical line \(LC_{U}\), \(x^{\prime }=g_{s1}\left( x\right) \) given in (30)

Full size image

For \(d>h\), at \(s=1\), both the 4-cycles MLMU and LLUU given in (18) and (21) exist and undergo a degenerate bifurcation with eigenvalue \(+1\) (Sushko and Gardini [33]), leading to segments filled with 4-cycles. They are stable but not attracting.

However, the segments filled with 4-cycles are different, depending on \(d\ge 2h\) (when the immediate basin of the segments filled with 2-cycles has no preimages, as in Fig. 5a, and we can use the first return map on \(LC_{U}\)), and \(h<d<2h\) (when the immediate basin of the segments filled with 2-cycles has other preimages, we cannot use the first return map on \(LC_{U}\)).

The two different cases are considered separately.

5.1 Case \(s=1\), \(d\ge 2h\)

The stable set of the 2-cycles described above is associated with the bifurcation of the fixed point O. It belongs to the quadrilateral region (in yellow in Fig. 5a) and does not intersect \(LC_{U}\). Thus, all points of \(LC_{U}\) are mapped into one of the existing 4-cycles. Considering the first return map \(x^{\prime }=g_{s1}\left( x\right) \) given in (30), shown in Fig. 5b, we have that an absorbing interval exists with \(x\in \left( g_{4}\left( x_{A}\right) ,x_{A}\right) =\left( -x_{A}-d,x_{A}\right) \). The points with \(x\in \left( -x_{B},-x_{A}\right) \) belong to 4-cycles with the symbolic sequence MLMU, while those of the remaining segments belong to 4-cycles with the symbolic sequence LLUU. Points outside the absorbing interval are mapped into one of these 4-cycles in a finite number of iterations, as it can be clearly seen in Fig. 5b.

A peculiarity of these 4-cycles is that only two are symmetric with respect to the fixed point O, the two with coordinates given in (18) and (21), which undergo a degenerate \(+1\) bifurcation. All the other 4-cycles, albeit with the same symbolic sequence, are not symmetric, and clearly, due to the symmetry property of the map, the symmetric ones also exist. Examples are shown in Fig. 5a; see the cycles colored in red and pink (with one periodic point inside the interval \(\left( -x_{B},-x_{A}\right) \) of the critical line \(LC_{U}\)) and the cycles colored in black and gray (with two periodic points on the absorbing interval on the critical line \(LC_{U}\) outside the interval \(\left( -x_{B},-x_{A}\right) \)).

The green point on the diagonal of the first return map \(x^{\prime }=g_{1}\left( x\right) \) represents the point of the 4-cycles MLMU given in (21). The segment on the diagonal, consisting in fixed points of the first return map \(g_{1}\left( x\right) \), represents points belonging to the 4-cycles for map T. These cycles have one periodic point inside the interval \(\left( -x_{B},-x_{A}\right) \) of the critical line \(LC_{U}\), and the same symbolic sequence of the bifurcating 4-cycle, i.e. with two periodic points in the middle partition \(D_{M}\). The other points outside the central segment of fixed points of the map \(x^{\prime }=g_{s1}\left( x\right) \) give two segments filled with 2-cycles of the first return map (including also the 4-cycle LLUU shown by two blue points) and represent points of 4-cycles of map T that have the same symbolic sequence of the bifurcating cycle. The points outside the absorbing interval \(\left( -x_{A}-d,x_{A}\right) \) are mapped into one of the 4-cycles mentioned above in a finite number of iterations.

5.2 Case \(s=1\), \(0<d<2h\)

Under these values, the immediate basin of the segment filled with 2-cycles intersects the two critical lines \(LC_{L/U}\). An example is shown in Fig. 6. The segment on \(LC_{L}\) with \(x\in [x_{A},h/2]\), and the symmetric one on \(LC_{U}\), have preimages on \(LC_{M}\) and further preimages on the segments of critical lines are inside the middle partition. In fact, the preimage by \(T_{L}^{-1}\) of the segment \(\left[ x_{A},h/2\right] \) on \(LC_{L}\) leads to the segment \(\left[ x^{*},x_{B}\right] \) on \(LC_{M}\) with \(x^{*}=d-h/2\), and its further preimage by \(T_{L}^{-1}\) leads to the segment \(\left[ -x_{B},-x^{*}\right] \) on \(LC_{U}\). Clearly, the symmetric segments also exist, leading to four segments on the critical lines of points that are mapped into a 2-cycle close to the origin.

The remaining dynamics can be commented by using points of the critical line \(LC_{U}\). The segment \(\left[ -x^{*},-h/2\right] \) in the middle partition consists of points of 4-cycles with the symbolic sequence MLMU, while the segments on \(LC_{U}\) with \(x\in [-x_{A},x_{A}]\) as well as \(x\in [-x_{A}-d,-x_{B}]\) are filled with points of 4-cycles with the symbolic sequence LLUU. Such segments also have images in the other critical lines, as shown in Fig. 6.

Fig. 6
figure 6

The \(\left( x,y\right) \) phase plane at \(h=1\), \(s=1\) and \(d=3.5\)

Full size image

In this case, too, the only symmetric 4-cycles are those with coordinates given in (18) and (21); all others are not symmetric with respect to the fixed point O, and the symmetric ones also exist. Two examples are shown in Fig. 6, a non symmetric 4-cycle with two periodic points on \(LC_{U}\) (blue points) and a non symmetric 4-cycle with one periodic point on \(LC_{U}\) (green points in Fig. 6).

As in the other case, any initial condition outside the segments listed above is mapped into one of these cycles in a finite number of iterations.

6 Instability regime \(\mathbf {s>1}\)

Classical nonlinear cobweb models typically display a period-two cycle, born via a standard flip bifurcation, as parameter s increases above 1. Of course, classical linear cobweb models yield divergent dynamics for \(s>1\). Our cobweb model gives rise to quite different dynamic behaviors.

As already mentioned, for \(s>1\), any existing cycle of map T is necessarily a saddle, which may be homoclinic or not. Moreover, the degenerate flip bifurcation is a global bifurcation. What occurs after it depends on the properties of the map. The fixed point O is no longer attracting, and it is possible to describe the dynamics via the first return map on the critical line \(LC_{U}\), consisting of a one-dimensional piecewise linear and discontinuous map, with several discontinuity points, characterized by all slopes in modulus larger than 1. Thus, when there are bounded dynamics, we expect chaotic intervals. Divergent dynamics also exist. In fact, one branch of the unstable set of the saddle 2-cycle described below, appearing at \(s=1\), goes to infinity.

To detect the existence of a 2-cycle with symbolic sequence LU, we consider a point \(\left( x_{1},y_{1}\right) \) in the lower partition belonging to \(LC_{U}\) (i.e. with \(y_{1}=-x_{1}/s-d\)). Its image \(\left( x_{2},y_{2}\right) =T_{L}\left( x_{1},y_{1}\right) \) must satisfy

$$\begin{aligned} T_{L}\left( x_{1},y_{1}\right) =\left( -x_{1},-y_{1}\right) \end{aligned}$$
(32)

leading to \(x_{1}=\widetilde{x}_{1}\), where \(\widetilde{x}_{1}=\frac{sd}{s-1}\). Hence, the point of the 2-cycle in the lower partition must be

$$\begin{aligned}{} & {} \left( \widetilde{x}_{1},y_{1}\right) =\left( \frac{sd}{s-1},-\frac{d}{s-1}-d\right) \nonumber \\{} & {} =\left( \frac{sd}{s-1},-\frac{sd}{s-1}\right) \end{aligned}$$
(33)

It can be easily verified that the existence condition \(y_{1}<\widetilde{x}_{1}\) is satisfied for \(s>1\). Thus, when the LU cycle exists, it is a saddle. For \(s=1\), it is at infinity. Thus, it appears at \(s=1\) via a degenerate transcritical bifurcation (see Sushko and Gardini [33]). However, for \(s>1\), the 2-cycle LU does not always exist, since it may disappear via a border collision bifurcation that occurs when the two periodic points have a contact with the discontinuity lines. This bifurcation is described below, together with the four different types of homoclinic bifurcations of the 2-cycle LU, due to different kinds of contacts of the chaotic attractor with the stable set of the saddle 2-cycle.

Besides the property that the chaotic segments must belong to the three critical lines, we can recall other properties of the chaotic sets in a discontinuous map. One relevant characteristic is that a chaotic attractor must have at least one discontinuity point belonging to the chaotic set. A second characteristic that does not apply to continuous maps is that the chaotic segments may be acyclic. In fact, in our map the chaotic segments are always acyclic, a consequence of the existence of a discontinuity point in the chaotic segments belonging to the critical line \(LC_{U}\) or \(LC_{L}\). A third characteristic is that the boundaries of the chaotic segments belonging to a chaotic attractor are images of the involved discontinuity points, obtained via the two different functions defined on the two sides. This implies that the bifurcations associated with the merging of chaotic intervals always involve some critical point. These properties are described for a one-dimensional discontinuous map in Avrutin et al. [3]. These can be applied to our map because in the range \(s>1\), it is possible to define a suitable first return map on the critical line \(LC_{U}\) (or, equivalently, on \(LC_{L}\)), representing all properties of the map, and for which the results of one-dimensional discontinuous maps apply.

The stable set of the saddle 2-cycle consists of vertical segments issuing from the 2-cycle and related preimages. When a chaotic attractor exists, the stable set of the 2-cycle bounds the set of divergent orbits, that is, it separates the divergent trajectories from those converging to the chaotic attractors. The chaotic set may be symmetric with respect to the origin or a symmetric chaotic set also exists.

The local unstable set of the saddle 2-cycle belongs to the critical lines \(LC_{U}\) and \(LC_{L}\) (eigenvector of the 2-cycle). One branch tends to infinity while the opposite branch tends to the chaotic attracting set, when existing. Thus, the \(\omega \)-limit set (of this branch of the unstable set) includes the existing chaotic intervals. It follows that a contact between the stable set and the chaotic set corresponds to an homoclinic bifurcation of the 2-cycle.

At its first homoclinic bifurcation, that can occur in different ways, there is a transition from chaotic attractors to a chaotic repelling set, and almost all the trajectories are divergent. It is worth noticing that for parameters at which the 2-cycle is homoclinic, almost all trajectories are divergent, but there exists a chaotic repellor (i.e. infinitely many saddle cycles exist). Differently, we show below that when, for \(s>1\), the 2-cycle LU does not exist, then all the trajectories different from the fixed point O are divergent (i.e. no saddle cycle exists).

So, the 2-cycle LU that appears due to a degenerate transcritical bifurcation at \(s=1\) may disappear via a BCB. In fact, it exists when \(\left( \widetilde{x}_{1},y_{1}\right) \) given in (33) belongs to the lower partition, that is, for \(y_{1}<\widetilde{x}_{1}-h\), leading to the condition \(d>h\frac{s-1}{2s}\). At the BCB

$$\begin{aligned} BCB_{2}: \ \ d=h\frac{s-1}{2s} \end{aligned}$$
(34)

the 2-cycle collides with the discontinuity lines on the border of the middle partition and disappears. We have the following.

Proposition 2

For \(s>1\) and \(0<d<h\frac{s-1}{2s}\) all trajectories except for the fixed point O are diverging.

Proof of Proposition 2

For \(s>1\), all existing cycles (all saddles) must belong to the critical lines \(LC_{L}\) and \(LC_{U}\) with points belonging to the range \(\left( -\widetilde{x}_{1},\widetilde{x}_{1}\right) \), and points may also belong to the critical line \(LC_{M}\). At the BCB of the 2-cycle, this range is reduced to the middle partition only, and no cycle can exist with all the points in the middle partition. It follows that any point that is not a fixed point has a divergent trajectory.\(\square \)

Let us first comment on some bifurcations of the chaotic attractors. We will then come back to the homoclinic bifurcations of the saddle 2-cycle.

An example of two different coexisting chaotic attractors, each consisting of six chaotic intervals, is shown in Fig. 7a.

Fig. 7
figure 7

a The \(\left( x,y\right) \) phase plane at \(h=1\), \(d=5\) and \(s=1.1\). One attractor has the six chaotic segments shown in black. Its symmetric chaotic set is shown in color. b The related one-dimensional first return map on the critical line \(LC_{U}\), \(x^{\prime }=g_{s}\left( x\right) \) given in (31)

Full size image

The related first return map \(g_{s}\left( x\right) \) on the critical line \(LC_{U}\) (given in (31)) is shown in Fig. 7b. The fixed point in green corresponds to the point of the 4-cycle MLMU belonging to the critical line \(LC_{U}\), while the 2-cycle of \(g_{s}\left( x\right) \) with points in blue corresponds to the two points of the 4-cycle LLUU belonging to the critical line \(LC_{U}\). The stable set of the 4-cycle MLMU separates the basins of the two symmetric chaotic sets, which is not homoclinic in Fig. 7. The first homoclinic bifurcation of the 4-cycle MLMU can be detected via the first return map \(g_{s}\left( x\right) \), since it occurs at the value of \(s\in \left( 1.1,1.2\right) \) that satisfies the following equation:

$$\begin{aligned} g_{4}\circ g_{2}\left( -x_{A}\right) =-\frac{sd}{1+s^{2}} \end{aligned}$$
(35)

where \(-x_{A}=-\frac{s\left( d-h\right) }{1+s}\), and \(-\frac{sd}{1+s^{2}}\) is the x-coordinate the point of the 4-cycle MLMU belonging to the critical line \(LC_{U}\) (green point in Fig. 7) given in (21). Numerically, we found the solution at \(s\approx 1.153467\). This homoclinic bifurcation leads to the reunion of the two chaotic sets into a unique chaotic attractor, symmetric with respect to the fixed point O, consisting of eight pieces (since the true merging involves only the pieces that have a contact with the 4-cycle MLMU), as shown in Fig. 8.

Fig. 8
figure 8

a The \(\left( x,y\right) \) phase plane at \(h=1\), \(d=3.5\) and \(s=1.2\). There exists only one attractor consisting of eight chaotic segments shown in black. b The related one-dimensional first return map on the critical line \(LC_{U}\), \(x^{\prime }=g_{s}\left( x\right) \) given in (31)

Full size image

Figure 8a shows the homoclinic 4-cycle MLMU inside the chaotic attractor with green points, while the 4-cycle LLUU is outside the chaotic intervals (blue points). The three chaotic intervals belonging to the critical line \(LC_{U}\) are marked in Fig. 8b. The homoclinic bifurcation of the 4-cycle LLUU, which occurs when the chaotic intervals have a contact with the 4-cycle, leads to the merging of the three pieces on \(LC_{U}\) into a unique piece on \(LC_{U}\) (and thus also a unique one on \(LC_{L}\)).

As before, we can detect when this bifurcation takes place via the first return map \(g_{s}\left( x\right) \), since it occurs at the value of \(s\in \left( 1.2,1.3\right) \) that satisfies the following equation:

$$\begin{aligned} g_{4}\left( -x_{A}\right) =\frac{s\left( s-1\right) d}{1+s^{2}} \end{aligned}$$
(36)

where \(-x_{A}=-\frac{s\left( d-h\right) }{1+s}\) and \(\frac{s\left( s-1\right) d}{1+s^{2}}\) is the \(x-\)coordinate of the point of the 4-cycle LLUU belonging to the critical line \(LC_{U}\) given in (18) (blue points in Fig. 8b). Numerically, we found the solution at \(s\simeq 1.284\). An example of the chaotic attractor in four pieces resulting from this homoclinic bifurcation is shown in Fig. 10.

6.1 Homoclinic bifurcations of the 2-cycle LU

In the existence region of the saddle 2-cycle, for \(s>1\) and \(d>h\frac{s-1}{2s}\), bounded trajectories may exist leading to chaotic attractors. For parameters belonging to the white region for \(s>1\) in Fig. 2, we have chaotic attractors. The gray region denotes that the generic trajectory diverges, but there exists a chaotic repellor; see also the enlargement in Fig. 9. The boundaries of the gray region are related to different kinds of homoclinic bifurcations of the 2-cycle. Since the boundary of the basin of the chaotic attractor is the stable set of the saddle 2-cycle, its first homoclinic bifurcation leads to generic divergence. This first contact can occur in different ways, as explained and detected here.

Fig. 9
figure 9

Enlargement of the \(\left( s,d\right) \) parameter plane at \(h=1\) (from Fig. 2a) showing the BCB related to the existence of the 2-cycle LU and the four boundaries associated with the four different homoclinic bifurcations of the 2-cycle LU identified in this section

Full size image

Proposition 3

For \(s>1\) and \(d>h\frac{s-1}{2s}\), the homoclinic bifurcation of the saddle 2-cycle occurs when the \(\left( s,d\right) \) parameter point crosses one of the following four curves \(HB_{2,i}\) for \(i=1,2,3,4\):

$$\begin{aligned} \begin{array}{lll} HB_{2,1}: \ \ d &{} = &{} h\frac{s\left( s-1\right) }{2\left( s^{2}-s-1\right) }\\ \\ HB_{2,2}: \ \ d &{} = &{} h\frac{s\left( s-1\right) }{1+2s-s^{2}}\\ \\ HB_{2,3}: \ \ d &{} = &{} h\frac{s^{2}\left( s-1\right) }{s^{3}-1-2s-s^{2}}\\ \\ HB_{2,4}: \ \ d &{} = &{} h\frac{s\left( s-1\right) }{1+s} \end{array} \end{aligned}$$
(37)

in the \(\left( s,d\right) \) parameter plane.

Proof of Proposition 3

Consider points \(P^{\prime }\) and \(Q^{\prime }\) at which the critical lines \(LC_{U}\) and \(LC_{O}\) intersect the stable set of the 2-cycle at \(x=-\widetilde{x}_{1}\), that is \(x=-\frac{sd}{s-1}\). The x-coordinate of their preimages (via \(T_{U}^{-1}\)) leads to points P and Q on the basin boundary (see Fig. 10a), with P (resp. Q) belonging to the upper (resp. lower) discontinuity line. These points are given by \(P=\left( x_{P},y_{P}\right) =\left( \frac{\widetilde{x}_{1}}{s}-d,\frac{\widetilde{x}_{1}}{s}-d+h\right) \) (resp. \(Q=\left( x_{Q},y_{Q}\right) =\left( \frac{\widetilde{x}_{1}}{s},\frac{\widetilde{x}_{1}}{s}-h\right) \)).

Fig. 10
figure 10

The \(\left( x,y\right) \) phase plane at \(h=1\), \(d=3\) and \(s=1.4\) in (a), \(s=1.7\) in (b)

Full size image

Note that the chaotic attractor also has points on the upper critical line \(LC_{L}\), i.e. on the unstable set of the saddle 2-cycle. When points A or B belong to the chaotic set, a homoclinic bifurcation occurs when point P merges with point A or when point Q merges with point B. The first condition \(x_{P}=x_{A}\), that is \(\frac{\widetilde{x}_{1}}{s}-d=\frac{s\left( d-h\right) }{1+s}\), leads to the bifurcation curve

$$\begin{aligned} HB_{2,1}: \ d=h\frac{s\left( s-1\right) }{2\left( s^{2}-s-1\right) } \end{aligned}$$
(38)

while the second condition \(x_{Q}=x_{B}\), that is \(\frac{\widetilde{x}_{1}}{s}=\frac{s\left( d+h\right) }{1+s}\), leads to the curve

$$\begin{aligned} HB_{2,2}: \ d=h\frac{s\left( s-1\right) }{1+2s-s^{2}} \end{aligned}$$
(39)

An example in which point P is close to merging with point A is shown in Fig. 10b.

However, the first homoclinic bifurcation of the 2-cycle may occur without involving directly the two points A or B on the critical line \(LC_{L}\).

Fig. 11
figure 11

The \(\left( x,y\right) \) phase plane at \(h=1\). In a \(s=1.75\) and \(d=0.725\). In b \(s=1.78\) and \(d=0.5\)

Full size image

In the case shown in Fig. 11(a), point B is not involved in the chaotic set. However, the image \(T_{U}\left( A\right) \) on the critical line \(LC_{U}\) is very close to the boundary of the divergence set issuing from \(-x_{Q}=-\frac{\widetilde{x}_{1}}{s}\) and the contact occurs when \(\left( -sx_{A}-d\right) =-\frac{\widetilde{x}_{1}}{s}\) holds, leading to

$$\begin{aligned} HB_{2,3}: \ \ d=h\frac{s^{2}\left( s-1\right) }{s^{3}-1-2s-s^{2}} \end{aligned}$$
(40)

A different case is shown in Fig. 11(b). Also here point B is not involved in the chaotic set. The contact of the chaotic set with the boundary of the divergence trajectories occurs when point Q merges with point M, where point M is the intersection of the critical line \(LC_{M}\) with the lower discontinuity \(y=x-h\). That is, \(M=\left( x_{M},x_{M}-h\right) \) with \(x_{M}=h\frac{s}{1+s}\). Thus, the contact occurs for \(h\frac{s}{1+s}=\frac{\widetilde{x}_{1}}{s}\), leading to

$$\begin{aligned} HB_{2,4}: \ \ d=h\frac{s\left( s-1\right) }{1+s} \end{aligned}$$
(41)

\(\square \)

In Fig. 12, we show one-dimensional bifurcation diagrams as a function of parameter s, representing the projection on the \(x-\)axis of the trajectories, where the presence of the two colors (red and black) denotes the coexistence of two chaotic attractors.

Fig. 12
figure 12

One-dimensional bifurcation diagrams as a function of parameter s at \(h=1\) and \(d=3.5\) in (a); \(d=5\) in (b) and related enlargement

Full size image
Fig. 13
figure 13

Example of dynamics in the time domain, assuming \(s=1.75\), \(d=2\) and \(h=1\)

Full size image

As it follows from the definition, an increase in parameter d (representing the jump at the discontinuity lines) corresponds to an increase in the width of the chaotic intervals.

Finally, Fig. 13 provides an example of the dynamics of map T in the time domain, assuming \(s=1.75\), \(d=2\) and \(h=1\). Note that our cobweb model has the capability to generate irregular commodity price fluctuations, oscillating between calm and turbulent periods, with alternating intervals of large and small amplitude in these fluctuations.

7 Conclusions

In this study, we explored a map that illustrates the dynamics of a cobweb model wherein firms rely on a regime-switching expectation rule. When the commodity price is relatively stable, firms believe it will remain constant. However, if the commodity price rises sharply, firms expect it to fall by a certain amount, and if it falls sharply, they anticipate a rise by a certain amount. Consequently, our cobweb model can be represented by a two-dimensional piecewise linear map. A key characteristic of this map is that its three different linear functions, defined in three distinct partitions of the phase plane, share the same Jacobian matrix, with real eigenvalues 0 and \(-s\). This peculiarity results in the asymptotic dynamics belonging to three critical lines of the phase plane, each with two discontinuity points. These discontinuity points are essential elements in establishing the properties of the dynamics that may occur.

As we have shown, the behavior of our cobweb model depends on whether the parameter s is in the stability regime (\(0<s<1\)), where all existing cycles are attracting nodes, or belongs to the instability regime (\(s>1\)), where all existing cycles are saddles and the attracting sets can only consist of chaotic intervals. These two different regimes are separated by a bifurcation case (\(s=1\)) that also has peculiar properties. At \(s=1\), all trajectories are convergent to a stable but not attracting cycle of period 2 or 4. These cycles fill suitable intervals, that have been detected on the critical lines. It is noteworthy that the behavior of our cobweb model, especially its capacity to generate cycles in the stability region and instantly induce chaos in the instability region, significantly expands upon what is typically reported in the relevant literature.

We have demonstrated that within the stability regime, the map’s real fixed point may coexist with one, two, or three cycles. The corresponding existence regions, bounded by border collision bifurcation curves in the \(\left( s,d\right) \) parameter plane, have been identified, revealing multiple overlapping areas. Another peculiarity is the structure of the basins of attraction in the \(\left( x,y\right) \) phase plane, which are bounded by vertical segments whose x-coordinate is determined by the preimages of the discontinuity points on the critical lines. It has been established that, for a significant portion of the parameter plane, the basin of attraction of the real fixed point forms a simple parallelogram situated in the middle partition of the map. In the presence of exogenous shocks, we may thus observe interesting attractor switching dynamics. Interestingly, however, endogenous irregular fluctuations between calm and turbulent periods may also arise in the instability region, where the dynamics occur in acyclic intervals. We have shown that the chaotic intervals are bounded by critical points, images of the discontinuity points on the critical lines, and the number and structure of the chaotic intervals change due to homoclinic bifurcations of some saddle cycle. We have also shown that, for a wide set of values of the parameters, the properties of the system may also be analyzed by means of the first return map on a critical line. By using the first return map we have detected the homoclinic bifurcations of repelling cycles leading to the merging of chaotic attractors. In the instability regime also divergent trajectories exist, and the stable set of a particular saddle 2-cycle with points in the external partitions bound in the phase plane the set of points having divergent trajectories. The dynamics are exploding (almost all the trajectoreis are divergent) when the saddle 2-cycle becomes homoclinic. We have shown that this occurs via four different kinds of homoclinic bifurcations due to contacts of this stable set with the chaotic attractor.

The results of the proposed system suggest a deeper analysis introducing some stochastic perturbation, that is left for future research work.