1 Introduction

Fluid–structure interaction (FSI) refers to the multiphysics coupling between the laws governing structural mechanics and fluid dynamics or between two fluids in relative motion. FSI has received growing interest among researchers for the past few decades due to its numerous industrial applications. It is also vital where mechanical systems' safety and reliability are concerned. A well-recognized specific instance of FSI, which has been investigated closely, is an aeroelastic phenomenon called the vortex-induced vibration (VIV). If the vortex shedding frequency matches the body's natural frequency, the ensuing vibration may cause the body to resonate to a threatening level. This range is defined as the ‘lock-in’ or ‘synchronization’ region [1,2,3,4,5]. Because the lock-in happens for a small flow velocity range, the vibration amplitude reaches high values, potentially exhibiting Limit Cycle Oscillation (LCO). Notably, the triggering mechanism of LCOs of an airfoil structure due to aeroelastic instability, which was shown to result from a cascade of resonance captures, was studied by Lee et al. [6]. Such high amplitude LCO causes undesirable noise, high cycle fatigue, and premature structural failure; hence, it should be avoided or attenuated. This is the focus of the current work. For other dynamic features, the reader is referred to a comprehensive review of the wind-induced vibrations [7]. For the current analysis, we specifically consider the case of turbine blades at the instant of frequency lock-in during VIV.

The VIV of structures can be analyzed using physical experiments or numerical analyses. However, physical experiments are very expensive to set up when compared with numerical methods. Therefore, numerical methods have been the focus of many researchers in VIV problems [8,9,10]. Further, the aeroelastic systems are nonlinear due to geometry, material, and flow separations [11, 12]. Thus, numerical methods are deemed to be successful due to the advancement in computations. More specifically, two numerical methods are widely used to determine the hydrodynamics forces acting on the structure that triggers the VIV. One way to predict VIV accurately using numerical methods is solving the Navier–Stokes equations coupled with the structural equations using a computational fluid dynamics (CFD) method [13]. Within the same context, the advancement of data-driven approaches to forecast bifurcations in dynamical systems is worth mentioning to explore the nonlinear dynamics of an aeroelastic system [14]. Such solution procedures, nevertheless, are computationally expensive and remarkably challenging at sufficiently high Reynolds numbers. The second method involves using the wake oscillator model, which uses a nonlinear oscillator to empirically determine the hydrodynamic forces. The apparent advantage of the wake oscillator is its lower computational cost compared to the CFD [15]. Bishop and Hassan [16] were the first to propose a self-exciting and self-limiting van der Pol (VDP) equation to simulate the lift force exerted on a structure in VIV. In 1971, Parkison [17] developed the first wake oscillator model, where a velocity coupling between the motion of the structure and the wake was proposed. Later, a displacement and an acceleration coupling between the structural equation and wake were proposed. Nevertheless, the most remarkable finding was proposed in [18], which used the acceleration coupling in the wake oscillator model and has been deemed successful by being verified in various works [19]. The current analysis only considers the acceleration coupling between the structure and the wake model.

The characteristics of the vortices, modeled by the VDP oscillator, have been analyzed in various applications to predict the VIV, such as an offshore riser [20], cylindrical structure [18], and turbine blade [21]. The LCO and frequency lock-in phenomena in a VDP oscillator were observed by Clark et al. [22] and, hence, laid the groundwork for modeling non-synchronous vibrations (NSV) in turbomachines. Subsequently, many scholars have investigated the VIVs of an airfoil extensively. For instance, Banerjee and Kennedy [23] provided a simplified model for rotating blades. They obtained an analytical solution of a uniform, straight rotating beam based on the Euler–Bernoulli theory. Pertinent to this discussion, a 3DOF FSI model simulating the VIV of turbine blades was proposed by Wang et al. [21]. They discussed the internal resonance between the fluid and the turbine blade by formulating the plunge and pitch motions of the airfoil coupled with the VDP oscillator to model the vortex force due to wake dynamics. Similarly, Hoskoti et al. [24] presented airfoils' coupled plunge-pitch oscillation to study the frequency lock-in and approximately calculated the vibration amplitude of the turbomachinery blade.

Numerous suppression techniques have been proposed to overcome the undesirable large amplitude VIV [25,26,27,28,29,30,31]. It is common to integrate piezoelectric materials in highly flexible airfoil structures to actuate wind warping, which alters the wind flow. Among the mitigation approaches, a novel active technique was proposed by Kassem et al. [29] to suppress the flutter of a 2DOF airfoil structure by using an active dynamic vibration absorber (ADVA). However, the drawback of this technique is the requirement of an auxiliary power source for the operation. Conversely, a damper in the form of a passive vibration absorber is a traditional technique to attenuate vibrations and requires no power source. In particular, damping is an effective parameter for increasing the critical wind speed at which vibrations in mechanical structures could occur, and the similar concept can be extended to VIV. Therefore, passive vibration absorbers have been applied in various wind-induced vibrations (WIV) research fields [32,33,34,35].

An alternative mitigation strategy involves using an entirely passive, internal Nonlinear Energy Sink (NES). An NES comprises a small mass coupled to the primary structure via a nonlinear spring and a linear viscous damper. In Vortex-Induced Vibrations (VIV), Blanchard et al. [35] developed a rotational NES to harvest energy and suppress vibrations in a fully turbulent sprung cylinder. Later, Vaurigaud et al. [36] explored passive nonlinear energy transfer between a two-degree-of-freedom (DOF) long-span bridge model susceptible to coupled flutter and a single-degree-of-freedom NES. Casalotti et al. [37] demonstrated that hysteretic vibration absorbers outperformed their linear counterparts in reducing vibrations in long-span suspension bridges.

Additionally, Lee et al. investigated the suppression of aeroelastic instabilities in a two-DOF NES-installed rigid wing model analytically [38] and experimentally [39], finding it effective for eliminating vibration instability. It is worth noting that NES systems are challenging to manufacture and install, particularly in more robust structures, making them less practical for real-world applications. Furthermore, the vibration frequency of an NES is sensitive to amplitude changes, unlike a linear vibration absorber [40]. If the amplitude surpasses a critical level, the NES frequency can deviate significantly from the host structure's natural frequency, negatively impacting energy transfer. Linear vibration absorbers, although limited in their frequency range of suppression, can offer better dissipation capacity near resonance frequencies when properly optimized [41]. They have been successfully used to mitigate limit cycle oscillations, as reported by Habib et al. [42], and have shown effectiveness in minimizing flutter instabilities [25, 28].

However, to the authors' best knowledge, no work has been done on mitigating the VIV in the 3DOF FSI aeroelastic system, which is composed of the airfoil's plunge and pitch degrees of freedom along with the VDP wake-oscillator model. Previous studies were focused on the onset of the flutter speed [14, 25, 29, 30, 37] rather than the synchronization region occurring due to the inclusion of the wake oscillator model. In this work, we investigate the suppression of large amplitudes of VIV in the lock-in region for a 3DOF FSI aeroelastic system using a passive linear and nonlinear vibration absorber. The current model consists of a turbine blade (modeled by a 2DOF airfoil coupled with a wake oscillator) embedded with a vibration absorber modeled as a spring-mass-damper subsystem. The entire system's mass is conserved, implying that any added mass to the absorber is taken from the mass of the host structure itself. The new aeroelastic system's parameters primarily consist of the absorber's stiffness, its distance from the elastic axis, the new coupling term, the absorber's damping coefficient, and the absorber's mass ratio. It has been shown that a proper selection of these parameters can significantly decrease the amplitude of the response of the structure and fluid as compared to the previously reported works where the aeroelastic system lacks vibration absorbers [21, 24]. This enables safe operations during the lock-in region speeds. On the other hand, the structural nonlinearity of the vibration absorbers is observed as ineffective in reducing the amplitude of the limit cycle oscillation during the synchronization region.

The remainder of the paper is organized as follows. In Sect. 2, we present a detailed mathematical model of the combined four-degrees-of-freedom aeroelastic system along with the numerical frequency response. In Sect. 3, the method of multiple scales is applied to derive the analytical expression of the frequency response, followed by a parametric study of the different absorber parameters on the system dynamics in the lock-in region in Sect. 4. Finally, some conclusions are drawn in Sect. 5.

2 Mathematical modeling

To systematically present the complex coupling between the turbine blade model and the vibration absorber with the wake oscillator, we first present the mathematical model of the blade with the absorber. Later, we present the coupled model of the turbine blade with the wake oscillator model and perform the nondimensionalization of the governing equations of motion to further simplify the analysis.

2.1 Lumped parameter model of the turbine blade with the absorber

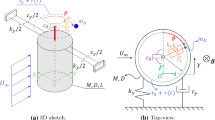
In aerodynamics, it is quite reasonable to assume the cross-section of a blade, namely, the airfoil, as the two-dimensional cascade model. Accordingly, the schematic of the aeroelastic system for the analysis is presented in Fig. 1. The model's rigid plunging (translation) and pitching (rotation) motions are restrained by linear springs and a local resonator. In engineering applications, the general trend is to maintain low vibration levels while minimizing weight using robust and lightweight materials. Hence, a conserved-mass system is considered in this work. The conserved-mass system implies that the additional mass of the absorber is equally cut from the host structure, making the system's total mass with the absorber a constant. The absorber, in practice, comprises a cantilever beam with a tip mass at a distance of \({l}_{1}b\) from the elastic axis, as shown in Fig. 1.

Fig. 1
figure 1

Schematic of the cross-section model of an isolated blade with an absorber

Full size image

It should be noted that the cantilever beam shown in Fig. 1 only serves as a practical realization of absorber installment in Aeroelastic system. As the classical inextensible viscoelastic cantilever beam is suitable for modeling a linear vibration absorber only [43], the nonlinearity in the beam can be introduced through geometric and material characteristics. For a nonlinear beam, usually the dominant nonlinearity in the first mode is geometrical and results in a hardening nonlineaity, while a softening type is imposed in the second or higher frequencies, through inertial nonlinearities [44]. Therefore, by adjusting the cantilever beam, such as employing a highly flexible beam as presented in [45] or incorporating an intermediate lumped mass as demonstrated in [46], we can effectively exhibit the characteristics of a nonlinear vibration absorber through a cantilever beam. In the current study, for the ease of the analysis of system with vibration absorber, we model the cantilever vibration absorber as an equivalent spring-mass-damper subsystem to access flexural rigidity and material damping of the cantilever beam.

Next, if the plunge translation, pitch rotation angle, and the absorber's motions are denoted by \(h,\alpha ,\) and \({x}_{1},\) respectively, then the coupled governing equations of motion for the systems' plunge and pitch motions are given by [12, 21]

$${m}_{T}\ddot{h}+{m}_{s}b{s}_{c}\ddot{\alpha }+{c}_{h}\dot{h}+{c}_{ab}\left(\dot{h}-\dot{{x}_{1}}-{l}_{1}b\dot{\alpha }\right)+{k}_{h1}h+{k}_{h2}{h}^{3}+\left({k}_{ab0}\right)\left(h-{x}_{1}-{l}_{1}b\alpha \right)+\left({k}_{ab2}\right){\left(h-{x}_{1}-{l}_{1}b\alpha \right)}^{3}= -L,$$
(1a)
$${m}_{s}b{s}_{c}\ddot{h}+{I}_{\alpha }\left(\frac{{m}_{T}}{{m}_{s}}\right)\ddot{\alpha }+{c}_{\alpha }\dot{\alpha }+{c}_{ab}\cdot {l}_{1}b\left(\dot{{x}_{1}}-\dot{h}+{l}_{1}b\dot{\alpha }\right)+{k}_{\alpha 1}\alpha +{k}_{\alpha 2}{\alpha }^{3}+\left({k}_{ab0}\right){l}_{1}b\left({x}_{1}-h+{l}_{1}b\alpha \right)+\left({k}_{ab2}\right){l}_{1}b{\left({x}_{1}-h+{l}_{1}b\alpha \right)}^{3}=M,$$

and the equation for the absorber motion is

$${m}_{ab}\ddot{{x}_{1}}+{c}_{ab}\left(\dot{{x}_{1}}-\dot{h}+{l}_{1}b\dot{\alpha }\right)+\left({k}_{ab0}\right)\left({x}_{1}-h+{l}_{1}b \alpha \right)+\left({k}_{ab2}\right){\left({x}_{1}-h+{l}_{1}b \alpha \right)}^{3}=0.$$
(1b)

In the above equations, \({m}_{T}=\left({m}_{s}+{m}_{f}\right)\) is the total mass with \({m}_{s}\) as the mass of the turbine blade and its support structure, while \({m}_{f}\) is the fluid-added mass; \({m}_{ab}\) is the mass of the absorber. Note that the total mass is conserved, which means that the additional mass of the absorber is equally cut from the host structure to keep the mass of the aeroelastic system constant. This step ensures that the mitigation of vibration occurs due to the absorber motion and not because of the addition of mass to the system. Further, \({I}_{\alpha }\) is the mass moment of inertia about the elastic axis; \(b\) is the half-chord length, and \({s}_{c}\), also known as static unbalance, indicates the dimensionless distance between the elastic axis and the center of mass; \({x}_{\alpha }\) is the nondimensional distance between the center of mass and the elastic axis; \(l\) is the nondimensional distance between the elastic axis and the position of the absorber. Linear viscous dampers are considered for the analysis with \({c}_{h}\),\({c}_{\alpha }\), \({c}_{ab}\) are the viscous damping coefficients for the plunge, pitch, and absorber, respectively. The absorber's linear and nonlinear stiffness coefficients are denoted by \({k}_{ab0}\) and \({k}_{ab2}\) respectively. Further, \({k}_{h1}\) and \({k}_{\alpha 1}\) are the linear stiffness of the spring in bending and torsion motion, respectively, while \({k}_{h2}\) and \({k}_{\alpha 2}\) are the nonlinear stiffness of the spring in bending and torsion motion, respectively. \(L\) and \(M\) denote the lift and the aerodynamic moment about the elastic axis, respectively. Moreover, we introduce the uncoupled, natural frequencies of the plunge, pitch, and absorber motions at zero airspeeds as.

$${\omega }_{h}=\sqrt{\frac{{k}_{h1}}{{m}_{s}}},{\omega }_{\alpha }=\sqrt{\frac{{k}_{\alpha 1}}{{I}_{\alpha }}} ,\,\, \text{and} \,\,{\omega }_{ab}=\sqrt{\frac{{k}_{ab}}{{m}_{ab}}} ,$$

respectively, the dimensionless time, \({t}^{*}={\omega }_{\alpha }\) t, the dimensionless plunge motion \({h}^{*}=h/b\) and the dimensionless absorber motion \({x}_{1}^{*}={x}_{1}/b\) to non-dimensionalize Eq. (1). The nondimensional governing equations are given by

$$\lambda \ddot{h}+{s}_{c}\ddot{\alpha }+2{\zeta }_{h}{\omega }_{\alpha } \dot{h}+2{\zeta }_{ab}{\omega }_{b}\left(\dot{h}-\dot{{x}_{1}}-{l}_{1}\dot{\alpha }\right)+{\omega }_{a}^{2} h+{\epsilon }_{h}{\omega }_{a}^{2} {h}^{3}+{\omega }_{b}^{2} \left(h-{x}_{1}-{l}_{1}\alpha \right)+{\epsilon }_{ab} {\omega }_{a}^{2} {\left(h-{x}_{1}-{l}_{1}\alpha \right)}^{3}=\widetilde{L},$$
(2)
$${s}_{c}\ddot{h}+\lambda {r}_{\alpha }^{2} \ddot{\alpha }+2{\zeta }_{\alpha }{r}_{\alpha }^{2} \dot{\alpha }+2{\zeta }_{ab}{\omega }_{b} {l}_{1} \left(\dot{{x}_{1}}-\dot{h}+{l}_{1}\dot{\alpha }\right)+{r}_{\alpha }^{2} \alpha +{\epsilon }_{\alpha }{r}_{\alpha }^{2} {\alpha }^{3}+{\omega }_{b}^{2} {l}_{1} \left({x}_{1}-h+{l}_{1}\alpha \right)+{\epsilon }_{ab} {\omega }_{a}^{2} {l}_{1} {\left({x}_{1}-h+{l}_{1}\alpha \right)}^{3}=\widetilde{M},$$
$${\mu }_{ab}\ddot{{x}_{1}}+2{\zeta }_{ab}{\omega }_{b}\left(\dot{{x}_{1}}-\dot{h}+{l}_{1}\dot{\alpha }\right)+{\omega }_{b}^{2}\left({x}_{1}-h+{l}_{1}\alpha \right)+{\epsilon }_{ab} {\omega }_{a}^{2}{\left({x}_{1}-h+{l}_{1}\alpha \right)}^{3}=0.$$

In the above equations (Eq. (2)), the nondimensional quantities are defined as

$$\lambda =\frac{{m}_{T}}{{m}_{s}},\quad {\mu }_{ab}=\frac{{m}_{ab}}{{m}_{s}},\quad {\omega }_{a}=\frac{{\omega }_{h}}{{\omega }_{\alpha }},\quad {\omega }_{b}= \frac{{\omega }_{ab}}{{\omega }_{\alpha }},$$
(3)
$${\zeta }_{h}=\frac{{c}_{h}}{2{m}_{s}{\omega }_{h}},\quad {\zeta }_{\alpha }=\frac{{c}_{\alpha }}{2{I}_{\alpha }{\omega }_{\alpha }},\quad {\zeta }_{ab}= \frac{{c}_{ab}}{2{m}_{s}{\omega }_{ab}},$$
$${\epsilon }_{h}=\frac{{k}_{h2}{b}^{2}}{{k}_{h1}},\quad {\epsilon }_{\alpha }=\frac{{k}_{\alpha 2}}{{k}_{\alpha 1}},\quad {\epsilon }_{ab}=\frac{{k}_{ab2}{b}^{2}}{{k}_{ab0}},\quad {r}_{\alpha }=\sqrt{\frac{{I}_{\alpha }}{{m}_{s}{b}^{2}}},$$
$$\widetilde{L}= \frac{-L}{{m}_{s}b{\omega }_{\alpha }^{2}},\quad {\text{and}}\quad \widetilde{M}=\frac{M}{{m}_{s}{b}^{2}{\omega }_{\alpha }^{2}} .$$

We emphasize that \({\left(\right)}^{*}\) is dropped from the notation for the sake of simplicity in writing. In the above equations, \({\mu }_{a}\) is the mass ratio; \({\omega }_{a}\) is the ratio of uncoupled plunge and pitch frequencies and \({\omega }_{b}\) is the ratio of the uncoupled absorber and pitch frequencies; \({\zeta }_{h}\), \({\zeta }_{\alpha }\) and \({\zeta }_{ab}\) are damping coefficients for plunge, pitch, and absorber, respectively; \({\epsilon }_{h}\) and \({\epsilon }_{\alpha }\) are the coefficients for cubic nonlinearity in plunge and pitch motion, respectively, and \({r}_{\alpha }\) is the dimensionless radius of gyration of the section about the elastic axis. To include the time-varying aerodynamic lift force and the aerodynamic moment, we use the VDP-based wake oscillator and presented in the next section.

2.2 The van der Pol oscillator

In the current work, the van der Pol oscillator represents the time-varying force caused by the alternate shedding of the vortices [18, 22]. The governing equation for this model can be expressed as follows:

$$\ddot{q}+\beta {f}_{v} \left({q}^{2}-1\right)\dot{q}+{f}_{v}^{2}q={f}_{s},$$
(4)

where the coefficient of unsteady vortex lift is expressed by the wake variable \(q\). The lift in terms of \(q\) is given by \({C}_{L}=\frac{1}{2}q{C}_{L0}\), with \({C}_{L0}\) as the reference lift coefficient of the fluctuating lift force when a fixed, rigid blade is subjected to VIV. \({f}_{v}=\frac{2\pi SV}{b}\) is the angular frequency of the vortex shedding with \(S\) as the Strouhal number and \(V\) as the free stream velocity. Moreover, \(\beta \) is the nonlinear damping coefficient of the wake-oscillator model. Using earlier mentioned nondimensional scales, the nondimensional form of Eq. (4) can be written as

$$\ddot{q}+\beta {\omega }_{v}\left({q}^{2}-1\right)\dot{q}+ {\omega }_{v}^{2}q={F}_{s},$$
(5)

where \({\omega }_{v}=2\pi S{U}_{r}\) is the dimensionless wake frequency in which \({U}_{r}(=V/(b{\omega }_{\alpha })\)) is the reduced velocity. The structural and fluid coupling terms are given by \({F}_{s}={f}_{s}/{\omega }_{\alpha }^{2}\).

2.3 Four-degree-of-freedom FSI model

Hodges and Pierce [10] demonstrated that the lift force and moment in the aeroelastic model of the time-varying vortex force from the wake dynamics near the blade is given by

$$L=\rho {V}^{2}b{C}_{L}, \mathrm{and } M=b\left({s}_{c}+\frac{1}{2}\right)L,$$
(6)

where \(\rho \) is the air density. Thus \(\widetilde{L}\) and \(\widetilde{M}\) in Eq. (2) will be modified to

$$\widetilde{L}=v{\omega }_{v}^{2}q, \mathrm{and }\widetilde{M}=\left({s}_{c}+0.5\right)v{\omega }_{v}^{2}q.$$
(7)

In the above expressions, \(v=\frac{{C}_{L0}}{8{\pi }^{2}{S}^{2}\mu }\) and \(\mu =\frac{{m}_{s}}{\rho {b}^{2}}\) are the mass number (to determine the scale of the vortex force on the blade) and the dimensionless mass ratio, respectively [18].

Accordingly, the forcing term in the wake-oscillator, Eq. (5), is assumed to be related to accelerations as

$${F}_{s}={\gamma }_{1}\ddot{h}+{\gamma }_{2}\ddot{\alpha }+{\gamma }_{3}\ddot{{x}_{1}},$$
(8)

where \({\gamma }_{1},{\gamma }_{2}\) and \({\gamma }_{3}\) are the wake oscillator's coupling coefficients with the plunge, pitch, and absorber motions, respectively.

Upon substituting all coupling terms, the governing equations of motion for the coupled 4DOF FSI aeroelastic system are given by

$$\ddot{h}+{s}_{1}\ddot{\alpha }+{\zeta }_{1} \dot{h}+{\zeta }_{abh}\left(\dot{h}-\dot{{x}_{1}}-{l}_{1}\dot{\alpha }\right)+{\omega }_{1}^{2} h+{\epsilon }_{1} {h}^{3}+\omega {}_{bh}^{2} \left(h-{x}_{1}-{l}_{1}\alpha \right)+{\epsilon }_{3} {\left(h-{x}_{1}-{l}_{1}\alpha \right)}^{3}=-{\eta }_{1}{\omega }_{v}^{2}q,$$
(9)
$$\ddot{\alpha }+{s}_{2}\ddot{h}+{\zeta }_{2} \dot{\alpha }+{\zeta }_{ab\alpha } {l}_{1} \left(\dot{{x}_{1}}-\dot{h}+{l}_{1}\dot{\alpha }\right)+{\omega }_{2}^{2} \alpha +{\epsilon }_{2} {\alpha }^{3} +{\omega }_{b\alpha }^{2} {l}_{1} \left({x}_{1}-h+{l}_{1}\alpha \right)+{\epsilon }_{3} {l}_{1} {\left({x}_{1}-h+{l}_{1}\alpha \right)}^{3}={\eta }_{2}{\omega }_{v}^{2}q,$$
$$\ddot{q}+\beta {\omega }_{v}\left({q}^{2}-1\right)\dot{q}+ {\omega }_{v}^{2}q={\gamma }_{1}\ddot{h}+{\gamma }_{2}\ddot{\alpha }+{\gamma }_{3}\ddot{{x}_{1}},$$
$$\ddot{{x}_{1}}+{\zeta }_{abx} \left(\dot{{x}_{1}}-\dot{h}+{l}_{1}\dot{\alpha }\right)+{\omega }_{bx}^{2}\left({x}_{1}-h+{l}_{1}\alpha \right)+{\epsilon }_{4}{\left({x}_{1}-h+{l}_{1}\alpha \right)}^{3}=0.$$

where

$$\begin{aligned} {\zeta }_{1}&= \frac{2{\zeta }_{h}{\omega }_{a}}{\lambda } , {\zeta }_{2}=\frac{2{\zeta }_{\alpha }}{\lambda } , \\ {\zeta }_{abh}&= \frac{2{\zeta }_{ab}{\omega }_{b}}{\lambda } , {\zeta }_{ab\alpha }= \frac{2{\zeta }_{ab}{\omega }_{b}}{\lambda {r}_{\alpha }^{2}} , \\{\zeta }_{abx}&= \frac{2{\zeta }_{ab}{\omega }_{b}}{\kappa } ,\end{aligned}$$
(10)
$${\omega }_{1}^{2}= \frac{{\omega }_{a}^{2}}{\lambda } , {\omega }_{2}^{2}=\frac{1}{\lambda } , \omega {}_{bh}^{2}=\frac{{\omega }_{b}^{2}}{\lambda } , {\omega }_{b\alpha }^{2}= \frac{{\omega }_{b}^{2}}{\lambda {r}_{\alpha }^{2}} , {\omega }_{bx}^{2}= \frac{{\omega }_{b}^{2}}{{\mu }_{ab}} ,$$
$$\begin{aligned}{s}_{1}&=\frac{{s}_{c}}{\lambda } , {s}_{2}= \frac{{s}_{c}}{\lambda {r}_{\alpha }^{2}} , \\{\epsilon }_{1}&=\frac{{\epsilon }_{h}{\omega }_{a}^{2}}{\lambda } , {\epsilon }_{2}=\frac{{\epsilon }_{\alpha }}{\lambda } , {\epsilon }_{3}=\frac{{\epsilon }_{ab}{\omega }_{a}^{2}}{\lambda } , {\epsilon }_{4}=\frac{{\epsilon }_{ab}{\omega }_{a}^{2}}{{\mu }_{ab}} ,\end{aligned}$$
$${\eta }_{1}=\frac{v}{\lambda } ,\,\, \text{and }\,\,{\eta }_{2}=\frac{v\left(s+0.5\right)}{\lambda {r}_{\alpha }^{2}} .$$

We first start with exploring the effect of the linear absorber on the vibration attenuation of the turbine blade to understand the frequency synchronization phenomenon. For this, the dimensionless linear undamped frequencies of the plunge, the pitch, the absorber, and the wake frequencies of the coupled system need to be determined. Accordingly, the coupled linear undamped equations are

$$\ddot{h}+{s}_{1}\ddot{\alpha }+{\omega }_{1}^{2} h+{\omega }_{bh}^{2} \left(h-{x}_{1}-{l}_{1}\alpha \right)+{\eta }_{1}{\omega }_{v}^{2}q=0,$$
(11)
$$\ddot{\alpha }+{s}_{2}\ddot{h}+{\omega }_{2}^{2} \alpha +{\omega }_{b\alpha }^{2} {l}_{1} \left({x}_{1}-h+{l}_{1}\alpha \right)- {\eta }_{2}{\omega }_{v}^{2}q=0,$$
$$\ddot{q}+{\omega }_{v}^{2}q- {\gamma }_{1}\ddot{h}-{\gamma }_{2}\ddot{\alpha }-{\gamma }_{3}\ddot{{x}_{1}}=0,$$
$$\ddot{{x}_{1}}+{\omega }_{bx}^{2}\left({x}_{1}-h+{l}_{1}\alpha \right)=0.$$

We assume the synchronous solution of Eq. (11) in the form of

$$\left\{h, \alpha, q \, {x}_{1}\right\}=\left\{{h}_{0} ,{\alpha }_{0}, {q}_{0}, {x}_{10}\right\} {e}^{i\mathrm{\Omega t}}.$$
(12)

Substituting the assumed form of the solution in Eq. (11), we get the characteristic equation

$$\left(1-{s}_{1}{s}_{2}\right) {{\varvec{\Omega}}}^{8}-\left({\omega }_{1}^{2}+{\omega }_{2}^{2}+{l}_{1}^{2}{\omega }_{b\alpha }^{2}+{l}_{1}{s}_{1}{\omega }_{b\alpha }^{2}+{\omega }_{bh}^{2}+{l}_{1}{s}_{2}{\omega }_{bh}^{2}+{\omega }_{bx}^{2}-{s}_{1}{s}_{2}{\omega }_{bx}^{2}+{\omega }_{v}^{2}-{s}_{1}{s}_{2}{\omega }_{v}^{2}+{\gamma }_{1}{\eta }_{1}{\omega }_{v}^{2}-{s}_{2}{\gamma }_{2}{\eta }_{1}{\omega }_{v}^{2}+{s}_{1}{\gamma }_{1}{\eta }_{2}{\omega }_{v}^{2}-{\gamma }_{2}{\eta }_{2}{\omega }_{v}^{2}\right) {{\varvec{\Omega}}}^{6}+\left({\omega }_{1}^{2}\left[{\omega }_{2}^{2}+{l}_{1}^{2}{\omega }_{b\alpha }^{2}+{\omega }_{bx}^{2}+{\omega }_{v}^{2}-{\gamma }_{2}{\eta }_{2}{\omega }_{v}^{2}\right]+{\omega }_{2}^{2}\left[{\omega }_{bh}^{2}+{\omega }_{bx}^{2}+\left(1+{\gamma }_{1}{\eta }_{1}\right){\omega }_{v}^{2}\right]+{\omega }_{v}^{2}\left[{l}_{1}^{2}{\omega }_{b\alpha }^{2}\left(1+{\gamma }_{1}{\eta }_{1}\right)+{\omega }_{bh}^{2}\left(1-{\gamma }_{2}{\eta }_{2}\right)+\left(1-{s}_{1}{s}_{2}+{\gamma }_{1}{\eta }_{1}-{s}_{2}{\eta }_{2}{\gamma }_{1}+{\gamma }_{3}{\eta }_{1}-{\gamma }_{2}{\eta }_{2}+{s}_{1}\left({\gamma }_{1}+{\gamma }_{3}\right) {\eta }_{2}\right){\omega }_{bx}^{2}+{l}_{1}\left({s}_{1}{\omega }_{b\alpha }^{2}+{\gamma }_{2}{\eta }_{1}{\omega }_{b\alpha }^{2}+{s}_{2}{\omega }_{bh}^{2}-{\gamma }_{1}{\eta }_{2}{\omega }_{bh}^{2}+{s}_{2}{\gamma }_{3}{\eta }_{1}{\omega }_{bx}^{2}+{\gamma }_{3}{\eta }_{2}{\omega }_{bx}^{2}\right)\right]\right) {{\varvec{\Omega}}}^{4}-\left({\omega }_{1}^{2}{\omega }_{v}^{2}\left[{l}_{1}^{2}{\omega }_{b\alpha }^{2}+{\omega }_{bx}^{2}-{\gamma }_{2}{\eta }_{2}{\omega }_{bx}^{2}+{l}_{1}{\gamma }_{3}{\eta }_{2}{\omega }_{bx}^{2}\right]+{\omega }_{2}^{2}{\omega }_{v}^{2}\left[{\omega }_{bh}^{2}+{\omega }_{bx}^{2}\left(1+{\gamma }_{1}{\eta }_{1}+{\gamma }_{3}{\eta }_{1}\right)\right]+{\omega }_{2}^{2}\left[{\omega }_{bx}^{2}+{\omega }_{v}^{2}\right]\right) {{\varvec{\Omega}}}^{2}+{\omega }_{1}^{2}{\omega }_{2}^{2}{\omega }_{v}^{2}{\omega }_{x}^{2}=0. $$
(13)

The roots of Eq. (13) are in the terms of \({\Omega }^{2}\) where \({\Omega }_{i}, i=1, 2, 3\) and 4 are the dimensionless frequencies of the coupled system associated with the pitch, plunge, wake-oscillator, and absorber motions, respectively. Moreover, the variation of the four natural frequencies of the coupled system with parameter \(\lambda \) determines the occurrence of internal resonance and is shown in Fig. 2a. Unlike the case for the system without absorbers, in the current case, \(\lambda \) is determined as a function of the absorber's and system parameter. It should be noted that by definition, the term \(\lambda \) includes the fluid-added mass in the system, which in the current case depends on the mass of the absorber, its location along the turbine blade, and the other factors that could interact with the wind. Therefore, making \(\lambda \) as a function of internal resonance for each configuration rather than being a constant. For instance, Fig. 2a demonstrates two cases where resonance occurs and corresponds to \(\lambda =0.9514\) and \(\lambda =1.014,\) respectively, for two different absorber locations. Note that there could be several possible internal resonance cases. However, from our calculations, the \(1:1\) internal resonance between the pitch and wake motion showed the lowest value of \(\lambda \) (i.e., fluid-added mass). Since the fluid-added mass is relatively small in this case compared to that of the blade in the turbomachinery [21], the internal resonance case between pitch and wake motion \({(\Omega }_{2}\approx {\Omega }_{3})\) will be the focus of the remainder of the analysis. This case of the internal resonance (plunge lock-in region) has been highlighted in Fig. 2. Furthermore, the heave natural frequencies for both configurations (different locations of the absorber represented by blue and green colors) are the same. Therefore, we plot it as a dotted line to distinguish it from the blue curve. The VDP and structural parameters are fixed for both scenarios in Fig. 2a and are adopted from [24] where \(\beta =0.3\), \({C}_{L0}=0.2\), \({s}_{c}=0.1, {r}_{\alpha }=0.5; {\omega }_{h}=73, {\omega }_{\alpha }=200, {\zeta }_{h}=0.016\) and \({\zeta }_{\alpha }=0.021.\) Note that for these variations \({\epsilon }_{h}={\epsilon }_{\alpha }=0\). The absorber's parameters used in each case are (blue) \({l}_{1}=0.5, {\omega }_{b}=0.2, {\mu }_{ab}=1.5\%\), \({\gamma }_{3}=2\) and (green) \({l}_{1}=0.1, {\omega }_{b}=0.2, {\mu }_{ab}=1.5\%\), \({\gamma }_{3}=2\).

Fig. 2
figure 2

a Variation of natural frequencies with the parameter \(\lambda ,\) with \(1:1\) resonance and b frequency of the coupled system with and without absorber

Full size image

Furthermore, the coupled natural frequencies of the system are plotted in Fig. 2b as functions of \({\omega }_{v}\) for the absorber parameters \({l}_{1}=0.5, {\omega }_{b}=0.2, {\mu }_{ab}=1\%\), \({\gamma }_{3}=2\) and \(\lambda =1.0252\). Figure 2b compares the variation of \({\Omega }_{i}\) with \({\omega }_{v}\) for two cases, viz., with and without [24] absorber. In both cases, it is apparent that the line \(\Omega ={\omega }_{v}\) corresponds to the wake mode \({\Omega }_{3}\). The frequency close to one is the mode associated with the torsional motion \({\Omega }_{2}\) whereas the higher and lower frequencies are associated with the absorber and plunging motion, respectively. The figure shows the impact of the addition of the absorber on the system's lock-in response. In both cases, the Strouhal Law relates to the \({\Omega }_{3}\) and \({\omega }_{v}\) (and eventually, the reduced velocity \({U}_{r}\)) proportionally. However, for certain \({\omega }_{v}\) values, when the wake mode is close to any of the other frequencies, the wake mode deviates from the Strouhal law, and the lock-in phenomena occur. A deeper visualization of these figures can be demonstrated with the frequency response curves plotted in Fig. 3. In both Figs. 2b, 3, we observe that the initial lock-in (bending) occurs for almost the same frequency range in both cases, with and without absorbers. Initially, Fig. 3a, c show the increase in the amplitude of \(h\) and \(q\) within this range. However, for the given system parameters, it has been shown that with few alterations on the absorber parameters, the amplitude during the initial lock-in can be mitigated. Furthermore, we can observe the noticeable shrinkage of the plunge lock-in region (blue vs. red background) with the addition of the absorber. Also, for the same range, with different values of absorber parameters, not only does the lock-in region shrink, but the amplitude of vibrations attenuates significantly.

Fig. 3
figure 3

Frequency response of the coupled system

Full size image

To demonstrate the absorber's effect on the aeroelastic system's dynamic response, we show the time histories of the different motions of the coupled system at a fixed reduced air stream velocity with and without the vibration absorbers. For this, we numerically integrate the coupled system using the Runge–Kutta method, and the time responses are shown in Fig. 4. The absorber values are \({l}_{1}=0.5, {\omega }_{b}=0.2, {\mu }_{ab}=1\%\), \({\gamma }_{3}=0.5\) and \({\zeta }_{ab}=0.1\). From Fig. 4, we can observe that for the given values of system and absorber parameters, the linear vibration absorber successfully attenuates the plunge and pitch motion of the turbine blades.

Fig. 4
figure 4

Dynamic response (time history) of the aeroelastic system at \({U}_{r}=1.16 {\text{m}}/{\text{s}}\) (with and without an absorber)

Full size image

Next, we explore the effect of a nonlinear vibration absorber on the system's dynamics. For this, we compare the frequency response of the system with a linear absorber and with a nonlinear absorber; the comparison is shown in Fig. 5. From Fig. 5, we can observe that within the range of operation, as suggested by the literature [24], the self-excited limit cycle oscillations do not seem to be significantly affected by the inclusion of nonlinearity in the vibration absorber. Since the system's response remains unchanged, it is suggested that the forcing amplitudes within this range of frequencies are not high enough to trigger the nonlinearities in the absorber. For the sake of theoretical investigation, Fig. 5b compares the system with a high coupling term and an intermediate coupling term, which in turn implies a high and moderate forcing to the system, respectively. We observe that the nonlinear vibration absorber outperforms its linear absorber counterpart for the smaller values of nonlinear stiffness in the nonlinear vibration absorber. However, as the nonlinear stiffness increases, higher amplitudes appear in the system than those of the linear vibration absorber. Figure 5b depicts that incorporating a nonlinear spring for the absorber can be effective for a specific choice of parameters, which ends up being an optimization problem. This is out of the scope of the current work and is left for future study. Therefore, we analyze the coupled system with a linear vibration absorber in the subsequent analysis. In the next section, we perform the method of multiple-scale to obtain an analytical frequency response relationship.

Fig. 5
figure 5

Frequency response curves for the van der Pol oscillation for a linear and a nonlinear absorber: a low coupling coefficient, b high coupling coefficient

Full size image

3 The method of multiple scales

As mentioned earlier, our prime interest in this section is to get an analytical solution for our coupled system with the linear vibration absorber. For this purpose, we use a perturbation technique, specifically the method of multiple scales. We follow the procedure outlined in [47] and introduce a small bookkeeping parameter \(\epsilon \) in the system by rescaling the fluid force, the damping, and the nonlinearity. This step ensures that the effect of damping and nonlinearity appears in the same order of \(\epsilon \). Using these rescales, we modify our governing equations of motion Eq. (9) as

$$\ddot{h}+{s}_{1}\ddot{\alpha }+{\omega }_{1}^{2} h+{\omega }_{bh}^{2} \left(h-{x}_{1}-{l}_{1}\alpha \right)=\epsilon \left\{-{\eta }_{1}{\omega }_{v}^{2}q-{\zeta }_{1} \dot{h}-{\zeta }_{abh}\left(\dot{h}-\dot{{x}_{1}}-{l}_{1}\dot{\alpha }\right)-{\epsilon }_{1} {h}^{3}\right\},$$
(14)
$$\ddot{\alpha }+{s}_{2}\ddot{h}+{\omega }_{2}^{2} \alpha +{\omega }_{b\alpha }^{2} {l}_{1} \left({x}_{1}-h+{l}_{1}\alpha \right)=\epsilon \left\{{\eta }_{2}{\omega }_{v}^{2}q-{\zeta }_{2} \dot{\alpha }-{\zeta }_{ab\alpha } {l}_{1} \left(\dot{{x}_{1}}-\dot{h}+{l}_{1}\dot{\alpha }\right)-{\epsilon }_{2} {\alpha }^{3}\right\},$$
$$\ddot{q}+{\omega }_{v}^{2}q=\epsilon \left\{{\gamma }_{1}\ddot{h}+{\gamma }_{2}\ddot{\alpha }+{\gamma }_{3}\ddot{{x}_{1}}-\beta {\omega }_{v}\left({q}^{2}-1\right)\dot{q}\right\},$$
$$\ddot{{x}_{1}}+{\omega }_{bx}^{2}\left({x}_{1}-h+{l}_{1}\alpha \right)=\epsilon \left\{-{\zeta }_{abx} \left(\dot{{x}_{1}}-\dot{h}+{l}_{1}\dot{\alpha }\right)\right\}.$$

Next, we introduce multiple time scales as \({T}_{j}={\epsilon }^{j}\tau \). The introduction of these scales leads to the perturbation in the differential operator as \(d/d\tau = {D}_{0}+\epsilon {D}_{1}+O\left({\epsilon }^{2}\right)\) and \({d}^{2}/d{\tau }^{2} ={D}_{0}^{2}+2\epsilon {D}_{0}{D}_{1}+O\left({\epsilon }^{2}\right)\), where \({D}_{i}^{j}={\partial }^{j}/\partial {T}_{i}^{j}\).

The approximate solution of the coupled system in multiple time scales can be expressed as

$$\begin{aligned} h&={h}_{0}\left({T}_{0},{T}_{1}\right)+\epsilon {h}_{1}\left({T}_{0},{T}_{1}\right)+O\left({\epsilon }^{2}\right), \\ \alpha &={\alpha }_{0}\left({T}_{0},{T}_{1}\right)+\epsilon {\alpha }_{1}\left({T}_{0},{T}_{1}\right)+O\left({\epsilon }^{2}\right),\\ q&={q}_{0}\left({T}_{0},{T}_{1}\right)+\epsilon {q}_{1}\left({T}_{0},{T}_{1}\right)+O\left({\epsilon }^{2}\right), \\ {x}_{1}&={x}_{10}\left({T}_{0},{T}_{1}\right)+\epsilon {x}_{11}\left({T}_{0},{T}_{1}\right)+O\left({\epsilon }^{2}\right). \end{aligned}$$
(15)

Substituting Eq. (15) along with the perturbed differential operator into Eq. (14) and equating coefficients of like powers of \(\epsilon \), we obtain

$${\epsilon }^{0}: {D}_{0}^{2}{h}_{0}+{s}_{1}{D}_{0}^{2}{\alpha }_{0}+{\omega }_{1}^{2}{h}_{0}+{\omega }_{bh}^{2}\left({h}_{0}-{l}_{1}{\alpha }_{0}-{x}_{10}\right)=0,$$
(16)
$${D}_{0}^{2}{\alpha }_{0}+{s}_{2}{D}_{0}^{2}{h}_{0}+{\omega }_{2}^{2}{\alpha }_{0}+{\omega }_{b\alpha }^{2}{l}_{1}\left({l}_{1}{\alpha }_{0}-{h}_{0}+{x}_{10}\right)=0,$$
$${D}_{0}^{2}{q}_{0}+{q}_{0}{\omega }_{v}^{2}=0,$$
$${D}_{0}^{2}{x}_{10}-{\omega }_{bx}^{2}\left({h}_{0}-{l}_{1}{\alpha }_{0}-{x}_{10}\right)=0.$$
$${\epsilon }^{1}: {D}_{0}^{2}{h}_{1}+{s}_{1}{D}_{0}^{2}{\alpha }_{1}+{\omega }_{1}^{2}{h}_{1}+{\omega }_{bh}^{2}\left({h}_{1}-{l}_{1}{\alpha }_{1}-{x}_{11}\right)=-{\eta }_{1}{\omega }_{v}^{2}{q}_{0}-2{s}_{1}{D}_{0}{D}_{1}{\alpha }_{0}-2{D}_{0}{D}_{1}{h}_{0}-{\zeta }_{1}{D}_{0}{h}_{0}-{\zeta }_{abh}\left({D}_{0}{h}_{0}-{l}_{1}{D}_{0}{\alpha }_{0}-{D}_{0}{x}_{10}\right)-{\epsilon }_{1}{h}_{0}^{3},$$
(17)
$${D}_{0}^{2}{\alpha }_{1}+{s}_{2}{D}_{0}^{2}{h}_{1}+{\omega }_{2}^{2}{\alpha }_{1}+{\omega }_{b\alpha }^{2}{l}_{1}\left({l}_{1}{\alpha }_{1}-{h}_{1}+{x}_{11}\right)={\eta }_{2}{\omega }_{v}^{2}{q}_{0}-2{s}_{2}{D}_{0}{D}_{1}{h}_{0}-2{D}_{0}{D}_{1}{\alpha }_{0}-{\zeta }_{2}{D}_{0}{\alpha }_{0}-{\zeta }_{ab\alpha }{l}_{1}\left({l}_{1}{D}_{0}{\alpha }_{0}-{D}_{0}{h}_{0}+{D}_{0}{x}_{10}\right)-{\epsilon }_{2}{\alpha }_{0}^{3},$$
$${D}_{0}^{2}{q}_{1}+{\omega }_{v}^{2}{q}_{1}={\gamma }_{1}{D}_{0}^{2}{h}_{0}+{\gamma }_{2}{D}_{0}^{2}{\alpha }_{0}+{\gamma }_{3}{D}_{0}^{2}{x}_{10}-2{D}_{0}{D}_{1}{q}_{0}-\beta {\omega }_{v}\left({q}_{0}^{2}-1\right){D}_{0}{q}_{1},$$
$${D}_{0}^{2}{x}_{11}-{\omega }_{bx}^{2}\left({h}_{1}-{l}_{1}{\alpha }_{1}-{x}_{11}\right)=-2{D}_{0}{D}_{1}{x}_{10}+{\zeta }_{abx}\left({D}_{0}{h}_{0}-{l}_{1}{D}_{0}{\alpha }_{0}-{D}_{0}{x}_{10}\right).$$

Equation (16) represents an undamped and unforced linear oscillator; hence, the general solutions of Eq. (16) can be written as:

$${h}_{0}={P}_{11}\left[A\left({T}_{1}\right){e}^{i{\Omega }_{1}{T}_{0}}\right]+{P}_{21}\left[B\left({T}_{1}\right){e}^{i{\Omega }_{2}{T}_{0}}\right]+{P}_{31}\left[D\left({T}_{1}\right){e}^{i{\Omega }_{3}{T}_{0}}\right]+c.c. ,$$
(18)
$${\alpha }_{0}={P}_{12}\left[A\left({T}_{1}\right){e}^{i{\Omega }_{1}{T}_{0}}\right]+{P}_{22}\left[B\left({T}_{1}\right){e}^{i{\Omega }_{2}{T}_{0}}\right]+{P}_{32}\left[D\left({T}_{1}\right){e}^{i{\Omega }_{3}{T}_{0}}\right] +c.c. ,$$
$${q}_{0}=C\left({T}_{1}\right){e}^{i{\omega }_{v}{T}_{0}}+c.c.,$$
$${x}_{10}={P}_{13}\left[A\left({T}_{1}\right){e}^{i{\Omega }_{1}{T}_{0}}\right]+{P}_{23}\left[B\left({T}_{1}\right){e}^{i{\Omega }_{2}{T}_{0}}\right]+{P}_{33}\left[D\left({T}_{1}\right){e}^{i{\Omega }_{3}{T}_{0}}\right] +c.c.$$

where \(A\left({T}_{1}\right), B\left({T}_{1}\right), C\left({T}_{1}\right)\) and \(D\left({T}_{1}\right)\) are the complex functions of time scale \({T}_{1}\) and \(c.c.\) represents the complex conjugate terms. Moreover, \({P}_{j3}=1 \left( j=\mathrm{1,2},3\right)\), while \({P}_{i1}\) and \({P}_{i2}\) \(\left(i=\mathrm{1,2},3\right)\) are given by

$${P}_{i1}=\frac{{{\upomega }_{2}^{2} {\upomega }_{{\text{bh}}}^{2}-\left({l}_{1}{s}_{1}{\omega }_{b\alpha }^{2}+{\omega }_{bh}^{2}\right)\Omega }_{i}^{2}}{\left(1-{s}_{1}{s}_{2}\right){\Omega }_{i}^{4}-\left({\omega }_{1}^{2}+{\omega }_{2}^{2}+{l}_{1}^{2}{\omega }_{\alpha }^{2}+{l}_{1}{s}_{1}{\omega }_{b\alpha }^{2}+{\omega }_{bh}^{2}+{l}_{1}{s}_{2}{\omega }_{bh}^{2}\right){\Omega }_{i}^{2}+{\omega }_{1}^{2}\left({\omega }_{2}^{2}+{l}_{1}^{2}{\omega }_{b\alpha }^{2}\right)+{\omega }_{2}^{2}{\omega }_{bh}^{2}} ,$$
(19)
$${P}_{i2}=\frac{{-{l}_{1}{\omega }_{1}^{2}{\omega }_{b\alpha }^{2}+\left({l}_{1}{\omega }_{b\alpha }^{2}+{{s}_{2}\omega }_{bh}^{2}\right)\Omega }_{i}^{2}}{\left(1-{s}_{1}{s}_{2}\right){\Omega }_{i}^{4}-\left({\omega }_{1}^{2}+{\omega }_{2}^{2}+{l}_{1}^{2}{\omega }_{\alpha }^{2}+{l}_{1}{s}_{1}{\omega }_{b\alpha }^{2}+{\omega }_{bh}^{2}+{l}_{1}{s}_{2}{\omega }_{bh}^{2}\right){\Omega }_{i}^{2}+{\omega }_{1}^{2}\left({\omega }_{2}^{2}+{l}_{1}^{2}{\omega }_{b\alpha }^{2}\right)+{\omega }_{2}^{2}{\omega }_{bh}^{2}} ,$$

and are the modal parameters. Further, the natural frequencies of the coupled equation can be obtained by solving the characteristic equation

$$\left(-1+{s}_{1}{s}_{2}\right){\Omega }^{6}+\left({\omega }_{1}^{2}+{\omega }_{2}^{2}+{l}_{1}^{2}{\omega }_{b\alpha }^{2}+{l}_{1}{s}_{1}{\omega }_{b\alpha }^{2}+{\omega }_{bh}^{2}+{l}_{1}{s}_{2}{\omega }_{bh}^{2}+{\omega }_{bx}^{2}-{s}_{1}{s}_{2}{\omega }_{bx}^{2}\right){\Omega }^{4}+\left(-{\omega }_{1}^{2}{\omega }_{2}^{2}-{l}_{1}^{2}{\omega }_{1}^{2}{\omega }_{b\alpha }^{2}-{\omega }_{2}^{2}{\omega }_{bh}^{2}-{\omega }_{1}^{2}{\omega }_{bx}^{2}-{\omega }_{2}^{2}{\omega }_{bx}^{2}\right){\Omega }^{2}+{\omega }_{1}^{2}{\omega }_{2}^{2}{\omega }_{bx}^{2}=0.$$
(20)

Substituting for \({h}_{0}, {\alpha }_{0}, {q}_{0}\) and \({x}_{10}\) from Eq. (18) into the first-order problem, Eq. (17) yields

$${\epsilon }^{1}: {D}_{0}^{2}{h}_{1}+{s}_{1}{D}_{0}^{2}{\alpha }_{1}+{\omega }_{1}^{2}{h}_{1}+{\omega }_{bh}^{2}\left({h}_{1}-{l}_{1}{\alpha }_{1}-{x}_{11}\right)={F}_{1}, $$
(21)
$${D}_{0}^{2}{\alpha }_{1}+{s}_{2}{D}_{0}^{2}{h}_{1}+{\omega }_{2}^{2}{\alpha }_{1}+{\omega }_{b\alpha }^{2}{l}_{1}\left({l}_{1}{\alpha }_{1}-{h}_{1}+{x}_{11}\right)={F}_{2},$$
$${D}_{0}^{2}{q}_{1}+{\omega }_{v}^{2}{q}_{1}={F}_{3},$$
$${D}_{0}^{2}{x}_{11}-{\omega }_{bx}^{2}\left({h}_{1}-{l}_{1}{\alpha }_{1}-{x}_{11}\right)={F}_{4}.$$

Here \({F}_{i}\left( i=\mathrm{1,2},\mathrm{3,4}\right)\) are lengthy expressions of system parameters. These terms are reported in the Appendix (A.1). We emphasize here that when \({\omega }_{v}\) is equal to the natural frequency \(\left({\Omega }_{1}\right)\), the resonance occurs. Accordingly, we can perturb \({\omega }_{v}\) by a detuning parameter and rewrite \({\omega }_{v}\) as

$${\omega }_{v}={\Omega }_{1}+\epsilon {\sigma }_{1} ,$$

where \({\sigma }_{1}\) is the detuning parameter. To eliminate secular terms in Eq. (21), the solvability condition needs to be satisfied.

$$i{\delta }_{11}{A}^{\prime}+i{\delta }_{12}A+{\delta }_{13}{A}^{2}\overline{A }+{\delta }_{14}AB\overline{B }+{\delta }_{15}AD\overline{D }-{\delta }_{16}C{e}^{i\sigma {T}_{1}}=0,$$
(22)
$${-2{\Omega }_{2}i\delta }_{21}{B}^{\prime}-{i{\Omega }_{2}\delta }_{22}B+{\delta }_{23}3{B}^{2}\overline{B }+{\delta }_{24}6AB\overline{A }+{\delta }_{25}6BD\overline{D }=0,$$
$${\delta }_{31}{C}^{\prime}+{\delta }_{32}\left({C}^{2}\overline{C }-C\right)-{\delta }_{33}i{A}^{-i{\sigma }_{1}{T}_{1}}=0, and$$
$${-2{\Omega }_{3}i\delta }_{41}{D}^{\prime}-i{{\Omega }_{3}\delta }_{42}D+{\delta }_{43}{3D}^{2}\overline{D }+{\delta }_{44}6BD\overline{B }+{\delta }_{45}6AD\overline{A }=0.$$

The \({\delta }_{ij}s\) are provided in Appendix (A.3) for brevity. Next, we write \(A,B,C,\) and \(D\) in the polar coordinates as

$$\begin{aligned} A& =\frac{1}{2}a\left({T}_{1}\right){e}^{i{\theta }_{1}\left({T}_{1}\right)}, B=\frac{1}{2}b\left({T}_{1}\right){e}^{i{\theta }_{2}\left({T}_{1}\right)}, \\C&=\frac{1}{2}c\left({T}_{1}\right){e}^{i{\theta }_{3}\left({T}_{1}\right)}, {\text{and}} \, D=\frac{1}{2}d\left({T}_{1}\right){e}^{i{\theta }_{4}\left({T}_{1}\right)}.\end{aligned}$$
(23)

Substituting the polar notation into Eq. (22) and separating real and imaginary parts, we obtain the following slow-flow equations

$${a}^{\prime}=\frac{{\delta }_{16}c{\text{sin}}\phi -{\delta }_{12}a}{{\delta }_{11}} , {\theta }_{1}^{\prime}=\frac{{\delta }_{13}{a}^{2}+{\delta }_{14}{b}^{2}+{\delta }_{15}{d}^{2}}{4{\delta }_{11}}-\frac{{\delta }_{16}c{\text{cos}}\phi }{a{\delta }_{11}} ,$$
(24)
$${b}^{\prime}=-\frac{{\delta }_{22}b}{{2\delta }_{21}} ,$$
$${\theta }_{2}^{\prime}=\frac{{-3 (2\delta }_{24}{a}^{2}+{\delta }_{23}{b}^{2}+2{\delta }_{25}{d}^{2})}{8{ \delta }_{21}{\Omega }_{2}} ,$$
$${c}^{\prime}=\frac{{\delta }_{33}\mathrm{a sin}\phi }{{\delta }_{31}}-\frac{{\delta }_{32}\left({c}^{3}-4c\right)}{4{\delta }_{31}} , {\theta }_{3}^{\prime}=\frac{{\delta }_{33}a{\text{cos}}\phi }{{\delta }_{31}c} ,$$
$${d}^{\prime}=-\frac{{\delta }_{42}d}{{2\delta }_{41}} , {\theta }_{4}^{\prime}=\frac{{-3(2\delta }_{45}{a}^{2}+{2\delta }_{44}{b}^{2}+{\delta }_{43}{d}^{2})}{8{\delta }_{41}{\Omega }_{3}} ,$$
$$\phi ={\theta }_{3}+\sigma {T}_{1}-{\theta }_{1},$$

where (\(\mathrm{^{\prime}})\) denotes the derivative with respect to \({T}_{1}\). The steady-states of the system can be obtained by setting \({a}^{\mathrm{^{\prime}}}={b}^{\mathrm{^{\prime}}}={c}^{\mathrm{^{\prime}}}={d}^{\mathrm{^{\prime}}}={\phi }^{\mathrm{^{\prime}}}=0\) in Eq. \((24)\), which leads to

$${\text{sin}}\phi =\frac{{\delta }_{12}a{\Omega }_{1}}{{\delta }_{16}c} , {\text{cos}}\phi =\frac{-ac{\delta }_{31}\left(3{a}^{2}{\delta }_{13}+8{\delta }_{11}\sigma {\Omega }_{1}\right)}{4\left({c}^{2}{\delta }_{15}{\delta }_{31}+2{a}^{2}{\delta }_{11}{\delta }_{33}{\Omega }_{1}\right) } ,$$
$$\frac{{\delta }_{12}{\delta }_{33}{\Omega }_{1}}{{\delta }_{16}}{a}^{2}=\frac{{\delta }_{32}}{4}\left({c}^{2}-4\right){c}^{2}.$$

By using the trigonometric identities, the frequency response equation can be obtained as

$$\sigma = \frac{{\delta }_{13}{a}^{2}}{4{\delta }_{11}} \pm \sqrt{ {\left(\frac{1}{ac} \left(\frac{{\delta }_{33}}{{\delta }_{31}}{a}^{2}+\frac{{\delta }_{16}}{{\delta }_{11}}{c}^{2}\right)\right)}^{2}- {\left(\frac{{\delta }_{12}}{{\delta }_{11}}+\frac{{\delta }_{32}}{4{\delta }_{31}} \left({c}^{2}-4\right)\right)}^{2}} .$$
(25)

Equation (25) reveals the relations for amplitudes \(a\) and \(c\) with respect to different parameters, including the detuning parameter \(\sigma \) and the dimensionless free-stream velocity \({U}_{r}\). In the subsequent section, we present the system's frequency response using the analytical results obtained in this section.

3.1 Boundary of the instability region

To determine the boundary of unstable regions of the wake oscillator as a function of the system parameters, the damping and nonlinear terms in the solvability condition are ignored. This is because for \(i=\mathrm{1,2},\mathrm{3,4}\), \({\delta }_{i2},\) the damping terms associated with the structural mode only affect the transient development of the amplitude but play an insignificant role in the resulting frequency of the coupled system. Similarly, the nonlinear terms \({\delta }_{i\mathrm{3,4},5}\) are weak by assumption and do not significantly affect the frequency. Accordingly, the solvability condition becomes

$${\delta }_{11}{A}^{\prime}=-{\delta }_{16}iC{e}^{i\sigma {T}_{1}}, {\delta }_{21}{B}^{\prime}=0,$$
(26)
$${\delta }_{31}{C}^{\prime}={\delta }_{33}iA{e}^{-\sigma {T}_{1}}, \mathrm{and }\,{\delta }_{21}{D}^{\prime}=0.$$

From Eq. (26), we can observe that the amplitudes \(B\) and \(D\) decrease to the trivial solution. Thus, the solutions of \(A\) and \(C\) of Eq. (26) can be assumed in the forms

$$A={a}_{1}\left({T}_{1}\right){e}^{\lambda {T}_{1}}, C={c}_{1}\left({T}_{1}\right){e}^{\left(\lambda +i\sigma \right){T}_{1}}$$
(27)

Substituting Eq. (27) into Eq. (26), the characteristic equation is obtained as

$$\left|\begin{array}{cc}\lambda & \frac{{\delta }_{16}}{{\delta }_{11}}i{e}^{2i\sigma {T}_{1}}\\ -\frac{{\delta }_{33}}{{\delta }_{31}}i{e}^{2i\sigma {T}_{1}}& \lambda +i\sigma \end{array}\right|=0, \mathrm{or }{\lambda }^{2}+i\sigma \lambda -\frac{{\delta }_{16}}{{\delta }_{11}} \frac{{\delta }_{33}}{{\delta }_{31}}=0.$$
(28)

Solving for the real parts of the roots of Eq. (28), the instability boundary reads

$$\sigma = \pm 2 \sqrt{\frac{{\delta }_{16}}{{\delta }_{11}} \frac{{\delta }_{33}}{{\delta }_{31}}} .$$
(29)

We observe that the boundary of the instability region is found to be a function of the coupling coefficients, \({\omega }_{b},\) the dimensionless distance of the absorber from the elastic axis \({l}_{1}\) and the absorber mass ratio \({\mu }_{ab}\). The effect of these parameters on the range of instability region can be analyzed using Eq. (29). The detailed discussion on the impact of each parameter on the instability boundary is presented in Sect. 4.2.

3.2 Selection of Parameters

To this end, we emphasize that aside from the absorber parameters, fluid and structural properties have been sourced from references [12, 18, 24, 48], which were determined experimentally. Additionally, the fluid parameters in this study are held constant at \(\beta =0.03\) and \({C}_{L0}=0.3\). A summary of the parameters used for the absorbers is listed in Table 1, along with their values. The discussion of the results obtained from the analytical method is presented next.

Table 1 Variation of various parameters used in the computation
Full size table

4 The analysis of the steady-state solutions

In this section, the results obtained from the method of multiple scales are analyzed through the frequency response curves. For this purpose, we used the absorber parameter values in Table 1. We emphasize that other system parameters in our system are chosen from the literature [12, 18, 24, 48]. The first part of this analysis is to validate the results obtained by the method of multiple scales (MMS). For this, we compare the time responses of the system obtained using MMS with the numerical simulation of the system. For the numerical simulations, we numerically integrate Eq. (14) using the Matlab built-in command 'ode45', which utilizes the Runge–Kutta method. The initial condition for the numerical simulations corresponds to the steady states. The comparison is shown in Fig. 6. From Fig. 6, we can observe that for the given values of \(\epsilon \), the analytical solution shows a good agreement with their numerical counterparts.

Fig. 6
figure 6

Comparison between the analytical and numerical results for the initial conditions \(h\left(0\right)=0,\dot{h}\left(0\right)=0,\alpha \left(0\right)=0.1,\dot{\alpha } \left(0\right)=0, q\left(0\right)=1.9, \dot{q}\left(0\right)=0, {x}_{1}\left(0\right)-0.1;\dot{{x}_{1}}\left(0\right)=0 :\) a the bending vibration, b the torsional vibration, c the van der Pol oscillation, d the absorber vibration

Full size image

4.1 Frequency response curves

In this section, we present the effect of different absorber parameters on the frequency response of the coupled system. This step also provides insight into the optimum selection of key design parameters of the vibration absorber for effective vibration suppression. The key design parameter of the linear vibration absorber includes the distance from the elastic axis, the new coupling term \({\gamma }_{3}\), the absorber's stiffness, damping of the absorber, and the absorber's mass ratio.

Furthermore, the effects of all the absorber parameters are compared to the original system [20], i.e., the system without any absorber. Figure 7 shows the effect of the distance of the absorber from the elastic axis on the system response. Four sets of frequency–response curves are presented for \({l}_{1}=\left\{0.1, 0.3, 0.5, 0.9\right\}\), while the other parameters are fixed, as listed in Table 1. From Fig. 7, we can observe that the distance of the absorber from the elastic axis can suppress the structure's vibration compared to the original system (black curve). This observation can be further explained by the fact that the absorber's interaction with the structure at an arbitrary location acts as a fixed-point force, and a moment is formed if the force is not on the elastic axis. Further, as the absorber is placed ahead of the elastic axis (closer to the leading edge), this creates a counter moment to the positive pitch response with the nose up. In Fig. 7, as \({l}_{1}\) increases, a more significant moment arm forms, and hence, a larger suppression in the amplitude of vibration occurs. We can further observe that for the first three sets of \({l}_{1}\), the system exhibits saddle-node bifurcations at lower values of \(\sigma \). However, when \({l}_{1}\) is set to \(0.9\), although the response of the system decreases significantly, the system does not show any bifurcation.

Fig. 7
figure 7

Influence of the absorber's distance from the elastic axis on the frequency response curves

Full size image

To investigate the effects of the absorber damping on the amplitude of the response, frequency responses are plotted for \({\zeta }_{ab}=0.1\), \({\zeta }_{ab}=0.5\), and \({\zeta }_{ab}=0.9\), while the other parameters are fixed. The variation in the frequency–response curves with \({\zeta }_{ab}\) is shown in Fig. 8. From Fig. 8, we can observe a trend in the responses similar to that seen in Fig. 7. The results depict that increasing the absorber's damping can mitigate the structural amplitude vibrations significantly. Furthermore, with a particular choice of damping, \({\zeta }_{ab}=0.9\), the response is stable for the entire frequency spectrum with a more than \(50\mathrm{\%}\) decrease in the structural amplitude compared to the original system without absorbers.

Fig. 8
figure 8

Influence of the absorber's damping coefficient on the frequency response curves

Full size image

Next, we present the effect of the absorber parameter \({\omega }_{b}\) on the system response. This variation is shown in Fig. 9 for the four sets of parameters, viz. \({\omega }_{b}=\left\{\mathrm{0.15,0.18,0.2,0.25}\right\}\). For all cases, a lower amplitude of vibration in the system is observed. Figure 9 shows a significant reduction in vibration as \({\omega }_{b}\) decreases. This observation can be justified by the definition of \({\omega }_{b}\). In the current cases, we fix the value of the mass of the absorber and vary \({\omega }_{b}\). Therefore, the variation in \({\omega }_{b}\) values can only be attained by lowering the stiffness of the absorber. It is plausible to suggest that for a specific range of stiffness values, a lower stiffness value of the absorber implies more absorption of vibration energy and, hence, lower amplitude vibrations. Furthermore, for \({\omega }_{b}\le 0.18,\) we only get a stable branch of the frequency response with a significant reduction in the amplitude of the system.

Fig. 9
figure 9

Frequency response curves with different values of frequency ratio \({\omega }_{b}.\)

Full size image

Next, the effect of the coupling parameter \({\gamma }_{3}\) on the frequency–response is analyzed and is shown in Fig. 10. The other parameters are listed in Table 1. It is observed that a higher coupling value of \({\gamma }_{3}\) leads to further mitigation of the amplitude of the response. It can be deduced from the last case of \({\gamma }_{3}=2\) that if all the system parameters are kept constant, a significant vibration suppression of the system can be achieved by merely increasing the new coupling parameter.

Fig. 10
figure 10

Impact of different coupling coefficients \({\gamma }_{3}\) on the frequency response curves

Full size image

Finally, the effect of the mass ratio on the system response is presented in Fig. 11. From Fig. 11; we can observe that the vibration absorber with a high mass ratio can suppress the amplitudes more than their lighter counterparts. However, in our case, as mentioned earlier, the mass of the absorber is accordingly cut from the host structure. Therefore, despite the larger suppression of vibration, the higher absorber mass ratio is deemed to be impractical due to the huge cut from the host structure. The result in Fig. 11 is simply a theoretical investigation depicting the absorber's influence in general.

Fig. 11
figure 11

Frequency response curves for different absorber mass ratio \({\mu }_{ab}\)

Full size image

4.2 Stability diagram

It should be noted here that another variable that represents the flow condition is the dimensionless free-stream velocity \({U}_{r}\). Hence, to get a thorough understanding of the system dynamics, we present the stability diagram with respect to the dimensionless free-stream velocity \({U}_{r}\) for different sets of parameters. This elucidates the sensitivity of different parameters on the lock-in range.

We start with the stability diagram for the parameter values given in Table 1, which is shown in Fig. 12. For the sake of completeness, we compare our current system with the system without any absorber [24]. In both cases, as the reduced velocity increases, the width of the lock-in region increases as well. However, the inclusion of a vibration absorber decreases the lock-in region at any given speed when compared to the system without an absorber.

Fig. 12
figure 12

Lock-in and unlock regions for \({l}_{1}=0.5, {\omega }_{b}=0.2, {\zeta }_{ab}=0.1, {\gamma }_{3}=0.1,{\mu }_{ab}=1\%.\)

Full size image

In Fig. 13, the sensitivity of different absorber parameters on the lock-in range is investigated. Figure 13a shows the effect of \({\omega }_{b}\) on the lock-in region, while the other parameters are fixed at \({l}_{1}=0.5, {\zeta }_{ab}=0.1, {\mu }_{ab}=1\%\), and \({\gamma }_{3}=0.1\). For a fixed value of the mass ratio, the parameter \({\omega }_{b}\) represents the stiffness of the absorber; therefore, a decrease in \({\omega }_{b}\) leads to lower absorber stiffness values, which further results in better suppression of the structural vibration. We further observe that the instability region increases with an increase in the parameter \({\omega }_{b}\). Moreover, the instability region is more sensitive to lower values of the parameter \({\omega }_{b}\) as compared to the higher values.

Fig. 13
figure 13

Effect of a frequency ratio \({\omega }_{b}\) b coupling coefficient \({\gamma }_{3}\) c distance from the elastic axis \({l}_{1}\) and d absorber mass ratio \({\mu }_{ab}\) on the stability curves

Full size image

Next, we present the effect of the coupling term, \({\gamma }_{3}\) as shown in Fig. 13b. The other parameters are fixed at \({l}_{1}=0.1, {\zeta }_{ab}=0.1, {\mu }_{ab}=1\%\), and \({\omega }_{b}=0.9\). This coupling parameter represents the action of the absorber motion on the wake that, in turn, affects the structural oscillation. The increase in the magnitude of the coupling coefficient decreases the lock-in region. This can be further explained by stating that at any given speed, a higher absorber coupling \({\gamma }_{3}\) will increase the effect of the absorber on the wake oscillator, which in turn decreases the lock-in region.

Figure 13c shows the effect of \({l}_{1}\) on the variation of the lock-in region. The other parameters are fixed at \({\gamma }_{3}=0.1, {\zeta }_{ab}=0.1, {\mu }_{ab}=1\%\), and \({\omega }_{b}=0.2\). From Fig. 13c, we observe that the lock-in region shrinks with increasing distance \({l}_{1}\). As mentioned earlier, the reverse moment effect created by the absorber increases with an increase in the moment arm. The figure also demonstrates that the instability region is sensitive to a slight increment in the distance \({l}_{1}\). Therefore, higher values of \({l}_{1}\) show greater improvements in the stable region.

Finally, the effect of the mass ratio of the absorber is shown in Fig. 13d. To depict the effect of this parameter, the other parameters were fixed at \({\gamma }_{3}=0.1, {\zeta }_{ab}=0.1,{l}_{1}=0.1\), and \({\omega }_{b}=0.5\). As shown, the stable regions increase with the increase in the mass ratio. The sensitivity is very small, nevertheless, as we incrementally increase the mass ratio. However, in the industry, it is favorable to keep the structure as light as possible, if applicable, while still being effective. In the cases shown, keeping the absorber at 1% of the host structure is deemed to be effective.

5 Conclusion

The effects of a vibration absorber on the vortex-induced vibrations (VIV) of turbine blades were investigated. This study demonstrated the capability of the absorber to mitigate the VIV amplitudes and decrease the lock-in frequency range. The 1:1 internal resonance of the nonlinear system was analyzed using the method of multiple scales, and the dynamic response characteristics of the system were revealed by deriving the modulation equations. The dynamic response included a parametric study on the frequency response and the stability regions analysis of each solution. The stability of the response was computed based on the nature of the Jacobian of modulation equations. Moreover, it was computed for a range of dimensionless free-stream velocities. Results of the frequency response indicated that placing the absorber close to the leading edge decreases the vibration amplitude. Moreover, the response did not show any bifurcation beyond a certain distance and became stable for the same frequency range. Decreasing the stiffness of the absorber was also very prominent in mitigating the amplitude noticeably. It was revealed that, for a range of stiffnesses, the lower stiffnesses were able to greatly attenuate the vibrations, and at certain values, the response was completely stable. Another frequency response showed that the bifurcation characteristics could also be changed by increasing the new coupling coefficient between the absorber and the fluid wake oscillator. Specific high coupling coefficients showed stable solutions for the same frequency range compared to the original system, which showed saddle-node bifurcations. In addition, the amplitude of the VIVs was mitigated. Moreover, the amplitude was further mitigated by increasing the damping of the absorber and its mass ratio. However, for practical reasons, a mass ratio of 1% could be chosen and still provide the required attenuation. Further, the linear analysis was carried out to understand the dependency of the synchronization region on the absorber's parameters by plotting the detuning parameters versus the free-stream velocity and different parameters. Results showed that the stiffness of the absorber is more sensitive compared to the other parameters. The present analysis results can be used to optimize the parameters for further reduction of the large-amplitude vibrations of blades during the frequency lock-in of VIVs of the blades.