Analysis and control of three-link planar robot with active last link: property and energy-based approach

Abstract

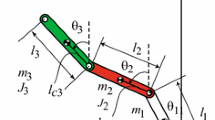
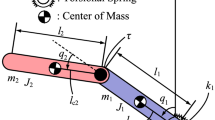
This paper investigates the nonlinear control of a three-link planar robot, which includes a passive first link, a passive second link, and an active last link (subsequently referred to as the PPA robot). Notably, only the angle between the last link and the vertical axis is actuated. First, this paper presents and strictly proves a property of the PPA robot, unaffected by its mechanical parameters. This property reveals that the two passive links of the PPA robot maintain static positions when the active last link remains fixed under a constant control input. Different from previous studies, the proof for the PPA robot demonstrates new challenges and distinctions originated from actuator configuration. Second, leveraging this property, this paper studies the energy-based control corresponding to the PPA robot’s upright equilibrium point (UEP), where all links extend upward. Under the derived energy-based controller, this paper conducts a global motion analysis of the closed-loop system to show that if the control gains satisfy certain requirements, then all initial states, apart from those in a set of Lebesgue measure zero, converge to an invariant set in which the last link extends upward and the robot’s total mechanical energy coincides with its value at the UEP. Finally, this paper provides numerical simulation to validate the developed theoretical results and to demonstrate the effectiveness of applying the derived controller along with an LQR controller to the swing-up and stabilizing task of the PPA robot.

Appendices

Proof of Theorem 1

We extend the method in [15] to prove Theorem 1. Algebraic manipulations are performed using Mathematica 12.1.

To start with, define coordinate transformation:

$$\begin{aligned} \phi _1=\theta _3^{*}-\theta _1,\quad \phi _2=\theta _3^{*}-\theta _2. \end{aligned}$$

(A1)

Using (A1) with $\theta _3=\theta _3^{*}$ and $u_3=u_3^{*}$, we rewrite the dynamics in (1) as

$$\begin{aligned}{} & {} -b\ddot{\phi }_1-\ddot{\phi }_2\cos \left( \phi _1-\phi _2\right) -{\dot{\phi }}_2^2\sin \left( \phi _1-\phi _2\right) \nonumber \\{} & {} \quad =f\sin \left( \theta _3^{*}-\phi _1\right) , \end{aligned}$$

(A2)

$$\begin{aligned}{} & {} -\ddot{\phi }_1\cos \left( \phi _1-\phi _2\right) -e\ddot{\phi }_2+{\dot{\phi }}_1^2\sin \left( \phi _1-\phi _2\right) \nonumber \\{} & {} \quad =d\sin \left( \theta _3^{*}-\phi _2\right) , \end{aligned}$$

(A3)

$$\begin{aligned}{} & {} -a\ddot{\phi }_1\cos \phi _1-\ddot{\phi }_2\cos \phi _2+a{\dot{\phi }}_1^2\sin \phi _1 +{\dot{\phi }}_2^2\sin \phi _2\nonumber \\{} & {} \quad =\displaystyle \frac{u_3^{*}+\beta _3\sin \theta _3^{*}}{\alpha _{23}}, \end{aligned}$$

(A4)

where

$$\begin{aligned} a=\frac{\alpha _{13}}{\alpha _{23}},\ b=\frac{\alpha _{11}}{\alpha _{12}},\ d=\frac{\beta _{2}}{\alpha _{12}},\ e=\frac{\alpha _{22}}{\alpha _{12}},\ f=\frac{\beta _{1}}{\alpha _{12}}. \end{aligned}$$

(A5)

The newly defined parameters in (A5) are determined by (2) and (3) and thus are positive constants. They are used to reduce the complexity of following discussion. Please refer Remark 2 for a detailed explanation about these parameters and the rewritten dynamics in comparison with the counterpart in [15].

Below, we present two lemmas concerning the properties of the parameters in (A5). To prove Theorem 1, we take full advantage of these properties.

Lemma 2

Regarding the parameters in (A5), the inequalities below hold:

$$\begin{aligned}&0<a<b, \end{aligned}$$

(A6)

$$\begin{aligned}&f>ad, \end{aligned}$$

(A7)

$$\begin{aligned}&be>1, \end{aligned}$$

(A8)

$$\begin{aligned}&b+e>2. \end{aligned}$$

(A9)

Proof

Equations (A6), (A7), and (A8) can be shown by using (2) and (3) directly. Using (A8) with (2) yields $b+e\ge 2\sqrt{be}>2$, which shows (A9). $\square$

Lemma 3

If

$$\begin{aligned} e=\frac{1+a^2-ab}{a}, \end{aligned}$$

(A10)

then $a\ne 1$.

Proof

Assume that $a=1$, we then obtain $b+e=2$ from (A10), which contradicts (A9). Thus, we have $a\ne 1$. $\square$

Using $\theta _3=\theta _3^{*}$ with (5) gives $E(\varvec{\theta },{{\dot{\varvec{\theta }}}})=E^{*}$, where $E^{*}$ is a constant. In what follows, two steps are undertaken to prove Theorem 1.

Step 1 By progressively eliminating the nonlinear coupling in (A2)–(A4), we obtain a holonomic constraint of underactuated variable $\phi _1$ (or $\theta _1$, equivalently) alone in the following high-order polynomial form:

$$\begin{aligned} L=\sum _{i=0}^{28}\xi _{i}\sin ^i\phi _1\left( t\right) =0,\quad \textrm{for}\ \forall t, \end{aligned}$$

(A11)

where $\xi _{i}\ (i=0,1,\ldots ,28)$ are constants consisting of the parameters in (A5), sine and cosine of any possible $\theta _3^{*}$, and any possible $E^{*}$. We partition Step 1 into the following substeps and present the details.

Step 1.1 Performing the integration of (A4) with respect to time t gives

$$\begin{aligned} -a{\dot{\phi }}_1\cos \phi _1-{\dot{\phi }}_2\cos \phi _2=\frac{\left( u_3^{*} +\beta _3\sin \theta _3^{*}\right) t}{\alpha _{23}}+\lambda _1, \end{aligned}$$

(A12)

with $\lambda _1$ being constant. The boundedness of ${\dot{\phi }}_1$ and ${\dot{\phi }}_2$ are guaranteed by $E=E^{*}$. This leads to $u_3^{*}+\beta _3\sin \theta _3^{*}=0$. Thus, integrating (A12) yields

$$\begin{aligned} -a\sin \phi _1-\sin \phi _2=\lambda _1t+\lambda , \end{aligned}$$

(A13)

with $\lambda$ being constant. Using the boundedness of sine and cosine in (A13) gives $\lambda _1=0$. Thus, from (A12) and (A13), we have

$$\begin{aligned}&a{\dot{\phi }}_1\cos \phi _1+{\dot{\phi }}_2\cos \phi _2=0, \end{aligned}$$

(A14)

$$\begin{aligned}&a\sin \phi _1+\sin \phi _2=\lambda . \end{aligned}$$

(A15)

In what follows, we replace $\sin \phi _2$ with (A15), and we keep the highest order of $\cos \phi _1$ or $\cos \phi _2$ equals to one by using

$$\begin{aligned}&\cos ^2\phi _1=1-\sin ^2\phi _1,\ \textrm{or}\nonumber \\&\cos ^2\phi _2=1-\sin ^2\phi _2=1-\left( \lambda -a\sin \phi _1\right) ^2. \end{aligned}$$

(A16)

Step 1.2 We eliminate $\ddot{\phi }_1$ and $\ddot{\phi }_2$ in this substep. To this end, using (A2)–(A4) gives

$$\begin{aligned} \begin{bmatrix} -b &{} -\cos \left( \phi _1-\phi _2\right) &{} \sigma _1\\ -\cos \left( \phi _1-\phi _2\right) &{} -e &{} \sigma _2\\ -a\cos \phi _1 &{} -\cos \phi _2 &{} \sigma _3 \end{bmatrix} \begin{bmatrix} \ddot{\phi }_1\\ \ddot{\phi }_2\\ 1 \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix}, \end{aligned}$$

where

$$\begin{aligned}&\sigma _1=-{\dot{\phi }}_2^2\sin \left( \phi _1-\phi _2\right) -f\sin \left( \theta _3^{*}-\phi _1\right) ,\\&\sigma _2={\dot{\phi }}_1^2\sin \left( \phi _1-\phi _2\right) -d\sin \left( \theta _3^{*}-\phi _2\right) ,\\&\sigma _3=a{\dot{\phi }}_1^2\sin \phi _1+{\dot{\phi }}_2^2\sin \phi _2. \end{aligned}$$

To avoid contradiction, the determinant of the square matrix in the above equation must equal zero. This leads to

$$\begin{aligned} F_1{\dot{\phi }}_1^2+F_2{\dot{\phi }}_2^2+F_3=0, \end{aligned}$$

(A17)

where $F_i\ (i=1,2,3)$ comprise $\sin \phi _1$, $\cos \phi _1$, and $\cos \phi _2$.

Step 1.3 We eliminate ${\dot{\phi }}_1$ and ${\dot{\phi }}_2$ in this substep. First, substituting (A1), (A15), and $E=E^{*}$ into (4) and using (A5), we obtain

$$\begin{aligned}&\frac{b}{2}{\dot{\phi }}_1^2+\frac{e}{2}{\dot{\phi }}_2^2+\cos \theta _3^{*} \left( f\cos \phi _1+d\cos \phi _2\right) \nonumber \\&\quad +\dot{\phi _1}{\dot{\phi }}_2\cos \left( \phi _1-\phi _2\right) \nonumber \\&\quad +\sin \theta _3^{*}\left( f\sin \phi _1+d\sin \phi _2\right) =\gamma , \end{aligned}$$

(A18)

where constant $\gamma$ is defined as

$$\begin{aligned} \gamma =\frac{E^{*}-\beta _3\cos \theta _3^{*}}{\alpha _{12}}. \end{aligned}$$

(A19)

Next, we use (A14) to eliminate terms of ${\dot{\phi }}_2$ via two ways. By computing ((A17)$\times e/2$-(A18)$\times F_2)\times \cos \phi _2$, we obtain

$$\begin{aligned} G_{11}+G_{12}{\dot{\phi }}_1^2=0. \end{aligned}$$

(A20)

By computing $E\times \cos ^2\phi _2$, we obtain

$$\begin{aligned} G_{21}+G_{22}{\dot{\phi }}_1^2=0, \end{aligned}$$

(A21)

where $G_{ij}\ (i,j=1,2)$ comprise $\sin \phi _1$, $\cos \phi _1$, and $\cos \phi _2$.

Finally, eliminating ${\dot{\phi }}_1$ from (A20) and (A21) gives

$$\begin{aligned} G_{11}G_{22}-G_{12}G_{21}=Q_1+Q_2\cos \phi _2=0, \end{aligned}$$

(A22)

where $Q_i\ (i=1,2)$ comprise $\sin \phi _1$ and $\cos \phi _1$. Note that the order of $\cos \theta _3^{*}$ remains to be one during the above derivation. Thus, $Q_i\ (i=1,2)$ can be expressed as

$$\begin{aligned}&Q_1=Q_{11}+Q_{12}\cos \theta _3^{*}, \end{aligned}$$

(A23)

$$\begin{aligned}&Q_2=Q_{21}+Q_{22}\cos \theta _3^{*}, \end{aligned}$$

(A24)

where the explicit expressions of $Q_{ij}\ (i=1,2)$ are omitted.

Step 1.4 Using (A22), we obtain

$$\begin{aligned} Q_1^2-Q_2^2\cos ^2\phi _2=Q_1^2-Q_2^2\left( 1-\sin ^2\phi _2\right) =0. \end{aligned}$$

(A25)

By using (A15), (A25) can be further expressed as

$$\begin{aligned} R_1+R_2\cos \phi _1=0, \end{aligned}$$

(A26)

where $R_1$ and $R_2$ are polynomials in terms of $\sin \phi _1$ with respective orders of 14 and 13. Deleting $\cos \phi _1$ from (A26) yields (A11); that is,

$$\begin{aligned} L=R_1^{2}-R_2^{2}\left( 1-\sin ^{2}\phi _{1}\right) =0. \end{aligned}$$

(A27)

Notably, if $\cos \theta _3^*=0$, then $R_2$ in (A26) equals zero, and $\cos \phi _1$ does not exist in (A25). Indeed, $Q_{11}$ can be written as ${\widehat{Q}}_{11}\times \cos \phi _1$ with ${\widehat{Q}}_{11}$ not containing $\cos \phi _1$, and $Q_{21}$ itself does not contain $\cos \phi _1$. Thus, from (A23) and (A24), if $\cos \theta _3^{*}=0$, then (A25) becomes $(1-\sin ^2\phi _1){\widehat{Q}}_{11}^2-Q_{21}^2(1-\sin ^2\phi _2)=0$, where $\cos \phi _1$ does not exist. In this case, (A27) can be simplified to $L=R_1$.

Step 2 Assume ${\dot{\phi }}_{1}=-{\dot{\theta }}_{1}\not \equiv 0$; that is, the PPA robot is not at an equilibrium configuration under the derived holonomic constraint in (A11). This is equivalent to the polynomial equation having infinite number of solutions, since $\sin \phi _1$ is time-varying. Thus, the coefficients in (A11) must satisfy

$$\begin{aligned} \xi _{i}=0,\quad i=0,1,\ldots ,28. \end{aligned}$$

(A28)

In this step, we reveal the existence of at least one nonzero coefficient for any possible mechanical parameters and any given values of $\theta _3^{*}$ and $E^{*}$. Consequently, this proves that (A28) does not hold. The details are given below.

To start with, consider $\xi _{28}$ in (A11); that is,

$$\begin{aligned}&\xi _{28}=16a^{16}\left( 1+a^2-ab-ae\right) ^2 \nonumber \\&\quad \left( \left( f-ad\right) ^2 +4adf\sin ^2\theta _3^{*}\right) \nonumber \\&\qquad \hspace{5.0pt}\times \left( \left( 1-3a^2+2ab\right) ad +\left( -3+a^2+2ae\right) f\right) ^2. \end{aligned}$$

(A29)

Using $f>ad$ in Lemma 2 yields $\left( f-ad\right) ^2+4adf\sin ^2\theta _3^{*}\ne 0$. Thus, from (A29) and $\xi _{28}=0$, we discuss the following two cases based on whether

$$\begin{aligned} 1+a^2-ab-ae\ne 0, \end{aligned}$$

(A30)

which is equivalent to $e\ne \left( 1+a^2-ab\right) /a$ holds or not:

Case 1: $e=\left( 1+a^2-ab\right) /a$

Case 2: $e\ne \left( 1+a^2-ab\right) /a$

Case 1: In this case, we obtain $\xi _{27}=0$ and

$$\begin{aligned}{} & {} \xi _{26}=1024a^{18}\left( a-b\right) ^4\left( f-ad\right) ^2\left( \left( f-ad\right) ^2\cos ^2\theta _3^{*} \right. \\{} & {} \quad \left. +\left( f+ad\right) ^2\sin ^2\theta _3^{*}\right) \lambda ^2. \end{aligned}$$

Since $0<a<b$ and $f>ad$ from Lemma 2, we see that $\xi _{26}=0$ shows $\lambda =0$. This further yields $\xi _{25}=0$ and

$$\begin{aligned}{} & {} \xi _{24}=a^{12}\left( -1+a^2\right) ^2\left( f-ad\right) ^2\left( \left( f-ad\right) ^2\cos ^2\theta _3^{*} \right. \\{} & {} \quad \left. +\left( f+ad\right) ^2\sin ^2\theta _3^{*}\right) \eta ^2, \end{aligned}$$

where

$$\begin{aligned} \eta =\left( 1+3a^2-4ab\right) \left( 1+5a^2-6ab\right) . \end{aligned}$$

(A31)

From Lemma 3, we have $a\ne 1$ for Case 1 and all its subcases. Thus, $\xi _{24}=0$ shows $\eta =0$. Regarding whether $b=\left( 1+3a^2\right) /\left( 4a\right)$, we consider the following two cases:

Case 1.1: $e=\left( 1+a^2-ab\right) /a$ and $b=\left( 1+3a^2\right) /\left( 4a\right)$

Case 1.2: $e=\left( 1+a^2-ab\right) /a$ and $b\ne \left( 1+3a^2\right) /\left( 4a\right)$

Below we present the details of each case.

Case 1.1: We have $\xi _{23}=\xi _{22}=\xi _{21}=0$, but

$$\begin{aligned}&\xi _{20}=\frac{1}{16}a^8\left( -1+a^2\right) ^6\left( 1+a^2\right) ^2\left( f-ad\right) ^2\\&\qquad \hspace{5.0pt}\times \left( \left( f-ad\right) ^2\cos ^2\theta _3^{*} +\left( f+ad\right) ^2\sin ^2\theta _3^{*}\right) >0, \end{aligned}$$

which contradicts (A28).

Case 1.2: From (A31) and $\eta =0$, we have $b=(1+5a^2)/(6a)$. This yields $\xi _{23}=0$ and

$$\begin{aligned}&\xi _{22}=\frac{4}{81}a^{12}\left( -1+a^2\right) ^6\gamma ^2\left( \left( f-ad\right) ^2 \cos ^2\theta _3^{*} \right. \nonumber \\&\quad \left. +\left( f+ad\right) ^2\sin ^2\theta _3^{*}\right) . \end{aligned}$$

(A32)

From (A32) and $\xi _{22}=0$, we have $\gamma =0$. To avoid analyzing complicated coefficients, we always search for the one with the simplest structure in the remainder of Step 2. For this case, we skip the intermediate coefficients and obtain

$$\begin{aligned} \xi _0=\frac{\left( -1+a^2\right) ^{12}\left( af-d\right) ^4\sin ^4\theta _3^{*}}{1679616a^8}. \end{aligned}$$

(A33)

From (A33) and $\xi _0=0$, if $\sin \theta _3^{*}=0$, we obtain

$$\begin{aligned} \xi _4=\frac{\left( -1+a^2\right) ^{12}\left( d^2-f^2\right) ^2}{20736a^4}. \end{aligned}$$

Note that $\xi _{4}=0$ shows $f=d$, and thus gives

$$\begin{aligned}{} & {} \xi _{20}=\frac{1}{144}a^8\left( -1+a^2\right) ^{10}\left( 1+a\right) ^6 \\{} & {} \quad \left( 5\left( -\frac{1}{5}+a\right) ^2+\frac{24}{5}\right) ^2d^4>0, \end{aligned}$$

which contradicts (A28).

If $\sin \theta _3^{*}\ne 0$, to render $\xi _0=0$, we have $f=d/a$ yielding

$$\begin{aligned} \xi _{20}&=\frac{25}{144}a^4\left( -1+a^2\right) ^8 \left( 1+a^2\right) ^2d^4\\&\quad \Big (\left( -1+a^2\right) ^2\cos ^4\theta _3^{*}\\&\quad +2\left( 1+a^4\right) \cos ^2\theta _3^{*} \sin ^2\theta _3^{*}\\&\quad +\left( 1+a^2\right) ^2\sin ^4\theta _3^{*}\Big )>0, \end{aligned}$$

which contradicts (A28).

Case 2: In this case, we obtain from (A29) and $\xi _{28}=0$ that

$$\begin{aligned} \left( 1-3a^2+2ab\right) ad+\left( -3+a^2+2ae\right) f=0. \end{aligned}$$

(A34)

Note that

$$\begin{aligned} -3+a^2+2ae\ne 0. \end{aligned}$$

(A35)

Otherwise, if $-3+a^2+2ae=0$, then (A34) yields $1-3a^2+2ab=0$; that is, $b=\left( -1+3a^2\right) /\left( 2a\right)$, since $ad>0$. This further yields

$$\begin{aligned} e=\frac{3-a^2}{2a}=\frac{1+a^2+a\displaystyle \frac{1-3a^2}{2a}}{a}=\frac{1+a^2-ab}{a}, \end{aligned}$$

which raises a contradiction. Thus, from (A34), we have

$$\begin{aligned} f=\frac{-\left( 1-3a^2+2ab\right) ad}{-3+a^2+2ae}. \end{aligned}$$

(A36)

By substituting (A36) into (A11), we obtain

$$\begin{aligned} \xi _{26}&=\frac{256a^{18}\left( 1+a^2-ab-ae\right) ^2}{\left( -3+a^2+2ae\right) ^4}\nonumber \\&\quad \Big (\left( 1+a^2-ab-ae\right) ^2\cos ^2\theta _3^{*}\nonumber \\&\quad \hspace{5.0pt}+\left( 2-2a^2+ab-ae\right) ^2\sin ^2 \theta _3^{*}\Big )d^2\epsilon , \end{aligned}$$

(A37)

where

$$\begin{aligned}&\epsilon \ =\epsilon _1^2+\epsilon _2^2,\nonumber \\&\epsilon _1=\left( 1-14a^2+a^4+6ab+6a^3e\right) d\lambda \cos \theta _3^{*}, \end{aligned}$$

(A38)

$$\begin{aligned}&\epsilon _2=\left( -1+a^2\right) \left( -3+a^2+2ae\right) \gamma \nonumber \\&\quad -\left( 1-14a^2+a^4+6ab+6a^3e\right) d\lambda \sin \theta _3^{*}. \end{aligned}$$

(A39)

Note that

$$\begin{aligned} 2-2a^2+ab-ae\ne 0. \end{aligned}$$

(A40)

Otherwise, putting $ae=2-2a^2+ab$ into (A36) yields $f=-ad$, which contradicts the fact that f in (A5) is always positive. Thus, from (A37) and $\xi _{26}=0$, we have $\epsilon =0$. This yields $\epsilon _1=0$ and $\epsilon _2=0$.

Before proceeding to discuss Case 2 further, we first analyze a special circumstance of $a=1$. From (A38) and (A39), if $a=1$, then we have $\epsilon =36d^2(-2+b+e)^2\lambda ^2=0$. This shows $\lambda =0$, since $b+e>2$ from Lemma 2. However, this further renders all the coefficients of polynomial L in (A11) to become zero; that is, (A28) holds. To deal with this, we derive and study another holonomic constraint of $\phi _1$. From (A15) and $\lambda =0$, we have

$$\begin{aligned} \phi _1=-\phi _2,\quad {\dot{\phi }}_1=-{\dot{\phi }}_2,\quad \ddot{\phi }_1=-\ddot{\phi }_2, \end{aligned}$$

(A41)

which implies a specific configuration for the PPA robot that $\theta _1+\theta _2=2\theta _3^{*}$. By adding (A41) into the derivation in Step 1 with $a=1$, $\lambda =0$, and (A36), the derived holonomic constraint becomes

$$\begin{aligned} L_{a}=\sum _{i=0}^{12}\xi _{ia}\sin ^i\phi _1\left( t\right) =0,\quad \textrm{for}\ \forall t. \end{aligned}$$

(A42)

Consider $\xi _{12a}$ in (A42); that is,

$$\begin{aligned} \xi _{12a}=\frac{16d^2\left( \left( -2+b+e\right) ^2\cos ^2\theta _3^{*} +\left( b-e\right) ^2\sin ^2\theta _3^{*}\right) }{\left( -1+e\right) ^2}. \end{aligned}$$

Note that $e\ne 1$. Otherwise, we have $-3+a^2+2ae=0$, which contradicts (A35). We now show $b-e\ne 0$. On the contrary, assume $b-e=0$, then putting $b=e$ and $a=1$ into (A36) yields $f=-d$. This, together with $b+e>2$ from Lemma 2, gives $\xi _{12a}>0$ and thus concludes the discussion for (A42).

Thus, returning to the analysis of (A11), we just need to consider $a\ne 1$ for Case 2 and all its subcases. In such circumstance, from (A38) and (A39), we have

$$\begin{aligned}&\left( 1-14a^2+a^4+6ab+6a^3e\right) \lambda \cos \theta _3^{*}=0, \end{aligned}$$

(A43)

$$\begin{aligned}&\gamma =\frac{\left( 1-14a^2+a^4+6ab+6a^3e\right) d\lambda \sin \theta _3^{*}}{\left( -1+a^2\right) \left( -3+a^2+2ae\right) }. \end{aligned}$$

(A44)

We start by proving

$$\begin{aligned} 1-14a^2+a^4+6ab+6a^3e>0 \end{aligned}$$

(A45)

in (A43) and (A44). By using $be>1$ in (A8), we have $6ab+6a^3e\ge 12a^2\sqrt{be}>12a^2$. This, together with $1+a^4\ge 2a^2$, yields $1-14a^2+a^4+6ab+6a^3e>2a^2+12a^2-14a^2=0$. Based on (A43) and (A44), we consider the following two cases for $\xi _{26}=0$:

Case 2.1: $e\ne \left( 1+a^2-ab\right) /a$ and $\cos \theta _3^{*}\ne 0$

Case 2.2: $e\ne \left( 1+a^2-ab\right) /a$ and $\cos \theta _3^{*}=0$

Below we present the details of each case.

Case 2.1: From (A43) and (A44), we have $\lambda =0$ and thus $\gamma =0$. These lead to

$$\begin{aligned} \xi _0=\frac{\left( -1+a^2\right) ^4\left( -2a+b+a^2e\right) ^4d^4 \omega ^4\sin ^4\theta _3^{*}}{\left( -3+a^2+2ae\right) ^4}, \end{aligned}$$

(A46)

where

$$\begin{aligned} \omega =4a-3b-3a^2e+2abe. \end{aligned}$$

(A47)

Note that $-2a+b+a^2e\ge -2a+2a\sqrt{be}>-2a+2a=0$ due to $be>1$ in (A8). We now show $\omega \ne 0$. On the contrary, assume $\omega =0$, substituting (A47) into (A36) gives $f=\left( 3a-2b\right) d$. It immediately follows that $0<a<b$ and $f>ad$ do not hold simultaneously. This contradicts Lemma 2.

Thus, from (A46) and $\xi _0=0$, we have $\sin \theta _3^{*}=0$ yielding

$$\begin{aligned} \xi _{24}=\frac{144a^{16}\left( -1+a^2\right) ^2\left( 1+a^2-ab-ae\right) ^ 4d^4\varepsilon ^2}{\left( -3+a^2+2ae\right) ^4}, \end{aligned}$$

(A48)

where

$$\begin{aligned} \varepsilon =1-6a^2+a^4+ab-a^3b+a\left( -1+a^2+4ab\right) e. \end{aligned}$$

(A49)

From (A30), we see that $\xi _{24}=0$ gives $\varepsilon =0$. We now show $-1+a^2+4ab\ne 0$ in (A49) by contradiction. Substituting $-1+a^2+4ab=0$ into (A49) gives $\left( -5+a^2\right) \left( -1+5a^2\right) /4=0$. If $-5+a^2=0$ holds, then $-1+a^2+4ab=4+4ab>0$. If $-1+5a^2=0$ holds, then by using (A6) we have $-1+a^2+4ab>-1+5a^2=0$.

Thus, from (A48) and $\xi _{24}=0$, we have

$$\begin{aligned} e=\frac{-1+6a^2-a^4-ab+a^3b}{a\left( -1+a^2+4ab\right) }. \end{aligned}$$

(A50)

This further yields

$$\begin{aligned} \xi _{20}&=\frac{1600a^{18}\left( -1+a^2\right) ^6\left( a-b\right) ^6\left( 1+a^2+6ab\right) ^2d^4}{\left( -1+a^2+4ab\right) ^2\left( -1-8a^2+a^4+14ab-6a^3b\right) ^4}\\&\quad \hspace{5.0pt}\times \left( \left( -7+a^2-2ab\right) ^2\left( -3+a^2+2ab\right) ^2\right) . \end{aligned}$$

Note that the denominator of $\xi _{20}$ does not equal zero. Otherwise, under (A36) and (A50), $-1-8a^2+a^4+14ab-6a^3b=0$ yields $-3+a^2+2ae=0$; $-7+a^2-2ab=0$ yields $a>b$; and $-3+a^2+2ab=0$ yields $f=ad$. These are all impossible due to (A35) and Lemma 2. Thus, we have $\xi _{20}>0$, which contradicts (A28).

Case 2.2: In this case, if $\lambda =0$, then $\gamma =0$ and we can use (A46) with $\sin \theta _3^*=\pm 1$ to show $\xi _0\ne 0$. Thus, we just need to consider $\lambda \ne 0$. Note that from Step 1.1, by substituting (A1) into (A15) with $\cos \theta _3^{*}=0$ and using (A5) with (2), we obtain

$$\begin{aligned} l_1\cos \theta _1+l_2\cos \theta _2=l_2\lambda . \end{aligned}$$

This implies that link 3 of the PPA robot is in the horizontal position and maintains a constant height. Moreover, from Step 1.4, we have $R_2=0$ when $\cos \theta _3^{*}=0$. Thus, in this case, we study $L=R_1=0$ instead of (A11). By using (A36) and (A44) with $\cos \theta _3^{*}=0$, we obtain from $R_1$ a polynomial equation of $\sin \phi _1$ with the highest order being equal to 12; that is,

$$\begin{aligned} L=\sum _{i=0}^{12}\xi _{i}\sin ^i\phi _1\left( t\right) =0,\quad \textrm{for}\ \forall t. \end{aligned}$$

(A51)

Consider $\xi _{12}$ in (A51); that is,

$$\begin{aligned}&\xi _{12}=\frac{4a^8\left( 1+a^2-ab-ae\right) \left( 2-2a^2+ab-ae\right) d^2}{\left( -1+a^2\right) \left( -3+a^2+2ae\right) ^2}\nonumber \\&\qquad \quad \times \left( \left( -1+a^2\right) ^2 \varTheta _{12}+12a\varDelta _{12}\lambda ^2\right) , \end{aligned}$$

(A52)

where

$$\begin{aligned} \varTheta _{12}&=6+20a^2+6a^4-9ab-3a^3b \nonumber \\&\quad -\left( 3a+9a^3+8a^2b\right) e, \end{aligned}$$

(A53)

$$\begin{aligned} \varDelta _{12}&=-6a-6a^3+b+3a^2b\nonumber \\&\quad +\left( 3a^2+a^4+2ab+2a^3b\right) e. \end{aligned}$$

(A54)

By using (A30), (A35), and (A40), from (A52) and $\xi _{12}=0$, we have

$$\begin{aligned} \left( -1+a^2\right) ^2\varTheta _{12}+12a\varDelta _{12}\lambda ^2=0. \end{aligned}$$

(A55)

Below we show $\varDelta _{12}\ne 0$. Suppose that $\varDelta _{12}$ equals zero, then from (A55), $\varTheta _{12}$ must also equal zero since $a\ne 1$. Using (A53) and (A54), we obtain b and the corresponding e from $\varTheta _{12}=0$ and $\varDelta _{12}=0$ as

$$\begin{aligned}&b=\frac{3-a^2}{2a},\quad \hspace{5.0pt}\; e=\frac{-1+3a^2}{2a}, \end{aligned}$$

(A56)

$$\begin{aligned}&\textrm{or}\nonumber \\&b=\frac{2a^3+6a^5}{5+3a^4},\ e=\frac{6+2a^2}{3a+5a^5}. \end{aligned}$$

(A57)

Substituting (A56) into (A36) gives $f=ad$, which contradicts Lemma 2. As for (A57), by using $be>1$ in (A8), we have $(2a^3+6a^5)(6+2a^2)-(5+3a^4)(3a+5a^5)=-3a(-1+a^2)^2(5+6a^2+5a^4)>0$, which raises a contradiction. Thus, $\varDelta _{12}\ne 0$.

From (A55), we have

$$\begin{aligned} \lambda ^2=-\frac{\left( -1+a^2\right) ^2\varTheta _{12}}{12a\varDelta _{12}}. \end{aligned}$$

(A58)

By using (A58), we obtain

$$\begin{aligned} \xi _i=k_i{\widehat{\xi }}_i,\quad i=11,10,9, \end{aligned}$$

(A59)

where $k_i\ (i=11,10,9)$ are guaranteed to be nonzero terms. We omit the explicit expressions of other ${\widehat{\xi }}_i$ in (A59) and present only that of ${\widehat{\xi }}_{11}$ below:

$$\begin{aligned} {\widehat{\xi }}_{11}&=-42+52a^2+124a^4\\&\quad +52a^6-42a^8+9ab-33a^3b-63a^5b+39a^7b\\&\quad \quad \hspace{5.0pt}-9a^2b^2+18a^4b^2-9a^6b^2\\&\quad +\big (39a-63b^3-33a^5+9a^7+24b-86a^2b\\&\quad \quad \hspace{5.0pt}-68a^4b-86a^6b+24a^8b+18ab^2\\&\quad +6a^3b^2+36a^5b^2-12a^7b^2\big )e\\&\quad \quad \hspace{5.0pt}+\big (-9a^2+18a^4-9a^6-12ab\\&\quad +36a^3b+6a^5b+18a^7b+16a^2b^2\\&\quad \quad \hspace{5.0pt}+16a^4b^2+16a^6b^2\big )e^2. \end{aligned}$$

Thus, $\xi _i=0\ (i=11,10,9)$ are equivalent to

$$\begin{aligned} {\widehat{\xi }}_i=0,\quad i=11,10,9. \end{aligned}$$

(A60)

Note that (A60) can be viewed as polynomial equations with a, b, and e as variables, where the highest order of e in ${\widehat{\xi }}_{11}$, ${\widehat{\xi }}_{10}$, and ${\widehat{\xi }}_{9}$ are equal to 2, 4, and 5, respectively. Moreover, we obtain $\xi _8$ from (A51). Below we show that (A60) and $\xi _8=0$ do not hold simultaneously.

Starting with the assumption that (A60) holds, we first eliminate e and derive the following three polynomial equations in terms of a and b from (A60):

$$\begin{aligned} \delta _i=0,\quad i=1,2,3. \end{aligned}$$

(A61)

To this end, we divide ${\widehat{\xi }}_{10}$ by ${\widehat{\xi }}_{11}$ with respect to e to obtain

$$\begin{aligned} {\widehat{\xi }}_{10}=p_{10}{\widehat{\xi }}_{11}+k_{10}r_{10}, \end{aligned}$$

(A62)

where $p_{10}$ is the quotient and $k_{10}r_{10}$ is the remainder with $k_{10}$ being the nonzero term. The same notations (or with bars) apply to the following process of the derivation of (A61). From ${\widehat{\xi }}_{10}=0$ and ${\widehat{\xi }}_{11}=0$ in (A62), we have $r_{10}=0$ in which the highest order of e has been reduced to 1. Moreover, we iterate the division by taking the divisor and nonzero part of the remainder in (A62) as the new dividend and divisor; that is, we divide ${\widehat{\xi }}_{11}$ by $r_{10}$ with respect to e to obtain

$$\begin{aligned} {\widehat{\xi }}_{11}=p_{11}r_{10}+k_{11}\delta _1, \end{aligned}$$

where $\delta _1=0$ is now the first polynomial equation, since ${\widehat{\xi }}_{11}=0$ and $r_{10}=0$. Similarly, we replace ${\widehat{\xi }}_{10}$ with ${\widehat{\xi }}_9$ and obtain

$$\begin{aligned} {\widehat{\xi }}_9=p_9{\widehat{\xi }}_{11}+k_{9}r_{9},\quad {\widehat{\xi }}_{11}={\overline{p}}_{11}r_9+{\overline{k}}_{11}\delta _2, \end{aligned}$$

where the highest order of e in $r_9$ is equal to 1. From ${\overline{k}}_{11}\delta _9$, we obtain the second polynomial equation $\delta _2=0$. Finally, we use $r_9$ and $r_{10}$ to obtain

$$\begin{aligned} r_9={\overline{p}}_{9}r_{10}+{\overline{k}}_{9}\delta _3. \end{aligned}$$

This gives the third polynomial equation $\delta _3=0$ and thus leads to (A61). Note that the highest orders of b in $\delta _1$, $\delta _2$, and $\delta _3$ are equal to 12, 12, and 10, respectively.

Next, by using (A61), we eliminate b and derive two polynomial equations solely in terms of a. To this end, we take $\delta _1$ and $\delta _3$ as the initial dividend and divisor with respect to b and obtain

$$\begin{aligned} \delta _1=m_1\delta _3+{\widetilde{k}}_1n_1, \end{aligned}$$

where $m_1$ is the quotient and ${\widetilde{k}}_1n_1$ is the remainder with ${\widetilde{k}}_1$ being the nonzero part. This gives $n_1=0$ with the highest order of b being equal to 9. We omit the subsequent process since it replicates the derivation of $\delta _1=0$ with more iteration. From the remainder of the final division, we obtain the following polynomial equation with $z=a^2>0$:

$$\begin{aligned} P_1=\sum _{i=0}^{362}\varsigma _{1,i}z^i=\varPhi {\widehat{P}}_1=0, \end{aligned}$$

(A63)

where $\varsigma _{1,i}\ (i=0,1,\ldots ,362)$ are constants and ${\widehat{P}}_1$ and $\varPhi$ are polynomials of z. Same derivation using $\delta _2$ as the initial dividend instead of $\delta _1$ yields the second polynomial equation with $z=a^2>0$:

$$\begin{aligned} P_2=\sum _{i=0}^{382}\varsigma _{2,i}z^i=\varPhi {\widehat{P}}_2=0, \end{aligned}$$

(A64)

where $\varsigma _{2,i}\ (i=0,1,\ldots ,382)$ are constants and ${\widehat{P}}_2$ is a polynomial of z. The explicit expressions of ${\widehat{P}}_1$, ${\widehat{P}}_2$, and $\varPhi$ are omitted.

Then, note that both $P_1=0$ and $P_2=0$ are derived from (A61), while (A61) is derived from (A60). Thus, a necessary condition for (A60) is that (A63) and (A64) hold simultaneously. In this case, it is equivalent to the common positive real solutions of ${\widehat{P}}_1=0$ and ${\widehat{P}}_2=0$ and the positive real solutions of $\varPhi =0$; that is,

$$\begin{aligned}&z=0.125043,\quad z=0.514811,\quad z=1.942459, \end{aligned}$$

(A65)

$$\begin{aligned}&\textrm{and}\nonumber \\&z=0.066778,\quad z=0.125043,\nonumber \\&\quad z=0.140556,\quad z=0.250000,\nonumber \\&z=4.000000,\quad z=7.114591,\nonumber \\&\quad z=7.997246,\quad z=14.97492, \end{aligned}$$

(A66)

respectively. We give a detailed explanation of these solutions in Remark 4.

Finally, we conduct an examination to see whether $\xi _8=0$ holds under these solutions. Specifically, we substitute each positive a obtained from (A65) and (A66) into $\delta _1=0$ in (A61), and solve b from the resulting equation. Combining with its corresponding a, we then substitute the obtained b into ${\widehat{\xi }}_{11}=0$ in (A60) to solve e and obtain the combination of (a, b, e). Now, for each combination, we first check whether the properties in Lemma 2 are satisfied with the aid of (A36). If so, we then substitute this combination into $\xi _8$ and check whether $\xi _8=0$ or not. Following such examination, we find that none of the solutions in (A65) or (A66) renders $\xi _8=0$; that is, (A60) and $\xi _8=0$ do not hold simultaneously. The details are omitted.

Thus, we conclude from (A59) that there exists at least one nonzero coefficient among $\xi _{11}$, $\xi _{10}$, $\xi _{9}$, and $\xi _{8}$, which contradicts (A28). We give some discussion concerning the analysis of Case 2.2 in Remark 3.

Thus far, we have located at least one nonzero coefficient for every case. This proves that (A28) does not hold in any circumstance. As a result, ${\dot{\theta }}_1=-{\dot{\phi }}_1\equiv 0$, which leads to $\sin \phi _2=\lambda _0$ with $\lambda _0$ being a constant. Consequently, ${\dot{\theta }}_2=-{\dot{\phi }}_2\equiv 0$, and hence completes the proof. $\square$

The three remarks given below concern the newly defined parameters in (A5), the analysis of Case 2.2 in comparison with [15], and the numerical solutions in (A65) and (A66), respectively.

Remark 2

The definition of newly defined parameters varies with actuator configuration of the three-link robot. From [15], the rewritten dynamics of the three-link planar robot with active first link are

$$\begin{aligned}&a\ddot{\phi }_2\cos \phi _2+\ddot{\phi }_3\cos \phi _3-a{\dot{\phi }}_2^2\sin \phi _2-{\dot{\phi }}_3^2 \sin \phi _3 \nonumber \\&\quad =\displaystyle \frac{\tau _1^{*}+\beta _1\sin \theta _1^{*}}{\alpha _{13}}, \end{aligned}$$

(A67)

$$\begin{aligned}&b\ddot{\phi }_2+\ddot{\phi }_3\cos \left( \phi _3-\phi _2\right) -{\dot{\phi }}_3^2\sin \left( \phi _3-\phi _2\right) \nonumber \\&\quad =ad\sin \left( \phi _2+\theta _1^{*}\right) , \end{aligned}$$

(A68)

$$\begin{aligned}&\ddot{\phi }_2\cos \left( \phi _3-\phi _2\right) +e\ddot{\phi }_3 +{\dot{\phi }}_2^2\sin \left( \phi _3-\phi _2\right) \nonumber \\&\quad =d\sin \left( \phi _3+\theta _1^{*}\right) , \end{aligned}$$

(A69)

where the angle of the first link and the control input are constants, and

$$\begin{aligned} a=\frac{\alpha _{12}}{\alpha _{13}},\ b=\frac{\alpha _{22}}{\alpha _{23}},\ d=\frac{\beta _3}{\alpha _{23}},\ e=\frac{\alpha _{33}}{\alpha _{23}}. \end{aligned}$$

(A70)

From (A70), we see that the set of newly defined parameters in (A5) inherits the notations but differs in content, since the PPA robot studied in this paper is actuated by the last link instead of the first. Note that although the underactuated parts of the dynamics in (A2) and (A3) coincide with (A68) and (A69) in structure, comparing (A5) with (A70) shows that there is one more newly added parameter f for the PPA robot. This difference takes root in the fundamental structure of mechanical parameters in (2) and (3). Indeed, the counterpart of f in (A68) can be expressed by $a\times d$, since $a=\alpha _{12}/\alpha _{13}=\beta _2/\beta _3$ holds. However, we cannot find similar connection between f and the rest in (A5). Consequently, the existence of f significantly complicates the coefficients of the polynomial in (A11) compared to that in [15]. To deal with this increased complexity, we take full advantage of the properties of the newly defined parameters in Lemma 2 to simplify the discussion and further identify nonzero coefficient(s).

Remark 3

The condition of Case 2.2 is similar to that of Case 2.2.2 in [15]; that is, the actuated link is in the horizontal position. It is very difficult to discuss these two cases, since no useful information can be drawn to directly ease the strong coupling of the newly defined parameters inside $\xi _i$. To unveil a nonzero coefficient, we obtain two polynomial equations solely in terms of a from $\xi _i$. This is achieved by performing a series of iterative polynomial division, which is a method used in [15] of eliminating targeted variable(s) from multi-variable polynomial equations at the expense of increasing the highest order of other variable(s). However, unlike the counterpart in [15] where parameter e is fixed, in Case 2.2 it remains indefinite, and thus should be treated as a targeted variable to eliminate in the same manner as for b. This difference inevitably aggravates the complexity of iteration, as demonstrated in Case 2.2. As a result, we end up with high-order polynomial equations of a, which demand further analysis and inspection not encountered in [15].

Remark 4

The numerical solutions in (A65) and (A66) are calculated using the Mathematica function “NSolve”. The “WorkingPrecision” option of this function is set to 50 to provide solutions with adequate precision of 50-digit, while a lower precision would also suffice to yield the same conclusion in Case 2.2. For brevity, we only present the first six digits of these solutions in (A65) and (A66).

Stability analysis of equilibrium points

By calculating the characteristic polynomial of the robot’s linearization at the down–up–up equilibrium point $(\theta _{1},\theta _{2},\theta _{3},{\dot{\theta }}_{1},{\dot{\theta }}_{2},{\dot{\theta }}_{3})=(\pi ,0,0,0,0,0)$, we obtain

$$\begin{aligned}{} & {} \left| s\varvec{I}-\varvec{J}_{duu} \right| \\{} & {} \quad =s^6+a_1s^5+a_2s^4+a_3s^3+a_4s^2+a_5s+a_6, \end{aligned}$$

where $\varvec{J}_{duu}$ is the corresponding Jacobian matrix, and

$$\begin{aligned}&a_1\cdot \varPi _{duu}=-k_V\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) ,\\&a_2\cdot \varPi _{duu}=-k_P\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) +k_D \left( -\alpha _{22}\beta _1+\alpha _{11}\beta _2\right) \\&\qquad +2\beta _1\Big (-\alpha _{23}^2\beta _1+\left( \alpha _{13}^2-\alpha _{11}\alpha _{33}\right) \beta _2 \\&\qquad +\alpha _{12}^2\beta _3+\alpha _{22}\left( \alpha _{33}\beta _1-\alpha _{11}\beta _3\right) \Big ),\\&a_3\cdot \varPi _{duu}=k_V\left( -\alpha _{22}\beta _{1}+\alpha _{11}\beta _2\right) ,\\&a_4\cdot \varPi _{duu}=k_P\left( -\alpha _{22}\beta _1+\alpha _{11}\beta _2\right) +\beta _1\Big (\left( k_D-2\alpha _{33}\beta _1\right) \beta _2\\&\qquad \qquad \quad \hspace{5.0pt}+2\left( -\alpha _{22}\beta _1+\alpha _{11}\beta _2\right) \beta _3\Big ),\\&a_5\cdot \varPi _{duu}=k_V\beta _1\beta _2,\quad a_6\cdot \varPi _{duu}=\beta _1\beta _2\left( k_P+2\beta _1\beta _3\right) , \end{aligned}$$

with

$$\begin{aligned} \varPi _{duu}&=-\Big (k_D\big (\alpha _{11}\alpha _{22}-\alpha _{12}^2\big ) +2\beta _1\nonumber \\&\quad \big (\alpha _{13}^2\alpha _{22}-2\alpha _{12}\alpha _{13}\alpha _{23}\nonumber \\&\quad \hspace{5.0pt}+\alpha _{11}\alpha _{23}^2-\big (\alpha _{11}\alpha _{22} -\alpha _{12}^2\big )\alpha _{33}\big )\Big ). \end{aligned}$$

(B1)

We recall the requirement on $k_D$ in Lemma 1 for the controller in (14) to be nonsingular. From (15), we have

$$\begin{aligned}&k_D>\left( E_\textrm{r}-P\left( \varvec{\theta }\right) \right) \left( \varvec{B}^\textrm{T}\varvec{M}^{-1} \left( \varvec{\theta }\right) \varvec{B}\right) ^{-1}\Big |_{\varvec{\theta }=[\pi ,0,0]^\textrm{T}}\nonumber \\&\quad \hspace{5.0pt}=\frac{-2\beta _1}{\alpha _{11}\alpha _{22}-\alpha _{12}^2} \left( \alpha _{13}^2\alpha _{22}-2\alpha _{12}\alpha _{13}\alpha _{23} \right. \nonumber \\&\quad \left. +\alpha _{11}\alpha _{23}^2+\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) \alpha _{33}\right) . \end{aligned}$$

(B2)

By using (B1), (B2), and $\alpha _{11}\alpha _{22}-\alpha _{12}^2>0$ due to $\varvec{M}(\varvec{\theta })|_{\varvec{\theta }=\varvec{0}_3}>0$, we have $\varPi _{duu}<0$. This leads to $a_5<0$ and $a_6<0$, regardless of control gains and mechanical parameters. Hence, it can be concluded that the down–up–up equilibrium point is strictly unstable, since $\varvec{J}_{duu}$ possesses no less than one eigenvalue in the open right-half plane. The instability of the up–down–up equilibrium point $(\theta _{1},\theta _{2},\theta _{3},{\dot{\theta }}_{1},{\dot{\theta }}_{2},{\dot{\theta }}_{3})=(0,\pi ,0,0,0,0)$ can be proved similarly.

Regarding the down–down–up equilibrium point $(\theta _{1},\theta _{2},\theta _{3},$ ${\dot{\theta }}_{1},{\dot{\theta }}_{2},{\dot{\theta }}_{3})=(\pi ,\pi ,0,$ 0, 0, 0), calculating its characteristic polynomial yields

$$\begin{aligned} \left| s\varvec{I}-\varvec{J}_{ddu} \right| =s^6+a_1s^5+a_2s^4+a_3s^3+a_4s^2+a_5s+a_6, \end{aligned}$$

where $\varvec{J}_{ddu}$ is the corresponding Jacobian matrix, and

$$\begin{aligned}&a_1\cdot \varPi _{ddu}=-k_V\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) ,\\&a_2\cdot \varPi _{ddu}=-k_P\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) \\&\quad -k_D \left( \alpha _{22}\beta _1+\alpha _{11}\beta _2\right) -2\left( \beta _1+\beta _2\right) \\&\quad \hspace{5.0pt}\times \left( \alpha _{23}^2\beta _1+\alpha _{13}^2\beta _2 -\alpha _{12}^2\beta _3 \right. \\&\quad \left. -\alpha _{33}\left( \alpha _{22}\beta _1+\alpha _{11}\beta _2\right) +\alpha _{11}\alpha _{22}\beta _3\right) ,\\&a_3\cdot \varPi _{ddu}=-k_V\left( \alpha _{22}\beta _1+\alpha _{11}\beta _2\right) ,\\&a_4\cdot \varPi _{ddu}=-k_P\left( \alpha _{22}\beta _1+\alpha _{11}\beta _2\right) \\&\quad -\beta _1\beta _2\left( k_D-2\alpha _{33}\left( \beta _1+\beta _2\right) \right) \\&\quad \qquad \quad \hspace{5.0pt}-2\left( \beta _1+\beta _2\right) \left( \alpha _{22}\beta _1 +\alpha _{11}\beta _2\right) \beta _3, \\&a_5\cdot \varPi _{ddu}=-k_V\beta _1\beta _2, a_6\cdot \varPi _{ddu}\\&\quad =-\beta _1\beta _2 \left( k_P+2\left( \beta _1+\beta _2\right) \beta _3\right) , \end{aligned}$$

with

$$\begin{aligned} \varPi _{ddu}&=-\Big (k_D\big (\alpha _{11}\alpha _{22}-\alpha _{12}^2\big )+2\big (\beta _1 +\beta _2\big )\\&\quad \big (\alpha _{13}^2\alpha _{22}-2\alpha _{12}\alpha _{13}\alpha _{23}\\&\quad \hspace{5.0pt}+\alpha _{11}\alpha _{23}^2 -\big (\alpha _{11}\alpha _{22}-\alpha _{12}^2\big )\alpha _{33}\big )\Big ). \end{aligned}$$

Similarly, exploiting the requirement on $k_D$ in Lemma 1 gives

$$\begin{aligned}&k_D>\left( E_\textrm{r}-P\left( \varvec{\theta }\right) \right) \left( \varvec{B}^\textrm{T}\varvec{M}^{-1} \left( \varvec{\theta }\right) \varvec{B}\right) ^{-1}\Big |_{\varvec{\theta }=[\pi ,\pi ,0]^\textrm{T}}\\&\quad \hspace{5.0pt}=\frac{-2\left( \beta _1+\beta _2\right) }{\alpha _{11}\alpha _{22} -\alpha _{12}^2}\\&\quad \left( \alpha _{13}^2\alpha _{22}-2\alpha _{12}\alpha _{13}\alpha _{23} +\alpha _{11}\alpha _{23}^2-\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) \alpha _{33}\right) , \end{aligned}$$

which leads to $\varPi _{ddu}<0$. Thus, we have $a_1$, $a_3$, $a_5$, and $a_6$ being positive, regardless of control gains and mechanical parameters. However, the signs of $a_2$ and $a_4$ are left undetermined. To reveal the instability of this equilibrium point, we further compute the Hurwitz determinant

$$\begin{aligned} D_3= \begin{vmatrix} a_1&\quad a_3&\quad a_5\\ 1&\quad a_2&\quad a_4\\ 0&\quad a_1&\quad a_3 \end{vmatrix} =a_1a_2a_3-a_3^2-a_1^2a_4+a_1a_5, \end{aligned}$$

which yields

$$\begin{aligned} D_3\cdot \varPi _{ddu}^3&=2k_V^2\left( \beta _1+\beta _2\right) \\&\quad \Big (\alpha _{22} \beta _1^2\left( \alpha _{13}\alpha _{22}-\alpha _{12}\alpha _{23}\right) ^2 +\alpha _{11}\beta _2^2\big (\alpha _{12}\alpha _{13}\\&\quad \hspace{5.0pt}-\alpha _{11}\alpha _{23}\big )^2 +2\alpha _{12}\beta _1\beta _2\left( \alpha _{13}\alpha _{22}-\alpha _{12}\alpha _{23}\right) \\&\quad \left( \alpha _{12}\alpha _{13}-\alpha _{11}\alpha _{23}\right) \Big ). \end{aligned}$$

Straightforward calculation with (2) and using $m_il_il_{ci}\ge J_i+m_il_{ci}^2$ from [28] shows $\alpha _{13}\alpha _{22}-\alpha _{12}\alpha _{23}\le 0$ and $\alpha _{12}\alpha _{13}-\alpha _{11}\alpha _{23}<0$. Thus, $D_3<0$ since $\varPi _{ddu}<0$. Hence, $\varvec{J}_{ddu}$ has one eigenvalue in the open right-half plane at a minimum, indicating that the down–down–up equilibrium point is strictly unstable. $\square$