1 Introduction

Electro-mechanical systems play a crucial role in engineering and are an integral part of a large variety of modern everyday devices. Combining together electrical and mechanical components, they are designed to perform various tasks utilizing the principles of both electromagnetism and mechanics, which makes them fundamental in automating processes, improving efficiency, and enhancing precision in manufacturing [1, 2]

Electro-mechanical systems consist of electrical components, such as sensors, actuators, motors, switches, and circuits, seamlessly integrated with mechanical systems like gears, levers, and belts [3,4,5]. Using a fascinating analogy, the electrical components provide the brain and power, while the mechanical components represent the muscles and the sensory apparatus, enabling physical movement, force transmission and physical interaction with the surrounding environment [6, 7].

A key feature of electro-mechanical systems is their versatility. They can be engineered to perform a wide range of functions. Their ability to convert electrical energy into mechanical motion allows them to respond to inputs and perform actions with unmatched accuracy and speed. An example is the use of silicon micro-technology to design cantilevers that can be exploited as micro-mechanical resonators. These have emerged as key elements in mass sensing applications, being characterized by very high quality factor, that makes their resonance frequency extremely sensitive to external forces and mass changes due to substance additions [8, 9]. On the other hand, in recent years, a new category of electro-mechanical systems has been realized, which explores the reverse mechanism. They are designed to convert mechanical kinetic energy dispersed in the environment that would otherwise be wasted, into usable electrical power, a solution that goes by the name of (vibrational) energy harvesting [10,11,12,13]. Energy harvesting aims to design electro-mechanical systems with self-powering capability, or at least able to recharge their internal battery prolonging its expected life, by scavenging energy dispersed in the ambient whenever available.

As technology progresses and with the rapid diffusion of new technological paradigms, such as Artificial Intelligence [14, 15] and the Internet of Things [16, 17], electro-mechanical systems are becoming increasingly intelligent, as well as increasingly interconnected. On the one hand, with the combined use of sensors, microcontrollers, and advanced algorithms, these systems can adapt to changing conditions, monitor their own performance, and optimize their operations in real-time. From the designer standpoint, new challenges arise especially in terms of system optimization and energy efficiency.

As the number of interconnected systems grows, the corresponding mathematical models involve larger number of variables, equations and parameters, resulting in large-scale systems that can be difficult to handle efficiently. In this view, model order reduction is a powerful technique used in engineering and science to simplify complex mathematical models while preserving their essential characteristic [18,19,20]. It permits the analysis and simulation of systems that would otherwise be computationally expensive or time-consuming to handle.

The simplified version of the mathematical model must retain the critical behavior and properties, while significantly reducing the computational complexity, allowing engineers and scientists to analyze and understand the system’s behavior more effectively. By projecting the system’s dynamics onto a lower-dimensional subspace, the number of equations, variables and parameters can be reduced, paying attention to retain the most important information while neglecting the less significant one. As a result, order reduced models significantly simplify design and optimization, reducing computational costs, prototyping time, and ultimately, fastening time-to-market.

In this contribution we propose a methodology for the analysis and design of electro-mechanical systems subject to random external perturbations. The method is based on a two step approach: (1) the first step consists in a model order reduction, such that the total number of variables (mechanical + electrical) is reduced to two for each mechanical degree of freedom, one representing the mechanical energy and the other an angle variable. The reduction is analogous to the well known action-angle representation for conservative systems [21], and is performed under the assumption that the mechanical friction and the action of electrical subsystems on the mechanical part are small perturbations of the mechanical equations. The electrical variables for the general equations are expressed as functions of the mechanical energy and of the angle, exploiting a spectral domain representation founded on Fourier (harmonic) series, which forms also the basis for the well known harmonic balance (HB) numerical solution technique [22]; (2) The second step is based on stochastic averaging [23]. Exploiting the time scale separation between the reduced variables, it is possible to eliminate the fast variable (in our case, the angle) so that a scalar equation for the energy is obtained. The main result is that the stationary energy probability density function can be analytically calculated in a relatively simple way, thus enabling the computation of all expected quantities for the electro-mechanical system. As a consequence, a significant simplification of the system modelling is obtained, opening the way to the definition of optimization and design procedures.

The paper is organized as follows: In Sect. 2 we introduce the general form of the electro-mechanical system to be modeled. The stochastic nature of the model, and its impact on the equation normalization procedure, are discussed in Sect. 3. Section 4 is devoted to the introduction of the model order reduction approach, whereas stochastic averaging is presented in Sect. 5. The application of the methodology to a vibration energy harvester with power factor correction is discussed in Sect. 6.1. In Sect. 6.2 the method is used to analyse a system composed by two coupled cantilevers for application to mass sensing. Finally Sect. 7 is devoted to conclusions.

2 Micro-electro-mechanical system modeling

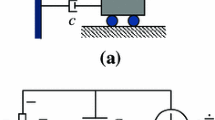
We consider an electro-mechanical system that can be represented as the two-port network shown in Fig. 1. Mechanical quantities (force and velocity) are applied at the left port, while electrical quantities (current and voltage) are at the right port. The right port is closed on a two terminal electrical element, representing a generic user which absorbs electrical power or receives information from the electro-mechanical network. In many practical applications, the user is a simple electrical resistor.

The internal structure of the electro-mechanical system can be very complicated, as it can be composed of several subsystems. For example, it may include a mechanical structure responsible for absorbing kinetic energy from external sources, one or more transducers that convert mechanical energy into electrical energy (or vice-versa), and an electrical domain. Possibly, a rectifier and/or a matching circuit may be interposed in front of the user. Thus, a large set of state variables, both mechanical and electrical, may be required for a detailed description.

Fig. 1
figure 1

Two-port network representation of an electro-mechanical system closed on a generic user

Full size image

We assume that the mechanical part is a one degree of freedom (DOF) system, described by the Lagrangian function \(\hat{{\mathcal {L}}}(z,\dot{z}) = {{\hat{T}}}(\dot{z}) - {{\hat{U}}}(z) = m \dot{z}^2/2 - {{\hat{U}}}(z)\), where \({{\hat{T}}}(\dot{z})\), \({{\hat{U}}}(z)\) are the kinetic and the potential energy, respectively, m is an inertial mass, and z, \(\dot{z}\) are the generalized coordinate and velocity, respectively. Such an assumption is quite reasonable for micro-electro-mechanical systems where, given the very small dimension involved, mass can be considered concentrated, and the displacement so small that the motion can be assumed to occur along a straight line. A generalization to systems with more than one mechanical DOF will be discussed in the second part of Sect. 4, and more specifically in Corollary 3.

For a mechanical systems with small internal friction, the dissipation can be approximated as a linear force, the dissipation potential being \(\mathcal {{{\hat{D}}}}(\dot{z}) = {{\hat{\varepsilon }}} \dot{z}^2/2\), where \({{\hat{\varepsilon }}}\) is the friction coefficient. The Lagrange equation of motion for the mechanical system takes the form

$$\begin{aligned} m \ddot{z} + {{\hat{\varepsilon }}} \dot{z} + {{\hat{U}}}'(z) = F(t) \end{aligned}$$
(1)

where \({\hat{U}}'(z) = \partial {\hat{U}}(z)/\partial z\), and F(t) is the resultant of the forces applied to the mechanical domain. In particular, we consider the case where F(t) is the sum of two contributions: an external force \(\eta (t)\) due to the action of the environment, and a force \({{\hat{b}}}_m({\textbf{z}}_e)\) due to the action of the electrical domain

$$\begin{aligned} F(t) = {{\hat{\varepsilon }}} {{\hat{b}}}_m({\textbf{z}}_e) + \sqrt{{{\hat{\varepsilon }}}} \, \eta (t) \end{aligned}$$
(2)

where \({\textbf{z}}_e: {{\mathbb {R}}}\mapsto {{\mathbb {R}}}^n\), denotes the collection of the electrical variables describing the state of the electrical domain (voltages across capacitors and currents through inductors, including the reactive elements of the transducer equivalent circuit [24,25,26]). For the sake of simplicity and without too much loss of generality, in (2) we have assumed that the electro-mechanical coupling force is of the same order of magnitude of the internal friction, while the external forcing has magnitude \(\sqrt{{{\hat{\varepsilon }}}}\).

The electrical domain is represented by an electrical circuit, composed by the interconnection of linear and nonlinear two-terminal and/or multi-terminal elements. External forces acting on the electrical domain, such as the action of transducers converting mechanical forces into electrical inputs, are modelled as equivalent voltage or current sources, either dependent or independent. For the sake of simplicity, we shall assume that this is the only force applied to the electrical domain. The state equations are a system of differential equations, that can be derived from Kirchhoff laws and the characteristic relationships of the electrical elements [27], thereby obtaining:

$$\begin{aligned} {{\dot{{\textbf{z}}}}}_e = {{\hat{{\textbf{a}}}}}_e({\textbf{z}}_e) + {{\hat{{\textbf{b}}}}}_e (z, \dot{z}) \end{aligned}$$
(3)

where \({{\hat{{\textbf{a}}}}}_e: {{\mathbb {R}}}^{n} \mapsto {{\mathbb {R}}}^n\), is the vector field which defines the internal state evolution, and \({{\hat{{\textbf{b}}}}}_e: {{\mathbb {R}}}^{2} \mapsto {{\mathbb {R}}}^n\) is the vector field of the sources associated to the action of the mechanical domain and the environment. We shall implicitly assume that all vector fields are smooth enough for all the following considerations.

Combining (1)–(3), and rewriting as a system of first order differential equations yields

$$\begin{aligned} \dot{z}_1&= z_2 \end{aligned}$$
(4a)
$$\begin{aligned} \dot{z}_2&= \left( - \dfrac{1}{m} {{\hat{U}}}'(z_1) - \dfrac{\hat{\varepsilon }}{m} z_2 + \dfrac{{{\hat{\varepsilon }}}}{m}{{\hat{b}}}_m({\textbf{z}}_e) \right) + \dfrac{\sqrt{{{\hat{\varepsilon }}}}}{m} \eta (t) \end{aligned}$$
(4b)
$$\begin{aligned} {{\dot{{\textbf{z}}}}}_e&= {{\hat{{\textbf{a}}}}}_e({\textbf{z}}_e) + {{\hat{{\textbf{b}}}}}_e({\textbf{z}}_m) \end{aligned}$$
(4c)

where \({\textbf{z}}_m = [z_1,z_2]^T=[z,\dot{z}]^T\) is the vector obtained collecting the mechanical variables. Again, in (4b) we have assumed that the electro-mechanical coupling force is of the same order of magnitude as the internal friction.

Finally we consider the external forcing. In a complex environment, the external force is the result of many distinct effects with very different nature, such as impacts or shocks, periodic or more complicated forces. If the sources are independent, the forces are uncorrelated, thus resembling a random signal. Moreover, if their number is large enough, their distribution becomes Gaussian. Typically, the energy of environmental forcings is spread over a wide frequency spectrum, and consequently the external force can be reasonably well modelled as a white Gaussian noise. Clearly a true white noise cannot exist in the real world, because the flat power spectrum would imply an infinite power. Nevertheless, white Gaussian noise is a widely adopted model for random forces, and the associated mathematical theory is well developed [28, 29].

3 Stochastic differential equations and dimensionless equations

Under the assumption that the external forcing is modelled as a white Gaussian noise, system (4) becomes a system of stochastic differential equations (SDEs).

Let \((\Omega ,{\mathcal {F}},{\mathcal {P}})\) be a probability space, where \(\Omega \) is the sample space, \({\mathcal {F}} = ({\mathcal {F}}_t)_{t\ge 0}\) is a filtration, that is the \(\sigma \)-algebra of all the events, and \({\mathcal {P}}\) is a probability measure. A vector valued stochastic process \({\textbf{X}}_t\) is a function mapping \({\textbf{X}}_t: \Omega \times T \mapsto {{\mathbb {R}}}^d\), i.e. a vector of random variables taking values in the sample space \(\Omega \), and parameterized by a real variable \(t \in T\). Usually, the parameter space T is the half-line \([0,+\infty [\) [29, 30]. We adopt the standard notation used in probability: capital letters denote stochastic processes, while lower case letters denote their possible values. A scalar Wiener process \(W_t=W(t)\), is a stochastic process characterized by the expectation value \(\mathrm E[W_t ] = 0\) (symbol \(\mathrm E[X_t]\) denotes expectation of the stochastic process \(X_t\)), by the covariance \(\textrm{cov}(W_t,W_s) = \mathrm E [W_t \, W_s] = \min (t,s)\) and by \(W_t \sim {\mathcal {N}}(0,t)\), where symbol \(\sim \) means “distributed as”, and \({\mathcal {N}}(0,t)\) denotes centered normal distribution. The Wiener process, also known as Brownian motion, represents the integral of a white noise Gaussian process.

A d-dimensional system of SDEs driven by a h-dimensional vector valued Wiener process \({\textbf{W}}_t: \Omega \times T \mapsto {{\mathbb {R}}}^h\), takes the form

$$\begin{aligned} \textrm{d}{\textbf{Z}}_t = {\textbf{a}}({\textbf{Z}}_t) dt + {\textbf{B}}({\textbf{Z}}_t) d {\textbf{W}}_t \end{aligned}$$
(5)

where \({\textbf{Z}}_t: \Omega \times T \mapsto {{\mathbb {R}}}^d\) is a vector valued stochastic process. The d-dimensional vector valued function \({\textbf{a}}: {{\mathbb {R}}}^d \mapsto {{\mathbb {R}}}^d\), is called the drift vector, while matrix \({\textbf{B}}: {{\mathbb {R}}}^d \mapsto {{\mathbb {R}}}^{d,h}\) is called the diffusion matrix. They are measurable functions satisfying a global Lipschitz condition, to ensure the existence and uniqueness solution Theorem [29]. For a constant diffusion matrix, the noise is called unmodulated (or additive), while in the general case \({\textbf{B}}({\textbf{Z}}_t)\) noise is modulated (or multiplicative).

The SDE system (4) can be rewritten in the form

$$\begin{aligned} \textrm{d}{\textbf{Z}}_t = \left( {{\hat{{\textbf{A}}}}} \, {\textbf{Z}}_t + {{\hat{{\textbf{n}}}}}({\textbf{Z}}_t) \right) \textrm{d}t + {{\hat{{\textbf{B}}}}}~\textrm{d}W_t \end{aligned}$$
(6)

where matrix \({{\hat{{\textbf{A}}}}} \in {{\mathbb {R}}}^{d,d}\) collects the linear terms, \({{\hat{{\textbf{n}}}}}: {{\mathbb {R}}}^d \mapsto {{\mathbb {R}}}^d\) represents the nonlinear parts, and \(d =n + 2\). Finally, \({{\hat{{\textbf{B}}}}} \in {{\mathbb {R}}}^d\) is a constant diffusion vector and \(W_t\) is a scalar Wiener process.

For the additive noise scenario, the two main possible interpretations for SDEs, namely Itô and Stratonovich, are equivalent, meaning that in both cases the solution of (5) is the same, irrespective of which interpretation is adopted [29]. However, the two interpretations imply a different set of calculus rules, thus requiring to specify the adopted approach: We shall assume hereafter Itô’s interpretation.

In many cases it is convenient to consider a transformed SDE system, for example rewritten in terms of dimensionless variables. Introducing dimensionless variables, including a dimensionless time, the number of parameters can be reduced, while a properly normalized dimensionless time, permits to adjust the time integration step used in numerical simulations, speeding up the integration and reducing numerical issues. Dimensionless equations are usually obtained by a linear change of variables, i.e. multiplying each variable, including time, by a proper normalizing parameter. The following theorem gives a systematic procedure for obtaining the transformed, possibly dimensionless, equations.

Theorem 1

Consider the SDE system (6). Let \({\textbf{P}}\in {{\mathbb {R}}}^{d,d}\) be a regular matrix, and let \(\tau (t) = \omega t\), \(\omega >0\), be the dimensionless time. Let \({\textbf{X}}_{\tau }\) be the solution of the SDE system

$$\begin{aligned} d {\textbf{X}}_{\tau } = \left( {\textbf{A}}{\textbf{X}}_{\tau } + {\textbf{n}}({\textbf{X}}_{\tau }) \right) dt + {\textbf{B}}dW_{\tau } \end{aligned}$$
(7)

with \({\textbf{A}}={\omega }^{-1} {\textbf{P}}{{\hat{{\textbf{A}}}}} {\textbf{P}}^{-1}\), \({\textbf{n}}({\textbf{x}}) = {\omega }^{-1} {\textbf{P}}{{\hat{{\textbf{n}}}}}({\textbf{P}}^{-1} {\textbf{x}})\), \({\textbf{B}}= {{\omega }}^{-1/2} {\textbf{P}}{{\hat{{\textbf{B}}}}}\). Then \({\textbf{X}}_{\tau } \sim {\textbf{P}}{\textbf{Z}}_{\tau }\).

Proof

Let \({\textbf{y}}= {\textbf{P}}{\textbf{z}}\). Application of Itô’s lemma [28, 29] to (6), yields the SDE system for the stochastic processes \({\textbf{Y}}_t\):

$$\begin{aligned} d {\textbf{Y}}_t = \left( {\textbf{P}}{{\hat{{\textbf{A}}}}} {\textbf{P}}^{-1} {\textbf{Y}}_t + {\textbf{P}}\hat{\textbf{n}}({\textbf{P}}^{-1} {\textbf{Y}}_t) \right) dt + {\textbf{P}}\, {{\hat{{\textbf{B}}}}}\, dW_t \end{aligned}$$
(8)

Consider the time change \(\tau (t) = \omega \, t\). If \({\textbf{Y}}_t\) solves (8), then \({\textbf{Y}}_{\tau }\) solves the SDE system

$$\begin{aligned} d {\textbf{Y}}_{\tau } = \dfrac{1}{\omega } \left( {\textbf{P}}{{\hat{{\textbf{A}}}}} {\textbf{P}}^{-1} {\textbf{Y}}_{\tau } + {\textbf{P}}{{\hat{{\textbf{n}}}}}({\textbf{P}}^{-1} {\textbf{Y}}_{\tau }) \right) d\tau + {\textbf{P}}\, {{\hat{{\textbf{B}}}}} \, dW_{t}\nonumber \\ \end{aligned}$$
(9)

The change of time theorem for Itô integrals [29, p. 156] implies that

$$\begin{aligned} W_{\tau (t)} \sim \sqrt{\tau '(t)} \, W_t = \sqrt{\omega } \, W_t \end{aligned}$$
(10)

Substituting (10) into (9), it follows that \({\textbf{X}}_{\tau }\) and \({\textbf{Y}}_{\tau }\) have the same probability distribution, because they are solutions of the same SDE system, but for two different realizations of the Wiener process. \(\square \)

The SDE system for the dimensionless variables is obtained by straightforward application of Theorem 1, where \({\textbf{P}}\) is a diagonal matrix which entries are the normalization parameters. The regularity of \({\textbf{P}}\) guarantees that the change of variables is invertible, which makes possible to retrieve the original variables. The dimensionless time is obtained introducing an appropriate normalizing frequency \(\omega \). The solution of the dimensionless SDE system converges in probability to the solution of the original SDE system, however for practical applications the probability density function (PDF) of the solution is the most relevant information, as it allows to calculate the expectation of all quantities. Therefore, knowledge of the PDF is more important that finding the pathwise solution for a specific realization of the noise process.

4 Model order reduction

According to Theorem 1, we shall consider the following dimensionless SDE system equivalent to (4):

$$\begin{aligned} d X_1 =&X_2 \, dt \end{aligned}$$
(11a)
$$\begin{aligned} dX_2 =&\left( - U'(X_1) - \varepsilon X_2 + \varepsilon \, b_m({\textbf{X}}_e) \right) dt + \sqrt{\varepsilon } B_m dW_t \end{aligned}$$
(11b)
$$\begin{aligned} d {\textbf{X}}_e =&\left( {\textbf{a}}_e({\textbf{X}}_e) + {\textbf{b}}_e(X_1,X_2) \right) dt \end{aligned}$$
(11c)

The final goal of the derivation will be the evaluation of the expectation \(\mathrm E[{\textbf{F}}(X_1,X_2,{\textbf{X}}_e)]\) of some relevant function \({\textbf{F}}\) (observable) of the state variables \((X_1,X_2,{\textbf{X}}_e)\). In general, finding an analytical solution of the SDEs system (11) is unfeasible, as it is nonlinear and of high order. Alternatively, one may resort to a numerical integration of (11). Various integration schemes are available for its numerical solution [31], however determining expectations \(\mathrm E[{\textbf{F}}(X_1,X_2,{\textbf{X}}_e)]\) requires time consuming simulations, making the approach unfeasible for the design and optimization of systems where a large parameter space must be explored.

An alternative solution, particularly well suited for the evaluation of expected quantities, amounts to consider the Fokker–Planck equation (FPE) associated to the SDEs system (11). The FPE is a partial differential equation describing the time evolution of the probability density function of the stochastic process [28, 32]. The FPE can be solved analytically only in few special cases. Otherwise, sophisticated numerical methods are required [32], whose implementation is rather cumbersome.

Yet another approach consists of deriving a reduced order model, that is, a SDEs system for a smaller set of variables that approximates the full solution. This procedure is based on observing that in the limit \(\varepsilon \downarrow 0\), the equations for the mechanical and the electrical parts are uncoupled, and the system becomes solvable. We expect that the solution of the reduced and of the original system are close enough, at least for small values of \(\varepsilon \). A general proof of the convergence of the two solutions is impossible, as well as to provide a good estimate of the error made. However, there is a large empirical evidence that the method gives accurate results for reasonably small values of \(\varepsilon \).

The first step in the derivation of a reduced order model, is to define a coordinate change,

$$\begin{aligned} {\textbf{X}}= {\textbf{h}}({\textbf{Y}}) \end{aligned}$$

where \({\textbf{X}}= [X_1,X_2, {\textbf{X}}_e^T]^T \in {{\mathbb {R}}}^{n+2} \) is the vector of the original coordinates (\(^T\) denotes transpose), \({\textbf{Y}}\in {{\mathbb {R}}}^p\), with \(p<n+2\) is the vector of the new coordinates, and \({\textbf{h}}: {{\mathbb {R}}}^{p}\mapsto {{\mathbb {R}}}^{n+2}\). The choice for \({\textbf{Y}}\) and \({\textbf{h}}\) is obviously not unique, and in general there is no a priori assessment on which option is better. The final choice is usually heuristic, being determined by a mix of physical considerations and experience.

Inspired by some recent works [33, 34], we take advantage of the fact that in the limit \(\varepsilon \downarrow 0\) the SDE system is solvable, thus allowing to rewrite the SDE system (11) in terms of the mechanical energy and of an angle variable. For \(\varepsilon = 0\), system (11a)–(11b) is Hamiltonian, with normalized mechanical energy \(E(X_1,X_2) =X_2^2/2 + U(X_1)\). Together with the energy we introduce an angle variable \(\theta (X_1,X_2)\), whose explicit form depends on the potential \(U(X_1)\). For \(\varepsilon \downarrow 0\) the Jacobian of the canonical transformation \((E, \theta ) \rightarrow (X_1,X_2)\) is regular, therefore the change of variables is invertible, and explicit expressions for \(X_1(E,\theta )\) and \(X_2(E,\theta )\) can be derived. To complete the reduction, we need an expression \({\textbf{X}}_e(E,\theta )\) for the electrical variables as functions of the mechanical energy and of the angle, to obtain the full transformation \([X_1,X_2,{\textbf{X}}_e^T]^T = {\textbf{h}}(E,\theta )\).

Proposition 1

(HB representation of \({\textbf{X}}_e(E,\theta )\)) In the limit \(\varepsilon \downarrow 0\), the electrical variables admit the representation

$$\begin{aligned} {\textbf{X}}_e(E,\theta )&= {\textbf{X}}_{e0}(E) + \sum _{m=0}^{+\infty } \big ( {\textbf{X}}_{ec,m}(E) \cos (m \, \theta ) \nonumber \\&\qquad + {\textbf{X}}_{es,m}(E) \sin (m \,\theta ) \big ) \end{aligned}$$
(12)

where the bias term \({\textbf{X}}_{e0}(E)\), and the amplitude of the harmonics \({\textbf{X}}_{ec,m}(E)\) and \({\textbf{X}}_{es,m}(E)\), are obtained from the associated Harmonic Balance system (see (21) in the proof).

Proof

The canonical mapping \((X_1,X_2) \rightarrow (E, \theta )\), transforms locally (for \(\varepsilon = 0\) and in the neighborhood of an invariant set) relations (11a)–(11b) into the equivalent ordinary differential equations (ODEs) system [21]:

$$\begin{aligned} \dfrac{dE}{dt}&= 0 \end{aligned}$$
(13a)
$$\begin{aligned} \dfrac{d\theta }{dt}&= \Omega (E) \end{aligned}$$
(13b)

where \(\Omega (E)\) is an energy dependent angular frequency. For the sake of simplicity, we assume a non degeneracy condition, e.g. we take for granted that the Jacobian matrix of the Hamiltonian system

$$\begin{aligned} \dfrac{d X_1}{dt}&= X_2 \end{aligned}$$
(14a)
$$\begin{aligned} \dfrac{d X_2}{dt}&= -U'(X_1) \end{aligned}$$
(14b)

does not have zero as a double eigenvalue. This condition is equivalent to assume that the only critical points of the potential \(U(X_1)\) are local maxima and minima. Then, the only possible invariant sets of the Hamiltonian system are saddles, e.g. unstable equilibrium points corresponding to local maxima of \(U(X_1)\), centres, e.g neutrally stable equilibrium points associated to local minima of \(U(X_1)\), surrounded by continuous families of periodic orbits, periodic orbits, and homoclinic or heteroclinic orbits (paths formed by the intersection of stable and unstable manifolds of saddles). Thus, we can expand \(X_1(E,\theta )\) in Fourier series with respect to the angle variable:

$$\begin{aligned} X_1(E,\theta )&= X_{10}(E) + \sum _{m=1}^{+\infty } \bigg ( X_{1c,m}(E) \cos (m \, \theta ) \nonumber \\&\qquad + X_{1s,m}(E) \sin (m \, \theta ) \bigg ) \end{aligned}$$
(15)

Using (11a) and (13), we find:

$$\begin{aligned} X_2(E,\theta )&= \sum _{m=1}^{+\infty } \bigg (- m \, \Omega (E) X_{1c,m}(E) \sin (m \, \theta ) \nonumber \\&\qquad + m\Omega (E) X_{1s,m}(E) \cos (m \, \theta ) \bigg ) \end{aligned}$$
(16)

Because \(X_1(E,\theta )\) and \(X_2(E,\theta )\) are periodic, \({\textbf{b}}_e(X_1,X_2)\) is periodic as well, and thus it can be expanded in Fourier series

$$\begin{aligned}&{\textbf{b}}_e(X_1(E,\theta ),X_2(E,\theta )) = {\textbf{b}}_{e0}(E) \nonumber \\&~+ \sum _{m=1}^{+\infty } \bigg ({\textbf{b}}_{ec,m}(E) \cos (m \, \theta ) + {\textbf{b}}_{es,m}(E) \sin (m \, \theta ) \bigg ) \end{aligned}$$
(17)

where the Fourier coefficients are linked to the mechanical variables by

$$\begin{aligned} {\textbf{b}}_{e0}(E)&= \dfrac{1}{2\pi } \int _0^{2\pi } {\textbf{b}}_{e}(X_1(E,\theta ),X_2(E,\theta ))\, d\theta \end{aligned}$$
(18a)
$$\begin{aligned} {\textbf{b}}_{ec,m}(E)&= \dfrac{1}{\pi } \int _0^{2\pi } {\textbf{b}}_{e}(X_1(E,\theta ),X_2(E,\theta )) \cos ( m \,\theta ) \, d\theta \end{aligned}$$
(18b)
$$\begin{aligned} {\textbf{b}}_{es,m}(E)&= \dfrac{1}{\pi } \int _0^{2\pi } {\textbf{b}}_{e}(X_1(E,\theta ),X_2(E,\theta )) \sin ( m \,\theta ) \, d\theta \end{aligned}$$
(18c)

We notice that for \(\epsilon \downarrow 0\) not only the mechanical system becomes conservative, but also it decouples from the electrical part. Consequently, (11c) becomes a nonlinear, non-homogeneous ODE system with source term \({\textbf{b}}_e(X_1,X_2)\), which is in turn a periodic function of \(\theta \). As a consequence, also the solution \({\textbf{X}}_e\) is a periodic function of \(\theta \), and thus it can be expressed according to the Fourier series (12). Therefore, also \({\textbf{a}}_e({\textbf{X}}_e(E,\theta ))\) can be expanded in Fourier series

$$\begin{aligned} {\textbf{a}}_e({\textbf{X}}_e(E,\theta ))&= {\textbf{a}}_{e0}(E) + \sum _{m=1}^{+\infty } \bigg ({\textbf{a}}_{ec,m}(E) \cos (m \, \theta ) \nonumber \\&\qquad + {\textbf{a}}_{es,m }(E) \sin (m \, \theta ) \bigg ) \end{aligned}$$
(19)

with coefficients

$$\begin{aligned} {\textbf{a}}_{e0}(E)&= \dfrac{1}{2\pi } \int _0^{2\pi } {\textbf{a}}_{e}({\textbf{X}}_e(E,\theta )) d\theta \end{aligned}$$
(20a)
$$\begin{aligned} {\textbf{a}}_{ec,m}(E)&= \dfrac{1}{\pi } \int _0^{2\pi } {\textbf{a}}_{e}({\textbf{X}}_e(E,\theta )) \cos ( m \, \theta ) \, d\theta \end{aligned}$$
(20b)
$$\begin{aligned} {\textbf{a}}_{es,m}(E)&= \dfrac{1}{\pi } \int _0^{2\pi } {\textbf{a}}_{e}({\textbf{X}}_e(E,\theta )) \sin ( m \, \theta ) \, d\theta \end{aligned}$$
(20c)

Introducing (17), (19) and the derivative of (12) into (11c), and using the orthogonality of the basis functions, we obtain the HB (infinite, as \(m=1,\ldots ,+\infty \)) system whose terms are nonlinear functions of the Fourier coefficients of \({\textbf{X}}_e(E,\theta )\)

$$\begin{aligned}&{\textbf{a}}_{e0}(E) + {\textbf{b}}_{e0}(E) = {\textbf{0}} \end{aligned}$$
(21a)
$$\begin{aligned}&m \Omega (E) {\textbf{X}}_{ec,m}(E) + {\textbf{a}}_{es,m}(E) + {\textbf{b}}_{es,m}(E) = {\textbf{0}} \end{aligned}$$
(21b)
$$\begin{aligned}&m \Omega (E) {\textbf{X}}_{es,m}(E) - {\textbf{a}}_{ec,m}(E) - {\textbf{b}}_{ec,m}(E) = {\textbf{0}} \end{aligned}$$
(21c)

The solution of (21) defines the constant component \({\textbf{X}}_{e0}(E)\) and the harmonic amplitudes \({\textbf{X}}_{ec,m}(E)\) and \( {\textbf{X}}_{es,m}(E)\) leading, to the representation (12) of \({\textbf{X}}_e(E,\theta )\). \(\square \)

Remark 1

Notice that the Fourier representation captures all the possible dynamic behaviors that we assumed feasible for the electro-mechanical system. Equilibrium points correspond to solutions with \(X_{1c,m}=X_{1s,m} = 0\) for all \(m=1,\ldots ,+\infty \). Periodic orbits correspond to solutions characterized by \(X_{1c,m}(E) \ne 0\) and/or \(X_{1s,m}(E) \ne 0\) for at least one m. Finally homoclinic and heteroclinic paths are obtained in the limit \(\Omega (E) \downarrow 0\). Thus, (15) and (16) represent all the invariant sets of the Hamiltonian system.

Remark 2

Using proposition 1, the electrical variables can be eliminated from the original equations, reducing the number of variables to the mechanical energy and angle. With respect to “traditional” applications of the harmonic balance method, which is mostly used as a numerical tool to study periodic solutions of ordinary differential equations, here the harmonic series is used to write electrical variables as functions of mechanical energy and angle, giving the ideal representation for application of the stochastic averaging method described in Sect. 5.

Corollary 1

(Linear electrical circuit) Consider a linear electrical circuit described by the ODE system

$$\begin{aligned} \dfrac{d {\textbf{X}}_e}{dt} = {\textbf{A}}_e {\textbf{X}}_e + {\textbf{b}}_1 X_1 + {\textbf{b}}_2 X_2 \end{aligned}$$
(22)

where \({\textbf{A}}_e \in {{\mathbb {R}}}^{n,n}\) and \({\textbf{b}}_1, {\textbf{b}}_2 \in {{\mathbb {R}}}^n\) are vectors of electro-mechanical coupling constants. The electrical variables admit the representation (\(j=\sqrt{-1}\))

$$\begin{aligned} {\textbf{X}}_e(E,\theta ) = {\textbf{X}}_{e0}(E) + \sum _{m=1}^{+\infty } {\text {Re}}[\hat{\textbf{X}}_{em}(E) \, e^{j m \theta }] \end{aligned}$$
(23)

with \({\textbf{X}}_{e0}(E) = - {\textbf{A}}_e^{-1} {\textbf{b}}_1 X_{10}(E)\), and

$$\begin{aligned} {{\hat{{\textbf{X}}}}}_{em}(E)&= (j m \Omega (E) {\varvec{I}}_n - {\textbf{A}}_e)^{-1} \nonumber \\&\qquad \times ({\textbf{b}}_1 + j m \Omega (E) {\textbf{b}}_2) {{\hat{X}}}_{1m}(E) \end{aligned}$$
(24)

where \({\varvec{I}}_n\) is the \(n\times n\) identity matrix, and \({{\hat{X}}}_{1m}(E)\) is the phasor representation of \(X_{1}(E)\).

Proof

Rewrite the representation (15) in the form

$$\begin{aligned} X_1(E,\theta ) = X_{10}(E) + \sum _{m=1}^{+\infty } X_{1m}(E) \cos (m\, \theta + \phi _m)\nonumber \\ \end{aligned}$$
(25)

with

$$\begin{aligned} X_{1m} =&\sqrt{ X_{1c,m}^2 + X_{1s,m}^2} \end{aligned}$$
(26a)
$$\begin{aligned} \phi _m =&-\arctan \dfrac{X_{1s,m}}{X_{1c,m}} \end{aligned}$$
(26b)

Substituting (23) and (25) in (22), and considering constant terms, relationship for \({\textbf{X}}_{e0}(E) \) immediately follows.

Transforming (22) in the phasor domain and using superposition, we obtain

$$\begin{aligned} j m \Omega (E) {{\hat{{\textbf{X}}}}}_{em}(E) =&{\textbf{A}}_e {{\hat{{\textbf{X}}}}}_{em}(E) \nonumber \\&+ ({\textbf{b}}_1 + j m \Omega (E) {\textbf{b}}_2) {{\hat{X}}}_{1m}(E) \end{aligned}$$
(27)

Solving for \({{\hat{{\textbf{X}}}}}_{em}(E)\), the thesis follows. \(\square \)

Corollary 2

The inverse matrix \((j m \Omega (E) {\varvec{I}}_n -{\textbf{A}}_e)^{-1}\) exists for every stable linear circuit.

Proof

Let \(\lambda _i\) be the eigenvalues of \({\textbf{A}}_e\). For a stable circuit, \({\text {Re}}[\lambda _i] < 0\), for all \(i=1,\ldots ,n\). Let \({\textbf{v}}_i\) be the corresponding eigenvectors. Then \({\textbf{v}}_i\) is also an eigenvector for \(j m \Omega (E) {\varvec{I}}_n\), with eigenvalue \(j m \Omega (E)\). The matrix \(j m \Omega (E) {\varvec{I}}_n -{\textbf{A}}_e\) has eigenvalues \(\mu _i = j m \Omega (E) - \lambda _i\), with positive real part for all \(i=1,\ldots ,n\). Therefore, zero is not an eigenvalue and the matrix is invertible. \(\square \)

Corollary 1 can be generalized to electro-mechanical systems with more than one mechanical DOF. For the sake of simplicity, we limit the discussion to systems with two mechanical DOF. Extension to higher numbers is straightforward, but the notation is more involved. Consider a system with two mechanical DOF:

$$\begin{aligned} d X_1 =&X_2 \, dt \end{aligned}$$
(28a)
$$\begin{aligned} dX_2 =&\big ( - U_1'(X_1) - \varepsilon X_2 + \varepsilon \, b_{m,1}({\textbf{X}}_e) \nonumber \\&+\varepsilon \, g_{1}(X_1,X_2,X_3,X_4) \big ) dt + \sqrt{\varepsilon } B_{m,1} dW_t \end{aligned}$$
(28b)
$$\begin{aligned} d X_3 =&X_4 \, dt \end{aligned}$$
(28c)
$$\begin{aligned} d X_4 =&\big ( - U_2'(X_3) - \varepsilon X_4 + \varepsilon \, b_{m,2}({\textbf{X}}_e) \nonumber \\&+ \varepsilon \, g_2(X_1,X_2,X_3,X_4) \big ) dt + \sqrt{\varepsilon } B_{m,2} dW_t \end{aligned}$$
(28d)

where \(X_1\), \(X_2\), \(X_3\), \(X_4\) are the mechanical variables, \({\textbf{X}}_e\) is the vector of electrical variables, and functions \(g_i: {{\mathbb {R}}}^4 \mapsto {{\mathbb {R}}}\), \(i=1,2\), represent couplings. Let \(E_1 = X_2^2/2 + U_1(X_1)\) and \(E_2 = X_4^2/2 + U_2(X_3)\) be the normalized energies associated to each DOF, and let \(\theta _1\), \(\theta _2\), be the corresponding angle variables. Again in the limit \(\varepsilon \downarrow 0\), due to periodicity with respect to the angle, \(X_1\) and \(X_3\) admit the following representations:

$$\begin{aligned} X_1(E_1,\theta _1)&= X_{10}(E_1) + \sum _{m=1}^{+\infty } X_{1m}(E_1) \cos (m\, \theta _1 + \phi _m) \end{aligned}$$
(29)
$$\begin{aligned} X_3(E_2,\theta _2)&= X_{30}(E_2) + \sum _{m=1}^{+\infty } X_{3m}(E_2) \cos (m\, \theta _2 + \varphi _m) \end{aligned}$$
(30)

Then the following proposition holds:

Corollary 3

(Mechanical 2-DOF system with linear electrical circuit) Consider a linear electrical circuit described by the ODE system

$$\begin{aligned} \dfrac{d {\textbf{X}}_e}{dt} = {\textbf{A}}_e {\textbf{X}}_e + \sum _{m=1}^4 {\textbf{b}}_m X_m \end{aligned}$$
(31)

where \({\textbf{A}}_e \in {{\mathbb {R}}}^{n,n}\) and \({\textbf{b}}_m, \in {{\mathbb {R}}}^n\), \(m=1,\ldots 4\), are vectors of electro-mechanical coupling constants. Then the electrical variables admit the representation

$$\begin{aligned}&{\textbf{X}}_e(E_1,\theta _1,E_2,\theta _2) = {\textbf{X}}_{e0}(E_1,E_2)\nonumber \\&+ \sum _{m=1}^{+\infty } \big ({\text {Re}}[{{\hat{{\textbf{X}}}}}_{em,1}(E_1) \, e^{j m \theta _1}] + {\text {Re}}[{{\hat{{\textbf{X}}}}}_{em,2}(E_2) \, e^{j m \theta _2}] \big ) \end{aligned}$$
(32)

where \({\textbf{X}}_{e0}(E_1,E_2) = - {\textbf{A}}_e^{-1} \left( {\textbf{b}}_1 X_{10}(E_1) + {\textbf{b}}_{3} X_{30}(E_2) \right) \), and

$$\begin{aligned}&{{\hat{{\textbf{X}}}}}_{em,1}(E_1) = (j m \Omega _1(E_1) {\varvec{I}}_n - {\textbf{A}}_e)^{-1} \nonumber \\&\quad \qquad \qquad \qquad \times ({\textbf{b}}_1 + j m \Omega _1(E_1) {\textbf{b}}_2) {{\hat{X}}}_{1m}(E_1) \end{aligned}$$
(33)
$$\begin{aligned}&{{\hat{{\textbf{X}}}}}_{em,2}(E_2) = (j m \Omega _2(E_2) {\varvec{I}}_n - {\textbf{A}}_e)^{-1} \nonumber \\&\quad \qquad \qquad \qquad \times ({\textbf{b}}_3 + j m \Omega _2(E_2) {\textbf{b}}_4) {{\hat{X}}}_{3m}(E_2) \end{aligned}$$
(34)

and \({{\hat{X}}}_{1m}(E_1)\), \({{\hat{X}}}_{3m}(E_2)\) are the phasor representation of \(X_{1m}(E_1)\), \(X_{3m}(E_2)\), respectively.

Proof

The proof is completely analogous to the case of Corollary 1, applying superposition and considering the contributions of \(X_1(E_1)\) and \(X_3(E_2)\) separately. \(\square \)

Remark 3

The previous result can be extended even to the case of a nonlinear electrical circuit. In fact, in this case a generalization of Proposition 1 can be proved by exploiting a multi-variate Fourier representation or, more effectively, by generalizing the HB system through the use of frequency remapping techniques [22].

Remark 4

Notice that if the mechanical DOF satisfy a resonant condition, i.e. \(m_1 \, \Omega _1(E_1) = m_2 \, \Omega _2(E_2)\), for some \(m_1,m_2 \in {{\mathbb {N}}}\), then the non-homogeneous part in (31) can be linearly combined, obtaining a problem analogous to (22). Conversely, if the angular frequencies are not resonant, the resulting motion for the unperturbed mechanical systems is quasi periodic, i.e. the trajectories wrap on a torus homeomorphic to \(S^1 \times S^1\), being S the unit radius circle.

The final step in the formulation of the reduced order model is the derivation of the SDEs system for the new variables.

Theorem 2

(Energy-angle SDEs given \(E(X_1,X_2)\) and \( \theta (X_1,X_2)\)) Consider the dimensionless SDEs system (11) and the canonical transformation \((X_1, X_2) \rightarrow (E,\theta )\), together with the HB representation of \({\textbf{X}}_e(E,\theta )\). Then, the energy and the angle are Itô processes solutions of the SDEs system:

$$\begin{aligned} d E&= \varepsilon \, a_E(E,\theta ) \, d t + \sqrt{\varepsilon } \, B_E(E,\theta ) \, d W_t \end{aligned}$$
(35a)
$$\begin{aligned} d\theta&= \big (\Omega (E) + \varepsilon \, a_{\theta }(E,\theta )\big ) \, d t + \sqrt{\varepsilon } \, B_{\theta }(E,\theta ) \, d W_t \end{aligned}$$
(35b)

where

$$\begin{aligned}&a_E(E,\theta ) = \dfrac{B_m^2}{2} - X_2^2(E,\theta ) + X_2(E,\theta ) \, b_m({\textbf{X}}_e(E,\theta )) \end{aligned}$$
(36a)
$$\begin{aligned}&B_E(E,\theta ) = X_2(E,\theta ) B_m \end{aligned}$$
(36b)
$$\begin{aligned}&\Omega (E) = \dfrac{\partial \theta }{\partial X_1} X_2(E,\theta ) - \dfrac{\partial \theta }{\partial X_2 } U'(X_1(E,\theta )) \end{aligned}$$
(36c)
$$\begin{aligned} a_{\theta }(E,\theta )&= \dfrac{\partial \theta }{\partial X_2} \big (b_m({\textbf{X}}_e(E,\theta )) - X_2(E,\theta ) \big ) \nonumber \\&\qquad + \dfrac{B_m^2}{2} \dfrac{\partial ^2 \theta }{\partial X_2^2} \end{aligned}$$
(36d)
$$\begin{aligned} B_{\theta }(E,\theta )&= \dfrac{\partial \theta }{\partial X_2} B_m \end{aligned}$$
(36e)

Proof

The energy and angle variables are Itô processes as a direct consequence of the implicit function theorem and of the fact that, for \(\varepsilon =0\), the coordinate transformation \((X_1, X_2) \rightarrow (E,\theta )\) is invertible. The SDEs system for the energy and angle is obtained directly applying Itô formula, using the definition of the normalized energy and of \(\theta (X_1,X_2)\). \(\square \)

In practical applications, the explicit expressions for \(X_1(E,\theta )\), \(X_2(E,\theta )\) often involve special functions. Therefore, finding an explicit form for \(\theta (X_1,X_2)\) may be impossible, or at least impractical. The following Corollary provides alternative expressions for the coefficients of the angle equations that may be useful in such cases.

Corollary 4

(SDE for the angle, given \(X_1(E,\theta )\)) The following alternative expressions for the coefficients of the angle equation (35b) hold:

$$\begin{aligned}&\Omega (E) = \left( \dfrac{\partial X_1}{\partial \theta } \right) ^{-1} X_2(E,\theta ) \end{aligned}$$
(37a)
$$\begin{aligned} a_{\theta }(E,\theta )&= - \left( \dfrac{\partial X_1}{\partial \theta } \right) ^{-1} \bigg ( \dfrac{\partial X_1}{\partial E} a_E(E,\theta ) \nonumber \\&\qquad + \dfrac{1}{2} \dfrac{\partial ^2 X_1}{\partial E^2} B^2_E(E,\theta ) + \dfrac{1}{2} \dfrac{\partial ^2 X_1}{\partial \theta ^2 } B^2_{\theta }(E,\theta ) \nonumber \\&\qquad + \dfrac{\partial ^2 X_1}{\partial E \partial \theta } B_E(E,\theta ) B_{\theta }(E,\theta ) \bigg ) \end{aligned}$$
(37b)
$$\begin{aligned} B_{\theta }(E,\theta )&= - \left( \dfrac{\partial X_1}{\partial \theta } \right) ^{-1} \dfrac{\partial X_1}{\partial E} B_E(E,\theta ) \end{aligned}$$
(37c)

Proof

Application of Itô formula to \(X_1 = X_1(E,\theta )\) gives

$$\begin{aligned} dX_1&= \dfrac{\partial X_1}{ \partial E } dE + \dfrac{\partial X_1}{\partial \theta } d \theta + \dfrac{1}{2} \dfrac{\partial ^2 X_1}{\partial E^2 } (dE)^2 \\&\qquad + \dfrac{1}{2} \dfrac{\partial ^2 X_1}{\partial \theta ^2 } (d\theta )^2 + \dfrac{\partial ^2 X_1}{\partial E\partial \theta } d E d\theta \end{aligned}$$

so that:

$$\begin{aligned} d \theta&= \left( \dfrac{\partial X_1}{\partial \theta } \right) ^{-1} \bigg ( dX_1 - \dfrac{\partial X_1}{\partial E} dE - \dfrac{1}{2} \dfrac{\partial ^2 X_1}{\partial E^2} (dE) ^2 \nonumber \\&- \dfrac{1}{2} \dfrac{\partial ^2 X_1}{\partial \theta ^2} (d\theta )^2 - \dfrac{\partial ^2 X_1}{\partial E\partial \theta } d E d\theta \bigg ) \end{aligned}$$
(38)

From the energy equation (35a), using Itô lemma we find \((dE)^2 = \varepsilon B^2_E(E,\theta ) dt\). On the other hand, being an Itô process, the angle must satisfy a SDE of the form

$$\begin{aligned} d \theta = \alpha _{\theta }(E,\theta ) \, dt + \beta _{\theta }(E,\theta ) \, dW_t \end{aligned}$$
(39)

where \(\alpha _{\theta }(E,\theta )\) and \(\beta _{\theta }(E,\theta )\) are unknown functions to be determined. By Itô lemma, we have

$$\begin{aligned} (d \theta )^2&= \beta ^2_{\theta } (E,\theta ) \, d t \end{aligned}$$
(40a)
$$\begin{aligned} dE \, d \theta&= \sqrt{\varepsilon } \beta _{\theta }(E,\theta ) \, B_E(E,\theta ) dt \end{aligned}$$
(40b)

Substituting (35a) and (40) in (38), and equating the coefficient of \(dW_t\), we find:

$$\begin{aligned} \beta _{\theta }(E,\theta ) = - \sqrt{\varepsilon } \left( \dfrac{\partial X_1}{\partial \theta } \right) ^{-1} \dfrac{\partial X_1}{\partial E}B_E(E,\theta ) \end{aligned}$$
(41)

Similarly, equating the coefficients of dt we find:

$$\begin{aligned} \alpha _{\theta }(E,\theta ) =&\left( \dfrac{\partial X_1}{\partial \theta } \right) ^{-1} \bigg [ X_2 - \varepsilon \dfrac{\partial X_1}{ \partial E} a_E(E,\theta ) \\&- \dfrac{\varepsilon }{2} \dfrac{\partial ^2 X_1}{\partial E^2} B^2_E(E,\theta ) - \dfrac{1}{2} \dfrac{\partial ^2 X_1}{\partial \theta ^2} \beta ^2_{\theta }(E,\theta ) \\&- \sqrt{\varepsilon } \dfrac{\partial ^2 X_1}{\partial E \partial \theta } B_E(E,\theta ) \beta _{\theta }(E,\theta ) \bigg ] \end{aligned}$$

Introducing these coefficients in (35b) and comparing with the angle equation (39) the thesis follows. \(\square \)

Remark 5

For \(\varepsilon = 0\), the SDE system (35) reduces to the energy-angle ODE system (13). Therefore, equations (36c) and (37a) can be used to determine the energy dependent angular frequency for the Hamiltonian system in the energy angle coordinates.

Remark 6

The SDE (35a), permits to derive a power balance equation for the mechanical domain of the system. Taking stochastic expectations on both sides of the equation, using the martingale property of Itô stochastic integral and (36a), we have

$$\begin{aligned} \mathrm E\left[ \dfrac{dE}{dt} \right]&= \varepsilon \Bigg ( \dfrac{B_m^2}{2} - \mathrm E[X_2^2(E,\theta ) ] \nonumber \\&\qquad + \mathrm E[X_2(E,\theta ) \, b_m({\textbf{X}}_e(E,\theta ))] \Bigg ) \end{aligned}$$
(42)

Using the passive sign convention, the first term on the right hand side, \(p_{in} = \varepsilon B_m^2/2\) represents the average power injected into the system by the noise. The second term, \(p_{dis} = - \varepsilon \, \mathrm E[X_2^2(E,\theta ) ]\) represents the average power dissipated by mechanical friction. Finally, term \(p_{tr} = \varepsilon \, \mathrm E[X_2(E,\theta ) \, b_m({\textbf{X}}_e(E,\theta ))]\), represents the average power transferred from the mechanical domain to the electrical domain (if \(p_{tr}<0\)) or in the opposite direction (if \(p_{tr} >0\)).

5 Stochastic averaging

In this section we present a method for the analysis of the reduced order SDE system, and we discuss how it can be used to design and optimize the electrical domain of an electro-mechanical system.

For \(\varepsilon \ll 1\), the reduced order SDE system (35) shows a time scale separation, with the energy being a slow (or nearly constant) variable with respect to the fast angle variable.

A classical theorem by Khasminskii [23] states that the slow varying process E converges weakly, i.e. in probability, to a one dimensional Markov process as \(\varepsilon \downarrow 0\), in a time interval \( 0 \le t \le T_{\varepsilon }\) with \(T_{\varepsilon } = {\mathcal {O}}(1/\varepsilon )\). The Itô SDE system for the one dimensional Markov process is obtained by averaging the original SDE system (35) with respect to the fast variable, while the slow quantity is kept constant [23, 35]. Therefore we obtain:

$$\begin{aligned} d E \simeq \varepsilon {{\overline{a}}}_E(E)d t + \sqrt{\varepsilon }\, {{\overline{B}}}_E(E) d W_t \end{aligned}$$
(43)

where the averaged coefficients read

$$\begin{aligned} {{\overline{a}}}_E(E)&= \lim _{T\rightarrow +\infty }\dfrac{1}{T} \int _0^{T} a_E(E,\theta (t)) \, d t \end{aligned}$$
(44a)
$$\begin{aligned} {{\overline{B}}}_E(E)&= \sqrt{\lim _{T\rightarrow +\infty }\dfrac{1}{T} \int _0^T B^2_E(E,\theta (t)) \, d t} \end{aligned}$$
(44b)

and \(\theta (t)\) is the solution of the fast equation, evaluated keeping the slow variable constant. In particular, for \(\varepsilon \downarrow 0\), the fast variable has the trivial solution \(\theta = \Omega (E) t + \theta _0\), where \(\theta _0\) is the initial condition, and the averaged coefficients become

$$\begin{aligned} {{\overline{a}}}_E(E)&= \dfrac{1}{2 \pi } \int _0^{2 \pi } a_E(E,\theta ) \, d \theta \end{aligned}$$
(45a)
$$\begin{aligned} {{\overline{B}}}_E(E)&= \sqrt{ \dfrac{1}{2 \pi } \int _0^{2\pi } B^2_E(E,\theta ) \, d \theta } \end{aligned}$$
(45b)

The reduced SDE for the energy (43) and that for the angle (35b) can be exploited to derive an accurate approximation for the probability density function. The time scale separation between the the two processes, suggests the following factorization for the stationary probability density function (PDF)

$$\begin{aligned} p_{st}(E,\theta ) = {{\hat{\rho }}}(E,\theta ) \, \rho (E) \end{aligned}$$
(46)

Exploiting again the limit \(\varepsilon \downarrow 0\) (where the energy is constant), the stationary Fokker–Planck equation (FPE) reads

$$\begin{aligned} \Omega (E) \dfrac{\partial p_{st}(E,\theta )}{\partial \theta } = 0 \end{aligned}$$
(47)

that implies \({{\hat{\rho }}}(E,\theta ) = h(E)\), where h(E) is an arbitrary function of the energy. Imposing the normalizing condition

$$\begin{aligned} \int _0^{2\pi } {{\hat{\rho }}}(E,\theta ) \textrm{d}\theta = 1 \end{aligned}$$
(48)

yields \({{\hat{\rho }}}(E,\theta )= (2\pi )^{-1}\).

The stationary FPE for the energy variable is thus

$$\begin{aligned} - \dfrac{\partial }{\partial E} \left( {{\overline{a}}}_E(E) \rho (E) \right) + \dfrac{1}{2} \dfrac{\partial ^2}{\partial E^2} \left( {{\overline{B}}}^2_E(E) \rho (E) \right) = 0\nonumber \\ \end{aligned}$$
(49)

Imposing zero flux boundary conditions, and by separation of variables, we find the following solution:

$$\begin{aligned} \rho (E) = \dfrac{{\mathcal {N}}}{{{\overline{B}}}^2_E(E)} \exp \left( 2 \int \dfrac{{{\overline{a}}}_E(E)}{{{\overline{B}}}^2_E(E)} \textrm{d}E \right) \end{aligned}$$
(50)

where \({\mathcal {N}}\) is a normalizing constant whose value is determined imposing \(\int _0^{+\infty } \rho (E) \textrm{d}E = 1\).

The stationary PDF (46) permits to calculate the expectations of any observable, generally expressed as \({\textbf{F}}(X_1(E,\theta ),X_2(E,\theta ),{\textbf{X}}_e(E,\theta ))\), computing the integral

$$\begin{aligned}&\mathrm E[{\textbf{F}}(X_1(E,\theta ),X_2(E,\theta ),{\textbf{X}}_e(E,\theta ))] \nonumber \\&\qquad = \dfrac{1}{2\pi } \int _0^{2\pi } \int _0^{+\infty } \; {\textbf{F}}(X_1(E,\theta ),X_2(E,\theta ),{\textbf{X}}_e(E,\theta )) \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \times \rho (E)\, d \theta \, d E \end{aligned}$$
(51)

Although in practical problems integral (51) can only be solved numerically, its calculation is still much simpler and much faster than the numerical integration of the full original SDEs system (11), making possible to optimize the design of the electrical domain exploring a wide parameter space.

Concerning systems with more than one mechanical DOF, stochastic averaging can be applied as well. A normalized energy and an angle are associated to each pair of mechanical variables \(X_i, \dot{X}_i\). Two different cases can be distinguished:

  1. 1.

    The natural frequencies \(\Omega _i(E_i)\) and \(\Omega _j(E_j)\) are not resonant. In this case, all angle variables can be eliminated through averaging, retaining only one energy variable for each mechanical DOF.

  2. 2.

    At least two frequencies are resonant, i.e. the condition \( m_i \Omega _i(E_i) = m_j \Omega _j(E_j)\) holds for some \(i\ne j\), with \(m_i,m_j \in {{\mathbb {N}}}\). In this case, some frequency components deriving from an algebraic sum of the fundamentals \(\Omega _i, \Omega _j\) may be rather small, and as such they are slow variables that cannot be eliminated through averaging. In this case we must retain one energy for each mechanical DOF plus such slow components (instead of only the two original frequencies).

Details on this can be found in [36, 37]. In both cases we obtain a system of SDEs, thus making impossible to find an analytical solution for the associated FPE. In this case we need to resort to ad hoc technique to find the expectations.

6 Applications

6.1 Piezoelectric energy harvester for ambient vibrations

As a first example, we consider the analysis and design of a piezoelectric energy harvester with Duffing type nonlinearity, such as the one discussed in [24, 25, 38]. The mechanical structure of the harvester consists of a cantilever beam, with an inertial tip mass to increase the amplitude of the oscillations. The dynamics of the mechanical part is described by (1), where F(t) is the sum of the force exerted by the environment and of that due to the piezoelectric transducer. The elastic potential of the beam is assumed of the form \(U(z_1) = k_1 z_1^2/2 + k_3 z_1^4/4\), where \(k_1\) and \(k_3\) are positive parameters, that correspond to a nonlinear elastic force with a stiffening effect.

The transducer is formed by a layer of piezoelectric material covering the beam. The governing equations for the transducer can be derived from the characterization of piezoelectric materials [4, 39, 40]. Assuming the representation shown in Fig. 2, the model reads

$$\begin{aligned}&b_m( {\textbf{Z}}_e) = - \alpha V \end{aligned}$$
(52a)
$$\begin{aligned}&C_{pz} \, \dot{V} = \alpha \dot{Z} + I \end{aligned}$$
(52b)

where \({\textbf{Z}}_e = [V,I]^T\) is the vector of the electrical variables (output voltage and current, respectively), \(\alpha \) is the electro-mechanical coupling constant (in N/V or As/m), and \(C_{pz}\) is the capacitance of the transducer.

Fig. 2
figure 2

Two-port representation of the electromechanical transducer with electrical load

Full size image

The electrical circuit is composed by a linear resistor, that models an electrical user which absorbs electrical energy, with a shunted linear inductor connected in parallel, see Fig. 2. The inductor is used for power factor correction, i.e. to reduce the time lag between the current through and the voltage across the load, thus maximizing the average absorbed power by the latter [24]. Using Kirchhoff current law and the voltage-current characteristic of a linear inductor, we have \(I + G\,V + I_L=0\), and \(\dot{I}_L = V/L\).

Finally, the external force is considered as the result of a complex environment, and it is modelled as a white Gaussian noise with intensity D.

Combining together the equations for the mechanical structure, the piezoelectric transducer and the electrical domain, and rewriting as a SDE system yields

$$\begin{aligned} d Z_1 =&Z_2 dt \end{aligned}$$
(53a)
$$\begin{aligned} d Z_2 =&\left( -\dfrac{1}{m} U'(Z_1) - \dfrac{{{\hat{\varepsilon }}}}{m} Z_2 - \dfrac{\alpha }{m} V\right) dt + \dfrac{D}{m} dW_t \end{aligned}$$
(53b)
$$\begin{aligned} d V =&\dfrac{1}{C_{pz}} \left( \alpha Z_2 - G V - I_L \right) dt \end{aligned}$$
(53c)
$$\begin{aligned} d I_L =&\dfrac{1}{L} \, V \, dt \end{aligned}$$
(53d)

where, for the sake of simplicity, we have written the circuit equation using the current through the inductor \(I_L(t)\) instead of the output current of the transducer I(t).

The dimensionless SDE system is obtained introducing the diagonal matrix

$$\begin{aligned} {\textbf{P}}= \text {diag}[l_0^{-1},T\,l_0^{-1},C_{pz} q_0^{-1}, T q_0^{-1}] \end{aligned}$$

where \(l_0\) and \(q_0\) are a normalizing length and charge, respectively, and \(T = \sqrt{{m}/{k_1}}\) is a normalization time. Assuming \(l_0=1\) m and \([q_0] = [\alpha ]\) C, the dimensionless equations take the form

$$\begin{aligned} d {\textbf{X}}_t = \left( {\textbf{A}}{\textbf{X}}_t + {\textbf{n}}({\textbf{X}}_t) \right) dt + \sqrt{\varepsilon } \, {\textbf{B}}\, dW_t \end{aligned}$$
(54)

where \({\textbf{X}}_t = [X_1,X_2,X_3,X_4]^T\) is the vector of the dimensionless variables,

$$\begin{aligned} {\textbf{A}}= \left[ \begin{array}{cccc} 0 &{} 1 &{} 0 &{} 0\\ -1 &{} -\varepsilon &{} -\varepsilon \beta &{} 0 \\ 0 &{} 1 &{} -\delta &{} -1 \\ 0 &{} 0 &{} \mu &{} 0 \end{array} \right] \end{aligned}$$
(55)

\({\textbf{n}}({\textbf{X}}_t) = [0,-\kappa X_1^3,0,0]^T\), \({\textbf{B}}= [0,\sigma ,0,0]^T\) and the parameters are

$$\begin{aligned}&\varepsilon = \dfrac{{{\hat{\varepsilon }}}}{\sqrt{m \, k_1}}, \quad \beta = \dfrac{q_0 \alpha }{C_{pz} \, l_0 \, \hat{\varepsilon }} \sqrt{\dfrac{m}{k_1}}, \quad \delta = \dfrac{G}{C_{pz}} \sqrt{\dfrac{m}{k_1}}, \nonumber \\&\qquad \mu = \dfrac{m}{C_{pz} L \, k_1}, \quad \sigma = \dfrac{D}{l_0 \sqrt{\hat{\varepsilon }\, k_1}}, \quad \kappa =\dfrac{k_3}{l_0 \, k_1} \end{aligned}$$
(56)

Notice that, in order to apply the method we propose, both \(\beta \) and \(\sigma \) must be of order \(\textrm{O}(1)\).

For \(\varepsilon \downarrow 0\), the equations for the mechanical part reduce to the Hamiltonian system

$$\begin{aligned} \dot{X}_1&= X_2 \end{aligned}$$
(57a)
$$\begin{aligned} \dot{X}_2&= -a X_1 - b X_1^3 \end{aligned}$$
(57b)

with \(a=1\) and \(b = \kappa \). The only invariant sets of (57a) are the origin, which is a centre, and the surrounding continuous family of periodic orbits. The latter are described by the solution

$$\begin{aligned} X_1(E,\theta )&= \left( \dfrac{ 4 E^2}{a^2 + 4 b E} \right) ^{1/4} \text {sd}(\theta ,k) \end{aligned}$$
(58a)
$$\begin{aligned} X_2(E,\theta )&= \sqrt{2E} \, \text {cd}(\theta ,k) \, \text {nd}(\theta ,k) \end{aligned}$$
(58b)

where \(E = X_2^2(0)/2 + U(X_1(0))\) is the energy level (determined by the initial conditions), \(\text {sd}(\theta ,k)\), \(\text {cd}(\theta ,k)\) and \(\text {nd}(\theta ,k)\) are the Jacobi elliptic functions and

$$\begin{aligned} k^2(E) = \dfrac{1}{2} \left( 1 - \dfrac{a}{\sqrt{a^2 + 4 b E}}\right) \end{aligned}$$
(59)

is the elliptic modulus [39]. The angle is \(\theta (t) = \Omega (E) t\) where the angular frequency takes the value

$$\begin{aligned} \Omega (E) = (a^2 + 4 b E)^{1/4} \end{aligned}$$
(60)

Remark 7

The angular frequency is bounded away from zero, which reflects the fact that neither homoclinic nor heteroclinic orbits exist in the system.

Alternatively, \(X_1(E,\theta )\) can be represented through the Fourier (or Lambert) series

$$\begin{aligned} X_1(E,\theta ) = \sum _{m=1}^{+\infty } X_{1s,m}(E) \sin \left( \dfrac{2m-1}{2{\mathcal {K}}(E)} \pi \, \theta \right) \end{aligned}$$
(61)

where (hereinfater we shall omit explicit dependence on the energy where not strictly necessary, for simplicity of notation)

$$\begin{aligned} X_{1s,m}(E,\theta ) = \left( \dfrac{4 E^2}{a^2+4bE}\right) ^{\frac{1}{4}} \dfrac{2\pi }{k\,k'\,{\mathcal {K}}} \dfrac{(-1)^{m-1} q^{m-\frac{1}{2}}}{1 + q^{2m-1}}\nonumber \\ \end{aligned}$$
(62)

\({\mathcal {K}}(E)\) is the complete elliptic integral of the first kind, \(k'(E)=\sqrt{1-k^2(E)}\) is the complementary modulus, \(q(E) = \exp \left( -\pi {\mathcal {K}}'/{\mathcal {K}} \right) \) is the nome, and finally \({\mathcal {K}}'(E) = {\mathcal {K}} (k^2(E))\). Similarly

$$\begin{aligned} X_2(E,\theta ) = \sum _{m=1}^{+\infty } X_{2c,m}(E) \cos \left( \dfrac{2m-1}{2{\mathcal {K}}(E)} \pi \theta \right) \end{aligned}$$
(63)

with

$$\begin{aligned} X_{2c,m}(E) = \sqrt{2E} \dfrac{2\pi }{k\,k'\,{\mathcal {K}}^2} \dfrac{(-1)^{m-1}(2m-1) q^{m-\frac{1}{2}}}{1 + q^{2m-1}}\nonumber \\ \end{aligned}$$
(64)

Figure 3 shows the angular frequency \(\Omega (E)\), and the amplitude of the first harmonics \(X_{1\,s,1}(E)\) and \(X_{2c,1}(E)\) as functions of the energy.

Fig. 3
figure 3

Angular frequency \(\Omega (E)\), and the amplitude of the first harmonic \(X_{1\,s,1}(E)\) and \(X_{2c,1}(E)\) as functions of the dimensionless energy. Normalized parameter values are listed in Table 2

Full size image

A straightforward application of Corollary 1 gives

$$\begin{aligned} {{\hat{X}}}_{3m}(E)&= K_3 \, X_{2c,m}(E) \end{aligned}$$
(65)
$$\begin{aligned} {{\hat{X}}}_{4m}(E)&= K_4 \, X_{2c,m}(E) \end{aligned}$$
(66)

where

$$\begin{aligned} K_3&= \dfrac{{j}\dfrac{2m-1}{2{\mathcal {K}}} \pi \Omega }{\mu - \left( \dfrac{2m-1}{2{\mathcal {K}}}\right) ^2 \pi ^2 \Omega ^2 + {j}\dfrac{2m-1}{2{\mathcal {K}}} \pi \Omega \delta } \end{aligned}$$
(67)
$$\begin{aligned} K_4&= \dfrac{\alpha \mu }{\mu - \left( \dfrac{2m-1}{2{\mathcal {K}}}\right) ^2 \pi ^2 \Omega ^2 + {j}\dfrac{2m-1}{2{\mathcal {K}}} \pi \Omega \delta } \end{aligned}$$
(68)

and \(j=\sqrt{-1}\).

Taking into account the relationships \(B_m = \sigma \) and \(b_m({\textbf{X}}_e(E,\theta )) = - \beta X_3(E,\theta )\), using (45) and the orthogonality of the basis function we obtain

$$\begin{aligned} {{\overline{a}}}_E(E)&= \dfrac{1}{2} \left( \sigma - \sum _{m=1}^{+\infty } \big (X_{2c,m}^2(E) \right. \nonumber \\&\qquad \qquad \left. + \beta X_{2c,m}(E) X_{3c,m}(E) \big ) \right) \end{aligned}$$
(69a)
$$\begin{aligned} {{\overline{B}}}_E(E)&= \sigma \left( \dfrac{1}{2} \sum _{m=1}^{\infty } X_{2c,m}^2(E) \right) ^{\frac{1}{2}} \end{aligned}$$
(69b)

where \(X_{3c,m}(E) = {\text {Re}}[{{\hat{X}}}_{3m}(E)]\).

These functions can be used to calculate the stationary PDF for the energy (50), which in turn allows to calculate the expectations of observables, according to (51).

Table 1 Values of the parameters for the piezoelectric energy harvester
Full size table

Table 1 summarizes the values of the parameters for the model of the nonlinear piezoelectric energy harvester adopted in our analysis. The corresponding values for the dimensionless parameters are summarized in Table 2. Optimization of the energy harvester requires to determine the value of the shunted inductance L, that maximizes the output voltage.

Table 2 Values of the parameters for the dimensionless SDE system
Full size table

The average power absorbed by the load is \(P_{av} = G v_{(rms)}^2\), where \(G = R^{-1}\) is the load conductance and \(v_{(rms)} = \sqrt{\mathrm E[V^2(t)]}\) is the root mean square value of the output voltage.

Using the results above, we have calculated the stationary PDF and the root mean square output voltage for values of the shunted inductance in the range \(L \in [0.5,20]\) H, as reported in Table 1. The result is shown in Fig. 4. The output voltage shows a maximum of \(v_{(rms), max} = 2.16\) V at \(L_{opt} = 2.33\) H.

To verify the accuracy of our theoretical analysis, we have compared theoretical predictions with numerical results, performing Monte-Carlo simulations for the dimensionless SDEs system (54). Results of Monte-Carlo simulations are shown by blue squares in Fig. 4. For each value of the shunted inductance, we have performed 30 numerical simulations for different realization of the Wiener process. The SDEs system (54) has been integrated numerically, using both Euler–Maruyama and stochastic Runge–Kutta method with strong order of convergence equal to one. In each simulation we have removed the initial transient, and then we averaged to calculate the output voltage. The simulation time length was set to \(\Delta T = 10^4\) (normalized time), the time integration step was \(\delta t \approx 75 \cdot 10^{-6}\) (\(2^{27}\) time samples). The theoretical prediction shows an excellent agreement with numerical simulations.

Fig. 4
figure 4

Root mean square output voltage \(v_{(rms)}\) versus the value of the shunted inductor L. Red line are theoretical predictions. Blue squares are results from Monte-Carlo simulations. Parameters values are summarized in Table 1

Full size image

Figure 5 shows the comparison between the stationary marginal PDF for the dimensionless energy, obtained using the proposed method based on model order reduction and stochastic averaging, and the result obtained through Monte-Carlo simulations. The probability to find the system in the energy range between E and \(E+\textrm{d}E\) has been evaluated as the number of samples in that interval, normalized to the total number of samples. The excellent matching between the two approaches validates the adopted stochastic averaging procedure.

Fig. 5
figure 5

Stationary probability density function for the dimensionless mechanical energy of the SDEs system (53). Blue vertical bars are the result of Monte-Carlo simulations. Red line is the theoretical prediction. Parameters values are those of Table 1. Inductance value is \(L = 0.5\) H

Full size image
Table 3 Comparison of root mean square output voltage, output average power and power efficiency for the energy harvester with two different load setups
Full size table

The method also permits to evaluate the efficacy of the power factor correction setup. In most of the cases the load is a simple resistor. As already mentioned, this generally implies that a large amount of the energy is reflected by the the load, i.e. a large amount of reactive power is present, because of the time lag between the voltage across and the current through the transducer. The shunted inductor in parallel with the resistor reduces this time lag. Obviously, complete elimination of the time lag is possible only at a single frequency, but choosing properly the inductance value, it is possible to achieve a significant time lag reduction over a relatively wide frequency band, thus maximizing the average power absorbed by the load and the power efficiency. Table 3 shows a comparison of the output voltage, average output power and power efficiency between a simple resistive load and the power factor corrected load.

Finally, some remarks on the computational advantage of our methodology. Determining the reduction in computational complexity and computation time is rather hard, because they depend on how efficient the implementation of the numerical integration scheme is, and on the specific algorithm used for generating the Wiener process. However we stress that a Monte-Carlo approach requires lengthy simulations (that must be repeated for each value of the parameters). On the contrary, with the proposed method most of the work can be done analytically. Only equations (50) and (51) are to be solved numerically, requiring few seconds only for their computation.

6.2 Example 2: Coupled micro-electro-mechanical resonators

As an example of application to systems with more than one mechanical DOF, we consider two coupled micro-electro-mechanical resonators. Micro-mechanical resonators, such as vibrating micro-cantilevers, emerged as key elements in mass sensing applications, as they are characterized by a very high quality factor, that makes their resonance frequency extremely sensitive to external forces and mass changes due to substance deposition [8, 9]. Micro-cantilevers can be fabricated at the wafer scale exploiting etching techniques, which allow to realize many cantilevers on a common substrate, acting as a physical coupling mean. The use of coupled micro-cantilevers forming arrays, permits to exploit more resonant frequencies, allowing the detection of several different substances with the same sensor system.

We consider a structure made of two micro-cantilevers coupled by an overhang at their bases. The array is attached to a piezoelectric actuator analogous to that described in the first example, that is connected to a resistor modelling power absorption by the sensing circuit. The external environment acts through random forces, modelled as a white Gaussian noise, and applied to each micro-cantilever.

Fig. 6
figure 6

Fourier transform (FFT) of one realization of the stochastic processes \(X_2(t)\) (left), \(X_4(t)\) (center), and \(X_5(t)\) (right). Stochastic processes are obtained through numerical integration of the SDEs system (70). Parameter values are listed in Table 4

Full size image

We consider the following SDE system written for the dimensionless variables:

$$\begin{aligned} d X_1&= X_2 \, dt \end{aligned}$$
(70a)
$$\begin{aligned} d X_2&= \big ( -U_1'(X_1) - \varepsilon X_2 - \varepsilon g_{1}(X_1,X_2,X_3,X_4) \nonumber \\&- \varepsilon \alpha _1 X_5 \big ) dt + \sqrt{\varepsilon } \, \sigma _1 \, dW_t \end{aligned}$$
(70b)
$$\begin{aligned} d X_3&= X_4 \, dt \end{aligned}$$
(70c)
$$\begin{aligned} d X_4&= \big ( -U_2'(X_3) - \varepsilon X_4 - \varepsilon g_{2}(X_1,X_2,X_3,X_4) \nonumber \\&- \varepsilon \alpha _2 X_5 \big ) dt + \sqrt{\varepsilon } \, \sigma _2 \, dW_t \end{aligned}$$
(70d)
$$\begin{aligned} dX_5&= \big ( - \delta X_5 + \beta _1 X_2 + \beta _2 X_4 \big ) dt \end{aligned}$$
(70e)

where \(X_1,\ldots ,X_4\) are the scalar, dimensionless mechanical variables, and \(X_5\) is the dimensionless output voltage. The elastic restoring forces are assumed to be of the form \(U'_1(X_1) = a_1 X_1 + b_1 X_1^3\), and \(U'_2(X_3) = a_2 X_3 + b_2 X_3^3\), where \(a_i, b_i\), \(i=1,2\) are positive parameters. The parameters \(\alpha _i\), \(\beta _i\), \(\sigma _i\), \(i=1,2\) and \(\delta \) are assumed real and positive.

Concerning the coupling functions, taking into account that \(\varepsilon \) is a small parameter, it is reasonable to assume that higher order terms of the coupling can be neglected. Retaining only the linear terms, the interaction is assumed of the form

$$\begin{aligned} g_{1}(X_1,X_2,X_3,X_4) = - g_{2}(X_1,X_2,X_3,X_4) \nonumber \\ = \mu (X_1-X_3) + \gamma (X_2-X_4) \end{aligned}$$
(71)

where \(\mu \) and \(\gamma \) are real positive dimensionless parameters.

To verify the assumption that each mechanical DOF is characterized by a different oscillation frequency \(\Omega _i\) \((i=1,2)\), we have performed Monte-Carlo numerical simulations integrating the SDE system (70). The numerical simulation methodology is the same as in Sect. 6.1. The parameter values used in the simulations are summarized in Table 4. Figure 6 shows the Fourier transform (evaluated through the FFT algorithm) of one realization of the stochastic processes \(X_2(t)\), \(X_4(t)\), and \(X_5(t)\), obtained through numerical integration of the SDE system for one realization of the Wiener process. As expected, the mechanical variables \(X_2(t)\) and \(X_4(t)\) show a single frequency peak at \(f_1 = 1.2616\) Hz and \(f_2 = 1.6603\) Hz, respectively. This proves the correctness of the initial assumption, that each mechanical variable can be expanded in a single frequency Fourier series. By contrast, the electrical variable \(X_5(t)\) shows two peaks, one per frequency, that correspond to a mixing of the individual oscillation frequencies of the two coupled cantilevers at the electrical level. Notice that because of the finite precision of digital computers, the two frequencies are always resonant (i.e., their ratio is rational). The parameter values have been chosen such that the ratio is far from an integer value.

Table 4 Values of the parameters for the dimensionless coupled micro-cantilevers model
Full size table

Introducing the dimensionless energy associated to each mechanical DOF, and using Itô calculus, the reduced SDE system can be easily derived

$$\begin{aligned} d E_1&= \varepsilon \big ( - X_2^2 - X_2 \, g_{1}(X_1,X_2,X_3,X_4) - \beta _1 \, X_2 \, X_5 \nonumber \\&+ \dfrac{1}{2} \sigma _1^2 \big ) dt + \sqrt{\varepsilon } \sigma _1 X_2 \, dW_t \end{aligned}$$
(72a)
$$\begin{aligned} d E_2&= \varepsilon \big ( - X_4^2 - X_4 \, g_{2}(X_1,X_2,X_3,X_4) - \beta _2 \, X_4 \, X_5 \nonumber \\&+ \dfrac{1}{2} \sigma _2^2 \big ) dt + \sqrt{\varepsilon } \sigma _2 X_4 \, dW_t \end{aligned}$$
(72b)

In (72), \(X_1(E_1,\theta _1)\) and \(X_3(E_2,\theta _2)\) are represented as in (61)–(62). Similarly, \(X_2(E_1,\theta _1)\) and \(X_4(E_2,\theta _2)\) follow (63)–(64). Notice also that \(\theta _i = \Omega _i(E_i) t\) (\(i=1,2\)), where \(\Omega _i(E_i)\) is given by (60) with the appropriate values of \(a_i, b_i\) and \(E_i\).

Assuming that the frequencies are not resonant, a direct application of Corollary 3 implies that the normalized voltage \(X_5\) admits the representation (32), with \(X_{50} = 0\), and

$$\begin{aligned} {{\hat{X}}}_{5m,1}(E_1)&= C_{1,m}(E_1) \, X_{2c,m}(E_1) \end{aligned}$$
(73)
$$\begin{aligned} {{\hat{X}}}_{5m,2}(E_2)&= C_{2,m}(E_2) \, X_{4c,m}(E_2) \end{aligned}$$
(74)

where

$$\begin{aligned} C_{i,m}(E_i) = \dfrac{\beta _i}{\delta + j \left( \dfrac{2m-1}{2 K(E_i)}\right) \pi \Omega _i(E_i)}, \quad i=1,2.\nonumber \\ \end{aligned}$$
(75)

Substituting into (72) and averaging yields

$$\begin{aligned} d E_1&= \dfrac{\varepsilon }{2} \bigg (\sigma _1^2 - (1+\gamma ) \sum _{m=1}^{+\infty } X_{2c,m}^2 (E_1) \nonumber \\&\qquad + \alpha _1 \sum _{m=1}^{+\infty } {\text {Re}}[C_{1,m}(E_1)] \, X_{2c,m}^2(E_1) \bigg ) dt \nonumber \\&\qquad + \sqrt{\dfrac{\varepsilon }{2}} \, \sigma _1 \, \Big (\sum _{m=1}^{+\infty } X_{2c,m}^2(E_1) \Big )^{\frac{1}{2}} \, dW_t \end{aligned}$$
(76a)
$$\begin{aligned} d E_2&= \dfrac{\varepsilon }{2} \bigg (\sigma _2^2 - (1+\gamma ) \sum _{m=1}^{+\infty } X_{4c,m}^2 (E_2) \nonumber \\&\qquad + \alpha _2 \sum _{m=1}^{+\infty } {\text {Re}}[C_{2,m}(E_2)] \, X_{4c,m}^2(E_2) \bigg ) dt \nonumber \\&\qquad + \sqrt{\dfrac{\varepsilon }{2}} \, \sigma _2 \, \Big (\sum _{m=1}^{+\infty } X_{4c,m}^2(E_2) \Big )^{\frac{1}{2}} \, dW_t \end{aligned}$$
(76b)

System (76) shows that the SDEs governing \(E_1\) and \(E_2\) are mutually independent. The mechanical coupling (described by \(g_i\)) introduces an additional damping proportional to \(\gamma \), while the coupling to the electrical domain gives a contribution proportional to the electro-mechanical coupling constants, without impairing the independence of the two SDEs. This somewhat surprising result is a consequence of the weak coupling assumption, and of the frequencies not being resonant. It has been proved in [41, p. 169, corollary 5.9], that a network of weakly coupled limit cycle oscillators organizes in “pools”, consisting of synchronized oscillators that share a common frequency. Oscillators from different pools behave independently of each other, i.e. the coupling becomes negligibly small, even if they are physically connected.

Because the energy equations are single variable, the marginal stationary PDFs can be found using the procedure described in Sect. 5. The joint stationary distribution for the energies reads

$$\begin{aligned} \rho (E_1,\theta _1,E_2,\rho _2) = \dfrac{1}{(2\pi )^2} \, \rho _1(E_1) \, \rho _2(E_2) \end{aligned}$$
(77)

where \(\rho _i(E_i)\) denotes the marginal stationary PDF for energy \(E_i\), \(i=1,2\). The expectation of an observable \({\textbf{F}}(E_1,\theta _1,E_2,\theta _2)\) function of the system variables is then expressed through the quadruple integral

$$\begin{aligned}&\mathrm E[{\textbf{F}}(E_1,\theta _1,E_2,\theta _2)] = \dfrac{1}{(2\pi )^2} \int _0^{2\pi }\int _0^{2\pi }\int _0^{+\infty } \int _0^{+\infty } \nonumber \\&\quad {\textbf{F}}(E_1,\theta _1,E_2,\theta _2) \, \rho _1(E_1) \, \rho _2(E_2)\, d E_2\,d E_1\, d \theta _2\,d\theta _1 \end{aligned}$$
(78)

Figure 7 shows a comparison of the stationary marginal probability density function \(\rho _1(E_1)\), obtained through Monte-Carlo simulations and from theoretical prediction. Blue vertical bars are the result of Monte-Carlo simulations, obtained through numerical integration of the SDE system (70), using the procedure described in the previous section. Red line is the theoretical prediction.

Fig. 7
figure 7

Stationary marginal probability density function \(\rho _1(E_1)\). Blue vertical bars are the result of Monte-Carlo simulations. Red line is the theoretical prediction. Parameters values are summarized in Table 1

Full size image

7 Conclusions

In this contribution, we have presented a method for the analysis and design of nonlinear electro-mechanical systems subject to random external perturbations, with particular reference to energy harvesting systems and coupled micro-resonators for mass sensing applications.

The proposed method is based on two steps: First we perform a model order reduction to reduce the total number of variables (mechanical + electrical) to two variables only, representing the mechanical energy and an angle variable. The electrical variables are expressed as functions of the mechanical energy and the angle, exploiting a spectral domain representation. Second, we apply stochastic averaging to eliminate the fast angle variable, so that a scalar equation for the energy is obtained. Thus, it is possible to solve the associated Fokker–Planck equation finding the stationary probability density function, and to calculate expected quantities.

Applying the proposed method, a significant simplification of the system model is obtained, opening the way to the definition of optimization and design procedures. As a first example, we have analysed a nonlinear piezoelectric energy harvester, with power factor correction. Power factor correction is obtained through the connection of a shunted inductor in parallel to the resistive load. The inductor reduces the time lag between the current through and voltage across the transducer, reducing the power reflected by the load (reactive power) and increasing the average power absorbed by the load and the power efficiency. Theoretical predictions are confirmed by Monte-Carlo simulations. As a second example, we have considered two coupled micro-resonators for mass sensing applications. This example shows the extension of the method to system with several mechanical degrees of freedom. Assuming a weak coupling and a non resonance condition, we show that after order reduction and averaging, the energy equations are mutually independent. The corresponding Fokker-Planck equations are solved to find the energy marginal probability density function.

The procedure reduces the computational complexity of the electro-mechanical system description significantly, paving the way towards derivation of fast, yet accurate models, enabling the optimized design of such systems. In particular, traditional approaches based on Monte-Carlo methods require lengthy, time consuming simulations, that become unfeasible whenever a large parameter space must be explored for design and optimization. Conversely, in the proposed approach most of the work can be done analytically, with only few numerical calculations that can be performed in a relatively short time.