1 Introduction

Control of dynamical systems in the presence of strict time constraints is a practically important problem which can be solved in several ways. Apart from a classical time-optimal control, one can find in the literature different alternative approaches to solve this problem. The first approach solves a finite-time stabilization problem, which ensures that there exists a finite upper bound of the settling times of the stabilization errors for any initial condition. The estimated upper bound depends on the initial conditions in this case. The problem of finite-time stability has been discussed, for example, in [1,2,3,4,5].

Another approach, called fixed-time stabilization, also guarantees that the settling time of the system error is no longer than the estimated upper bound, but here the estimated upper bound is independent of the initial conditions. This concept has been discussed and developed, for example, in [6,7,8], while the papers [9,10,11] proposed methods for estimating the upper bound. Moreover, the authors in [12] introduced an estimation method that is less conservative relative to others.

Yet another approach is called the predefined-time stabilization (some authors call this problem the prescribed-time stabilization—see, e.g., [13] and [14]), which is similar to the fixed-time stabilization but assumes a change in the parametrization of the closed-loop system. Namely, the upper bound of the settling time is not estimated in this case but prescribed by a designer, while the controller parameters can be tuned upon a selected value of the upper bound. Predefined-time stability and stabilization have been an area of intensive research, for example, in [15,16,17,18,19,20,21], while in [22] the authors presented several general forms of predefined-time stable systems. From a practical point of view, the predefined-time controllers can be useful in many applications where time is crucial for some reasons like, for example, synchronization or safety issues. A flexible transportation task or a spatio-temporal synchronization for multi-agent systems are examples of practical problems, which can be solved by predefined-time control laws.

The feedback stabilization problem for non-holonomic systems has been widely addressed in the literature (see the fundamental limitations related to this problem presented in [23] and [24]). Among various solutions to the asymptotic stabilization task, the discontinuous control laws represent an important class of solutions. The Vector-Field-Orientation (VFO) controllers belong to this class [25]. According to the practical experience, application of the VFO design methodology leads to control laws which result in non-oscillatory transient states and well-predictable vehicle behavior in its workspace (see, e.g., [26] and [27]). In the literature, one can find also the finite-time (see [28]), and fixed-time (see [29]) versions of the VFO control laws.

The predefined-time control solutions are scarce in the literature, especially for nonholonomic mobile robots (see, e.g., [14, 16, 30]). We try to fill this gap by proposing a feedback set-point control law for unicycle-like mobile robots (modeling not only wheeled mobile robots but also some unmanned aerial vehicles flying on a constant altitude, [31, 32]) which inherits beneficial properties of the VFO control strategy and additionally preserves explicit time-constraints imposed on the closed-loop dynamics. In this work, we propose a predefined-time VFO control law for non-holonomic mobile robots, which is an extension of the fixed-time VFO controller in [29]. It is worth noting that in [29], the upper bound of the settling time cannot be easily prescribed by the designer. In the sequel, apart from a formal stability analysis performed for the closed-loop dynamics, we also present the results of extensive numerical simulations and experimental tests. To reveal the benefits coming from an application of the predefined-time VFO control law, we compare it with an alternative predefined-time stabilizer, recently proposed for nonholonomic chained-form systems in [16].

This paper is organized as follows. Section 2 is devoted to the formulation of the control problem, as well as a discussion of assumptions and prerequisites. Section 3 presents the predefined-time VFO control design. Section 4 provides a formal stability analysis based on the Lyapunov theory, and Sect. 5 presents the results of numerical simulations and experimental tests of the proposed control system.

2 Prerequisites and assumptions

2.1 Model of the mobile robot

Let us consider the kinematic model of a mobile robot:

$$\begin{aligned} {\dot{\varvec{q}}} = \varvec{G}(\varvec{q})\varvec{u}= \begin{bmatrix} 1 &{}\quad 0 \\ 0 &{}\quad \cos \theta \\ 0 &{}\quad \sin \theta \end{bmatrix} \begin{bmatrix} u_1 \\ u_2\end{bmatrix} = \varvec{g}_1u_1 + \varvec{g}_2(\theta )u_2,\nonumber \\ \end{aligned}$$
(1)

where \(\varvec{q}= \begin{bmatrix} \theta \ x \ y \end{bmatrix}^\top = \begin{bmatrix} \theta \ \overline{\varvec{q}}^\top \end{bmatrix}^\top \in \mathbb {R}^3\) is the configuration vector consisting of the orientation angle \(\theta \) and the position coordinates (x, y) of a guidance point expressed in a global frame. The control input vector \(\varvec{u}= \begin{bmatrix} u_1 \ u_2 \end{bmatrix}^\top \in \mathbb {R}^2\) contains angular velocity \(u_1\) and longitudinal velocity \(u_2\). The guidance point is located in the middle of the axis connecting the right and left wheels of the unicycle.

2.2 The concept of predefined-time stability

Let us introduce the concept of (nearly) predefined-time stability:

Definition 1

( [15, 33]) The equilibrium point \(\varvec{w}= \textbf{0}\) of a dynamical system \(S: {\dot{\varvec{w}}}(t) = f(\varvec{w}(t), \varvec{p})\), \(\varvec{w}(0) = \varvec{w}_0 \in {\mathbb {R}^{n}}\) is said to be (nearly) predefined-time stable if:

  • it is (nearly) fixed-time stable, i.e., it is Lyapunov stable and for any neighborhood \(M \subset \mathbb {R}^n\) of the origin there exists an upper bound \(T_c\) of the settling time function \(t_s(\varvec{w}_0, \varvec{p})\) of system S such that \(0~<~t_s(\varvec{w}_0, \varvec{p})~<~T_c~<~\infty \), and

    $$\begin{aligned} \forall \varvec{w}_0 \in \mathbb {R}^n, \ \forall t \ge T_c, \quad \varvec{w}(t, \varvec{w}_0, \varvec{p}) \in M, \end{aligned}$$

  • and for any predefined \(T_c\) (i.e., prescribed by a designer) there exist some parameters \(\varvec{p}\in \mathbb {R}^l\) of system S such that

    $$\begin{aligned} \sup _{\varvec{w}_0 \in \mathbb {R}^n} t_s(\varvec{w}_0, \varvec{p}) \le T_c. \end{aligned}$$

Remark 1

The equilibrium point \(\varvec{w}= \textbf{0}\) of the system S is said to be predefined-time stable if \(M = \{ \textbf{0 }\}\).

Based on the work [12], let us recall the following lemma.

Lemma 1

The equilibrium point \(\varvec{w}= 0\) of a dynamical system \(S: {\dot{\varvec{w}}}(t) = f(\varvec{w}(t), \varvec{p})\), \(\varvec{w}(0) = \varvec{w}_0 \in \mathbb {R}^n\) is said to be predefined-time stable, with a predefined time \(T_c\), if there exists a continuous radially unbounded positive defined function \(V: \mathbb {R}^n \rightarrow \mathbb {R}_+ \cup \{0\}\), and a vector of parameters \(\varvec{p}\), such that any solution \(\varvec{w}(t, \varvec{w}_0, \varvec{p}) \in \mathbb {R}^n \backslash \{ \textbf{0 }\}\) of system S satisfies:

$$\begin{aligned} {\dot{V}}(\varvec{w}) \le - \frac{\gamma }{T_c} \left( \alpha V^P(\varvec{w}) + \beta V^R(\varvec{w}) \right) ^k, \end{aligned}$$
(2)

where \(\alpha , \beta , P, R, k > 0\), \(kP < 1\), \(kR >1\) and \(\gamma \) is given by:

$$\begin{aligned} \gamma = \frac{\displaystyle \Gamma (m_P)\Gamma (m_R)}{\displaystyle \alpha ^k\Gamma (k)(R-P)}\left( \frac{\alpha }{\beta }\right) ^{m_P}, \end{aligned}$$
(3)

with \(m_P = \frac{1-kP}{R-P}\), \(m_R = \frac{kR - 1}{R-P}\) and where \(\Gamma (\cdot )\) is the gamma function defined as \(\Gamma (z)~\triangleq ~\int _{0}^{\infty } e^{-t}t^{z-1}dt\). As a consequence, the settling time function satisfies \(\sup _{\varvec{w}_0 \in \mathbb {R}^n} t_s(\varvec{w}_0, \varvec{p})~\le ~T_c\), and moreover, if (2) is an equality, then \(\sup _{\varvec{w}_0 \in \mathbb {R}^n} t_s(\varvec{w}_0, \varvec{p}) = T_c\).

2.3 Control problem formulation

We are interested in designing a predefined-time control law for the unicycle-like kinematics (1). In order to simplify the reasoning, we assume that the desired configuration is defined as the origin of the global frame (i.e., \(\varvec{q}_d = \begin{bmatrix} \theta _d \ \overline{\varvec{q}}_d^\top \end{bmatrix}^\top \triangleq \begin{bmatrix} 0 \ 0 \ 0 \end{bmatrix}^\top \)), and the error vector can be defined as follows:

$$\begin{aligned} \varvec{e}= \begin{bmatrix} e_\theta \\ e_x \\ e_y \end{bmatrix} = \begin{bmatrix} e_\theta \\ \overline{\varvec{e}} \end{bmatrix} \triangleq \begin{bmatrix} f_\theta (\theta _d - \theta ) \\ \overline{\varvec{q}}_d - \overline{\varvec{q}} \end{bmatrix} = \begin{bmatrix} f_\theta (-\theta ) \\ -\overline{\varvec{q}} \end{bmatrix}, \end{aligned}$$
(4)

where \(f_\theta (\cdot ): \mathbb {R}\rightarrow (-\pi , \pi ]\), i.e., for the angular part we will understand the value of zero modulo \(2 \pi \). The control problem can be formulated as follows:

Problem 1

For system (1), find a feedback control law \(\varvec{u}(\varvec{e}, \varvec{p})\), such that for any initial configuration error \(\varvec{e}(0) = \varvec{e}_0 \in \mathbb {R}^3{\setminus } M\), \(M \triangleq \left\{ \varvec{e}: \Vert \varvec{e}\Vert \le \psi \right\} \), \(\psi \ge 0\), and a prescribed upper bound \(0<T_c<\infty \), there exists a set of controller parameters \(\varvec{p}(T_c)\) which guarantees that the solution \(\varvec{q}(t, \varvec{q}_0, \varvec{p})\) of the closed-loop dynamics \({\dot{\varvec{q}}} = \varvec{G}(\varvec{q})\varvec{u}\left( \varvec{e}, \varvec{p}(T_c)\right) \) implies:

  • \(\forall t \ge 0 \quad \Vert \varvec{e}(t, \varvec{e}_0, \varvec{p}) \Vert < \infty \),

  • \(\forall t \ge t_s(\varvec{e}_0, \varvec{p}) \quad \varvec{e}(t, \varvec{e}_0, \varvec{p}) \in M\),

  • \(\displaystyle {\sup _{\varvec{e}_0 \in \mathbb {R}^3}} \ t_s(\varvec{e}_0, \varvec{p}) \le T_c\),

where \(t_s(\varvec{e}_0, \varvec{p})\) is the settling time function.

Remark 2

If \(\psi > 0\), then Problem 1 corresponds to the predefined-time ultimate boundedness [15], which can be called, the nearly predefined-time stability. If \(\psi = 0\), then \(M~=~\{ \textbf{0 }\}\) and Problem 1 corresponds to the predefined-time stability (see Remark 1).

3 Predefined-time VFO control design

Let us begin the design process of the VFO control law with a decomposition of the kinematic model (1) into the orientation dynamics and the positional dynamics:

$$\begin{aligned} {\dot{\theta }} = u_1, \qquad \dot{\overline{\varvec{q}}} = \overline{\varvec{g}}_2(\theta ) u_2, \end{aligned}$$
(5)

where \(\overline{\varvec{g}}_2(\theta ) = \begin{bmatrix} \cos \theta \ \sin \theta \end{bmatrix}^\top \). Next, we introduce the so-called convergence vector field \(\varvec{h}\) defined as follows:

$$\begin{aligned} \varvec{h}= \begin{bmatrix} h_\theta \\ \overline{\varvec{h}} \end{bmatrix} \triangleq \begin{bmatrix} K_a \left( \left| e_a\right| ^{\delta _1} + \left| e_a\right| ^{\delta _2} \right) \textrm{sign}(e_a) + {\dot{\theta }}_{a} \\ K_p \overline{\varvec{e}} + \varvec{v}\end{bmatrix}, \end{aligned}$$
(6)

where \(\textrm{sign}(\cdot )\) is a conventional sign function, such that

$$\begin{aligned} \textrm{sign}(z) \triangleq \left\{ \begin{array}{ccc} 1 &{}\quad \text {if} &{}\quad z > 0 \\ 0 &{}\quad \text {if} &{}\quad z = 0 \\ -1 &{}\quad \text {if} &{}\quad z < 0 \end{array}\right. , \end{aligned}$$
(7)

and

$$\begin{aligned} \varvec{v}\triangleq - \eta \sigma \Vert \overline{\varvec{e}}\Vert \overline{\varvec{g}}_{2d}, \end{aligned}$$
(8)

where \(\overline{\varvec{g}}_{2d} = \begin{bmatrix} \cos \theta _d \ \sin \theta _d \end{bmatrix}^\top = \begin{bmatrix} 1 \ 0 \end{bmatrix}^\top \), while

$$\begin{aligned} \delta _1 = 1 - \overline{\delta }, \qquad \delta _2 = 1 + \overline{\delta }, \qquad \overline{\delta } \in (0,1), \end{aligned}$$
(9)

and \(K_a, K_p>0\), \(\eta \in (0,K_p)\) are the design coefficients. The values of \(K_a\) and \(K_p\) will depend on a prescribed upper bound of the settling time, and will be determined in the sequel.

The decision variable \(\sigma \) used in (8) determines the motion strategy: forward if \(\sigma = 1\) and backward if \(\sigma = -1\). Its value can be chosen arbitrarily for almost all initial conditions of the robot configuration, or can depend on the sign of the initial position error as follows:

$$\begin{aligned} \sigma \triangleq \text {sgn}(e_x(0) \cos \theta _d + e_y(0) \sin \theta _d ) \in \{-1,+1\} \end{aligned}$$
(10)

where

$$\begin{aligned} \text {sgn}(z) \triangleq \left\{ \begin{array}{ccc} 1 &{}\quad \text {if} &{}\quad z \ge 0 \\ -1 &{}\quad \text {if} &{}\quad z < 0 \end{array}\right. . \end{aligned}$$
(11)

Assuming \(\theta _d \triangleq 0\), one can observe that (10) takes the following form:

$$\begin{aligned} \sigma \triangleq \text {sgn}(e_x(0) )\in \{-1,+1\}. \end{aligned}$$
(12)

Remark 3

The value of the coefficient \(\eta \) can be determined as follows:

$$\begin{aligned} \eta = \overline{\eta } K_p, \quad \overline{\eta } \in \left( 0, 1\right) , \end{aligned}$$
(13)

where \(\overline{\eta }\) is related to the so-called directing effect (see [25]). Furthermore, it is beneficial to select \(\overline{\eta } \in \left( 0.5, 1\right) \). Moreover, for \(\overline{\eta } = 0.82\) a maximum nominal curvature rate of a robot motion reaches the minimum (for details, see [25] and [34]).

Now, let us define the auxiliary orientation error introduced in (6), namely:

$$\begin{aligned} e_a(t) \triangleq \theta _a(t) - \theta (t) \in \mathbb {R}, \end{aligned}$$
(14)

where the term

$$\begin{aligned} \theta _a\left( \overline{\varvec{h}}(\overline{\varvec{e}})\right) \triangleq \left\{ \begin{array}{ccc} \text {Atan2c}\left( {\sigma h_y},{\sigma h_x}\right) &{} \text {if} &{} \Vert {\overline{\varvec{e}}(t)}\Vert > \epsilon \\ \theta _{a,\epsilon } &{} \text {if} &{} \Vert {\overline{\varvec{e}}(t)}\Vert \le \epsilon \end{array}\right. \end{aligned}$$
(15)

is an auxiliary orientation angle, while \(\epsilon \ge 0\) is a small vicinity of zero chosen by a designer. A time derivative of the auxiliary orientation angle is defined as follows:

$$\begin{aligned} {\dot{\theta }}_{a} \triangleq \left\{ \begin{array}{ccc} \frac{\displaystyle \left( {\dot{h}}_{y}h_x - h_y{\dot{h}}_{x}\right) }{\displaystyle \Vert {\overline{\varvec{h}}}\Vert ^2} &{} \text {if} &{} \Vert {\overline{\varvec{e}}(t)}\Vert >\epsilon \\ 0 &{} \text {if} &{} \Vert {\overline{\varvec{e}}(t)}\Vert \le \epsilon \end{array}\right. , \end{aligned}$$
(16)

where

$$\begin{aligned} \dot{\overline{\varvec{h}}} = \begin{bmatrix} {\dot{h}}_{x} \\ {\dot{h}}_{y} \end{bmatrix} = K_p \dot{\overline{\varvec{e}}} - \eta \sigma \frac{\displaystyle \overline{\varvec{e}}^\top \dot{\overline{\varvec{e}}}}{\displaystyle \Vert \overline{\varvec{e}} \Vert } \overline{\varvec{g}}_{2d} \end{aligned}$$
(17)

and \(\displaystyle {\theta _{a,\epsilon } \triangleq \lim _{\Vert {\overline{\varvec{e}}(t)}\Vert \rightarrow \epsilon } \theta _a\left( \overline{\varvec{h}}(\overline{\varvec{e}})\right) } \). The operator \(\text {Atan2c}\left( {\cdot },{\cdot }\right) :\,\mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}\), used in (15), is a continuous version of the four-quadrant inverse tangent function \(\text {Atan2}\left( {\cdot },{\cdot }\right) :\,\mathbb {R}\times \mathbb {R}\rightarrow (-\pi ;\pi ]\).

The VFO control formulas are defined as follows:

$$\begin{aligned} u_{1}&\triangleq h_\theta {{\mathop {=}\limits ^{(\small {}6)}}} K_a \left( \left| e_a\right| ^{\delta _1} +\left| e_a\right| ^{\delta _2} \right) \textrm{sign}(e_a) + {\dot{\theta }}_{a}, \end{aligned}$$
(18)
$$\begin{aligned} u_{2}&\triangleq \rho \varvec{h}^\top \varvec{g}_2(\theta ) = \rho \Vert \overline{\varvec{h}}\Vert \cos \alpha , \end{aligned}$$
(19)

where the angle \(\alpha \triangleq \angle (\overline{\varvec{h}},\overline{\varvec{g}}_2(\theta ))\) and

$$\begin{aligned} \rho \triangleq \left\{ \begin{array}{lll} \frac{\rho _0}{\Vert \overline{\varvec{h}}\Vert } \left( \Vert \overline{\varvec{e}}\Vert ^{\mu _1} + \Vert \overline{\varvec{e}}\Vert ^{\mu _2}\right) &{} \text {if} &{} \Vert {\overline{\varvec{e}}(t)}\Vert >\epsilon \\ \qquad \qquad \qquad 0 &{} \text {if} &{} \Vert {\overline{\varvec{e}}(t)}\Vert \le \epsilon \end{array}\right. , \end{aligned}$$
(20)

with additional design parameters

$$\begin{aligned} \mu _1 = 1 - \overline{\mu }, \qquad \mu _2 = 1 + \overline{\mu }, \qquad \overline{\mu } \in (0,1), \end{aligned}$$
(21)

and where \(\rho _0 > 0\) provides an additional design degree of freedom which will depend on a given upper bound of the settling time, and will be determined in Sect. 4.2.

4 Stability analysis

In order to show that the control law (18)–(19) solves Problem 1, formulated in Sect. 2.3, a stability analysis based on the Lyapunov stability method will be presented separately for the auxiliary orientation error and for the positional error. Next, the convergence of the orientation error will be shown. Note that the analysis will be prepared for \(\epsilon = 0\), which corresponds to \(\psi = 0\) in Problem 1.

4.1 Analysis for the auxiliary orientation error

First, let us derive the dynamics of the auxiliary orientation error (14):

$$\begin{aligned} {\dot{e}}_a&{{\mathop {=}\limits ^{(\small {}14)}}} {\dot{\theta }}_{a}-{\dot{\theta }} {{\mathop {=}\limits ^{(\small {}5)}}} {\dot{\theta }}_{a}-u_1 \nonumber \\&{{\mathop {=}\limits ^{(\small {}18)}}} {\dot{\theta }}_{a} - K_a \left( \left| e_a\right| ^{\delta _1} + \left| e_a\right| ^{\delta _2} \right) \textrm{sign}(e_a) - {\dot{\theta }}_{a} \nonumber \\&= - K_a \left( \left| e_a\right| ^{\delta _1} + \left| e_a\right| ^{\delta _2} \right) \textrm{sign}(e_a). \end{aligned}$$
(22)

One can conclude, that \(e_a = 0\) is the equilibrium point of (22).

Now, let us consider the positive-definite function \(V_a \triangleq \frac{1}{2}e_a^2\). A time-derivative of \(V_a\) can be computed as follows:

$$\begin{aligned} {\dot{V}}_a&= e_a{\dot{e}}_a {{\mathop {=}\limits ^{(\small {}22)}}} e_a\left[ - K_a \left( \left| e_a\right| ^{\delta _1} + \left| e_a\right| ^{\delta _2} \right) \textrm{sign}(e_a)\right] \nonumber \\&= - K_a\left( \left| e_a\right| ^{(\delta _1 + 1)} + \left| e_a\right| ^{(\delta _2 + 1)} \right) \nonumber \\&{{\mathop {=}\limits ^{(2)}}} - \frac{\displaystyle \gamma _a}{\displaystyle T_{c,a}}\left( \alpha _a V_a^{P_a} + \beta _a V_a^{R_a}\right) , \end{aligned}$$
(23)

where \(\alpha _a = \sqrt{2}^{\left( \delta _1 + 1\right) },\) \(\beta _a = \sqrt{2}^{\left( \delta _2 + 1\right) },\) \( P_a =\left( \frac{\delta _1 + 1}{2}\right) \), \( R_a = \left( \frac{\delta _2 + 1}{2}\right) \), \( k = 1\), and \(\frac{\displaystyle \gamma _a}{\displaystyle T_{c,a}} = K_a\). By comparing (23) with (2), one can conclude that the equilibrium point \(e_a = 0\) of the auxiliary orientation error dynamics is predefined-time stable. Moreover, upon (3) one can write:

$$\begin{aligned} \gamma _a&{{\mathop {=}\limits ^{(3)}}} \frac{\displaystyle \Gamma \left( \frac{\displaystyle 1 - \delta _1}{\displaystyle \delta _2 - \delta _1}\right) \Gamma \left( \frac{\displaystyle \delta _2 - 1}{\displaystyle \delta _2 - \delta _1}\right) }{\displaystyle \delta _2 - \delta _1} \nonumber \\&{{\mathop {=}\limits ^{(9)}}} \frac{\displaystyle \Gamma ^2\left( \frac{\displaystyle 1}{\displaystyle 2}\right) }{\displaystyle 2 \overline{\delta }} = \frac{\displaystyle \pi }{\displaystyle 2 \overline{\delta }}, \end{aligned}$$
(24)

where \(\Gamma \left( \frac{1}{2}\right) = \sqrt{\pi }\), according to [35], and \(\gamma _a\) corresponds to (3) evaluated for the auxiliary orientation error dynamics. Now, the gain \(K_a\), which is used in the control formula (18), can be selected as follows:

$$\begin{aligned} K_a = \frac{\displaystyle \gamma _a}{\displaystyle T_{c,a}} {{\mathop {=}\limits ^{(\small {}24)}}} \frac{\displaystyle \pi }{\displaystyle 2 T_{c,a} \overline{\delta }}, \end{aligned}$$
(25)

where \(T_{c,a}\) means the prescribed upper bound of the settling time \(t_{s,a}\) of the auxiliary orientation error \(e_a\). Since (23) is an equality, then: \(\sup _{e_a(0) \in \mathbb {R}} t_{s,a}(e_a(0)) = T_{c,a}\).

Remark 4

(cf. [28] or [29]) According to the practical experience, one can suggest the following heuristic tuning rule:

$$\begin{aligned} K_p = \frac{1}{2} K_a {{\mathop {=}\limits ^{(\small {}25)}}} \frac{\displaystyle \pi }{\displaystyle 4 T_{c,a} \overline{\delta }} . \end{aligned}$$
(26)

4.2 Analysis for the positional error

The positive-definite function \(V_p \triangleq \frac{1}{2} \overline{\varvec{e}}^T \overline{\varvec{e}}\) is chosen to analyze the dynamics of the positional error. First, let us derive the closed-loop positional error equation:

$$\begin{aligned} \dot{\overline{\varvec{e}}}&= -\dot{\overline{\varvec{q}}} {{\mathop {=}\limits ^{(5)}}} -\overline{\varvec{g}}_2(\theta ) u_2 \nonumber \\&{{\mathop {=}\limits ^{(6)}}} - \overline{\varvec{g}}_2(\theta ) u_2 + \rho \overline{\varvec{h}} - \rho (K_p \overline{\varvec{e}} + \varvec{v}) \nonumber \\&= -\rho K_p\overline{\varvec{e}} + \rho \overline{\varvec{h}} - \overline{\varvec{g}}_2(\theta ) u_2 - \rho \varvec{v}\nonumber \\&= -\rho K_p\overline{\varvec{e}} + \rho \varvec{r}- \rho \varvec{v}, \end{aligned}$$
(27)

where \(\varvec{r}= \overline{\varvec{h}} - \overline{\varvec{g}}_2(\theta ) \frac{\displaystyle u_2}{\displaystyle \rho }\) and \(\varvec{v}\) is defined in (8).

Remark 5

Let us consider the positional error dynamics (27): \(\dot{\overline{\varvec{e}}} {{\mathop {=}\limits ^{(\small {}5)}}} -\overline{\varvec{g}}_2(\theta ) u_2 {{\mathop {=}\limits ^{(19)}}} \rho \Vert \overline{\varvec{h}}\Vert \cos \alpha {{\mathop {=}\limits ^{(\small {}20)}}} \rho _0 \left( \Vert \overline{\varvec{e}}\Vert ^{\mu _1} \right. \) \(\left. + \Vert \overline{\varvec{e}}\Vert ^{\mu _2}\right) \cos \alpha \) and \(\forall t \ge T_{c,a} \ |\cos \alpha | = |\cos e_a| = 1\). Thus, one can conclude that \(\overline{\varvec{e}} = \textbf{0}\) is the equilibrium point of (27).

Next, let us define the function \(\chi (e_a) {=}\sqrt{1 {-} \cos ^2 e_a} \in [0,1]\). One can observe that:

$$\begin{aligned} \Vert \overline{\varvec{h}}\Vert {{\mathop {=}\limits ^{(6)}}} \Vert K_p \overline{\varvec{e}} + \varvec{v}\Vert \le \left( K_p + \eta \right) \Vert \overline{\varvec{e}} \Vert \end{aligned}$$

and \(\Vert \varvec{r}\Vert = \Vert \overline{\varvec{h}}\Vert \chi (e_a) \) (for details, see [28]). Now, let us analyze the time derivative of function \(V_p\):

$$\begin{aligned} {\dot{V}}_p&= \overline{\varvec{e}}^\top \dot{\overline{\varvec{e}}} = \overline{\varvec{e}}^\top \left[ -\rho K_p\overline{\varvec{e}} + \rho \varvec{r}- \rho \varvec{v}\right] \nonumber \\&= -\rho K_p\Vert \overline{\varvec{e}}\Vert ^2 + \rho \overline{\varvec{e}}^\top \varvec{r}- \rho \overline{\varvec{e}}^\top \varvec{v}\nonumber \\&\le -\rho \left[ K_p\Vert \overline{\varvec{e}}\Vert ^2 - \Vert \overline{\varvec{e}}\Vert \Vert \varvec{r}\Vert - \Vert \overline{\varvec{e}}\Vert \Vert \varvec{v}\Vert \right] \nonumber \\&\le -\rho \left[ K_p\Vert \overline{\varvec{e}}\Vert ^2 - \Vert \overline{\varvec{e}}\Vert \Vert \overline{\varvec{h}}\Vert \chi -\eta \Vert \overline{\varvec{e}}\Vert ^2 \right] \nonumber \\&{{\mathop {=}\limits ^{(\small {}6)}}} -\rho \left[ K_p\Vert \overline{\varvec{e}}\Vert ^2 - \Vert \overline{\varvec{e}}\Vert \Vert K_p\overline{\varvec{e}}+\varvec{v}\Vert \chi -\eta \Vert \overline{\varvec{e}}\Vert ^2 \right] \nonumber \\&\le -\rho \left[ K_p\Vert \overline{\varvec{e}}\Vert ^2 - \chi K_p\Vert \overline{\varvec{e}}\Vert ^2 - \chi \eta \Vert \overline{\varvec{e}}\Vert ^2 -\eta \Vert \overline{\varvec{e}}\Vert ^2 \right] \nonumber \\&= -\rho \Vert \overline{\varvec{e}}\Vert ^2 \underbrace{\left[ (K_p - \eta ) - \chi (K_p + \eta )\right] }_{\xi (\chi )} \nonumber \\&= -\rho \Vert \overline{\varvec{e}}\Vert ^2\xi (\chi ) \nonumber \\&{{\mathop {=}\limits ^{(\small {}20)}}} -\frac{\rho _0\xi (\chi )}{\Vert \overline{\varvec{h}}\Vert } \Vert \overline{\varvec{e}} \Vert \left( \left\| \, \!\overline{\varvec{e}}\right\| ^{\mu _1+1} + \left\| \, \!\overline{\varvec{e}}\right\| ^{\mu _2+1}\right) \nonumber \\&\le -\frac{\rho _0\xi (\chi )}{K_p+\eta } \left( \Vert \overline{\varvec{e}}\Vert ^{\mu _1+1} + \Vert \overline{\varvec{e}}\Vert ^{\mu _2+1}\right) . \end{aligned}$$
(28)

Based on (28), one can conclude that \(V_p < \infty \) for \(t~\in ~[0,T_{c,a})\), since \(|\xi (\chi )| < \infty \), thus \(\Vert \overline{\varvec{e}} \Vert < \infty \) for \(t~\in ~[0,T_{c,a})\), and consequently the finite-time-escape effect is not possible for dynamics (27).

Note that \(\chi (e_a)\rightarrow 0\) as \(e_a\rightarrow 0\), and as a consequence, \(\xi (\chi (e_a))\rightarrow (K_p-\eta )\) as \(e_a\rightarrow 0\). Thus, for \(t \ge T_{c,a}\) the inequality (28) can be replaced by the following relation:

$$\begin{aligned} {\forall t {\ge } T_{c,a}} \quad {\dot{V}}_p&{\le } {-}\frac{\displaystyle \rho _0(K_p - \eta )}{\displaystyle K_p+\eta } \left( \Vert \overline{\varvec{e}}\Vert ^{\mu _1+1} {+} \Vert \overline{\varvec{e}}\Vert ^{\mu _2+1}\right) \nonumber \\&{{\mathop {=}\limits ^{(\small {}2)}}} -\frac{\displaystyle \gamma _p}{\displaystyle T_{c,p}} \left( \alpha _p V_p^{P_p} +\beta _p V_p^{R_p}\right) , \end{aligned}$$
(29)

which depends only on the positional error, and where \(\alpha _p = \sqrt{2}^{\left( \mu _1+1\right) }\), \(\beta _p = \sqrt{2}^{\left( \mu _2+1\right) }\), \( P_p =\left( \frac{\mu _1+1}{2}\right) \), \( R_p = \left( \frac{\mu _2+1}{2}\right) \), and \(\frac{\displaystyle \gamma _p}{\displaystyle T_{c,p}} = \frac{\displaystyle \rho _0(K_p - \eta )}{\displaystyle K_p+\eta }\). Now, by comparing (29) with (2) one can conclude that the equilibrium point \(\overline{\varvec{e}} = \textbf{0}\) of the positional error dynamic is predefined-time stable and, upon (3), one can write:

$$\begin{aligned} \gamma _p&{{\mathop {=}\limits ^{(\small {}3)}}} \frac{\displaystyle \Gamma \left( \frac{\displaystyle 1 - \mu _1}{\displaystyle \mu _2 - \mu _1}\right) \Gamma \left( \frac{\displaystyle \mu _2 - 1}{\displaystyle \mu _2 - \mu _1}\right) }{\displaystyle \mu _2 - \mu _1} \nonumber \\&{{\mathop {=}\limits ^{(\small {}21)}}} \frac{\displaystyle \Gamma ^2\left( \frac{\displaystyle 1}{\displaystyle 2}\right) }{\displaystyle 2 \overline{\mu }} = \frac{\displaystyle \pi }{\displaystyle 2 \overline{\mu }}, \end{aligned}$$
(30)

where \(\gamma _p\) corresponds to (3) evaluated for the positional error dynamics.

When a designer prescribes the upper bound \(T_{c,p}\) on the settling time \(t_{s,p}\) of the positional error, the parameter \(\rho _0\) can be computed as follows:

$$\begin{aligned} \rho _0&= \frac{\displaystyle \gamma _p(K_p + \eta )}{\displaystyle T_{c,p}(K_p - \eta )} {{\mathop {=}\limits ^{(\small {}30)}}} \frac{\displaystyle \pi (K_p + \eta )}{\displaystyle 2 T_{c,p}(K_p - \eta )\overline{\mu }} \nonumber \\&{{\mathop {=}\limits ^{(\small {}13)}}} \frac{\displaystyle \pi (1 + \overline{\eta })}{\displaystyle 2 T_{c,p}(1 - \overline{\eta })\overline{\mu }}. \end{aligned}$$
(31)

Remark 6

Note that (29) holds for \(\forall t \ge T_{c,a}\). Thus, assuming that \(T_{c,a}<T_{c,p}\), the total upper bound of the settling time for the error \({\varvec{e}}(t)\) from (4) has to be (conservatively) estimated as

$$\begin{aligned} T_c = T_{c,a} + T_{c,p}. \end{aligned}$$
(32)

4.3 Convergence of the orientation error

Let us also analyze the convergence of the orientation error \(e_\theta \) as follows. From (4) and (14), one can write:

$$\begin{aligned} e_\theta {{\mathop {=}\limits ^{(\small {}4)}}} f_\theta (-\theta ) {{\mathop {=}\limits ^{(\small {}14)}}} f_\theta (e_a - \theta _a). \end{aligned}$$
(33)

Next, one can observe that

$$\begin{aligned} \forall t \ge T_{c,a} \quad e_\theta = f_\theta (- \theta _a). \end{aligned}$$
(34)

Assuming that \(T_{c,a} < T_{c,p}\), one can proceed as follows. According to [36], it can be shown that \(h_x(t)~\xrightarrow {t\rightarrow \tau _x}~0\), \(h_y(t)~\xrightarrow {t\rightarrow \tau _y}~0\), for \(\tau _y < \tau _x \le T_{c,p}\), and as a consequence, \(\forall t \ge {T_c} \quad \theta _a {{\mathop {=}\limits ^{(\small {}15)}}} 2k\pi \), \(k \in \mathbb {Z}\), thus one can conclude that \(e_\theta \rightarrow 0\) as \(t \rightarrow {T_c}\).

Remark 7

It should be noted that for \(\epsilon > 0\), \(\theta _a(t)~\rightarrow ~\) \(\theta _{a,\epsilon }\) as \(t \rightarrow {T_c}\), and as a consequence \(e_\theta (t) \rightarrow f_\theta (- \theta _{a,\epsilon })\) as \(t \rightarrow {T_c}\). Moreover, for \(\epsilon > 0\) one gets \(\Vert \overline{\varvec{e}}(t) \Vert = \epsilon \) for \(t \rightarrow {T_c}\).

4.4 Summary of the analysis

Considering the reasoning presented in Sects. 4.1–4.3, and recalling Remark 7, the following corollary can be formulated:

Corollary 1

Prescribing the positive upper bounds \(T_{c,a}< T_{c,p} < \infty \) and if the coefficients \(K_a\), \(K_p\), \(\eta \) and \(\rho _0\) are selected according to (25), (26), (13) and (31), respectively, the control law (18)–(19), when applied to system (1), solves Problem 1 for \(T_c~=~{T_{c,a}+T_{c,p}}\), and such that:

  • taking \(\epsilon = 0 \implies \psi = 0,\)

  • taking \(\epsilon > 0 \implies \psi = \sqrt{ \epsilon ^2 + f_\theta ^2 \left( - \theta _{a,\epsilon } \right) }\).

5 Control system validation

5.1 Simulation results

In order to verify the predefined-time convergence, numerical simulations were prepared with the following parameters: \(\overline{\delta } = \overline{\mu } = 0.2\), \(\epsilon = 10^{-15} \ \text {m}\) and \(\overline{\eta } = 0.82\). The values for the upper bounds of the settling time were chosen as follows: \(T_{c,a} = 5 \ \text {s}\) and \(T_{c,p} = 50 \ \text {s}\). The parameters \(K_a\) and \(\rho _0\) were calculated according to (25) and (31), respectively, while we took \(K_p = \frac{\displaystyle 1}{\displaystyle 2} K_a\).

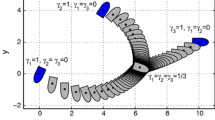
Figure 1 shows the results obtained for the far initial position, i.e., \(\varvec{q}_0 = \begin{bmatrix} -\frac{\displaystyle \pi }{\displaystyle 2} \ -10^3 \ 10^3 \end{bmatrix}^\top \). The following real values of settling times for the auxiliary orientation error and the positional error were obtained: \(t_{s,a} = 2.5 \ \text {s}\) and \(t_{s,p} = 6.77 \ \text {s}\).

Fig. 1
figure 1

Results of a simulation scenario obtained for \(\varvec{q}_0 = \begin{bmatrix} {-\frac{\displaystyle \pi }{\displaystyle 2}} \ {-10^3} \ 10^3 \end{bmatrix}^\top \) (the initial robot configuration is denoted by a solid-line triangle)

Full size image

The closed-loop system was also tested for a grid of initial conditions determined by the following discrete set of values:

$$\begin{aligned} x_0, y_0 \in&\left\{ {-2}, {-\frac{\displaystyle 3}{\displaystyle 2}}, {-1}, {-\frac{\displaystyle 1}{\displaystyle 2}}, 0, \frac{\displaystyle 1}{\displaystyle 2}, 1, \frac{\displaystyle 3}{\displaystyle 2}, 2 \right\} , \\ \theta _0 \in&\left\{ {-\frac{\displaystyle \pi }{\displaystyle 2}}, 0, \frac{\displaystyle \pi }{\displaystyle 2}, \pi \right\} . \end{aligned}$$

The largest true values of settling times on the grid were obtained as: \(t_{s,a} = 3.37 \ \text {s}\) and \(t_{s,p} = 4.98 \ \text {s}\). The results of the simulations are presented in Fig. 2.

It should be noted that the prescribed upper bounds were satisfied and \(\forall t \ge 0 \ |u_1(t)|,|u_2(t)| < \infty \).

Fig. 2
figure 2

Set of numerical simulation results for \(x_0, y_0 \in \{{-2}, {-\frac{\displaystyle 3}{\displaystyle 2}}, {-1}, {-\frac{\displaystyle 1}{\displaystyle 2}}, 0, \frac{\displaystyle 1}{\displaystyle 2}, 1, \frac{\displaystyle 3}{\displaystyle 2}, 2 \}\) and \(\theta _0 \in \{{-\frac{\displaystyle \pi }{\displaystyle 2}}, 0, \frac{\displaystyle \pi }{\displaystyle 2}, \pi \}\) (the initial robot positions are denoted by red crosses—for each initial position, a simulation was performed with 4 different initial orientations)

Full size image

In order to study the effect of the settling-time ratio

$$\begin{aligned} T_r = \frac{\displaystyle T_{c,p}}{\displaystyle T_{c,a}} \end{aligned}$$
(35)

on the control performance, additional simulations have been conducted (see Fig. 3 and Table 1). The following values of the upper bounds: \(T_{c,p} = 10 \ \text {s}\) and \(T_{c,a} \in \{0.1 \ \text {s}, 1 \ \text {s}, 10 \ \text {s}\}\) were chosen.

Fig. 3
figure 3

Set of numerical simulations obtained for \(T_r~\in ~\{100, 10, 1\}\) and \(\varvec{q}_0 = \begin{bmatrix} 0 \ {-2} \ {-2} \end{bmatrix}^\top \) (the initial robot configuration is denoted by a solid-line triangle)

Full size image

Upon the results, it can be concluded that the control performance is affected by both the individual values of \(T_{c,a}\) and the ratio \(T_r\). Choosing lower values of \(T_{c,a}\) will lead to faster convergence of the auxiliary orientation error \(e_a\), increasing also the amplitude of the orienting control \(u_1\). Similarly, a selection of smaller values of \(T_{c,p}\) will give a faster convergence of the positional error, though at the expense of higher absolute values of pushing control \(u_2\). The ratio \(T_r\) mainly affects the shapes of paths drawn by the robot’s guidance point, that is, values \(T_r \le 1\) mean that the positional error will converge too fast relative to the auxiliary orientation error, which can lead to a loss of the so-called directing effect, which is crucial for ensuring convergence of the robot’s orientation angle in a terminal motion stage (the lack of orientation convergence can be observed in Fig. 3c).

5.2 Experimental results

The experimental results were obtained using the MTracker—a small differentially driven mobile robot developed in the Institute of Automatic Control and Robotics at the Poznan University of Technology (see Fig. 4). For the experimental validation purposes, the following values of the design parameters were used: \(\overline{\delta } = \overline{\mu } = 0.2\), \(\overline{\eta } = 0.82\), and \(\epsilon = 0.003 \ \text {m}\). In order to guarantee that the control signals are not saturated, the following values of the upper bounds were selected: \(T_{c,a} = 60 \ \text {s}\) and \(T_{c,p} = 600 \ \text {s}\). The experimental tests were prepared for two different initial configurations and movement strategies, namely:

$$\begin{aligned} \text {E1}:&\quad \varvec{q}_0 = \left[ \begin{array}{cc} 0 \ \ 0.375 \ \ 0.4 \end{array}\right] ^\top , \quad \sigma = -1, \\ \text {E2}:&\quad \varvec{q}_0 = \left[ \begin{array}{cc} 0 \ \ {-0.75} \ \ {{-0.4}} \end{array}\right] ^\top , \quad \sigma = 1. \end{aligned}$$

The results for both experimental scenarios are shown in Figs. 5 and 6, respectively. The real values of the settling times obtained during the tests are as follows:

$$\begin{aligned} \text {E1}:&\quad t_{s,a} \approx 21.16 \ \text {s}, \quad t_{s,p} \approx 15.26 \ \text {s}, \\ \text {E2}:&\quad t_{s,a} \approx 24.62 \ \text {s}, \quad t_{s,p} \approx 17.18 \ \text {s}. \end{aligned}$$

The prescribed upper bounds on the settling times are satisfied and the system errors converge toward zero.

Table 1 Influence of \(T_{c,a}\) and the settling-time ratio \(T_r\) on control performance
Full size table
Fig. 4
figure 4

MTracker—differentially driven mobile robot used for the experimental validation

Full size image
Fig. 5
figure 5

Results of experimental test for case E1: \(\varvec{q}_0 = \begin{bmatrix} 0 \ 0.375 \ 0.4 \end{bmatrix}^\top \) (the initial robot configuration is denoted by a solid-line triangle)

Full size image
Fig. 6
figure 6

Results of experimental test for case E2: \(\varvec{q}_0~=~\begin{bmatrix} 0 \ {-0.75} \ {{-0.4}} \end{bmatrix}^\top \) (the initial robot configuration is denoted by a solid-line triangle)

Full size image

5.3 Comparison study

In order to reveal advantages of the proposed predefined-time set-point VFO control law, we compared our solution (using the same control scenario) with the predefined-time stabilizer proposed for the chained-form nonholonomic system in [16].

The control strategy characteristic to the solution shown in [16], and other similar approaches which also use the chained-form transformation [14, 16, 30], can be summarized as follows:

  • a system in the chained form is decomposed into two subsystems:

    $$\begin{aligned}&\dot{x}_0 = v_0 \end{aligned}$$
    (36)

    and

    $$\begin{aligned}&\dot{x}_1 = x_2 v_0, \end{aligned}$$
    (37)
    $$\begin{aligned}&\dot{x}_2 = v_1, \end{aligned}$$
    (38)

  • the subsystem (37)–(38) is stabilized first in a predefined time while the subsystem (36) is controlled by some constant value (i.e., \(v_0=a\)) to overcome the loss of controllability of subsystem (37)–(38),

  • when the stabilization process of the subsystem (37)–(38) finishes, then the control law \(v_0\) switches to guarantee the predefined time stabilization of the subsystem (36).

A connection between the chained-form system (36) - (38) and (1) is determined by the following state and input transformations (cf. [16]):

$$\begin{aligned} x_0&= x, \nonumber \\ x_1&= y, \nonumber \\ x_2&= \tan \theta , \nonumber \\ v_0&= u_2 \cos \theta , \nonumber \\ v_1&= \frac{\displaystyle u_1}{\displaystyle \cos ^2 \theta }, \end{aligned}$$
(39)

valid for \(\theta \not = \frac{\displaystyle 2k+1}{\displaystyle 2}\pi \), \(k \in \mathbb {Z}\). The authors of [16] proposed the following control law for the chained-form system:

$$\begin{aligned} v_0&\triangleq \left\{ \begin{array}{clc} a, &{} \text {if} &{} t \le T_{c1} + T_{c2} \\ v_0^*, &{} \text {else} &{} \end{array}\right. , \end{aligned}$$
(40)
$$\begin{aligned} v_1&\triangleq \left\{ \begin{array}{clc} \frac{\displaystyle \varphi \left( x_1, ax_2 \right) }{\displaystyle a}, &{} \text {if} &{} t \le T_{c1} + T_{c2} \\ -\gamma \ \textrm{sign}{(x_2)}, &{} \text {else} \end{array}\right. , \end{aligned}$$
(41)

where a is a constant chosen by a designer, and

$$\begin{aligned} v_0^* = - \frac{\displaystyle \sqrt{\pi }}{\displaystyle T_{c3}}\exp {\left( |x_0|\right) }\lfloor x_0 \rceil ^{\frac{1}{2}} - \zeta _0 \textrm{sign}{(x_0)}, \end{aligned}$$
(42)

with

$$\begin{aligned}&\varphi \left( z_1, z_2 \right) = \nonumber \\&- \frac{\displaystyle \alpha _2^{\frac{\displaystyle \beta _2 q_2 - 1}{\displaystyle p_2}} \Gamma \left( \frac{\displaystyle 1 - \beta _2 q_2}{\displaystyle p_2} \right) }{\displaystyle p_2 T_{c2}}\exp {\left( \alpha _2 |\sigma |^{p_2} \right) } \lfloor \sigma \rceil ^{\beta _2 q_2} \nonumber \\&- \zeta \textrm{sign}{(\sigma )} - \overline{\sigma }\left( q_1 + p_1 \lfloor z_1 \rceil ^{p_1} \right) |z_1|^{q_1 - 1} \nonumber \\&\times \exp \left( |z_1|^{p_1} \right) \textrm{sign}{\left( \sigma \right) }, \end{aligned}$$
(43)

while \(\lfloor z_1 \rceil ^{z_2} \triangleq |z_1|^{z_2} \textrm{sign}{(z_1)}\),

$$\begin{aligned} \sigma = z_2 + \big \lfloor \lfloor z_2 \rceil ^{2} + 2\overline{\sigma } \exp {(|z_1|^{p_1})} \lfloor z_1 \rceil ^{q_1} \big \rceil ^\frac{1}{2} \end{aligned}$$
(44)

and

$$\begin{aligned} \overline{\sigma } = \left( \frac{\displaystyle 2^{\frac{\displaystyle 1-q_1/2}{\displaystyle p_1}} \Gamma \left( \frac{1 - q_1/2}{p_1} \right) }{\displaystyle p_1 T_{c1}} \right) ^2. \end{aligned}$$
(45)

Note that the VFO methodology also assumes decomposition of the state dynamics into two subsystems, but at any time instant none of them are controlled by a constant value chosen by a designer, and switching of the pushing control (19) is necessary only in a terminal control stage, i.e., when the positional error enters into a prescribed vicinity \(\epsilon \) (cf. (20)). The comparison shown below has been prepared only with the controller taken from [16] to highlight the benefits of using the VFO design methodology over the representative one proposed for the chained-form system in [16].

Fig. 7
figure 7

Results obtained for the comparison of the predefined-time VFO controller with the controller proposed in [16]: \(\varvec{q}_0~=~\begin{bmatrix} 0 \ 3 \ {-1} \end{bmatrix}^\top \) (the initial robot configuration is denoted by a solid-line triangle).

Full size image
Table 2 Summary of the comparison of the predefined-time VFO controller with the controller proposed in [16].
Full size table

For the control law (40)–(41), the simulation was conducted with the following parameters: \(T_{c1} = 50 \ \text {s}\), \(T_{c2} = 9 \ \text {s}\), \(T_{c3} = 41 \ \text {s}\), \(p_1 = 1\), \(q_1 = 1.2\), \(p_2 = 1\), \(q_2 = 0.8\), \(\alpha _2 = 10^{-3}\), \(\zeta _0 = 0.1\), \(\zeta = 0.03\), \(\beta _2 = 1\), \(a = 0.01\) and \(\gamma = 0.3\). For the VFO control law, the upper bounds were chosen as: \(T_{c,a} = 10 \ \text {s}\), \(T_{c,p} = 90 \ \text {s}\) and other parameters were selected as in Sect. 5.1. The obtained comparative results are shown in Fig. 7 and are summarized in Table 2.

In both cases, the total upper bound on the settling time of the stabilization errors is 100 s—for the VFO control law \(T_c = T_{c,p} + T_{c,a}\), and for the controller from [16] the total upper bound is \(T_c = T_{c1} + T_{c2} + T_{c3} \). One can observe that the configuration errors converge faster for the VFO controller than for the controller from [16]. Moreover, the control design proposed in [16] is characterized by a control-chattering effect observed in the plots of the control signals. The control oscillations are caused by the use of a discontinuous sign function in (41) and (43). One can replace the sign function, e.g., by a sigmoid function to reduce the chattering phenomenon, however, at the cost of significant performance degradation (robustness and accuracy issues). In contrast, the VFO controller is characterized by non-oscillatory time evolution of transient states, which can be also observed in Fig. 7.

Moreover, the controller from [16] is characterized by discontinuities in \(u_2\) and higher supremum values of \({u_1}\) (see Table 2). Hence, the controller from [16] provides control inputs which will be saturated due to physical limitations on the robot actuators contrary to our proposed scheme. The switching scheme in [16] significantly impacts the transient states. It is also worth mentioning, that the proposed predefined-time VFO controller generates noticeably smaller absolute value of \(u_1\) and a well predictable time evolution of transient states. Moreover, for the VFO controller, the path taken by the robot is shorter, is characterized by a smaller maximum curvature, and needs less movement direction changes.

6 Conclusions

In the paper, the predefined-time VFO control law has been proposed for the nonholonomic unicycle-like mobile robots, based on the definition of global predefined-time stability proposed in [12], which guarantees less conservative estimation of the upper bounds for the settling time of configuration errors relative to alternative estimation approaches introduced in [9,10,11]. For the predefined-time VFO control law, the well-predictable and non-oscillatory transient behavior (characteristic to the previous versions of VFO controllers) has been preserved. Some practical benefits of the proposed control law relative to the predefined-time chained-form stabilizer proposed in [16] have been highlighted in this paper.

It is worth noting that despite the less conservative method of the upper bound estimation for settling times utilized during the VFO control design, the differences between achieved settling times and the predefined upper bounds are still noticeable (some level of conservatism seems to be unavoidable for the global stability results). In order to decrease the conservatism, local versions of fixed- and predefined-time stability concepts seem to be necessary. A combination of time constraints with control input constraints for mobile robots is the next interesting and practically important research problem, which the authors are going to address in their future investigations.