1 Introduction

Nowadays, with the trend for increasing flexibility and extreme loading environments, engineering structures are likely to work outside of the linear envelope and oscillate at a high amplitude level. In these cases, many nonlinear phenomena can be induced by geometric nonlinearities [1, 2]. Thanks to the development of the finite element (FE) method and commercial software, structures with large displacement can be modelled accurately [3]. However, the computational demands quickly become prohibitive, especially when considering the dynamical analysis of systems with a large number degrees-of-freedom (DoFs) [4], referred to as full-order models. To alleviate the computational burden, model reduction techniques are developed extensively to construct reduced-order models (ROMs). These ROMs can capture the full-order model’s salient dynamical characteristics by using a low-dimensional dynamical system [5, 6].

Conventionally, the equations of motion of an FE model are projected to a small set of linear normal modes (LNMs) to achieve the model reduction. This garlekin-based projection can output a very accurate result under a small amplitude level [7]. When the displacement increases, the result from this linear projection departs from the accurate one, as the modal interaction induced by geometric nonlinearities occurs, e.g. the modal coupling between bending modes and membrane modes. In this case, the updating of the modal basis is essential to provide an accurate dynamic response under large amplitudes [8, 9]. In addition, the proper orthogonal decomposition (POD) method may be used to generate a set of POD modes as the optimal reduction basis in terms of the energy contribution [10]. However, the identification of POD modes requires dynamic simulation of the FE model, which is time-consuming for complex structures.

In nonlinear dynamics, the response frequencies, and the resulting modeshapes, are both dependent on the amplitude of the system, and the LNMs are only accurate under the small-amplitude displacement. Motivated by this fact, the modal derivatives (MDs) have been used to model this dependence by differentiating the eigenvalue problem, whilst the modal reduction is achieved by incorporating the LNMs and the corresponding MDs into the reduction basis [11, 12]. One limitation is that, when the nonlinearity becomes significant, the number of MDs increases quadratically with respect to the number of LNMs in the basis, which requires a rapid increase in the size of the reduction basis. To circumvent this issue, the concept of a quadratic manifold is proposed to illustrate the nonlinear mapping from the physical coordinates to the reduced coordinates [13]. In the quadratic manifold approach, the amplitudes of the MDs are dependent on the amplitudes of the LNMs; i.e. they are not included as independent variables. References [14, 15] show that the quadratic manifold can output reliable results only when the assumption of the slow/fast decomposition holds (see Ref. [16]), i.e. the remaining modes should be stiffer than the reduced modes. In the FE context, the computational procedure of the MDs is not explicit, since some terms in the computational formula do not correspond to standard FE executions. Hence, a simplified version, static modal derivatives (SMDs), is introduced by neglecting the inertial effects, which can be applied to any commercial FE software [13].

In nonlinear analysis, the nonlinear normal modes (NNMs) represent an important concept as the extension to LNMs. The NNMs are firstly defined as synchronous periodic responses in a conservative system, and then relaxed to periodic, but not necessarily synchronous, responses [17,18,19], which provide a good metric for evaluating the ROM’s accuracy [20]. Meanwhile, on account of the concept of the invariant manifold, the NNM motion can be defined directly on the invariant manifold, which is tangent to the linear modal subspace at the equilibrium point. Using this concept, every component’s motion in a system can be expressed by a functional dependence of the displacement/velocity pairs in a set of invariant normal coordinates, and the ROM is constructed based on these invariant normal coordinates [21, 22]. Studies show that the ROM based on the invariant manifold is able to capture the system’s nonlinear phenomena accurately, e.g. hardening/softening behaviour [23] and internal resonance [24]. Besides, the invariant manifold can also be described and parametrised using the normal form theory, in which a nonlinear relationship between a set of new normal coordinates and the initial modal coordinates is bulit. The dynamics related to these new coordinates represent the motion on NNMs [23, 25]. Normally, the invariance relationship derived from normal form theory can be solved using the asymptotic expansion, whose validity in the case of the third expansion is discussed in Refs. [15, 23, 25]. Considering FE models with a large number of DoFs, the direct computation of nonlinear mapping from physical coordinates to invariant manifolds is derived from the normal form theory, which is named direct normal form [26, 27]. Using this technique, the cumbersome modal coordinate change and stiffness evaluation procedure in high-dimensional FE models can be avoided during the reduction process [26]. Meanwhile, the arbitrary order of expansion to calculate the nonlinear mapping from the FE discretisation is proposed to consider complex dynamic behaviours [28,29,30].

Besides the methods mentioned above, there are two indirect/non-intrusive methods for modal reduction in geometrically nonlinear structures, the enforced modal displacement (EMD) method and the applied modal force (AMF) method, which do not explicitly require the equations of motion. Unlike the rigorous mathematical framework in the manifold-based methods, both of these indirect methods use only the static dataset extracted from FE models to calculate the nonlinear coefficients in the ROM’s construction, therefore they are applicable to FE commercial software where the equations of motion are normally not available.

The EMD method, or the related stiffness evaluation procedure (STEP), was firstly introduced by Muravyov and Rizzi [31], and then developed by Perez et al. [32]. This method evaluates an FE model’s nonlinear modal stiffness coefficients using a set of modal displacements and the static forces required to reach these displacements. When applying the EMD method, all relevant modes coupling to the modes of interest, e.g. the bending modes and the coupled membrane modes, must be explicitly included in the reduction basis, otherwise, the insufficient size of the basis can cause a non-negligible error [20, 33]. This leads to a large number of modes in the reduction basis [32]. In recent studies, this STEP approach is more often used as a method to identify the coupling coefficients of nonlinear terms in an FE model instead of using it to construct the ROM [34, 35]. Starting from this STEP approach, the coupling coefficients which correspond to the modes that potentially exhibit dynamic interaction may be calculated for further reduction, e.g. using manifold-based methods [24]. In addition, two numerical characteristics in the STEP approach should be noticed. The first is that parameters identified from the STEP approach are not sensitive within a large displacement range [34, 36], and the second is the slow convergence with respect to the number of coupled modes in the reduction basis [34, 35]. The latter issue makes this method less appealing, as it’s difficult to identify all coupled modes in complex structures [37]. However, this issue can be overcome using different methods e.g. static modal derivatives [35], modified STEP method [35], dual modes [38] or companion modes [37].

The applied modal force (AMF) method, or implicit condensation (IC) method, was first discussed by McEwan et al. [39, 40]. The AMF method constructs the ROM using a set of static load cases imposed on an FE model and the corresponding displacements extracted from the static analysis. The ROM’s stiffness coefficients are then estimated using a regression analysis. In this method, only the modes of interest are included in the reduction basis as reduced modes, while the coupling effects of remaining modes can be condensed implicitly [37]. The dynamics of these condensed modes are then recovered using a recovering step, which, when combined with the IC method, leads to a more comprehensive model reduction procedure, which is named as ‘Implicit Condensation and Expansion’ (ICE) [41]. Compared with the STEP approach, a significant advantage of the IC/ICE method is its small volume reduction basis [35]. Nevertheless, the ROM’s coefficients estimated by the ICE method are sensitive to the distribution range of load cases controlled by the ‘scale factor’, and a proper scale factor needs to be selected carefully to ensure the ROM’s accuracy [20, 42].

To alleviate the variation in ROM’s coefficients, Nicolaidou et al. suggest that the highest term in the nonlinear restoring forces of ROMs should be higher than the counterpart in FE models, due to the quasi-static coupling between reduced and condensed modes, and they show that the parameters of higher-order ROMs are much less sensitive to the change of the scale factor [43]. Meanwhile, the introduction of higher-order ROMs is helpful to improve the ROM’s accuracy in terms of the backbone curve predictions in complex structures, e.g. the curved beam [44]. In earlier studies, the ICE method neglects the inertial contribution from the condensed modes, which leads to an incorrect result for structures with a large in-plane kinetic energy, e.g. the over-hardening behaviour prediction in a cantilever beam [14, 45]. Motivated by this fact, Reference [45] proposes the concept of ‘Inertial Compensation’ to consider the kinetic energy contributed by condensed modes. This extension can be constructed without adding computational cost compared to the original ICE method.

The ICE’s procedure described above is based on the static analysis and does not consider the dynamic interaction between the reduced modes and condensed modes [20], and it can only enable the accuracy of ROMs when the system fulfills the slow/fast decomposition [14, 24]. This suggests that a multi-mode ROM is required to capture dynamic interaction between modes in the full-order model. However, it is not trivial to identify these dynamically significant modes without a prior computation. To achieve this, Nicolaidou et al. introduce time-dependent terms, which represent the error of the quasi-static coupling relationship, to detect the dynamic interaction in the system efficiently [46]. Monitoring these errors allows for a modal selection strategy for developing a multi-mode ROM, since the mode with a large error is deemed as dynamically significant and should be added to the reduction basis. In addition, the analytical results inspired by this idea have also been discussed based on a general two-mode oscillator [47].

Besides using NNMs to evaluate the accuracy of ROMs [4, 45], recent studies demonstrate that the ROM’s ability to capture the static behaviour of an FE model is important to reproduce this FE model’s dynamic response [42, 44], which suggests that a ROM’s accuracy may be reflected by its capacity to capture the static behaviour.

In this study, we present a method to ensure the accuracy of ROMs without requiring dynamic FE analysis for validation. To be specific, the proposed method aims to capture the static behaviour of FE models to a high accuracy level within the range related to a given energy level. This objective is achieved by introducing a computationally efficient error metric, along with a strategy for selecting the additional load cases based on this metric. It is found that the proposed method can effectively alleviate the complexity of the construction of multi-mode ROMs in which the multi-dimensional fitting procedure is seen as a shortcoming of the ICE method in the past. To this end, the rest of the paper is organised as follows.

In Sect. 2, the procedure of the ICE method is reviewed, and a curved beam is utilised to demonstrate the limitation of the standard error measurement. Then, a method to construct a ROM within a specific fitting range, defined using energy, is described in Sect. 3. Here, an algorithm is proposed to ensure the accuracy of ROMs within this range, and an efficient error metric is proposed. This is first demonstrated for the single-mode case and later extended to the multi-mode case. Meanwhile, the characteristic of the error metric, in terms of guiding the load case selection to improve the ROM’s accuracy, is described. Finally, the generalisation of the proposed method to the higher-order case is given in Sect. 4.

2 Motivation

2.1 An overview of the implicit condensation and expansion (ICE) technique

In this section, we explore the evaluation and construction of a ROM under the ICE’s framework. In an FE model, a continuous system is discretised into N DoFs, and written as,

$$\begin{aligned} \textbf{M}\ddot{\textbf{x}}+\textbf{Kx}+ \tilde{\textbf{f}}_\textbf{x}{} \mathbf{(x)=\textbf{0}} \end{aligned}$$
(1)

where \(\textbf{x}\) is the \(N \times 1\) displacement vector in the physical space, \(\textbf{M}\), \(\textbf{K}\) are the \(N \times N\) mass and stiffness matrices, and \(\tilde{\textbf{f}}_\textbf{x}{} \mathbf{(x)}\) represents the \(N \times 1\) vector of the nonlinear restoring forcesFootnote 1. Due to the orthogonality between linear normal modes, this full-order model’s displacement in physical space is transformed into the linear modal space using,

$$\begin{aligned} \textbf{x}={\varvec{\Phi }} \textbf{q} \end{aligned}$$
(2)

where \(\textbf{q}\) is the \(N \times 1\) displacement vector in the modal space and \({\varvec{\Phi }}\) is the mass-normalised linear modeshape matrix with dimension \(N \times N\). The column vector \({\varvec{\phi }}_{i}\;(i=1 \sim N)\) in \({\varvec{\Phi }}\) is solved from the eigenvalue problem, \((\textbf{K}-\omega _{n,i}^{2}\textbf{M}){\varvec{\phi }}_{i}=0\), where \(\omega _{n,i}^2\) is the square of the linear natural frequency corresponding to this ith linear modeshape \(\varvec{\phi }_{i}\). Using Eq. (2), the matrices \(\textbf{M}\) and \(\textbf{K}\) can be fully uncoupled and Eq. (1) can be projected into the linear modal space,

$$\begin{aligned} {{{\ddot{\textbf{q}}}}+ {\varvec{\Lambda }} \textbf{q}}+\tilde{\textbf{f}}(\textbf{q})=\textbf{0} \end{aligned}$$
(3)

where \({\varvec{\Lambda }}\) is the diagonal \(N \times N\) matrix consisting of \(\omega _{n,i}^2\;(i=1 \sim N)\), and \(\tilde{\textbf{f}}(\textbf{q})={{\varvec{\Phi }}}^\textrm{T}\tilde{\textbf{f}}_\textbf{x}(\varvec{\Phi } \textbf{q})\) represents the nonlinear restoring forces in the modal space. It is noted that \(\tilde{\textbf{f}}(\textbf{q})\) is likely to be coupled when the FE model contains geometric, or other, nonlinear features – in FE models with geometric nonlinearities, \(\tilde{\textbf{f}}(\textbf{q})\) is normally described as the combination of quadratic and cubic polynomials that couple all coordinates in the displacement vector, \(\textbf{q}\) [6]. In addition, the algebraic form of \(\tilde{\textbf{f}}(\textbf{q})\) generally cannot be accessed in commercial FE software.

To reduce the full-order model, the reduced modes,(i.e. the modes forming the reduction basis), should be selected first. The modes of the FE model, \(\textbf{q}\), can be separated into two parts: (1) the dynamically important modes, \(\textbf{q}_\textbf{r}\), which are normally some low-frequency modes and contain the majority of the energy in the motion, (2) the remaining modes, \(\textbf{q}_\textbf{s}\), which can be viewed as being quasi-statically coupled to \(\textbf{q}_\textbf{r}\), induced by geometric nonlinearities [45]. Based on these, Eq. (3) is rewritten as,

$$\begin{aligned} \begin{bmatrix} { \ddot{\textbf{q}}}_\textbf{r} \\ { \ddot{\textbf{q}}}_\textbf{s} \\ \end{bmatrix}+ \begin{bmatrix} \varvec{\Lambda }_\textbf{r}&{}\textbf{0 }\\ \textbf{0}&{}\varvec{\Lambda }_\textbf{s} \\ \end{bmatrix}\begin{bmatrix} \mathbf{q_r} \\ \mathbf{q_s} \\ \end{bmatrix}+\begin{bmatrix} {\tilde{\textbf{f}}_\textbf{r}}(\mathbf{q_r},\mathbf{q_s}) \\ {\tilde{\textbf{f}}_\textbf{s}}(\mathbf{q_r},\mathbf{q_s}) \\ \end{bmatrix}=\begin{bmatrix} \textbf{0} \\ \textbf{0 }\\ \end{bmatrix} \end{aligned}$$
(4)

where \(\mathbf{q_{r}}\) and \(\mathbf{q_{s}}\) are the \(R \times 1\) and \(S \times 1\) vectors, respectively. The ICE method assumes that the dynamics of \(\textbf{q}_\textbf{r}\) can be governed by a lower dimensional reduced-order model (ROM) which consists of a reduced set of modes,

$$\begin{aligned} \ddot{\textbf{r}}+ {\varvec{\Lambda }}_\textbf{r} \textbf{r}+\tilde{\textbf{f}}_{n}(\textbf{r})=\textbf{0} \end{aligned}$$
(5)

where \(\textbf{r} \approx \mathbf{q_{r}}\), and \({\varvec{\Lambda }_\textbf{r}}\) is the diagonal \(R \times R\) matrix representing the square of ROM’s linear natural frequencies, \(\omega _{n,ri}^2\), \(\tilde{\textbf{f}}_{n}(\textbf{r})\) is a \(R \times 1\) vector representing the ROM’s nonlinear restoring forces. Normally, \(\tilde{\textbf{f}}_{n}(\textbf{r})\) can be approximated by an nth-order polynomial whose parameters must be estimated. Similarly, the quasi-static coupling relationship between \(\mathbf{q_{r}}\) and \(\mathbf{q_{s}}\) can be approximated as a vector function, \(\mathbf{s=g(r)}\), where we treat \(\textbf{s} \approx \mathbf{q_{s}}\).Footnote 2

According to the ICE’s framework, the static load cases, \( {\hat{\textbf{F}}}_{\textbf{r}}\), in the modal space are projected into the physical space,

$$\begin{aligned} {\hat{\mathbf{{F}}}_{\textbf{x}}=\textbf{M}\varvec{\Phi }_\textbf{r}\hat{\mathbf{{F}}}_{\textbf{r}}} \end{aligned}$$
(6)

where \({\varvec{\Phi }}_\textbf{r}\) contains the modeshapes related to \(\textbf{q}_r\), and the variable with “ \(\hat{}\) ” denotes that this variable is related to an FE execution in this paper. Then, \(\hat{\mathbf{{F}}}_{\textbf{x}}\) is imposed on the FE model, and the static FE analysis is executed in commercial FE software (e.g. Abaqus) to solve the static equation,

$$\begin{aligned} \textbf{K}\hat{\mathbf{{x}}}+{\tilde{\textbf{f}}_\textbf{x}}(\hat{\mathbf{{x}}})=\hat{\mathbf{{F}}}_{\textbf{x}} \end{aligned}$$
(7)

where the resulting physical displacement, \(\hat{\mathbf{{x}}}\), will be extracted. After running the static FE analysis, the corresponding modal displacement, \(\hat{\mathbf{{r}}}\), is obtainedFootnote 3,

$$\begin{aligned} \hat{\mathbf{{r}}}={\varvec{\Phi }}_\textbf{r}^\textrm{T}{} \textbf{M}\hat{\mathbf{{x}}} \end{aligned}$$
(8)

Finally, the static dataset, \(\{\hat{\mathbf{{r}}},\hat{\mathbf{{F}}}_{\textbf{r}}\}\), is substituted into the static equation of the ROM to estimate parameters in the ROM’s nonlinear restoring force, \(\tilde{\textbf{f}}_{n}(\textbf{r})\), via the least-square regression,

$$\begin{aligned} \tilde{\textbf{f}}_{n}(\hat{\mathbf{{r}}})=\hat{\mathbf{{F}}}_{\textbf{r}}-{\varvec{\Lambda }_\textbf{r}}\hat{\mathbf{{r}}} \end{aligned}$$
(9)

In previous work, it is noted that the ROM’s performance is sensitive to the scale factor if the order of the ROM is insufficient [20, 42], but this issue can be alleviated by introducing higher-order ROMs [43]. However, the accuracy of higher-order ROMs is easily violated by the selection of load cases and the fitting procedure, especially when the ROM is composed of multiple modes [24]. In this paper, we propose a method to ensure the ROM’s accuracy within a given energy level. We then demonstrate that this method can effectively be applied to the construction of higher-order and multi-mode ROMs.

2.2 Motivating example: a curved beam

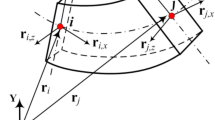
To discuss the issues around the current ICE framework, a motivating example in which the ICE method is applied to an Abaqus FE model of a geometrically nonlinear curved beam is presented, which is a segment of a circle. The schematic and main parameters of this curved beam are presented in Fig. 1 and Table 1, respectively. Based on these parameters, this curved beam is modelled using 130 beam elements of type B32, resulting in 1554 DoFs.

Fig. 1
figure 1

The schematic of the curved beam

Full size image
Table 1 The main parameters of the curved beam
Full size table

In this section, only the 1st mode is included in the ROM, and the natural frequency of this mode is \(\omega _{n,r1}=233.28\;\mathrm{rad\;s^{-1}}\). For this single-mode ROM case, the restoring force, \(f_{n}(r_{1})\), is approximated as the polynomial,

$$\begin{aligned} f_{n}(r_{1})= & {} \omega _{n,r1}^{2}r_{1}+{\tilde{f}}_{n}(r_1)\nonumber \\= & {} \omega _{n,r1}^{2}r_{1}+\sum _{k=2}^{n} (k+1)A_{k}r_{1}^{k} \end{aligned}$$
(10)

Note that \((k+1)\) term results from Lagrangian energy considerations – this is described in Sect. 3. To estimate the ROM’s parameters, \(A_{k}\), in the nonlinear restoring force, \({\tilde{f}}_{n}(r_1)\), 10 static load cases (denoted \(\hat{\mathbf{{F}}}_{r1}\)) are applied. These load cases, which are evenly distributed between \(-100\) and 100, and the corresponding modal displacements, \(\hat{\mathbf{{r}}}_{1}\), generate the static dataset, \(\{\hat{\mathbf{{r}}}_{1},\hat{\mathbf{{F}}}_{r1}\}\), that is used in the fitting procedure. As described in Ref. [44], the ROM’s accuracy is dependent on the fitting results, and a good performance in the backbone curve prediction requires a small fitting error. In this paper, the fitting error of an nth-order ROM is evaluated by the error function,

$$\begin{aligned} {\hat{\varepsilon }}_{n}(r_1)=\frac{\Vert f_{n}(r_1)-{\hat{f}}_\textrm{FE}(r_1)\Vert }{\textrm{max}\Vert {\hat{f}}_\textrm{FE}(r_1)\Vert } \end{aligned}$$
(11)

where \({\hat{\varepsilon }}_{n}(r_1)\) is the error representing the fitting result in the ROM’s construction, \(f_{n}(r_1)\) and \({\hat{f}}_\textrm{FE}(r_1)\) are the restoring forces used in the ROM (see Eq. (10)) and the true modal force extracted from the FE model, respectively. Once \(f_{n}(r_1)\) is known, the fitting result can be evaluated from Eq. (11). Here, we term \({\hat{\varepsilon }}_{n}(r_1)\) as the ‘FE error metric’, as this error is benchmarked against the FE model. Note that, in practice, \({\hat{\varepsilon }}_{n}(r_1)\) is not a convenient metric as it requires extra load cases across the range of interest, denoted as dots in Fig. 2a, rather than just the 10 data points used to construct the ROM. The extraction of these extra load cases increases the computational burden, i.e. more FE static analyses are required, especially in multi-mode cases. In the next section, a less computationally intensive approach is introduced to alleviate the computational burden.

Using the static dataset generated from these 10 load cases, Fig. 2 shows the fitting error, \({\hat{\varepsilon }}_{n}(r_1)\), given by Eq. (11), and backbone curves found using the numerical continuation toolbox COCO [49]. In Fig. 2a, \({\hat{\varepsilon }}_{n}(r_1)\) is evaluated within the displacement range covered by \(\hat{\textbf{r}}_{1}\), which shows a strongly asymmetric behaviour. In this range, \({\hat{\varepsilon }}_{n}(r_1)\) significantly decreases as the ROM’s order increases from 3 to 11, and the 11th-order ROM has the smallest fitting error. Meanwhile, it is found that, in Fig. 2b, the backbone curves converge as the order of the ROM increases. This is to be expected as the accuracy of the fitting is improved as the order increases (see Fig. 2a).

Fig. 2
figure 2

The fitting error analysis and backbone curve comparison between 3rd, 5th, 7th, 9th and 11th-order ROMs. The left panel is in the projection of the first static modal displacement, \(r_1\), against the error distributions, \({\hat{\varepsilon }}_{n}(r_1)\), described by Eq. (11). Note that the dots in panel a indicates that \({\hat{\varepsilon }}_{n}(r_1)\) is calculated at discrete points, corresponding to extracted load cases. Panel b is in the projection of the response frequency, \(\Omega \), against the first modal displacement amplitude, \(R_1\), for different order ROMs

Full size image

In addition, an important consideration is the range over which the static behaviour of an FE model needs to be captured accurately (referred to here as the fitting range), which has yet to be defined clearly. If this range is too large, an excessively high-order ROM will be required. More critically, if the range is too small, the ROM’s accuracy cannot be guaranteed. According to the theory of NNMs, a point on the backbone curve represents a NNM motion, and the range of this motion, i.e. velocities and displacements of the coordinates, is limited by the energy of the system, which consists of the kinetic energy and potential energy. The forces coupling the modes are only related to the potential energy. Motivated by this, the method for constructing a ROM based on the energy level will be proposed in this paper, which dictates the fitting range. To illustrate the relationship, Fig. 3 depicts a schematic representation of the energy level across the fitting range for a single-mode case. Note that the extreme amplitudes towards the positive and negative directions have the same potential energy, \(E_\textrm{level}\), but not necessary the same displacement or load amplitude, allowing structures with asymmetry to be accurately captured. We propose that the ROM should be accurate within the fitting range, which determines the ROM’s validity range, i.e. this fitting range can cover all possible motions of NNMs up to \(E_\textrm{level}\)Footnote 4. In the following sections we develop a strategy to find additional static load cases by exploiting the fitting range, such that we can ensure the ROM’s accuracy within a given energy level.

Fig. 3
figure 3

The relationship between the energy level and fitting range. The blue curve is the potential function, \(V(r_1)\), at which the modal displacements, \(r_{1,p}\) and \(r_{1,m}\), have the same energy level, \(E_\textrm{level}\), defining the fitting range, but \(r_{1,p}\) is not necessarily equal to \(r_{1,m}\). The red dots on the \(r_{1}\) and \(F_{r1}\)-axis denote load cases in the static dataset, \(\{{\hat{\textbf{r}}}_{1},\hat{\mathbf{{F}}}_{r1}\}\), used for the fitting procedure

Full size image

According to Fig. 2, a higher-order ROM can reach a smaller fitting error; however, the fitting procedure becomes more complex as well due to the increasing parameters. Considering this issue, the following section first starts from a 5th-order ROM to demonstrate the proposed method, and the construction of higher-order ROMs would be discussed in Sect. 4.

3 Using energy to define the fitting range

In this section, we propose a method to construct an accurate ROM within the fitting range defined by energy. For a given energy level, we first use the potential energy function in a ROM to specify the range for the fitting procedure in which the minimum number of load cases for constructing a ROM is illustrated. Then, a computationally efficient error metric is proposed, as the extension of Eq. (11), to evaluate the accuracy of ROMs within this fitting range. This error metric is used to find additional load cases for enriching the static dataset. By combining the error metric and the strategy of the load case selection, we propose a method for constructing ROMs that can ensure the desired accuracy up to the energy level. The curved beam used in Sect. 2 is used to illustrate the proposed method’s application to the single-mode case and the extension to the multi-mode case, as discussed in Sects. 3.2 and 3.3.

3.1 The energy level and static dataset in the ROM’s construction

3.1.1 The definition of the energy level

Ideally, we would describe the energy in terms of the FE model’s potential energy function; however this is non-trivial to obtain, and we will consider the potential energy function of ROMs. For an nth-order ROM, we write the potential energy as \(V(\textbf{r})\), which can be approximated as a polynomial function, and using the given energy level, \(E_\textrm{level}\), the fitting range is given by,

$$\begin{aligned} 0 \le V(\textbf{r}) \le E_\textrm{level} \end{aligned}$$
(12)

Considering Eq. (5), the relationship between the ROM’s potential energy, \(V(\textbf{r})\), and restoring forces, \(\textbf{f}_{n}(\textbf{r})\), is given by,

$$\begin{aligned} \textbf{f}_{n}(\textbf{r})=\frac{\partial V(\textbf{r})}{\partial \textbf{r}}={\varvec{\Lambda }_\textbf{r}{} \textbf{r}}+ \tilde{\textbf{f}}_{n}(\textbf{r}) \end{aligned}$$
(13)

In the single-mode case, the potential energy for an nth-order ROM may be written as,

$$\begin{aligned} V(r_1)=\frac{1}{2}\omega _{n,r1}^2r_{1}^2+A_{2}r_{1}^3+\cdots +A_{n}r_{1}^{n+1} \end{aligned}$$
(14)

which, using Eq. (13), leads to the ROM’s restoring force,

$$\begin{aligned} \begin{aligned} f_{n}(r_1)=&\omega _{n,r1}^2r_1+3A_2r_{1}^2\\&+4A_3r_{1}^3+\cdots +(n+1)A_{n}r_{1}^{n}\\ \end{aligned} \end{aligned}$$
(15)

Note that \(A_{i}\;(i=2 \sim n)\) are parameters that need to be estimated using the static dataset. Similarly, the nth-order ROM’s potential energy in the two-mode case is written as,

$$\begin{aligned} V(r_1,r_2)= & {} \frac{1}{2}\omega _{n,r1}^2r_{1}^2+\frac{1}{2}\omega _{n,r2}^2r_{2}^2\nonumber \\{} & {} +A_{2,1}r_{1}^{3}+A_{2,2}r_{1}^{2}r_{2}+A_{2,3}r_{1}r_{2}^2+A_{2,4}r_{2}^{3}\nonumber \\{} & {} +A_{3,1}r_{1}^{4}+A_{3,2}r_{1}^{3}r_{2}+\cdots +A_{3,4}r_{1}r_{2}^{3}\nonumber \\{} & {} +A_{3,5}r_{2}^{4}+\cdots \nonumber \\{} & {} +A_{n,1}r_{1}^{n+1}+\cdots +A_{n,n+2}r_{2}^{n+1} \end{aligned}$$
(16)

This will lead to the restoring forces,

$$\begin{aligned} \left\{ \begin{aligned} f_{n,1}(r_1,&r_2)=\omega _{n,r1}^2r_1\\&+3A_{2,1}r_{1}^2+2A_{2,2}r_{1}r_{2}+A_{2,3}r_{2}^2+\cdots \\&+(n+1)A_{n,1}r_{1}^n+ \cdots + A_{n,n+1}r_{2}^{n}\\ f_{n,2}(r_1,&r_2)=\omega _{n,r2}^2r_2\\&+A_{2,2}r_{1}^2+2A_{2,3}r_{1}r_{2}+3A_{2,4}r_{2}^2+\cdots \\&+ A_{n,2}r_{1}^n+ \cdots + (n+1)A_{n,n+2}r_{2}^n\\ \end{aligned}\right. \nonumber \\ \end{aligned}$$
(17)

where \(A_{i,j}\;(i=2 \sim n,j=1 \sim i+2)\) need to be estimated. It can be seen that some parameters appear in both restoring force expressions (e.g. \(A_{2,2}\)), which arises from the Lagrangian derivation of the force from the energy function, Eq. (16), and ensures energy balances across these force functions. Considering these parameter relationships in the construction of multi-mode ROMs can make the results more stable and robust, and is known as the ‘Constrained IC’ method [51]. This also allows the ROM’s potential energy and the fitting range to be found after the ROM’s parameters are estimated (e.g. using Eqs. (16) and (12) in the two-mode case).

3.1.2 The minimum number of load cases

In the ICE method, the fitting procedure requires that the number of static relationships, which can be seen as the number of static equations in Eq. (9), contributed by load cases in the static dataset, \(\{\hat{\mathbf{{r}}},\hat{\mathbf{{F}}}_{\textbf{r}}\}\), should be at least equal to the number of independent parameters in the ROM. For example, a single-mode 3rd-order ROM has 2 independent parameters (see Eq. (15)), \(A_2\), \(A_3\). This indicates at least 2 unique static relationships should be included in the static dataset, such that \(A_2\), \(A_{3}\) may be computed using,

$$\begin{aligned} \left\{ \begin{aligned} 3A_2{\hat{r}}_{1(1)}^2+4A_{3}{\hat{r}}_{1(1)}^3&={\hat{F}}_{r1(1)}-\omega _{n,r1}^2{\hat{r}}_{1(1)}\\ 3A_2{\hat{r}}_{1(2)}^2+4A_{3}{\hat{r}}_{1(2)}^3&={\hat{F}}_{r1(2)}-\omega _{n,r1}^2{\hat{r}}_{1(2)}\\ \end{aligned}\right. \end{aligned}$$
(18)

where \(\{{\hat{r}}_{1(1)},{\hat{F}}_{r1(1)}\}\), \(\{{\hat{r}}_{1(2)},{\hat{F}}_{r1(2)}\}\) are two unique load cases in the static dataset.

When considering the two-mode case, the number of independent parameters in a 3rd-order ROM increases to 9, and each load case contributes two static relationships in Eq.  (9) (see Appendix A). Hence, at least 5 load cases should be used for constructing a 3rd-order ROM in the two-mode case. Table 2 summarises the relationship between the ROM’s independent parameters, \(N_{f}\), and the minimum number of load cases, \(N_{m}\), for the construction of ROMs. Note that a similar procedure may be followed for a case with a higher number of modes.

Table 2 The number of independent parameters (\(N_f\)) and minimum number of load cases (\(N_{m}\)) in the construction of ROMs
Full size table

3.2 Construction and evaluation of a single-mode ROM

3.2.1 An efficient metric to evaluate a ROM’s accuracy

As previously mentioned, the FE error metric given in Eq. (11) is not computationally efficient for evaluating the accuracy of ROMs, as extra validation load cases are required. In this section, an alternative error metric is proposed. This exploits the observation that a higher-order ROM (with a higher-order polynomial) is able to capture the restoring force with greater accuracy [43, 44]. Motivated by this fact, \({\hat{f}}_\textrm{FE}(r_1)\) (i.e. the true modal force extracted from the FE model in Eq. (11)) is approximated by \(f_{n+2}(r_1)\), i.e. the restoring force in a ROM with order \((n+2)\). As such, the error function Eq. (11) can be approximated as,

$$\begin{aligned} {\hat{\varepsilon }}_{n}(r_1)\approx \varepsilon _{n}(r_1)=\frac{\Vert f_{n}(r_1)-f_{n+2}(r_1)\Vert }{\textrm{max}\Vert f_{n+2}(r_1)\Vert } \end{aligned}$$
(19)

Compared with Eq. (11), computing Eq. (19) is much more efficient, as it does not require extra load cases from the FE model beyond the necessary load cases to fit a ROM of order \((n+2)\) (see Table 2). If the ROM’s order is sufficient, a small maximum fitting error, \(\textrm{max}\{\varepsilon _{n}(r_1)\}\), suggests that ROMs of order n and \((n+2)\) are both accurate.

Fig. 4
figure 4

The main algorithm of the proposed method for the construction and evaluation of ROMs. Note that this is generally applicable for all cases, and the technical details in the single-mode case and multi-mode case are illustrated in Sects. 3.2 and 3.3, respectively

Full size image

3.2.2 Description of the proposed algorithm

The construction and evaluation of ROMs based on energy level, \(E_\textrm{level}\), is discussed using an approximate error metric,Footnote 5 \(\varepsilon _{n}(\textbf{r})\). After the parameters of the ROM are estimated, two extra procedures are conducted: (1) quantifying the fitting error using the error metric, \(\varepsilon _{n}(\textbf{r})\),  (2) identifying additional load cases to improve the accuracy, if necessary. After the FE model’s structural parameters (i.e. mass and stiffness matrices) and modal properties (i.e. frequencies and modeshapes) are known, the algorithm to construct an accurate ROM is presented in Fig. 4. Technical details in some of the steps for the single-mode caseFootnote 6 are:

  1. 1.

    In Step (2), the number of load cases in the initial load dataset should at least match the independent parameters, \(N_{f}\), in the ROM with order \((n+2)\) (see Table 2). Here, we select these load cases based on the initial assumption that the system is linear (as no nonlinear parameters are predicted at this stage); hence energy level is assumed to be given by the linear energy formula,

    $$\begin{aligned} \begin{aligned} E_\textrm{level}=&\frac{1}{2}\omega _{n,r1}^{2}r_{1}^2=\frac{F_{r1}^2}{2\omega _{n,r1}^2} \end{aligned} \end{aligned}$$
    (20)

    In this paper, the initial load cases are then evenly distributed between \(-\sqrt{2\omega _{n,r1}^2E_\textrm{level}}\) and \(\sqrt{2\omega _{n,r1}^2E_\textrm{level}}\).

  2. 2.

    Steps (3) and (9c) represent the procedure related to static FE analyses. In this procedure, the load cases, \(\hat{\mathbf{{F}}}_{\textbf{r}}\) (or \(\hat{\mathbf{{F}}}_{\textbf{r},\textrm{add}}\)), are transformed into the physical space for imposing on the FE model, and then the modal displacement, \(\hat{\mathbf{{r}}}\) (or \(\hat{\mathbf{{r}}}_\textrm{add}\)), for generating the static dataset, \(\{\hat{\mathbf{{r}}},\hat{\mathbf{{F}}}_{\textbf{r}}\}\) (or \(\{\hat{\mathbf{{r}}}_\textrm{add},\hat{\mathbf{{F}}}_{\textbf{r},\textrm{add}}\}\)), is extracted. The corresponding equations refer to Eqs. (6)–(8).

  3. 3.

    In Step (9b), the additional load case, \(\hat{\mathbf{{F}}}_{\textbf{r},\textrm{add}}\), are calculated using the maximum error point, \(\textbf{r}_\textrm{max}\), which is given by \(\hat{\mathbf{{F}}}_{\textbf{r},\textrm{add}}={\varvec{\Lambda }}_\textbf{r}{} \textbf{r}_\textrm{max}+ {\tilde{\textbf{f}}}_{n}(\textbf{r}_\textrm{max})\).

3.2.3 Application to an FE model

To illustrate the validity of the proposed algorithm, a single-mode ROM of a curved beam is constructed. This curved beam’s schematic and main parameters have been presented in Sect. 2 (see Fig. 1 and Table 1). In this case, the ROM only consists of the 1st mode, \(r_{1}\), and the related natural frequency is \(\omega _{n,r1}=233.28\;\mathrm{rad\;s}^{-1}\). According to Fig. 2, a 5th-order ROM is firstly considered to demonstrate the proposed algorithm given in Fig. 4 due to the simpler fitting procedure. The application of this algorithm to the higher-order (11th-order) case is investigated in Sect. 4. The energy level, \(E_\textrm{level}\), is set to \(5 \times 10^{-2}\;J\) in this example.

Following the procedure outlined in Sect. 3.2.2, the initial load cases are selected between \(-\sqrt{2\omega _{n,r1}^2E_\textrm{level}}\) and \(\sqrt{2\omega _{n,r1}^2E_\textrm{level}}\), which is presented schematically in Fig. 5. Once the initial load dataset is determined, a 5th-order ROM can be constructed following the algorithm shown in Fig. 4.

Figure 6 shows the distribution of the fitting error represented by two error metrics, \({\hat{\varepsilon }}_{5}(r_1)\) and \(\varepsilon _{5}(r_1)\), under different static datasets, \(S_{i}\) \((i=1 \sim 5)\). The initial load cases are applied and the resulting displacement components are represented by black circles in Fig. 6a. The initial static dataset, \(S_{1}\), is then used to estimate the parameters in the restoring force, \(f_{n}(r_1)\), of ROMs with order of \(n=5\) and 7. These force functions are then used to compute the error metric, \(\varepsilon _{5}(r_1)\), represented by the light blue line in Fig. 6a. Note that the results are only considered within the fitting range (given by the computed energy). The maximum error point, representing the maximum fitting error, \(\textrm{max}\{\varepsilon _{5}(r_1)\}\), is then selected (red circle in Fig. 6a) and the location of this point, \(r_\textrm{max}\), is substituted into \(f_{5}(r_1)\), i.e. \(\omega _{n,r1}^{2}r_{1}+{\tilde{f}}_{5}(r_1)\), to identify the additional load case, \(F_{r1,\textrm{add}}\).

Fig. 5
figure 5

The load cases in the initial load dataset

Full size image
Fig. 6
figure 6

The fitting result in the single-mode ROM’s construction. In each panel, the light blue curve and green dots indicate the distribution of the error metric, \(\varepsilon _{5}(r_1)\), and the FE error metric, \({\hat{\varepsilon }}_{5}(r_1)\), which are calculated using Eq. (19) and Eq. (11), respectively. The black circles denote the load cases used to construct the ROM, while the red circle represents the maximum error point for determining the additional load case, \({\hat{F}}_{r1,\textrm{add}}\)

Full size image

Meanwhile, the FE error metric, \({\hat{\varepsilon }}_{5}(r_1)\), is also calculated for comparison where additional FE analyses are required to extract extra load cases, denoted as green dots, covering the fitting range. The black dashed line denotes the critical error, \(\varepsilon _\textrm{cri}\), which is set as \(2 \times 10^{-3}\). After \({\hat{F}}_{r1,\textrm{add}}\) is found, the corresponding displacement, \({\hat{r}}_{1,\textrm{add}}\), is obtained by a single static FE analysis, which leads to the enriched static dataset, \(S_{2}\), according to Step (9d). The fitting result under \(S_{2}\) is presented in Fig. 6b where \(\textrm{max}\{\varepsilon _{5}(r_1)\}\) is smaller when compared with the value in Fig. 6a. Following the same procedure, more load cases can be found, and it is shown that, when the static dataset evolves to \(S_{5}\), \(\textrm{max}\{\varepsilon _{5}(r_1)\}\) is smaller than \(\varepsilon _\textrm{cri}\) (see Fig. 6e).

During this process, the maximum value of the FE error metric, \(\textrm{max}\{{\hat{\varepsilon }}_{5}(r_1)\}\), also decreases until it is smaller than \(\varepsilon _\textrm{cri}\) in the 5th iteration. As \(\textrm{max}\{{\hat{\varepsilon }}_{5}(r_1)\}\) decreases, \({\hat{\varepsilon }}_{5}(r_1)\) converges to the error metric, \(\varepsilon _{5}(r_1)\), e.g. they are much closer in Fig. 6e than in Fig. 6a within the fitting range. This indicates the additional load case has improved the accuracy of the restoring force, \(f_{5}(r_1)\).

Fig. 7
figure 7

The ROM’s construction in the single-mode case. Panel a shows the number of static analyses, \(N_\textrm{st}\), against the maximum fitting error, \(\textrm{max}\{\varepsilon _{5}(r_1)\}\). The dashed black line denotes the critical error, \(\varepsilon _\textrm{cri}\). Panel b shows the response frequency, \(\Omega \), against to the ROM’s maximum displacement amplitude, \(R_1\), under different static datasets (marked as \(S_1\), \(S_2\), \(S_3\), \(S_4\), \(S_5\), \(S_{25}\) in panel a)

Full size image

Figure 7a depicts the relationship between the maximum fitting error, \(\textrm{max}\{\varepsilon _{5}(r_1)\}\), and the number of static analyses, \(N_\textrm{st}\), for a number of iterations under the proposed algorithm. It is found that \(\textrm{max}\{\varepsilon _{5}(r_1)\}\) decreases rapidly as additional load cases enrich the static dataset. However, the new additional load cases do not reduce \(\textrm{max}\{\varepsilon _{5}(r_1)\}\) significantly after the 5th iteration, corresponding to the static dataset \(S_{5}\). This suggests that the limit of accuracy of the 5th-order ROM has been reached. If a smaller critical error is required, a higher-order ROM should be considered, which is discussed further in the construction of multi-mode ROMs in Sect. 4.

Figure 7b compares the backbone curves of 5th-order ROMs which have been found by fitting to the static datasets \(S_1 \sim S_{5}\) and \(S_{25}\). As the ROMs are only valid up to the energy level, \(E_\textrm{level}\), the backbone curves are terminated at this energy, indicated by circles. From this figure, it is noted that the backbone curves from \(S_{1}\) to \(S_{5}\) become closer to the backbone curve generated by \(S_{25}\), which might be seen as a baseline for comparison because of the converged value of \(\textrm{max}\{\varepsilon _{5}(r_1)\}\) in Fig. 7a. Compared with \(S_{1}\) to \(S_{3}\), the backbone curves generated by \(S_4\) and \(S_{5}\) are more consistent with those generated by \(S_{25}\). These results are to be expected as \(\textrm{max}\{\varepsilon _{5}(r_1)\}\) decreases from \(S_1\) to \(S_5\) in Fig. 7a. As defined in Fig. 4, the algorithm is terminated at \(i=5\) and the ROM constructed using dataset \(S_5\) is deemed as accurate as it meets the predefined critical error level.

To summarise, the algorithm outlined in Fig. 4 provides an effective method to construct a ROM of the FE model. The proposed approximate error, \(\varepsilon _{n}(\textbf{r})\), is utilised as a measurable metric to evaluate the ROM’s accuracy before calculating ROM’s backbone curves. Also, the proposed algorithm provides a means for selecting additional load cases to improve the ROM’s accuracy. These characteristics are discussed further in the construction of multi-mode ROMs in the following subsection.

3.3 Extending the proposed method to the multi-mode case

3.3.1 Definitions for the multi-mode case

In the multi-mode case, the number of independent parameters, \(N_{f}\), and the minimum number of load cases, \(N_{m}\), are both much larger than the values in the single-mode case (see Table 2). Note that many FE packages utilise incremental load steps to analyse nonlinear static problems, and are able to output the data of all incremental steps, e.g. Abaqus [52]. Hence, the data from all increments are utilised to generate the static dataset, \(\{\hat{\mathbf{{r}}},\hat{\mathbf{{F}}}_{\textbf{r}}\}\), to ensure that the total number of load cases in the static dataset satisfies the requirement described in Sect. 3.1.2 whilst reducing the number of the nonlinear FE analyses required. In this paper, we denote the final incremental load steps as ‘Target points’, and the remaining points as ‘Intermediate points’.

To extend the proposed method to the multi-mode case, the approximate error metric, \(\varepsilon _{n}(\textbf{r})\), is calculated for all reduced modes. For an nth-order ROM with R modes, the error metric in the ith (\(i=1 \sim R\)) reduced mode can be defined as,

$$\begin{aligned} \varepsilon _{n,i}(\textbf{r})=\frac{\Vert f_{n,i}(\textbf{r})-f_{n+2,i}(\textbf{r})\Vert }{\textrm{max}\Vert f_{n+2,i}(\textbf{r})\Vert } \end{aligned}$$
(21)

where \(\textbf{r}=(r_1,r_2,\cdots ,r_R)^\textrm{T}\), and where \(f_{n,i}(\textbf{r})\) and \(f_{n+2,i}(\textbf{r})\) are the restoring forces in ith mode of the ROMs with order n and \((n+2)\), respectively. With reference to Fig. 4, the necessary technical details in terms of the multi-mode case are clarified as,

  1. 1.

    In Step (2), the initial load dataset can be determined from the linear energy contour related to \(E_\textrm{level}\),

    $$\begin{aligned} E_\textrm{level}=\sum _{i=1}^{R}\frac{1}{2}\omega _{n,ri}^{2}r_{i}^2=\sum _{i=1}^{R}\frac{F_{ri}^2}{2\omega _{n,ri}^2} \end{aligned}$$
    (22)
  2. 2.

    In Step (7), the fitting error is calculated using Eq. (21) for all modes, while the fitting range is found by rejecting the data outside the energy bounds, such that the inequality Eq. (12) is not solved exactly. This is detailed in Sect. 4. Considering the variation of ROM’s parameters, which leads to the change of the fitting range, the load cases outside the fitting range are temporarily excluded from the fitting procedure and reused if they belong to the fitting range in future iterations.

  3. 3.

    From Step (8) to (9a), the largest error value across all the reduced modes, \(\textrm{max}\{\varepsilon _{n,i}(\textbf{r})\}\), is labelled as \(\textrm{max}\{\varepsilon _{n}(\textbf{r})\}\), whose location corresponds to the maximum error point, \(\textbf{r}_\textrm{max}=(r_{1,m},r_{2,m},\cdots ,r_{R,m})^\textrm{T}\).

  4. 4.

    In Steps (9b) and (9c), \(\textbf{r}_\textrm{max}\) is used to calculate the target point of additional load cases, \(\hat{\mathbf{{F}}}_{\textbf{r},\textrm{targ}}\) \(=({\hat{F}}_{r1,\textrm{targ}},{\hat{F}}_{r2,\textrm{targ}},\cdots ,{\hat{F}}_{rR,\textrm{targ}})^\textrm{T}\), imposed on the FE model for the next iteration, which is given by,

    $$\begin{aligned} \hat{\mathbf{{F}}}_{\textbf{r},\textrm{targ}}={\varvec{\Lambda }_\textbf{r}}{} \textbf{r}_\textrm{max}+{\tilde{\textbf{f}}}_{n}(\textbf{r}_\textrm{max}) \end{aligned}$$
    (23)

    Based on this new target point, the additional load cases, \({\hat{\mathbf{{r}}}_\textrm{add}}\) and \(\hat{\mathbf{{F}}}_{\textbf{r}, \textrm{add}}\), now include all incremental data generated by the static FE analysis.

3.3.2 Application to an FE model

The curved beam used in the single-mode case is also used here to demonstrate the algorithm’s application in the multi-mode case – specifically the two-mode case. The ROM now consists of the 1st and 3rd modes, which are denoted \(r_1\) and \(r_2\), respectively. The corresponding natural frequencies are \(\omega _{n,r1}=233.28\;\)\(\mathrm{rad\;s}^{-1}\) and \(\omega _{n,r2}=853.91\;\mathrm{rad\;s}^{-1}\). Here, a single static FE analysis is configured to include 20 incremental load steps, as discussed in Sect. 3.3.1.Footnote 7

According to Step (2) in Fig. 4, the load cases in the initial load dataset can be found from the linear energy contour related to the energy level, \(E_\textrm{level}\). Here, 4 target points related to these load cases are located at \((\pm {\hat{F}}_{r1},0)\) and \((0,\pm {\hat{F}}_{r2})\). Force amplitudes \({\hat{F}}_{r1}\) and \({\hat{F}}_{r2}\) are given by Eq. (22), i.e. \({\hat{F}}_{r1}=\sqrt{2\omega _{n,r1}^{2}E_\textrm{level}}\) and \({\hat{F}}_{r2}=\sqrt{2\omega _{n,r2}^{2}E_\textrm{level}}\). These target points lead to a total of \((19\;(\textit{ intermediate points})+1\;(\textit{ target point})) \times 4\;(\mathrm{static\;analysis}) = 80\) load cases. These load cases are represented by black dots in Fig. 8, and demonstrate that the intermediate points provide data across a range of energies, even though every target point is at a single energy.

Following Table 2, a 15th-order ROM may theoretically be generated from such a large initial load dataset, but a 5th-order ROM continues to be used here to demonstrate the application of the proposed method in the multi-mode case. The generalisation of this method to higher-order ROMs is discussed in the next section.

Fig. 8
figure 8

The load cases in the initial load dataset. The pink ellipse represents the linear energy contour given by Eq. ( 22), and black dots denote the load cases resulting from the FE analyses. The target points, relating to the final incremental load steps, are labelled as black circles

Full size image
Fig. 9
figure 9

The demonstration of the load case selection in the construction of multi-mode ROMs. Panels a and b show the cases under the 1st and 11th iteration, respectively. The blue ellipse-like loops represent the nonlinear energy contour related to the energy level, \(E_\textrm{level}\), projected in the \((F_{r1},F_{r2})\)-plane, calculated using Eqs. (12) and (13) for the relevant iteration. The pink ellipses represent the linear energy contour related to \(E_\textrm{level}\) for determining the initial load dataset. The black dots and circles represent the load cases in the static dataset and the corresponding target points, respectively. In these load cases, those points outside the fitting range are labelled as grey. The red circles in the panels denote the new target point, \(\hat{\mathbf{{F}}}_{\textbf{r},\textrm{targ}}\), given by Eq. (23), for generating additional load cases (red dots)

Full size image
Fig. 10
figure 10

The ROM’s construction in the two-mode case. Panel a shows the number of static analyses, \(N_\textrm{st}\), against the maximum fitting error, \(\textrm{max}\{\varepsilon _{5}(r_1,r_2)\}\). The dashed black line denotes the critical error, \(\varepsilon _\textrm{cri}\). Panels b and c show the response frequency, \(\Omega \), against the maximum displacement amplitude of the ROM’s first mode, \(R_1\), and second mode, \(R_2\), under different static datasets (marked as \(S_{1}\), \(S_{11}\), \(S_{27}\) in panel a, respectively)

Full size image

Similarly to the single-mode case, the algorithm given in Fig. 4 also instructs the additional load cases based on the maximum fitting error, \(\textrm{max}\{\varepsilon _{n}(\textbf{r})\}\), in the multi-mode case. Figure 9 presents the procedure of the load case selection under the 1st and 11th iteration, respectively. In Fig. 9a, after the ROM’s parameters are identified using the initial load cases (black dots), the maximum error point, \(\textbf{r}_\textrm{max}\), is found to calculate the new target point (red circle), \(\hat{\mathbf{{F}}}_{\textbf{r},\textrm{targ}}\), using Eq. (23), which leads to the additional load cases (red dots) by exploiting the incremental data. Following the algorithm, these additional load cases are incorporated in the existing load cases for the subsequent iterations. Figure 9b shows the result of the load case selection under the static dataset \(S_{11}\) where 10 target points have been found and the resulting load cases have been added in the static dataset. These additional load cases can reduce \(\textrm{max}\{{\hat{\varepsilon }}_{n}(\textbf{r})\}\), which is illustrated subsequently. Meanwhile, considering the variations of the ROM’s parameters, which leads to the change of the fitting range (or its mapping in the \((F_{r1},F_{r2})\)-plane), only the load cases within the fitting range are considered for the fitting range in the next iteration. Those points outside the fitting range, checked using Eq. (12), are excluded (see grey dots and circles in Fig. 9b).

Figure 10a depicts the relationship between the number of static analyses, \(N_\textrm{st}\), and the maximum fitting error, \(\max \{\varepsilon _{5}(r_1,r_2)\}\). This shows a steady decrease in \(\max \{\varepsilon _{5}(r_1,r_2)\}\) as additional load cases enrich the static dataset. The static dataset, \(S_{11}\), whose load cases have been presented in Fig. 9b, has an error, \(\max \{\varepsilon _{5}(r_1,r_2)\}\), below \(4 \times 10^{-4}\) (the critical error selected for this example), which indicates the algorithm in Fig. 4 can be terminated here and an accurate ROM can be generated; however, we show the effect of further data leading towards convergence for illustration. After \(S_{11}\), the new additional load cases do not reduce \(\max \{\varepsilon _{5}(r_1,r_2)\}\) significantly, which implies that a higher-order ROM would need to be considered if a smaller fitting error is required.

Figure 10b and 10c compares the backbone curves of the ROMs constructed by static datasets \(S_{1}\), \(S_{11}\), and \(S_{27}\), and show that the backbone curves exhibit an internal resonance branch. Throughout the captured responses, the \(S_{11}\) backbone curves show a good agreement to the \(S_{27}\) backbone curves. Meanwhile, the \(S_{1}\) backbone curves show a less good agreement at the internal resonance and high energy region, which corresponds to a larger fitting error in Fig. 10a predicted by the proposed method.

3.3.3 Comparing load case selection methods

In previous analysis, it has been seen that additional load cases can improve the accuracy of the ROM (see Figs. 7a and 10a). However, it is unclear whether this improvement is due to the strategic selection of additional load cases, as proposed in the algorithm, or simply the increased volume of data. To explore this, the characteristics of different load case selection methods are compared in this section. Three methods are used for comparison: (1) where the load cases are determined by scale factors, (2) where the load cases are determined randomly, (3) where the load cases are determined using \(\max \{\varepsilon _{n}(\textbf{r})\}\), i.e. the proposed algorithm.

Considering the method based on scale factors, in the single-mode case, there is a scale factor that can produce the optimal results [20, 42], while the optimal scale factors in the two-mode case refer to searching in the \((F_{r1},F_{r2})\)-plane, which is not feasible in practice. Here, we simplify this procedure to demonstrate the characteristics of this method in the multi-mode case.

Assuming that the force amplitudes of target points in load cases, \({\hat{F}}_{r1}\) and \({\hat{F}}_{r2}\), controlled by a single scale factor, \(F_{s}\), are given by,

$$\begin{aligned} \left\{ \begin{aligned} {\hat{F}}_{r1}=F_{s}F_{r1,0}\\ {\hat{F}}_{r2}=F_{s}F_{r2,0} \end{aligned} \right. \end{aligned}$$
(24)

where \(F_{r1,0}\) and \(F_{r2,0}\) are linked to the linear energy contour at the energy level, \(E_\textrm{level}\), which is given by Eq. (22), i.e. \(F_{r1,0}=\sqrt{2\omega _{n,r1}^{2}E_\textrm{level}}\) and \(F_{r2,0}=\sqrt{2\omega _{n,r2}^{2}E_\textrm{level}}\). When \({\hat{F}}_{r1}\) and \({\hat{F}}_{r2}\) are both non-zero, a reduction factor, \(\dfrac{1}{2}\), is utilised, i.e. \(\{\dfrac{1}{2}{\hat{F}}_{r1},\dfrac{1}{2}{\hat{F}}_{r2}\}\), as shown in Refs. [20, 51]. In addition, note that \(F_{s}\) is defined as 1 when \({\hat{F}}_{r1}=F_{r1,0}\) and \({\hat{F}}_{r2}=F_{r2,0}\), where we term the generating load dataset as ‘basic load dataset’ (the target points of this load dataset are depicted as black circles in Fig. 11). Under different \(F_{s}\) values, the target points have the same shape as in the basic case, but \({\hat{F}}_{r1}\) and \({\hat{F}}_{r2}\) are scaled by \(F_{s}\) (blue and red circles in Fig. 11).

Fig. 11
figure 11

The target points of load datasets under different \(F_s\) values

Full size image

The total number of load cases used in Method (1) (based on scale factors) is 280, which is equivalent to the number of load cases in the 11th iteration (see Fig. 9b) from our proposed method (labelled as Method (3)). In Method (1), these load cases are generated via 8 static FE analyses with 35 incremental load steps. In addition, the fitting results for different \(F_s\) values are both evaluated within the fitting range giving by \(S_{11}\). Methods (2) and (3) follow the same framework, however, the target point of the additional load cases in Method (2) are selected randomly within the fitting range identified by Eq. (12).

Fig. 12
figure 12

The maximum fitting error comparison between different load case selection methods. Panel a shows the scale factor, \(F_{s}\), described in Method (1), against the maximum fitting error, \(\max \{\varepsilon _{5}(r_1,r_2)\}\). Panel b shows the number of static analyses, \(N_\textrm{st}\), against \(\max \{\varepsilon _{5}(r_1,r_2)\}\). Note that, in panel b, Method (2) consists of random load case selection within the fitting range (blue asterisk line), while the load cases in Method (3) are selected within the fitting range based on \(\max \{\varepsilon _{5}(r_1,r_2)\}\) (red circle line)

Full size image

Figure 12 shows the results of the three load case selection methods. Figure 12a shows that there is an optimal scale factor, \(F_s\), that can produce the smallest \(\textrm{max}\{\varepsilon _{5}(r_1,r_2)\}\). However, this optimal result does not satisfy the critical error, \(\varepsilon _\textrm{cri}\), while \(\textrm{max}\{\varepsilon _{5}(r_1,r_2)\}\) in the 11th iteration, which has the same number of load cases, is smaller than \(\varepsilon _\textrm{cri}\) (see Fig. 10a) and the scale factor at which the minimum occurs would be unknown without running many simulations at different scale factors which is computationally expensive. On the other hand, Fig. 12b compares \(\textrm{max}\{\varepsilon _{5}(r_1,r_2)\}\) between Method (2) and Method (3). It shows that, under the same initial load dataset, Method (2), whose additional load cases are selected randomly within the fitting range, has a slow speed in terms of reducing \(\textrm{max}\{\varepsilon _{5}(r_1,r_2)\}\) and cannot satisfy the critical error, \(\varepsilon _\textrm{cri}\), within the number of static analyses shown here, while the load cases guided by \(\textrm{max}\{\varepsilon _{5}(r_1,r_2)\}\) can expect a steady decrease and eventually converge. These results indicate the importance of the load case selection for the accuracy of ROMs, and shows the proposed method provides a meaningful and efficient way to choose these additional load cases in the construction of multi-mode ROMs.

In Sect. 3, we have shown that the proposed method works well in both the single-mode and multi-mode cases. The accuracy of ROMs is reflected by a measurable error metric, \(\textrm{max}\{\varepsilon _{n}(\textbf{r})\}\), and the given critical error, \(\varepsilon _\textrm{cri}\). However, \(\textrm{max}\{\varepsilon _{n}(\textbf{r})\}\) might always be larger than \(\varepsilon _\textrm{cri}\), no matter how many load cases have been added to the static dataset. For example, \(\textrm{max}\{\varepsilon _{5}(r_1,r_2)\}\) can be smaller than \(4 \times 10^{-4}\) for the case we considered, but cannot reach, for example, \(1 \times 10^{-4}\) (Fig. 10a). In that case, a higher-order ROM should be considered, as this may be able to achieve a higher accuracy. However, as the number of independent parameters increases, the fitting results become extremely sensitive to the static datasets. Motivated by this fact, the application of the proposed method to the more generalised case, e.g. higher ROM’s order and higher energy level, is discussed in the next section.

4 Generalisation to higher-order cases

Section 3 focussed on how to apply the proposed error metric (Eqs. (19) and (21)) to construct an accurate ROM within a given energy level, and a 5th-order ROM was used to illustrate the proposed algorithm given in Fig. 4. The results show that the ROM’s performance, in terms of the maximum fitting error, \(\textrm{max}\{\varepsilon _{n}(\textbf{r})\}\), converges as the size of the dataset increases (see Figs. 7a and 10a). For example, a 5th-order ROM is unable to satisfy the error level, \(1 \times 10^{-4}\), regardless of the size of data used in the two-mode case due to the limitation of ROM’s order (see Fig. 10a). In multi-mode cases, the ROM with a large fitting error may not capture the response in the regions of the internal resonance and high energy (see Fig. 10). Here we consider the use of a higher-order polynomial in the ROM, in this case an 11th-order polynomial, to further reduce the error. This requires a more complex fitting procedure. Specifically, we must refine the method of selecting the next data point to be added to the data set to ensure that the dataset remains appropriately bounded in terms of displacements and forces.

The construction of this 11th-order ROM is based on the energy level, \(1 \times 10^{-1}\;J\), and the initial load dataset in this section is presented in Fig. 13. Note that 8 target points with their 20 related increments are used to help ensure the stability of convergence. Besides the points \((\pm {\hat{F}}_{r1},0)\) and \((0,\pm {\hat{F}}_{r2})\), 4 extra target points, \((\pm \gamma _{1} {\hat{F}}_{r1},\pm \gamma _{2} {\hat{F}}_{r2})\), are included in the initial load dataset, which are the intersection points between the linear energy contour and the straight lines, \(F_{r2}=\pm \dfrac{{\hat{F}}_{r2}}{{\hat{F}}_{r1}}F_{r1}\), as shown in Fig. 13 using dashed red line.

Fig. 13
figure 13

The initial load dataset with 8 target points. The pink ellipse represents the linear energy contour. The black dots and circles are load cases and the corresponding target points, respectively. The red dashed lines represent the straight lines, \(F_{r2}=\pm \dfrac{{\hat{F}}_{r2}}{{\hat{F}}_{r1}}F_{r1}\), which are used to determine the target points \((\pm \gamma _{1}{\hat{F}}_{r1},\pm \gamma _{2}{\hat{F}}_{r2})\)

Full size image

According to the proposed algorithm, the ROM’s accuracy is evaluated within the fitting range in the \((r_1,r_2)\)-plane, under the static dataset, \(S_{i}\), and the new target point for generating \(S_{i+1}\) is identified from Eq. (23). As mentioned in Sect. 3.3, the fitting range is not obtained by exactly solving the boundary of the inequality (Eq. (12)), but by checking if the ROM’s energy satisfies the criterion in Eq. (12). After the ROM’s parameters are estimated, Fig. 14a assesses the potential energy of this 11th-order ROM over a grid, labelled as computing points. The points that satisfy the criterion are deemed as belonging to the fitting range, which are named as ‘Energy points’ (light blue dots) and occupy an irregular region. This irregularity arises because fitting such a high-order ROM is very sensitive, and hence the fitting result is likely to be less stable when the static dataset is poorly distributed (note that, in the previous section, the 5th-order ROM led to a near-elliptical shape in the \((F_{r1},F_{r2})\)-plane – see, for example, Fig. 9). In this case, although the maximum error point in the \((r_1,r_2)\)-plane can be found, it is far away from the existing load cases and hence represents a much larger amplitude case. To alleviate this issue, we limit the range of computing points, marked as \(\Gamma _{c}\), within every iteration, as shown in Fig. 14b.

In the ith iteration, we suggest that the coordinates of computing points in \(\Gamma _{c}\) are given by,

$$\begin{aligned} \Gamma _{c,i}=\left\{ (r_{1c},r_{2c})\left| {\left\{ \begin{array}{ll} r_{1c,\textrm{min}} \le r_{1c} \le r_{1c,\textrm{max}}\\ r_{2c,\textrm{min}} \le r_{2c} \le r_{2c,\textrm{max}} \end{array}\right. }\right. \right\} \end{aligned}$$
(25)

where we utilise the displacement component, \(\hat{\mathbf{{r}}}\), in the static dataset \(S_{i}\), to determine a rectangle (see Fig. 14b), which is centred about \(\hat{\mathbf{{r}}}\). Formally, the range of this rectangle is given by,

$$\begin{aligned} {\left\{ \begin{array}{ll} r_{1c,\textrm{min}}=\dfrac{1-\alpha }{2}\textrm{max}\{\hat{\mathbf{{r}}}_{1}\}+\dfrac{1+\alpha }{2}\textrm{min}\{\hat{\mathbf{{r}}}_{1}\} \\ r_{1c,\textrm{max}}=\dfrac{1+\alpha }{2}\textrm{max}\{\hat{\mathbf{{r}}}_{1}\}+\dfrac{1-\alpha }{2}\textrm{min}\{\hat{\mathbf{{r}}}_{1}\}\\ r_{2c,\textrm{min}}=\dfrac{1-\alpha }{2}\textrm{max}\{\hat{\mathbf{{r}}}_{2}\}+\dfrac{1+\alpha }{2}\textrm{min}\{\hat{\mathbf{{r}}}_{2}\} \\ r_{2c,\textrm{max}}=\dfrac{1+\alpha }{2}\textrm{max}\{\hat{\mathbf{{r}}}_{2}\}+\dfrac{1-\alpha }{2}\textrm{min}\{\hat{\mathbf{{r}}}_{2}\}\\ \end{array}\right. } \end{aligned}$$
(26)

where the size of the rectangle is controlled by \(\alpha \) (where \(\alpha >1\)), and \(\hat{\mathbf{{r}}}_{1}\) and \(\hat{\mathbf{{r}}}_{2}\) are the data in \(\hat{\mathbf{{r}}}\) related to the 1st and 2nd modes in the ROM, respectively. Using Eq. (25), the ROM’s potential energy within \(\Gamma _{c,i}\) is assessed based on an evenly distributed grid, and the corresponding energy points are the points satisfying the condition in Eq. (12). Note that this is extremely computationally cheap, and does not require an energy contour (blue loops in Fig. 9) to be calculated explicitly. Following the algorithm in Fig. 4, the maximum error point within the energy points, which is expressed as a modal displacement vector, \(\textbf{r}_\textrm{max}\), is used to generate the new target point. As previously, \(\textbf{r}_\textrm{max}\) is converted to a target force, \(\hat{\mathbf{{F}}}_{\textbf{r},\textrm{targ}}\), using the identified restoring force (see Eq. (23)). Fig. 14c shows all energy points are projected into the \((F_{r1,},F_{r2})\)-plane using Eq. (13) and the maximum error point is marked again as the red circle. However, Fig. 14c shows that this maximum error point includes a very large force level compared to existing load cases, which suggests a large fitting error. Furthermore, the mapping of the remaining points again occupies an irregular region (unlike the roughly elliptical region seen in Fig. 9a previously); this again suggests that the identified ROM is highly inaccurate, due to the high-order polynomial in the restoring forces. To control the force level of the new target point, we place a further limit in the \((F_{r1},F_{r2})\)-plane, and only energy points within this limit, which we name as ‘Force bounded points’ in Fig. 14d, are considered for the load case selection.

Fig. 14
figure 14

The energy assessment and load case selection in the construction of an 11th-order ROM under the initial static dataset \(S_{1}\). In panel a, green dots represent the computing points used to find the ROM’s potential energy, while light blue dots, named as ‘Energy points’, denote the subset of these points which satisfy the energy criterion. In panel b, computing points within a given range are named as \(\Gamma _{c,1}\), while the blue points are corresponding energy points within \(\Gamma _{c,1}\). In panels a and b, the black circles denote the target points of load cases in the static dataset, and the red circle represents the maximum error point within the energy points. Panels c and d show the procedure of selecting the new target point, \({{{\hat{\textbf{F}}}}_{\textbf{r},\textrm{targ}}}\). In panel c, all blue dots represent the projection of energy points from panel b, and the red circle again represents the maximum error point. In panel d, energy points are limited to a given range and are named as ‘Force bounded points’, denoted as \(\Gamma _{f,1}\). The points in \(\Gamma _{f,1}\) with the maximum fitting error represents the new target point, \(\hat{\mathbf{{F}}}_{\textbf{r},\textrm{targ}}\). Note that the objective of these panels is twofold. It demonstrates the introduced constraints in the \((r_1,r_2)\) and \((F_{r1},F_{r2})\)-planes. Meanwhile, these panels also show the specific computing procedure and results under \(S_{1}\) with \(\alpha =\beta =1.25\)

Full size image
Fig. 15
figure 15

The 11th-order ROM’s construction in the two-mode case. Panel a shows the number of static analyses, \(N_\textrm{st}\), against the maximum fitting error, \(\textrm{max}\{\varepsilon _{11}(r_1,r_2)\}\), under four different parameter groups. The dashed black line denotes the critical error, \(\varepsilon _\textrm{cri}\). Panels b and c show the response frequency, \(\Omega \), against the maximum displacement amplitude of the ROM’s first mode, \(R_1\), and second mode, \(R_2\), respectively. These static datasets, where \(\textrm{max}\{\varepsilon _{11}(r_1,r_2)\}\) is smaller than \(\varepsilon _\textrm{cri}\), are labelled as \(S_{45}\), \(S_{29}\), \(S_{25}\) in parameter groups (1), (2) and (3), respectively. The black dashed lines denote the backbone curves predicted by \(S_{1}\) whose fitting result is presented in Fig. 14a

Full size image

In Fig. 14d, the force bounded points are denoted as \(\Gamma _{f}\), and the maximum error point in \(\Gamma _{f}\) is related to the new target point, \(\hat{\mathbf{{F}}}_{\textbf{r},\textrm{targ}}\), for generating additional load cases. In this Figure, the coordinates of the points in \(\Gamma _{f}\) should satisfy,

$$\begin{aligned} \begin{aligned} \Gamma _{f,i}=\left\{ (F_{r1,f},F_{r2,f})\left| \left( \frac{F_{r1,f}^{'}}{F_{r1,m}}\right) ^2+\right. \right. \\ \left. \left( \frac{F_{r2,f}^{'}}{F_{r2,m}}\right) ^2 \le 1 \right\} \end{aligned} \end{aligned}$$
(27)

where we determine an elliptical constraint centred on the force component, \(\hat{\mathbf{{F}}}_{\textbf{r}}\), in the static dataset \(S_{i}\), which depends on an ellipse encompassing load cases in \(S_{i}\), e.g. linear energy contour in \(S_{1}\). In the ith iteration, this ellipse is constructed as below steps:

  1. 1.

    Find the maximum distance from load cases in \(S_{i}\) to the centre of load cases, labelled as \((\overline{{\hat{F}}}_{r1},\overline{{\hat{F}}}_{r2})\), which corresponds to a specific load case, \(\{{\hat{F}}_{r1(m)},{\hat{F}}_{r2(m)}\}\). This load case determines the half-major axis, \(l_{d1,\textrm{max}}\), and the direction of the required ellipse, which indicates the angle, \(\theta _{m}\), between the half-major axis and \(F_{r1}\)-axis.

  2. 2.

    Then, a set of ellipses can be constructed using every remaining load cases, and the one with the maximum half-minor axis, labelled as \(l_{d2,\textrm{max}}\), is selected to ensure that all existing load cases are included within the ellipse.

Using \(\theta _{m}\), \(l_{d1,\textrm{max}}\) and \(l_{d2,\textrm{max}}\), \(F_{r1,m}\) and \(F_{r2,m}\) in Eq. (27) are defined as,

$$\begin{aligned} {\left\{ \begin{array}{ll} F_{r1,m}=\beta l_{d1,\textrm{max}} \\ F_{r2,m}=\beta l_{d2,\textrm{max}} \\ \begin{aligned} F_{r1,f}^{'}=(F_{r1,f}-\overline{{\hat{F}}}_{r1})&{}\textrm{cos}\theta _{m}\\ &{}+(F_{r2,f}-\overline{{\hat{F}}}_{r2})\textrm{sin}\theta _{m} \\ F_{r2,f}^{'}=(F_{r2,f}-\overline{{\hat{F}}}_{r2})&{}\textrm{cos}\theta _{m}\\ &{}-(F_{r1,f}-\overline{{\hat{F}}}_{r1})\textrm{sin}\theta _{m} \\ \end{aligned}\\ \overline{{\hat{F}}}_{r1}=\dfrac{1}{2}(\textrm{min}\{\hat{\mathbf{{F}}}_{r1}\}+\textrm{max}\{\hat{\mathbf{{F}}}_{r1}\})\\ \overline{{\hat{F}}}_{r2}=\dfrac{1}{2}(\textrm{min}\{\hat{\mathbf{{F}}}_{r2}\}+\textrm{max}\{\hat{\mathbf{{F}}}_{r2}\}) \end{array}\right. } \end{aligned}$$
(28)

where the size of the force constraint is controlled by \(\beta \) (where \(\beta >1\)), \(\hat{\mathbf{{F}}}_{r1}\) and \(\hat{\mathbf{{F}}}_{r2}\) are data in \(\hat{\mathbf{{F}}}_\textbf{r}\) related to the 1st and 2nd modes in the ROM, respectively.

Using constraints Eqs. (25) and (27), we can effectively control the force level of additional load cases in every iteration, such that the algorithm in Fig. 4 is able to construct higher-order ROMs in a robust manner, despite the instability when data is poorly distributed. The related results under the initial static dataset, \(S_{1}\), are summarised in Fig. 14 where the parameters \(\alpha \) and \(\beta \) are both set as 1.25.

To demonstrate the application of this method to an 11th-order ROM, Fig. 15 presents the maximum fitting error, \(\textrm{max}\{\varepsilon _{11}(r_1,r_2)\}\), and the backbone curves under different groups of parameters, \(\alpha \) and \(\beta \). The \(\alpha \) and \(\beta \) values in these groups are, (1) \(\alpha =\beta =1.03\), (2) \(\alpha =\beta =1.1\), (3) \(\alpha =\beta =1.25\), (4) \(\alpha =\beta =2.5\). Figure 15a shows that the proposed algorithm with the first three parameter sets can make \(\textrm{max}\{\varepsilon _{11}(r_1,r_2)\}\) smaller than the critical error, \(\varepsilon _\textrm{cri}\), which is set as \(1 \times 10^{-4}\). The algorithm using small \(\alpha \) and \(\beta \) values, e.g. \(\alpha =\beta =1.03\), requires more iterations to reach the critical error level (the purple line), whereas larger \(\alpha \) and \(\beta \) values can lead to faster convergence. Under overly large \(\alpha \) and \(\beta \) values (\(\alpha =\beta =2.5\)), which performs similarly to the case without constraints, the algorithm outputs a diverged result (the grey dashed line), due to the sensitivity of fitting such a high-order polynomial. This shows that, while larger \(\alpha \) and \(\beta \) parameters may lead to faster convergence, they may also cause unstable behaviour and non-convergence. According to the proposed algorithm, the results from all parameter groups are accurate as long as \(\textrm{max}\{\varepsilon _{11}(r_1,r_2)\}\) is smaller than \(\varepsilon _\textrm{cri}\), which is corresponding to the static datasets, \(S_{45}\), in group (1) and \(S_{29}\), \(S_{25}\) in groups (2) and (3), respectively. The results of backbone curves from these three parameter groups are presented in Figs. 15b and 15c. Specifically, it is clear that the ROM constructed by \(S_{1}\) cannot capture the internal resonance and provide a diverged result at the high energy level. This is expected due to the large fitting error as shown in Fig. 15a and the irregular region occupied by energy points, shown in Fig. 14a. As the introduction of constraints, the proposed algorithm now can construct the ROM satisfying a desired accuracy level in higher-order cases.

5 Conclusions

In this paper, we propose a method to produce an accurate ROM for a given modal basis under the ICE framework. We also demonstrate that this method can be effectively utilised to construct higher-order and multi-mode ROMs.

The paper first demonstrates that a ROM’s accuracy in the ICE method is dependent on the fitting data. In our proposed method, an algorithm is presented to ensure a small fitting error within the fitting range which is linked to a given energy level, \(E_\textrm{level}\). This is achieved by introducing a computationally efficient error metric and a strategy for selecting load cases. We have shown that the proposed error metric can efficiently represent the error within the fitting range and can be readily extended to the multi-mode case. Meanwhile, the method provides a meaningful way to find additional load cases for improving a ROM’s accuracy based on the fitting results. A curved beam is used to validate these characteristics in the single-mode and two-mode cases, and the results show that these additional load cases instructed by our method effectively reduce the maximum fitting error, \(\textrm{max}\{\varepsilon (\textbf{r})\}\). Furthermore, we compare our method with two other methods, based on scale factors and random selection, in terms of the load case selection. It is shown that randomly selected load cases are inefficient at reducing the fitting error, which indicates the significance of the locations of load cases. In addition, the method based on scale factors can output optimal results only when the scale factors are selected carefully, which requires a search procedure with a large computational burden.

To address the difficulties arising from the multi-dimensional fitting procedure, we further generalise the proposed algorithm to the higher-order and multi-mode cases. In the two-mode case, we demonstrate that the fitting range and the additional load cases are both unreliable due to the poor fitting result if the ROM’s order is too high. Some constraints in both the \((r_1,r_2)\)-plane and \((F_{r1},F_{r2})\)-plane are introduced to limit the range for assessing the ROM’s potential energy and selecting additional load cases, which helps to avoid excessive additional load cases. The numerical results show that these additional constraints can effectively enhance the proposed algorithm’s robustness and potential in the construction of higher-order and multi-mode ROMs.

Based on the proposed algorithm, we can quantitatively monitor and control the accuracy of ROMs. The algorithm enables additional load cases to be selected in an efficient and strategic manner to enable the accuracy of the ROMs to reach the desired level. This algorithmic procedure allows ROMs to be constructed without user input whilst guaranteeing their accuracy, allowing ROMs to be used in model updating and optimisation, for example. Furthermore, by achieving very high levels of accuracy, this approach may be used in conjunction with methods that require low levels of uncertainty, such as gradient-based methods.