Calculation of dynamic responses of railway sleepers on a nonlinear foundation

Abstract

The safety of a passing train depends on different factors, of which one of the most important is the behavior of the foundation. Therefore, the effects of the nonlinearity of ballast on the dynamic responses of the railway track are a key research interest. In this paper, a new model of railway sleepers posed on a nonlinear foundation has been developed. By coupling the finite element method (FEM) of the sleeper with an analytical model of the periodically supported beam model, the dynamic equation of the sleeper is developed. On the other hand, by considering a periodic series of moving loads, this equation can be transformed to a forced nonlinear oscillation. Iteration procedures have been built to calculate the periodic solution. This method has demonstrated a good convergence of results by comparison with the analytical solution in the linear case. The influence of the nonlinear foundation has been investigated by two examples: cubic-nonlinear and bi-linear foundations. The parametric studies demonstrate that numerical results converge with a small number of iterations.

Appendices

A Mathematical transformation

By performing the Fourier transform, and then the inverse Fourier transform of the right term of Eq. (7), we can obtain the following result:

$$\begin{aligned} k_{rp}w_r(t) + \zeta _{rp} \dot{w}_r(t) = \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty k_p(\omega ) \hat{w}_r(\omega ) \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \nonumber \\ \end{aligned}$$

(20)

The right term of the last equation depends on the rail displacements. It can be rewritten as a function of the sleeper displacement by substituting Eq. (6) into Eq. (20) as follows:

$$\begin{aligned}{} & {} \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty k_p(\omega ) \hat{w}_r(\omega ) \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \\{} & {} \quad = \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty \dfrac{k_p^2(\omega ) \hat{u}_{R_{k_z}}(\omega )}{k_p(\omega )+ \mathcal {K}_e(\omega )} \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \\{} & {} \qquad - \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty \dfrac{k_p(\omega ) \mathcal {Q}_e(\omega )}{k_p(\omega )+ \mathcal {K}_e(\omega )} \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \end{aligned}$$

By combining the previous result and Eq. (7), we obtain the following result:

$$\begin{aligned} \begin{aligned}&\textbf{M} {\ddot{\textbf{u}}} + \textbf{C} {\dot{\textbf{u}}} +\textbf{K} \textbf{u} + \textbf{f}_{NL} (\textbf{u}, {\dot{\textbf{u}}}) \\&\quad = \left[ \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty \dfrac{k_p^2(\omega ) \hat{u}_{R_{1_z}}(\omega )}{k_p(\omega )+ \mathcal {K}_e(\omega )} \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \right] \textbf{e}_{R_1} \\&\qquad - \left[ \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty \dfrac{k_p(\omega ) \mathcal {Q}_1(\omega )}{k_p(\omega )+ \mathcal {K}_e(\omega )} \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \right] \textbf{e}_{R_1} \\&\qquad + \left[ \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty \dfrac{k_p^2(\omega ) \hat{u}_{R_{2_z}}(\omega )}{k_p(\omega )+ \mathcal {K}_e(\omega )} \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \right] \textbf{e}_{R_2} \\&\qquad - \left[ \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty \dfrac{k_p(\omega ) \mathcal {Q}_2(\omega )}{k_p(\omega )+ \mathcal {K}_e(\omega )} \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \right] \textbf{e}_{R_2} \end{aligned} \end{aligned}$$

(21)

where $\mathcal {Q}_1(\omega )$ and $\mathcal {Q}_2(\omega )$ are the equivalent train loads at the rail 1 and rail 2, respectively (see Appendix 1). $\hat{u}_{R_{1_z}} (\omega )$ and $\hat{u}_{R_{2_z}} (\omega )$ are, respectively, the two displacement of the sleeper at the crossing points with the two rails in the frequency domain. By developing the first and the third terms on the right side of Eq. (8), it can be rewritten as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\left[ \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty \dfrac{k_p^2(\omega ) \hat{u}_{R_{1_z}}(\omega )}{k_p(\omega )+ \mathcal {K}_e(\omega )} \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \right] \textbf{e}_{R_1} \\&\quad = \textbf{I}_{R_1} \left[ \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty \dfrac{k_p^2(\omega ) \textbf{u}(\omega )}{k_p(\omega )+ \mathcal {K}_e(\omega )} \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \right] \\&\left[ \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty \dfrac{k_p^2(\omega ) \hat{u}_{R_{2_z}}(\omega )}{k_p(\omega )+ \mathcal {K}_e(\omega )} \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \right] \textbf{e}_{R_1} \\&\quad = \textbf{I}_{R_2} \left[ \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty \dfrac{k_p^2(\omega ) \textbf{u}(\omega )}{k_p(\omega )+ \mathcal {K}_e(\omega )} \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \right] \end{aligned} \right. \end{aligned}$$

Finally, by inserting the last result in Eq. (21), we have:

$$\begin{aligned} \begin{aligned}&\textbf{M} {\ddot{\textbf{u}}} + \textbf{C} {\dot{\textbf{u}}} +\textbf{K} \textbf{u} + \textbf{f}_{NL} (\textbf{u}, {\dot{\textbf{u}}}) \\&\quad = \textbf{I}_{R} \left[ \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty \dfrac{k_p^2(\omega ) \textbf{u}(\omega )}{k_p(\omega )+ \mathcal {K}_e(\omega )} \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \right] \\&\qquad - \left[ \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty \dfrac{k_p(\omega ) \mathcal {Q}_1(\omega )}{k_p(\omega )+ \mathcal {K}_e(\omega )} \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \right] \textbf{e}_{R_1} \\&\qquad - \left[ \dfrac{1}{2 \pi } \int \limits _{-\infty }^\infty \dfrac{k_p(\omega ) \mathcal {Q}_2(\omega )}{k_p(\omega )+ \mathcal {K}_e(\omega )} \textrm{e}^{\textrm{i} \omega t} \textrm{d}\omega \right] \textbf{e}_{R_2} \end{aligned} \end{aligned}$$

(22)

B Periodically supported beam in steady-state

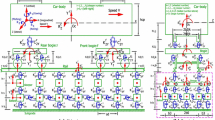
Figure 12 presents a periodically supported beam model. In this model, each rail k of the track is modeled by an infinite beam posed on periodic supports. The sleeper spacing is l. The train loads are considered by the concentrated loads $Q^{(k)}_j$. Each load is characterized by its distance $D_j$ to the first axle and the train speed v.

Fig. 12

Periodically supported beam model

In the frequency domain, Hoang et al. [45, 46] have demonstrated a relation between the reaction force $\hat{R}_k(\omega )$ and the displacement of the rail $\hat{w}_r(0, \omega )$ in the frequency domain as follows:

$$\begin{aligned} \hat{R}_k(\omega ) = \mathcal {K}_e(\omega ) \hat{w}_r(0, \omega ) + \mathcal {Q}_k(\omega ) \end{aligned}$$

(23)

where: $\mathcal {K}_e(\omega )$ and $\mathcal {Q}_k(\omega )$ are the equivalent stiffness and equivalent loads of the system. The two functions are calculated by the parameters of the rail and the train loads as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\mathcal {K}_e(\omega ) = 4 \lambda _r^3 E_r I_r \left[ \dfrac{\sin l\lambda _r}{\cos l\lambda _r - \cos \frac{\omega l}{v}} \right. \\&\qquad \left. - \dfrac{\sinh l\lambda _r}{\cosh l\lambda _r - \cos \frac{\omega l}{v}}\right] ^{-1} \\&\mathcal {Q}_k(\omega ) = \dfrac{\mathcal {K}_e(\omega )}{v E_r I_r \left[ \left( \frac{\omega }{v}\right) ^4-\lambda _r^4\right] } \sum _{q=1}^K Q_q^{(k)} \textrm{e}^{- \textrm{i} \omega \frac{D_j}{v}} \end{aligned} \right. \end{aligned}$$

(24)

where: $\lambda _r = \root 4 \of {\dfrac{\rho _r S_r \omega ^2}{E_r I_r}}$. $E_r$, $I_r$, $\rho _r$ and $S_r$ are, respectively, the Young’s modulus of rail, the second moment of area of the rail, the density of rail and cross-sectional area of rail. The expressions show that Eq. (23) is applicable for any foundation behavior. In this paper, the rail parameters are given in Table 2.

Table 2 Parameters of the periodically supported beam model [45]

C Calculation of equivalent load

By substituting Eq. (9) into Eq. (24) and together with the assumption as shown in Eq. (10), a new expression of the equivalent charge $\mathcal {Q}_k(\omega )$ can be expressed as follows:

$$\begin{aligned}{} & {} \mathcal {Q}_k(\omega ) \nonumber \\{} & {} \quad = \dfrac{Q \mathcal {K}_e(\omega )}{v E_r I_r} \dfrac{\left( 1 + \textrm{e}^{-\textrm{i} \omega \frac{D_w}{v}} + \textrm{e}^{-\textrm{i} \omega \frac{D_w + L_w}{v}} + \textrm{e}^{-\textrm{i} \omega \frac{2D_w + L_w}{v}} \right) }{\left( \frac{\omega }{v}\right) ^4-\lambda _r^4}\nonumber \\{} & {} \quad \sum _{j=-\infty }^\infty \textrm{e}^{-\textrm{i} \omega \frac{H_w}{v}j} \end{aligned}$$

(25)

The parameters of Eq. (25) are explained in Appendix 1. Moreover, a property of the Dirac comb [54] gives the following result:

$$\begin{aligned} \sum _{j=-\infty }^\infty \textrm{e}^{-\textrm{i} \omega \frac{H_w}{v}j} = 2 \pi \dfrac{v}{H_w} \sum _{j=-\infty }^\infty \delta \left( \omega + \dfrac{2 \pi v}{H_w}j\right) \end{aligned}$$

(26)

By introducing this property into Eq. (25), the equivalent loads can be expressed as follows:

$$\begin{aligned}{} & {} \mathcal {Q}_k(\omega ) = \dfrac{2 \pi Q \mathcal {K}_e(\omega )}{E_r I_r H_w}\nonumber \\{} & {} \quad \dfrac{\left( 1 + \textrm{e}^{-\textrm{i} \omega \frac{D_w}{v}} + \textrm{e}^{-\textrm{i} \omega \frac{D_w + L_w}{v}} + \textrm{e}^{-\textrm{i} \omega \frac{2D_w + L_w}{v}} \right) }{\left( \frac{\omega }{v}\right) ^4-\lambda _r^4}\nonumber \\{} & {} \quad \sum _{j=-\infty }^\infty \delta \left( \omega + \dfrac{2 \pi v}{H_w}j\right) \end{aligned}$$

(27)

Thus, Eq. (27) leads to the following result:

$$\begin{aligned} \dfrac{1}{2\pi } \int \limits _{-\infty }^{+\infty }\dfrac{k_p(\omega ) \mathcal {Q}_k(\omega )}{k_p(\omega ) + \mathcal {K}_e(\omega )}\textrm{e}^{\textrm{i}\omega t} \textrm{d}\omega = \sum _{j=-\infty }^\infty F_j \textrm{e}^{\textrm{i}\omega _j t} \end{aligned}$$

(28)

where $F_j$ is calculated by:

$$\begin{aligned}{} & {} F_j = \dfrac{Q }{E_r I_r H_w} \nonumber \\{} & {} \qquad \left[ \dfrac{1 + \textrm{e}^{-\textrm{i} \omega \frac{D_w}{v}} + \textrm{e}^{-\textrm{i} \omega \frac{D_w + L_w}{v}} + \textrm{e}^{-\textrm{i} \omega \frac{2D_w + L_w}{v}}}{\left( \frac{\omega }{v}\right) ^4-\lambda _r^4}\right. \nonumber \\{} & {} \qquad \left. \dfrac{k_p(\omega ) \mathcal {K}_e(\omega )}{k_p(\omega ) + \mathcal {K}_e(\omega )} \right] _{\omega = \omega _j} \end{aligned}$$

(29)

The last equation describes a forced oscillation with the exciting force $\sum F_j \textrm{e}^{\textrm{i} \omega _j t}$ with frequency $f_0 = v/H_w$. We remark that $\omega _j = 2 \pi f_j = 2 \pi j f_0$. We suppose that the solution of the nonlinear problem can admit the same frequencies as the excitation force. Therefore, with this assumption, there exists a periodic solution of $\textbf{u}(t)$ which can be represented as follows:

$$\begin{aligned} \textbf{u}(t) = \sum _{j=-\infty }^\infty \Phi _j \textrm{e}^{\textrm{i} \omega _j t} \end{aligned}$$

(30)

Moreover, by performing the Fourier transform, Eq. (30) can be explained in the frequency domain as follows:

$$\begin{aligned} \hat{\textbf{u}}(\omega ) = 2 \pi \sum _{j=-\infty }^\infty \Phi _j \delta (\omega - \omega _j) \end{aligned}$$

(31)

So that, we can deduce the following result:

$$\begin{aligned} \dfrac{1}{2\pi } \int \limits _{-\infty }^{+\infty }\dfrac{k_p^2(\omega ) \hat{\textbf{u}}(\omega )}{k_p(\omega ) + \mathcal {K}_e(\omega )}\textrm{e}^{\textrm{i}\omega t} \textrm{d}\omega = \sum _{j=-\infty }^\infty \Phi _j P_j \textrm{e}^{\textrm{i}\omega t} \nonumber \\ \end{aligned}$$

(32)

where

$$\begin{aligned} P_j = \left[ \dfrac{k_p^2(\omega )}{k_p(\omega ) + \mathcal {K}_e(\omega )}\right] _{\omega =\omega _j} \end{aligned}$$

(33)