A novel resonant parametric feedback controller (RPFC) for suppressing nonlinear resonances and chaos in a cantilever beam

Abstract

This paper presents a novel resonant parametric feedback controller (RPFC) for suppressing nonlinear resonances and chaos in a cantilever beam using acceleration feedback. The excitation of the system may be due to 1:1 direct excitation, 1:3 subharmonic direct excitation, 3:1 superharmonic direct excitation, 1:2 parametric excitation, 1:4 subharmonic parametric excitation, self excitations, and combinations of two or more of these. The controller is designed in two stages. First, the measured acceleration signal of the beam is fedback to a second-order filter. Subsequently, the states of the second-order filter are used to formulate the nonlinear control function that is applied to the structure as a parametric input such that the controlled parametric variation produces dissipative force at the resonance. The analysis of the system is carried out using the method of multiple time-scales. A number of special cases demonstrating the efficacy of the controller in suppressing various nonlinear resonances and their combinations are studied. Finally, a novel frequency adaptation law is proposed to deal with the uncertainty in the system's natural frequency. The results are verified by numerical simulations and some experiments. Though the analysis is carried out for an SDOF system, the proposed control scheme can easily be extended to any MDOF system, and it can target any mode by tuning the filter frequency.

Appendices

Appendix A

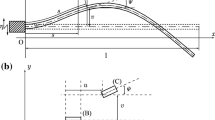
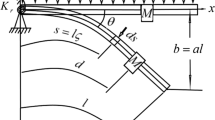
Derivation of the governing equation of a cantilever beam vibrating due to the axial and transverse motion of the base.

List of variables used:

$w$:

Transverse deflection of the beam

$u$:

Axial deflection of the beam

$s$:

Coordinate along the length of the beam

$\rho$:

Density of the beam

$A$:

Cross section area of the beam

$L$:

Length of the cantilever beam

$m$:

Tip mass

$x_{e}$:

Axial displacement of base/support

$y_{e}$:

Transverse displacement of base/support

$v_{s}$:

Normalized mode shape of the beam

$v$:

Time dependent scaling factor

$\omega_{n}$:

First mode of the beam

1.1 Strain energy

$$ {\text{U}} = \frac{1}{2}\int_{0}^{l} {\int_{A}^{{}} {Ez^{2} \kappa^{2} dA} ds} , $$

(A.1)

where $z$ is the distance from the neutral axis, and $\kappa$ is the curvature. Assuming that the beam is inextensible

$$ \kappa = \frac{\partial }{\partial s}\alpha (s,t) = w^{(2,0)} (s,t) + \frac{1}{2}w^{(2,0)} (s,t)w^{(1,0)} (s,t)^{2} + \cdots $$

(A.2)

where $w\left( {s,t} \right)$ is the transverse displacement at a distance $s$ from the fixed end and $w^{{\left( {i,j} \right)}} \left( {s,t} \right) = \frac{{\partial^{i} }}{{\partial s^{i} }}\left( {\frac{{\partial^{j} w}}{{\partial t^{j} }}} \right)$

Substituting Eq. (A2) in Eq. (A1) and neglecting the higher order terms,

$$ U = \frac{1}{2}\int\limits_{0}^{l} {\int_{A} {Ez^{2} \left( {\left[ {w^{(2,0)} (s,t)} \right]^{2} + \left[ {w^{(2,0)} (s,t)w^{(1,0)} (s,t)} \right]^{2} } \right)} } dAds $$

(A.3)

$$ U = \frac{1}{2}\int_{0}^{l} {EI\left[ {w^{(2,0)} (s,t)} \right]^{2} ds} + \frac{1}{2}\int\limits_{0}^{l} {EI\left[ {w^{(1,0)} (s,t)w^{(2,0)} (s,t)} \right]^{2} ds} $$

(A.4)

Applying the variational operator,

$$ \begin{aligned} & \delta U = \int_{0}^{L} {EI\left[ {w^{(2,0)} (s,t)\left( {1 + \left( {w^{(1,0)} (s,t)} \right)^{2} } \right)} \right]\delta w^{(2,0)} (s,t)ds} \\ & \quad + \int_{0}^{l} {EI\left[ {w^{(1,0)} (s,t)\left( {w^{(2,0)} (s,t)} \right)^{2} \delta w^{(1,0)} (s,t)} \right]ds} \\ \end{aligned} $$

(A.5)

Integrating by parts one obtains

$$ \delta U = EI\left( \begin{aligned} & \left( {w^{(2,0)} (s,t)\left( {1 + \left( {w^{(1,0)} (s,t)} \right)^{2} } \right)\delta w^{(1,0)} (s,t)} \right)_{0}^{L} \\ & - \left( {\left( {w^{(3,0)} (s,t)\left( {1 + \left( {w^{(1,0)} (s,t)} \right)^{2} } \right) + w^{(1,0)} (s,t)\left( {w^{(2,0)} (s,t)} \right)^{2} } \right)\delta w(s,t)} \right)_{0}^{L} \\ & + \int_{0}^{L} {\left( \begin{gathered} w^{(4,0)} (s,t)\left( {1 + \left( {w^{(1,0)} (s,t)} \right)^{2} } \right) + \left( {w^{(2,0)} (s,t)} \right)^{3} \hfill \\ + 4w^{(1,0)} (s,t)w^{(2,0)} (s,t)w^{(3,0)} (s,t) \hfill \\ \end{gathered} \right)\delta w(s,t)ds} \\ \end{aligned} \right) $$

(A.6)

1.2 Inextensibility constraint

$$ \left( {1 + u^{{\left( {1,0} \right)}} \left( {s,t} \right)} \right)^{2} + w^{{\left( {1,0} \right)}} \left( {s,t} \right)^{2} = 1 $$

$$ C = \int_{0}^{L} {\frac{\lambda }{2}\left( {1 - \left( {1 + u^{{\left( {1,0} \right)}} \left( {s,t} \right)} \right)^{2} - w^{{\left( {1,0} \right)}} \left( {s,t} \right)^{2} } \right)ds} , $$

(A.7)

where $\lambda$ is a Lagrange multiplier. Applying variational operator to the Eq. (A7) and integrating by parts yields,

$$ \begin{aligned} \delta C & = \left[ { - \lambda \left( {\left( {1 + u^{{\left( {1,0} \right)}} \left( {s,t} \right)} \right)\delta u\left( {s,t} \right) + w^{{\left( {1,0} \right)}} \left( {s,t} \right)\delta w\left( {s,t} \right)} \right)} \right]_{0}^{L} \\ & \quad + \int_{0}^{L} {\left( {\left( {\lambda \left( {1 + u^{{\left( {1,0} \right)}} \left( {s,t} \right)} \right)} \right)^{\prime } \delta u\left( {s,t} \right) + \left( {\lambda w^{{\left( {2,0} \right)}} \left( {s,t} \right) + \lambda^{\prime}w^{{\left( {1,0} \right)}} \left( {s,t} \right)} \right)\delta w\left( {s,t} \right)} \right)ds} \\ \end{aligned} $$

(A.8)

1.3 Kinetic energy

$$ T = \frac{1}{2}m\int_{0}^{L} {\left( {\left[ {\dot{x}_{e} + \dot{u}} \right]^{2} + \left[ {\dot{y}_{e} + \dot{w}} \right]^{2} } \right)\delta^{*} \left( {s - L} \right)ds} + \frac{1}{2}\rho A\int_{0}^{L} {\left( {\left[ {\dot{x}_{e} + \dot{u}} \right]^{2} + \left[ {\dot{y}_{e} + \dot{w}} \right]^{2} } \right)ds} , $$

(A.9)

where $\delta^{*}$ is the Dirac delta function. Applying a variational operator to Eq. (A9) and integrating by parts, one obtains

$$ \begin{aligned} & \int_{{t_{1} }}^{{t_{2} }} {\delta T} dt = - m\int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {\left( {\left[ {\ddot{u} + \ddot{x}_{e} } \right]\delta u + \left[ {\ddot{w} + \ddot{y}_{e} } \right]\delta w} \right)\delta^{*} \left( {s - L} \right)ds} dt} \\ & \quad - \rho A\int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {\left( {\left[ {\ddot{u} + \ddot{x}_{e} } \right]\delta u + \left[ {\ddot{w} + \ddot{y}_{e} } \right]\delta w} \right)ds} dt} \\ \end{aligned} $$

(A.10)

1.4 Hamilton's principle

$$ \delta \int_{{t_{1} }}^{{t_{2} }} {\left( {T - \left( {U + V} \right) + C} \right)dt} = 0 $$

(A.11)

Substituting Eq. (A6), (A8), and (A10) in eq. (A11) one obtains Eq. (A12)

$$ \begin{aligned} \int_{{t_{1} }}^{{t_{2} }} {\left( {\delta T - \delta U + \delta C} \right)dt} & = - m\int_{{t_{1} }}^{{t_{2} }} {\left( {\left[ {\ddot{u} + \ddot{x}_{e} } \right]\delta u + \left[ {\ddot{w} + \ddot{y}_{e} } \right]\delta w} \right)_{s = L} dt} \\ & \quad - \rho A\int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {\left( {\left[ {\ddot{u} + \ddot{x}_{e} } \right]\delta u + \left[ {\ddot{w} + \ddot{y}_{e} } \right]\delta w} \right)ds} dt} \\ & \quad - \int_{{t_{1} }}^{{t_{2} }} {EI\left( \begin{gathered} \left( {\left[ {w^{(2,0)} (s,t)\left( {1 + \left( {w^{(1,0)} (s,t)} \right)^{2} } \right)} \right]\delta w^{(1,0)} (s,t)} \right)_{0}^{L} \\ - \left( {\left[ {w^{(3,0)} (s,t)\left( {1 + \left( {w^{(1,0)} (s,t)} \right)^{2} } \right) + w^{(1,0)} (s,t)\left( {w^{(2,0)} (s,t)} \right)^{2} } \right]\delta w(s,t)} \right)_{0}^{L} \\ + \int_{0}^{L} {\left[ \begin{gathered} w^{(4,0)} (s,t)\left( {1 + \left( {w^{(1,0)} (s,t)} \right)^{2} } \right) + \left( {w^{(2,0)} (s,t)} \right)^{3} \hfill \\ + 4w^{(1,0)} (s,t)w^{(2,0)} (s,t)w^{(3,0)} (s,t) \hfill \\ \end{gathered} \right]\delta w(s,t)ds} \\ \end{gathered} \right)dt} \\ & \quad - \int_{{t_{1} }}^{{t_{2} }} {\left[ {\lambda \left( {\left( {1 + u^{{\left( {1,0} \right)}} \left( {s,t} \right)} \right)\delta u\left( {s,t} \right) + w^{{\left( {1,0} \right)}} \left( {s,t} \right)\delta w\left( {s,t} \right)} \right)} \right]_{0}^{L} dt} \\ & \quad + \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {\left( {\left( {\lambda \left( {1 + u^{{\left( {1,0} \right)}} \left( {s,t} \right)} \right)} \right)^{\prime } \delta u\left( {s,t} \right) + \left( {\lambda w^{{\left( {1,0} \right)}} \left( {s,t} \right)} \right)^{\prime } \delta w\left( {s,t} \right)} \right)ds} dt} \\ \end{aligned} $$

(A.12)

1.5 Boundary conditions

From Eq. (A12) following boundary conditions are obtained.

At $s = 0$

$$ w^{{\left( {1,0} \right)}} \left( {0,t} \right) = 0 $$

(A.13)

$$ u\left( {0,t} \right) = 0 $$

(A.14)

$$ w\left( {0,t} \right) = 0 $$

(A.15)

At $s = L$

$$ w^{{\left( {2,0} \right)}} \left( {L,t} \right) = 0 $$

(A.16)

$$ \lambda = - \frac{{m\left( {\ddot{u} + \ddot{x}_{e} } \right)}}{{1 + u^{{\left( {1,0} \right)}} \left( {s,t} \right)}} $$

(A.17)

$$ EIw^{(3,0)} (s,t) = \frac{m}{{1 + \left( {w^{(1,0)} (s,t)} \right)^{2} }}\left( {\left( {\ddot{w} + \ddot{y}_{e} } \right) - \left( {\ddot{u} + \ddot{x}_{e} } \right)\left( {\frac{{w^{{\left( {1,0} \right)}} \left( {s,t} \right)}}{{1 + u^{{\left( {1,0} \right)}} \left( {s,t} \right)}}} \right)} \right) $$

(A.18)

1.6 Equations of motion

From Eq. (A12) following equations of motion are obtained

$$ - \rho A\left( {\ddot{u} + \ddot{x}_{e} } \right) + \left( {\lambda \left( {1 + u^{\prime}} \right)} \right)^{\prime } = 0 $$

(A.19)

$$ - \rho A\left( {\ddot{w} + \ddot{y}_{e} } \right) + \left( {\lambda w^{\prime}} \right)^{\prime } - EI\left( \begin{aligned} & w^{(4,0)} (s,t)\left( {1 + \left( {w^{(1,0)} (s,t)} \right)^{2} } \right) + \left( {w^{(2,0)} (s,t)} \right)^{3} \\ & + 4w^{(1,0)} (s,t)w^{(2,0)} (s,t)w^{(3,0)} (s,t) \\ \end{aligned} \right) = 0 $$

(A.20)

From Eq. (A19)

$$ \lambda \left( {1 + u^{\prime}} \right) = \int_{0}^{s} {\rho A\left( {\ddot{u} + \ddot{x}_{e} } \right)} ds + c\left( t \right) $$

(A.21)

From Eqs. (A17) and (A21)

$$ c\left( t \right) = - \left[ {m\left( {\ddot{u} + \ddot{x}_{e} } \right) + \int_{0}^{s} {\rho A\left( {\ddot{u} + \ddot{x}_{e} } \right)} ds} \right]_{s = L} $$

(A.22)

From Eq. (A21) and (A22) the Lagrange multiplier is obtained as

$$ \lambda = \frac{ - 1}{{1 + u^{\prime}}}\left( {m\left( {\ddot{u} + \ddot{x}_{e} } \right)_{s = L} + \rho A\int_{s}^{L} {\left( {\ddot{u} + \ddot{x}_{e} } \right)ds} } \right) $$

(A.23)

Substituting Eq. (A23) and $u = \int_{0}^{s} {\left( {\sqrt {1 - w^{{\prime}{2}} } - 1} \right)ds} \approx \int_{0}^{s} {\left( { - w^{{\prime}{2}} /2} \right)ds}$ in Eq. (A20), following equation is obtained

$$ \begin{aligned} & \rho A\left( {\ddot{w} + \ddot{y}_{e} } \right) + \left( {\frac{{\left( {1 - 2w^{\prime 2} } \right)w^{\prime \prime } }}{{\left( {1 - w^{\prime 2} } \right)^{3/2} }}\left( \begin{gathered} m\left( {\frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\int_{0}^{s} {\left( { - w^{\prime 2} /2} \right)ds} } \right) + \ddot{x}_{e} } \right)_{s = L} \hfill \\ + \rho A\int_{s}^{L} {\left( {\frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\int_{0}^{s} {\left( { - w^{\prime 2} /2} \right)ds} } \right) + \ddot{x}_{e} } \right)ds} \hfill \\ \end{gathered} \right)} \right) \\ & \quad - \rho A\frac{{w^{\prime}}}{{\sqrt {1 - w^{\prime 2} } }}\left( {\frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\int_{0}^{s} {\left( { - w^{\prime 2} /2} \right)ds} } \right) + \ddot{x}_{e} } \right) \\ & \quad + EI\left( \begin{gathered} w^{(4,0)} (s,t)\left( {1 + \left( {w^{(1,0)} (s,t)} \right)^{2} } \right) + \left( {w^{(2,0)} (s,t)} \right)^{3} \hfill \\ + 4w^{(1,0)} (s,t)w^{(2,0)} (s,t)w^{(3,0)} (s,t) \hfill \\ \end{gathered} \right) = 0 \\ \end{aligned} $$

(A.24)

Using Binomial expansion Eq. (A24) can be simplified to the following equation

$$ \begin{aligned} & \rho A\left( {\ddot{w} + \ddot{y}_{e} } \right) + \left( {\left( {1 - 2w^{\prime 2} } \right)w^{\prime \prime } \left( {1 + \frac{3}{2}w^{\prime 2} } \right)\left( \begin{gathered} m\left( {\frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\int_{0}^{s} {\left( { - w^{\prime 2} /2} \right)ds} } \right) + \ddot{x}_{e} } \right)_{s = L} \hfill \\ + \rho A\int_{s}^{L} {\left( {\frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\int_{0}^{s} {\left( { - w^{\prime 2} /2} \right)ds} } \right) + \ddot{x}_{e} } \right)ds} \hfill \\ \end{gathered} \right)} \right) \\ & \quad - \rho A\frac{{w^{\prime}}}{{\sqrt {1 - w^{\prime 2} } }}\left( {1 + \frac{1}{2}w^{\prime 2} } \right)\left( {\frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\int_{0}^{s} {\left( { - w^{\prime 2} /2} \right)ds} } \right) + \ddot{x}_{e} } \right) \\ & \quad + EI\left( \begin{gathered} w^{(4,0)} (s,t)\left( {1 + \left( {w^{(1,0)} (s,t)} \right)^{2} } \right) + \left( {w^{(2,0)} (s,t)} \right)^{3} \hfill \\ + 4w^{(1,0)} (s,t)w^{(2,0)} (s,t)w^{(3,0)} (s,t) \hfill \\ \end{gathered} \right) = 0 \\ \end{aligned} $$

(A.25)

Neglecting the higher order terms,

$$ \begin{aligned} & \rho A\left( {\ddot{w} + \ddot{y}_{e} } \right) + w^{\prime \prime } \left( \begin{gathered} m\left( {\frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\int_{0}^{L} {\left( { - w^{\prime 2} /2} \right)ds} } \right) + \ddot{x}_{e} } \right) \hfill \\ + \rho A\int_{s}^{L} {\left( {\frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\int_{0}^{s} {\left( { - w^{\prime 2} /2} \right)ds} } \right) + \ddot{x}_{e} } \right)ds} \hfill \\ \end{gathered} \right) \\ & \quad - \rho Aw^{\prime}\left( {\frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\int_{0}^{s} {\left( { - w^{\prime 2} /2} \right)ds} } \right) + \ddot{x}_{e} } \right) \\ & \quad + EI\left( \begin{gathered} w^{(4,0)} (s,t)\left( {1 + \left( {w^{(1,0)} (s,t)} \right)^{2} } \right) + \left( {w^{(2,0)} (s,t)} \right)^{3} \hfill \\ + 4w^{(1,0)} (s,t)w^{(2,0)} (s,t)w^{(3,0)} (s,t) \hfill \\ \end{gathered} \right) = 0 \\ \end{aligned} $$

(A.26)

Separating the variables assuming that the beam vibrates around the first mode

$$ w\left( {s,t} \right) = v_{s} \left( s \right)v\left( t \right) $$

(A.27)

where $v_{s}$ is the mode shape function at first mode. Substituting the above equation in Eq. (A.26)

$$ \begin{aligned} & \rho Av_{s} \ddot{v} + v\left( {v\ddot{v} + \dot{v}^{2} } \right)\left( { - mv_{s2} \left( {\int_{0}^{L} {v_{s1}^{2} ds} } \right) + \rho Av_{s1} \left( {\int_{0}^{s} {v_{s1}^{2} ds} } \right) - \rho Av_{s2} \int_{s}^{L} {\int_{0}^{s} {v_{s1}^{2} ds} ds} } \right) \\ & \quad + \left( {mv_{s2} + \rho A\left( {v_{s2} \left( {L - s} \right) - v_{s1} } \right)} \right)v\ddot{x}_{e} + \rho A\ddot{y}_{e} + EIvv_{s4} + EIv^{3} \left( {v_{s4} v_{s1}^{2} + v_{s2}^{3} + 4v_{s1} v_{s2} v_{s3} } \right) = R \\ \end{aligned} $$

(A.28)

where $R$ is the residual.

After Galerkin projection, the above equation can be expressed as

$$ \hat{\gamma }_{0} \ddot{v} + \hat{\gamma }_{1} \left( {\dot{v}^{2} + v\ddot{v}} \right)v + \hat{\gamma }_{2} v + \hat{\gamma }_{3} v^{3} + \hat{\lambda }_{2} v\ddot{x}_{e} + \hat{\lambda }_{1} \ddot{y}_{e} = 0 $$

(A.29)

where

$$ \hat{\gamma }_{0} = \rho A\int_{0}^{L} {v_{s}^{2} ds} $$

$$ \hat{\gamma }_{1} = \int_{0}^{L} {v_{s} \left( {\rho Av_{s1} \int_{0}^{s} {v_{s1}^{2} ds} - v_{s2} \left( {m\int_{0}^{L} {v_{s1}^{2} ds} + \rho A\int_{s}^{L} {\int_{0}^{s} {v_{s1}^{2} ds} ds} } \right)} \right)ds} $$

$$ \hat{\gamma }_{2} = EI\int_{0}^{L} {v_{s} v_{s4} ds} $$

$$ \hat{\gamma }_{3} = EI\int_{0}^{L} {v_{s} } \left( {v_{s4} v_{s1}^{2} + v_{s2}^{3} + 4v_{s1} v_{s2} v_{s3} } \right)ds $$

$$ \hat{\lambda }_{1} = \rho A\int_{0}^{L} {v_{s} ds} $$

$$ \hat{\lambda }_{2} = \int_{0}^{L} {mv_{s2} v_{s} ds} + \int_{0}^{L} {\rho Av_{s} \left( {v_{s2} \left( {L - s} \right) - v_{s1} } \right)ds} $$

The above equation when converted to the non-dimensional form, gives the following equation

$$ \ddot{x} + \gamma_{1} \left( {\dot{x}^{2} + x\ddot{x}} \right)x + x + \gamma_{3} x^{3} = \lambda_{2} F_{2} x + F_{1} $$

(A.30)

where $v = Lx$, $\tau = \omega_{n} t$ and $\omega_{n}$ is the first mode of the system and is given by, $\omega_{n}^{2} = \frac{{\hat{\gamma }_{2} }}{{\hat{\gamma }_{0} }} = \frac{{EI\int_{0}^{L} {v_{s} v_{s4} ds} }}{{\rho A\int_{0}^{L} {v_{s}^{2} ds} }} = \frac{EI}{{\rho AL^{4} }}\frac{{\int_{0}^{1} {v_{p} v_{p4} dp} }}{{\int_{0}^{1} {v_{p}^{2} dp} }}$

where $v_{p}$ is a normalized mode shape and $v_{pi}$ denotes the i^th derivative of $v_{p}$.

The non-dimensional parameters from Eq. (A28) can be obtained from the following expressions

$$ \boxed{\gamma_{1} = \frac{{\hat{\gamma }_{1} }}{{\hat{\gamma }_{0} }}L^{2} = \frac{{\gamma_{11} - m_{r} \gamma_{12} }}{{\gamma_{13} }}} $$

where $m_{r}$ is the ratio of mass at the tip and the total mass of beam.

$$ \begin{aligned} \gamma_{11} & = \int_{0}^{1} {\left( {v_{p} v_{p1} \int_{0}^{p} {v_{p1}^{2} dp} } \right)dp} - \int_{0}^{1} {\left( {v_{p} v_{p2} \int_{p}^{1} {\left( {\int_{0}^{p} {v_{p1}^{2} dp} } \right)dp} } \right)dp} \\ \gamma_{12} & = \int_{0}^{1} {\left( {v_{p} v_{p2} \int_{0}^{1} {v_{p1}^{2} dp} } \right)dp} \\ \gamma_{13} & = \int_{0}^{1} {v_{p}^{2} dp} \\ \end{aligned} $$

$$ \boxed{\gamma_{3} = \frac{{\hat{\gamma }_{3} }}{{\hat{\gamma }_{2} }}L^{2} = \frac{{\int_{0}^{1} {v_{p} } \left( {v_{p4} v_{p1}^{2} + v_{p2}^{3} + 4v_{p1} v_{p2} v_{p3} } \right)dp}}{{\int_{0}^{1} {v_{p} v_{p4} dp} }}} $$

$$ \boxed{\lambda_{2} = - L\frac{{\hat{\lambda }_{2} }}{{\hat{\gamma }_{0} }} = \frac{{\lambda_{21} + \lambda_{22} m_{r} }}{{\lambda_{23} }}} $$

$$ \begin{aligned} & \lambda_{21} = - \int_{0}^{1} {v_{p} \left( {v_{p2} \left( {1 - p} \right) - v_{p1} } \right)dp} \\ & \lambda_{22} = - \int_{0}^{1} {v_{p2} v_{p} dp} \\ & \lambda_{23} = \int_{0}^{1} {v_{p}^{2} dp} \\ \end{aligned} $$

Appendix B

The objective of introducing the adaptation equation is to maintain the phase difference between the displacement signal and the control signal at $\frac{\pi }{2}$ which results in improved damping irrespective of the excitation frequency. The phase difference can be adjusted by tuning the filter frequency. The product of two harmonic signals with the same frequency ($\omega$, say) gives a biased signal with $2\omega$ frequency. The bias is directly proportional to the cosine of the phase difference between the input signals. Using this property, a first-order differential equation can be constructed as follows

$$ \frac{{d\Omega_{f} }}{dt} = k_{b} xy $$

(B.1)

The rate of convergence for this equation depends on the amplitudes of the system variable and the control force. This leads to a slow response of the adaptation equation for low amplitude vibration suppression. To make the adaptation law independent of the amplitudes, a signum function is used, as shown in Eq. (B.2)

$$ \frac{{d\Omega_{f} }}{dt} = k_{b} {\text{sgn}} \left( x \right){\text{sgn}} \left( y \right) $$

(B.2)

Equtaion (B.2) is shown graphically in Fig. 

Fig. 31

Graphical representation of the adaptation equation

31. One can observe that at a steady state, the right-hand side of the adaption equation gives a square wave which results in the chattering of filtering frequency. To remove this chattering, another square wave is added to the right-hand side of the adaption equation but with the phase difference of $\pi$ radians. This secondary square wave is generated from the already available state variables of the filter. The modified adaption law is,

$$ \frac{{d\Omega_{f} }}{dt} = k_{b} \left( {{\text{sgn}} \left( x \right){\text{sgn}} \left( y \right) + {\text{sgn}} \left( y \right){\text{sgn}} \left( {\dot{y}} \right)} \right) $$

(B.3)

Addition of secondary square wave results in either positive or negative pulses. Where pulse width is directly proportional to $\left( {\frac{\pi }{2} - \theta } \right)$ as shown in Fig. 31. This completely removes the chattering in theory and suppresses the chattering in practice.

For the signal dominated by a single frequency, ${\text{sgn}} \left( x \right)$ can be replaced by $- {\text{sgn}} \left( {\ddot{x}} \right)$. Therefore, the same adaptation equation can be used for both displacement and acceleration signals.

$$ \frac{{d\Omega_{f} }}{dt} = - k_{b} {\text{sgn}} \left( y \right)\left( {{\text{sgn}} \left( {\ddot{x}} \right) - {\text{sgn}} \left( {\dot{y}} \right)} \right) $$

(B.4)

Here, $y = z$.

$$ \frac{{d\Omega_{f} }}{dt} = k_{b} {\text{sgn}} \left( z \right)\left( {{\text{sgn}} \left( {\ddot{x}} \right) - {\text{sgn}} \left( {\dot{z}} \right)} \right) $$

(B.5)

Appendix C

Procedure to calculate the coefficients $c_{i}$ in Eqs. (2a) and (3e).

The approximated function is given by

$$ u = \sum\limits_{i = 1}^{n} {c_{i} \left( {\cos \left( {\Omega t + \alpha } \right)} \right)^{2i - 1} {\text{sgn}} \left( {\sin \left( {\Omega t + \alpha } \right)} \right)} $$

(C.1)

The desired function is

$$ u_{0} = \cot \left( {\Omega t + \alpha } \right) $$

(C.2)

Since the polynomial approximation is independent of $\Omega$, let $\Omega = 1$. Further shifting the time in the above signals, one obtains

$$ u = \sum\limits_{i = 1}^{n} {c_{i} \left( {\cos t} \right)^{2i - 1} {\text{sgn}} \left( {\sin t} \right)} $$

(C.3)

$$ u_{0} = \cot t $$

(C.4)

Since $\cot t$ is a periodic function with a period $\pi$, the error function is defined as

$$ e_{j} = \sum\limits_{i = 1}^{n} {c_{i} \left( {\cos t_{j} } \right)^{2i - 1} } - \cot t_{j} \;\;t_{j} \in \left( {0,\pi } \right) $$

(C.5)

The above equation contains $n$ variables. In order to apply the least square optimization method, $n$ linearly spaced points are selected in the range $t \in \left( {0,\pi } \right)$. This results in $n$ error functions. The above optimization problem is then solved using the built-in MATLAB function lsqnonlin.

Appendix D

Consider a harmonic signal $z = a_{2,1} \sin \left( {\Omega t} \right)$. Squaring on both sides, one obtains,

$$ z^{2} = \frac{{\left( {a_{2,1} } \right)^{2} }}{2}\left( {1 - \cos \left( {2\Omega t} \right)} \right) $$

(D.1)

Here, the objective is to find the controlling equation for a parameter (say $k_{11} > 0$) such that at steady state $k_{11} a_{2,1} = 1$. First, consider the lowest order of the differential equation. It is clear that the rate of change of $k_{11}$ should be proportional to $\left[ {1 - \left( {k_{11} a_{2,1} } \right)^{2} } \right]$. So, the differential equation should look like this,

$$ \dot{k}_{11} = k_{a1} \left[ {1 - \left( {k_{11} a_{2,1} } \right)^{2} } \right] $$

(D.2)

The problem in employing Eq. (D.2) is that the amplitude of the signal is unknown. But from Eq. (D.1) it is clear that the term $z^{2}$ consists of a bias and a periodic signal where bias is proportional to the square of the amplitude of the signal. One can replace the term $\left( {a_{2,1} } \right)^{2}$ with $2z^{2}$. There is a periodic component in $z^{2}$, but the overall change in $k_{11}$ due to this component over a time period $T = \frac{\pi }{\Omega }$ is zero. Therefore the governing equation for the parameter $k_{11}$ is

$$ \dot{k}_{11} = k_{a1} \left( {1 - 2\left( {k_{11} z} \right)^{2} } \right) $$

(D.3)

Or

$$ \dot{k}_{11} = k_{a} \left( {\frac{1}{2} - \left( {k_{11} z} \right)^{2} } \right) $$

(D.4)