Trade-off dynamics and chaotic behavior in nonautonomous prey-predator model with group defense

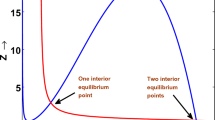
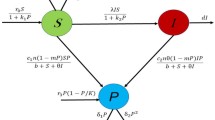
Abstract

Ecological “trade-off” is prioritising one trait over another. Predators put their lives at danger to pursue dangerous prey, and their injuries can reduce their chances of survival. Prey must “trade-off” between reproduction rate and safety, whereas predators must “trade-off” between food and safety. We present a two-dimensional prey and predator model that takes into account prey logistic growth rate and Monod-Haldane type functional response to reflect prey collective defense. We investigate the cost of fear in order to depict prey trade-off dynamics, and we change the predator’s mortality rate by incorporating a function that reflects predator loss as a result of encountering dangerous prey. Our model shows bistability and goes through transcritical bifurcation, saddle node bifurcation, Hopf bifurcation, Bogdanov-Takens bifurcation, Bautin bifurcation, Homoclinic bifurcation, and Limit point of cycle bifurcation. We investigated the effects of our critical parameters on both populations and discovered that predators become extinct if their loss of predator is too high due to encounters with dangerous prey, demonstrating how predators risk their own health for food. We find that fear can lead to global stability in a system by causing the stable and unstable limit cycles to collide. We also see that the degree of seasonality in the level of fear in the nonautonomous model might lead to chaos. Sensitivity analysis, the positivity of the maximal Lyapunov exponent, and the uneven distribution of points observed in the Poincaré map shown are the established signs of chaotic nature. We note that variations in intensity of seasonality in carry-over can cause a system to shift under many different periodic windows. The findings presented in this article may be beneficial in comprehending the biological insights derived from investigating prey-predator interactions.

Appendices

Appendix A Proof of Theorem (4)

The interior equilibrium $E_1^*$ becomes unstable owing to Hopf-bifurcation. Parameter k is taken into consideration as the bifurcation parameter. The eigenvalues are complex conjugate with zero real parts at the Hopf bifurcation point.

Let us assume $\lambda (k)=\lambda _r(k)+i \lambda _i(k)$ be an eigenvalue of the characteristic equation. Replacing the value of $\lambda (k)$ in Eq. (3.10), and separating the real and imaginary parts, we get

$$\begin{aligned} \begin{aligned} \lambda _r^2-\lambda _i^2-A_{11} \lambda _r-A_{12} A_{21}&=0, \\ 2 \lambda _r \lambda _i-A_{11} \lambda _i&=0. \end{aligned} \end{aligned}$$

(A1)

At the point where Hopf bifurcation occurs, we consider $\lambda _r(k)=0$. We denote $k=k_h, \lambda _r\left( k_h\right) =0$, and substitute $\lambda _r=0$ in (A1). Therefore,

$$\begin{aligned} \begin{array}{ccc} \lambda _i^2+A_{12} A_{21} &{} = 0, \\ A_{11} \lambda _i &{} =0, &{} \text{ where } \lambda _i \ne 0. \end{array} \end{aligned}$$

Therefore, based on the equations shown above, we get $A_{11}\left( k_h\right) =0$, and $\lambda _i\left( k_h\right) =\sqrt{-A_{12}\left( k_h\right) A_{21}\left( k_h\right) }>0$, i.e., $\left. {\text {det}}\left( A_{E_1^*}\right) \right| _{k=k_h}=-A_{12}\left( k_h\right) A_{21}\left( k_h\right) >0$. At the Hopf-bifurcation point, we have $A_{11}\left( k_h\right) =0$ and $k_h$ is the positive root of the quadratic equation

$$\begin{aligned} \eta _1 k^2+\eta _2 k+\eta _3 k=0 \end{aligned}$$

where $\eta _1,\eta _2 \text { and } \eta _3$ are given by:

$$\begin{aligned} \eta _1&= -2\,h{x_1}^{*5}{y_1}^{*2}-4\,bh{x_1}^{*3}{y_1}^{*2}-d{x_1}^{*4}{y_1}^{*2}\\&\quad +a{x_1}^{*2}{y_1}^{*3 }-2\,{b}^{2}hx_1^*{y_1}^{*2}-2\,\\&bd{x_1}^{*2}{y_1}^{*2}-ab{y_1}^{*3}-{b}^{2}d{y_1}^{*2}, \\ \eta _2&=-4\,ch{x_1}^{*6}y_1^*-8\,bch{x_1}^{*4}y_1^*-2\,cd{x_1}^{*5}y_1\\&\quad +2\,cr{x_1}^{*5}y_1^*+2\,ac{x_1}^{*3} {y_1}^{*2}-4\,{b}^{2}ch{x_1}^{*2}y-4\,\\&bcd{x_1}^{*3}y+4\,bcr{x_1}^{*3}y_1^*\\&~~~ -4\,h{x_1}^{*5}y_1^*-2\,abcx_1^*{y_1}^{*2}- 2\,{b}^{2}cdx_1^*y_1^*\\&\quad +2\,{b}^{2}crx_1^*y_1^*-8\,bh{x_1}^{*3}y_1^* - 2\,d{x_1}^{* 4}y_1^*\\&\quad +r{x_1}^{*4}y+2\,a{x_1}^{*2}{y_1}^{*2}\\&~~~ -4\,{b}^{2}hx_1^*y_1^*-4\,bd{x_1}^{*2}y_1^*+2\,br{x_1}^ {*2}y_1^*\\&\quad -2\,ab{y_1}^{*2}-2\,{b}^{2}dy_1^*+{b}^{2}ry_1^*\\ \eta _3&= -2\,{c}^{2}h{x_1}^{*7}-4\,b{c}^{2}h{x_1}^{*5}-{c}^{2}d{x_1}^{*6}+{c}^{2}r{x_1}^{*6 }\\&\quad +a{c}^{2}{x_1}^{*4}y_1^*-2\,{b}^{2}{c}^{2}h{x_1}^{*3}-2\,\\&b{c}^{2}d{x_1}^{*4}+2\,b{ c}^{2}r{x_1}^{*4}-4\,ch{x_1}^{*6}\\&~~~-ab{c}^{2}{x_1}^{*2}y_1-{b}^{2}{c}^{2}d{x_1}^{*2}+ { b}^{2}{c}^{2}r{x_1}^{*2}-8\,bch{x_1}^{*4}\\&\quad -2\,cd{x_1}^{*5}+2\,cr{x_1}^{*5}+2\,ac{x_1} ^{*3}y\\&\quad - 4\,{b}^{2}ch{x_1}^{*2}-4\,bcd{x_1}^{*3}\\&~~~ +4\,bcr{x_1}^{*3}-2\,h{x_1}^{*5}-2\,a bcx_1^*y_1^*\\&\quad -2\,{b}^{2}cdx_1^*+ 2\,{b}^{2}crx_1^*-4\,bh{x_1}^{*3}\\&\quad -d{x_1}^{*4}+r{x_1}^{*4}+a{x_1}^{* 2}y_1^*\\&~~~ -2\,{b}^{2}hx_1^*-2\,bd{x_1}^{*2}\\&\quad +2\,br{x_1}^{*2}-aby_1^*-{b}^{2}d+{b}^{2}r.\\ \end{aligned}$$

We differentiate Eq. (A1), w.r.t. k and putting $\lambda _r(k)=0$, we have

$$\begin{aligned} \begin{array}{r} -A_{11} \frac{d\left( \lambda _r\right) }{d k}-2 \lambda _i \frac{d\left( \lambda _i\right) }{d k}=\frac{d\left( A_{12} A_{21}\right) }{d k} \\ 2 \lambda _i \frac{d\left( \lambda _r\right) }{d k}-A_{11} \frac{d\left( \lambda _i\right) }{d k}=\lambda _i \frac{d\left( A_{11}\right) }{d k} \end{array} \end{aligned}$$

By resolving the above system of equations, we have

$$\begin{aligned} \left. \frac{d\left( \lambda _r\right) }{d k}\right| _{k=k_h}=\left. \frac{2 \lambda _i^2 \frac{d\left( A_{11}\right) }{d k}-A_{11} \frac{d\left( A_{12} A_{21}\right) }{d k}}{A_{11}^2+4 \lambda _i^2}\right| _{k=k_h} \ne 0 \end{aligned}$$

$\left. {\text {provided}}\left[ 2 \lambda _i^2 \frac{d\left( A_{11}\right) }{d k}-A_{11} \frac{d\left( A_{12} A_{21}\right) }{d k}\right] \right| _{k=k_h} \ne 0$

Appendix B Proof of Theorem (5)

We use a sequence of transformations to derive a normal form using the approaches and steps described in Kuznetsov’s book [50]. We consider the system (2.3) and keeping all other parameters constant and arbitrarily selecting the trade-off parameters k and l. Without loss of generality, we define $x_0(k,l)=x_0$ and $y_0(k,l)=y_0$. Since all the parameters are positive and y is non-negative, so in the model (2.3), $\frac{d x}{d t}=f(x,y)$ and $\frac{d y}{d t}=g(x,y)$ are smooth functions of x and y. Assume that $k = k_{BT}$ and $l = l_{BT}$, also $T(x_0,y_0)=0$ and $D(x_0,y_0)=0$, where $T(x_0,y_0)$ and $D(x_0,y_0)$ are the trace and determinant of the Jacobian matrix in (3.8) evaluated at $E_0(x_0,y_0)$. This matrix has a zero eigenvalue of algebraic multiplicity two. Now we consider the following parametric region

$$\begin{aligned}{} & {} \Gamma = \left\{ (r,a,b,c,d,e,h,k,l,m)\in \mathbb {R}{^{10}_+}: T(x_0,y_0)\right. \\ {}{} & {} \quad \left. =0, D(x_0,y_0)=0\right\} . \end{aligned}$$

Mathematically, $\Gamma$ represents a BT surface. In what follows, we will try to reduce the system (2.3) in the canonical form of BT bifurcation by employing a series of $C^\infty$ change of coordinates in a small neighborhood of (0, 0). For these, first we use the transformation $x = x_1+x_0$ and $y =x_2+y_0$, so that the equilibrium point of the system (2.3) shifted to the origin. We take a small perturbation of the model (2.3) at $k = k_{BT}$ and $l =l_{BT}$. Then the model system (2.3) we get,

$$\begin{aligned} \begin{array}{l} \frac{d x_1}{d t}=\frac{r( x_1+x_0) (1+c(x_1+x_0))}{1+c (x_1+x_0)+(k+\theta _1) (x_2+y_0)}-d (x_1+x_0) \\ \quad -h (x_1+x_0)^2-\frac{a (x_1+x_0) (x_2+y_0)}{b+(x_1+x_0)^2}, \\ \frac{d x_2}{d t}=-m (x_2+y_0) \left( \frac{(l+\theta _2)( x_1+x_0)}{1+(l+\theta _2) (x_1+x_0)}+1\right) \\ \quad +\frac{a e (x_1+x_0) (x_2+y_0)}{b+(x_1+x_0)^2}, \end{array} \end{aligned}$$

(B1)

where $\theta = (\theta _1,\theta _2)$ is a parameter vector vary in the small neighbourhood of (0,0). Expanding the Taylor’s series of system (B1) at $(x_1,x_2)=(0,0)$ up to the terms of order 2, produces the following system.

$$\begin{aligned} \begin{array}{l} {\frac{{dx_1}}{{dt}}}=m_{00} \left( \theta \right) +m_{10} \left( \theta \right) {x_1}+m_{01} \left( \theta \right) { x_2}+m_{20} \left( \theta \right) {{x_1}}^{2}\\ \quad +m_{11} \left( \theta \right) {x_1 x_2}+m_{02} \left( \theta \right) {{ x_2}}^{2}+O \left( \left( \left| x \right| \right) ^{3} \right) , \\ {\frac{{dx_2}}{{dt}}}=n_{00} \left( \theta \right) + n_{10} \left( \theta \right) {x_1}+n_{01} \left( \theta \right) { x_2}+n_{20} \left( \theta \right) {{x_1}}^{2}\\ \quad +n_{11} \left( \theta \right) {x_1 x_2} +n_{02} \left( \theta \right) {{ x_2}}^{2}+O \left( \left( \left| x \right| \right) ^{3} \right) , \end{array} \end{aligned}$$

(B2)

where

$m_{00}=x_0 \left( -\frac{a y_0}{b+x_0^2}+\frac{r (c x_0+1)}{c x_0+y_0 (k_{BT}+\theta _1)+1}-d-h x_0\right) ,$

$n_{00}=y_0 \left( \frac{a e x_0}{b+x_0^2}+m \left( \frac{1}{x_0 (l_{BT}+\theta _2)+1}-2\right) \right) ,$

$m_{10}=-\frac{a y_0 \left( b-x_0^2\right) }{\left( b+x_0^2\right) ^2} +\frac{r \left( c^2 x_0^2+2 c x_0 (y_0 (k_{BT}+\theta _1)+1)+y_0 (k_{BT}+\theta _1)+1\right) }{(c x_0+y_0 (k_{BT}+\theta _1)+1)^2}-d-2\,h x_0,$

$m_{01}=x_0 \left( -\frac{a}{b+x_0^2}-\frac{r (c x_0+1) (k_{BT}+\theta _1)}{(c x_0+y_0 (k_{BT}+\theta _1)+1)^2}\right) ,$ $m_{20}=2 y_0 \left( \frac{c r (k_{BT}+\theta _1) (y_0 (k_{BT}+\theta _1)+1)}{(c x_0+y_0 (k_{BT}+\theta _1)+1)^3}-\frac{a x_0 \left( x_0^2-3 b\right) }{\left( b+x_0^2\right) ^3}\right) -2\,h,$

$m_{02}=\frac{2 r x_0 (c x_0+1) (k_{BT}+\theta _1)^2}{(c x_0+y_0 (k_{BT}+\theta _1)+1)^3},$ $m_{11}=\frac{a \left( x_0^2-b\right) }{\left( b+x_0^2\right) ^2}+\frac{r (k_{BT}+\theta _1) (-c x_0 (2 y_0 (k_{BT}+\theta _1)+1)+y_0 (-(k_{BT}+\theta _1))-1)}{(c x_0+y_0 (k_{BT}+\theta _1)+1)^3},$

$n_{10}=y_0 \left( \frac{a e \left( b-x_0^2\right) }{\left( b+x_0^2\right) ^2}-\frac{m (l_{BT}+\theta _2)}{(x_0 (l_{BT}+\theta _2)+1)^2}\right) ,$ $n_{01}=\frac{a e x_0}{b+x_0^2}+m \left( \frac{1}{x_0 (l_{BT}+\theta _2)+1}-2\right) ,$

$n_{20}=y_0 \left( \frac{2 a e x_0 \left( x_0^2-3 b\right) }{\left( b+x_0^2\right) ^3}+\frac{2\,m (l_{BT}+\theta _2)^2}{(x_0 (l_{BT}+\theta _2)+1)^3}\right) ,$ $n_{02}=0,$ and $n_{11}=\frac{a e \left( b-x_0^2\right) }{\left( b+x_0^2\right) ^2}-\frac{m (l_{BT}+\theta _2)}{(x_0 (l_{BT}+\theta _2)+1)^2}.$ Here we assume that,

$$\begin{aligned}{} & {} m_{10}(0)+n_{01}(0)=0 \text { and } \\ {}{} & {} m_{10}(0)n_{10}(0)-m_{01}(0)n_{10}(0)=0. \end{aligned}$$

Now we introduce affine transformation,

$$\begin{aligned} u_1 = x_1 \text { and } u_2 = m_{10} x_1+m_{01} x_2, \end{aligned}$$

which reduces the system (B2) to

$$\begin{aligned} \begin{array}{l} \frac{d u_1}{d t}=m_{00}(\theta )+u_2+p_{20}(\theta ) u_1^2+p_{11}(\theta ) u_1 u_2\\ \quad +p_{02}(\theta ) u_2^2+O\left( \Vert u\Vert ^3\right) , \\ \frac{d u_2}{d t}=q_{00}(\theta )+q_{10}(\theta ) u_1+q_{01}(\theta ) u_2+q_{20}(\theta ) u_1^2\\ \quad +q_{11}(\theta ) u_1 u_2+q_{02}(\theta ) u_1^2+O\left( \Vert u\Vert ^3\right) , \end{array} \end{aligned}$$

(B3)

where

$$\begin{aligned} \begin{array}{l} p_{20}(\theta )=m_{20}-\frac{m_{11} m_{10}}{m_{01}}+\frac{m_{02} m_{10}^2}{m_{01}^2},\\ p_{11}(\theta )=\frac{m_{11}}{m_{01}}-\frac{2 m_{10} m_{02}}{m_{01}^2}, ~ p_{02}(\theta )=\frac{m_{02}}{m_{10}^2}, ~\\ q_{00}(\theta )=m_{10} m_{00}+m_{01} n_{00}, ~ q_{10}(\theta )=m_{01} n_{10}-m_{10} n_{01},\\ q_{01}(\theta )=m_{10}+n_{01}, \\ q_{20}(\theta )=m_{10} m_{20}-\frac{m_{11} m_{10}^2}{m_{01}}+\frac{m_{02}~ m_{10}^3}{m_{01}^2}\\ +m_{01} n_{20}-m_{10} n_{11}+\frac{n_{02} m_{10}^2}{m_{01}}, \\ q_{11}(\theta )=n_{11}+\frac{m_{11} m_{10}}{m_{01}}-\frac{2 m_{10}^2 m_{02}}{m_{01}^2}-\frac{2 m_{10} n_{02}}{m_{01}},\\ q_{02}(\theta )=\frac{m_{10} m_{02}}{m_{01}^2}+\frac{n_{02}}{m_{01}}. \end{array} \end{aligned}$$

The function $q_{00}(\theta ),\alpha _{kl}(\theta ),\beta _{kl}(\theta )$ are smooth functions of $\theta$ and we take $\theta ^*=(0,0)$. We assume $q_{00}(\theta ^*)=0$ and consider the fact $q_{10}(\theta ^*)=q_{01}(\theta ^*)=0.$ Next, under the preceding $C^{\infty }$ change of coordinates in a small neighbourhood of (0, 0)

$$\begin{aligned} \begin{array}{l} z_1= u_1\\ z_2 =m_{00}(\theta )+u_2+p_{20}(\theta ) u_1^2+p_{11}(\theta ) u_1 u_2\\ +p_{02}(\theta ) u_2^2+O\left( \Vert u\Vert ^3\right) , \end{array} \end{aligned}$$

the system (B3) becomes,

$$\begin{aligned} \begin{array}{l} \frac{d z_1}{d t}=z_2, \\ \frac{d z_2}{d t}=s_{00}(\theta )+s_{10}(\theta ) z_1+s_{01}(\theta ) z_2+s_{20}(\theta ) z_1^2\\ \quad +s_{11}(\theta ) z_1 z_2+s_{02}(\theta ) z_2^2+O\left( \Vert z\Vert ^3\right) , \end{array} \end{aligned}$$

(B4)

where

$$\begin{aligned} \begin{aligned} s_{00}(\theta )&=q_{00}(\theta )-m_{00}(\theta ) q_{01}(\theta ) +\cdots , \\ s_{10}(\theta )&=q_{10}(\theta )+p_{11}(\theta ) q_{00}(\theta )-m_{00}(\theta ) q_{11}(\theta ) +\cdots , \\ s_{01}(\theta )&=q_{01}(\theta )-m_{00}(\theta ) p_{11}(\theta )+2 m_{00}(\theta ) q_{02}(\theta )\\&-2 m_{00}(\theta ) q_{02}(\theta )+\cdots ,\\ s_{20}(\theta )&=q_{20}(\theta )+p_{11}(\theta ) q_{10}(\theta )-q_{01}(\theta ) p_{20}(\theta )+\cdots , \\ s_{11}(\theta )&=q_{11}(\theta )+2 p_{20}(\theta )+2 p_{02}(\theta ) q_{10}(\theta )+\cdots , \\ s_{02}(\theta )&=q_{02}(\theta )-p_{02}(\theta ) q_{01}(\theta )+p_{11}(\theta ) +\cdots . \end{aligned} \end{aligned}$$

Here we observe that $s_{00}(0)=s_{10}(0)=s_{01}(0)=0$, since $q_{00}(0)=0=q_{10}(0)=q_{01}(0)$ and $s_{20}(0)=q_{20}(0), \quad s_{11}(0)=q_{11}(0)+2 p_{20}(0), \quad s_{02}(0)=q_{02}(0)+p_{11}(0).$ We analyze the following parameter-dependent shift of coordinates in the $z_1$-direction to annihilate the $z_2$ term on the RHS of the second equation of (B4)

$$\begin{aligned} \begin{aligned}&z_1=j_1+\gamma (\theta ) \text { and }z_2=j_2.\\ \end{aligned} \end{aligned}$$

Using the above transformation system (B4) reduces to

$$\begin{aligned} \begin{array}{ll} \frac{d j_1}{d t}= j_2 \\ \frac{d j_2}{d t}=g_{00}(\theta )+g_{10}(\theta ) j_1+g_{01}(\theta ) j_2+g_{20}(\theta ) j_1^2\\ +g_{11}(\theta ) j_1 j_2+g_{02}(\theta ) j_2^2+O\left( \Vert j\Vert ^3\right) , \end{array}\nonumber \\ \end{aligned}$$

(B5)

where $g_{00}=s_{00}+s_{10} \gamma +s_{20} \gamma ^2+\cdots , \quad g_{10}=s_{10}+2 s_{20} \gamma +\cdots , \quad g_{01}=s_{01}+s_{11} \gamma +\cdots$, $g_{20}=s_{20}+\cdots , \quad g_{11}=s_{11}+\cdots , \quad g_{02}=s_{02}+\cdots$.

The coefficient of $j_2$ in right hand side of the second equation of (B5) is written by $g_{01}=s_{01}+s_{11} \gamma +O\left( \Vert \gamma \Vert ^2\right) .$ Thus we assume that

$$\begin{aligned} \begin{aligned} g_{01}&=s_{01}\left( \theta ^*\right) =0,\left. \quad \frac{\partial g_{01}}{\partial \gamma }\right| _{\left( 0, \theta ^*\right) }\\&=q_{11}(\theta ^*)+2 p_{20}(\theta ^*)= \rho _2 \ne 0. \end{aligned} \end{aligned}$$

(B6)

We can imply that there exists a smooth function locally $\gamma =\gamma \left( \theta ^*\right)$ such that $\gamma \left( \theta ^*\right) =0, g_{01}(\gamma (\theta ),\theta )=0$ for any $\theta \in N\left( \theta ^*\right) ,$ where $N\left( \theta ^*\right)$ denotes the a small neighbourhood of $\theta = \theta ^*.$

Let any $\theta \in N\left( \theta ^*\right) \text { we have } \gamma (\theta ) \in M$. Then in the open connected region $M, \gamma (\theta )$ can be approximated by

$$\begin{aligned} \begin{aligned} \gamma (\theta )&\approx -\frac{s_{01}(\theta )}{s_{11}(\theta )} \approx -\frac{s_{01}(\theta )}{s_{11}\left( \theta ^*\right) }. \end{aligned} \end{aligned}$$

Thus, (B5) reduces to the following

$$\begin{aligned} \begin{aligned} \frac{d j_1}{d t}=&j_2, \\ \frac{d j_2}{d t}=&g_{00}(\theta )+g_{10}(\theta ) j_1+g_{20}(\theta ) j_1^2\\&+g_{11}(\theta ) j_1 j_2 +g_{02}(\theta ) j_2^2+O\left( \Vert j\Vert ^3\right) . \end{aligned} \end{aligned}$$

(B7)

The essential terms of $g_{i j}(\theta ), i+j=2$, are, at $\theta =\theta ^*, g_{20}\left( \theta ^*\right) =s_{20}\left( \theta ^*\right) , g_{11}\left( \theta ^*\right) =s_{11}\left( \theta ^*\right) , g_{02}\left( \theta ^*\right) =s_{02}\left( \theta ^*\right)$, where $s_{i j}\left( \theta ^*\right) ; i+j=2$ are determined earlier. We have $g_{00}\left( \theta ^*\right) =g_{10}\left( \theta ^*\right) =0$.

We take a new timescale that is determined by $d t=\left( 1+\psi j_1\right) d \tau$ where $\psi =\psi (\theta )$ is a smooth function to be defined ahead. Due to this transformation, (B7) reduces to

$$\begin{aligned} \begin{aligned} \frac{d j_1}{d \tau }=&j_2\left( 1+\psi j_1\right) ,\\ \frac{d j_2}{d \tau }=&g_{00}+\left( g_{10}+g_{00} \psi \right) j_1+\left( g_{20}+g_{10} \psi \right) j_1^2 \\&+g_{11} j_1 j_2+g_{02} j_2^2+O\left( \Vert j\Vert ^3\right) . \end{aligned} \end{aligned}$$

Assume $v_1=j_1, v_2=j_2\left( 1+\psi j_1\right) .$ Then we obtain

$$\begin{aligned} \begin{aligned} \frac{d v_1}{d \tau }=&v_2, \\ \frac{d v_2}{d \tau }=&w_{00}(\theta )+w_{10}(\theta ) v_1+w_{20}(\theta ) v_1^2\\&+w_{11}(\theta ) v_1 v_2 +w_{02}(\theta ) v_2^2+\textrm{O}\left( \Vert v\Vert ^3\right) , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&w_{00}(\theta )=g_{00}(\theta ), ~ w_{10}(\theta )=g_{10}(\theta )\\&+2 g_{00}(\theta ) \psi (\theta ),w_{11}(\theta )=g_{11}(\theta ), \\&w_{20}(\theta )=g_{20}(\theta )+2 g_{10}(\theta ) \psi (\theta )\\&+g_{00}(\theta ) \psi ^2(\theta ),~ w_{02}(\theta )=g_{02}(\theta )+\psi (\theta ). \end{aligned} \end{aligned}$$

Now we take $\psi (\theta )=-g_{02}(\theta )$ in order to remove $v_2^2$-term. We then have

$$\begin{aligned} \begin{aligned}&\frac{d v_1}{d \tau }=v_2, \\&\frac{d v_2}{d \tau }=A_1(\theta )+A_2(\theta ) v_1+{N_1}(\theta ) v_1^2\\&+{N_2}(\theta ) v_1 v_2+O\left( \Vert v\Vert ^3\right) , \end{aligned} \end{aligned}$$

(B8)

where

$$\begin{aligned} \begin{aligned}&A_1(\theta )=g_{00}(\theta ), ~ A_2(\theta )=g_{10}(\theta )-2 g_{00}(\theta ) g_{02}(\theta ), \\&{N_1}(\theta )=g_{20}(\theta )-2 g_{10}(\theta ) g_{02}(\theta )+g_{02}^2(\theta ) g_{00}(\theta ), \\&{N_2}(\theta )=g_{11}(\theta ). \end{aligned} \end{aligned}$$

We always have,

$$\begin{aligned}&A_1\left( \theta ^*\right) =A_2\left( \theta ^*\right) =0 \text { and }{N_1}\left( \theta ^*\right) =g_{20}\left( \theta ^*\right) \nonumber \\&= s_{20}\left( \theta ^*\right) \ne 0, {N_2}\left( \theta ^*\right) =s_{11}\left( \theta ^*\right) =\rho _2 \ne 0. \end{aligned}$$

(B9)

We present a different time scale denoted by $t=\left| \frac{{N_2}(\theta )}{{N_1}(\theta )}\right| \tau ,$ with the distinct variables $B_1=\left( \frac{N_1(\theta )}{{L}^2(\theta )}\right) v_1$ and $B_2=s\left( \frac{N_1^2(\theta )}{{N_2}^3(\theta )}\right) v_2$ such that $s={\text {sign}}\left( \frac{L(\theta )}{N_1(\theta )}\right) ={\text {sign}}\left( \frac{N_2\left( \theta ^*\right) }{N_1\left( \theta ^*\right) }\right) =\pm 1.$ This yields (B8) into the form

$$\begin{aligned} \begin{aligned}&\frac{d C_1}{d \tau }=C_2, \\&\frac{d C_2}{d \tau }=B_1+B_2 C_1+C_1^2+\omega C_1 C_2+O\left( \Vert C\Vert ^3\right) , \end{aligned} \end{aligned}$$

(B10)

where

$$\begin{aligned} B_1(\theta )=\frac{{N_2}^4(\theta )}{{N_1}^3(\theta )} A_1(\theta ), \end{aligned}$$

$$\begin{aligned} B_2(\theta )=\frac{{N_2}^2(\theta )}{{N_1}^2(\theta )} A_2(\theta ). \end{aligned}$$

(B11)

The system (B10) is locally topologically equivalent close to the origin for small $\Vert B\Vert$ to the system

$$\begin{aligned} \begin{aligned}&\frac{d C_1}{d \tau }=C_2, \\&\frac{d C_2}{d \tau }=B_1+B_2 C_1+C_1^2+\omega C_1 C_2, \end{aligned} \end{aligned}$$

(B12)

where $\omega =\pm 1$. We have determined the generic normal form of the Bogdanov-Takens bifurcation for the system (2.3). In order to evaluate whether there exists original parameter $\theta \in \mathbb {R}^{10}$ for Bogdanov-Takens bifurcation is comparable to the condition of regularity of the map $\theta \rightarrow \left( B_1(\theta ), B_2(\theta )\right)$ at $\theta =\theta ^*$ i.e., ${\text {rank}}\left( \frac{\partial \left( B_1, B_2\right) }{\partial \theta }\right) _{\theta =\theta ^*}=2.$ The parameters may then be selected as $\theta _k, k=1,2, \ldots , 10$ and $\theta _l, l(\ne k)=1,2, \ldots ,10$ or any components of $\theta$ as bifurcation parameters so that

$$\begin{aligned} \left| \begin{array}{ll} \frac{\partial B_1}{\partial \theta _k} &{} \frac{\partial B_1}{\partial \dot{\theta }_l} \\ \frac{\partial B_2}{\partial \dot{\theta }_k} &{} \frac{\partial B_2}{\partial \dot{\theta }_l} \end{array}\right| \ne 0. \end{aligned}$$

(B13)

The system (B10) is labelled as normal form of Bogdanov-Takens bifurcation. Assuming the non-degeneracy conditions (B6), (B9) and (B10), the system (2.3) can be transformed into the system (B10). Thus the system (2.3) undergoes Bogdanov-Takens bifurcation with respect to k and l as varying parameters in a small neighbourhood of origin.

Appendix C Proof of Theorem (8)

Let $x(t)= \exp (u(t)) \text { and } y(t)= \exp (v(t)),$ then the system (2.4) may then be rewritten as follows:

$$\begin{aligned} \begin{array}{ll} \frac{d u}{d t}=\frac{r (1+c(t) \exp (u(t)))}{1+c(t) \exp (u(t))+k(t) \exp (v(t))}-d-h \exp (u(t))\\ \qquad -\frac{a \exp (v(t))}{b+\exp (2u(t))}, \\ \frac{d v}{d t}=-m \left( \frac{l \exp (u(t))}{1+l \exp (u(t))}+1\right) +\frac{a e \exp (u(t))}{b+\exp (2u(t))}. \end{array} \end{aligned}$$

(C1)

Thus, if (u(t), v(t)) is a $\omega -$periodic solution of the system (C1), then $(x(t),y(t))=(\exp (u(t)),\exp (v(t)))$ is a positive $\omega -$periodic solution of (2.4). To utilise the continuation theorem, we choose

$$\begin{aligned}{} & {} U=V=\left\{ \left( u, v\right) ^T \in C\left( \mathbb {R}, \mathbb {R}^2\right) \mid u(t+\omega )\right. \\ {}{} & {} \left. \quad =u(t) \text { and } v(t+\omega )=v(t), t \in \mathbb {R}\right\} , \end{aligned}$$

equipped with the norm $\left\| \left( u, v\right) \right\| =\max _{t \in [0, \omega ]}\left| u(t)\right| +\max _{t \in [0, \omega ]}\left| v(t)\right|$. Then $(U,\Vert \cdot \Vert )$ and $(V,\Vert \cdot \Vert )$ are both Banach spaces.

Let

$$\begin{aligned}{} & {} M\left[ \begin{array}{c}u\\ v\end{array}\right] = \left[ \begin{array}{c}u'\\ v'\end{array}\right] ,~ N\left[ \begin{array}{c}u\\ v\end{array}\right] = P\left[ \begin{array}{c}u\\ v\end{array}\right] = \left[ \begin{array}{c}\frac{1}{\omega }\underset{0}{\overset{\omega }{\int }}u\left( t\right) dt \\ \frac{1}{\omega }\underset{0}{\overset{\omega }{\int }}v\left( t\right) dt\end{array}\right] ,\\{} & {} Q\left[ \begin{array}{l} u \\ v \end{array}\right] =\left[ \begin{array}{l} \frac{r (1+c(t) \exp (u(t)))}{1+c(t) \exp (u(t))+k(t) \exp (v(t))}-d-h \exp (u(t))-\frac{a \exp (v(t))}{b+\exp (2u(t))}\\ -m \left( 1+\frac{l \exp (u(t))}{1+l \exp (u(t))}\right) +\frac{a e \exp (u(t))}{b+\exp (2u(t))} \end{array}\right] ,\left[ \begin{array}{l} u \\ v \end{array}\right] \in U. \end{aligned}$$

Then system (C1) is identical to the operator equation $Ms=Qs, s =\left( u, v\right) ^T \in U$. We merely need to confirm the operator equation’s conditions in Lemma (4.1) and establish that at least one $\omega$-periodic solution of system (C1) exists. It’s simple to observe that

$$\begin{aligned} \begin{aligned}&{\text {Ker}} M=\left\{ \left( u, v\right) \in U \mid \left( u, v\right) =\left( c_1, c_2\right) \in \mathbb {R}^2\right\} , \\&{\text {Im}} M=\left\{ \left( u, v\right) \in U \mid \int _0^\omega u(t) d t =0 \text { and } \right. \\&\qquad \left. \int _0^\omega v(t) d t =0 \right\} , \end{aligned} \end{aligned}$$

and ${\text {dim}} {\text {Ker}} M=2=$ codim ${\text {Im}} M$. Since ${\text {Im}} M$ is closed in V, M is a Fredholm mapping of index zero. We know that $N(=P)$ is a continuous projection such that ${\text {Im}} N={\text {Ker}} M,~ {\text {Im}} M={\text {Ker}} P={\text {Im}}(I-P). M_N^{-1}$: ${\text {Im}} M \rightarrow {\text {dom}} M \cap {\text {Ker}} N$ exists and is given by

$$\begin{aligned} M_N^{-1}\left[ \begin{array}{l} u \\ v \end{array}\right] =\left[ \begin{array}{c} \int _0^t u(s) d s-\frac{1}{\omega } \int _0^\omega \int _0^t u(s) d s d t \\ \int _0^t v(s) d s-\frac{1}{\omega } \int _0^\omega \int _0^t v(s) d s d t \end{array}\right] . \end{aligned}$$

Since PQ and $M_N^{-1}(I-P) Q$ are continuous, we can easily verify that Q is M-compact on an any closed bounded set in U.

Let $s=(u,v)^T \in U$ be a solution of $M s =\lambda Qs$ for a specific $\lambda \in (0,1)$. Then

$$\begin{aligned} \frac{d u}{d t}= & {} \lambda \left[ \frac{r (1+c(t) \exp (u(t)))}{1+c (t)\exp (u(t))+k(t)\exp (v(t))}\right. \nonumber \\{} & {} \left. -d-h \exp (u(t))-\frac{a \exp (v(t))}{b+\exp (2u(t))} \right] , \end{aligned}$$

(C2)

$$\begin{aligned} \frac{d v}{d t}= & {} \lambda \left[ -m \left( \frac{l \exp (u(t))}{1+l \exp (u(t))}+1\right) +\frac{a e \exp (u(t))}{b+\exp (2u(t))} \right] .\nonumber \\ \end{aligned}$$

(C3)

After integrating above Eq. (C2) over $[0, \omega ]$, we have

$$\begin{aligned} d\omega= & {} \int _0^\omega \left[ \frac{r (1+c(t) \exp (u(t)))}{1+c(t) \exp (u(t))+k(t)\exp (v(t))}\right. \nonumber \\{} & {} \left. -h \exp (u(t))-\frac{a \exp (v(t))}{b+\exp (2u(t))} \right] dt, \end{aligned}$$

(C4)

$$\begin{aligned}{} & {} \implies d\omega + \int _0^\omega h \exp (u(t))+\frac{a \exp (v(t))}{b+\exp (2u(t))} dt \nonumber \\{} & {} = \int _0^\omega \frac{r (1+c(t) \exp (u(t)))}{1+c(t) \exp (u(t))+k(t)\exp (v(t))} dt. \end{aligned}$$

(C5)

From above we can conclude that,

$$\begin{aligned} \begin{aligned} \int _0^\omega |u'(t)|dt&\le 2 \Big ( d\omega + \int _0^\omega h \exp (u(t))\\&+\frac{a \exp (v(t))}{b+\exp (2u(t))} dt)\Big ) \le 2\omega K_1, \end{aligned} \end{aligned}$$

(C6)

where $K_1= d + \frac{1}{\omega } \int _0^\omega h \exp (u(t))+\frac{a \exp (v(t))}{b+\exp (2u(t))} dt.$

After integrating Eq. (C3) over $[0, \omega ]$, we have

$$\begin{aligned} m\omega = \int _0^\omega \left[ -m \left( \frac{l \exp (u(t))}{1+l \exp (u(t))}\right) +\frac{a e \exp (u(t))}{b+\exp (2u(t))} \right] dt,\nonumber \\ \end{aligned}$$

(C7)

$$\begin{aligned}{} & {} \implies m\omega +\int _0^\omega m \left( \frac{l \exp (u(t))}{1+l \exp (u(t))}\right) \nonumber \\{} & {} = \int _0^\omega \frac{a e \exp (u(t))}{b+\exp (2u(t))} dt. \end{aligned}$$

(C8)

We can deduce from the preceding that,

$$\begin{aligned} \begin{aligned} \int _0^\omega |v'(t)|dt&\le 2 \Big ( m\omega +\int _0^\omega \frac{a e \exp (u(t))}{b+\exp (2u(t))} dt)\Big )\\&\le 2\omega K_2, \end{aligned} \end{aligned}$$

(C9)

where $K_2= m+ \frac{1}{\omega }\int _0^\omega \frac{a e \exp (u(t))}{b+\exp (2u(t))} dt).$

Let us denote

$$\begin{aligned}{} & {} u\left( \xi _1\right) =\min _{t \in [0, \omega ]} u(t), \quad u\left( \eta _1\right) =\max _{t \in [0, \omega ]} u(t) \text { and }\\{} & {} v\left( \xi _2\right) =\min _{t \in [0, \omega ]} v(t), \quad v\left( \eta _2\right) =\max _{t \in [0, \omega ]} v(t). \end{aligned}$$

From Theorem (6), we can deduce that

$$\begin{aligned} u(\xi _1)\le \ln (M_1),~ v(\xi _2)\le \ln (M_2) \end{aligned}$$

and let $M'= \max \{ln(M_1),ln(M_2)\}$. Then

$$\begin{aligned} u(t) \le u\left( \xi _1\right) +\int _0^\omega \left| u^{\prime }(t)\right| d t \le \ln (M_1)+2 K_1 \omega :=A_1. \end{aligned}$$

And similarly we have

$$\begin{aligned} v(t) \le v\left( \xi _2\right) +\int _0^\omega \left| v^{\prime }(t)\right| d t \le \ln (M_2)+2 K_2 \omega :=A_2. \end{aligned}$$

Again from Theorem (6), we can deduce that

$$\begin{aligned} u(\eta _1)\ge \ln (m_1),~ v(\eta _2)\ge \ln (m_2). \end{aligned}$$

Then

$$\begin{aligned} u(t) \ge u\left( \eta _1\right) -\int _0^\omega \left| u^{\prime }(t)\right| d t \ge \ln (m_1)-2 K_1 \omega :=B_1. \end{aligned}$$

and similarly we have

$$\begin{aligned} v(t) \ge v\left( \eta _2\right) -\int _0^\omega \left| v^{\prime }(t)\right| d t \ge \ln (m_2)-2 K_2 \omega :=B_2. \end{aligned}$$

Let $\max _{t \in [0, \omega ]}\left| u(t)\right| \le \max \left\{ \left| A_{1}\right| ,\left| B_{1}\right| \right\} := K_1$ and $\max _{t \in [0, \omega ]}\left| v(t)\right| \le \max \left\{ \left| A_{2}\right| ,\left| B_{2}\right| \right\} :=K_2.$

Define $\Omega =\left\{ \left( u, v\right) ^T \in X \mid \left\| \left( u, v\right) \right\| <K\right\}$, where $K=K_1+K_2+K_3$ and $K_3>0$ is sufficiently large such that for each $\lambda \in (0,1)$, every solution $s=\left( u, v\right) ^T$ of $M s=\lambda Q s$ satisfies $s \notin \partial \Omega$.

In order to verify the second condition of Lemma (4.1), we need to consider the following algebraic equations:

$$\begin{aligned} \begin{aligned}&\frac{\mu }{\omega } \int _0^\omega \left[ \frac{r (1+c(t) \exp (u(t)))}{1+c(t) \exp (u(t))+k(t) \exp (v(t))}-d-h\right. \\&\left. \exp (u(t))-\frac{a \exp (v(t))}{b+\exp (2u(t))} \right] d t=0, \\&\frac{\mu }{\omega } \int _0^\omega \left[ -m \left( \frac{l \exp (u(t))}{1+l \exp (u(t))}+1\right) \right. \\&\left. +\frac{a e \exp (u(t))}{b+\exp (2u(t))} \right] d t=0, \end{aligned} \end{aligned}$$

(C10)

where $\left( u, v\right) \in \mathbb {R}^2$ and $\mu \in [0,1]$ is a parameter. Similarly to the previously stated arguments, it is simple to verify that any solution $\left( u^*, v^*\right)$ with $\mu \in [0,1]$ satisfies $\left\| \left( u^*, v^*\right) \right\| <K$.

Following that, for each $s=\left( u, v\right) ^T \in \partial \Omega \cap {\text {Ker}} M=\partial \Omega \cap \mathbb {R}^2, PQ s \ne 0$, i.e.,

$$\begin{aligned} PQ\left[ \begin{array}{l} u \\ v \end{array}\right] =\left[ \begin{array}{l} \frac{1}{\omega } \int _0^\omega \left[ \frac{r (1+c(t) \exp (u(t)))}{1+c(t) \exp (u(t))+k(t) \exp (v(t))}-d-h \exp (u(t))-\frac{a \exp (v(t))}{b+\exp (2u(t))} \right] d t\\ \frac{1}{\omega } \int _0^\omega \left[ -m \left( \frac{l \exp (u(t))}{1+l \exp (u(t))}+1\right) +\frac{a e \exp (u(t))}{b+\exp (2u(t))} \right] d t \end{array}\right] \ne \left[ \begin{array}{l} 0 \\ 0 \end{array}\right] \end{aligned}$$

Hence the second part of the condition of Lemma (4.1) is satisfied. Now, we must verify that Brouwer degree $deg(JPQ,\Omega \cap Ker M,0) \ne 0.$ For this purpose, we define a homomorphism

$$\begin{aligned} J: {\text {Im}} P \rightarrow {\text {Ker}} M,\left( u, v\right) ^T \rightarrow \left( u, v\right) ^T, \end{aligned}$$

then

$$\begin{aligned} {\text {deg}}(J P Q, \Omega \cap {\text {Ker}} M, 0)={\text {deg}}(PQ, \Omega \cap {\text {Ker}} M, 0). \end{aligned}$$

In our analysis, we make the assumption that the equation $PQs=0$ has a finite number of real-valued solutions $\left( u_{i}^*, v_{i}^*\right) , i=1,2, \ldots , n$ such that

$$\begin{aligned} \sum _{i=1}^n {\text {sign}} {\text {det}}(PQ)^{\prime }\left( u_{i}^*, v_{i}^*\right) \ne 0, \end{aligned}$$

(C11)

therefore, given the assumption stated in (C11), we can derive the following result

$$\begin{aligned} {\text {deg}}(J PQ,\Omega \cap {\text {Ker}} M, 0) \ne 0. \end{aligned}$$

Therefore, each of the requirements of Lemma (4.1) are proved. Thus $M s= Qs$ possess at minimum one solution in ${\text {Dom}} M \cap \bar{\Omega }$ i.e., system (C1) has at minimum one $\omega$-periodic solution $\left( u_{i}^*, v_{i}^*\right) \in {\text {Dom}} M \cap \bar{\Omega }$. Therefore, $\left( x^*, y^*\right) =$ $\left( e^{u^*}, e^{v^*}\right)$ is a strictly positive $\omega$-periodic solution of model (2.4).

Appendix D Proof of Theorem (9)

Let (x(t), y(t)) and $(x_1(t),y_1(t))$ be two positive periodic solutions for the non-autonomous system with positive initial conditions. Let us define

$$\begin{aligned} \begin{aligned}&\alpha _1(t)=\left| \ln x(t)-\ln x_1(t)\right| \text { and }\\&\alpha _2(t)=\left| \ln y(t)-\ln y_1(t)\right| . \end{aligned} \end{aligned}$$

After determining the right derivative $D^+$ of $\alpha _i(t)$ along the system (2.4), we obtain

$$\begin{aligned} \begin{aligned}&D^{+} \alpha _1(t)={\text {sgn}}\left( x(t)-x_1(t)\right) \left( \frac{{\dot{x}}(t)}{x(t)}-\frac{{\dot{x}}_1(t)}{x_1(t)}\right) \\&\le \Big \{\frac{k(t) r c(t) y_1(t)}{(1+c(t) x(t)+k(t) y(t))(1+c(t) x_1(t)+k(t) y_1(t))}\\&-h+\frac{a y(t)(x_1(t)+x(t))}{(x(t)^2+b)(x_1(t)^2+b)} \Big \}| x(t)-x_1(t)|\\&-\Big \{\frac{ab}{(x(t)^2+b)(x_1(t)^2+b)}\\&+\frac{rk(t)+rc(t)k(t)x_1(t)}{(1+c(t) x(t)+k(t) y(t))(1+c(t)x_1(t)+k(t) y_1(t))}\Big \}\\&|y(t)-y_1(t)|; \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned}&D^{+} \alpha _2(t)={\text {sgn}}\left( y(t)-y_1(t)\right) \left( \frac{{\dot{y}}(t)}{y(t)}-\frac{{\dot{y}}_1(t)}{y_1(t)}\right) \\&\le \Big \{\frac{-ml}{(1+lx(t))(1+lx_1(t))}\\&+\frac{aeb-aex(t)x_1(t)}{(x(t)^2+b)(x_1(t)^2+b)} \Big \}\\&| x(t)-x_1(t)|; \end{aligned} \end{aligned}$$

Let $\alpha (t) = \alpha _1(t)+\alpha _2(t).$ Then using the inequalities mentioned above incorporating $\alpha _1(t),\alpha _2(t)$, the Dini derivative of $\alpha (t)$ is calculated as follows:

$$\begin{aligned} \begin{aligned}&D^{+} \alpha (t)\le -\Big \{\frac{-k(t) r c(t) y_1(t)}{(1+c(t) x(t)+k(t) y(t))(1+c(t) x_1(t)+k(t) y_1(t))}\\&+h-\frac{a y(t)(x_1(t)+x(t))}{(x(t)^2+b)(x_1(t)^2+b)}\\&~~~+ \frac{ml}{(1+lx(t))(1+lx_1(t))}-\frac{aeb-aex(t)x_1(t)}{(x(t)^2+b)(x_1(t)^2+b)} \Big \}\\&| x(t)-x_1(t)|\\&~~~-\Big \{ \frac{ab}{(x(t)^2+b)(x_1(t)^2+b)}\\&+\frac{rk(t)+rc(t)k(t)x_1(t)}{(1+c(t) x(t)+k(t) y(t))(1(t)+c(t) x_1(t)+k(t) y_1(t))} \Big \}\\&|y(t)-y_1(t)|. \end{aligned} \end{aligned}$$

Then, applying Theorem (6), we get

$$\begin{aligned} \begin{aligned}&D^{+} \alpha (t)\le -\Big \{\frac{-k(t) r c M_2}{(1+c(t) m_1(t)+k(t) m_2(t))^2}\\&+h-\frac{2a M_1 M_2}{((m_1(t))^2+b)^2}+ \frac{ml}{(1+l M_1)^2}\\&~~~-\frac{aeb}{((m_1(t))^2+b)^2}+\frac{ae(m_1(t))^2}{((M_1)^2+b)^2} \Big \}| x(t)-x_1(t)|\\&~~~-\Big \{ \frac{ab}{(M_1^2+b)^2}+\frac{rk(t)+rc(t)k(t)m_1(t)}{(1+c(t) M_1+k(t) M_2)^2} \Big \}\\&|y(t)-y_1(t)|. \end{aligned} \end{aligned}$$

Thus

$$\begin{aligned} D^{+} \alpha (t) \le -\mathcal {R}_1\left| x(t)-x_1(t)\right| -\mathcal {R}_2\left| y(t)-y_1(t)\right| ,\nonumber \\ \end{aligned}$$

(D1)

where $\mathcal {R}_1=\frac{-k(t) r c(t) M_2}{(1+c(t) m_1(t)+k(t) m_2(t))^2}+h-\frac{2a M_1 M_2}{((m_1(t))^2+b)^2}+ \frac{ml}{(1+l M_1)^2}-\frac{aeb}{((m_1(t))^2+b)^2}+\frac{ae(m_1(t))^2}{((M_1)^2+b)^2}$, $\mathcal {R}_2= \frac{ab}{((M_1)^2+b)^2}$ $+\frac{rk(t)+rc(t)k(t)m_1(t)}{(1+c(t) M_1+k(t) M_2)^2}$.

Therefore, given the conditions described in (4.3), $\alpha (t)$ is non-increasing on the interval $[0, \infty )$, integrating (D1), we get

$$\begin{aligned}{} & {} \alpha (t)+\mathcal {R}_1 \int _0^t\left| x(s)-x_1(s)\right| d s+\mathcal {R}_2 \int _0^t\left| y(s)-y_1(s)\right| \\{} & {} d s \le \alpha (0)<\infty ~ \forall ~t~\ge 0 \end{aligned}$$

which implies that $|x(t)-x_1(t)| \text { and } |y(t)-y_1(t)| \in \mathcal {L}^1([0,\infty ))$. By using Lemma (4.2), we have

$$\begin{aligned} \begin{aligned}&\lim _{t \rightarrow \infty }\left| x(t)-x_1(t)\right| =0, \lim _{t \rightarrow \infty }\left| y(t)-y_1(t)\right| =0. \end{aligned} \end{aligned}$$

As a result, the positive periodic solution of the seasonal system (2.4) is globally attractive.