Identifying bifurcations underlying a neuronal bursting of mixed-mode oscillations with two slow variables in inner hair cell

Abstract

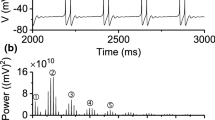
Neuronal bursting patterns are nonlinear behaviors related to various brain functions and diseases. Bursting modulated by two slow variables manifest more complex dynamics than that with one slow variable, due to involved with more bifurcations of fast subsystem. The traditional dissection method or singular perturbation method often fails to analyze the bursting with two slow variables, for instance, a complex mixed-mode oscillation (MMO) bursting observed in the immature inner hair cell related to the development of auditory function. The MMO bursting exhibits alternation between a single spike with large amplitude and a pseudo-plateau burst behaving as fast burst with small oscillations. In the present paper, the MMO bursting is successfully analyzed using a novel dissection process. With two slow variables c and h regarded as bifurcation parameters of the fast subsystem, various dynamical behaviors and bifurcation curves are obtained. By identifying real intersections between the bursting trajectory and bifurcation curves in the (c, h, V) space instead of (c, h) plane, the pseudo-plateau burst is built relationships to the depolarization block and subcritical Hopf bifurcation of the fast subsystem, and the spike is associated with coexisting firing and limit point bifurcation of cycles. Interestingly, no quiescent state is identified to be related to the resting state or saddle-node bifurcation on an invariant cycle (SNIC), due to that c is not slow enough. As c becomes sufficiently slow, the bursting pattern is associated with the resting state and the SNIC. In addition, the bursting trajectory exhibits a narrow shape around an oblique line in the (c, h) plane, and the bifurcations along the line presents a simple and effective candidate to characterize the bursting. The results present effective process of dissection method and deep understanding of the MMO bursting, which are helpful for modulating the development of auditory functions related to the inner hair cell.

Appendix: Bifurcations of 3-dimensional fast subsystem fails to explain the bursting dynamics

As expected, bifurcations of 3-dimensional fast subsystem fail to explain the bursting dynamics fails to explain the dynamics of the “$1+4$” burst. In the present Appendix, we show that the failure results and compared with the results of the main text. Such a comparison is helpful for comprehensive and deep understanding to the dynamics of “$1+4$” bursting

1.1 Fast subsystem

Similar to many nervous systems, the concentration of intracellular calcium ion c is the slow variable. Therefore, the dissection method with c taken as a single slow variable is used to identify the bifurcation mechanism underlying the MMO bursting “$1+4$”. Then, the fast subsystem is described as follows:

$$\begin{aligned}{} & {} \begin{aligned} C_{\textrm{m}}\dfrac{\textrm{d}V}{\textrm{d}t}&= -(I_{\textrm{Ca}}+I_{\textrm{K}}+I_{\textrm{KCa}}+I_{\textrm{leak}})+I_{\textrm{app}}, \end{aligned} \end{aligned}$$

(A1)

$$\begin{aligned}{} & {} \begin{aligned} \dfrac{\textrm{d}n}{\textrm{d}t}&= \dfrac{n_{\infty }-n}{\tau _{n}}, \end{aligned} \end{aligned}$$

(A2)

$$\begin{aligned}{} & {} \begin{aligned} \dfrac{\textrm{d}h}{\textrm{d}t}&= \dfrac{h_{\infty }-h}{\tau _{h}}, \end{aligned} \end{aligned}$$

(A3)

where $I_{\textrm{Ca}} = g_{\textrm{Ca}}m_{\mathrm{\infty }}q_{\mathrm{\infty }}(V-V_{\textrm{Ca}})$ with $q_{\mathrm{\infty }} =(1+\dfrac{c}{K_{\textrm{q}}})^{-1}$, and c is taken as bifurcation parameter.

1.2 Dynamics of the 3-dimenional fast subsystem

The bifurcations of equilibrium points and limit cycles with respect to c are illustrated in Fig. 15a. The lower branch (red solid) represents a stable node, which corresponds to the resting state with a lower membrane potential. The middle branch (black short dots) represents a saddle. The upper branch is divided into 2 parts by a subcritical Hopf bifurcation ($\mathrm {HB_{\textrm{1}}}$) occurring at c $\approx$ 0.5763 $\upmu \textrm{M}$. The red solid part left to the $\mathrm {HB_{\textrm{1}}}$ represents a stable focus, which corresponds to the depolarization block with a higher membrane potential, and the part (black short dots) right to $\mathrm {HB_{\textrm{1}}}$ denotes an unstable focus. The right turning point of the equilibrium point curve is a saddle-node (SN) bifurcation at c $\approx$ 0.5948 $\upmu \textrm{M}$, and the left turning point is a saddle-node bifurcation on an invariant cycle (SNIC) at c $\approx$ 0.4683 $\upmu \textrm{M}$. An unstable limit cycle (blue short dash line) appears via the Hopf bifurcation $\mathrm {HB_{\textrm{1}}}$ and disappears via a limit point bifurcation of cycles (LPC) appearing at c $\approx$ 0.3038 $\upmu \textrm{M}$. Meanwhile, a stable limit cycle (green solid line) emerges via the LPC and terminates via the SNIC at c $\approx$ 0.4683 $\upmu \textrm{M}$, as shown in Fig. 15a. The spiking and resting state coexist between the LPC and SNIC points. In addition, the insert figure represents the enlargement around the SN point. A subcritical Hopf bifurcation ($\mathrm {HB_{\textrm{2}}}$) appears on the middle branch at c $\approx$ 0.5946 $\upmu \textrm{M}$. The unstable limit cycle (blue short dash curves) emerges from $\mathrm {HB_{\textrm{2}}}$ and disappears via a saddle homoclinic orbit bifurcation (HC) at c $\approx$ 0.5945 $\upmu \textrm{M}$. Both the $\mathrm {HB_{\textrm{2}}}$ and HC points have little influences on the dynamics of the MMO bursting “$1+4$”.

Fig. 15

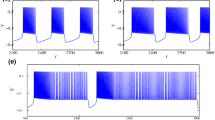
The dynamics of the MMO bursting “$1+4$” with c taken as a single slow variable. a The dynamics of the fast subsystem. The upper and lower red solid curves represent stable focus (depolarization block) and node (resting state), respectively, the black short dot curve of the upper branch denotes unstable focus. The black short dot curve of the middle branch represents unstable equilibrium. The SN, $\mathrm {HB_{\textrm{1}}}$, and SNIC represent the corresponding bifurcations. The green solid (blue short dash) curve represents stable (unstable) limit cycle. The LPC represents limit point bifurcation of cycles. The insert represents the enlargement around the SN. The blue short dash curve represents unstable limit cycle, $\mathrm {HB_{\textrm{2}}}$ represents Hopf bifurcation, and HC represents saddle homoclinic orbit bifurcation; b The bursting trajectory (black bold solid curve) and the critical phase points superimposed with panel (a). The phase points A1 and B1 (red circle) represent the extreme values of the single spike “1”, and A2 and B2 (red circle) represent the extreme values of the pseudo-plateau burst “4”. (Color figure online)

Fig. 16

The difference of the bifurcations with respect to c between the two-dimensional fast subsystem [Eqs. (15–16)] at h $\approx$ 0.9387 and the three-dimensional fast subsystem [Eqs. (A1–A3)] (thin curves, same as Fig. 15b). Black symbols HB and LPC are for the two-dimensional fast subsystem, green symbols $\mathrm {HB_{\textrm{1}}}$, $\mathrm {HB_{\textrm{2}}}$, HC, and LPC are for the 3-dimensional fast subsystem, and red SNIC is for both fast subsystems. (Color figure online)

1.3 No relationships between the bifurcations of the 3-dimensional fast subsystem and the bursting trajectory

The trajectory (black bold solid curve) of the MMO bursting “$1+4$” and four critical phase points A1, A2, B1, and B2 are superimposed to Fig. 15a to form Fig. 15b, and the direction of the trajectory is denoted by the arrows. As can be found from Fig. 3b, the amplitude (between point A1 and point B1) of the spike “1” is consistent with the amplitude of the stable limit cycle. But there is no obvious relationship between the bursting trajectory and the bifurcations, as addressed in the following three aspects.

• (1) The pseudo-plateau burst “4” has no relationship to the stable behaviors on the upper branch (red solid), which is different from the general bursting. For a general bursting, the burst always runs along the stable limit cycle [40].

• (2) No any part of the bursting trajectory is overlap with the lower branch, which is different from the general bursting. For a general bursting, the trajectory of quiescent state is overlap with the stable behavior on the lower branch. Although the two durations begging from the point B1 and from the point B2 look like the quiescent state of the bursting “$1+4$” in appearance, both durations are not overlap with the lower branch (lower red curve). Therefore, the two durations begging from the point B1 and from the point B2 should not be the quiescent state indeed.

• (3) The begging and ending phases of the spike “1” have no relationships to the bifurcations of the fast system such as the SNIC, LPC, or $\mathrm {HB_{\textrm{1}}}$, which differs from the general bursting. For a general bursting, such phases should be related to the bifurcations.

1.4 Distinction of dynamics between the two-dimensional and three-dimensional fast subsystems

The bifurcations of the 3-dimensional fast subsystem [Eqs. (A1–A3)] fail to explain the “$1+4$” bursting, due to that h is regarded as fast variables. In Sect. 3.2, the bifurcations of the 2-dimensional fast subsystem [Eqs. (15–16)] can explain the dynamics of the bursting. The distinction of bifurcations between the 3-dimensional (thin curves) and 2-dimensional (bold curves) fast subsystems can be found from Fig. 16. The most important difference is that the upper branch (upper bold red) of the equilibrium (DB) for the 2-dimensional fast subsystem (h $\approx$ 0.9387) becomes lower, compared with that (upper thin red) of the 3-dimensional fast subsystem. The pseudo-plateau burst “4” rotates around the lower membrane potential of the DB of the 2-dimensional fast system, while has no relationship to the DB of the 3-dimensional fast system. Then, the bifurcations of the two-dimensional fast subsystem modulated by both c and h are more effective to analyze the “$1+4$” bursting than those of the 3-dimensional fast system modulated by c.