Dynamics in a memristive neuron under an electromagnetic field

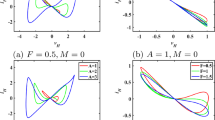
Abstract

Propagation and exchange of electrical signals between neurons mainly depend on the controllability of synapses. These electrical signals will affect the dynamic characteristics of ion channels on the neuron membrane and the firing activity of neurons can be changes. Polarization and magnetization of media exposed to electromagnetic field encode energy distribution and the neural activities will be changed greatly. The incorporation of memristors is effective to estimate the energy effect from the physical field on neurons. In this work, a charge-controlled memristor (CCM) and a magnetic flux-controlled memristor (MFCF) are connected in parallel to a FitzHugh–Nagumo (FHN) neural circuit for building a new neural circuit, which can perceive modulation from external electric and magnetic fields. Furthermore, the dynamical equation of the memristive neural circuit and the field energy of electrical elements are obtained based on Kirchhoff’s law and Helmholtz’s theorem. The firing patterns of the memristive neuron and energy proportion can be controlled when the external electric and magnetic fields are adjusted. Continuous energy injection into the memristive channels enables memristive synapses to become self-adaptive under energy flow. Noisy disturbance and radiation are applied to discern the occurrence of coherent resonance in this memristive neuron. The results can be used to explore the collective behaviors and creation of heterogeneity in networks in the presence of an electromagnetic field.

Appendices

Appendix A: Approach of energy proportion in memristive neuron model

$$ \left\{ \begin{gathered} p_{1} = \frac{{\int_{0}^{T} {\frac{1}{2}x^{2} d\tau } }}{{\int_{0}^{T} {\left( {\frac{1}{2}x^{2} + \frac{1}{2c}y^{2} } \right)d\tau + \left| {\int_{0}^{T} {\frac{1}{2}xzd\tau } } \right| + \left| {\int_{0}^{T} {\frac{1}{2}\mu w^{2} xd\tau } } \right|} }} \approx \frac{{\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i}^{2} } }}{{\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i}^{2} } + \sum\limits_{i = 1}^{N} {\frac{1}{2c}y_{i}^{2} } + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i} z_{i} } } \right| + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}\mu w_{i}^{2} x_{i} } } \right|}}; \hfill \\ p_{2} = \frac{{\int_{0}^{T} {\frac{1}{2c}y^{2} d\tau } }}{{\int_{0}^{T} {\left( {\frac{1}{2}x^{2} + \frac{1}{2c}y^{2} } \right)d\tau + \left| {\int_{0}^{T} {\frac{1}{2}xzd\tau } } \right| + \left| {\int_{0}^{T} {\frac{1}{2}\mu w^{2} xd\tau } } \right|} }} \approx \frac{{\sum\limits_{i = 1}^{N} {\frac{1}{2c}y_{i}^{2} } }}{{\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i}^{2} } + \sum\limits_{i = 1}^{N} {\frac{1}{2c}y_{i}^{2} } + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i} z_{i} } } \right| + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}\mu w_{i}^{2} x_{i} } } \right|}}; \hfill \\ p_{3} = \frac{{\left| {\int_{0}^{T} {\frac{1}{2}xzd\tau } } \right|}}{{\int_{0}^{T} {\left( {\frac{1}{2}x^{2} + \frac{1}{2c}y^{2} } \right)d\tau + \left| {\int_{0}^{T} {\frac{1}{2}xzd\tau } } \right| + \left| {\int_{0}^{T} {\frac{1}{2}\mu w^{2} xd\tau } } \right|} }} \approx \frac{{\left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i} z_{i} } } \right|}}{{\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i}^{2} } + \sum\limits_{i = 1}^{N} {\frac{1}{2c}y_{i}^{2} } + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i} z_{i} } } \right| + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}\mu w_{i}^{2} x_{i} } } \right|}}; \hfill \\ p_{4} = \frac{{\left| {\int_{0}^{T} {\frac{1}{2}\mu w^{2} xd\tau } } \right|}}{{\int_{0}^{T} {\left( {\frac{1}{2}x^{2} + \frac{1}{2c}y^{2} } \right)d\tau + \left| {\int_{0}^{T} {\frac{1}{2}xzd\tau } } \right| + \left| {\int_{0}^{T} {\frac{1}{2}\mu w^{2} xd\tau } } \right|} }} \approx \frac{{\left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}\mu w_{i}^{2} x_{i} } } \right|}}{{\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i}^{2} } + \sum\limits_{i = 1}^{N} {\frac{1}{2c}y_{i}^{2} } + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i} z_{i} } } \right| + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}\mu w_{i}^{2} x_{i} } } \right|}}; \hfill \\ \end{gathered} \right. $$

(18)

Appendix B: The proof of the Hamilton energy for the memristive neuron by applying a Helmholtz theorem

The memristive neuron model in Eq. (5) is rewritten with equivalent form as follows

$$ \begin{aligned} \left( \begin{gathered} {\dot{x}} \hfill \\ {\dot{y}} \hfill \\ {\dot{z}} \hfill \\ {\dot{w}} \hfill \\ \end{gathered} \right) & = \left( \begin{gathered} u_{s} - \xi x - y - k_{1} x(\alpha^{\prime } + \beta^{\prime } z^{2} ) + gz - \mu wx \hfill \\ c(x + 1 - y) \hfill \\ k_{1} x(\alpha^{\prime } + \beta^{\prime } z^{2} ) - gz + E_{ext} \hfill \\ \lambda^{\prime } \tanh (w) - \gamma^{\prime } w + \delta x + \varphi_{ext} \hfill \\ \end{gathered} \right) = F_{c} + F_{d} \\ & = \left( \begin{array}{c} - y - \frac{1}{2}k_{1} \alpha^{\prime } x - \delta \mu wx \hfill \\ cx \hfill \\ k_{1} \alpha^{\prime } x \hfill \\ \delta x + a_{1} + \frac{1}{2x}wy + a_{2} \hfill \\ \end{array} \right) + \left( \begin{gathered} u_{s} - \xi x - k_{1} x\beta^{\prime } z^{2} + gz + \frac{3}{2}k_{1} \alpha^{\prime } x - \mu wx + \delta \mu wx \hfill \\ c(1 - y) \hfill \\ k_{1} \beta^{\prime } xz^{2} - gz + E_{ext} \hfill \\ \lambda^{\prime } \tanh (w) - \gamma^{\prime } w + \varphi_{ext} - a_{1} - \frac{1}{2x}wy - a_{2} \hfill \\ \end{gathered} \right) \\ & = \left( {\begin{array}{*{20}c} 0 & { - c} & { - k_{1} \alpha^{\prime } } & { - \delta } \\ c & 0 & { - \frac{cz}{x}} & { - \frac{cw}{{2x}}} \\ {k_{1} \alpha^{\prime } } & \frac{cz}{x} & 0 & { - a_{2} } \\ \delta & {\frac{cw}{{2x}}} & {a_{2} } & 0 \\ \end{array} } \right)\left( \begin{gathered} x + \frac{z}{2} + \frac{{\mu w^{2} }}{2} \hfill \\ \frac{y}{c} \hfill \\ \frac{x}{2} \hfill \\ \mu wx \hfill \\ \end{gathered} \right) \\ & \quad + \left( {\begin{array}{*{20}c} {a_{11} } & 0 & 0 & 0 \\ 0 & {c^{2} \left( {\frac{1}{y} - 1} \right)} & 0 & 0 \\ 0 & 0 & {2k_{1} \beta^{\prime } z^{2} - \frac{2}{x}gz + \frac{2}{x}E_{ext} } & 0 \\ 0 & 0 & 0 & {a_{44} } \\ \end{array} } \right)\left( \begin{array}{c} x + \frac{z}{2} + \frac{{\mu w^{2} }}{2} \hfill \\ \frac{y}{c} \hfill \\ \frac{x}{2} \hfill \\ \mu wx \hfill \\ \end{array} \right); \\ \end{aligned} $$

(19)

$$ \begin{gathered} \left\{ \begin{gathered} a_{1} = \delta \left( {\frac{1}{2}z + \frac{1}{2}\mu w^{2} } \right); \hfill \\ a_{2} = \frac{{k_{1} \alpha^{\prime } \left( {\frac{1}{2}z + \frac{1}{2}\mu w^{2} } \right) + \frac{wy}{x}}}{2\mu w}; \hfill \\ a_{11} = \frac{{2(u_{s} - \xi x - k_{1} x\beta^{\prime } z^{2} + gz + \frac{3}{2}k_{1} \alpha^{\prime } x - \mu wx + \delta \mu wx)}}{{2x + z + \mu w^{2} }}; \hfill \\ a_{44} = \frac{{\lambda^{\prime } \tanh (w) - \gamma^{\prime } w + \varphi_{ext} - a_{1} - \frac{1}{2x}wy - a_{2} }}{\mu wx} \hfill \\ \end{gathered} \right. \hfill \\ \quad \; \hfill \\ \end{gathered} $$

(20)

According to the Helmholtz theorem, the dimensionless Hamilton energy H for the neuron model meets the following criterion.

$$ {\kern 1pt} \nabla H^{T} F_{c} (x,y,z,w) = 0;\quad \nabla H^{T} F_{d} (x,y,z,w) = \frac{dH}{{d\tau }}; $$

(21)

Therefore, the energy function can be an exact solution for the formula as follows

$$ {\kern 1pt} \left( { - y - \frac{1}{2}k_{1} \alpha^{\prime } x - \delta \mu wx} \right)\frac{\partial H}{{\partial x}} + (cx)\frac{\partial H}{{\partial y}} + (k_{1} \alpha^{\prime } x)\frac{\partial H}{{\partial z}} + \left( {\delta x + a_{1} + \frac{wy}{{2x}} + a_{2} } \right)\frac{\partial H}{{\partial w}} = 0; $$

(22)

According to Eq. (21), an solution is obtained to match the Hamilton energy function as follows

$$ H = \frac{1}{2}x^{2} + \frac{{y^{2} }}{2c} + \frac{1}{2}xz + \frac{1}{2}\mu w^{2} x; $$

(23)

That is, the energy function for the memristive neuron can be confirmed and changes in the parameters (c, μ) have direct impact on the energy value, and firing mode in electric activities is regulated synchronously.