Sharp changes in fractal basin of attraction in passive dynamic walking

Abstract

A passive dynamic walker is a mechanical system that walks down a slope without any control, and gives useful insights into the dynamic mechanism of stable walking. This system shows specific attractor characteristics depending on the slope angle due to nonlinear dynamics, such as period-doubling to chaos and its disappearance by a boundary crisis. However, it remains unclear what happens to the basin of attraction. In our previous studies, we showed that a fractal basin of attraction is generated using a simple model over a critical slope angle by iteratively applying the inverse image of the Poincaré map, which has stretching and bending effects. In the present study, we show that the size and fractality of the basin of attraction sharply change many times by changing the slope angle. Furthermore, we improved our previous analysis to clarify the mechanisms for these changes and the disappearance of the basin of attraction based on the stretching and bending deformation in the basin formation process. These findings will improve our understanding of the governing dynamics to generate the basin of attraction in walking.

1 Introduction

A passive dynamic walker is a mechanical system that walks down a slope without any control [27], and gives useful insights into the dynamic mechanism of stable walking. This system has been used extensively for the study of human walking with low energy consumption [4, 5, 9, 21, 23,24,25, 29, 33, 37] and has been the basis for the design of energy-efficient bipedal robots [2, 3, 6, 7, 20, 22, 28, 38, 39]. Because the walking speed for this system changes with slope angle, it is important to clarify its influence on walking. In particular, this system shows specific characteristics due to nonlinear dynamics depending on the slope angle. For example, a chaotic attractor appears through a period-doubling cascade when the slope angle increases [12], and it abruptly disappears at a critical slope angle [17, 31]. Furthermore, fractal basin boundaries appear even without period-doubling  [1, 31, 34]. To understand the dynamics that generate walking, it is important to elucidate the mechanism for these characteristics.

The change in the attractor by the slope angle and its mechanism have been clarified in previous studies [10,11,12, 17,18,19], whereas the change in the basin of attraction and its mechanism remain largely unclear. In our previous studies [31, 32], we showed that the basin of attraction is produced through iterative stretching and bending deformation by the inverse image of the Poincaré map. As a result, the basin boundaries become fractal when the slope angle exceeds a critical value. However, other characteristics of the basin of attraction remain unclear.

In this study, we focused on the size, fractality, and disappearance of the basin of attraction. Because the basin of attraction is the set of initial states that converge to an attractor, the basin size indicates the robustness of walking and is thus an important feature for walking. The fractal basin boundary has a final state sensitivity [13, 26]. This means that even when the system is deterministic, unpredictability exists for the attractor or final state when the initial condition contains uncertainties. Although the unpredictability of chaotic attractors has been investigated based on the initial-state sensitivity [11, 12], the final state sensitivity in fractal basin boundaries has not been investigated thoroughly. The final state sensitivity makes the prediction of walking easily affected by inevitable noise and is thus also an important feature for walking. The disappearance of the chaotic attractor and its basin of attraction indicates that the system cannot produce stable walking and falls down regardless of the initial state. While the disappearance of the chaotic attractor can be explained by a boundary crisis  [17, 31], the mechanism for the disappearance of the basin of attraction remains unclear.

Fig. 1

Simplest walking model for analysis of passive dynamic walking

The stretching-bending deformation revealed in our previous study [32] creates horseshoes [35] that cause complex phenomena, such as chaos and fractals, and is an important property in nonlinear dynamics. It is expected to play an important role in determining the size, fractality, and disappearance of the basin of attraction in passive dynamic walking. In the present study, we first calculated the size and fractality of the basin of attraction for passive dynamic walking depending on the slope angle using the simplest walking model, which is useful for the analysis of passive dynamic walking, and found sharp changes in these parameters at specific slope angles. We then clarified the mechanism for the sharp changes and disappearance of the basin of attraction based on stretching-bending deformation in the basin of attraction by improving our previous analysis [32].

2 Passive dynamic walking

2.1 Model

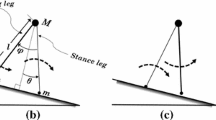
In this study, we analyzed passive dynamic walking using the simplest walking model [11] (Fig. 1). This model has two legs, swing and stance legs, connected by a frictionless hip joint and walks down a slope of angle $\gamma$ without any control. The leg length is l. The tip of the stance leg is fixed on the slope, and the stance leg rotates around the leg tip without friction. The angles between the stance leg and slope normal and between the stance and swing legs are denoted by $\theta$ and $\varphi$, respectively. The hip mass and leg tip mass are M and m, respectively. We assumed $m/M \rightarrow 0$ as in [11]. The gravitational acceleration is g.

2.2 Governing equations

This model is governed by hybrid dynamics that consist of continuous dynamics generated by the equations of motion when the swing leg is in motion and discontinuous dynamics generated by the impact when the foot makes contact with the ground.

The equations of motion are given by

$$\begin{aligned}{} & {} \!\!\!\ddot{\theta }-\sin (\theta -\gamma ) = 0 \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \!\!\!(\cos \varphi -1) \ddot{\theta }+\ddot{\varphi }-\dot{\theta }^{2} \sin \varphi +\sin (\varphi -\theta +\gamma ) = 0.\nonumber \\ \end{aligned}$$

(2)

The equations are made dimensionless by the timescale $\sqrt{l/g}$. The swing leg tip touches the slope (touchdown) when the following conditions are satisfied:

$$\begin{aligned}{} & {} 2 \theta -\varphi = 0 \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \theta < 0 \end{aligned}$$

(4)

$$\begin{aligned}{} & {} 2 \dot{\theta }-\dot{\varphi } < 0. \end{aligned}$$

(5)

We utilized the condition (4) to ensure that touchdown takes place exclusively in front of the model to move forward, and condition (5) to disregard the scuffing of the leg tip on the slope when the swing leg moves forward. We considered the touchdown as a completely inelastic collision, where no slip or bounce occurs, and assumed that the stance leg lifts off without interaction just after touchdown. Because the roles of the swing and stance legs are reversed just after touchdown, we obtain

$$\begin{aligned} \begin{bmatrix} \theta ^{+} \\ \dot{\theta }^{+} \\ \varphi ^{+} \\ \dot{\varphi }^{+} \end{bmatrix} = \begin{bmatrix} -\theta ^{-} \\ \dot{\theta }^{-} \cos 2 \theta ^{-} \\ -2 \theta ^{-} \\ \cos 2 \theta ^{-}\left( 1-\cos 2 \theta ^{-}\right) \dot{\theta }^{-} \end{bmatrix} \end{aligned}$$

(6)

where the notations $*^-$ and $*^+$ indicate the state of $*$ just before and after touchdown, respectively. The key aspect of this relationship is that the state just after touchdown, denoted by $(\theta ^{+}, \dot{\theta }^{+}, \varphi ^{+}, \dot{\varphi }^{+})$, depends solely on $(\theta ^{-}, \dot{\theta }^{-})$ and is not influenced by $(\varphi ^{-},\dot{\varphi }^{-})$.

Fig. 2

Schematic diagram of the structure of phase space. A Hybrid dynamics composed of the section H, jump T, map U, and Poincaré map S. B Relationship among the regions $D_n$ and $S(D_n)$, and the range R of S on T(H)

2.3 Structure of phase space by hybrid dynamics

The structure of the phase space is determined by the hybrid dynamic system, as shown in Fig. 2A. The section H is defined by the touchdown conditions (3)–(5) and forms a three-dimensional space in four-dimensional phase space. The jump T in the phase space from the state just before touchdown to the state just after touchdown is defined by (6). Therefore, the image of T, T(H), represents all states just after touchdown, and a new step starts from T(H). The map U is defined by the equations of motion (1) and (2) from the start of a step to the next touchdown instance, i.e., from T(H) to H. The Poincaré section is defined as T(H) and the Poincaré map S is defined by $S=T \circ U: T(H) \rightarrow T(H)$, which represents one step. T(H) is two-dimensional in the simplest walking model as shown in (6), which is useful for analyzing S. S is parameterized only by the slope angle $\gamma$ and an attractor of S represents stable walking. In particular, S has an attracting fixed point at $0< \gamma < 0.015$, and there is a period-doubling cascade to chaos for $0.015< \gamma < 0.019$  [11]. While the basin of attraction of S has smooth boundaries for $\gamma <0.0075$, it has fractal boundaries for $\gamma >0.0075$  [32].

Fig. 3

Basin of attraction for $\gamma$. A Basin of attraction for $\gamma =0.01$, 0.012, and 0.016. Blue and orange lines show the boundaries of the basin of attractions and the lower edge of range R, respectively. Black lines show the regions used to calculate the uncertainty exponent $\alpha$: $(\theta +\dot{\theta } \times \theta -\dot{\theta })=[0.00133,0.00633]\times [0.4233,0.5233]$ for $\gamma =0.010$, $[0.00266,0.00766]\times [0.4366,0.5366]$ for $\gamma =0.012$, and $[0.00533,0.01033]\times [0.4633,0.5633]$ for $\gamma =0.016$. B Basin size versus $\gamma$. C Proportion of uncertainty box $f_{\varepsilon }$ versus $\varepsilon$ for various $\gamma$ values. Dotted lines represent corresponding linear regression lines. D Uncertainty exponent $\alpha$ versus $\gamma$. E Number of non-R-penetrating slits versus $\gamma$

3 Characteristics of basin of attraction

3.1 Basin size

Because the basin of attraction is the collection of initial conditions on T(H) from which the model keeps walking, we computed the basin using the governing equations (1)–(6). Specifically, we used 1560 bins for $0.1<\theta \le \pi /2$ with increments of 0.001 and 1500 bins for $-1.5<\dot{\theta }\le 0$ with increments of 0.001 for the initial conditions on T(H); that is, we used $2.34\times 10^6$ initial conditions in total. This range of $\theta$ and $\dot{\theta }$ was sufficient to contain the basin of attraction irrespective of $\gamma$. We approximated the basin of attraction by the set of initial states from which the model can walk at least 50 steps, and determined the size of the basin of attraction by counting the number of initial conditions within it.

Figure 3A shows the basins of attraction for $\gamma =0.01$, 0.012, and 0.016, where $\theta +\dot{\theta }$ and $\theta -\dot{\theta }$ are used for the axes to clarify the geometric characteristics as in [30,31,32]. Because $\gamma >0.0075$ in these figures, the basins have an infinite number of slits and fractal boundaries  [32]. The size of the basin decreases as $\gamma$ increases, as shown in Fig. 3B. In particular, it abruptly decreases around $\gamma = 0.0103$, 0.0135, and 0.019.

3.2 Fractality of basin boundary

We evaluated the fractality of the basin boundary based on the uncertainty exponent [13, 26], which is defined as follows:

$$\begin{aligned} \alpha = \textrm{dim}(B)-\textrm{dim}(\partial B) \end{aligned}$$

(7)

where $\alpha$ is the uncertainty exponent, B is the basin of attraction, $\partial B$ is the basin boundary, and $\text {dim}(\xi )$ is the dimension of set $\xi$. If $0<\alpha <1$, the basin boundary has a non-integer dimension and is fractal.

We calculated the uncertainty exponent $\alpha$ using a previously reported method [13, 26]. First, we placed many squares with a length $\varepsilon$, which is sufficiently larger than the bin size in the initial conditions, randomly on a limited range of the Poincaré section. We calculated the proportion $f_{\varepsilon }$ of the squares that touch the basin boundary. When the square is coarse-grained as a single point, it is “uncertain” whether the point is inside or outside the basin. Therefore, $\alpha$ describes not only the fractality but also the final state sensitivity. The following relationship between $\alpha$ and $\varepsilon$ holds:

$$\begin{aligned} f_{\varepsilon } \propto \varepsilon ^{\alpha }. \end{aligned}$$

(8)

Therefore, we can obtain $\alpha$ by calculating the slope of the linear regression line for $f_{\varepsilon }$ versus $\varepsilon$ using a log-log plot.

We placed 30, 000 squares randomly in a limited region to calculate $\alpha$, as shown in Fig. 3A. Because the basin of attraction moves depending on $\gamma$, the limited region moves in the same way as the basin of attraction. However, the area of the limited region is identical for all $\gamma$. Figure 3C shows $f_{\varepsilon }$ versus $\varepsilon$ for $\gamma =0.01$, 0.012, 0.016, and 0.01925, and linear regression lines using a log-log graph. We obtained the uncertainty exponent $\alpha$ from the coefficient for this regression. Figure 3D shows a plot of $\alpha$ versus $\gamma$. When $\gamma <0.008$, the basin boundary is not fractal because $\alpha \approx 1$. When $\gamma >0.008$, the basin boundary becomes fractal because $0< \alpha < 1$. We can find dramatic changes in $\alpha$ at certain values of $\gamma$, which include $\gamma \approx 0.0103, 0.0135$, and 0.019, where the basin size shows remarkable changes in Fig. 3C.

4 Mechanism for sharp changes in the basin of attraction

4.1 Formation of basin of attraction through stretch-bending deformation by $S^{-1}$

We introduce the notation $D_{n}$ $(n=1,2, \ldots )$ to denote the set of initial conditions on the Poincaré section T(H) from which the model walks at least n steps. As n increases to infinity, $D_n$ approximates the basin of attraction. Furthermore, this set satisfies $D_{n+1} \subseteq D_{n}$ (Fig. 2B), which means that if the initial condition is in $D_{n}$ but not in $D_{n+1}$, the model will fall down at the ($n+1$)th step. In our previous study [32], we showed that $S(D_{n})$ represents the state on T(H) after the model walked one step starting from $D_{n}$, which is in $D_{n-1}$ (Fig. 2B) because the Poincaré map S represents walking one step. Moreover, $S(D_n)$ is also in the range R of S, which is given by $R=S(D_1)$ because $D_1$ is the domain of S. Therefore, the following condition is satisfied: $S(D_{n})=D_{n-1} \cap R$, which gives

$$\begin{aligned} D_{n}=S^{-1}(S^{-1}(\cdots (S^{-1}(D_{1} \cap R) \cap R) \cdots \cap R) \cap R). \end{aligned}$$

(9)

This indicates that the basin of attraction is obtained by iterative processes to extract the intersection with R of S and to apply the inverse image $S^{-1}$ starting from $D_1$. Because saddle instability due to the inverted pendulum induces a stretching-bending effect in $S^{-1}$ [31, 32], $D_1$ is stretched and bent many times to create many slits (Fig. 4).

Fig. 4

Schematic diagram of process to deform $D_1$ to $D_2$, to $D_3, \cdots ,$ to $D_{\infty }$ and generate slits. $D_1 \cap R$ (B) is extracted from $D_1$ (A) and stretched and bent by $S^{-1}$ to form U-shaped $D_2$ with one slit (C). In the same way, $D_2 \cap R$ is extracted (D) and stretched and bent by $S^{-1}$ to form $D_3$ with two slits (E). $D_3 \cap R$ is extracted (F) and stretched and bent by $S^{-1}$ to form $D_4$ with three slits (G). $D_{\infty }$ has many slits through this process (H)

Fig. 5

Formation process for fractal basin of attraction. When a red slit in $D_N$ penetrates the lower edge of the range R for the first time (A), $D_N\cap R$ is separated into two regions (B). $D_{N+1}$ has a red $D_n$-penetrating slit near the outer edge (C) and it is separated into two red slits in $D_{N+1}\cap R$ (D). $D_{N+2}$ and $D_{N+2}\cap R$ have a red $D_n$-penetrating slit, which surrounds the center blue slit (E, F). $D_{N+3}$ has a red $D_n$-penetrating slit, which surrounds a blue slit and penetrates the lower edge of R (G), and it is also separated into two red slits in $D_{N+3}\cap R$ (H). These slits produce new penetrating slits, and the number of slits increases at an accelerated rate as n increases after $D_{N+4}$ (I)

Suppose that a slit (red) in $D_n$ penetrates the lower edge of R for the first time at $n = N$, as shown in Fig. 5A. By applying $S^{-1}$ to $D_N\cap R$ (Fig. 5B) in the same manner as in Fig. 4, the slit penetrates the U-shaped $D_{N+1}$ along and near the outer edge (Fig. 5C). When a slit penetrates $D_n$, we call it a $D_n$-penetrating slit. When it does not, we call it a non-$D_n$-penetrating slit. The $D_n$-penetrating slit in $D_{N+1}$ corresponds to two slits near the left and right edges in $D_{N+1} \cap R$ (Fig. 5D). The right slit penetrates $D_{N+2}$ along and near the inner edge and surrounds the slit (blue) generated by the inner edge (Fig. 5E). Because these slits do not penetrate R, they remain in $D_{N+2}\cap R$ (Fig. 5F) and $D_{N+3}$ (Fig. 5G). However, these two slits in $D_{N+3}$ penetrate R and one of them (red) corresponds to two slits in $D_{N+3}\cap R$ (Fig. 5H). The number of slits increases at an accelerated rate as n increases, and some slits are surrounded by many $D_n$-penetrating slits (Fig. 5I). Through these procedures, the basin boundaries become fractal in $\gamma >0.0075$.

4.2 Comparison of basin state before and after sharp changes in its characteristics

Figure 6A and B show the basin of attraction at $\gamma =0.0134$ (before the sharp changes in the basin characteristics at $\gamma \approx 0.0135$) and $\gamma =0.0136$ (after the sharp changes), respectively. In the specific region of each figure, we used at least $1500\times 1500$ initial conditions to obtain accurate boundaries, which was confirmed by investigating if the boundary remained unchanged even when we used $3000\times 3000$ initial conditions (we used the same conditions to calculate $D_n$ in the following sections). As shown in the enlarged figures, a purple non-$D_n$-penetrating slit is surrounded by $D_n$-penetrating slits. While these slits do not reach the lower edge of the range R in Fig. 6A, many slits reach and penetrate the lower edge of R in Fig. 6B. This difference could cause the sharp changes in the basin characteristics.

Fig. 6

Penetration of the lower edge of the range R by $D_n$-penetrating slits in the basin of attraction at $\gamma \approx 0.0135$. A $\gamma = 0.0134$ (before penetration). B $\gamma = 0.0136$ (after penetration). The orange and blue regions are R and the basin of attraction $D_{\infty }$, respectively. The orange, blue, and red lines are the boundaries of R, $D_{\infty }$, and $D_{\infty }^1$, respectively

Fig. 7

Regions and slits when basin boundaries become fractal. A $D_n$ is separated into $D_n^i$ $(i=1,2,\dots ,\infty )$ by $D_n$-penetrating slits, where $D_n^1$ contains the attractor. B R-penetrating and non-R-penetrating slits in $D_n^1$. A R-penetrating slit reaches and penetrates the lower edge of R and a non-R-penetrating slit does not

When the basin boundaries become fractal ($\gamma >0.0075$), non-$D_n$-penetrating slits are surrounded by $D_n$-penetrating slits through the formation process for the basin of attraction, as shown in Fig. 5E and G. For large enough n, $D_n$ has many such $D_n$-penetrating slits and consists of an infinite number of regions separated by the $D_n$-penetrating slits. We define $D_n=\bigcup ^{\infty }_{i=1}D_n^i$ as shown in Fig. 7A, where $D_n^i$ ($i=1,2,\dots$) is the separated region and $D_n^1$ contains the attractor. If a non-$D_n$-penetrating slit in $D_n^1$ reaches and penetrates the lower edge of R, we call it a R-penetrating slit (Fig. 7B). If it does not penetrate the lower edge, we call it a non-R-penetrating slit.

In Fig. 3A, we can find three non-R-penetrating slits in $D_{50}^1(\approx D_{\infty }^1)$ for $\gamma =0.01$, two for $\gamma =0.012$, and one for $\gamma =0.016$, which means that the number of non-R-penetrating slits decreases as they penetrate R through the increase of $\gamma$. Figure 3E shows the number of non-R-penetrating slits versus $\gamma$ and confirms that it decreases as $\gamma$ increases. There could be an infinite number of non-R-penetrating slits for $\gamma \approx 0.0075$, where fractal basin boundaries appear. By comparing Fig. 3C–E, we can find that when the number of non-R-penetrating slits changes, the basin characteristics sharply change.

4.3 Mechanism for sharp changes in basin characteristics based on the number of non-R-penetrating slits

Because the basin of attraction is the set of initial states that asymptotically converge to an attractor, any state in the basin of attraction moves toward the attractor by repeated application of S. That is, the basin of attraction is obtained by the iterative application of the inverse image $S^{-1}$ to the proximity of the attractor. Therefore, the formation process for the basin of attraction can be explained by the iterative application of $S^{-1}$ not only to $D_n$ as in Figs. 4 and 5, but also to $D_n^1$ that contains the attractor.

We investigated the relationship between the sharp change in the basin characteristics with $\gamma$ and the change in the number of non-R-penetrating slits in $D_{\infty }^1$. First, we examined how the number of slits increases in the formation process for the basin of attraction by focusing on the deformation of $D_n^1$ with n when the basin boundary is not fractal, when it is fractal with one non-R-penetrating slit, and when it is fractal with two non-R-penetrating slits. Second, we investigated the mechanism for the sharp changes in the basin characteristics when the number of non-R-penetrating slits decreases from 2 to 1. Finally, we determined that this mechanism is applicable when the number of non-R-penetrating slits decreases from $k+1$ to k $(k=1,2,\dots )$.

4.3.1 Increase of number of slits in formation process for basin of attraction for n

First, we investigated how the number of slits increases in the formation process for the basin of attraction when no slit reaches the lower edge of R and the basin boundary is not fractal as in Fig. 4 ($\gamma <0.0075$). Although a red slit in $D_2$ in Fig. 4C is stretched and bent by $S^{-1}$, it never reaches the lower edge of R and there is only one red slit in both $D_3$ in Fig. 4E and $D_4$ in Fig. 4G. No matter how many times $S^{-1}$ is applied, there is only one red slit in $D_n$ ($n\ge 2$).

Second, we investigated how the number of slits increases when the basin boundary is fractal and there is one non-R-penetrating slit in $D_{\infty }^1$ ($0.0135<\gamma <0.019$). Because the formation process for the basin of attraction is explained by $D_n^1$, Fig. 5 explains the basin formation for one non-R-penetrating slit by replacing $D_N$ by $D_N^1$ in Fig. 5A. We define $\hat{D}_{n}^1$ $(n\ge N+1)$ as the region obtained by applying $S^{-1}$ to $D_N^1$. Figure 5A shows one red R-penetrating slit and one yellow non-R-penetrating slit in $D_N^1$. The red R-penetrating slit generates red $D_n$-penetrating slits in $\hat{D}_{N+1}^1$, $\hat{D}_{N+2}^1$, and $\hat{D}_{N+3}^1$ in Fig. 5C, E, and G, respectively. Because these $D_n$-penetrating slits also reach and penetrate the lower edge of R, these slits are divided into two slits in $\hat{D}_{N+1}^1\cap R$, $\hat{D}_{N+2}^1\cap R$, and $\hat{D}_{N+3}^1\cap R$ in Fig. 5D, F, and H, respectively. Therefore, the number of red $D_n$-penetrating slits increases one by one in $\hat{D}_{N+1}^1\rightarrow \hat{D}_{N+2}^1\rightarrow \hat{D}_{N+3}^1$ (one red slit in $\hat{D}_{N+1}^1$, two red slits in $\hat{D}_{N+2}^1$, and three red slits in $\hat{D}_{N+3}^1$). In addition, $\hat{D}_{N+3}^1$ has a red $D_n$-penetrating slit, which surrounds a blue R-penetrating slit and penetrates the lower edge of R as shown in Fig. 5G. This red slit is also divided into two slits in $\hat{D}_{N+3}^1\cap R$, as shown in Fig. 5H. Therefore, while the number of red slits increases one by one in $\hat{D}_{N+1}^1\rightarrow \hat{D}_{N+2}^1\rightarrow \hat{D}_{N+3}^1$, it increases by two in $\hat{D}_{N+3}^1\rightarrow \hat{D}_{N+4}^1$. In addition, the red slits divided in $\hat{D}_{N+3}^1\cap R$ generate two $D_n$-penetrating slits in $\hat{D}_{N+4}^1$ (Fig. 5I), each of which is also divided into two slits in $\hat{D}_{N+4}^1\cap R$. These findings indicate that the number of red slits increases at an accelerating rate by two effects: a $D_n$-penetrating slit at the left of $\hat{D}_n^1$ is divided into two slits in $\hat{D}_n^1\cap R$ and a $D_n$-penetrating slit surrounding a R-penetrating slit is divided into two slits in $\hat{D}_n^1\cap R$. Figure 8 shows the formation process for the basin of attraction for $\gamma =0.018$, where the basin boundary is fractal and there is one non-R-penetrating slit. A non-$D_n$-penetrating slit penetrates the lower edge of R in $D_4$ ($N=4$, $D_4^1=D_4$). A $D_n$-penetrating slit surrounds the R-penetrating slit in $D_7$ ($N+3=7$, $\hat{D}_7^1=D_7$), which penetrates the lower edge of R and is divided into two slits in $D_7\cap R$.

Fig. 8

Formation process for basin of attraction from $D_3$ to $D_7$ (A–F) for $\gamma =0.018$, where there is one non-R-penetrating slit in $D_{\infty }^1$. The red slits correspond to those for $N=4$ in Fig. 5. A non-$D_n$-penetrating slit penetrates the lower edge of the range of R in $D_4$ and a $D_n$-penetrating slit surrounding the R-penetrating slit penetrates R in $D_7$

Fig. 9

Formation process for fractal basin of attraction when there are two non-R-penetrating slits. When a red slit in $D_N$ penetrates the lower edge of the range R for the first time (A), $D_N\cap R$ is separated into two regions (B). $D_{N+1}$ has a red $D_n$-penetrating slit near the outer edge (C), and it is separated into two red slits in $D_{N+1}\cap R$ (D). $D_{N+2}$ and $D_{N+2}\cap R$ have a red $D_n$-penetrating slit, which surrounds the center, yellow non-R-penetrating slit (E, F). $D_{N+3}$ and $D_{N+3}\cap R$ have a red $D_n$-penetrating slit, which surrounds the non-R-penetrating slit at the left of the center, yellow non-R-penetrating slit (G, H). $D_{N+4}$ has a red $D_n$-penetrating slit, which surrounds a yellow R-penetrating slit and penetrates the lower edge of R (I), and it is also separated into two red slits in $D_{N+4}\cap R$ (J). While it takes three applications of $S^{-1}$ to surround the R-penetrating slit by a $D_n$-penetrating slit for one non-R-penetrating slit (Fig. 5), it takes four applications for two non-R-penetrating slits

Finally, we investigated how the number of slits increases when the basin boundary is fractal and there are two non-R-penetrating slits in $D_{\infty }^1$ ($0.0103<\gamma <0.0135$). Figure 9 explains the basin formation process for two non-R-penetrating slits. Figure 9A shows one red R-penetrating slit and one blue and one purple non-R-penetrating slits in $D_N^1$. The red R-penetrating slit generates red $D_n$-penetrating slits in $\hat{D}_{N+1}^1$, $\hat{D}_{N+2}^1$, $\hat{D}_{N+3}^1$, and $\hat{D}_{N+4}^1$ in Fig. 9C, E, G, and I, respectively. Because these $D_n$-penetrating slits also reach and penetrate the lower edge of R, these slits are divided into two slits in $\hat{D}_{N+1}^1\cap R$, $\hat{D}_{N+2}^1\cap R$, $\hat{D}_{N+3}^1\cap R$, and $\hat{D}_{N+4}^1\cap R$ in Fig. 5D, F, H, and J, respectively. Therefore, the number of red $D_n$-penetrating slits increases one by one in $\hat{D}_{N+1}^1\rightarrow \hat{D}_{N+2}^1\rightarrow \hat{D}_{N+3}^1\rightarrow \hat{D}_{N+4}^1$ (one red slit in $\hat{D}_{N+1}^1$, two red slits in $\hat{D}_{N+2}^1$, three red slits in $\hat{D}_{N+3}^1$, and four red slits in $\hat{D}_{N+4}^1$). In addition, $\hat{D}_{N+4}^1$ has a red $D_n$-penetrating slit, which surrounds a yellow R-penetrating slit and penetrates the lower edge of R, as shown in Fig. 9I. This red slit is divided into two slits in $\hat{D}_{N+4}^1\cap R$, as shown in Fig. 9J. In addition, the red slits divided in $\hat{D}_{N+4}^1\cap R$ generate two $D_n$-penetrating slits in $\hat{D}_{N+5}^1$, each of which is also divided into two slits in $\hat{D}_{N+5}^1\cap R$. The number of red slits increases at an accelerating rate in the same way as that when there is one non-R-penetrating slit in $D_{\infty }^1$. Figure 10 shows the formation process for the basin of attraction for $\gamma =0.013$, where the basin boundary is fractal and there are two non-R-penetrating slits. A non-$D_n$-penetrating slit penetrates the lower edge of R in $D_5$ ($N=5$, $D_5^1=D_5$). A $D_n$-penetrating slit surrounds the R-penetrating slit in $D_9$ ($N+4=9$, $\hat{D}_9^1=D_9$), which penetrates the lower edge of R and is divided into two slits in $D_9\cap R$.

4.3.2 Mechanism for sharp changes in basin characteristics when number of non-R-penetrating slits decreases from 2 to 1

In the comparison of the basin formation processes when one non-R-penetrating slit exists in $D_{\infty }^1$ and when two exist, it is common that the number of slits in $D_n^1$ increases at an accelerating rate to generate fractal basin boundaries. However, how the number of slits increases in the basin formation processes is different. Specifically, it takes three applications of $S^{-1}$ to surround the R-penetrating slit by a $D_n$-penetrating slit and to be divided into two slits in $\hat{D}_n^1\cap R$ for one non-R-penetrating slit. In contrast, it takes four applications for two non-R-penetrating slits. This implies that one non-R-penetrating slit has a faster rate of increase than two non-R-penetrating slits. This difference is due to the formation process for $D_n$-penetrating slits. Specifically, $\hat{D}_{N+1}^1$ has a red $D_n$-penetrating slit near the outer edge, as shown in Figs. 5C and 9C. $\hat{D}_{N+2}^1$ also has another red $D_n$-penetrating slit, which surrounds the non-R-penetrating slit at the middle, as shown in Figs. 5E and 9E. For two non-R-penetrating slits, $\hat{D}_{N+3}^1$ has another red $D_n$-penetrating slit, which surrounds the non-R-penetrating slit left of the middle non-R-penetrating slit, as shown in Fig. 9G. Finally, $\hat{D}_{N+3}^1$ for one non-R-penetrating slit and $\hat{D}_{N+4}^1$ for two non-R-penetrating slits have a red $D_n$-penetrating slit, which surrounds a R-penetrating slit, as shown in Figs. 5G and 9I. This means that the surrounding $D_n$-penetrating slits appear one by one from $D_{N+2}^1$ to $D_{N+k+2}^1$, where k is the number of non-R-penetrating slits. As a result, one non-R-penetrating slit forms a larger number of slits and more complex boundaries in $D_n$ for any n than two non-R-penetrating slits, which leads to a smaller basin size and a lower uncertainty exponent for basin boundaries. This mechanism induces the sharp changes in the basin characteristics at $\gamma \approx 0.0135$, where the number of non-R-penetrating slits decreases from 2 to 1.

Fig. 10

Formation process for basin of attraction from $D_4$ to $D_9$ (A–G) for $\gamma =0.013$, where two non-R-penetrating slits exist in $D_{\infty }^1$. The red slits correspond to those for $N=5$ in Fig. 9. A non-$D_n$-penetrating slit penetrates the lower edge of the range of R in $D_5$ and a $D_n$-penetrating slit surrounding the R-penetrating slit penetrates R in $D_9$

4.3.3 Mechanism for sharp changes in basin characteristics when number of non-R-penetrating slits decreases from $k+1$ to k

The mechanism for the sharp change in the basin characteristics described in the previous section is applicable when the number of non-R-penetrating slits decreases from $k+1$ to k ($k=1,2,\dots$). Suppose that there are ($k+1$) non-R-penetrating slits. When $\hat{D}_N^1$ has an R-penetrating slit, $\hat{D}_{N+1}^1$ has a $D_n$-penetrating slit near the outer edge in the same way for one and two non-R-penetrating slits in Figs. 5C and 9C, respectively. $\hat{D}_{N+2}^1$ has a $D_n$-penetrating slit, which surrounds the center non-R-penetrating slit. $\hat{D}_{N+n}^1$ ($3\le n\le k+2$) has a $D_n$-penetrating slit, which surrounds the non-R-penetrating slit at the ($n-2$)th slit left from the center non-R-penetrating slit. Finally, $\hat{D}_{N+k+3}^1$ has a $D_n$-penetrating slit that surrounds an R-penetrating slit. This means that it takes $k+3$ applications of $S^{-1}$ to generate the $D_n$-penetrating slit that surrounds the R-penetrating slit. Therefore, when the number of non-R-penetrating slits decreases from $k+1$ to k, the number of iterations changes from $k+3$ to $k+2$. The rate of this change is $\frac{k+2}{k+3}$, which is $\frac{3}{4}$ for $k=1$ for $\gamma \approx 0.0135$ and $\frac{4}{5}$ for $k=2$ at $\gamma \approx 0.0105$. It is almost 1 for $k\gg 1$ for $0.0075<\gamma <0.01$. Therefore, the change in the basin of attraction is most remarkable for $\gamma \approx 0.0135$ with $k=1$, and is less significant for smaller $\gamma$ with larger k, as shown in Fig. 3C and D. In particular, the changes for $0.0075<\gamma <0.01$ are difficult to recognize.

Fig. 11

Formation process for basin of attraction when all non-$D_n$-penetrating slits penetrate lower edge of range R. When the last non-R-penetrating slit penetrates R at $n=N$ (A), $D_N^1\cap R$ has one red slit (B). $\hat{D}_{N+1}^1$ has one red $D_n$-penetrating slit inside the U-shaped region (C). $\hat{D}_{N+1}^1\cap R$ has two red slits (D). $\hat{D}_{N+2}^1$ has two red $D_n$-penetrating slits inside the U-shaped region (E). $\hat{D}_{N+2}^1\cap R$ has four red slits (D). $\hat{D}_n^1\cap R$ ($n=N,N+1,\dots$) can be assumed as a one-dimensional Cantor set

4.4 Mechanism for disappearance of basin of attraction

The mechanism for the sharp changes in the basin characteristics described in the previous section is applicable when the number of non-R-penetrating slits decreases from $k+1$ to k for $k=1,2,\dots$. In this section, we investigate the formation process for the basin of attraction when the number of non-R-penetrating slits decreases from 1 to 0 and all non-$D_n$-penetrating slits penetrate the lower edge of R.

Figure 11 explains the basin formation process when all non-$D_n$-penetrating slits penetrate the lower edge of R. Suppose that all non-$D_n$-penetrating slits penetrate R at $n=N$ in $D_N^1$ (Fig. 11A). Then, a $D_n$-penetrating slit is generated in $\hat{D}_{N+1}^{1}$, which penetrates the lower edge of R (Fig. 11C) and is divided into two slits in $\hat{D}_{N+1}^{1}\cap R$ (Fig. 11D). Moreover, each divided slit also penetrates the lower edge of R in $\hat{D}_{N+2}^{1}$ (Fig. 11E) and is divided into two slits in $\hat{D}_{N+2}^{1}\cap R$ (Fig. 11F). Each application of $S^{-1}$ produces this penetration of R and subsequent division into two slits. This formation process for the basin of attraction can be assumed as a one-dimensional Cantor set [36]. Therefore, the area of $\hat{D}_{n}^{1}$ decreases as n increases and it finally disappears. That is, the basin of attraction disappears when the number of non-R-penetrating slits decreases from 1 to 0. However, note that we cannot observe that the number of non-R-penetrating slits is 0 as in Fig. 3E. This is because we cannot calculate the number of non-R-penetrating slits when the basin of attraction disappears. (Actually, $D_n^1$ does not exist when all non-$D_n$-penetrating slits penetrate R because there is neither an attractor nor a basin of attraction. However, we used it only in the basin formation process to simply explain the disappearance mechanism for the basin of attraction.)

Figure 12 shows the disappearance process for the basin of attraction for $\gamma =0.021$, where all non-$D_n$-penetrating slits penetrate the lower edge of R. A non-$D_n$-penetrating slit penetrates R in $D_6^1$ ($N=6$) and non-R-penetrating slits disappear in Fig. 12B. As a result, ${D}_7$ has one red $D_n$-penetrating slit (Fig. 12C), as shown in Fig. 11C. Furthermore, ${D}_8$ and ${D}_9$ have two and four red $D_n$-penetrating slits (Fig. 12D and E), respectively. $D_n$ becomes thinner as n increases. By repeating these processes, the basin of attraction disappears.

Fig. 12

Formation process for basin of attraction from $D_5$ to $D_9$ (A–E) for $\gamma =0.021$, where all non-$D_n$-penetrating slits penetrate lower edge of range R. The red slits correspond to the red slits for $N=6$ in Fig. 11. $D_7$ has one red $D_n$-penetrating slit inside the U-shaped region. $D_8$ and $D_9$ have two and four red $D_n$-penetrating slits, respectively

5 Conclusion

In this study, we showed that sharp changes in the size and fractality of the basin of attraction for passive dynamic walking depends on the slope angle $\gamma$. In addition, we clarified the mechanism for the sharp changes based on the formation process by improving our previous analysis. We also proposed a mechanism for the disappearance of the basin of attraction, which was previously explained by a boundary crisis [17, 31], based on the formation process for the basin of attraction. These mechanisms are commonly based on the stretching-bending deformation caused by the inverse image of the Poincaré map. Specifically, abrupt alterations of the overlap between region $D_n$ and the range R of the Poincaré map in the formation process for the basin of attraction induce these sharp changes in the basin of attraction.

We used a computational resolution that allowed us to identify sharp changes in fractal dimension at $\gamma = 0.0103$, 0.0135, and 0.019. However, even at higher resolution, two technical difficulties prevented us from finding sharp changes for $0.0075<\gamma <0.01$. The first difficulty is the regional dependence of the fractal dimension, since different parts of the basin of attraction have different fractal dimensions. In addition, the basin of attraction moves in phase space depending on $\gamma$. Because we cannot necessarily calculate the fractal dimension in the same region of the basin boundary for each $\gamma$, this region-dependent effect is a serious problem. The second difficulty is the accuracy of the calculation for the basin of attraction. To determine if an initial state is inside or outside the basin of attraction, we determined whether or not the model fell within 50 steps, as described in Sect. 3.1. Near the fractal basin boundary, it takes an extremely long time for the model to fall, which affects the fractality of the basin boundary.

Our model is a hybrid system. The boundaries of the domain and the range of the Poincaré map for our model are mainly obtained from touchdown conditions (Eqs. (4) and (5), respectively), as previously described [31, 32]. Because the basin boundary is obtained from the inverse image of the Poincaré map of these boundaries, it can be considered to have the same properties as the boundaries for the domain and the range. Therefore, the basin boundary in our model is dominated by the touchdown conditions and does not correspond to a stable manifold as in continuous systems. In future studies, we intend to investigate the relationship between manifolds and basin boundaries.

Sharp changes in the basin of attraction are also observed in the Hénon map, which is a well-studied example of a nonlinear dynamical system exhibiting chaotic attractors [14]. Because the inverse image of the Hénon map also induces a stretching-bending effect, a common mechanism is expected for the sharp changes in the basin of attraction between passive dynamic walking and the Hénon map. However, sharp changes occur countless times during passive dynamic walking, whereas they occur only twice in the Hénon map [14]. Furthermore, the Poincaré map for passive dynamic walking is neither surjective nor injective because the system is a hybrid system, whereas the Hénon map is bijective. Therefore, different mechanisms are expected for the Hénon map. Clarifying common and specific features of the basin of attraction for dynamical systems is a subject for future study.

To understand the stabilization mechanism for bipedal walking, not only the simplest walking model used in this study, but also more general models with knees and an upper body have been considered [7, 8, 10]. To carry out a stability analysis of these models, a method for designing an explicit expression for the Poincaré map has been proposed [40,41,42]. The disappearance of attractors in these models is not solely attributed to the boundary crisis, but also to other bifurcations, such as flip bifurcation and saddle-node bifurcation [8, 15, 16]. However, the basin characteristics for these models remain largely unclear. The principal dynamic characteristic of bipedal walking is saddle instability due to the inverted pendulum, which induces the stretching-bending effect in the inverse image of the Poincaré map [31]. Therefore, the formation process for the basin of attraction clarified in this study is expected to be applicable to the formation mechanisms for the basin of attraction of other models, and for clarifying their basin characteristics.