Skip to main content
SpringerLink
Log in

Dynamics of plane waves on two-dimensional isotropic and anisotropic dissipative systems near subcritical bifurcation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

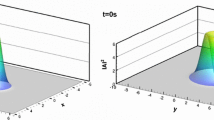
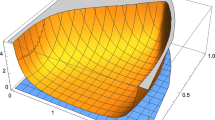
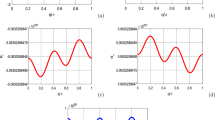
In this work, stability analysis of plane wave solutions of the cubic-quintic complex Ginzburg–Landau equation for isotropic and anisotropic systems is carried out. In this regard, we perform extensive numerical simulations based on a two-dimensional spatial Fourier discretization and an explicit scheme for temporal differentiation to find the domain of existence of the space-time dynamical behavior of the two-dimensional complex Ginzburg–Landau equation with cubic and quintic nonlinearities. One of the nonlinearity parameters is fixed and the others are varied one by one to determine the regimes in which plane wave solutions exist as stable/instable structures. Moreover, the stability criterion which has been plotted with the state diagram and the different dynamic structures obtained in space parameters has been established. Energy function was also used to characterize spatiotemporal dynamics observed in our system. By performing long simulations for the different parameters of the equation, we found the existence of stable (plane wave, localized defect), intermittent (intermittency state), and unstable (bichaos, phase turbulence, and defect turbulence) structures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Data accessibility

The datasets generated and analyzed in the current study are available from the corresponding author on reasonable request.

References

  1. Ott, E., Grebogi, C., Yorke, J.A.: Controlling chaos. Phys. Rev. Lett. 64(11), 1196 (1990)

    MathSciNet  MATH  Google Scholar 

  2. Tchakounte, F.M., Nana, V.B., Nana, L.: Time-delayed feedback with global and local contributions on spatiotemporal dynamics of waves in fiber cavity. Eur. Phys. J. Plus 136(1), 94 (2021)

    Google Scholar 

  3. Kyrychko, Y.N., Blyuss, K.B., Hogan, J., Scholl, E.: Control of spatiotemporal patterns in the Gray–Scott model. Chaos 19(4), 043126 (2009)

    Google Scholar 

  4. Cross, M., Hohenberg, P.: Pattern formation outside of equilibrium. Rev. Mod. Phys. 65(3), 851 (1993)

    MATH  Google Scholar 

  5. Alvarez-Garrido, F., Clerc, M.G., Gonzalez-Cortes, G.: Transition to spatiotemporal intermittency and defect turbulence in systems under translational coupling. Phys. Rev. Lett. 124(16), 164101 (2020)

    Google Scholar 

  6. Cross, M., Greenside, H.: Pattern Formation and Dynamics in Nonequilibrium Systems. Cambridge University Press, Cambridge (2009)

    MATH  Google Scholar 

  7. Ledesma-durán, A., Aragón, J.L.: Spatio-temporal secondary instabilities near the Turing–Hopf bifurcation. Sci. Rep. 9(1), 11287 (2019)

    Google Scholar 

  8. Tu, M., Shen, J., Zhou, Z.: Traveling fronts of a real supercritical Ginzburg–Landau equation coupled by a slow diffusion. Qualit. Theory Dyn. Syst. 17, 29–48 (2018)

    MathSciNet  MATH  Google Scholar 

  9. Bennett, J., Sherratt, J.: How do dispersal rates affect the transition from periodic to irregular spatio-temporal oscillations in invasive predatorprey systems. Appl. Math. Lett. 94, 8086 (2019)

    MATH  Google Scholar 

  10. Skinner, G.S., Swinney, H.L.: Periodic to quasiperiodic transition of chemical spiral rotation. Physica D 48(1), 1–16 (1991)

    MATH  Google Scholar 

  11. Daviaud, F., Lega, J., Bergé, P., Coullet, P., Dubois, M.: Spatio-temporal intermittency in a 1D convective pattern: theoretical model and experiments. Physica D 55(3–4), 287–308 (1992)

  12. Rehberg, I., Rasenat, S., Steinberg, V.: Traveling waves and defect-initiated turbulence in electroconvecting nematics. Phys. Rev. Lett. 62(7), 756 (1989)

    Google Scholar 

  13. Coullet, P., Lega, J.: Defect-mediated turbulence in wave patterns. Europhys. Lett. 7(6), 511 (1988)

    Google Scholar 

  14. Kidachi, H.: Side wall effect on the pattern formation of the Rayleigh–Bénard convection. Prog. Theor. Phys. 64(5), 1861–1864 (1980)

    MathSciNet  Google Scholar 

  15. Aranson, I.S., Kramer, L.: The world of the complex Ginzburg–Landau equation. Rev. Mod. Phys. 74(1), 99 (2002)

    MathSciNet  MATH  Google Scholar 

  16. Drazin, P.G., Reid, W.H.: Hydrodynamic stability. NASA STI/Recon Tech. Rep. A 82, 17950 (1981)

    Google Scholar 

  17. Kuetche, G.S., Nana, L.: Higher-order spectral filtering effects on the dynamics of stationary soliton in dissipative systems in the presence of linear and nonlinear gain/loss. Nonlinear Dyn. 105(3), 2559–2573 (2021)

    Google Scholar 

  18. van Saarloos, W., Hohenberg, P.C.: Fronts, pulses, sources and sinks in generalized complex Ginzburg–Landau equations. Physica D 56(4), 303–367 (1992)

    MathSciNet  MATH  Google Scholar 

  19. Grelu, P., Akhmediev, N.: Group interactions of dissipative solitons in a laser cavity: the case of 2+1. Opt. Express 12(14), 3184–3189 (2004)

    Google Scholar 

  20. Yan, Y., Liu, W., Zhou, Q., Biswas, A.: Dromion-like structures and periodic wave solutions for variable-coefficients complex cubic-quintic Ginzburg–Landau equation influenced by higher-order effects and nonlinear gain. Nonlinear Dyn. 99(2), 1313–1319 (2020)

    Google Scholar 

  21. Staliunas, K., Herrero, R., de Valcarcel, G.J.: Arresting soliton collapse in two-dimensional nonlinear Schrödinger systems via spatiotemporal modulation of the external potential. Phys. Rev. A 75(1), 011604 (2007)

    Google Scholar 

  22. Thual, O., Fauve, S.: Localized structures generated by subcritical instabilities. J. Phys. 49(11), 1829–1833 (1988)

    Google Scholar 

  23. Bazhenov, M., Rabinovich, M.: Synchronized disorder in a 2D complex Ginzburg–Landau equation. Physica D 73(4), 318–334 (1994)

    MathSciNet  MATH  Google Scholar 

  24. Chaté, H., Manneville, P.: Phase diagram of the two-dimensional complex Ginzburg–Landau equation. Phys. A 224(1–2), 348–368 (1996)

    MathSciNet  MATH  Google Scholar 

  25. Petviashvili, V.I., Sergeev, A.M.: Spiral solitons in active media with an excitation threshold. Dokl. Akad. Nauk SSSR 276(6), 1380–1834 (1984)

    Google Scholar 

  26. Pismen, L.M.: Vortices in Nonlinear Fields: From Liquid Crystals to Superfluids, from Non-Equilibrium Patterns to Cosmic Strings, vol. 100. Oxford University Press, Oxford (1999)

    MATH  Google Scholar 

  27. Mancas, S.C., Choudhury, R.S.: Pulses and snakes in Ginzburg–Landau equation. Nonlinear Dyn. 79(1), 549–571 (2015)

    MathSciNet  Google Scholar 

  28. Aranson, I.S., Pismen, L.M.: Interaction of vortices in a complex vector field and stability of a “vortex molecule’’. Phys. Rev. Lett. 84(4), 634 (2000)

    Google Scholar 

  29. Sanchez-Morcillo, V.J., Staliunas, K.: Stability of localized structures in the Swift–Hohenberg equation. Phys. Rev. E 60(5), 6153 (1999)

    Google Scholar 

  30. Crasovan, L., Malomed, B.A., Mihalache, D.: Stable vortex solitons in the two-dimensional Ginzburg–Landau equation. Phys. Rev. E 63(1), 016605 (2001)

    MATH  Google Scholar 

  31. Bérard, F., Vandamme, C.J., Mancas, S.C.: Two-dimensional structures in the quintic Ginzburg–Landau equation. Nonlinear Dyn. 81(3), 1413–1433 (2015)

    MathSciNet  Google Scholar 

  32. Brown, R., Fabrikant, A.L., Rabinovich, M.I.: Evolution of patterns in the anisotropic complex Ginzburg–Landau equation: modulational instability. Phys. Rev. E 47(6), 4141 (1993)

    MathSciNet  Google Scholar 

  33. Vanishree, R.K.: Convection in anisotropic porous medium with gravity modulation using Ginzburg–Landau model. J. Eng. Res. Appl. 10(4), 59–64 (2020)

    MathSciNet  Google Scholar 

  34. El Achab, A., Amine, A.: A construction of new exact periodic wave and solitary wave solutions for the 2D Ginzburg–Landau equation. Nonlinear Dyn. 91(2), 995–999 (2018)

    Google Scholar 

  35. Tafo, J.B.G., Nana, L., Kofane, T.C.: Dynamics of a traveling hole in one-dimensional systems near subcritical bifurcation. Eur. Phys. J. Plus 126(11), 105 (2011)

    Google Scholar 

  36. Komarov, A., Leblond, H., Sanchez, F.: Multistability and hysteresis phenomena in passively mode-locked fiber lasers. Phys. Rev. A 71(5), 053809 (2005)

    Google Scholar 

  37. Akhmediev, N., Afanasjev, V.V.: Novel arbitrary-amplitude soliton solutions of the cubic-quintic complex Ginzburg–Landau equation. Phys. Rev. Lett. 75(12), 2320 (1995)

    Google Scholar 

  38. Akhmediev, N.N., Afanasjev, V.V., Soto-Crespo, J.M.: Singularities and special soliton solutions of the cubic-quintic complex Ginzburg–Landau equation. Phys. Rev. E 53(1), 1190 (1996)

    Google Scholar 

  39. Malomed, B.A.: Evolution of nonsoliton and “quasi-classical’’ wavetrains in nonlinear Schrödinger and Korteweg–de Vries equations with dissipative perturbations. Physica D 29(1–2), 155–172 (1987)

    MathSciNet  MATH  Google Scholar 

  40. Hakim, V., Jakobsen, P., Pomeau, Y.: Fronts vs. solitary waves in nonequilibrium systems. Europhys. Lett. 11(1), 19 (1990)

    Google Scholar 

  41. Fauve, S., Thual, O.: Solitary waves generated by subcritical instabilities in dissipative systems. Phys. Rev. Lett. 64(3), 282 (1990)

    Google Scholar 

  42. Brand, H.R., Deissler, R.J.: Interaction of localized solutions for subcritical bifurcations. Phys. Rev. Lett. 63(26), 2801 (1989)

    Google Scholar 

  43. Segur, H., Henderson, D., Carter, J., Hammack, J., Li, C., Pheiff, D., Socha, K.: Stabilizing the Benjamin–Feir instability. J. Fluid Mech. 539, 229–271 (2005)

    MathSciNet  MATH  Google Scholar 

  44. Benjamin, T.B., Feir, J.E.: The disintegration of wave trains on deep water Part 1. Theory. J. Fluid Mech. 27(3), 417–430 (1967)

    MATH  Google Scholar 

  45. Tiofack, C.G.L., Tchepemen, N.N., Mohamadou, A., Kofané, T.C.: Stability of Gaussian-type soliton in the cubic-quintic nonlinear media with fourth-order diffraction and PT-symmetric potentials. Nonlinear Dyn. 98(1), 317–326 (2019)

    MATH  Google Scholar 

  46. Liu, C.S.: The Gaussian soliton in the Fermi–Pasta–Ulam chain. Nonlinear Dyn. 106, 899–905 (2021)

  47. Kai, Y., Huang, L.: Dynamic properties, Gaussian soliton and chaotic behaviors of general Degasperis–Procesi model. Nonlinear Dyn. 111(9), 8687–8700 (2023)

    MathSciNet  Google Scholar 

  48. Liu, Y., Ecke, R.E.: Eckhaus–Benjamin–Feir instability in rotating convection. Phys. Rev. Lett. 78(23), 4391 (1997)

    Google Scholar 

  49. Chaté, H.: Spatiotemporal intermittency regimes of the one-dimensional complex Ginzburg–Landau equation. Nonlinearity 7(1), 185 (1994)

    MathSciNet  MATH  Google Scholar 

  50. Huber, G., Alstrom, P., Bohr, T.: Nucleation and transients at the onset of vortex turbulence. Phys. Rev. Lett. 69(16), 2380 (1992)

    Google Scholar 

  51. Coullet, P., Gil, L., Lega, J.: Defect-mediated turbulence. Phys. Rev. Lett. 62(14), 1619 (1989)

    Google Scholar 

  52. Manneville, P., Chaté, H.: Phase turbulence in the two-dimensional complex Ginzburg–Landau equation. Physica D 96(1–4), 30–46 (1996)

    MATH  Google Scholar 

  53. Tafo, J.B.G., Nana, L., Tabi, C.B., Kofane, T.C.: Nonlinear Dynamical Regimes and Control of Turbulence Through the Complex Ginzburg–Landau Equation. Research Advances in Chaos Theory. Intechopen, New York (2020)

    Google Scholar 

  54. Ciszak, M., Mayol, C., Mirasso, C.R., Toral, R.: Anticipated synchronization in coupled complex Ginzburg–Landau systems. Phys. Rev. E 92(3), 032911 (2015)

    MathSciNet  Google Scholar 

  55. Montagne, R., Hermandez-Gracia, E., San Miguel, M.: Winding number instability in the phase-turbulence regime of the complex Ginzburg–Landau equation. Phys. Rev. Lett. 77(2), 267 (1996)

    Google Scholar 

  56. Wabnitz, S.: Spatiotemporal chaos and order in fiber lasers. Rev. Cub. Fis. 33(1E), E32–E34 (2016)

    Google Scholar 

  57. Bodenschatz, E., Pesch, W., Ahlers, G.: Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32(1), 709–778 (2000)

    MATH  Google Scholar 

  58. Tsague, M.N., Bami, N.V., Waffo, T.F., Nana, L.: Stabilization of traveling waves on dissipative system near subcritical bifurcation through a combination of global and local feedback. Eur. Phys. J. Plus 137(10), 1139 (2022)

    Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous reviewers for their useful and valuable comments and suggestions.

Author information

Authors and Affiliations

  1. Pure Physics Laboratory, Group of Nonlinear phenomena in Complex Systems, Department of Physics, Faculty of Sciences, University of Douala, P.O. Box 24157, Douala, Cameroon

    Jimmy Franklin Beltchui Nzoukeu, Thibaut Patient Nana Leufak & Laurent Nana

Authors
  1. Jimmy Franklin Beltchui Nzoukeu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Thibaut Patient Nana Leufak
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Laurent Nana
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Laurent Nana.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest concerning the publication of this manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Beltchui Nzoukeu, J.F., Nana Leufak, T.P. & Nana, L. Dynamics of plane waves on two-dimensional isotropic and anisotropic dissipative systems near subcritical bifurcation. Nonlinear Dyn 111, 17427–17438 (2023). https://doi.org/10.1007/s11071-023-08753-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-023-08753-8

Keywords

Search

Navigation