Reduced-order modeling of geometrically nonlinear structures. Part II: Correspondence and unified perspectives on different reduction techniques

Abstract

Reduced-order models derived by routine finite mode Galerkin truncation of nonlinear continuous structures may lead to errors in the results, especially for quadratic nonlinearity dominated structures (say, sagged cables, shallow arches, imperfect beams). Many different approaches like invariant manifold method (including center manifold, nonlinear normal modes (NNMs), and spectral submanifolds (SSMs)), normal form method, full-basis or direct perturbation techniques, rectified Galerkin method, and low-order elimination approach have been proposed to refine reduced models, i.e., to improve the routine finite mode truncation, and they indeed succeed in correcting the unreliable Galerkin reduction. This is not by coincidence because, essentially, all these refined reduction methods are interconnected with each other in a subtle manner, albeit some of the underlying intrinsic connections still need to be fully unveiled. A manifold parametrization formulation has been recently introduced for nonlinear model reduction in the context of SSMs theory, which suggests an underlying link between the NNMs method and normal form method. This paper aims at establishing an expanded correspondence also including other methods, by focusing on refined treatment of geometric nonlinearity (with weak damping/forcing). This will allow to frame perturbation method, rectified Galerkin, and low-order elimination technique (presented in Part I of the current sequential work) within the overall picture of refined nonlinear reduction, and also to provide an additional interpretation of the mentioned subtle connections from the perspective of nonlinear decomposition, by extending the classical linear expansion. All the comparative arguments will lead to a unified and coherent elucidation of nominally different approaches, fully revisited in the background of the low-order elimination formulation using passive pattern concept, despite being originally designed according to different perspectives.

Appendix

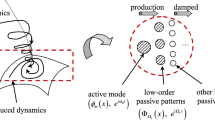
In the sense of correspondence with the reduction methods as detailed in the current work (Fig. 1), two more reduction methods for geometrically nonlinear structures, i.e., static condensation technique [48, 49], and quadratic manifolds method [37, 45] using a mode derivative concept, are briefly discussed below (whose advantages and limitations have also been summarized in the general review [5]).

Firstly, the static condensation technique (also termed adiabatic elimination [50, 51]), as a degenerate version of slow-fast decomposition method [38, 52], has been widely employed, e.g., in the continuous framework, for enslaving fast longitudinal dynamics to the slow transversal one in extensible one-dimension nonlinear structures (generally assumed to be fixed at both ends) [48, 49]. Essentially, nonlinear model reduction is built upon a slow-fast approximation, i.e., inertia effect of nonessential fast dynamics is ignored, which is thus statically enslaved to the master dynamics near a critical (constraint) manifold M_ε (ε → 0), with ε being the small ratio of the fast time scale over the slow one of interest. Similarly, within the discrete framework, static condensation of nonessential dynamics is definitely an improvement with respect to routine/standard Galerkin truncation based on simply skipping essential modes. Later, deficiency of static condensation, say, incorrect prediction of nonlinear softening/hardening behaviors has been pointed out, and the method has been improved by employing a shifted perturbation scheme (see, e.g., [34, 35] as well as Sect. 3.2 and 4.2). Similarly, as a more recent version of static condensation (in the finite-element formulation), the implicit condensation/expansion method [37] has been found unable to predict nonlinear internal resonance due to ignorance of velocity dependence in the critical constraint manifolds, and has been improved through employing the NNMs (invariant manifolds) method [53], by pointing out that, only in the slow-fast partition limit ($\omega_{l} \gg \omega_{m} ,\;\;l \ne m$), the static condensation and NNMs method give the same manifolds [53]. We claim that, with our expanded correspondence (Fig. 1) in mind, it is equivalent to replace the static condensation by either the shifted perturbation [34, 35] or the NNMs (invariant manifolds) method [53], both of which essentially improve the static condensation to a dynamic condensation. What is more, and in accordance with the expanded correspondence (Fig. 1), we conclude that only in the slow-fast partition limit, the static condensation (or implicit condensation/expansion) can predict equivalent results to those of other nonlinear reduction methods in Fig. 1, where all methods belong to dynamic condensation.

However, we also point out that dynamic condensation using shifted perturbation or NNMs [34, 35, 53], and even all methods detailed in Fig. 1, are locally valid in the vicinity of an attractor (say, around a certain active mode), while static condensation itself, due to the slow-fast partition condition ($\omega_{l} \gg \omega_{m} ,\;\;l \ne m$), is more globally valid and can be applied even without modal information (as a limit case of slow-fast decomposition technique [38, 52]).

As another refinement of static condensation, a ‘more global’ dynamic condensation can be achieved through a slow-fast decomposition near a slow manifold M_ε (ε ≠ 0, ε << 1) [52, 54], rather than the critical one M_ε (ε → 0), or by including longitudinal kinetic energy [55, 56] in the Hamiltonian or Lagrangian formulations. Even more, the dynamic condensation has to be further improved for treating non-condensable (stronger longitudinal–transversal coupling) cases, i.e., to include approaching-manifold fast (in the current context, longitudinal) dynamics or to expand master coordinates, either away from [57, 58] or close to longitudinal–transversal internal resonance [59,60,61].

Secondly, the quadratic manifolds method [37, 45] follows the spirit of nonlinearly extending the linear expansion/decomposition: a nonlinear additional term, named mode derivative, is built by sensitivity analysis of nonlinear eigenvalue problem and nonlinear amplitude dependence (typical of nonlinear vibration), and it is suggested to complement the classical linear decomposition, leading to a manifold parametrized by the master modal coordinate, say, $q_{m}$

$$ w\left( {x,t} \right) = \phi_{m} q_{m} + \Theta_{mm} q_{m}^{2} $$

(98)

where the mode derivative $\Theta_{mm}$ has been explicitly derived as a second-order tensor (discrete) [37, 45]. It is recommended here to interpret $\Theta_{mm}$ as a spatial shape function (continuous), naturally leading to an augmented expansion basis $\left[ {\phi_{m} ,\;\;\Theta_{mm} } \right]$. As pointed out in [38, 39], due to ignorance of velocity dependence in Eq. (98), the quadratic manifold method fails to predict internal resonance, and is thus inconsistent with the normal form method. More generally, with our expanded correspondence in mind, the quadratic manifold method is inconsistent with the nonlinear reduction methods in Fig. 1, all of which, being of a dynamic condensation type, are capable to predict internal resonance. Indeed, the low-order elimination suggested decomposition is, say, Eq. (75)

$$ w\left( {x,t} \right) = \phi_{m} p_{m} + \left( {\Phi_{0} + \Phi_{{2\omega_{m} }} } \right)\frac{{p_{m}^{2} }}{2} + \left( {\Phi_{0} - \Phi_{{2\omega_{m} }} } \right)\frac{{\dot{p}_{m}^{2} }}{{2\omega_{m}^{2} }} $$

(99)

and the rectified Galerkin method suggested decomposition (weak excitation) is, say, Eq. (45)

$$ w\left( {x,t} \right) = \phi_{m} \eta_{m} + \frac{{\tilde{\psi }_{0} + \tilde{\psi }_{2} }}{2}\eta_{m}^{2} + \frac{{\tilde{\psi }_{0} - \tilde{\psi }_{2} }}{{2\omega_{m}^{2} }}\dot{\eta }_{m}^{2} + \cdots $$

(100)

Both of them clearly indicate that a reliable nonlinear decomposition requires nonlinear velocity dependence. This velocity dependence is clear from non-invariance of the subspace of homogeneous polynomial, i.e., ${\text{span}}\left\{ {p_{m}^{2} } \right\}$ is not invariant but ${\text{span}}\left\{ {p_{m}^{2} ,\dot{p}_{m}^{2} } \right\}$ is under action of the differentiation operator ${{{\hat{\text{d}}}^{2} } \mathord{\left/ {\vphantom {{{\hat{\text{d}}}^{2} } {{\hat{\text{d}}}t^{2} }}} \right. \kern-0pt} {{\hat{\text{d}}}t^{2} }}$ defined in Eq. (78) (or Sect. 2.3 and Appendix C of Part I [1]). Thus, a sole source nonlinearity $p_{m}^{2}$ will possibly induce both displacement and velocity dependence as given in Eqs. (99) or (100).

Note that only in the slow-fast partition limit ($\omega_{l} \gg \omega_{m} ,\;\;l \ne m$), $\tilde{\psi }_{0} \to \tilde{\psi }_{2}$ (see Eq. (42)) and velocity dependence in nonlinear decomposition (100) vanishes. Consequently, in such a limit case, the quadratic manifold method (or static condensation method) will be possibly consistent with other nonlinear reduction methods in Fig. 1, as also discussed in [38, 39, 45]. Essentially, the following assumptions used for slave modal dynamics in various reduction methods are equivalent versions of static condensation: ignoring the inertia effect, skipping kinetic energy, a slow(active)-fast(slave) partition limit, non-velocity dependence, a vanishing operator ${{{\hat{\text{d}}}^{2} } \mathord{\left/ {\vphantom {{{\hat{\text{d}}}^{2} } {{\hat{\text{d}}}t^{2} }}} \right. \kern-0pt} {{\hat{\text{d}}}t^{2} }} \to 0$ (otherwise, due to non-invariance of subspace spanned by $\left\{ {p_{m}^{2} } \right\}$, both displacement and velocity dependence will be induced). All of them lead to failure of internal resonance prediction, being a unified explanation of observations given in various different contexts.

Therefore, there are some inherent theoretical limitations associated with the mode derivative concept. This means that the original definition of mode derivative using sensitivity analysis of nonlinear eigenvalue problem, intuitively extended from linear sensitivity analysis, demands for some re-evaluation. A more recent refined definition using Volterra series method [62] produces a nonlinear decomposition compatible with the passive pattern-based one (99), leading to a future possibility of framing it, too, within the expanded correspondence (Fig. 1).

Finally, although the current focus is mainly reduction methods built upon first-principle derived dynamic equations and relevant modal knowledge, it is worth mentioning the non-intrusive indirect reduction methods [56, 60] using finite-element models plus response data. Further, data-driven reduction methods using only response data/snapshots (fully equation-free) [63, 64] have demonstrated good applicability to complex dynamical systems and, in particular, the recent fractional-powered SSMs [65] going beyond the traditional reduction framework built upon integer-powered polynomials, pose new challenges to framing them within the general big picture of reliable nonlinear model reduction.