1 Introduction

Neurons form the fundamental units of the central and peripheral nervous systems. By the exchange of electrical and chemical signals between them, neurons supervise the mechanisms of complex information processing and response to stimuli. These complex dynamical behaviors exhibited by neurons can be represented and studied with the help of dynamical systems [1, 2] like ordinary differential equations and maps, leading to the science of neurodynamics. Recently, neurodynamics has become an emerging field of research and has attracted a lot of attention [1] from mathematicians, biologists, and computer scientists, to name a few. These dynamical systems-oriented models, which mimic many neuron behaviors, have been confirmed experimentally [3] as well. Examples of models that are represented by continuous dynamical systems include the Hodgkin–Huxley model [4], Hindmarsh–Rose system [5], FitzHugh–Nagumo neuron system [6], etc., whereas examples for the ones represented by discrete systems involve Rulkov neuron system [7] and Chialvo neuron system [8]. Scarcely any research attention is given to the study of the discrete version. Motivated, we focus on an improved model: a network of Chialvo neurons with spatiotemporal heterogeneities. We believe this is a good imitation of a real-world nervous system. It is important to study the corresponding dynamical behaviors to gain insight into how a nervous system might behave in reality.

The paper takes a step further in realizing a realistic neuron network. Heterogeneities in neuron networks have been incorporated in various forms and structures by researchers previously. For example, a FitzHugh–Nagumo neuron was coupled with a Hindmarsh–Rose neuron model to form a heterogeneous coupled neural network in [9]. Heterogeneity, in this case, was realized in terms of coupling two different already established neuron models. Other works include the achievement of exponential synchronization in a memristor synapse-coupled neuron network [10] and the realization of heterogeneity in terms of coupling a two-dimensional Hindmarsh–Rose neuron model to a three-dimensional Hindmarsh–Rose neuron model via a multistable memristive synapse [11] or a gap junction [12]. Furthermore, in [13], it was reported that variation of energy influx between two adjacent neurons installs heterogeneity in the ensemble over time. In another study, synaptic heterogeneity was studied in a weakly coupled network of Wang–Buzsaki and Hodgkin–Huxley neuron models [14]. In [15], it was also noted that continuous energy accumulation in neurons, under external stimulation, produces shape deformation, leading to heterogeneities. Thus, “heterogeneity” is an important phenomenon to study. One of the major differences between the literature on heterogeneous neuron networks cataloged here and our work is that our system is based on a discrete-time dynamical system, in contrast to the continuous-time dynamical systems neuron models reported herein. The other major difference being our adaptive neuron network is heterogeneous not only over time but also over space, focusing on how the synapse between two adjacent neurons mutates on the application of connection probabilities and noise source. Note that the neurons are identical, that is they are one of a kind: a two-dimensional Chialvo neuron. Heterogeneous neuron networks are believed to be applicable in a wide range of scientific fields: promoting robust learning [16], realizing a real-world neural network, neurocomputing, and secure image encryptions [17], among others.

One of the striking features exhibited by an ensemble of neurons is the phenomenon of synchronization. Synchronization is a universal concept in dynamical systems that have been studied in fields ranging from biology to physics, to neuroscience, to economics [18,19,20,21,22,23,24]. Relevant to our study in neurodynamics, a synchronized state can both pertain to a normal or abnormal cognitive state [25]. In the latter case, it is of utmost importance to study and understand the dynamics of neurons that are not completely synchronized, as has been mentioned in the paper [26]. Two of the interesting states that represent asynchronicity in the neural nodes are chimera states and solitary nodes. A “chimera” state [27,28,29,30,31], discovered by Kuramoto, is characterized by the simultaneous existence of coherent and incoherent nodes from a specific ensemble after a precise time. Chimera states have been reported in various natural phenomena like sleeping patterns of animals [32,33,34], flashing of fireflies [35], and many more [28, 36, 37]. On the other hand, nodes falling under the “solitary” regime [26, 38,39,40,41,42,43] are the ones which behave completely different from the coherent nodes in a particular ensemble at a specific time. They get separated from the main typical cluster and oscillate with their own particular amplitude.

There have been works concerning networks of dynamical systems in which the nodal behaviors were found to be rich. It is interesting to note that in a network of neurodynamical systems, the researchers have found chimera states, cluster synchronization, solitary states, etc. A variety of spatiotemporal patterns are reported in the heterogeneous network considered in this study: solitary states, synchronized states, asynchronized states, etc.

The fact that the dynamical behaviors portrayed by neurons are remarkably complex, demands the requirement of statistical tools to study and quantify their complexity. Measures like spatial average density and entropy are effective tools to study the complexity in the dynamics of neurons. Banerjee and Petrovskii [44] applied the spatial average density approach to show that the spatial irregularity in an ecological model is indeed chaotic. A similar approach is considered in the reference [45]. Entropy is a ubiquitous concept first introduced by C. E. Shannon in his revolutionary work [46]. Since then, it has had a widespread application in various domains of research, including neuroscience [47, 48]. In another study [49], authors report the study of applying entropy to EEG data from patients and report that Alzheimer’s disease could result in complexity loss. More relevant papers [50] related to this topic can also be found. Other applications of entropy in neuroscience include the study of topological connectivity in neuron networks [51,52,53], and estimation of the upper limit on the information contained in the action potential of neurons [54]. Motivated by these, we utilize the tool of sample entropy [55] to analyze time series data of the spatially averaged action potential generated from our model and study the complexity of the dynamics.

Empirical evidence says that the functioning of neurons is affected by many external factors such as temperature [56], pressure [57] light [58], electromagnetic radiations [59,60,61], and many more. For example, the signature of growth in embryo neuron cells was observed with the application of electromagnetic flux [62]. These shreds of evidence motivate us to perform a study on the effect of external electromagnetic flux in a network of Chialvo neurons. The ring-star network topology [63] serves as a promising candidate. Most recently, the dynamical effects of discrete Chialvo neuron map under the influence of electromagnetic flux have been studied [60], where after understanding a single neuron system, analysis on a ring-star network of the neurons has been conducted, making it flexible to work with all the possible scenarios of ring, star, and ring-star topologies. The network that has been mathematically set up in the work consists of N Chialvo neurons arranged in the formation of a ring-star topology, where the central node is connected to all the \(N-1\) nodes with the homogeneous coupling strength \(\mu \) and the peripheral nodes are connected to each of their R neighbors with a coupling strength \(\sigma \). The nodes follow a periodic boundary condition, meaning that the \((N-1)^{th}\) node is connected to the 2nd node to complete the loop. Although the studies in the paper have exhibited some rich dynamics, the topology of the network is too simple to be close to a real-world connection of the nervous system. The study of these neurodynamical systems on this simple network topology gave further motivation to consider even more complex topologies to mimic the real-world connection between the neurons in the brain. Extending on the work, we have tried to tackle this issue by studying the spatiotemporal dynamics of the introduction of heterogeneous and time-varying coupling strengths to the network topology of the ring-star Chialvo neurons under the influence of electromagnetic flux.

In this paper, we mainly catalog the presence of several interesting temporal phenomena, i.e., solitary nodes, and chimera, to name a few, exhibited by the nodes in a heterogeneous network of Chialvo neurons. Heterogeneity is introduced in both space and time. In another study [64], the authors have reported chimera states in time-varying links of a network formed from two coupled populations of Kuramoto oscillators. To quantify what solitary states mean in our system model, we work with a metric called “cross-correlation” coefficient [65]. This metric lets us decide the regime a node lies in.

The goals of this paper are as follows:

  1. 1.

    Improve the ring-star topology of the Chialvo neuron network introduced in the original paper [60], by the inclusion of heterogeneous links between nodes that vary not only in space but also in time, depending on noise modulations and specific coupling probabilities,

  2. 2.

    Report the appearance of rich spatiotemporal patterns throughout the temporal dynamics of the heterogeneous network,

  3. 3.

    Study the emergence of an important asynchronous behavior called solitary nodes and characterize it using quantitative measures like cross-correlation coefficient and synchronization error that we set up according to our network topology,

  4. 4.

    Use the statistical tool called sample entropy on the time series data of spatially averaged action potential, to gain intuition on the extent of complexity, and

  5. 5.

    Develop an understanding of the innate mechanism of whether and how the various measures relate by employing numerical simulations.

We organize the paper in the following way: in Sect. 2, we introduce our improved heterogeneous model for a ring-star network of Chialvo neurons, followed by setting up of the quantitative metrics like cross-correlation coefficient and synchronization error in Sect. 3. Next, in Sect. 3.3 we establish how we are going to apply the measure of sample entropy on time series data that get generated from our model dynamics. Then in Sect. 4, we show results from running various numerical experiments (plotting phase portraits, spatiotemporal patterns, recurrence plots, time series plots, several two regime color plots, bifurcation plots for synchronization, etc.), perform time series analysis, and try drawing inferences about the behavior and dynamics of our heterogeneous neuron network model. Note that all simulations are performed in Python. Finally, in Sect. 5 we provide concluding remarks and future directions.

2 System modeling

The two-dimensional discrete map proposed by Chialvo [8] in 1995 that corresponds to the single neuron dynamics is given by

$$\begin{aligned} x(n+1)&= x(n)^{2} e^{(y(n) - x(n))} + k_{0}, \end{aligned}$$
(1)
$$\begin{aligned} y(n+1)&= a y(n) - b x(n) + c, \end{aligned}$$
(2)

where x and y are the dynamical variables representing activation and recovery, respectively. Two of the control parameters are \(a<1\) and \(b<1\) which indicate the time constant of recovery and the activation dependence of recovery, respectively, during the neuron dynamics. Control parameters c and \(k_0\) are the offset and the time-independent additive perturbation. Throughout this study, we have kept \(a = 0.89, b = 0.6, c = 0.28,\) and \(k_0 = 0.04\).

The model was improved [60] to a three-dimensional smooth map by the inclusion of electromagnetic flux, realized by a memristor. The improved system of equations is given by

$$\begin{aligned} x(n+1)=&x(n)^{2} e^{(y(n)-x(n))} + k_{0} \nonumber \\&+ k x(n) M(\phi (n)), \end{aligned}$$
(3)
$$\begin{aligned} y(n+1) =&a y(n) - bx(n) + c, \end{aligned}$$
(4)
$$\begin{aligned} \phi (n+1) =&k_{1}x(n) - k_{2}\phi (n), \end{aligned}$$
(5)

where \(M(\phi ) = \alpha + 3 \beta \phi ^2\) is the commonly used memconductance function [66] in the literature with \(\alpha , \beta , k_1\) and \(k_2\) as the electromagnetic flux parameters. In (3), the \(k_{1}x\) term denotes the membrane potential induced changes on magnetic flux and the \(k_{2}\phi \) term denotes the leakage of magnetic flux [60]. The parameter k denotes the electromagnetic flux coupling strength with \(kxM(\phi )\) as the induction current. We note that k can take both positive and negative values. Throughout the paper, we have used \(\alpha = 0.1, \beta = 0.2, k_1 = 0.1, k_2 = 0.2\). We also restrict k in the range \([-1, 4]\).

Recently [60], a ring-star network of the Chialvo neurons under the effect of electromagnetic flux has been considered where the coupling strength is set to be homogeneous, and they do not vary with time. We further improve the ring-star model with the incorporation of heterogeneous coupling strengths \(\mu _m(n)\) and \(\sigma _m(n)\). The improved version is then given by

$$\begin{aligned} x_m(n+1)=&x_m(n)^2e^{y_m(n)-x_m(n)} + k_0 \nonumber \\&+ kx_m(n)M(\phi _m(n)) \nonumber \\&+\mu _m(n)(x_m(n)-x_1(n)) \nonumber \\&+\frac{1}{2R}\sum _{i=m-R}^{m+R}\sigma _i(n)(x_i(n)-x_m(n)), \end{aligned}$$
(6)
$$\begin{aligned} y_m(n+1)=&ay_m(n)-bx_m(n)+c, \end{aligned}$$
(7)
$$\begin{aligned} \phi _m(n+1) =&k_1x_{m}(n)-k_2\phi _m(n), \end{aligned}$$
(8)

whose central node is further defined as

$$\begin{aligned} x_1(n+1) =&x_1(n)^2e^{(y_1(n)-x_1(n))}+k_0\nonumber \\&+kx_1(n)M(\phi _1(n)) \nonumber \\&+ \sum _{i=1}^N\mu _i(n)(x_i(n)-x_1(n)), \end{aligned}$$
(9)
$$\begin{aligned} y_1(n+1) =&ay_1(n) - bx_1(n)+c, \end{aligned}$$
(10)
$$\begin{aligned} \phi _1(n+1) =&k_1x_1(n) - k_2\phi _1(n), \end{aligned}$$
(11)

having the following boundary conditions:

$$\begin{aligned} x_{m+N-1}(n)=&x_m(n), \end{aligned}$$
(12)
$$\begin{aligned} y_{m+N-1}(n) =&y_m(n), \end{aligned}$$
(13)
$$\begin{aligned} \phi _{m+N-1}(n) =&\phi _m(n), \end{aligned}$$
(14)

where n represents the \(n^{\textrm{th}}\) iteration, and \(m = 1, \ldots , N\) with N as the total number of neuron nodes in the system. For the sake of making the model more complex and closer to a realistic nervous system, we introduce heterogeneities to the coupling strengths \(\sigma _m(n)\) and \(\mu _m(n)\) in both space and time. In space, the heterogeneities are realized following the application of a noise source with a uniform distribution [65, 67] given by

$$\begin{aligned} \sigma _m(n)&= \sigma _0 + D_{\sigma }\xi _{\sigma }^{m, n}, \end{aligned}$$
(15)
$$\begin{aligned} \mu _m(n)&= \mu _0 + D_{\mu }\xi _{\mu }^{m, n}, \end{aligned}$$
(16)

where \(\sigma _0\) and \(\mu _0\) are the mean values of the coupling strengths \(\mu _m\) and \(\sigma _m\), respectively. Throughout the paper, we keep \(\sigma _0 \in [-0.01, 0.01]\) and \(\mu _0\in [-0.001, 0.001]\). The noise sources \(\xi _{\sigma }\) and \(\xi _{\mu }\) for the corresponding coupling strengths are real numbers randomly sampled from the uniform distribution \([-0.001, 0.001]\). Finally, the D’s refer to the “noise intensity” which we restrict in the range [0, 0.1]. Note that we have used negative (inhibitory) coupling strengths in this study. They represent a significant proportion of neuron connectivity in the human nervous system. The authors in the papers [68, 69] have mentioned them in their course of simulations of the leaky integrate-and-fire (LIF) model. Also, negative coupling strengths are included via a rotational coupling matrix (See Eq. (2) in the paper [70]) during simulations of FitzHugh–Nagumo neuron models. Heterogeneity in time is introduced by considering the network having time-varying links [71,72,73] depending on the two coupling probabilities \(P_{\mu }\) and \(P_{\sigma }\), which govern the update of the coupling topology with each iteration n. The probability with which the central node is connected to all the peripheral nodes at a particular n is denoted by \(P_{\mu }\). Likewise, the probability with which the peripheral nodes are connected to their R neighboring nodes is given by \(P_{\sigma }\). We have studied the spatiotemporal dynamics of the improved topological model under the variation of the seven most important parameters which are \(k, \sigma _0, \mu _0, D_{\sigma }, D_{\mu }, P_{\sigma }\), and \(P_{\mu }\).

Fig. 1
figure 1

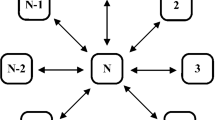
Heterogeneous ring-star network of Chialvo neurons. The nodes are numbered from \(1, \ldots , N\). The star and ring coupling strengths are denoted by \(\mu _{m}\) and \(\sigma _{m}\) for each node \(m=1, \ldots , N\), respectively. Different colors in the ring-star topology signify a range of heterogeneous values of \(\mu _m\) and \(\sigma _m\)

Full size image

3 Quantitative metrics and time series analysis

To quantize the solitary nodes and determine the extent of synchronization in the system after a satisfactory number of iterations, we employ two metrics known as the cross-correlation coefficient [40, 65] and the synchronization error [74]. We also realize the complexity of the time series data that get generated from our simulations using a measure known as sample entropy.

Fig. 2
figure 2

a represents a phase portrait of single neuron dynamics. Parameters are set to be \(a = 0.89, b = 0.6, c = 0.28, k_0 = 0.04, \alpha = 0.1, \beta = 0.2, k_1 = 0.1,\) and \(k_2 = 0.2\). A closed invariant curve (quasiperiodicity) is observed. b the time series plot for the corresponding neuron is illustrated. The sample entropy is 0.041, which is quite low. This indicates less disorderedness in the dynamics as can also be seen from not-so-irregular behavior in the time series

Full size image

3.1 Cross-correlation coefficient

Fig. 3
figure 3

Coherent and solitary nodes giving rise to a two-clustered state. Parameters: \(\sigma _0 = 0, \mu _0=-0.001, D_{\sigma }=0.005, D_{\mu }=0.005, P_{\sigma }=0.66666, P_{\mu }=1,\) and \(k=-1\). The normalized cross-correlation coefficient and the normalized synchronization error values are \(\Gamma = 0.585,\) and \(E = 0.063\), respectively

Full size image
Fig. 4
figure 4

Mostly synced in the coherent domain with two solitary nodes. Parameters: \(\sigma _0 = -0.01, \mu _0=0.001, D_{\sigma }=0.1, D_{\mu }=0.1, P_{\sigma }=1, P_{\mu }=0,\) and \(k=-1\). The normalized cross-correlation coefficient and the normalized synchronization error values are \(\Gamma = 0.932\), and \(E = 0.033\), respectively

Full size image
Fig. 5
figure 5

Two-clustered state. Parameters: \(\sigma _0 = 0, \mu _0=-0.001, D_{\sigma }=0.005, D_{\mu }=0.005, P_{\sigma }=1, P_{\mu }=1,\) and \(k=-1\). The normalized cross-correlation coefficient and the normalized synchronization error values are \(\Gamma = 0.306,\) and \(E = 0.104\), respectively

Full size image
Fig. 6
figure 6

Some random nodes in the solitary domain. Parameters: \(\sigma _0 = -0.01, \mu _0=0.001, D_{\sigma }=0.005, D_{\mu }=0.005, P_{\sigma }=0, P_{\mu }=1,\) and \(k=-1\). The normalized cross-correlation coefficient and the normalized synchronization error values are \(\Gamma = 0.481\), and \(E = 0.058\), respectively

Full size image
Fig. 7
figure 7

Chimera pattern. Parameters: \(\sigma _0 = -0.01, \mu _0=0.001, D_{\sigma }=0.005, D_{\mu }=0.005, P_{\sigma }=0.6667, P_{\mu }=0.3333,\) and \(k=-1\). The normalized cross-correlation coefficient and the normalized synchronization error values are \(\Gamma = 0.185\), and \(E = 0.128\), respectively

Full size image
Fig. 8
figure 8

Asynchrony. Parameters: \(\sigma _0 =-0.01, \mu _0=-0.001, D_{\sigma }=0.005, D_{\mu }=0.005, P_{\sigma }=0.33333, P_{\mu }=0,\) and \(k=3.5\). The normalized cross-correlation coefficient and the normalized synchronization error values are \(\Gamma = 0.777\), and \(E = 0.147\), respectively

Full size image

Keeping in mind that our system has a ring-star topology, we must define the coefficient in such a way that it captures the correct collective behavior of the network dynamics. The general definition of the cross-coefficient denoted by \(\Gamma _{\textrm{i,m}}\) is given by

$$\begin{aligned} \Gamma _{\textrm{i,m}} = \frac{\langle \tilde{x}_i(n) \tilde{x}_m(n)\rangle }{\sqrt{\langle (\tilde{x}_i(n))^2 \rangle \langle (\tilde{x}_m(n))^2 \rangle }}. \end{aligned}$$
(17)

The averaged cross-correlation coefficient over all the units of the network is given by,

$$\begin{aligned} \Gamma = \frac{1}{N-1}\sum _{m=1, m \ne i}^N \Gamma _{\textrm{i,m}}. \end{aligned}$$
(18)

Throughout the paper, we use \(\Gamma _{2,m}\), denoting the degree of correlation between the first peripheral node of the ring-star network and all the other nodes, including the central node. The average is calculated over time with transient dynamics removed and \(\tilde{x}(n) = x(n) - \langle x(n) \rangle \) refers to the variation from the mean. Note that \(\langle \rangle \) denotes the average over time. Everywhere in the paper, we take 20000 iterations in time, of which we discard the first 10000 points for the dynamical variables, such that the transient dynamics is discarded, and thereafter perform all the calculations and simulations. We use \(\Gamma _{\textrm{2,m}}\) to characterize all the necessary regimes for our study. When the nodes have \(\Gamma _{\textrm{2,m}} \sim 1\), they lie in the coherent domain. Due to the noise modulations, there might be node behaviors that are realized by their \(\Gamma _\textrm{2,m}\) values lying in the range \([-0.15, 0.75]\). Finally, the solitary regime is characterized by the domain where the nodes have a high probability of having \(\Gamma _{\textrm{2,m}} \in [-0.38, -0.15]\). Note that these values were selected after running numerous simulations confirming the fact that it is the local dynamics of the network of oscillators that govern the characteristics of solitary nodes from system to system. Interestingly there exist cases where some nodes might cluster in the solitary regime having almost the same density as the nodes clustered in the coherent domain, giving rise to two-clustered states. \(\Gamma \rightarrow 1\) implies that almost all the nodes are clustered in the coherent regime after a specific time without any transient dynamics.

3.2 Synchronization error

The averaged synchronization error for the nodes in a system is given by

$$\begin{aligned} E = \frac{1}{N-1} \sum _{m=1, m \ne 2}^{N} \langle |x_2(n) - x_m(n) |\rangle , \end{aligned}$$
(19)

where we again consider node number \(N=2\) as the baseline for the calculation as has been done in the case of cross-correlation coefficient, and n represents the \(n^{\textrm{th}}\) iteration. Note that \(E \rightarrow 1\) implies that the nodes in the system are moving toward an asynchronous behavior, with \(E=1\) depicting a complete asynchrony. Similarly, \(E \rightarrow 0\) implies synchronization. Like the first metric, \(\langle \rangle \) denotes the average over time.

3.3 Sample entropy: a measure for complexity

Additionally, we perform a statistical analysis of the dynamics of our system to determine how complex it is. In order to do so, we take the spatial average of all the N nodes at a particular time n and generate time series data for the action potential, which we utilize to calculate the sample entropy (SE) of the network in consideration. Next, we provide a brief discussion on the algorithm of SE according to [75]. We start with a time series data \(\left\{ x(n), n = 1,\ldots , {\mathcal {N}}\right\} \). Let \(e \le {\mathcal {N}}\) be a nonnegative integer, which helps us define the \({\mathcal {N}}-e+1\) vectors

$$\begin{aligned} x'_e(j) =\left\{ x(j+k)\big |0 \le k \le e-1 \right\} , \end{aligned}$$

where \(1 \le j \le {\mathcal {N}}-e+1\). The set \(x'_e(j)\) consists of e data points that runs from x(j) to \(x(j+e-1)\). Now, the Euclidean distance can be defined as

$$\begin{aligned} d\left( x'_e(j), x'_e(n) \right) = \max _{0 \le k \le e-1} \left\{ |x(j+k) - x(n+k) |\right\} . \end{aligned}$$

Now, for a positive real tolerance value \(\varepsilon \), the authors in [75] define the term \(B^e_j(\varepsilon )\) as the ratio of the number of vectors \(x'_e(n)\) within \(\varepsilon \) of \(x'_e(j)\) and \(({\mathcal {N}} -e - 1)\) where n ranges from 1 to \({\mathcal {N}} - e\), with \(n \ne j\). Then,

$$\begin{aligned} B^e(\varepsilon ) = \frac{1}{{\mathcal {N}}-e} \sum _{j=1}^{{\mathcal {N}}-e} B^e_j(\varepsilon ). \end{aligned}$$

In a similar fashion, one can define \(B^{e+1}(\varepsilon )\) as well, which finally allows to define the SE measure as

$$\begin{aligned} \textrm{SE}(e, \varepsilon , {\mathcal {N}}) = \lim _{{\mathcal {N}} \rightarrow \infty } \left( -\ln {\frac{B^{e+1}(\varepsilon )}{B^e(\varepsilon )}} \right) . \end{aligned}$$
(20)

SE tells us about how complex the time series data is. A high value indicates unpredictability in the behavior, thus offering more complexity. For more works revolving around or utilizing sample entropy, please refer to [76, 77]. To calculate SE from the time series data, we utilize an open-source package called nolds [78], which provides us with the function nolds.sampen(), which is again built on the algorithm by [75]. The default value of e is 2, and that of \(\varepsilon \) is \(0.2 \times \mathrm{std(data)}\), where \(\mathrm{std(data)}\) represents the standard deviation of the time series data. Note that \({\mathcal {N}}\) is 10000 in our case.

4 Results

Every time we run a computer experiment, we use a pseudo-random generator to initialize the action potential x between 0 and 1. Additionally y and \(\phi \) are initialized to 1. This is done for all the \(N=100\) nodes. In each simulation, the total number of iterations is set to 20, 000, of which we discard the first 10000 to remove transient dynamics. First, we briefly cover the single neuron dynamics under the fixed parameter values as mentioned in the previous sections, before moving to the analysis of the network.

4.1 Single neuron dynamics

For a single neuron, we set the parameter values to \(a = 0.89, b = 0.6, c = 0.28, k_0 = 0.04, \alpha = 0.1, \beta = 0.2, k_1 = 0.1,\) and \(k_2 = 0.2\). Additionally, we set \(k=-1\). The corresponding phase portrait and the time series are given in Fig. 2a , b, respectively. The sample entropy value is calculated to be 0.041, indicating quite a low complexity. Looking at the phase portrait, we observe that the attractor is a closed invariant curve. Using the \(QR-\)factorization method as was done recently [60], it can be noted that the maximum Lyapunov exponent is \(\sim 0\), exhibiting a quasi-periodic dynamics for the fixed set of parameter values. Keeping this in mind, we analyze the system of \(N=100\) such neurons arranged in ring-star topology in the next sections. Note that for the above selected local dynamical parameters \(a, b, c, k_0, \alpha , \beta , k_1,\) and \(k_2\), we perform the whole analysis throughout. In case, these parameters are set differently, the dynamical behaviors of the single neuron and the network of neurons are expected to change accordingly.

Fig. 9
figure 9

Time series plots along with the sample entropy values for the spatially averaged action potential obtained from Figs. 3, 4, 5, 6, 7, and 8. a–c correspond to Figs. 3, 4 and 5, respectively, and figures d–f correspond to Figs. 6, 78, respectively. SE values reported are a 0.114, b 0.041, c 0.11, d 0.196, e 0.092, and f 0.134. The starting time is 8000 because it helps with the illustration of the feasible temporal behavior of x

Full size image

4.2 Phase portraits, spatiotemporal patterns, and recurrence plots

In this section, we have numerically plotted and gathered some interesting behaviors exhibited by the network under variations of different parameter values. We showcase a variety of different phase portraits, and spatiotemporal patterns exhibited by the heterogeneous Chialvo ring-star network in Eq. 6 and Eq. 9. For each simulation, we have shown five separate plots corresponding to different responses. In Figs. 3, 4, 5, 6, 7, and 8,

  1. 1.

    panel (a) (first row, first column) indicates the phase portrait of all the N nodes with the transients removed,

  2. 2.

    panel (b) (first row, second column) refers to the \(\Gamma _{2,m}\) values for all the N nodes,

  3. 3.

    panel (c) (second row, first column) denotes the spatiotemporal dynamics of the nodes with time,

  4. 4.

    panel (d) (second row, second column) portrays the last instance of all the units in space after a sufficient number of iterations n with the transient dynamics removed, and

  5. 5.

    panel (e) (third row, first column) corresponds to the recurrence plot [59] comparing the distance between the final position of each node with all the other nodes in space after n iterations.

In the first, second, and fourth plots, the nodes lying in the solitary regime are denoted by red dots, the nodes with \(\Gamma _\textrm{2,m} \in [-0.15, 0.75]\) are denoted by green dots, and the nodes in the coherent domain are denoted by blue dots. Additionally, the second node is denoted by a black dot in the first (phase portrait) plot.

Figure 3 displays the solitary nodes and the coherent nodes clustered in their respective domains with almost equal density giving rise to a two-clustered state. The blue nodes have cluttered with \(\Gamma _{\textrm{2,m}} \in [0.75, 1]\) and the solitary nodes have accumulated with \(\Gamma _{\textrm{2,m}} \sim -0.1716\). We notice that the solitary nodes are distributed over the whole ensemble. The fact that there exists an almost equal number of nodes in both clusters is evident from the tiny squares in the recurrence plot. In Fig. 4, we see that all the nodes have been clustered and in synchrony except two, which are solitary. Synchronization is also confirmed by the very small value of the normalized synchronization error, i.e., \(E = 0.033\). Here, the solitary nodes consist of \(\Gamma _{\textrm{2,m}} \sim -0.1735\), very similar to the last case. In the corresponding recurrence plot, we notice a deep blue region that covers almost the whole space, visually denoting the fact that the nodes are synchronized. Figure 5 has similar dynamics as that of Fig. 3. The solitary nodes mostly accumulate with \(\Gamma _{\textrm{2,m}} \sim -0.1689\). Note that after sufficient time iterations, the blue and the green nodes can rest together in a single cluster (See the fourth plot in Figs. 4 and  5). As expected, the recurrence plots of Figs. 3 and 5 look very similar to each other as well. In Fig. 6, we see that very few random nodes have clustered in the solitary regime having \(\Gamma _{\textrm{2,m}} \sim -0.1705\) and the remaining clutter in the region with \(\Gamma _{\textrm{2,m}} \sim 0.5\). Here in the recurrence plot, although we see squares denoting multi clusters in the dynamics, they are obviously bigger in area than the ones appearing in Figs. 3 and 5, due to the fact that the number of nodes in one of the clusters is much higher. The behavior in Fig. 7 refers to the phenomenon of “chimera” where nodes within a particular boundary (approximately in \(40 \le m \le 43\) and in \(98 \le m \le 5\)) are completely asynchronous compared to the other nodes in the space which are convincingly synchronous, and they coexist [39]. The recurrence plots in Fig. 7 visually support the fact that we indeed notice chimera. In Fig. 8, we observe asynchrony.

4.3 Time series analysis

Next, we perform statistical analysis on the time series data of the action potential x corresponding to the parameter combinations reported in Figs. 3, 4, 5, 6, 7, and 8. As. mentioned in Sect. 3.3, we take the spatial average of all the nodes at a particular time n, denoted by \({\overline{x}}\), and this is illustrated in Fig. 9. The plots of the spatial average against time for the parameter combinations in Figs. 3, 4 and 5 and Figs. 6, 7 and 8 are shown in Figs. 9a–f, respectively. The time series plots are visualized with 8000 as the starting time, as this helps us illustrate the feasible temporal behavior of the dynamical variable x. As seen in Fig. 9, the oscillations are irregular and do not appear to converge to any steady state of the system. To further our analysis of complex dynamics, we use nolds to compute the sample entropy for each of these cases and record them on each time series plot. What we clearly observe is the presence of fairly complex behavior in all of them, giving us an intuition about the extent of disorderedness. Visually, we also notice irregular oscillatory behavior in the firing pattern of \({\overline{x}}\), not converging to any stable steady state. Note that Fig. 9b which corresponds to the mostly synchronized case (\(E = 0.033\)) Fig. 4 has the lowest value of sample entropy (SE=0.041) and thus the lowest disorderedness as compared to the other five cases. Furthermore, out of the above six cases, the highest value of synchronization error is observed in Fig. 8, having \(E=0.147\). The corresponding time series Fig. 9a too has a very high value of sample entropy, SE=0.114 (third highest). Statistically speaking, it can be expected that an increase in asynchrony leads to an increase in the complexity of the system dynamics. From the color plots and their corresponding E vs. SE plots in the next section, we can infer the above phenomenon.

Fig. 10
figure 10

Collection of two-dimensional color plots of a \(\Gamma ,\) b E,  c \(\frac{N_s}{N},\) and d SE in the parameter space defined by \((\sigma _0, \mu _0)\) with \(k=-1, P_{\mu }=1, P_{\sigma } \sim 0.666, D_{\mu }=D_{\sigma }=0.005\). An almost definitive bifurcation boundary is observed. Solitary nodes appear around \(\sigma _0 \sim 0\) and \(\mu _0>0\)

Full size image
Fig. 11
figure 11

Comparison plots for the various measures: a E vs. \(\Gamma \), b SE vs. E, and c SE vs. \(\Gamma \), collected from Fig. 10. a and c show an inverse trend, whereas b shows a proportional trend

Full size image
Fig. 12
figure 12

Collection of two-dimensional color plots of a \(\Gamma ,\) b E,  c \(\frac{N_s}{N},\) and d SE in the parameter space defined by \((P_{\sigma }, P_{\mu })\) with \(\sigma _0=0, \mu _0 = -0.001, D_{\sigma }=D_{\mu }=0.005\) and \(k=-1\). For values close to \(P_{\mu }=0\), for all \(P_{\sigma }\), highly asynchronous behavior is observed, whereas for \(P_{\mu }>0.5\), the region is randomly distributed between both types of extreme behaviors

Full size image
Fig. 13
figure 13

Comparison plots for the various measures: a E vs. \(\Gamma \), b SE vs. E, and c SE vs. \(\Gamma \), collected from Fig. 12. a and c show an inverse trend, whereas b shows a proportional trend

Full size image

4.4 Two-dimensional color-coded plots

In this section, we visualize a collection of two-dimensional color-coded plots representing a reduced parameter space. These plots help us with an understanding of the bifurcation structure of the dynamics that this system portrays.

4.4.1 Parameter space defined by \((\sigma _0, \mu _0)\)

Figure 10 is a collection of two-dimensional color plots of \(\Gamma , E, \frac{N_s}{N}\), and SE in the parameter space defined by \((\sigma _0, \mu _0)\). The parameter space is a \(40 \times 40\) grid with \(k=-1, P_{\mu }=1, P_{\sigma } \sim 0.666, D_{\mu }=D_{\sigma }=0.005\). From the plot that depicts the normalized cross-correlation coefficient (Fig. 10a), we observe an almost definitive bifurcation boundary within which most of the nodes lie in the coherent regime, i.e., \(\Gamma \sim 1\) and outside which the nodes behave incoherently, i.e., \(\Gamma < 0.75\). A similar kind of bifurcation boundary is observed in the normalized synchronization error color plot (Fig. 10b). In the region where \(\Gamma \sim 1\), the nodes tend to adopt a complete synchronization behavior, making \(E \sim 0\). Moving on to the sample entropy plot (Fig. 10d), interestingly we once again notice an almost similar bifurcation boundary between no complexity (SE\(\sim 0\)) and the onset of complexity (SE \(>0\)). Whenever, \(\Gamma \sim 1\) and \(E \sim 0\) then SE\(\sim 0\) too. Now in the parameter region where \(\Gamma <1\), we notice a transition in the behavior of the nodes from complete synchrony to a degree of asynchrony, such that the normalized synchronization rate lies in the range \(0<E<0.3\) approximately. In an analogous mechanism, the sample entropy increases too when \(\Gamma < 1\) pertaining to a more disordered system dynamics. When \(\Gamma < 1\), and the mean coupling strength \(\sigma _0 \sim 0\), there appears a tinge of the violet region in the color plot, implying \(\Gamma \in (-0.15, -0.38)\), for which there appear solitary nodes (as evident from the \(\frac{N_s}{N}\) color plot, Fig. 10c) and a further peak in the value of sample entropy (\(0.3< \textrm{SE} < 0.75\) approximately). Otherwise, throughout the parameter space, there exist no solitary nodes. In Fig. 11, we have collected the values of \(E, \Gamma \), and SE and plotted them against each other. Notice in Fig. 11a that it gives a clear inversely proportional trend for E and \(\Gamma \). In Fig. 11b, we notice that with an increase in E, the sample entropy shows a fairly increasing trend, whereas in Fig. 11c, with an increase in \(\Gamma \), the sample entropy decreases as expected.

4.4.2 Parameter space defined by \((P_{\mu }, P_{\sigma })\)

Figure 12 is a collection of two-dimensional color plots in the parameter space defined by \((P_{\mu }, P_{\sigma })\) with \(\sigma _0=0, \mu _0 = -0.001, D_{\sigma }=D_{\mu }=0.005\) and \(k=-1\). From Fig. 12a, we see that for values close to \(P_{\mu }=0\), for all \(P_{\sigma }\), there exist regions where \(\Gamma <0.75\), where nodes behave asynchronously (Fig. 12b), having very high sample entropy value (Fig. 12d) and are solitary (Fig. 12c). Above this region of \(P_{\mu }\) where \(P_{\mu }<0.5\), mostly the nodes are synchronized in the coherent domain having a very small value of sample entropy. As soon as \(P_{\mu }>0.5\), the region is randomly distributed between both types of extreme behaviors, denoted by the contrasting colored boxes in all four color-coded plots. We notice a cluster settling down toward the bottom of where \(P_{\mu }\) is closer to 0, but not exactly 0. This implies the phenomenon of the peripheral nodes having little chance to be connected to the central node, which is not nonexistent. We believe this contributes to the disturbance, however small, that amplifies to high asynchrony among the nodes. When \(P_{\mu } = 0\), there is a high chance the peripheral nodes again fall back to synchrony, as evident from the two-dimensional color plot. This might be due to the reason that there exist no disturbances at all via the coupling strength \(\mu _m\) from the central node. However, when \(P_{\mu }>0.5\) there exists an almost equal probability of all the N nodes to be in synchrony and asynchrony, depending on the values of \(\mu _m\) as evident from the equal distribution of the values of E when \(P_{\mu }>0.5\). In Fig. 13, we have collected the values of \(E, \Gamma \), and SE and plotted them against each other. Notice in Fig. 13a that it clearly indicates an inversely proportional trend for E and \(\Gamma \). In Fig. 13b, we notice that with an increase in E, the sample entropy shows a fairly increasing trend, whereas in Fig. 13c, with an increase in \(\Gamma \), the sample entropy decreases as expected.

Fig. 14
figure 14

Collection of two-dimensional color plots of a \(\Gamma ,\) b E,  c \(\frac{N_s}{N},\) and d SE in the parameter space defined by \((\sigma _0, k)\) with \(\mu _0=-0.001, P_{\mu }=1, P_{\sigma } \sim 0.666, D_{\mu }=D_{\sigma }=0.005\). The nodes are mostly asynchronous having \(\Gamma \) in \((-0.38, 0.75)\). There exist two moderately distinct regions portraying coherence. SE is the highest at \(\sigma _0 \sim 0\) and \(k \in (0, 1.5)\)

Full size image
Fig. 15
figure 15

Comparison plots for the various measures: a E versus \(\Gamma \), b SE vs. E, and c SE vs. \(\Gamma \), collected from Fig. 14. a and c show an inverse trend, whereas b shows a proportional trend

Full size image

4.4.3 Parameter space defined by \((\sigma _0, k)\)

Figure 14 is a collection of two-dimensional color plots in the parameter space defined by \((\sigma _0, k)\) with \(\mu _0=-0.001, P_{\mu }=1, P_{\sigma } \sim 0.666, D_{\mu }=D_{\sigma }=0.005\). We observe that the \(\Gamma \) colored plot (Fig 14a) is mostly dominated by values that lie in \((-0.38, 0.75)\), for which the nodes behave in a fairly asynchronous manner as depicted from the corresponding synchronization error plot E (Fig 14b). There exist two moderately distinct regions in the \(\Gamma \) plot where the nodes all lie in the coherent region and they are almost completely synchronous (see the deep yellow regions and the deep black regions in the \(\Gamma \) and E plots, respectively). Comparing the synchronization error plot and the sample entropy plot, we observe again a fairly increasing relationship between the two measures. The sample entropy (Fig 14d) has the maximum value at the region \(\sigma _0 \sim 0\) and \(k \in (0, 1.5)\). Looking into the plot depicting the normalized number of solitary nodes (Fig 14c), we detect a space where almost all the nodes are solitary in the region \(k \in (-0.5, 0.5), \sigma _0 \in (0.005, 0.01)\). In Fig. 15, we have collected the values of \(E, \Gamma \), and SE and plotted them against each other. Notice in Fig. 15a that it clearly indicates an inversely proportional trend for E and \(\Gamma \). In Fig. 15b, we notice that with an increase in E, the sample entropy shows a fairly increasing trend, whereas in Fig. 15c, with an increase in \(\Gamma \), the sample entropy decreases as expected.

5 Conclusion

In this article, we have made a substantial improvement in the ring-star network of Chialvo neurons under the influence of an electromagnetic flux by considering a heterogeneous topology of the network. The motivation behind this was to study the spatiotemporal dynamics of an ensemble of neurons that mimics a realistic nervous system. Heterogeneity is realized not only in space but also in time. We have introduced a noise modulation to incorporate heterogeneity in space and a time-varying structure of the links between neurons that update probabilistically. Noise sources are sampled from a uniform distribution. How the network dynamics change on induction of other complicated distributions opens a future scope of the study. Exploring various computer-generated diagrams like phase portraits, spatiotemporal plots, and recurrent plots, we observe rich dynamical behaviors like two-cluster states, solitary nodes, chimera states, traveling waves, and coherent states. We observe the appearance of solitary nodes and chimeras corresponding to substantial asynchrony in the ensemble. We also notice two-cluster states where one cluster corresponds to the coherent domain, whereas the other corresponds to the solitary domain.

One of the purposes of the paper was to study the appearance of this special kind of asynchronous behavior called solitary nodes and characterize them using a metric called cross-correlation coefficient. It was observed that the cross-correlation coefficient indeed characterizes the solitary nodes in an efficient manner. Two more measures that we implemented here were the synchronization error to study how synchronized the nodes behave, and sample entropy to study the complexity of the network dynamics. Under different pairwise combinations of the model parameters, we have studied the response of each of these three measures and have tried to conclude how efficiently they relate. Asynchronization and sample entropy, for example, portray a fairly convincing proportional relationship, whereas asynchronization and cross-correlation coefficient exhibit an inverse relation to each other. These imply that a higher synchronization error will correspond to a high sample entropy and a low cross-correlation coefficient, whereas a lower value of synchronization error will add up to a low sample entropy value and a high cross-correlation coefficient. These open a research direction to study how exactly they relate and if it is possible to establish an analytical relationship between them. Note that the trend obtained was a bit noisy. We hypothesize that this may be due to the heterogeneity introduced by noise modulations and time-varying links in the system. It would be interesting to see a noise-free relationship in a noise-free system which we plan to address in the future. Also, it would be very interesting to analytically and numerically study the existence of chaos in the ring-star network dynamics (by studying the Lyapunov exponent of the network system and methods to compute it). The two-dimensional color-coded plots representing two-dimensional bifurcation diagrams (by varying two parameters at the axes) reveal a wide range of dynamical behaviors, helping us visualize the global behavior of the neuron network. The time series data/plots generated from the model help us apply sample entropy to study the statistical property of the system, exposing the fact that the more chaotic and disordered the system is, the more the value of the sample entropy measure will be.

The fact that a ring-star network of Chialvo neurons exhibits rich dynamics, this study raises the question of how identical or contrasting the reported dynamical behaviors would be if we had considered different topologies and/or perturbations. Keeping this in mind, we plan to study the behaviors of an ensemble of Chialvo neurons under different topological arrangements: heterogeneous but quenched (no change in topology with time); has coupling strengths that are dependent on a normalized distance between a pair of neurons; is a multiplex heterogeneous network (See the recent work [79]); is perturbed by either temperature or photosensitivity. The fact that solitary nodes oscillate in a completely different phase from the main coherent ensemble, raises a future direction of exploring anti-phase synchronization with different coupling forms such as attractive and/or nonlinear repulsive couplings. A recent similar study [80] with Van der Pol oscillators has also been published. Finally, a similar complexity analysis for an adaptive ring-star network of neuron models represented by continuous-time dynamical systems (FitzHugh–Nagumo, Hindmarsh–Rose, etc.) is a rich problem to look at in the future as well.

As with any other models, the model put forward in this work is not limitations-free as well. One of the major hurdles that the authors have faced is computational efficiency while creating the simulation plots. Python is indisputably slow, despite the extensive use of numpy having C and Fortran dependencies. An interested reader is encouraged to try different software to reproduce the results. Furthermore, parallel processing can be utilized to achieve high performance, especially while generating two-dimensional color-coded parameter plots. This would allow the readers to realize smoother bifurcation boundaries, if any. On a more theoretical side, the authors believe that further increment of the node number along with the dimension of the network from two to three (by establishing additional links between the layers) will help achieve more accurate results as well. These might generate new dynamical behaviors not encountered before.