1 Introduction

Dynamical systems with time-periodic coefficients, also named parametrically excited systems, have been investigated since the nineteenth century to explain different wave phenomena in fluids or solids. Nowadays, parametric excitation is a cornerstone in various fields of science and engineering, including mechanical resonators [1], optics [2], microwave systems [3] and atomic physics [4]. The archetypical and simplest mathematical form of these parametrically excited systems appears in the Mathieu equation. Subsequently, significant attention was given to these systems studying the stability of their trivial solutions. In a nonlinear system, however, a parametric resonance could lead to steady-state non-trivial solutions and limit cycles, in which the amplitudes are governed by the system’s nonlinearities. Among nonlinear differential equations, the Duffing equation used to be one of the most influential examples in modeling nonlinear systems, where micro- and nanomechanical resonators are no exception [5]. A special concern is given to the parametrically excited Duffing equation, which in its simplest form carries the name Mathieu–Duffing equation [6, 7].

In applications, and more specifically micro- and nanosensors, increasing the sensitivity of these devices by amplifying their response to the environment is a key performance indicator. However, the signal-to-noise ratio (SNR) is always an obstacle for the amplification of these systems. Perfectly suited to these challenges, parametric excitation offers an increase in sensitivity through amplification with minimal noise production, compared to electronic techniques [8]. Of more interest is the parametric excitation in these systems due to the accompanying thermal squeezing effect [9]. For these reasons, parametric resonances and amplification were automatically exploited to increase the sensitivity of micro- and nanosensors.

The utilization of parametric excitation in micro- and nanosystems was known for decades [1], which was used usually in high-Q systems for amplification [10]. In addition, combining nonlinearity to parametric excitation was found to be influential in these systems, especially for sensing applications [11]. Several examples are discussed in the literature, for instance, in microgyroscopes [12, 13]. Moreover, acquiring a broadband parametric excitation showed several advantages: either in terms of frequency tuning capability [14], for noise squeezing [15], or for energy harvesting [16, 17]. Although the parametric pumping of micro- and nanosystems seems to be discussed extensively in the literature, a lesser effort was given to corresponding multi-degree-of-freedom (M-DoF) systems. Despite the complexity of these systems, they reveal other interesting phenomena which could be significantly advantageous for these applications in terms of sensitivity and noise reduction.

From a theoretical point of view, parametrically excited two-DoF linear systems were studied for decades, since they represent the simplest form of M-DoF systems. In addition to the principle parametric resonances at twice the system’s eigenfrequencies, a bimodal parametric excitation could initiate resonances at combination frequencies, namely difference and summation frequencies [7, 18, 19]. At these frequencies, the solutions of these systems could be significantly amplified [20] or even suppressed [21, 22]. Moreover, by controlling the phase of these excitation terms more interesting phenomena could be found. A special effect was observed when the coupling between two degrees of freedom is applied through a phase-shifted parametric excitation, called asynchronous parametric excitation [23, 24]. In this case a phenomenon called “total instability” was found, where the system exhibits a destabilization effect at all parametric excitation frequencies [25]. This effect was broadly studied in the recent years, and it was found that this type of excitation causes global stability conditions, which means not being localized at resonant frequencies [26]. Furthermore, only recently this excitation method was brought to the microsystems industry, where the mathematical model could be validated experimentally in a microsystem [27]. Moreover, the effects of broadband destabilization or broadband parametric amplification were discussed for microgyroscopes [28], which could serve as a typical example for this theoretical study.

Motivated by the mentioned theoretical findings and by the significance of parametric excitation methods in micro- and nanoapplications, the two-degree-of-freedom Mathieu–Duffing equation is discussed in this work in a generic configuration, especially where the broadband destabilization effect is exhibited. Parametrically excited nonlinear two-DoF systems were investigated before in different configurations. In addition to cubic nonlinearities, some systems included either quadratic or coupling nonlinear terms were studied analytically [29, 30]. Some works were focused on two-DoF systems for specific applications using numerical [31] or experimental methods [32, 33], where different nonlinear terms were included depending on the application involved. Theoretical works were more interested in systems with bimodal coupled parametric excitation [34,35,36], where the diagonal terms in the parametric excitation matrix were not considered. In these studies, the non-trivial solutions were considered at combination resonances [34, 36] using averaging approximation methods and at non-resonant frequencies under asynchronous excitation  [35] using the method of normal forms; however, principle resonances were not considered since the diagonal excitation terms did not exist. The influence of the diagonal or the off-diagonal terms on parametric resonances will be discussed in this study.

In this work, the asynchronous parametric excitation is considered in a two-DoF nonlinear system, with a fully populated excitation matrix, providing a generic form of the two-degree-of-freedom Mathieu–Duffing system. Moreover, the non-trivial solutions are discussed at all resonant and non-resonant frequencies, and a detailed bifurcation analysis using the multiple scales method is carried out. In addition, a special case of a 1:1 internal resonance is also considered due to its relevance to systems with degenerate or similar eigenfrequencies found in different applications [28, 37].

To this end, the following two-DoF nonlinear system is proposed

$$\begin{aligned} \begin{aligned}&u_1''+\omega _1^2 u_1+\mu _1 u_1'+\gamma _1 u_1^3+\alpha _1 u_1'^3+\eta _{11} u_1 \cos (\varOmega _p t)\\&\qquad +\eta _{12} u_2 \cos (\varOmega _p t)=0\\&u_2''+\omega _2^2 u_2+\mu _2 u_2'+\gamma _2 u_2^3+\alpha _2 u_2'^3\\&\qquad +\eta _{21} u_1 \cos (\varOmega _p t+\zeta )+\eta _{22} u_2 \cos (\varOmega _p t)=0 \end{aligned} \end{aligned}$$
(1)

with cubic stiffness and damping nonlinearities having the coefficients \(\gamma _i\) and \(\alpha _i\), \(i=1,2\), respectively, and having natural frequencies \(\omega _1,\omega _2\). Without the given parametric excitation, the two DoF would be rather uncoupled, the coupling is then achieved through the parametric excitation terms, which have the coefficients \(\eta _{12}\) and \(\eta _{21}\), where the latter includes a phase-shift \(\zeta \). In addition, the system includes intrinsic parametric excitation terms as well with coefficients \(\eta _{ii}\), \(i=1,2\). Thus, there is no forced excitation, that is, the system is purely parametrically excited.

2 Stability of the trivial solution

As a first step to investigate the dynamics of the system (1), the stability of its trivial solution is discussed. Therefore, the system is linearized around the trivial solution to give

$$\begin{aligned} \begin{aligned}&u_1''+\omega _1^2 u_1+\mu _1 u_1'+\eta _{11} u_1 \cos (\varOmega _p t)\\&\qquad +\eta _{12} u_2 \cos (\varOmega _p t)=0,\\&u_2''+\omega _2^2 u_2+\mu _2 u_2'+\eta _{21} u_1 \cos (\varOmega _p t+\zeta )\\&\qquad +\eta _{22} u_2 \cos (\varOmega _p t)=0. \end{aligned} \end{aligned}$$
(2)

This linearized system was discussed in [22, 26, 34] either in more general or specific forms. Since this system is non-autonomous, the eigenvalues cannot be deduced. Therefore, Floquet theory is then used to determine the stability of the trivial solution. To this end, the system is put in a first-order form

$$\begin{aligned} z_1'&=z_2,\nonumber \\ z_2'&{=}{-}\omega _1^2 z_1{-}\mu _1 z_2{-}\eta _{11} z_1 \cos (\varOmega _p t){-}\eta _{12} z_3 \cos (\varOmega _p t),\nonumber \\ z_3'&=z_4,\nonumber \\ z_4'&=-\omega _2^2 z_3-\mu _2 z_4-\eta _{21} z_1 \cos (\varOmega _p t+\zeta )\nonumber \\&\quad -\eta _{22} z_3 \cos (\varOmega _p t), \end{aligned}$$
(3)

which could be written in the compact form

$$\begin{aligned} \varvec{\dot{z}}=\varvec{A}(t)\varvec{z}. \end{aligned}$$
(4)

According to Floquet theory [6], each fundamental matrix \(\varvec{Z}(t)\) can be written as

$$\begin{aligned} \varvec{Z}(t)=\varvec{P}(t)e^{\varvec{B} t}, \end{aligned}$$
(5)

where each of \(\varvec{Z,P,B}\) is an \(n\times n\) matrix, \(\varvec{P}(t)=\varvec{P}(t+T)\), and \(\varvec{B}\) is constant. By evaluating the eigenvalues of the monodromy matrix \(e^{\varvec{B} t}=\varvec{C}\) at the periodic time T, we get the Floquet characteristic multipliers \(\nu \). Then,

$$\begin{aligned} \lambda _i=\frac{1}{T}\ln (\nu _i),\quad i=1,2,...,n, \end{aligned}$$
(6)

are the system’s Floquet characteristic exponents, and their real parts are found to be Lyapunov characteristic exponents [38].

The same criterion of stability of a fixed point can be extended here for periodic solution of a non-autonomous system. If all Lyapunov exponents are negative, which means that all Floquet multipliers are inside the unit circle of the complex plane, the solution is said to be asymptotically stable. While if any Lyapunov exponent is negative, which means that any Floquet multiplier lies outside the unit circle, the system is said to be unstable. For nonlinear systems, if none of the Floquet multipliers associated with a non-hyperbolic solution lies outside the unit circle, then a nonlinear analysis is necessary to determine the stability [39].

Fig. 1
figure 1

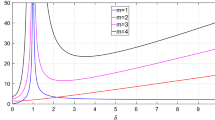
Maximum Lyapunov characteristic exponent \(Re(\lambda )_{max}\) against the parametric excitation frequency \(\varOmega _p\) for system (3) at the amplitude \(\eta =0.4\), where \(\omega _1=1,\omega _2=\sqrt{5},\mu _1=\mu _2=0.01\)

Full size image

According to this criterion, the Lyapunov characteristic exponents \(Re(\lambda )\) are evaluated in the parameter space of parametric excitation frequency and amplitude (\(\varOmega _p\text {-}\eta \)). For instance, at an excitation amplitude \(\eta =0.4\) the maximum exponent is calculated against the parametric excitation frequency \(\varOmega _p\) and plotted in Fig. 1 for synchronous (\(\zeta =0\)) and asynchronous (\(\zeta =-\pi /2\)) excitation. Throughout this paper, a comparison is held between these two cases. The specific phase-shift, \(\zeta =-\pi /2\), is chosen as an example for the asynchronicity, since it leads to total instability according to [25] and more specifically, it allows for broadband destabilization and amplification in microsystems [28]. It can be observed in the figure that when \(\zeta =0\), resonances occur at \(\varOmega _p=(\omega _i+\omega _j)/n\), that is, at the principle resonance frequency (\(i=j\)) and at the summation combination frequency (\(i\ne j\)) and their fractions, where \(n\in \mathbb {N}\). However, at the difference combination frequency \(\varOmega _p=\omega _2-\omega _1\) an anti-resonance takes place. While in the case of asynchronous parametric excitation \(\zeta =-\pi /2\), resonances occur at all principle and combination frequencies. Moreover, in the latter case, a broadband destabilization can be observed between the combination frequencies, where the maximum characteristic Lyapunov exponent is increased in this frequency interval. The demonstration in this figure was discussed before in [26] and is comparable to the effective damping in [40], specifically for Fig. 1a.

Applying the instability criterion explained before, i.e., \(max(Re(\lambda ))>0\), and plotting only the points of instability at different excitation levels \(\eta \) gives the so-called stability chart of the system’s trivial solution in the parameter space \(\varOmega _p\text {-}\eta \). The stability chart is again evaluated in the synchronous and asynchronous excitation cases. The stability chart for the synchronous excitation case is depicted in Fig. 2, while Fig. 3 shows the asynchronous case, where in each case the blue points represent unstable trivial solutions. Under synchronous excitation, the expected Arnold’s tongues are found at principle and combination resonant frequencies \(\varOmega _p=(|\omega _i\pm \omega _j|)/n,\> n\in \mathbb {N}\). The occurrence of instability tongues at principle resonance frequencies and their fractions are dependent on the existence of the diagonal terms, in addition, they occur either at the summation frequency when \(\zeta =0\) or at the difference frequency when \(\zeta =\pi \). However, when the phase-shift \(\zeta =-\pi /2\) is introduced, an instability tongue at both combination frequencies is found, in addition, they are merged and a large instability region is formed between both combination frequencies \([|\omega _i-\omega _j|,\omega _i+\omega _j]\), which results in a broadband instability region. This explains the broadband destabilization effect [28].

Fig. 2
figure 2

Stability chart of the system (2) under synchronous parametric excitation (white is stable, blue/gray is unstable), where \(\omega _1=1,\omega _2=\sqrt{5},\mu _1=\mu _2=0.01\) and \(\zeta =0\)

Full size image
Fig. 3
figure 3

Stability chart of the system (2) under asynchronous parametric excitation (white is stable, blue/gray is unstable), where \(\omega _1=1,\omega _2=\sqrt{5},\mu _1=\mu _2=0.01\) and \(\zeta =-\pi /2\)

Full size image

The importance of this phenomenon is considered for applications that seek broadband parametric amplification as mentioned in the introduction and was emphasized in [28] for microgyroscopes, which also applies for micro- and nanosystems with similar eigenfrequencies. Since in these devices the summation frequency is in the order of hundreds of kHz while the difference frequency is in the order of hundreds of Hz, the broadband destabilization spans approximately the whole frequency bandwidth up to the summation frequency. This effect cannot be attained using a synchronous excitation except at extremely high excitation amplitudes when the Arnold’s tongues meet, see Fig. 2; however, using an asynchronous excitation allows it to happen at reasonable excitation levels, see Fig. 3. These findings and their significance in applications intrigued the authors to study the dynamics of the system inside the regions of instability under asynchronous excitation and compare it to the conventional synchronous parametric excitation. However, if the trivial solution is destabilized, a linear system would suggest an unbounded response, which does not occur in reality. For these reasons, the system is modeled nonlinearly, and the non-trivial solutions and their stability are studied in the next sections.

3 Perturbation analysis of the nonlinear system

The method of multiple scales is used to analyze the given problem up to the first order [7, 41]. To this end, the linear system of (1) is perturbed to give

$$\begin{aligned}{} & {} u_1''{+}\omega _1^2 u_1{+}\epsilon [\mu _1 u_1'{+}\gamma _1 u_1^3{+}\alpha _1 u_1'^3+\eta _{11} u_1 \cos (\varOmega _p t)\nonumber \\{} & {} \qquad +\eta _{12} u_2 \cos (\varOmega _p t)]=0 \nonumber \\{} & {} u_2''+\omega _2^2 u_2+\epsilon [\mu _2 u_2'+\gamma _2 u_2^3+\alpha _2 u_2'^3\nonumber \\{} & {} \qquad +\eta _{21} u_1 \cos (\varOmega _p t+\zeta )+\eta _{22} u_2 \cos (\varOmega _p t)]=0,\nonumber \\ \end{aligned}$$
(7)

where all terms but the linear oscillator terms are considered to be small, which is indicated by the perturbation arbitrary parameter \(\epsilon<<1\).

One seeks an expansion in the form

$$\begin{aligned}{} & {} u_1(t;\epsilon )=u_{10}(T_0,T_1)+\epsilon u_{11}(T_0,T_1)+\cdots , \end{aligned}$$
(8a)
$$\begin{aligned}{} & {} u_2(t;\epsilon )=u_{20}(T_0,T_1)+\epsilon u_{21}(T_0,T_1)+\cdots , \end{aligned}$$
(8b)

where \(T_i=\epsilon ^i t,\> D_i=\partial /\partial T_i\) and

$$\begin{aligned} \begin{aligned}&\frac{\partial }{\partial t}=D_0+\epsilon D_1+...,\\&\frac{\partial ^2}{\partial t^2}=D_0^2+2\epsilon D_0 D_1+...\> . \end{aligned} \end{aligned}$$
(9)

Inserting (8) and  (9) in (7) and separating according to the order of \(\epsilon \) results in the following: for \(\varvec{\epsilon ^0}\), we obtain

$$\begin{aligned}{} & {} D_0^2u_{10}+\omega _1^2 u_{10}=0, \end{aligned}$$
(10a)
$$\begin{aligned}{} & {} D_0^2u_{20}+\omega _2^2 u_{20}=0, \end{aligned}$$
(10b)

while for \(\varvec{\epsilon ^1}\), the equations read

$$\begin{aligned}{} & {} D_0^2u_{11}+\omega _1^2 u_{11}=-\mu _1 D_0u_{10}-\gamma _1 u_{10}^3-\alpha _1D_0 u_{10}^3\nonumber \\{} & {} \quad -\eta _{11} u_{10} \cos (\varOmega _p t)-\eta _{12} u_{20} \cos (\varOmega _p t)\nonumber \\{} & {} \quad -2D_0D_1u_{10}, \end{aligned}$$
(11a)
$$\begin{aligned}{} & {} D_0^2u_{21}+\omega _2^2 u_{21}=-\mu _2 D_0u_{20}-\gamma _2 u_{20}^3-\alpha _2D_0 u_{20}^3 \nonumber \\{} & {} \quad -\eta _{21} u_{10} \cos (\varOmega _p t+\zeta )-\eta _{22} u_{20} \cos (\varOmega _p t)\nonumber \\{} & {} \quad -2D_0D_1u_{20}. \end{aligned}$$
(11b)

Solving (10) gives

$$\begin{aligned}{} & {} u_{10}(T_0,T_1)=A_1(T_1)e^{i\omega _1T_0}+\bar{A_1}(T_1)e^{-i\omega _1T_0},\end{aligned}$$
(12a)
$$\begin{aligned}{} & {} u_{20}(T_0,T_1)=A_2(T_1)e^{i\omega _2T_0}+\bar{A_2}(T_1)e^{-i\omega _2T_0}, \end{aligned}$$
(12b)

where the amplitudes \(A_1,A_2\) represent the slow time-scale variables, which will exhibit the system’s stability in the further calculations, while the exponential expressions represent the fast time-scale periodic solution. Inserting (12) in (11) gives

$$\begin{aligned}&\begin{aligned}&D_0^2u_{11}+\omega _1^2u_{11}=-\gamma _1(A_1^3e^{i3\omega _1T_0}+3A_1^2\bar{A_1}e^{i\omega _1T_0})\\&\qquad -\alpha _1(-i\omega _1^3A_1^3e^{i3\omega _1T_0}+i3\omega _1^3A_1^2\bar{A_1}e^{i\omega _1T_0})\\&\qquad -\frac{1}{2}\eta _{11}A_1(e^{i(\omega _1-\varOmega _p)T_0}+e^{i(\omega _1+\varOmega _p)T_0})\\&\qquad -\frac{1}{2}\eta _{12}A_2(e^{i(\omega _2-\varOmega _p)T_0}+e^{i(\omega _2+\varOmega _p)T_0})\\&\qquad -i2\omega _1D_1A_1e^{i\omega _1T_0}-i\mu _1\omega _1A_1e^{i\omega _1T_0}+CC, \end{aligned} \end{aligned}$$
(13a)
$$\begin{aligned}&\begin{aligned}&D_0^2u_{21}+\omega _1^2u_{21}=-\gamma _2(A_2^3e^{i3\omega _2T_0}+3A_2^2\bar{A_2}e^{i\omega _2T_0})\\&\qquad -\alpha _2(-i\omega _2^3A_2^3e^{i3\omega _2T_0}+i3\omega _2^3A_2^2\bar{A_2}e^{i\omega _2T_0})\\&\qquad -\frac{1}{2}\eta _{21}A_1(e^{i(\omega _1-\varOmega _p)T_0-i\zeta }+e^{i(\omega _1+\varOmega _p)T_0+i\zeta })\\&\qquad -\frac{1}{2}\eta _{22}A_2(e^{i(\omega _2-\varOmega _p)T_0}+e^{i(\omega _2+\varOmega _p)T_0})\\&\qquad -i2\omega _2D_1A_2e^{i\omega _2T_0}-i\mu _2\omega _2A_2e^{i\omega _2T_0}+CC, \end{aligned} \end{aligned}$$
(13b)

where CC stands for the complex conjugates of the preceding terms in each equation.

Equations (13) have secular terms that must vanish (see [7, 42]). However, these secular terms are found to be dependent on the frequency interval chosen for the solution, whether it is away from resonance frequencies or nearly tuned to them. For this reason, the following sections will represent the different cases according to the resonant conditions: near principle resonance frequencies, that is when \(\varOmega _p\simeq 2\omega _i\); near combination resonance frequencies, i.e., when \(\varOmega _p\simeq \omega _i\pm \omega _j\); or at non-resonant frequencies. The latter concludes our goal for discussing parametric destabilization and amplification in the broad frequency band as explained before.

4 Principle parametric resonance

Although this case can be found in [7] or [43] using the multiple scales method when \(\alpha _i=0\), a further analysis reveals more interesting properties for \(\alpha _i\ne 0\) as follows. Being interested in the dynamics around the principle parametric resonance, a detuning parameter \(\sigma _p=\mathcal {O}(1)\) is introduced to give

$$\begin{aligned} \varOmega _p=2\omega _1+\epsilon \sigma _p. \end{aligned}$$
(14)

Inserting (14) in (13) and equating secular terms to zero, then transforming into the polar coordinates using

$$\begin{aligned} A_1(T_1)=\frac{1}{2}a_1(T_1)e^{i\phi _1(T_1)},\quad A_2(T_1)=\frac{1}{2}a_2(T_1)e^{i\phi _2(T_1)}. \end{aligned}$$
(15)

gives the resonance equation. The reader is referred to [7] for more details. The steady-state solution of the second oscillator \(a_2\) vanishes, while that of the first one \(a_1\) is given by the resonance equation

$$\begin{aligned}{} & {} -9(\gamma _1^2+\alpha _1^2\omega _1^6)a_1^5+24(\gamma _1\sigma _p\omega _1-\alpha _1\mu _1\omega _1^4)a_1^3\nonumber \\{} & {} \qquad +(4\eta _{11}^2-16(\mu _1^2+\sigma _p^2)\omega _1^2)a_1=0. \end{aligned}$$
(16)

and the steady-state solutions

$$\begin{aligned}{} & {} a_1=\pm \sqrt{\frac{2}{3}}\nonumber \\{} & {} \quad \sqrt{\frac{2\gamma _1\sigma _p\omega _1-2\alpha _1\mu _1\omega _1^4\pm \sqrt{-8\alpha _1\gamma _1\mu _1\sigma _p\omega _1^5+\gamma _1^2(\eta _{11}^2-4\mu _1^2\omega _1^2)+\alpha _1^2\omega _1^6(\eta _{11}^2-4\sigma _p^2\omega _1^2)}}{\gamma _1^2+\alpha _1^2\omega _1^6}},\qquad \qquad \qquad \qquad \qquad \end{aligned}$$
(17)

or the trivial solution

$$\begin{aligned} a_1=0. \end{aligned}$$
(18)
Fig. 4
figure 4

Frequency–response curve at the principle parametric resonance of the first DoF, where \(\omega _1=1,\mu _1=0,\gamma _1=0.07, \alpha _1=0.03\) and \(\eta _{11}=0.2.\) Blue and red points represent stable and unstable limit cycles, respectively

Full size image
Fig. 5
figure 5

Phase plot for the complex plane of the \(A_1\)

Full size image

The frequency–response curve corresponding to the non-trivial solution (17) is presented in Fig. 4. A nonlinear resonance behavior is exhibited, and a stable limit cycle is born after a bifurcation at \(\sigma _p =-0.1\) and extends up to \(\sigma _p \simeq 0.25\). Although the system incorporates Duffing-type nonlinearities, the non-trivial solution here differs substantially from that of a forced Duffing oscillator with regard to the type of excitation. At the point (\(\sigma _p=0.1\)) another bifurcation occurs, where a smaller unstable limit cycle appears in addition to the stable one and extends also up to \(\sigma _p \simeq 0.25\), where both limit cycles annihilate each other. This creates two frequency intervals, the first one (\(\sigma _p \in ]-0.1,0.1[\)) involves only a stable limit cycle with an unstable trivial solution, while the second (\(\sigma _p \in ]0.1,0.25[\)) includes a stable limit cycle, an unstable limit cycle and a stable trivial solution. However, only a stable trivial solution exists at other frequency intervals. The phase portrait before and after the bifurcation point (\(\sigma _p=0.1\)) is represented in Fig. 5 in complex phase space of the slow variable \(A_1\) represented in the complex form

$$\begin{aligned} A_1=(a_{Re}-ia_{Im})e^{\frac{1}{2}i\sigma _p T_1} \end{aligned}$$
(19)

instead of the polar one used in the analysis. This is depicted as having a saddle trivial fixed point (\(s_1\)) in the first interval and a stable focus (\(f_1,f_1'\)), where the negative “image” of each non-trivial solution is denoted by a prime. In the second interval, the stable focus (\(f_1,f_1'\)) persists, while the saddle point (\(s_1\)) splits into a stable focus (\(f_2\)) for the trivial solution and a new saddle point (\(s_2,s_2'\)).

A further insight could be drawn from this analysis by setting the detuning parameter \(\sigma _p=0\) and at the same time canceling the linear damping, i.e., \(\mu _1=0\). In this case, the non-trivial solution (17) reduces to

$$\begin{aligned} a_1=\varGamma =\left( \frac{4\eta _{11}^2}{9(\gamma _1^2+\alpha _1^2\omega _1^6)}\right) ^{1/4}, \end{aligned}$$
(20)

which will be called \(\varGamma \) for further analysis. As we see in this expression, the amplitude of the oscillation is determined mainly by the parametric excitation amplitude \(\eta _{11}\) and the nonlinear terms \(\gamma _1,\alpha _1\). Here, it is obviously clear that in the case of the absence of any of them, we will be left with only the trivial solution. Although it might seem to contradict the fact that the unforced Duffing oscillator has non-trivial solutions even without any parametric excitation, but the main difference here is that the linear damping was set to zero [42]. The \(\varGamma \) value is considered here to represent a non-trivial solution neither with a perturbing linear damping nor with the detuning of the excitation frequency. The effect of perturbing this solution through varying both of them will be studied next.

Substituting the value of \(\varGamma \) back in (16) while keeping the detuning parameter \(\sigma _p=0\) but allowing the linear damping \(\mu _1\) to vary gives

$$\begin{aligned} a_1^5+\varGamma ^4\left( \frac{6\alpha _1\mu _1\omega _1^4}{\eta _{11}^2}\right) a_1^3+\varGamma ^4\left( \frac{4\mu _1^2\omega _1^2}{\eta _{11}^2}-1\right) a_1=0, \end{aligned}$$
(21)

solving this resonance equation gives again

$$\begin{aligned} a_1=0 \end{aligned}$$
(22)

or

$$\begin{aligned} a_1^4+\varGamma ^4\left( \frac{6\alpha _1\mu _1\omega _1^4}{\eta _{11}^2}\right) a_1^2+\varGamma ^4\left( \frac{4\mu _1^2\omega _1^2}{\eta _{11}^2}-1\right) =0, \end{aligned}$$
(23)

which is clearly a quadratic equation in \(a_1\). Using combined parameters \(\varXi _1,\varXi _2\) for the terms between brackets and rewriting, it gives

$$\begin{aligned} a_1^4+\varGamma ^4\varXi _1a_1^2+\varGamma ^4\varXi _2=0, \end{aligned}$$
(24)

which has a solution of

$$\begin{aligned} a_1^2=\frac{-\varGamma ^4\varXi _1}{2}\pm \frac{1}{2}\sqrt{\varGamma ^8\varXi _1^2-4\varGamma ^4\varXi _2}. \end{aligned}$$
(25)

For relatively high excitation amplitudes with respect to system parameters, we find the combined parameters \(\varXi _1,\varXi _2\) and \(\varGamma \) to have values smaller than one. In this case \(\varXi _2\) will dominate the solution. And in order to have a real-valued \(a_1\), i.e., positive-valued \(a_1^2\), \(\varXi _2\) must then be negative. Thus, a real-valued \(a_1\) can only take place if positive square root solution was selected and if \(\varXi _2<0\). Reading the \(\varXi _2\) term from (23) and applying this condition yields

$$\begin{aligned} -\frac{\eta _{11}}{2\omega _1}<\mu _1<\frac{\eta _{11}}{2\omega _1}, \end{aligned}$$
(26)

which could be confirmed by numerically solving (23) and plotting the solution in Fig. 6a.

Fig. 6
figure 6

Non-trivial solutions by varying the system linear damping \(\mu _1\), while \(\sigma _p=0\). Other parameter values read \(\omega _1=1, \gamma _1=0.07,\alpha _1=0.03\)

Full size image
Fig. 7
figure 7

Non-trivial solution by varying the system linear damping \(\mu _1\) at two different values for the detuning parameter \(\sigma _p\). Other parameter values read \(\omega _1=1, \gamma _1=0.07,\alpha _1=0.03,\eta _{11}=0.2\)

Full size image

However, if the excitation amplitudes were relatively small, giving the combined parameters values larger than one, we find \(\varXi _1\) to be dominating. In this case a real-valued \(a_1\) is only possible for \(\mu _1<0\), as shown in the same figure. The plotted solution in Fig. 6 corresponds to the solution of the main resonance equation at \(\sigma _p=0\) in Fig. 4, where only a stable limit cycle exists. However, if another value of \(\sigma _p\) was chosen which includes an unstable solution as well, this should give another dimension to the problem. Thereby, by returning back to (16) it can be written in

$$\begin{aligned} a_1^4{+}\varGamma ^4\left( \varXi _1{-}\frac{6\gamma _1\omega _1}{\eta _{11}^2}\sigma _p\right) a_1^2{+}\varGamma ^4\left( \varXi _2{+}\frac{4\omega _1^2}{\eta _{11}^2}\sigma _p^2\right) {=}0,\nonumber \\ \end{aligned}$$
(27)

which gives the admissible amplitude values shown in Fig. 7 by varying the linear damping \(\mu _1\) again. The figure shows isolated stable and unstable steady-state solutions. This is particularly interesting, since the variation of the linear damping could cause an abrupt increase or decrease in the amplitude of the response at a bifurcation point. This high sensitivity of the response at the bifurcation point could be of significant importance for systems, where high sensitivity is pursued using a bifurcation control scheme.

5 Internal resonance under parametric excitation

The case of 1:1 internal resonance stands to be relevant for systems involving degenerate or similar eigenvalues \(\omega _1\simeq \omega _2\). This happens to be the case for structures with axis-symmetric geometry. A motivating example is the micro-ring gyroscope [28], where it was shown that the degeneracy of eigenvalues or even the nearness to one another leads to a large broadband destabilization effect between the difference and summation combination frequencies. In the nonlinear case, however, an additional phenomenon takes place, which is the internal resonance, provided that one eigenfrequency is in the vicinity of the other.

In this case, we introduce an additional detuning parameter \(\sigma _{in}\) where

$$\begin{aligned} \omega _2=\omega _1+\epsilon \sigma _\textrm{in}, \end{aligned}$$
(28)

while the previous one (14) remains effective.

Returning to (13) and this time inserting both (14) and (28) gives the solvability conditions

$$\begin{aligned}{} & {} i2\omega _1D_1A_1+i\mu _1\omega _1A_1+3(\gamma _1+i\alpha _1\omega _1^3)A_1^2\bar{A_1}\nonumber \\{} & {} \qquad +\frac{1}{2}\eta _{11}\bar{A_1}e^{i\sigma _p T_1}+\frac{1}{2}\eta _{12}\bar{A_2}e^{i(\sigma _p-\sigma _{in})T_1}=0,\nonumber \\ \end{aligned}$$
(29a)
$$\begin{aligned}{} & {} i2\omega _2e^{i\sigma _{in}T_1}D_1A_2+i\mu _2\omega _2e^{i\sigma _{in} T_1}A_1\nonumber \\{} & {} \qquad +3(\gamma _2+i\alpha _2\omega _2^3)A_2^2\bar{A_2}e^{i\sigma _{in} T_1}+\frac{1}{2}\eta _{21}\bar{A_1}e^{i\sigma _p T_1+i\zeta }\nonumber \\{} & {} \qquad +\frac{1}{2}\eta _{22}\bar{A_2}e^{i(\sigma _p-\sigma _{in})T_1}=0. \end{aligned}$$
(29b)

In order to investigate the exchange of energy when only one DoF is parametrically excited, we put \(\eta _{22}=0\), and the phase-shift is firstly not taken into consideration, i.e., \(\zeta =0\). As previously done, we insert (15) in (29) then separate real and imaginary parts to yield the modulation equations

$$\begin{aligned} D_1a_1&=-\frac{\mu \omega _1a_1}{2\omega _1}-\frac{3\alpha _1\omega _1^3a_1^3}{8\omega _1}+\frac{\eta _{12}a_2\sin (\theta _1)}{4\omega _1}\nonumber \\&-\frac{\eta _{11}a_1\sin (\theta _2)}{4\omega _1}, \end{aligned}$$
(30a)
$$\begin{aligned} D_1a_2&=-\frac{\mu _2\omega _2a_2}{2\omega _2}-\frac{3\alpha _2\omega _2^3a_2^3}{8\omega _2}+\frac{\eta _{21}a_1\sin (\theta _1)}{4\omega _2}, \end{aligned}$$
(30b)
$$\begin{aligned} D_1\theta _1&=-\sigma _p+\sigma _{in}+\frac{3\gamma _1a_1^2}{8\omega _1}+\frac{3\gamma _2a_2^2}{8\omega _2}\nonumber \\&+\frac{1}{4\omega _2}\eta _{21}\frac{a_1}{a_2}\cos (\theta _1)+\frac{1}{4\omega _1}\eta _{12}\frac{a_2}{a_1}\cos (\theta _1)\nonumber \\&+\frac{\eta _{11}\cos (\theta _2)}{4\omega _1}, \end{aligned}$$
(30c)
$$\begin{aligned} D_1\theta _2&=\sigma _p-\frac{3\gamma _1a_1^2}{4\omega _1}-\frac{\eta _{12}a_2\cos (\theta _1)}{2\omega _1 a_1}-\frac{\eta _{11}\cos (\theta _2)}{2\omega _1}, \end{aligned}$$
(30d)

where \(\theta _1=\phi _1+\phi _2+(\sigma _{in}-\sigma _p)T_1\) and \(\theta _2=-2\phi _1+\sigma _p T_1\).

Fig. 8
figure 8

Non-trivial solutions for \(a_1\) and \(a_2\) by detuning \(\sigma _p\) in case of tuned 1:1 internal resonance, where \(\omega _i=1,\mu _i=0,\gamma _i=0.1,\alpha _i=0.02,\eta _{11}=\eta _{12}=\eta _{21}=1,\eta _{22}=0\) and \(\sigma _{in}=0\), for \(i=1,2\). Blue and red points represent stable and unstable limit cycles, respectively

Full size image
Fig. 9
figure 9

Non-trivial solutions for \(a_1\) and \(a_2\) by detuning \(\sigma _p\) in case of tuned 1:1 internal resonance, where \(\omega _i=1,\mu _i=0,\gamma _i=0.1,\alpha _i=0.02,\eta _{12}=\eta _{21}=1,\eta _{22}=0,\sigma _{in}=0\) and \(\eta _{11}=0\), for \(i=1,2\). Blue and red points represent stable and unstable limit cycles, respectively

Full size image

The steady-state solutions are then sought when \(D_1a_i=0,D_1\theta _i=0,\>i={1,2}\), which when substituted in (30) and solved for \(a_1\) and \(a_2\) give the two resonance equations

$$\begin{aligned}{} & {} \!\!\!9(\gamma _2^2{+}\alpha _2^2\omega _2^6)a_2^6{+}24\omega _2(-\gamma _2\sigma _p+2\gamma _2\sigma _{in}{+}\alpha _2\mu _2\omega _2^3)a_2^4\nonumber \\{} & {} \qquad +16\omega _2^2(\mu _2^2+(\sigma _p-2\sigma _{in})^2)a_2^2-4\eta _{21}^2a_1^2=0,\nonumber \\ \end{aligned}$$
(31a)
$$\begin{aligned}{} & {} \begin{aligned}&9\eta _{21}^2(\gamma _1^2+\alpha _1^2\omega _1^6)a_1^7+24\eta _{21}^2(\alpha _1\mu _1\omega _1^4-\gamma _1\sigma _p\omega _1)a_1^5\\&\quad \quad +a_1^3\left[ -4\eta _{21}^2(\eta _{11}^2-4(\mu _1^2+\sigma _p^2)\omega _1^2)\right. \\&\qquad +24\eta _{12}\eta _{21}(\gamma _1(\sigma _p-2\sigma _{in})-\alpha _1\mu _2\omega _1^3)\omega _2a_2^2\\&\qquad \left. -18\eta _{12}\eta _{21}(\gamma _1\gamma _2+\alpha _1\alpha _2\omega _1^3\omega _2^3)a_2^4\right] \\&\qquad +4\eta _{12}\eta _{21}a_1\left[ (\eta _{12}\eta _{21}-8(\mu _1\mu _2+\sigma _p(\sigma _p-\right. \\&\qquad 2\sigma _{in}))\omega _1\omega _2)a_2^2\\&\qquad \left. +6\omega _1(\gamma _2\sigma _p-\alpha _2\mu _1\omega _2^3)a_2^4\right] =0. \end{aligned} \end{aligned}$$
(31b)

5.1 Stability analysis

In order to determine the stability of the obtained non-trivial solutions, the solution is perturbed using

$$\begin{aligned} a_1(T_1)= & {} a_{10}+\varDelta a_1(T_1),\quad a_2(T_1)=a_{20}+\varDelta a_2(T_1),\nonumber \\ \theta _1(T_1)= & {} \theta _{10}+\varDelta \theta _1(T_1),\nonumber \\{} & {} \quad \theta _2(T_1)=\theta _{20}+\varDelta \theta _2(T_1), \end{aligned}$$
(32)

compactly written

$$\begin{aligned} \varvec{z}(T_1)=\varvec{z_0}+\varvec{\varDelta z}(T_1), \end{aligned}$$
(33)

which is then inserted in the modulation equations (30) to give

$$\begin{aligned} \varvec{\varDelta \dot{ z}}=\frac{\partial \varvec{f}(\varvec{\varDelta z},\varvec{z_0})}{\partial \varvec{\varDelta z}}|_{\varvec{\varDelta z}=\varvec{z_0}}+NLT, \end{aligned}$$
(34)

where \(\varvec{J}=\frac{\partial \varvec{f}(\varvec{\varDelta z},\varvec{z_0})}{\partial \varvec{\varDelta z}}|_{\varvec{\varDelta z}=\varvec{0}}\) is the Jacobian matrix evaluated at the fixed point, NLT represents the nonlinear terms.

After eliminating the nonlinear terms, the linearized system presents an eigensystem with the eigenvectors being tangent to the system’s nonlinear manifolds. The stability of the fixed point of the nonlinear system can be deduced from the eigenvalues of the linearized system, as long as the fixed point is hyperbolic according to Hartman–Grobman theorem [44]. In this view, if all the eigenvalues at the investigated fixed point have negative real parts, the fixed point and the corresponding solution is considered asymptotically stable. While the existence of a single positive eigenvalue implies the instability of the solution. However, if the largest eigenvalue is strictly zero, then the stability of the solution cannot be determined by a linear analysis [39].

Figure 8 depicts the frequency–response curves for the amplitudes of both degrees of freedom, which were calculated by solving (31). The parameter values used represent a perfectly symmetrical system with zero linear damping. The resonance curves show the typical “M” shape due to the internal resonance; moreover, the hardening nonlinear stiffness causes all curves to bend to the right. This figure shows a similar behavior as in [45] for a 1:3 internal resonance, however, with different stability analysis results. In addition, multiple stationary points could be calculated by detuning the excitation frequency. This results in a complex phase space containing various fixed points at a given excitation frequency.

However, when the external parametric excitation \(\eta _{11}\) is turned off, the internal resonance’s typical behavior vanishes (see Fig. 9), and the frequency–response curves show only stable and unstable limit cycles similar to the case of principle parametric resonance discussed before. Nevertheless, a distinction should be made here between this case and the case of parametric resonance. In the case of principle resonance, we have only one excitation source, which is \(\eta _{11}\), that is, the effect of the coupling parametric excitation terms \(\eta _{12},\eta _{21}\) does not exist. This is a general remark that the coupling excitation terms influence only combination resonances, while intrinsic excitation terms \(\eta _{11},\eta _{22}\) influence only the respective principle parametric resonance [22]. However, we present here a different phenomenon, where the energy is transferred to the other degree of freedom, not through coupling excitation terms but through internal resonance. Thus, in the case of internal resonance, we do have three excitation sources, \(\eta _{11},\eta _{12}\) and \(\eta _{21}\). If the first one is turned off, the other two remain effective, causing a transfer of energy at the principle resonance frequency. These coupling excitation terms will show up again to be influencing the system’s behavior under combination resonance, as will be discussed afterward. In other words, while having zero \(\eta _{11}\) and \(\eta _{22}\), we have a cross parametric resonance through \(\eta _{12}\) and \(\eta _{21}\). This leads to the response depicted in Fig. 9.

6 Combination parametric resonances

We apply the same analysis as before for the case of combination parametric resonances, where the parametric excitation frequency is in the neighborhood of the summation or the difference frequencies, that is \(\varOmega _p\simeq |\omega _1\pm \omega _2|\). To perturb around any of both frequencies, we introduced the detuning parameter \(\sigma \), where

$$\begin{aligned} \varOmega _p=\omega _1\pm \omega _2+\epsilon \sigma , \end{aligned}$$
(35)

then as before the resonance condition (35) is then inserted in (13), to give the solvability conditions for the summation frequency

$$\begin{aligned}{} & {} i2\omega _1D_1A_1+i\mu _1\omega _1A_1+3\gamma _1A_1^2\bar{A_1}+i3\alpha _1\omega _1^3A_1^2\bar{A_1}\nonumber \\{} & {} \qquad +\frac{1}{2}\eta _{12}\bar{A_2}e^{i\sigma _s T_1}=0, \end{aligned}$$
(36a)
$$\begin{aligned}{} & {} i2\omega _2D_1A_2+i\mu _2\omega _2A_2+3\gamma _2A_2^2\bar{A_2}+i3\alpha _2\omega _2^3A_2^2\bar{A_2}\nonumber \\{} & {} \qquad +\frac{1}{2}\eta _{21}\bar{A_1}e^{i(\sigma _s T_1+\zeta )}=0, \end{aligned}$$
(36b)

or for the difference frequency

$$\begin{aligned}{} & {} i2\omega _1D_1A_1+i\mu _1\omega _1A_1+3\gamma _1A_1^2\bar{A_1}+i3\alpha _1\omega _1^3A_1^2\bar{A_1}\nonumber \\{} & {} \qquad +\frac{1}{2}\eta _{12}A_2e^{-i\sigma _d T_1}=0, \end{aligned}$$
(37a)
$$\begin{aligned}{} & {} i2\omega _2D_1A_2+i\mu _2\omega _2A_2+3\gamma _2A_2^2\bar{A_2}+i3\alpha _2\omega _2^3A_2^2\bar{A_2}\nonumber \\{} & {} \qquad +\frac{1}{2}\eta _{21}A_1e^{i(\sigma _d T_1+\zeta )}=0. \end{aligned}$$
(37b)

Putting the amplitudes \(A_1(T_1),A_2(T_1)\) in polar form according to (15), substituting in (36) or (37) and separating real and imaginary terms gives

$$\begin{aligned} D_1a_1&=-\frac{1}{2}\mu _1a_1-\frac{3}{8}\alpha _1\omega _1^2a_1^3-\frac{1}{4\omega _1}\eta _{12}a_2\sin (\theta _1) \end{aligned}$$
(38a)
$$\begin{aligned} D_1a_2&{=}{-}\frac{1}{2}\mu _2a_2{-}\frac{3}{8}\alpha _2\omega _2^2a_2^3\mp \frac{1}{4\omega _2}\eta _{21}a_1\sin (\theta _1)\cos (\zeta )\nonumber \\&-\frac{1}{4\omega _2}\eta _{21}a_1\cos (\theta _1)\sin (\zeta ) \end{aligned}$$
(38b)
$$\begin{aligned} D_1\theta _1&{=}\pm \sigma {-}\frac{3\gamma _1a_1^2}{8\omega _1}\mp \frac{3\gamma _2a_2^2}{8\omega _2}\mp \frac{1}{4\omega _2}\eta _{21}\frac{a_1}{a_2}\cos (\theta _1)\cos (\zeta )\nonumber \\&+\frac{1}{4\omega _2}\eta _{21}\frac{a_1}{a_2}\sin (\theta _1)\sin (\zeta )-\frac{1}{4\omega _1}\eta _{12}\frac{a_2}{a_1}\cos (\theta _1), \end{aligned}$$
(38c)
$$\begin{aligned} D_1\theta _2&=\frac{3\gamma _2a_2^2}{8\omega _2}+\frac{1}{4\omega _2}\eta _{21}\frac{a_1}{a_2}\cos (\theta _1)\cos (\zeta )\nonumber \\&\mp \frac{1}{4\omega _2}\eta _{21}\frac{a_1}{a_2}\sin (\theta _1)\sin (\zeta ), \end{aligned}$$
(38d)

where \(\theta _1=\pm \sigma T_1-\phi _1\mp \phi _2\) and \(\theta _2=\phi _2\), where the upper and lower signs in the terms with combined signs correspond to the summation and difference frequency cases, respectively. Steady-state solutions are then obtained by calculating the fixed points of (38), that is when \(D_1a_i=0\) and \(D_1\theta _i=0\), for \(i=1,2\), and then the stability of each fixed point is determined as explained before. However, in this case the effect of the asynchronicity of the parametric excitation, i.e., the presence of the phase-shift \(\zeta \), heavily influences the non-trivial solutions. Therefore, we present the steady-state solutions in two different cases, synchronous \(\zeta =0\) and asynchronous \(\zeta =-\pi /2\). This latter particular phase-shift is chosen according to our analysis of the trivial solution discussed before.

Fig. 10
figure 10

Non-trivial solutions for \(a_1\) and \(a_2\) by detuning \(\sigma \) about the summation frequency, when \(\omega _1=1,\omega _2=\sqrt{5},\mu _i=0,\gamma _i=0.07, \alpha _i=0.03,\eta _{ij}=1,\> i,j={1,2}\) and \(\zeta =0\)

Full size image
Fig. 11
figure 11

Non-trivial solutions for \(a_1\) and \(a_2\) by detuning \(\sigma \) about the summation frequency, when \(\omega _1=1,\omega _2=\sqrt{5},\mu _i=0,\gamma _i=0.07, \alpha _i=0.03,\eta _{ij}=1,\> i,j={1,2}\) and \(\zeta =-\pi /2\)

Full size image

From (38), it can be observed that although these equations are in four variables, only three of them influence the vector fields excluding \(\theta _2\), which lead to three algebraic equations in three variables to determine the fixed points.

In the synchronous excitation case, the steady-state solutions are deduced and plotted in Fig. 10 for the summation resonance frequency, where the blue and red points represent stable and unstable limit cycles, respectively. However, by solving the equations for the difference frequency case, an interesting result is observed: non-trivial solutions do not exist. This comes in line with our stability analysis of the trivial solution, where no resonance was found at the difference combination frequency, instead an anti-resonance could be detected. According to this observation, a correspondence between the stability of the trivial solution and the existence of the non-trivial ones can be proposed. Moreover, the parametric resonance curve for the summation frequency case is shown to be similar to principle resonances (see Fig. 4), where the amplitude of the second degree of freedom \(a_2\) is lower than the first one \(a_1\).

Fig. 12
figure 12

Non-trivial solutions for \(a_1\) and \(a_2\) by detuning \(\sigma \) about the difference frequency, when \(\omega _1=1,\omega _2=\sqrt{5},\mu _i=0,\gamma _i=0.07, \alpha _i=0.03,\eta _{ij}=1,\> i,j={1,2}\) and \(\zeta =-\pi /2\)

Full size image

In the other case, when \(\zeta =-\pi /2\), the fixed points of (38) are again determined and the resonance curves in this case are then depicted in Figs. 11 and 12. In these figures it can be observed that all the non-trivial steady-state solutions, or limit cycles, are found to be stable for the given detuning interval. However, the resonance curves of both degrees of freedom have different profiles. Furthermore, detuning the excitation frequency has opposite effects on the amplitudes of the limit cycles of both degrees of freedom: for the summation frequency case, by positive detuning \(a_2\) exhibits higher amplitude than \(a_1\), while by negative detuning the opposite occurs, and vice versa for the difference frequency case. Moreover, the resonance curves around the difference frequency are shown to be significantly similar and mirrored around the zero detuning parameter when compared to those calculated around the summation resonance. This result should be related to the difference in the solvability conditions (36) and (37) where the excitation terms in each case are found to be the complex conjugate of the corresponding ones in the other case.

7 Non-resonant limit cycles

As illustrated in Sect. 2, the uniqueness of the phase-shifted parametric excitation lies in the destabilization of the trivial solution in a broad band of excitation frequencies. This means, when the trivial solution turns unstable, we should look for a non-trivial solution. In this case, as previously noted, the non-trivial solutions represent limit cycles due to the parametric excitation. In order to find these solutions, the system (7) is restudied without specifying a resonance condition. However, in order to capture the required phenomenon the approximation up to the second order is then required. In this case we rewrite (8) and (9) to be

$$\begin{aligned} u_1(t;\epsilon )= & {} u_{10}(T_0,T_1,T_2)+\epsilon u_{11}(T_0,T_1,T2)\nonumber \\{} & {} +\epsilon ^2u_{12}(T_0,T_1,T_2)+..., \end{aligned}$$
(39a)
$$\begin{aligned} u_2(t;\epsilon )= & {} u_{20}(T_0,T_1,T_2)+\epsilon u_{21}(T_0,T_1,T_2)\nonumber \\{} & {} +\epsilon ^2u_{22}(T_0,T_1,T_2)+..., \end{aligned}$$
(39b)

and

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial t}&=D_0+\epsilon D_1+\epsilon ^2D_2...,\\ \frac{\partial ^2}{\partial t^2}&=D_0^2+2\epsilon D_0 D_1+\epsilon ^2(D_1^2+D_0D_2). \end{aligned} \end{aligned}$$
(40)

Inserting (39) and (40) in the perturbed differential equations (7) gives an additional couple of equations for the second order \(\epsilon ^2\), which are

$$\begin{aligned}&\begin{aligned}&D_0^2u_{12}+\omega _1^2 u_{12}=-\mu _1 (D_0u_{11}+D_1u_{10})\\&\qquad -\eta _{11} u_{11} \cos (\varOmega _p t)-\eta _{12} u_{21} \cos (\varOmega _p t)\\&\qquad -D_1^2u_{10}-2D_0D_2u_{10}-2D_0D_1u_{11}, \end{aligned} \end{aligned}$$
(41a)
$$\begin{aligned}&\begin{aligned}&D_0^2u_{22}+\omega _2^2 u_{22}=-\mu _2 (D_0u_{211}+D_1u_{20})-\\&\qquad \eta _{21} u_{11} \cos (\varOmega _p t+\zeta )-\eta _{22} u_{21} \cos (\varOmega _p t)\\&\qquad -D_1^2u_{20}-2D_0D_2u_{20}-2D_0D_1u_{21}. \end{aligned} \end{aligned}$$
(41b)

While the excitation frequency \(\varOmega _p\) is chosen to be away from all resonance frequencies, the solvability conditions of (13) in the non-resonant case then read

$$\begin{aligned}{} & {} i2\omega _1D_1A_1+i\mu _1\omega _1A_1+3\gamma _1A_1^2\bar{A_1}\nonumber \\{} & {} \qquad +i3\alpha _1\omega _1^3A_1^2\bar{A_1}=0, \end{aligned}$$
(42a)
$$\begin{aligned}{} & {} i2\omega _2D_1A_2+i\mu _2\omega _2A_2+3\gamma _2A_2^2\bar{A_2}\nonumber \\{} & {} \qquad +i3\alpha _2\omega _2^3A_2^2\bar{A_2}=0, \end{aligned}$$
(42b)

which show no influence of the parametric excitation. However, as pointed out in Sect. 2, the trivial solution shows instability in a broad band of frequencies, which suggests the presence of secular terms at non-resonant frequencies that depend on parametric excitation terms. Moreover, in a nonlinear system this could lead to the presence of non-trivial solutions or limit cycles. For this reason, the analysis is then extended to the second-order approximation.

Up to this point, it was not required to obtain the first-order correction terms \(u_{11},u_{12}\), since we were only interested in the amplitudes of the basic solution \(u_{01}, u_{02}\). In this current case the first-order correction terms are needed to solve (41), noting that the solutions should be functions of three time scales here \(T_0,T_1,T_2\), which also applies to (12) and (13). By eliminating the secular terms and solving (13), then applying these solutions to (41) and extracting the secular terms, the solvability conditions then read

$$\begin{aligned}&\begin{aligned}&\left( 4\omega _1^2\left( \frac{\eta _{11}^2}{4\omega _1^2-\varOmega _p^2}\right. \right. \\&\qquad \left. +\frac{\eta _{12}\eta _{21}(2i\omega _1\varOmega _p\sin (\zeta )-(\varOmega _p^2+\omega _1^2-\omega _2^2)\cos (\zeta ))}{(\varOmega _p^2-(\omega _1-\omega _2)^2)(\varOmega _p^2-(\omega _1+\omega _2)^2)}\right) \\&\qquad \left. -3(\gamma _1-i\alpha _1\omega _1^3)(\gamma _1-3i\alpha _1\omega _1^3)|A_1|^4\right) A_1\\&\qquad -8\omega _1^2D_1^2A_1-8\omega _1^2(\mu _1+6\alpha _1\omega _1|A_1|^2)D_1A_1\\&\qquad -16i\omega _1^3D_2A_1\\&\qquad +24\alpha _1\omega _1^4A_1^2D_1\bar{A_1}+CC=0, \end{aligned} \end{aligned}$$
(43a)
$$\begin{aligned}&\begin{aligned}&\left( 4\omega _2^2\left( \frac{\eta _{22}^2}{4\omega _2^2-\varOmega _p^2}\right. \right. \\&\qquad \left. -\frac{\eta _{12}\eta _{21}(2i\omega _2\varOmega _p\sin (\zeta )+(\varOmega _p^2+\omega _2^2-\omega _1^2)\cos (\zeta ))}{(\varOmega _p^2-(\omega _1-\omega _2)^2)(\varOmega _p^2-(\omega _1+\omega _2)^2)}\right) \\&\qquad \left. -3(\gamma _2-i\alpha _2\omega _2^3)(\gamma _2-3i\alpha _2\omega _2^3)|A_2|^4\right) A_2\\&\qquad -8\omega _2^2D_1^2A_2-8\omega _2^2(\mu _2+6\alpha _2\omega _2|A_2|^2)D_1A_2\\&\qquad -16i\omega _2^3D_2A_2\\&\qquad +24\alpha _2\omega _2^4A_2^2D_1\bar{A_2}+CC=0, \end{aligned} \end{aligned}$$
(43b)

where they surprisingly represent two decoupled equations in \(A_1(T_1,T_2)\) and \(A_1(T_1,T_2)\). Unlike the conditions (42), we observe here the influence of both nonlinear and parametric excitation terms, which should be a correct representative of the slow time-scale dynamics at non-resonant frequencies.

The solvability equations (43) show the amplitudes \(A_1,A_2\) differentiated with respect to \(T_1\) and \(T_2\), whereas those in (42) were only differentiated with respect to \(T_1\). In this case, instead of being solved as partial differential equations, they could be combined using the method of reconstitution [46] to give

$$\begin{aligned} \frac{\textrm{d}A}{\textrm{d}t}=\dot{A_i}=\epsilon D_1A_i+\epsilon ^2 D_2A_i+\cdots ,\quad i=1,2. \end{aligned}$$
(44)

Thus, using (42) and (43), while \(D_1^2A_1,D_1^2A_2\) are obtained by the time differentiation of (42), we arrive at the differential equations of the slow varying amplitudes \(A_1,A_2\). Afterward, using the polar coordinates \(A_n=\dfrac{1}{2}a_n(t)e^{i\phi _n(t)},\>n={1,2}\) and separating real and imaginary parts yield

$$\begin{aligned}&\dot{a}_1=\frac{1}{2}\left( -\mu _1+\frac{\eta _{12}\eta _{21}\varOmega _p\sin (\zeta )}{(\varOmega _p^2-(\omega _1-\omega _2)^2)(\varOmega _p^2-(\omega _1+\omega _2)^2)}\right) a_1\nonumber \\&\qquad +\frac{3(\gamma _1\mu _1-2\alpha _1\omega _1^4)}{16\omega _1^2}a_1^3-\frac{3}{32}\alpha _1\gamma _1a_1^5, \end{aligned}$$
(45a)
$$\begin{aligned}&\dot{a}_2=\frac{1}{2}\left( -\mu _2-\frac{\eta _{12}\eta _{21}\varOmega _p\sin (\zeta )}{(\varOmega _p^2-(\omega _1-\omega _2)^2)(\varOmega _p^2-(\omega _1+\omega _2)^2)}\right) a_2\nonumber \\&\qquad +\frac{3(\gamma _2\mu _2-2\alpha _2\omega _2^4)}{16\omega _2^2}a_2^3-\frac{3}{32}\alpha _2\gamma _2a_2^5, \end{aligned}$$
(45b)
$$\begin{aligned}&\phi '_1=-\frac{\mu _1^2}{8\omega _1}-\frac{\eta _{11}^2}{4\omega _1(4\omega _1^2-\varOmega _p^2)}\nonumber \\&\qquad +\frac{\eta _{12}\eta _{21}(\omega _1^2-\omega _2^2+\varOmega _p^2)\cos (\zeta )}{4\omega _1(\varOmega _p^2-(\omega _1-\omega _2)^2)(\varOmega _p^2-(\omega _1+\omega _2)^2)}\nonumber \\&\qquad +\frac{3\gamma _1}{8\omega _1}a_1^2+\frac{3(-5\gamma _1^2+3\alpha _1^2\omega _1^6)}{256\omega _1^3}a_1^4, \end{aligned}$$
(45c)
$$\begin{aligned}&\phi '_2=-\frac{\mu _2^2}{8\omega _2}-\frac{\eta _{22}^2}{4\omega _2(4\omega _2^2-\varOmega _p^2)}\nonumber \\&\qquad +\frac{\eta _{12}\eta _{21}(\omega _2^2-\omega _1^2+\varOmega _p^2)\cos (\zeta )}{4\omega _2(\varOmega _p^2-(\omega _1-\omega _2)^2)(\varOmega _p^2-(\omega _1+\omega _2)^2)}\nonumber \\&\qquad +\frac{3\gamma _2}{8\omega _2}a_2^2+\frac{3(-5\gamma _2^2+3\alpha _2^2\omega _2^6)}{256\omega _2^3}a_2^4. \end{aligned}$$
(45d)
Fig. 13
figure 13

Limit cycle amplitudes \(a_1,a_2\) at non-resonant frequencies, when \(\omega _1=1,\omega _2=\sqrt{5},\mu _i=0,\gamma _i=0.07, \alpha _i=0.03,\eta _{ij}=1,\> i,j={1,2}\) and \(\zeta =-\pi /2\)

Full size image

It can be noticed in (45) that the amplitude equations (a,b) are composed of linear and nonlinear terms. The linear terms represent an effective damping coefficient modified by the parametric excitation, while the nonlinear terms are primarily composed of the nonlinear coefficients of the original system (1). This affirms the expected dependency of the existence of non-trivial solutions on the nonlinearity of the original system. A similar modulation equation could be obtained in [35] using the method of normal forms; however, the nonlinear stiffness terms did not appear.

By plotting the non-trivial solutions for the amplitudes \(a_1,a_2\) in Fig. 13, we find the non-trivial solutions of each degree of freedom existing in a different band of frequencies for \(\zeta =-\pi /2\), while when the phase-shift vanishes, \(\zeta =0\), no non-trivial solutions could be found. In this figure, \(a_1\) has non-trivial values between the two combination frequencies \(|\omega _2\pm \omega _1|\), while \(a_2\) has only the trivial solution, and vice versa. This can be attributed to the denominator of the parametric excitation term, that is \( (\varOmega _p^2-(\omega _1-\omega _2)^2)(\varOmega _p^2-(\omega _1+\omega _2)^2)\) which changes signs at both combination frequencies, giving a negative value in-between and a positive one otherwise. This change of sign influences the existence of non-trivial solutions for \(a_1\) and \(a_2\). However, their non-trivial solutions exist at different intervals due to the sign change of the whole parametric excitation term, see (45a,b).

Furthermore, (12) can be rewritten using (15) to yield

$$\begin{aligned} u_1= & {} \frac{1}{2}a_1\left( e^{i(\omega _1t+\phi _1)}+e^{-i(\omega _1t+\phi _1)}\right) ,\nonumber \\{} & {} \quad \quad u_2=\frac{1}{2}a_2\left( e^{i(\omega _2t+\phi _2)}+e^{-i(\omega _2t+\phi _2)}\right) , \end{aligned}$$
(46)

which shows the main frequency of the oscillations of each degree of freedom to be \(\omega _1\) and \(\omega _2\) modified by the slow varying \(\phi _1\) and \(\phi _2\), respectively.

To summarize all the non-trivial solutions obtained: the analysis carried out at the non-resonant frequencies represents a global solution with respect to the excitation frequency, whereas the solutions obtained in the previous sections at resonant frequencies correspond to local solutions. In combining the global and local pictures of the system response under asynchronous excitation (\(\zeta =-\pi /2\)), see Figs. 4, 11, 12 and 13, we obtain a full representation of the dynamics of the system (1) at all excitation frequencies.

Furthermore and most importantly, stable limit cycles are proved to exist at non-resonant frequencies, where the trivial solution exhibits instability. This result affirms our hypothesis, which is the broadband parametric amplification acquired through this method of excitation as a result of a broadband destabilization of the trivial solution discussed in Sect. 2.

8 Conclusion

Nonlinear time-periodic systems exhibit several types of instability which occur due to different reasons. Resonances and transfer of energy between coupled degrees of freedom contribute to this destabilization; moreover, the addition of a phase-shift between the coupling parametric excitation terms adds other non-trivial steady-state solutions. Through the variation of the linear damping coefficient at the principle parametric resonance, the non-trivial solutions seem to exist in a limited interval of the damping coefficient values, but more interestingly it could cause isolated steady-state solutions as well when the excitation frequency is detuned in a region of multiple stationary points. In addition, the case of internal resonance shows an influence of each excitation term. Even when the intrinsic excitation terms, i.e., the diagonal terms in the parametric excitation matrix, do not exist, the coupling excitation terms could cause a cross excitation in both degrees of freedom. At the summation combination frequency, the non-trivial solutions were obtained for both synchronous and asynchronous excitations. In the former case, the resonance curves are shown to be similar to those occurring at the principle resonance frequency; however, in the latter case only stable limit cycles could be found for the given parameter values. Furthermore, it could be shown that non-trivial solutions appear at the difference frequency under asynchronicity, which is not the case when the phase-shift vanishes. This is found to be in accordance with the stability analysis of the trivial solution, since at the difference frequency an anti-resonance occurs causing the stabilization of the trivial solution. Finally, limit cycles are found at non-resonant frequencies under asynchronous parametric excitation. This last result supports the aim of this work to find a broadband parametric amplification through the destabilization of the trivial solution.

In summary, the system’s dynamics are investigated at all resonant and non-resonant frequencies, thus giving a global picture of the system’s response. Through the analysis, the influence of the asynchronous parametric excitation on the stability of the trivial and non-trivial solutions is highlighted, which corresponds directly to parametric amplification.

Therefore, these findings provide a better understanding of the nonlinear dynamics of parametrically excited M-DoF systems which are particularly important for micro- and nanosystems, such as micro- and nanomechanical resonators. Through these conclusions, the proposed method of asynchronous parametric excitation is shown to be promising for the sake of increasing the amplification and thereby enhancing the sensitivity of these systems in the sensors industry.