Extreme nonlinear dynamics of cantilever beams: effect of gravity and slenderness on the nonlinear modes

Abstract

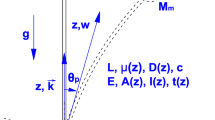
In this paper, the effect of gravity on the nonlinear extreme amplitude vibrations of a slender, vertically oriented cantilever beam is investigated. The extreme nonlinear vibrations are modeled using a finite element discretization of the geometrically exact beam model solved in the frequency domain through a combination of harmonic balance and a continuation method for periodic solutions. The geometrically exact model is ideal for dynamic simulations at extreme amplitudes as there is no limitation on the rotation of the cross sections due to the terms governing the rotation being kept exact. It is shown that the very large amplitude vibrations of dimensionless beam structures depend principally on two parameters, a geometrical parameter and a gravity parameter. By varying these two parameters, the effect of gravity in either a standing or hanging configuration on the natural (linear) modes as well as on the nonlinear modes in extreme amplitude vibration is studied. It is shown that gravity, in the case of a standing cantilever, is responsible for a linear softening behavior and a nonlinear hardening behavior, particularly pronounced on the first bending mode. These behaviors are reversed for a hanging cantilever.

Appendices

A. Effect of shear parameter $\mu$

As detailed in Sect. 2, a third dimensionless parameter related to the shear stiffness of the beam (which is present exclusively in the case of Timoshenko kinematics), called $\mu$ in §2, appears in the equations of motion Eqs. (7) and (8). Recalling Eq. (6), $\mu$ is found to depend on three parameters: the shear coefficient k, the Poisson’s ratio $\nu$ and the slenderness parameter $\eta$. Considering only slender beams such that $\eta$ is very small ($\eta \le 2 \cdot 10^{-4}$), it naturally follows that $\mu$ is also very small, being proportional to $\eta$. Recalling Eq. (8), a very small $\mu$ tends the overall shear stiffness toward infinity, i.e., to the point of no shearing of the cross section as in Euler–Bernoulli kinematics. Therefore, for very small $\mu$, it can be considered that there is very little effect of shearing of the cross section (even at high amplitudes of rotation) and little difference between Timoshenko and Euler–Bernoulli kinematics.

In order to confirm the minor influence of the dimensionless parameter $\mu$, the simulations of Sect. 4 were performed again with different values of k and $\nu$ while keeping $\eta$ and $\alpha$ the same. As mentioned in Sect. 2.2, typical values of k and $\nu$ are in the ranges of $0.8 \le k \le 0.9$ and $0 \le \nu \le 0.5$, respectively. The two extremities of $\mu$ within these ranges for k and $\nu$ were selected, $\mu = 2.22 \cdot 10^{-7}$ and $3.75 \cdot 10^{-7}$ for $\eta = 1 \cdot 10^{-7}$, in order to compare with the simulations of Sect. 4, where $k = 1, \nu = 0.3$. The breakdown of these parameters is shown in Table 3.

Table 3 Values of $\mu$ for different values of k and $\nu$, with $\eta = 1\cdot 10^{-7}$

The simulations of Sect. 4.1 and 4.2 (where $\mu = 2.60 \cdot 10^{-7}$ for $\eta = 10^{-7}$) are recomputed using these two additional values of $\mu$. For the latter, $\alpha = 5$ is chosen. The results of these simulations are summarized in Fig. 18; the orange curves in both figures are the same as their counterparts in Sect. 4.

Fig. 18

Effect of dimensionless parameters on the first nonlinear mode, isolation of the effect of $\mu$: a amplitude of the first harmonic H1 of $\theta$ at the free end of the beam for different values of $\mu$, no-gravity condition ($\alpha = 0$), b the same as a but with gravity condition ($\alpha = 5$)

In both conditions, regardless of the presence of gravity in Fig. 18b, the variation in $\mu$ between its minimum and maximum values has next to no effect on the backbone curve of the first nonlinear mode; the three curves overlap to the point of being indistinguishable. These comparisons prove the negligible influence of shearing on the mechanics of very slender beams and, therefore, justify the omission of the third dimensionless parameter $\mu$ from the analyses presented in this work.

B. Tangent stiffness computation

According to Eq. (24), the tangent stiffness $\textbf{K}_\text {t}$ is defined as the first derivative of the internal force vector $\textbf{f}_\text {int}$ with respect to the vector of degrees of freedom:

$$\begin{aligned} \textbf{K}_\text {t}=\frac{\partial \textbf{f}_\text {int}}{\partial \textbf{q}}. \end{aligned}$$

(35)

In practice, it can be computed at the elementary level and then assembled according to standard finite element procedures.

All details having been explained in previous work [4, 44], we recall here only the main parts of the reasoning. First, the strains of Eq. (2) are discretized according to Eq. (12), yielding the elementary strain expressions:

$$\begin{aligned} e^e&= \left( 1 + \dfrac{u_2 - u_1}{L^e} \right) \cos {\theta }^e + \left( \dfrac{w_2 - w_1}{L^e} \right) \sin {\theta }^e - 1, \end{aligned}$$

(36a)

$$\begin{aligned} \gamma ^e&= \left( \dfrac{w_2 - w_1}{L^e} \right) \cos {\theta }^e - \left( 1 + \dfrac{u_2 - u_1}{L^e} \right) \sin {\theta }^e, \end{aligned}$$

(36b)

$$\begin{aligned} \kappa ^e&= \dfrac{\theta _2 - \theta _1}{L^e}. \end{aligned}$$

(36c)

Then, the elementary discretized gradient matrix is defined as:

$$\begin{aligned}{} & {} \delta \varvec{\varepsilon }^e=\textbf{B}^e \delta \textbf{q}^e\nonumber \\{} & {} \quad \Rightarrow \quad \textbf{B}^e = \frac{1}{L_e}\begin{bmatrix} -\cos \theta ^e &{} -\sin \theta ^e &{} N_1(x)L^e\gamma ^e &{} \cos \theta ^e &{} \sin \theta ^e &{} N_2(x)L^e\gamma ^e \\ \sin \theta ^e &{} -\cos \theta ^e &{} -N_1(x)L^e(1+e^e) &{} -\sin \theta ^e &{} \cos \theta ^e &{} -N_2(x)L^e(1+e^e) \\ 0 &{} 0 &{} -1 &{} 0 &{} 0 &{} 1 \end{bmatrix}, \end{aligned}$$

(37)

with $\varvec{\varepsilon }^e = [e^e\;\gamma ^e\;\kappa ^e]^{{\text {T}}}$. Considering the internal virtual work (see [4, 44]), the elementary internal force vector is written:

$$\begin{aligned} \textbf{f}_{\textrm{int}}^e(\textbf{q}^e) = \int _0^{L^e} (\textbf{B}^e)^{{\text {T}}}\textbf{C}\varvec{\varepsilon }^e\,\textrm{d}x, \end{aligned}$$

(38)

with:

$$\begin{aligned} \textbf{C}=\begin{bmatrix} EA &{} 0 &{} 0 \\ &{} kGA &{} 0\\ &{} &{} EI \end{bmatrix}. \end{aligned}$$

(39)

Recalling Eqs. (35) and (36), the first variation of Eq. (38) can be written:

$$\begin{aligned}{} & {} \delta \textbf{f}_{\textrm{int}}^e(\textbf{q}^e)=\left\{ \int _0^{L^e} (\textbf{B}^e)^{{\text {T}}}\textbf{C} \textbf{B}^e \,\textrm{d}x \right. \nonumber \\{} & {} \quad \left. + \int _0^{L^e} \left( \frac{\partial \textbf{B}^e}{\partial \textbf{q}^e}\right) ^{{\text {T}}}\textbf{C}\varvec{\varepsilon }^e \,\textrm{d}x\right\} \delta \textbf{q}^e = \textbf{K}^e_\text {t} \delta \textbf{q}^e, \end{aligned}$$

(40)

where $\textbf{K}^e_\text {t}$ is the elementary tangent stiffness matrix. Finally, $\textbf{K}^e_\text {t}$ is computed $\textbf{K}^e_\text {t} = \textbf{K}^e_e + \textbf{K}^e_\gamma + \textbf{K}^e_\kappa$, with

$$\begin{aligned} \textbf{K}_e^e&= \frac{E A}{L^e} \begin{bmatrix} {K}_1 &{} {K}_3 &{} {K}_4 &{} -{K}_1 &{} -{K}_3 &{} {K}_4 \\ {} &{} {K}_2 &{} {K}_5 &{} -{K}_3 &{} -{K}_2 &{} {K}_5 \\ {} &{} &{} {K}_6 &{} -{K}_4 &{} -{K}_5 &{} {K}_6 \\ {} &{} &{} &{} {K}_1 &{} {K}_3 &{} -{K}_4 \\ {} &{} &{} &{} &{} {K}_2 &{} -{K}_5 \\ {} &{} &{} &{} &{} &{} {K}_6 \end{bmatrix}, \end{aligned}$$

(41a)

$$\begin{aligned} \textbf{K}_\gamma ^e&= \frac{kG A}{L^e} \begin{bmatrix} {K}_2 &{} -{K}_3 &{} {K}_7 &{} -{K}_2 &{} {K}_3 &{} {K}_7 \\ {} &{} {K}_1 &{} {K}_8 &{} {K}_3 &{} -{K}_1 &{} {K}_8 \\ {} &{} &{} {K}_9 &{} -{K}_7 &{} -{K}_8 &{} {K}_9 \\ {} &{} &{} &{} {K}_2 &{} -{K}_3 &{} -{K}_7 \\ {} &{} &{} &{} &{} {K}_1 &{} -{K}_8 \\ {} &{} &{} &{} &{} &{} {K}_9 \end{bmatrix}, \end{aligned}$$

(41b)

$$\begin{aligned} \textbf{K}_\kappa ^e&= \frac{E I}{L^e} \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ {} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ {} &{} &{} 1 &{} 0 &{} 0 &{} -1 \\ {} &{} &{} &{} 0 &{} 0 &{} 0 \\ {} &{} &{} &{} &{} 0 &{} 0 \\ {} &{} &{} &{} &{} &{} 1 \end{bmatrix}, \end{aligned}$$

(41c)

and with:

$$\begin{aligned}{} & {} {K}_1 = \cos ^2{\bar{\theta }}, \quad {K}_2 = \sin ^2{\bar{\theta }}, \quad {K}_3 = \cos {\bar{\theta }}\sin {\bar{\theta }}, \nonumber \\{} & {} {K}_4 = \frac{L^e}{2} (\bar{e}^e\sin {\bar{\theta }} - \bar{\gamma }^e\cos {\bar{\theta }}), \\{} & {} {K}_5 = -\frac{L^e}{2} (\bar{e}^e\cos {\bar{\theta }} + \bar{\gamma }^e\sin {\bar{\theta }}), \nonumber \\{} & {} {K}_6 = \frac{(L^e)^2}{4}\left[ (\bar{\gamma }^e)^2 - \bar{e}^e(\bar{e}^e + 1)\right] , \nonumber \\{} & {} {K}_7 = \frac{L^e}{2}[\bar{\gamma }^e\cos {\bar{\theta }} - \sin {\bar{\theta }}(\bar{e}^e + 1)], \\{} & {} {K}_8 = \frac{L^e}{2} [\bar{\gamma }^e\sin {\bar{\theta }} + \cos {\bar{\theta }}(\bar{e}^e + 1)],\nonumber \\{} & {} {K}_9 = \frac{(L^e)^2}{4}\left[ \left( \bar{e}^e + 1\right) ^2 - (\bar{\gamma }^e)^2\right] . \end{aligned}$$

In the above expressions for $K_i$, $i=1,\ldots 9$, $\bar{\theta } = (\theta _1 + \theta _2)/2$, $\bar{e} = e(\bar{\theta })$, and $\bar{\gamma } = \gamma (\bar{\theta })$ since the internal force vector integration is evaluated using a single-point Gaussian quadrature at $x= L^e/2$ to avoid shear locking (see [4, 44, 49]). Then, $\textbf{K}^e_\text {t}$ is assembly according to standard finite element procedures in order to obtain the full tangent stiffness matrix $\textbf{K}_\text {t}$.

Notice that $\textbf{K}^e_\text {t}=\textbf{K}^e_\text {t}(\textbf{q}^e)$ and, by extension, $\textbf{K}_\text {t}=\textbf{K}_\text {t}(\textbf{q})$ depend on the degrees of freedom $u_i$, $w_i$ and $\theta _i$ through their presence in $\bar{\theta }$, $\bar{e}$ and $\bar{\gamma }$ (see Eq. (36)); in other words, due to the presence of geometrical nonlinearities, the tangent stiffness of the structure is a function of its deformed state. This serves to explain the dependence of the natural frequencies of the cantilever on the gravitational field, as seen in Eq. (26) and Sect. 3.

As explained in Sect. 2.4, the tangent stiffness matrix is also used in computing the equilibrium solution $\textbf{q}_\text {s}$ of the cantilever subjected to the gravitational field. In this case, the tangent stiffness is evaluated at $\textbf{q}= \textbf{0}$, such that the elementary tangent stiffness prior to assembly takes the form of Eq. (41) with $\textbf{q}^e=\textbf{0}\;\Rightarrow \; u_1=u_2=w_1=w_2=\theta _1=\theta _2=0\;\Rightarrow \;\bar{\theta }=e^e=\gamma ^e=0$, which is with $K_1=1$, $K_2=K_3=K_4=K_5=K_6=K_7=0$, $K_8= L^e/2$ and $K_9=(L^e)^2/4$.

C. Analytical backbone computation with the third-order inextensible beam model

In this appendix, additional details are provided regarding the approximate inextensible cantilever beam model first introduced by Crespo da Silva et al. in [26, 27], serving in Sect. 4 (represented as the black dashed lines in Figs. 5 and 9) as a comparison to the geometrically exact finite element model. This model is very interesting as it is both analytical and valid up to a moderate (but not inconsiderable) amplitude of vibration and has thus been used widely in the literature on nonlinear beam dynamics [54, 63]. In our case, it is advantageous to use this model for comparison since, when restricting the modal projection to a single mode and solving via a first-order harmonic balance, the computation of the backbone curve itself becomes analytical.

The derivation of the full inextensible beam model is shown in detail in Section 3.2 of [44], which we use as the starting point for our development. We begin with the strong form of the geometrically exact model, Eq. (3), to which four assumptions are added:

• 1. The condition of inextensibility;

• 2. Euler–Bernoulli kinematics along with elimination of the rotatory inertia;

• 3. Truncation of the geometrical nonlinearities up to order 3 in w;

• 4. A free end boundary condition.

Based on assumptions 1 and 2, $e = \gamma =0$, so that Eq. (3c), taking into account the constitutive Eqs. (4), simplifies to $T=-M'-q=-EI\theta ''-q$. Then, eliminating N in Eq. (3b) using (3a) and assumption 4 ($N(L,t)=T(L,t)=0$ $\forall t$), the following partial differential equation is obtained:

$$\begin{aligned} \rho A \ddot{w} + \left( \frac{EI\theta ''+q}{\cos {\theta }}\right) ' - \left[ \tan {\theta } \int _L^x \left( \rho A \ddot{u} -n\right) \,\textrm{d}x\right] ' = p. \end{aligned}$$

(42)

Table 4 Bending parameters of the k-th bending mode for the first three bending modes of a cantilever beam

To recover the model of Crespo da Silva et al., we first assume no external axial load ($n=0$) or moment ($q=0$). Then, the inextensibility condition, written explicitly as $\sqrt{(1+u')^2 + w'^2} - 1 = 0$ [44], is used in order to rewrite the axial displacement as a function of w in Eq. (42) according to $u' = \sqrt{1 - w'^2} - 1$. In addition, the geometrically exact kinematics of the beam with the inclusion of the inextensibility condition simplify to:

$$\begin{aligned} \sin \theta = w',\qquad \cos \theta = 1 + u'=\sqrt{1-w'^2}. \end{aligned}$$

(43)

Finally, performing a Taylor expansion up to order three in w leads to:

$$\begin{aligned}{} & {} \rho A \ddot{w} + EI\left( w''' + w'w''^2 + w'''w'^2 \right) ' \nonumber \\{} & {} \quad +\frac{\rho A}{2}\left[ w' \int _L^x \frac{\partial ^2}{\partial t^2} \left( \int _0^x w'^2 \textrm{d}x \right) \textrm{d}x \right] ' = p. \end{aligned}$$

(44)

The same normalization as that of Sect. 2 (Eq. (6)) is carried out, so that Eq. (44) becomes:

$$\begin{aligned}{} & {} \ddot{\bar{w}} + \bar{w}'''' + \left( \bar{w}'\bar{w}''^2 + \bar{w}'''\bar{w}'^2 \right) ' \nonumber \\{} & {} \quad + \frac{1}{2}\left[ \bar{w}' \int _1^{\bar{x}} \frac{\partial ^2}{\partial \bar{t}^2} \left( \int _0^{\bar{x}} \bar{w}'^2 \textrm{d}\bar{x} \right) \textrm{d}\bar{x} \right] ' = \bar{p}, \end{aligned}$$

(45)

where all terms are now dimensionless.

Next, the model is discretized via a projection of the transverse displacement w onto a single eigenmode $\Phi _k(x)$, for a given $k\in {\mathbb {N}}$:

$$\begin{aligned} \bar{w}(\bar{x},t) = \Phi _k(\bar{x}) q_k(t), \end{aligned}$$

(46)

where $q_k(t)$ are the modal coordinates and the transverse mode shapes $\Phi _k$ represent those of a cantilever beam, solutions of the linear part of the equations of motion, i.e., $\Phi '''' + \beta ^4\Phi =0$ with boundary conditions $\Phi (0)=\Phi '(0)=\Phi ''(1)=\Phi '''(1)=0$. Written explicitly:

$$\begin{aligned} \Phi _k(\bar{x}) = \cos {\beta _k \bar{x}} - \cosh {\beta _k \bar{x}} - a_k \left( \sin {\beta _k \bar{x}} - \sinh {\beta _k \bar{x}} \right) . \end{aligned}$$

(47)

In Eq. (47), the coefficients $\beta _k$ are related to the dimensionless natural frequencies, such that $\bar{\omega }_k=\beta _k^2$ [50], and the coefficient $a_k$ can be calculated by normalizing the mode shapes $\Phi _k$ such that $\int _0^1 \Phi _k^2 \textrm{d}\bar{x} = 1$. The values of $\beta _k$ and $a_k$ for the first three bending modes are shown in Table 4.

In a standard procedure, the modal projection (46) is injected into Eq. (45), and the result is multiplied by $\Phi _k(\bar{x})$ and integrated over the length of the beam. Additionally, as we are here deriving an expression for the nonlinear modes/backbone curve (i.e., the free and undamped solution), the damping terms and external forcing are removed, so that Eq. (45) after the modal projection becomes:

$$\begin{aligned} \ddot{q}_k + \bar{\omega }^2_k q_k + \Gamma _k q_k^3 + \Pi _k \left( \ddot{q}_k q_k + \dot{q}_k^2 \right) q_k = 0, \end{aligned}$$

(48)

with:

where the expressions for $\Gamma _k$ and $\Pi _k$ have been evaluated for the first three bending modes based on Eq. (47) and are shown in Table 4.

Next, we seek to solve Eq. (48) using a harmonic balance (HBM) expansion truncated to a single harmonic: $q_k(t) = Q_k \cos \Omega t$ with $Q_k$ the amplitude of the oscillation. Injecting this expression for $q_k(t)$ into Eq. (48) and keeping only terms in $\cos \Omega t$ lead to the analytical expression for the amplitude $Q_k$ as a function of the frequency $\Omega$ and thus of the backbone curve:

$$\begin{aligned} Q_k = 2\sqrt{\frac{\Omega ^2 - \omega _k^2}{3\Gamma _k - 2\Omega ^2\Pi _k}}. \end{aligned}$$

(50)

Finally, the dimensionless transverse displacement is recovered according to Eq. (46) restricted to one mode as $\bar{w}(\bar{x},t)=\Phi _k(\bar{x})Q_k \cos \Omega t$. The black dashed backbone curve in Fig. 5b is traced by sweeping its amplitude $\Phi _k(1)Q_k(\Omega )$ as a function of $\Omega$. Then, $\bar{w}$ is used to compute the amplitudes of the cross-section rotation according to Eq. (43): $\theta (\bar{x},t) = \sin ^{-1}[{\bar{w}'}(\bar{x},t)]$. To trace the analytical black dashed curves in Figs. 5a and 6 in $\theta$, the first harmonic of $\theta (1,t)$ is computed as the amplitude of the first Fourier coefficient of $\sin ^{-1}[\Phi _k(1)Q_k(\Omega )\cos \Omega t]$. It is noted that this Fourier coefficient necessarily has an amplitude less than $\simeq 0.4\pi$ rad due to the limitations of the inverse sine function itself, limiting in turn the maximum amplitude of $\theta (L,t)$ plotted in Figs. 5a and 6.