Skip to main content
SpringerLink
Log in

Boussinesq equation solved by the physics-informed neural networks

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

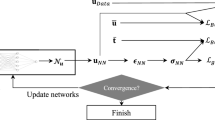
Physics-informed neural networks (PINNs) model is utilized to achieve the first- and second-order rogue wave solvers of the Boussinesq equation with different initial and boundary conditions. A new generalized loss term handling the initial first-order derivate is included in the simulations to guarantee the high prediction accuracies in the adaptive PINNs (APINNs) and the gradient-optimized PINNs (GPINNs) models, with a new regularization parameter being considered in the latter case. Learned results with high precision are fulfilled in the large domain simulations by applying more collocation points and more weight parameters in the neural network architecture. The APINNs model currently can be made use of in more situations with high prediction accuracies, while the GPINNs model is more robust in the current research where the initial condition is distributed in the localized sharp areas. Parallel computing is carried out to get the mean relative \(L_2\)-norm errors efficiently in the GPINNs model due to the random choosing of the simulation points during the training iterations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

  1. LeCun, Y., Bengio, Y., Hinton, G.: Deep learning. Nature 521(7553), 436–444 (2015)

    Google Scholar 

  2. Krizhevsky, A., Sutskever, I., Hinton, G.E.: Imagenet classification with deep convolutional neural networks. Commun. ACM 60(6), 84–90 (2017)

    Google Scholar 

  3. Voulodimos, A., Doulamis, N., Doulamis, A., Eftychios, P., et al.: Deep learning for computer vision: a brief review. Comput. Intel. Neurosci. (2018)

  4. Hirschberg, J., Manning, C.D.: Advances in natural language processing. Science 349(6245), 261–266 (2015)

    MathSciNet  MATH  Google Scholar 

  5. Lagaris, I.E., Likas, A., Fotiadis, D.I.: Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neur. Netw. 9(5), 987–1000 (1998)

    Google Scholar 

  6. Han, J., Jentzen, A., et al.: Deep learning-based numerical methods for high-dimensional parabolic partial differential equations and backward stochastic differential equations. Commun. Math. Stat. 5(4), 349–380 (2017)

    MathSciNet  MATH  Google Scholar 

  7. Rudy, S.H., Brunton, S.L., et al.: Data-driven discovery of partial differential equations. Sci. Adv. 3, 4 (2017)

    Google Scholar 

  8. Sirignano, J., Spiliopoulos, K.: Dgm: a deep learning algorithm for solving partial differential equations. J. Comput. Phys. 375, 1339–1364 (2018)

    MathSciNet  MATH  Google Scholar 

  9. Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019)

    MathSciNet  MATH  Google Scholar 

  10. Jagtap, A.D., Kawaguchi, K., Karniadakis, G.E.: Adaptive activation functions accelerate convergence in deep and physics-informed neural networks. J. Comput. Phys. 404, 109136 (2020)

    MathSciNet  MATH  Google Scholar 

  11. Jagtap, A.D., Kawaguchi, K., Karniadakis, G.E.: Locally adaptive activation functions with slope recovery for deep and physics-informed neural networks. Proc. R. Soc. A 476(2239), 20200334 (2020)

    MathSciNet  MATH  Google Scholar 

  12. Jagtap, A.D., Shin, Y., Kawaguchi, K., Karniadakis, G.E.: Deep kronecker neural networks: a general framework for neural networks with adaptive activation functions. Neurocomputing 468, 165–180 (2022)

    Google Scholar 

  13. Jagtap, A.D., Karniadakis, G.E.: Extended physics-informed neural networks (xpinns): a generalized space-time domain decomposition based deep learning framework for nonlinear partial differential equations. In: AAAI Spring Symposium: MLPS, pp. 2002–2041, (2021)

  14. Jagtap, A.D., Kharazmi, E., Karniadakis, G.E.: Conservative physics-informed neural networks on discrete domains for conservation laws: applications to forward and inverse problems. Comput. Method Appl. Mech. Eng. 365, 113028 (2020)

    MathSciNet  MATH  Google Scholar 

  15. Shukla, K., Jagtap, A.D., Karniadakis, G.E.: Parallel physics-informed neural networks via domain decomposition. J. Comput. Phys. 447, 110683 (2021)

    MathSciNet  MATH  Google Scholar 

  16. Glorot, X., Bengio, Y.: Understanding the difficulty of training deep feedforward neural networks. In: Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, pp. 249–256. JMLR Workshop and Conference Proceedings, (2010)

  17. Wang, S., Teng, Y., Perdikaris, P.: Understanding and mitigating gradient flow pathologies in physics-informed neural networks. SIAM J. Sci. Comput. 43(5), A3055–A3081 (2021)

    MathSciNet  MATH  Google Scholar 

  18. Li, J., Chen, J., Li, B.: Gradient-optimized physics-informed neural networks (gopinns): a deep learning method for solving the complex modified kdv equation. Nonlinear Dyn. 107, 781–792 (2022)

    Google Scholar 

  19. Wang, S., Xinling, Yu., Perdikaris, P.: When and why pinns fail to train: a neural tangent kernel perspective. J. Comput. Phys. 449, 110768 (2022)

    MathSciNet  MATH  Google Scholar 

  20. Yu, J., Lu, L., Meng, X., Karniadakis, G.E.: Gradient-enhanced physics-informed neural networks for forward and inverse pde problems. Comput. Methods Appl. Mech. Eng. 393, 114823 (2022)

    MathSciNet  MATH  Google Scholar 

  21. Li, J., Chen, Y.: Solving second-order nonlinear evolution partial differential equations using deep learning. Commun. Theor. Phys. 72(10), 105005 (2020)

    MathSciNet  Google Scholar 

  22. Li, J., Chen, Y.: A deep learning method for solving third-order nonlinear evolution equations. Commun. Theor. Phys. 72(11), 115003 (2020)

    MathSciNet  Google Scholar 

  23. Juncai, P., Li, J., Chen, Y.: Solving localized wave solutions of the derivative nonlinear schrödinger equation using an improved pinn method. Nonlinear Dyn. 105, 1723–1739 (2021)

    Google Scholar 

  24. Zhang, R.-F., Bilige, S.: Bilinear neural network method to obtain the exact analytical solutions of nonlinear partial differential equations and its application to p-gbkp equation. Nonlinear Dyn. 95, 3041–3048 (2019)

    MATH  Google Scholar 

  25. Zhang, R.-F., Li, M.-C.: Bilinear residual network method for solving the exactly explicit solutions of nonlinear evolution equations. Nonlinear Dyn. 108(1), 521–531 (2022)

    Google Scholar 

  26. Zhang, R.-F., Li, M.-C., Gan, J.-Y., Li, Q., Lan, Z.-Z.: Novel trial functions and rogue waves of generalized breaking soliton equation via bilinear neural network method. Chaos Solit. Fract. 154, 111692 (2022)

    MathSciNet  MATH  Google Scholar 

  27. Zhang, R.-F., Li, M.-C., Albishari, M., Zheng, F.-C., Lan, Z.-Z.: Generalized lump solutions, classical lump solutions and rogue waves of the (2+ 1)-dimensional caudrey-dodd-gibbon-kotera-sawada-like equation. Appl. Math. Comput. 403, 126201 (2021)

    MathSciNet  MATH  Google Scholar 

  28. Zhang, R.-F., Li, M.-C., Cherraf, A., Vadyala, S.R.: The interference wave and the bright and dark soliton for two integro-differential equation by using bnnm. Nonlinear Dyn. 111(9), 8637–8646 (2023)

    Google Scholar 

  29. Zhang, R.-F., Li, M.-C., Yin, H.-M.: Rogue wave solutions and the bright and dark solitons of the (3+ 1)-dimensional jimbo-miwa equation. Nonlinear Dyn. 103, 1071–1079 (2021)

    Google Scholar 

  30. Zhang, R.-F., Bilige, S., Liu, J.-G., Li, M.: Bright-dark solitons and interaction phenomenon for p-gbkp equation by using bilinear neural network method. Phys. Scrip. 96(2), 025224 (2020)

    Google Scholar 

  31. Ankiewicz, A., Akhmediev, N.: Rogue wave-type solutions of the mkdv equation and their relation to known nlse rogue wave solutions. Nonlinear Dyn. 91, 1931–1938 (2018)

    Google Scholar 

  32. El-Tantawy, S.A., Alharbey, R.A., Salas, A.H.: Novel approximate analytical and numerical cylindrical rogue wave and breathers solutions: an application to electronegative plasma. Chaos Solit. Fract. 155, 111776 (2022)

    MathSciNet  MATH  Google Scholar 

  33. Li, J., Li, B.: Mix-training physics-informed neural networks for the rogue waves of nonlinear schrödinger equation. Chaos Solit. Fract. 164, 112712 (2022)

    Google Scholar 

  34. Wazwaz, A.-M.: New (3+ 1)-dimensional painlevé integrable fifth-order equation with third-order temporal dispersion. Nonlinear Dyn. 106(1), 891–897 (2021)

    Google Scholar 

  35. Wazwaz, A.-M.: Painlevé integrability and lump solutions for two extended (3+ 1)-and (2+ 1)-dimensional kadomtsev-petviashvili equations. Nonlinear Dyn. 111(4), 3623–3632 (2023)

    Google Scholar 

  36. Wazwaz, A.-M., Albalawi, W., El-Tantawy, S.A.: Optical envelope soliton solutions for coupled nonlinear schrödinger equations applicable to high birefringence fibers. Optik 255, 168673 (2022)

    Google Scholar 

  37. Kaur, L., Wazwaz, A.-M.: Optical soliton solutions of variable coefficient biswas-milovic (bm) model comprising kerr law and damping effect. Optik 266, 169617 (2022)

    Google Scholar 

  38. Boussinesq, J.: Théorie de l’intumescence liquide appelée onde solitaire ou de translation se propageant dans un canal rectangulaire. CR Acad. Sci. Paris 72(755–759), 1871 (1871)

    MATH  Google Scholar 

  39. Boussinesq, J.: Théorie des ondes et des remous qui se propagent le long d’un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond. Journal de mathématiques pures et appliquées 17, 55–108 (1872)

    MathSciNet  MATH  Google Scholar 

  40. Ursell, F.: The long-wave paradox in the theory of gravity waves. Math. Proc. Camb. Philos. Soc. 49, 685–694 (1953)

    MathSciNet  MATH  Google Scholar 

  41. Whitham, G.B.: Linear and Nonlinear Waves, p. 651. Wiley-Interscience, New York (1974)

    MATH  Google Scholar 

  42. Ablowitz, M. J., Ablowitz, M.A., Clarkson, P.A.: Solitons, Nonlinear Evolution Equations and Inverse Scattering, vol. 149. Cambridge University Press (1991)

  43. Ablowitz, M.J., Haberman, R.: Resonantly coupled nonlinear evolution equations. J. Math. Phys. 16(11), 2301–2305 (1975)

    MathSciNet  Google Scholar 

  44. Ablowitz, M.J., Segur, H.: Solitons and the Inverse Scattering Transform. SIAM, (1981)

  45. Toda, M.: Studies of a non-linear lattice. Phys. Rep. 18(1), 1–123 (1975)

    MathSciNet  Google Scholar 

  46. Zabusky, N.J.: A synergetic approach to problems of nonlinear dispersive wave propagation and interaction. In: Nonlinear Partial Differential Equations, pp. 223–258. Elsevier (1967)

  47. Zakharov, V.E.: On stochastization of one-dimensional chains of nonlinear oscillations. Sov. Phys. JETP 38, 108–110 (1974)

  48. Infeld, E., Rowlands, G.: Nonlinear Waves, Solitons and Chaos. Cambridge University Press (2000)

  49. Scott, A.C.: The application of bäcklund transforms to physical problems. In: Bäcklund Transformations, the Inverse Scattering Method, Solitons, and Their Applications: NSF Research Workshop on Contact Transformations, pp. 80–105. Springer (2006)

  50. Wazwaz, A.-M.: Solitons and singular solitons for a variety of Boussinesq-like equations. Ocean Eng. 53, 1–5 (2012)

    Google Scholar 

  51. Wazwaz, A.-M.: Gaussian solitary waves for the logarithmic Boussinesq equation and the logarithmic regularized Boussinesq equation. Ocean Eng. 94, 111–115 (2015)

    Google Scholar 

  52. Gao, J., Zhou, X., Zang, J., Chen, Q., Zhou, L.: Influence of offshore fringing reefs on infragravity period oscillations within a harbor. Ocean Eng. 158, 286–298 (2018)

    Google Scholar 

  53. Yan, S., Liu, Z.Y.: Numerical model of sloshing in rectangular tank based on boussinesq-type equations. Ocean Eng. 121, 166–173 (2016)

    Google Scholar 

  54. Chen, M., Niu, R., Zheng, W.: Adaptive multi-scale neural network with resnet blocks for solving partial differential equations. Nonlinear Dyn. 111, 1–20 (2022)

    Google Scholar 

  55. Sana, D.: Approximating the Wave Equation Via Physics Informed Neural Networks: Various Forward and Inverse Problems (2022)

  56. Fang, Y., Gang-Zhou, W., Wang, Y.-Y., Dai, C.-Q.: Data-driven femtosecond optical soliton excitations and parameters discovery of the high-order nlse using the pinn. Nonlinear Dynamics 105(1), 603–616 (2021)

    Google Scholar 

Download references

Funding

This work was supported by the Scientific Research Fund of Zhejiang Provincial Education Department under Grant No. Y202148297 and the National Natural Science Foundation of China under Grant No. 11975008.

Author information

Authors and Affiliations

  1. College of Engineering, Lishui University, Lishui, 323000, China

    Ruozhou Gao, Wei Hu, Jinxi Fei & Hongyu Wu

Authors
  1. Ruozhou Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wei Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jinxi Fei
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hongyu Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wei Hu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

This research does not involve human participants and/or animals.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gao, R., Hu, W., Fei, J. et al. Boussinesq equation solved by the physics-informed neural networks. Nonlinear Dyn 111, 15279–15291 (2023). https://doi.org/10.1007/s11071-023-08614-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-023-08614-4

Keywords

Search

Navigation