Kuznetsov–Ma rogue wave clusters of the nonlinear Schrödinger equation

Abstract

In this work, we investigate rogue wave (RW) clusters of different shapes, composed of Kuznetsov–Ma solitons (KMSs) from the nonlinear Schrödinger equation (NLSE) with Kerr nonlinearity. We present three classes of exact higher-order solutions on uniform background that are calculated using the Darboux transformation (DT) scheme with precisely chosen parameters. The first solution class is characterized by strong intensity narrow peaks that are periodic along the evolution x-axis, when the eigenvalues in DT scheme generate KMSs with commensurate frequencies. The second solution class exhibits a form of elliptical rogue wave clusters; it is derived from the first solution class when the first m evolution shifts in the nth-order DT scheme are nonzero and equal. We show that the high-intensity peaks built on KMSs of order $n-2m$ periodically appear along the x-axis. This structure, considered as the central rogue wave, is enclosed by m ellipses consisting of a certain number of the first-order KMSs determined by the ellipse index and the solution order. The third class of KMS clusters is obtained when purely imaginary DT eigenvalues tend to some preset offset value higher than one, while keeping the x-shifts unchanged. We show that the central rogue wave at (0, 0) always retains its $n-2m$ order. The n tails composed of the first-order KMSs are formed above and below the central maximum. When n is even, more complicated patterns are generated, with m and $m-1$ loops above and below the central RW, respectively. Finally, we compute an additional solution class on a wavy background, defined by the Jacobi elliptic dnoidal function, which displays specific intensity patterns that are consistent with the background wavy perturbation. This work demonstrates an incredible power of the DT scheme in creating new solutions of the NLSE and a tremendous richness in form and function of those solutions.

1 Introduction

In this paper, we present and analyze new solutions of the well-known partial differential equation, the nonlinear Schrödinger equation (NLSE) with Kerr nonlinearity. This equation is generally used for describing various nonlinear phenomena in nature [1,2,3]:

$$\begin{aligned} i{\psi _x} + \frac{1}{2}{\psi _{tt}} + {\left| \psi \right| ^2}\psi = 0, \end{aligned}$$

(1.1)

where $\psi \equiv \psi \left( x,t\right)$ is the slowly varying envelope of the physical field under study and the nature of independent variables x and t depends on the nature of the problem considered. Here, we adopt the standard notation used in optical fibers, where t denotes the transverse spatial variable and x is the retarded time in the moving frame of reference. Another “standard” notation is used in the propagation problems of laser beams, in which x is the propagation distance, usually denoted by z, and t is the transverse spatial variable, denoted by x. We confine our attention to the localized optical waves generated on a constant intensity background that can be considered as high-order rogue waves.

Under certain approximations, NLSE can be used to describe the propagation of optical pulses in nonlinear dispersive media, i.e., in optical fibers and waveguides [4,5,6,7]. The usefulness of NLSE in photonics stems from the fact that it is formally equivalent to the paraxial wave equation in nonlinear optics. It is also used in plasma physics for describing the coupled dynamics of the electric field amplitude and the low-frequency density fluctuations of ions [8]. This equation also describes the interaction of the intra-molecular vibrations forming Davydov solitons with the acoustic disturbances in a molecular chain [8]. NLSE governs nonlinear optical modes in dilute Bose–Einstein condensates (BECs) [9], where it is known as the Gross–Pitaevskii equation. It also determines the evolution of an envelope that modulates long-crested surface gravity waves in deep water [10,11,12].

In recent times, an extended family of nonlinear Schrödinger equations (ENLSEs) has been proposed and investigated [13, 14]. These equations consistently include any number of higher-order dispersion terms with the corresponding additional nonlinear terms that are conveniently grouped together in certain named equations of the hierarchy of NLSEs. The effort to derive and solve higher-order equations in the NLSE hierarchy comes from the need to understand and describe the propagation of ultrashort pulses through optical fibers [15, 16]. Most attention so far was focused on the Hirota equation [17, 18] (containing the third-order dispersion) and quintic equation (with dispersions up to the fifth-order) [19,20,21,22]. In general, the entire family of extended NLSE offers a subtlety of possible forms for an additional shaping of basic NLSE solutions.

Nevertheless, the basic NLSE mentioned above remains a subject of broad interest, despite its relatively simple form (having only a cubic nonlinear term). Primarily, this is because of its complete integrability in one dimension. It contains infinitely many solutions, depending on the integration procedure and the form of solutions. The integrability feature has initiated a number of experimental and theoretical studies in many branches of physics, where the cubic NLSE can model the dynamics of various systems. In addition, the same mathematical procedure used for deriving the cubic NLSE solutions can be easily generalized and applied to the entire hierarchy of NLSEs. This implies that the features of the basic NLSE solutions are similar to those of the more complicated ENLSE family. Thus, by finding and analyzing the simple NLSE solutions, one can predict and describe the properties of similar solution classes of the extended family.

There are many methods for solving various partial differential equations (PDEs) with applications in nonlinear dynamics [23,24,25,26] and even in medicine [27, 28]. The most basic is the inverse scattering method (ISM) [29], originating from the seminal work by Gardner, Greene, Kruskal, and Miura, in 1967 [30]. An extension of ISM, directly applicable to NLSE, was introduced by Zakharov and Shabat in 1972 [31] and later (1974) generalized by Ablowitz, Kaup, Newell, and Segur [32] to include other nonlinear PDEs into what is today known as the AKNS method. Other useful methods include the Bäcklund and Darboux transformations, based on the treatment of the Lax pair matrix operators [29]. Recently, the propagation of internal solitary waves in the ocean has been described by the solitary solutions of another PDE, called the generalized nonlinear Schrödinger equation, containing a third-order dispersion, in addition to the usual second-order [33].

Here, we are focused on the Darboux transformation (DT) technique [34], which is widely used to derive exact analytical solutions of both NLSE and ENLSEs [18, 34, 35]. Briefly, DT is based on the Lax pair eigenvalue problem and the resulting recursive relations, with the aim to calculate higher-order solutions starting from the trivial zeroth-order seed function that satisfies Eq. (1.1) (for more details, see Appendix). Different solution classes can be derived by selecting the DT order n, the zeroth seed, and a set of n complex eigenvalues, with arbitrary real shifts along the x- and t-axes. The major advantage of DT scheme is the straightforward algorithm for calculating infinitely many NLSE wave functions with incredible richness of solutions’ patterns. The minor drawback of DT technique is that only specific analytical solutions can be computed that do not include the general NLSE evolution from arbitrary initial conditions. Also, by increasing the DT order n, the DT procedure becomes computationally expensive.

We also mention that the DT technique has similarity to other techniques of PDE integration, such as He’s semi-inverse variational principle (HVP) [36]. In the HVP technique, the given PDE is transformed into ordinary differential equations (similar to the Lax pair in DT). Also, an ansatz is assumed, in parallel to the DT seed solution. The difference between HVP and DT schemes is the procedure for generating the final solution: In HVP, it is calculated using the variational formula and finding its stationary point, while in DT the algebraic recursive relations are employed (see Appendix).

The basic solutions of the cubic NLSE (and ENLSEs) that can be calculated using DT are the Akhmediev breathers (ABs) [37, 38] (localized in x, but periodic along t-axis) and the Kuznetsov–Ma solitons (KMSs) [31, 39,40,41] (localized in t, but periodic along x-axis). The Peregrine soliton (PS) (localized along both axes) can be considered as the limiting case of both ABs and KMSs when their corresponding periods go to infinity [42, 43]. All these basic solutions ride on a background and can be considered as the prototype first-order RWs.

These solutions may also be considered as the fingerprints of NLSE—it is experimentally shown that such structures spontaneously appear during the NLSE evolution, even from the white noise [44]. Furthermore, the first-order ABs, PS, and KMSs are the building blocks for generating higher-order solutions of the NLSE. Such solutions, characterized by a narrow peak of high intensity, are considered as the true rogue waves. The simplest example of a RW is the PS [45]. The research on RWs is currently a hot topic, since these giant nonlinear waves can appear in nonlinear optics [46, 47], deep ocean [12, 48], quantum optics [49, 50], and elsewhere. A recent paper proposed a new way for RW excitation [51], via the electromagnetically induced transparency (EIT) [52,53,54,55]. Significant effort has been expended to understand the nature and generating mechanisms of optical rogue waves [56, 57]. The root of their appearance is related to the modulation instability [56, 58]. A very recent paper succinctly summarizes the main characteristics of the RWs: They are nonlinear, deterministic, and physical in nature [59].

Our main objective in this paper is to present new analytical RW solutions of the cubic NLSE arising on the uniform background and indicate new intensity patterns in the nonlinear systems governed by the NLSE. To achieve this goal, we are using three different nonlinear superpositions of KMSs. The first class has the form of a periodic array of RW peaks along the evolution x-axis. It is calculated by applying the commensurate periods of KMSs in the DT scheme of order n. To calculate the second solution class, we introduce m nonzero DT shifts $(m<n)$ along x-axis, to achieve the transformation of vertical (along evolution axis) RWs into multi-elliptic RW clusters composed of KMSs (KM MERWCs). The third solution class is obtained by breaking the proportionality relation among the DT constituents’ frequencies, while retaining the evolution shifts. Imaginary parts of the eigenvalues are chosen to be slightly higher than 1 (i.e., to lie in close vicinity of 1), which could be approximately regarded as a degenerate DT problem. In this manner, we came up to cluster solutions characterized by a single high-order rogue wave in the center of the xt-plane, with n tails emanating before and after it, composed of the first-order (KMS1) solitons. We show that the parity of n determines whether the wave function contains the loops of the first-order KMSs around the (0, 0) point.

The results presented here represent an extension and closure of our recent work [60], in which elliptic rogue wave clusters were obtained from the ABs of NLSE (AB MERWCs). We thus add new and complementary solutions to the previously described rogue wave triplets [61], triangular cascades [62,63,64], and circular clusters [35, 65,66,67], but now based on the KMSs. The classification of multi-RW structures into different families was presented in a series of papers by Akhmediev’s group [67,68,69]. We believe that the contribution of the three new KMS clusters, which were not presented before, represents a necessary symmetric closure on the possible higher-order RW clusters that can be obtained by the DT scheme. We also show that these solutions can be computed numerically on the elliptic dn background. Finally, the same sets of DT eigenvalues and shifts can be employed to all equations in the extended NLSE hierarchy, to generalize KMS rogue wave clusters of more complex systems (not presented here).

The paper is organized as follows. In Sect. 2, we present the periodic array of RW peaks composed of higher-order KMSs. In Sect. 3, we display NLSE solutions in the form of multi-elliptic rogue wave clusters on a uniform background, built from KMSs. In Sect. 4, we analyze the third class of KMS clusters obtained when all imaginary parts of DT eigenvalues are higher than but close to 1. In Sect. 5, we exhibit the NLSE KMS cluster solutions on a nonuniform background, formed by the Jacobi elliptic dnoidal function. In Sect. 6, we summarize our results. A short introduction into the general DT scheme for NLSE is provided in Appendix.

2 Periodic arrays of RWs composed by KMSs

The expression that describes all first-order solutions, the AB, PS, and KMS on uniform background [37, 38], is given by:

$$\begin{aligned} \psi (t,x)=\biggl [\!1\!+\! \frac{2(1\!-\!2a)\cosh \lambda x\!+\!i\lambda \sinh \lambda x}{\sqrt{2a}\cos \omega t-\cosh \lambda x}\!\biggr ]\,e^{ ix}.\!\!\!\!\!\ \ \ \ \nonumber \\ \end{aligned}$$

(2.1)

Here, parameter a determines the type of solution: If $a<0.5$, one gets an AB that is periodic along the t-axis, with the period $L = \frac{\pi }{{\sqrt{1 - 2a} }}$. For $a=0.5$, one obtains a single peak at the coordinate center, known as the Peregrine soliton. In this paper, we consider in detail the case $a>0.5$, when Eq. (2.1) describes the Kuznetsov–Ma solitons. To analyze it further, we write the following expressions for the growth factor $\lambda$ and the transverse frequency $\omega$, present in (2.1):

$$\begin{aligned} \lambda = \sqrt{8a\left( 1-2a\right) }, \end{aligned}$$

(2.2)

$$\begin{aligned} \omega = 2\sqrt{1-2a}. \end{aligned}$$

(2.3)

Note that the parameter a is closely related to the imaginary part $\nu$ of $\lambda _{DT}$:

$$\begin{aligned} \nu = \sqrt{2a}. \end{aligned}$$

(2.4)

Therefore, we ignore the real parts of any DT eigenvalue $\lambda _{DT}$ (assuming them equal to zero throughout this paper) and concentrate only on the imaginary parts. When $a>0.5$, $\nu >1$ and both $\lambda$ and $\omega$ become imaginary numbers, so $\cosh \lambda x$ and $\sinh \lambda x$ in (2.1) turn into $\cos$ and $\sin$ functions, while $\cos \omega t$ transforms into hyperbolic cosine. This means that KMSs are periodic along the evolution x-axis and localized along the transverse t-axis. The period $T_x$ and frequency $\omega _x$ along x-axis are, respectively:

$$\begin{aligned} {T_x} = \frac{\pi }{{\nu \sqrt{{\nu ^2} - 1} }} \end{aligned}$$

(2.5)

and

$$\begin{aligned} {\omega _x} = \frac{{2\pi }}{{{T_x}}} = 2\nu \sqrt{{\nu ^2} - 1}. \end{aligned}$$

(2.6)

Our idea is to build the periodic rogue waves from the higher-order KMSs, using the DT scheme. The DT equations for conducting such a task for NLSE were presented in detail elsewhere [57], and a short description is provided in Appendix. The DT order n is also the order of RW peaks along the x-axis. In this scheme, we have n first-order KMSs (each defined by an imaginary eigenvalue $\lambda _{j}=i\nu _j$ $\left( \nu \equiv \nu _1\right)$, with real vertical shifts $x_j$, and horizontal shifts $t_j$ preset to zero) that are building blocks for a final solution. To produce a vertical array of high-intensity peaks, with a complex pattern in their vicinity, we employ the idea of commensurate KMS frequencies:

$$\begin{aligned} \omega _{xj} = j\omega _{x}, \end{aligned}$$

(2.7)

where $\omega _{x}\equiv \omega _{x1}$ is the frequency of the first KMS in the DT scheme. This insures that all DT constituents will eventually collide at the same points along x-axis, thus producing periodic and strong intensity maxima. By combining last equations, one can easily obtain the DT eigenvalues needed to achieve the periodicity condition:

$$\begin{aligned} {\nu _j} = \sqrt{\frac{{1 + \sqrt{1 + 4{j^2}{\nu ^2}\left( {{\nu ^2} - 1} \right) } }}{2}}. \end{aligned}$$

(2.8)

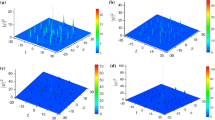
We present analytical results when $\nu =1.1$ for the second-order $\left( n=2\right)$ and third-order $\left( n=3\right)$ commensurate KMSs in Fig. 1a and b, respectively. Other eigenvalues in the DT scheme can be calculated using Eq. (2.8). One can clearly see the vertical periodic array of RWs having equal periods $T_x=6.24$ along x-axis in both figures, which is in agreement with Eq. (2.5). The intensity $I_{\text {max}}$ of each peak in the vertical array is even higher than in the case of higher-order Akhmediev breathers $\left( \nu <1\right)$. This can be simply explained by means of the peak-height formula (PHF) [70, 71]:

$$\begin{aligned} \left| \psi \left( {0,0} \right) \right| ^2 = \left( 1 + \sum \limits _{j = 1}^n {2{\nu _j}}\right) ^2. \end{aligned}$$

(2.9)

By this equation, one can easily calculate the maximum intensity of higher-order ABs or KMSs, under the condition that all DT eigenvalues nonlinearly collide at the same point, say (0, 0). When one builds higher-order ABs, all imaginary parts are less than one, while for the KMSs they are higher than 1. This is the reason why KMSs are characterized by higher peaks. For the KMS RW of order $n=2$, we obtained $I_{\text {max}}=33.06$, and for $n=3$ the value is $I_{\text {max}}=74.7$. This is in agreement with Eq. (2.8) and PHF for the starting value of $\nu =1.1$.

We next performed numerical integration of these solutions, to check the influence of modulation instability (MI) on the dynamical generation of higher-order KMSs. The results are presented in Fig. 1c and d for the second-order and third-order KMSs, respectively. In both figures, one can see that higher Fourier modes arise quickly after the iteration onset, due to MI. This leads to the disintegration of the periodic array of RWs, in favor of the irregular growth of lower intensity peaks elsewhere in the (x, t) plane—in contrast to the desired dynamic generation of higher-order ABs. Namely, the Fourier transform (FT) in our split-step beam propagation method assumes periodicity along the transverse axis, which is characteristic of ABs. This enables the matching of constituent AB periods to the box size and neat generation of RWs along the t-axis, as analyzed in our previous papers [18, 21, 70]. Since KMSs are periodic along the evolution axis, it is impossible to match the periods of KMSs to the horizontal box, which is the reason why MI destroys RWs soon after the integration starts.

Fig. 1

3D color plots of higher-order Kuznetsov–Ma solitons with commensurate frequency components on a uniform background. a The second-order DT solution with eigenvalues $\nu =\nu _1=1.1$ and $\nu _2$, calculated using Eq. (2.8). b The third-order DT solution with eigenvalues $\nu =\nu _1=1.1$, $\nu _2$, and $\nu _3$, calculated using Eq. (2.8). The modulation instability of higher-order KMSs is tested for (c) the second-order solution from figure (a) and for (d) the third-order solution from figure (b), by executing the second-order beam propagation method from the analytical DT wave function at some fixed time $x_0$ between the two peaks. The modulation instability appearing soon after the iteration onset destroys the intensity distribution and periodicity of higher-order KMS peaks

3 Multi-elliptic rogue wave clusters of Kuznetsov–Ma solitons

To generate KM MERWCs, we follow an analogous procedure to the one described in our previous paper for Akhmediev breathers [60]. The first condition is to keep commensurate frequencies of constituent first-order KMSs, as in the previous section (Eq. 2.7). The second requirement is to adjust the first m shifts along the evolution axis ($x_j$) to be nonzero and equal: $x_j \ne 0$ for $j \le m$, and $x_j=0$ when $m<j\le n$. All transverse shifts are $t_j=0$. Here, we use the same expression for calculating x-shifts from the AB MERWCs paper [60] (to keep close analogy with the Akhmediev breather clusters):

$$\begin{aligned} {x_j}= & {} \sum \limits _{l = 1}^\infty {{X_{jl}}{\omega ^{2\left( {l - 1} \right) }}} = {X_{j1}} + {X_{j2}}{\omega ^2} \nonumber \\{} & {} \quad + {X_{j3}}{\omega ^4} + {X_{j4}}{\omega ^6} + \cdots , \end{aligned}$$

(3.1)

in which $\omega$ denotes a number close to zero. Note that $\omega$ is a main DT frequency in the AB MERWCs case, but that is not the case for the KM MERWCs. The reader should not confuse $\omega \rightarrow 0$, which we retain for $x_j$ calculation, with $\omega _x$ of the KMSs (Eq. (2.6)).

In Fig. 2, we present KM MERWCs on uniform background, having one ellipse around the central peak. The frequency $\omega$ in the expansion (Eq. (3.1)) is set to $10^{-1}$, while $X_{j4}=10^6$. This way, one gets evolution shift $x_j$ in the order of 1. The imaginary part of the first eigenvalue is chosen as $\nu =1.1$, while other $\nu _j$ values are calculated using Eq. (2.8). We set $m=1$ and vary the value of n, to change the order of the central RW. For $n=4$, one gets seven KMSs of order one (KMS1), situated on an ellipse around the second-order KMS (Fig. 2a). When $n=5$, one obtains a third-order KMS, surrounded by 9 KMS1 distributed along a single ring (Fig. 2b).

The second example of KM MERWCs is shown in Fig. 3. Here, $m=2$ so the two rings are formed around each central peak. Since m is increased compared to Fig. 2, we need to increase the solution order n. For $n=6$, one obtains the second-order KMS at the center, with 11 and 7 KMS1 on the outer and inner ellipses, respectively (Fig. 3a). When $n=7$, an array of the third-order KMSs is formed, with 13 and 9 KMS1 on two ellipses around each central RW peak (Fig. 3b). As for the $m=1$ case, we left $\omega =10^{-1}$ and $X_{j4}=10^6$ unchanged. In both Figs. 2 and 3, one can easily observe the periodicity of the cluster along x-axis. The period $T_x$ is calculated from Eq. (2.5) and is not perturbed by evolution shifts, meaning that the numerical value remains $T_x=6.24$ in Fig. 2, since we did not change the $\nu$ value from Fig. 1. In Fig. 3, we set $\nu =1.02$, to increase the $T_x$ period according to equation (2.5). This was done to zoom in the three clusters in the selected numerical box, so the reader can clearly see the two rings around each RW at the center.

Fig. 2

3D color plots of KM MERWCs on the uniform background, having one ellipse ($m=1$) around each $n-2m$ order rogue wave. The clusters are formed periodically along the evolution x-axis. Shifts of the constituent DT components are obtained for $X_{j4}=10^6$. The orders of Darboux transformation and the high-intensity encircled peaks are, respectively: a $n=4$ with the second-order rogue wave, and b $n=5$ with the third-order rogue wave

Fig. 3

3D color plots of KM MERWCs on the uniform background, having two ellipses ($m=2$) around each $n-2m$ order rogue wave. The clusters are formed periodically along the evolution x-axis. Shifts of the constituent DT components are obtained for $X_{j4}=10^6$. The orders of Darboux transformation and the high-intensity encircled peaks are, respectively: a $n=6$ with the second-order rogue wave, and b $n=7$ with the third-order rogue wave

Our final conjecture is that the RW of $n-2m$ order (denoted hereafter as KMS$_{n-2m}$ or KMS $(n-2m)$ or RW$_{n-2m}$) is obtained at (0, 0), with m ellipses around the peak for $n \ge 2\,m+2$. The outer ellipse contains $2n-1$ KMS1, while each following ring toward the center has four KMS1 less. If the rings are indexed from 1 to m, going from outer to the inner one, the number of KMS1 on each ring is $c_i=2n-4i+3$. This is the same conclusion as for the AB MERWCs [60, 67, 68]. The two differences are the lower intensity of AB MERWCs as compared to the KM MERWC case (due to PHF) and the direction of periodicity (AB MERWC is periodic along the $t-$axis).

The explanation of KMS cluster’s appearance is similar to the AB case. If all $x_j$ shifts are zero, the nonlinear superposition of all n DT components will take place at equidistant points along the x-axis (including coordinate origin), producing the periodic array of RWs, as shown in Fig. 1a and b. However, if one sets x-shifts to be nonzero for the first $m \ge 1$ DT components, the intensity distribution will decrease and split over the xt-plane. The understanding of why KM MERWC appears in such a way could be theoretically possible if one applies the mathematical analysis of exact analytical DT solutions. It is well known that deriving very complex DT expression for big n is extremely hard work with relatively little theoretical insight, so it was not performed anywhere before. Thus, we will not conduct that analysis here either.

4 Third solution class of nearly degenerate eigenvalues

Here, we present the third class of KMS cluster solutions that do not display a multi-elliptic form. This class is characterized by long-tail structure distributions, with loops of KMS1 in certain cases. We were motivated to explore new KMS patterns in order to compare them with the AB solutions obtained under similar computational conditions. Namely, the first requirement for generating AB MERWCs was to provide the proportionality condition for higher-order DT components ($\omega _j=j\omega$), which lead to the simple equation for the imaginary part of $j^{\text {th}}$ eigenvalue $\nu _j = \sqrt{1 - \frac{1}{4}{j^2}{\omega ^2}}$, with $\omega \rightarrow 0$ [60]. For the KMS case, all $\nu _j$ must be greater than one, so we slightly modified the last equation to:

$$\begin{aligned} \nu _j = \nu _0 + \sqrt{1 - \frac{1}{4}{j^2}{\omega ^2}}, \end{aligned}$$

(4.1)

where $\nu _0$ denotes the offset of KMS eigenvalues. Consequently, all $\nu _j$ are close to the $1+\nu _0$ value (in analogy to the AB case, when $\nu _j \rightarrow 1$). The difference, however, is significant: In the AB case, one retains the commensurate frequencies and AB MERWCs are obtained, while for the KMS a new $\nu _j$ set destroys the proportionality of frequencies. In this section, we show the appearance of new KMS clusters under the condition of Eq. (4.1).

The algorithm for calculating long-tail KMS clusters is as follows: First, we set an offset $\nu _0$ and some small value of $\omega$. We choose values for n and m and calculate all x-shifts using Eq. (3.1). Next, we compute all eigenvalues in the DT scheme from Eq. (4.1) $\left( 1 \le j \le n\right)$. Finally, we apply the DT procedure, to numerically calculate wave function $\psi \left( x,t\right)$ at all grid points with an arbitrary precision.

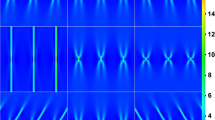
In Fig. 4, we show the intensity distribution for $n=4$, $\nu _0=0.1$, and $\omega =0.05$. When $m=0$, a fourth-order peak is obtained at the origin $\left( 0,0\right)$, with a peak intensity of 95.67 (in agreement with the PHF). The intensity distribution is shown in Fig. 4a. One can easily discern the central RW and four tails containing the KMS1 solutions spreading below and above the peak. In Fig. 4b, we show the intensity distribution for $m=1$. In this case, the second-order KMS peak is formed at the origin, with 28.97 maximal intensity. The one nonzero shift clearly moved apart constituent KMSs, producing a lower-order DT solution at the $\left( 0,0\right)$ point. Four KMS1 tails are also formed on both sides of the central RW, but are separated in groups of two in the lower half plane, for a given box. Further on, above the KMS2, a single loop consisting of KMS1 is formed, stretching out from $x=0$ to $x \approx 43$. Note that the range of pseudo-color scales on both figures are set to $\left( 0,10\right)$ interval, to emphasize the central peak and KMS1 along the tails. We also display the insets, to show the central RW and its vicinity in more detail.

Fig. 4

2D color plots of the long-tail KMS clusters on the uniform background, having one rogue wave of the $n-2m$ order formed at (0, 0) of the (x, t) plane. The starting offset for cluster formation is $\nu _0=0.1$. DT shifts are obtained for $X_{j4}=10^6$ and $\omega =0.05$. The DT order is $n=4$. The number of nonzero shifts m and the order of high-intensity central peaks are, respectively: a $m=0$ with the fourth-order rogue wave and b $m=1$ with the second-order rogue wave. The insets in both images show the enlarged central RW and its vicinity

We next show the $n=5$ case, for $m=0$ (Fig. 5a), $m=1$ (Fig. 5b), and $m=2$ (Fig. 5c). The values of $\nu _0=0.1$ and $\omega =0.05$ are left unchanged. When $m=0$, RW5 is formed at the origin (peak intensity 143.17, in agreement with the PHF). Since n is changed, five symmetric KMS1 tails are observed on both sides of the central peak. For $m=1$, one can see the RW3 at the (0, 0) point (max. intensity 57.26, see the inset) and also five tails, but the outer two are not participating in the building of the central structure. If we set $m=2$, no central RW emerges. Instead, a group of six KMS1 appears at the origin, while five tails are still preserved. The first clue of the solution structure can now be deduced from Figs. 4 and 5. The central peak at the origin, composed of the constituent KMS1 solitons, has the $n-2m$ order, as expected for the KM MERWCs. Next, the number of tails above and below the high-intensity peak is equal to the overall DT solution order n.

Fig. 5

2D color plots of the long-tail KMS clusters on the uniform background. The rogue wave of $n-2m$ order is conditionally formed at (0, 0) of the (x, t) plane. The starting offset for cluster formation is $\nu _0=0.1$. Shifts in the DT scheme are calculated for $X_{j4}=10^6$ and $\omega =0.05$. The DT order is $n=5$ and the number of nonzero shifts is m. a The fifth-order rogue wave for $m=0$. b The third-order rogue wave for $m=1$. c For $m=2$, the central structure resembles a single Akhmediev breather, since $n-2m=1$. The insets in all images show the enlarged regions centered around (0, 0)

In Fig. 6, we present three long-tail KMS clusters for the $n=6$ case, with $\nu _0=0.1$ and $\omega =0.05$. The RW6 is formed at the origin, with the peak intensity of 199.83 (in agreement with the PHF), when $m=0$ (Fig. 6a). Below and above the sharp RW peak (KMS of the sixth-order: KMS6), six symmetric tails can be observed. In Fig. 6b, the intensity distribution is presented for $m=1$. One can observe the RW4 at (0, 0) (max. intensity 94.95, see the inset) and six tails emerging from the origin, but the outer two are not contributing to the central RW4 structure. In the upper half plane, the tails are formed in three groups of two. Above the RW, one loop of KMS1 appears stretching out from $x=0$ to $x \approx 69$. This solution has a similar form to the $n=4$, $m=1$ case shown in Fig. 4b. However, the loop is not present when $n=5$. One may conclude that the loop is formed only for even values of n. This is supported by the next case of $n=6$ and $m=2$, when the second-order KMS is generated at the center, with two KMS1 loops above, one KMS1 loop below the RW, and six tails (Fig. 6c). The tails are divided into three groups of two, but only in the lower half of the plane.

Fig. 6

2D color plots of the long-tail KMS clusters on the uniform background. The rogue wave of $n-2m$ order is conditionally formed at (0, 0) of the (x, t) plane. The starting offset for cluster formation is $\nu _0=0.1$. Shifts in the DT scheme are calculated for $X_{j4}=10^6$ and $\omega =0.05$. The DT order is $n=6$, and the number of nonzero shifts is m. a The sixth-order rogue wave is formed for $m=0$. b The fourth-order rogue wave is formed for $m=1$. c The second-order rogue wave is formed for $m=2$. The insets on three images show the enlarged central RW and its vicinity

Finally, we analyze the third class of solutions for even higher DT order: $n=7$ ($\nu _0=0.1$ and $\omega =0.05$) and $n=8$ ($\nu _0=0.07$ and $\omega =0.05$). When $n=7$ and $m=2$, the third-order KMS at (0, 0), along with seven tails, is formed (Fig. 7a). No loop appears in this case. For $n=7$ and $m=3$, there is no RW at the center, only an AB-like cluster, since $n-2m=1$ (Fig. 7b). Again, seven tails are seen in both figures, but without KMS1 loops. The appearance of the cluster is different when $n=8$. For $m=2$, the KMS4 is found at the origin $(n-2m=4)$, with eight tails on both sides of the peak. In the upper plane, the tails are formed in four groups of two. Two KMS1 loops are obtained above the peak and one loop is formed below the peak (Fig. 7c). When $n=8$ and $m=3$, one sees KMS2 at the xt-plane center and eight tails. Three/two KMS1 loops are generated above/below the RW (Fig. 7d).

From Figs. 4, 5, 6, and 7, we conclude the following: Kuznetsov–Ma solitons of order $n-2m$ appear at the origin (0, 0) when the overall solution order is n and when the first m nonzero and equal shifts in the DT scheme are used. Above and below the central RW, n tails are formed, each consisting of KMS1 solitons. For even values of n, the m ($m-1$) KMS1 loops emerge above (below) the RW. We emphasize that if one changes the sign of x-shifts, the entire cluster simply flips about the $x=0$ line (results not shown).

Fig. 7

2D color plots of the long-tail KMS clusters on the uniform background, for higher values of DT order n. The high-intensity central rogue wave is formed when $n-2m>1$. DT shifts are obtained for $X_{j4}=10^6$ and $\omega =0.05$. Values of n, nonzero shifts m, and the starting offset $\nu _0$ are, respectively: a $n=7$, $m=2$, $\nu _0=0.1$ (third-order RW at the center), b $n=7$, $m=3$, $\nu _0=0.1$ (single AB at the center), c $n=8$, $m=2$, $\nu _0=0.07$ (fourth-order RW at the center), and d $n=8$, $m=3$, $\nu _0=0.07$ (second-order RW at the center). The insets in all images show the enlarged regions centered around (0, 0)

5 Long-tail KMS clusters on Jacobi elliptic dnoidal background

In this section, we show the long-tail KMS clusters computed on a wavy background, defined by the Jacobi elliptic dnoidal function $\text {dn}$. For this calculation, we use the modified DT scheme for the NLSE [72]. We start from the seed function $\psi _{\text {dn}}(x,t)=\text {dn}(t,g)e^{i(1-g^2/2)x}$, where the elliptic modulus is denoted by g ($0< g < 1$) and the elliptic modulus squared is $m_{\text {dn}}=g^2$. Although the choice of shifts and eigenvalues is the same as in the previous section, the procedure for calculating wave function is different. Namely, the exact analytical values of $\psi$ can be obtained only when $t=0$ [72]. We therefore use the fourth-order Runge–Kutta algorithm to calculate $\psi (x,t \ne 0)$ values in the grid along the t-line for the fixed x from the initial values of $\psi (x,t=0)$.

In Fig. 8, we show the intensity distribution of the long-tail KMS cluster built on the dn background with $m_{dn}=0.4^2$. The order of DT solution is $n=6$, and the number of nonzero shifts is $m=2$. The computational parameters are: $\nu _0=0.1$, $\omega =0.05$, and $X_{j4}=10^6$. We report the formation of the second-order RW at the origin (clearly observable in the inset). Since n is even, we obtained two KMS1 loops above and one KMS1 loop below the central peak. The peak maximum is 28.61, but we set the maximum of pseudo-color scale to 10, to emphasize the fine vertical stripes representing the crests and troughs of the dnoidal background. Although the long-tail cluster is clearly visible, the tops of the two upper loops are blurred by the background wave.

Fig. 8

2D color plot of the long-tail KMS cluster on the Jacobi elliptic dnoidal background, with elliptic modulus squared $m_{dn}=0.4^2$. The starting offset is $\nu _0=0.1$, while DT shifts are obtained for $X_{j4}=10^6$ and $\omega =0.05$. The DT order value of $n=6$ and the number of nonzero shifts $m=2$ lead to generation of the second-order RW at $(x,t)=(0,0)$. The inset shows the enlarged central RW and its vicinity

6 Conclusion

In this paper, we presented the three classes of NLSE solutions built from Kuznetsov–Ma solitons in the DT scheme of order n. The first class is obtained for the commensurate frequencies of DT components, with all evolution shifts set to zero. These solutions have the form of vertically periodic arrays of RWs, composed of the nth-order KMSs. We discussed the difficulties in generating these solutions dynamically, since the higher Fourier modes arise quickly after the simulation onset, due to the modulation instability, and lead to the disintegration of the periodic array of rogue waves.

Next, we showed the multi-elliptic KMS clusters, also periodic along the x-axis, computed using the same set of eigenvalues, but with the first m evolution shifts set to be equal and nonzero. The KMS of order $n-2m$ (considered as the central rogue wave) is surrounded by m ellipses composed of KMS1 peaks. The number of KMS1 peaks on the outermost ellipse is $2n-1$. On each following ring, we counted four KMS1 peaks less.

The third solution class are the long-tail KMS clusters. They are computed for a set of n nearly degenerate eigenvalues that are all close to some predefined value greater than one. The first m shifts were equal and zero, as for the second solution class. The computation was conducted to emphasize the analogy to multi-elliptic clusters of Akhmediev breathers. The central part of the KMS cluster consists of the $n-2m$-order Kuznetsov–Ma soliton at the origin. Above and below this high-intensity narrow peak, the n tails composed of KMS1s are observed. For $m=0$, the tails are perfectly symmetric. If $m \ge 1$, the symmetry is partially broken down, especially for even values of n. Namely, in this case ($n=4$, $n=6$, $n=8$) one observes the loops consisting of the first-order KMSs around the peak. The numbers of loops above and below the RW are m and $m-1$, respectively. Depending on the particular values of even n and m, the tails can be grouped in n/2 groups by two, in the upper or lower half planes. Finally, these specific features are not observed for the odd n cases ($n=5$ and $n=7$).

We numerically built the long-tail KMS cluster on a periodic background, using the modified Darboux transformation scheme. The intensity of higher-order Kuznetsov–Ma solitons at the plane origin significantly surpasses the amplitude of elliptic AB waves. However, we are still able to spot the weak background oscillations, on which the KMS cluster is constructed.

The results presented in this paper represent an extension and conclusion of our previous work on the multi-elliptic RW clusters composed of Akhmediev breathers. A perfect agreement with all facets of the complex DT analysis is demonstrated, often after complicated calculations. Nevertheless, our opinion is that even such complex investigation of various wave clusters can be of further research interest—after many years of NLSE research, new and interesting solutions emerge, due to the rich variety of parameters and possibilities in the Darboux transformation scheme. The research potential is increased even more if one considers the cluster solutions for the infinite hierarchy of extended nonlinear Schrödinger equations. The material presented in this paper can be a starting point to understand in more detail the rogue wave features in more complex physical systems that are governed by the extended nonlinear Schrödinger equations (Hirota, quintic, etc.)

Appendix: The general Darboux transformation scheme

The NLSE solution of order N is a nonlinear superposition of N independent components, where each one is determined by the complex eigenvalue $\lambda _j$ ($1 \le j \le N$). The corresponding wave function is:

$$\begin{aligned} {\psi _n} = {\psi _{n - 1}} + \frac{{2\left( {\lambda _n^* - {\lambda _n}} \right) {s_{n,1}}r_{n,1}^*}}{{{{\left| {{r_{n,1}}} \right| }^2} + {{\left| {{s_{n,1}}} \right| }^2}}}. \end{aligned}$$

(A.1)

The functions $r_{n,1}$ and $s_{n,1}$ are given by the recursive relations involving $r_{n,p}(x,t)$ and $s_{n,p}(x,t)$:

$$\begin{aligned} {r_{n,p}}={} & {} [\left( {\lambda _{n - 1}^* - {\lambda _{n - 1}}} \right) s_{n - 1,1}^*{r_{n - 1,1}}{s_{n - 1,p + 1}}\nonumber \\{} & {} + \left( {{\lambda _{p + n - 1}} - {\lambda _{n - 1}}} \right) {\left| {{r_{n - 1,1}}} \right| ^2}{r_{n - 1,p + 1}}\nonumber \\{} & {} + \left( {{\lambda _{p + n - 1}} - \lambda _{n - 1}^*} \right) {\left| {{s_{n - 1,1}}} \right| ^2}{r_{n - 1,p + 1}}]\nonumber \\{} & {} /\left( {{{\left| {{r_{n - 1,1}}} \right| }^2} + {{\left| {{s_{n - 1,1}}} \right| }^2}} \right) , \nonumber \\ {s_{n,p}} ={} & {} [\left( {\lambda _{n - 1}^* - {\lambda _{n - 1}}} \right) {s_{n - 1,1}}r_{n - 1,1}^*{r_{n - 1,p + 1}} \\{} & {} + \left( {{\lambda _{p + n - 1}} - {\lambda _{n - 1}}} \right) {\left| {{s_{n - 1,1}}} \right| ^2}{s_{n - 1,p + 1}} \nonumber \\ {}{} & {} + \left( {{\lambda _{p + n - 1}} - \lambda _{n - 1}^*} \right) {\left| {{r_{n - 1,1}}} \right| ^2}{s_{n - 1,p + 1}}] \nonumber \\{} & {} /\left( {{{\left| {{r_{n - 1,1}}} \right| }^2} + {{\left| {{s_{n - 1,1}}} \right| }^2}} \right) .\nonumber \end{aligned}$$

(A.2)

Thus, all pairs $r_{n,p}$ and $s_{n,p}$ can be determined starting from $r_{1,j}$ and $s_{1,j}$. The functions $r_{1,j}(x,t)$ and $s_{1,j}(x,t)$, forming the Lax pair $R = \left( {\begin{array}{*{20}{c}} r \\ s \\ \end{array}} \right) \equiv \left( {\begin{array}{*{20}{c}} {{r_{1,j}}} \\ {{s_{1,j}}} \\ \end{array}} \right) ,$ are determined by the eigenvalue $\lambda \equiv \lambda _j$ and real shifts of the solution $\left( x_{j},t_{j}\right)$.

The Lax pair satisfies a system of linear differential equations

$$\begin{aligned} \frac{{\partial R}}{{\partial t}} = U \cdot R,\quad \frac{{\partial R}}{{\partial x}} = V \cdot R, \end{aligned}$$

(A.3)

where matrices U and V for the NLSE are defined as ($\psi \equiv \psi _0$):

$$\begin{aligned}{} & {} U = i\left[ {\begin{array}{*{20}{c}} \lambda &{}\quad {\psi {{(x,t)}^*}} \\ {\psi (x,t)} &{}\quad { - \lambda } \\ \end{array}} \right] ,\nonumber \\{} & {} V = \sum \limits _{k = 0}^2 {{\lambda ^k} \cdot i\left[ {\begin{array}{*{20}{c}} {{A_k}} &{}\quad {B_k^*} \\ {{B_k}} &{}\quad { - {A_k}} \\ \end{array}} \right] }. \end{aligned}$$

(A.4)

The coefficients $A_k$ and $B_k$ are given by:

$$\begin{aligned} \begin{aligned} {A_0} =&- \frac{1}{2}{\left| \psi \right| ^2}, \end{aligned} \end{aligned}$$

(A.5)

$$\begin{aligned} \begin{aligned} {B_0}&= \frac{i}{2}{\psi _t},\\ {A_1}&= 0,\\ {B_1}&= \psi ,\\ {A_2}&= 1,\\ {B_2}&= 0. \end{aligned} \end{aligned}$$

We next define the following terms:

$$\begin{aligned} \begin{aligned} {\kappa _j}&= 2\sqrt{1 + \lambda _j^2}\\ {A_j}&= \frac{1}{2}\arccos \frac{{{\kappa _j}}}{2} \\&\quad + \frac{{{\kappa _j}}}{2}\left[ {\left( {t - {t_j}} \right) + {\lambda _j}\left( {x - {x_j}} \right) } \right] - \frac{\pi }{4}\\ {B_j}&= - \frac{1}{2}\arccos \frac{{{\kappa _j}}}{2} \\&\quad +\frac{{{\kappa _j}}}{2}\left[ {\left( {t - {t_j}} \right) + {\lambda _j}\left( {x - {x_j}} \right) } \right] - \frac{\pi }{4}. \end{aligned} \end{aligned}$$

(A.6)

From Eqs. (A.3)–(A.6), one can calculate $r_{1,j}$ and $s_{1,j}$:

$$\begin{aligned} \begin{aligned} {r_{1,j}}&= 2i{e^{ - ix/2}}\sin {A_j}\\ {s_{1,j}}&= 2{e^{ix/2}}\cos {B_j}. \end{aligned} \end{aligned}$$

(A.7)

To emphasize again, $r_{n,1}$ and $s_{n,1}$ are calculated from $r_{1,j}$ and $r_{1,j}$, by applying Eq. (A.2) multiple times. Finally, the nth-order DT solution $\psi _n$ is then calculated from $\psi _{n-1},...,\psi _0$ using Eq. (A.1).