1 Introduction

Metamaterials are man-made materials exhibiting remarkable and unique physical properties which are not present in natural materials, but emerge as result of a suitable theoretical–experimental design [1]. These peculiarities contribute to create an extremely fascinating research field. The smart capabilities of metamaterials can be achieved by their designable micro-geometry and/or by their composition [2] and their potential applications range from wave impact mitigation [3, 4] to sound and vibrations control [5,6,7,8,9,10,11]. At a very general conceptual level, it can be said that the study of wave propagation in periodic lattices, with the inherent dispersive properties, constitutes the theoretical framework which allows to give birth to the idea of metamaterial. More precisely, the exotic features, such as negative refraction [12, 13] and tunnelling effect [14,15,16], characterising these new materials are generally recognised as a consequence of the existence of frequency ranges in which wave propagation is inhibited, so-called bandgaps. The frequencies and width of these bandgaps are ruled by the mismatch between the mechanical properties of the constituent phases and the lattice parameters. Indeed, in phononic crystals the two main mechanisms responsible of the formation of bandgaps rely in the Bragg interference of waves scattered by periodic inhomogeneites and hybridization of local resonances due to the resonant modes of the constituents interacting with the embedding continuum [17,18,19,20,21,22,23]. Lately, locally resonant metamaterials get attention because they are able to generate bandgaps at wavelengths much longer than the lattice size [24,25,26,27], for this reason they are good candidates for efficient energy harvesters, that is materials where energy harvesting is obtained converting the localised vibrational kinetic energy into electrical energy [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43].

The mass–spring system is a well-known classical physical model which can explain the most of resonance phenomena although it has been applied mainly to 1D metamaterials [44,45,46,47,48,49,50,51,52]. Some attempts have been made to represent a 2D metamaterial into a mass–spring system, but nonlinear coupling terms between the oscillators are generally not considered: actually, the most of such research works focus on the linear behaviour [53,54,55,56,57,58].

To gain quantitative descriptions of these facts, in order to plan rational design tools, the analytical studies mostly focus on the spectral properties of the (linear) operator governing the motion equations of the system. Bandgaps dictate frequency ranges where vibrations propagation is forbidden, so enabling the localisation of vibrational kinetic energy in the form of oscillatory motion. Nevertheless, a clear explanation of the mechanism by which resonances lead to the occurrence of energy localisations seems to be a challenging issue which, in our opinion, can be addressed by considering the nonlinear coupling of a mass–spring system.

In the present work, we show, in a conservative 2D mass–spring metamaterial, the occurrence of energy localisation at short wavelengths. We note that the localisation arises only because oscillators interact (by springs) in resonance with one another and not because there is an external disturbance or host structure with which they resonate at long wavelengths [59, 60].

In the light of the above, understanding the mechanism leading to the energy transfer and its localisation, which is the main goal of the present paper, is a key problem in the study of metamaterials and it is connected with the search of elementary excitations preserving their characteristic under mutual interactions. This leads to the concept of nonlinear normal modes (NNM) introduced in [61]. In order to find NNMs, we take advantage from the fact that we deal with symmetrical system whose equations are of the kind

$$\begin{aligned} \ddot{x}_i+\frac{\partial V(x_1,...,x_n)}{\partial x_i}=0, \quad \quad i=1,2,...,n, \end{aligned}$$
(1)

where n is the number of degrees of freedom (in our case \(n=4\)) and the potential V is defined as

$$\begin{aligned} V(x_1,...,x_n)= & {} \sum _{m=1}^{\infty }(m+1)^{-1}\nonumber \\{} & {} \sum _{i=1}^n\sum _{j=i+1}^{n}a_{ij}^{(m)}(x_i-x_j)^{m+1}\nonumber \\{} & {} +\sum _{m=1}^{\infty }\sum _{i=1}^{\infty }(m+1)^{-1}b^{(m)}x_{i}^{m+1}, \end{aligned}$$
(2)

where \(a_{ij}^{(m)}\) and \(b^{(m)}\) represent elastic coefficients. This system admits similar NNMs as solutions and it possesses always solutions of the type \(x_1=\pm x_m\) with \(m=2,...,n\) which correspond to in-phase and anti-phase similar NNMs [61, 62]. These NNMs correspond to the stationary points of the system. By Lyapunov Theorem [63], we know that in a neighbourhood of stable equilibrium points of an n degrees of freedom (DOF) system there exist at least n NNMs. This theorem was extended by Weinsten [64] and Moser [65] to systems with internal resonances. However, NNMs technique is effective only for the analysis of stationary states and cannot be applied for highly non-stationary resonant processes in weakly nonlinear oscillators. For this reason, the concept of limiting phase trajectory (LPT) was first introduced by Manevitch [66] for 1D mass–spring system with two degrees of freedom (DOF) and it has been showed that it places a key role in understanding intense resonant energy exchange for highly non-stationary resonant processes [66].

More precisely, localised excitations originate from two transitions in the phase space: the instability of bifurcating NNMs and, then, the instability of LPTs. On the one hand, NNMs individuate the stationary points and the encircling curves close enough to them. On the other hand, the LPT individuates the outer curve of a set of curves encircling the stationary points which represents a highly non-stationary resonant process [67, 68]. The instability of the NNMs corresponds to a partial energy exchange between the oscillators and leads to weak energy localisation, whereas the instability of the LPT corresponds to the maximum energy transfer between the weakly interacting nonlinear oscillators and leads to strong energy localisation. When this transfer is broken the maximum possible energy is localised in one of the oscillators; in other words, the vibrations are concentrated mainly on one of the masses. As a result, strongly modulated non-stationary oscillations appear.

It is worth to highlight that the investigation of the NNMs and LPT evolution in the phase plane is applied only to 1D mass–spring system with two DOF in the Manevitch’s works, and as soon as the degrees of freedom become more than two, the continuous limit (strong nonlinearity) is considered instead of the discrete limit (weak nonlinearity). This is due to the mathematical difficulties in dealing with more than two DOF and, a fortiori, with a 2D or 3D mass–spring system [69, 70]. Manevitch’s approach in more than two DOF has some weak points:

  • The investigation is conducted at long wavelengths (wavelengths larger than the oscillators interspaces) leaving aside the possibility of probing the mechanism of energy exchange between the oscillators detected at smaller wavelengths (high frequencies).

  • The searching for stationary points by the equations of motion is not possible in case of non-canonical transformations or if dealing with many DOF.

Here, we propose a more general method in order to find energy localisation in a 2D mass–spring system with more than two DOF. We consider weak nonlinear equations of motion in the discrete regime for a unit cell with 4 DOF generating by periodicity a plane metamaterial, we name it the Z cell. To detect the occurrence of energy localisation, our strategy is to focus on the Hamiltonian by computing its Hessian and related eigenvalues in order to classify the stationary points in the whole 4D phase space. Once done that, we take into account every 2D subspace and we see if the nature of the stationary points changes in dependence of the physical parameters. In such subspaces, we follow the evolution of NNMs and LPTs following Manevitch’s method. It is worth to highlight that almost all critical points are saddle points rather than maxima or minima as the dimension of the space increases, this observation was first made in the physics of the p-spin spherical spin glasses (see, for instance, [71, 72] and literature therein). This condition suggests us to focus on a 2D subspace instead of the entire phase space. Furthermore, we note that energy localisation occurs in the 2D subspace and not in the whole phase space.

The weak nonlinearity approximation, and so the discrete framework, implies the existence of the slow timescale and the emergence of slowly modulated fast oscillations. For this reason, we employ the multiple timescale approximation [73] and introduce complex variables (see [74] and literature therein).

Eventually, we perform a numerical simulation adapting the Fermi–Pasta–Ulam–Tsingou (FPUT) code [75, 76] to the present case with periodic initial conditions. We add a fixed boundary surrounding the 2D metamaterial and we impose restriction on the modes amplitude. In this particular case, we observe a partial exchange and weak energy localisation between two modes (i.e. the FPUT recurrence) and the maximum energy exchange between the other two other modes (i.e. the FPUT super-recurrence). Ultimately, these last modes contribute to the kinetic energy and to the nonlinear coupling, but not to the linear coupling. Since the trend of the energy does not change as the linear coupling parameter changes, we can state that the energy localisation for the 2D metamaterial with fixed boundaries and with these particular conditions occurs for any generic value of the stiffnesses. On the contrary, in the general model without fixed boundary discussed above, energy localisation takes place only for a particular value of the stiffnesses.

The numerical experiments are implemented for a 2D metamaterial composed by 4 and 16 moving oscillators and we observe energy localisation in both the cases.

Fig. 1
figure 1

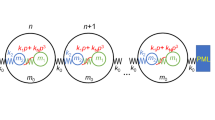
The metamaterial when all the nodes are in their rest positions. The coordinates \(\textbf{r}^{k}_{\nu \mu }=(x^{k}_{\nu \mu },y^{k}_{\nu \mu })\) are labelled by two subscripted indices: the \(\mu \)-index discretizes the y-coordinate and the \(\nu \)-index discretizes the x-axis, such that \((x^{k}_{\nu \mu },y^{k}_{\nu \mu })=(\nu a,\mu b)\), \(\nu ,\mu =1,...,N\). The constants a and b are the horizontal and vertical spacings between the two nearest nodes in their rest positions

Full size image

Moreover, at the best of our knowledge, it is an important open question to know if the FPUT recurrence occurs in a 2D system. We have found the conditions at which FPUT recurrence occurs in the 2D metamaterial and we shall prove that the energy of the 2D metamaterial of \(N\times N\) moving oscillators (with generic N) can be meant as the sum of the energies of N FPUT chains.

The paper is organised as follows. In Sect. 2, we present the model of the 2D metamaterial and write down the equations of motion considering small oscillations of the masses around their equilibrium positions. In Sect. 3, we introduce the Z cell as a model generating a plane metamaterial and we carry out the time scale approximation. In Sect. 4, we lead the phase analysis and show that energy localisations occur via NNMs and LPTs instabilities for a particular value of the stiffnesses ratio. In Sect. 5, we generalise the FPUT numerical experiment to the case of the 2D metamaterial and we show the occurrence of energy localisations related to the observation of FPUT recurrence and FPUT super-recurrence.

2 Dynamics of a plane metamaterial

Let \(N\in \mathbb {N}\) be given, we consider the periodic plane metamaterial in Fig. 1 with \(N\times N\) number of nodes. Here, we distinguish nodes of type 0 (green dots) from the nodes of type 1 (blue dots). Any 0-node is connected with the two nearest 1-nodes by elastic rods with stiffness \(k_0\) (dashed lines) and, in addition, any 1-node interacts by rods with stiffness \(k_1\) (solid lines) with other four 1-nodes. All the types of nodes carry unitary masses.

We denote by \(t\mapsto \textbf{r}^{k}_{\nu \mu }(t)\in \mathbb {R}^2\), with \(k=0,1\), the positions at time \(t\in \mathbb {R}^{+}\) of the 0-nodes and 1-nodes, respectively, and the \(\textbf{p}^{k}_{\nu \mu }(t)={\dot{\textbf{r}}}^{k}_{\nu \mu }(t)=\frac{d\textbf{r}^k_{\nu \mu }(t)}{dt}\) their associated momenta relative to the positions \((x_{\nu \mu }^k(t),y_{\nu \mu }^k(t))\), for \(\nu ,\mu =1,...N\) and \(k=0,1\). The \(\nu \)-index discretizes the x-axis, whereas the \(\mu \)-index discretizes the y-axis as explained in details later. Let us suppose that all the nodes oscillate along the y-axis only, such that

$$\begin{aligned} x^{k}_{\nu \mu }=\nu a, \quad y^{k}_{\nu \mu }= {\left\{ \begin{array}{ll} \mu b+\bar{w}_{\nu \mu },\quad \textrm{if}\quad k=0, \\ \mu b+\bar{v}_{\nu \mu }, \quad \,\textrm{if} \quad k=1, \end{array}\right. } \end{aligned}$$
(3)

where the variables \(\bar{w}_{\nu \mu }=\bar{w}_{\nu \mu }(t)\) and \(\bar{v}_{\nu \mu }=\bar{v}_{\nu \mu }(t)\) are the displacements from the rest positions along the y-axis of the 0-nodes and 1-nodes, respectively, whereas the constants a and b are the horizontal and vertical spacings between the nearest nodes at the rest position. In particular, the displacements \({\bar{w}_{\nu \mu }}\) and \(\bar{v}_{\nu \mu }\) are zero when the nodes are at the rest positions, i.e. \(\bar{w}_{\nu \mu }=0\) and \(\bar{v}_{\nu \mu }=0\). In this case, the coordinates of every node reduce to \((x^{k}_{\nu \mu },y^{k}_{\nu \mu })=(\nu a,\mu b)\) (Fig. 1). We highlight that the mass in \(\textbf{r}^1_{11}=(x^1_{11},y^1_{11})\) is at the rest position (a, b) and it does not lay on the origin (0, 0) (Fig. 1).

Taking into account that within the metamaterial the 0-nodes alternate their positions with the 1-nodes, the Hamiltonian can be written in the following way

$$\begin{aligned} \begin{aligned} \mathcal {H}=K+U, \end{aligned} \end{aligned}$$
(4)

where K and U are the kinetic energy and the potential energy, respectively, and they are given by

(5)
(6)

where \(\delta _{\ell ,k}\) denotes the Kronecker delta. Moreover, we put to zero the potential energies \(U_0\) and \(U_1\) in any case they would contain self-interaction terms, that is the outer nodes placed at the boundaries are not fixed and some contributions to the potential should be vanished with the following criteria:

  • when \(\nu =N\), for every \(\mu =1,...,N\),

    $$\begin{aligned} \begin{aligned}&U_0\left( \textbf{r}^{1}_{N+1\mu }-\textbf{r}^0_{N\mu }\right) =0,\\&U_1\left( \textbf{r}^{1}_{N+1\mu +1}-\textbf{r}^1_{N\mu }\right) +U_1\left( \textbf{r}^{1}_{N+1\mu -1}-\textbf{r}^1_{N\mu }\right) =0, \end{aligned} \end{aligned}$$
    (7a)

  • when \(\nu =1\), for every \(\mu =1,...,N\)

    $$\begin{aligned} U_0\left( \textbf{r}^{1}_{0\mu }-\textbf{r}^0_{1\mu }\right) =0, \end{aligned}$$
    (7b)

  • when \(\mu =N\), for every \(\nu =1,...,N\),

    $$\begin{aligned} U_1\left( \textbf{r}^{1}_{\nu +1N+1}-\textbf{r}^1_{\nu N}\right) =0, \end{aligned}$$
    (7c)

  • when \(\mu =1\), for every \(\nu =1,..,N\)

    $$\begin{aligned} U_1\left( \textbf{r}^{1}_{\nu +10}-\textbf{r}^1_{\nu 1}\right) =0. \end{aligned}$$
    (7d)

We write the interaction potential between a 0-node with coordinates \(\textbf{r}^{0}_{\nu \mu }\) and the two nearest nodes 1 with coordinates \(\textbf{r}^{1}_{\nu -1\mu }\) and \(\textbf{r}^{1}_{\nu +1\mu }\), is

$$\begin{aligned} U_0= & {} k_0\left[ \left( \sqrt{a^2+(\bar{v}_{\nu -1\mu }-\bar{w}_{\nu \mu })^2}-a\right) ^2\right. \nonumber \\{} & {} \left. +\left( \sqrt{a^2+(\bar{v}_{\nu +1\mu }-\bar{w}_{\nu \mu })^2}-a\right) ^2\right] , \end{aligned}$$
(8)

and the interaction potential between a node 1 with coordinates \(\textbf{r}^{1}_{\nu \mu }\) and the other two forwards nearest 1-node with coordinates \(\textbf{r}^{1}_{\nu +1\mu -1}\), \(\textbf{r}^{1}_{\nu +1\mu +1}\) is

$$\begin{aligned} U_1= & {} k_1\left[ \left( \sqrt{a^2+(b+\bar{v}_{\nu +1\mu +1}-\bar{v}_{\nu \mu })^2}-\ell \right) ^2\right. \nonumber \\{} & {} \left. +\left( \sqrt{a^2+(b+\bar{v}_{\nu \mu }-\bar{v}_{\nu +1\mu -1})^2}-\ell \right) ^2\right] , \end{aligned}$$
(9)

where \(\ell =\sqrt{a^2+b^2}\).

Considering small oscillations \(\bar{w}_{\nu \mu },\bar{v}_{\nu \mu }=O(\delta ^2)\)

$$\begin{aligned} \bar{v}_{\nu \mu }:=\delta ^2v_{\nu \mu } \quad \quad \bar{w}_{\nu \mu }:=\delta ^2w_{\nu \mu }, \end{aligned}$$
(10)

and using the Taylor expansion, we get the perturbed potentials

$$\begin{aligned} U_0&= \frac{k_0}{4a^2}\delta ^8\left[ \left( v_{\nu -1\mu }-w_{\nu \mu }\right) ^4 +\left( v_{\nu +1\mu }-w_{\nu \mu }\right) ^4\right] , \end{aligned}$$
(11)
$$\begin{aligned} U_1&=k_1\frac{b^2}{\ell ^2}\delta ^4\left[ \left( v_{\nu +1\mu +1}-v_{\nu \mu }\right) ^2+\left( v_{\nu \mu }-v_{\nu +1\mu -1}\right) ^2\right] \nonumber \\&\quad -k_1b_1\delta ^6\left[ \left( v_{\nu +1\mu +1}-v_{\nu \mu }\right) ^3+\left( v_{\nu \mu }-v_{\nu +1\mu -1}\right) ^3\right] \nonumber \\&\quad +\frac{k_1}{4}b_2\delta ^8\left[ \left( v_{\nu +1\mu +1}-v_{\nu \mu }\right) ^4+\left( v_{\nu \mu }-v_{\nu +1\mu -1}\right) ^4\right] , \end{aligned}$$
(12)

where

$$\begin{aligned} b_1= & {} \frac{b}{\ell ^2}\left( \frac{b^2}{\ell ^2}-1\right) ,\nonumber \\ b_2= & {} \frac{1}{\ell ^2}\left( \frac{b^2}{\ell ^2}-1\right) \left( 5\frac{b^2}{\ell ^2}-1\right) . \end{aligned}$$
(13)

We compute the equations of motion from the Hamiltonian (4) with the potentials (11) and (12) after scaling time

$$\begin{aligned} t=\frac{\tau }{\sqrt{k_0}}, \quad \quad \beta =\frac{k_1}{k_0}, \end{aligned}$$
(14)

and the characteristic scale L such that the scaled solutions \(w\rightarrow \frac{w}{L}\) and \(v\rightarrow \frac{v}{L}\) are dimensionless.

For any fixed \(\nu \) and \(\mu \), the perturbed equations of motion are

$$\begin{aligned} \displaystyle \ddot{{w}}_{\nu \mu }=-\frac{\partial \mathcal {H}}{\partial w_{\nu \mu }},\quad \quad \displaystyle \ddot{{v}}_{\nu \mu }=-\frac{\partial \mathcal {H}}{\partial v_{\nu \mu }}, \end{aligned}$$
(15)

that is

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \ddot{{w}}_{\nu \mu }&{}=\displaystyle \frac{L^2}{a^2}\delta ^4\sum \left[ (v_{\nu -1\mu }-w_{\nu \mu })^3\right. \\ &{}\left. \quad +(v_{\nu +1\mu }-w_{\nu \mu })^3\right] \\ &{}\left( \delta _{\nu ,2n-1}\delta _{\mu ,2m}+\delta _{\nu ,2n}\delta _{\mu ,2m-1}\right) ,\\ \displaystyle \ddot{{v}}_{\nu \mu }&{}=\displaystyle \frac{L^2}{a^2}\delta ^4\sum \left[ (w_{\nu +1\mu }-v_{\nu \mu })^3\right. \\ &{}\left. \quad +(w_{\nu -1\mu }-v_{\nu \mu })^3\right] \\ &{}\left( \delta _{\nu ,2n-1}\delta _{\mu ,2m}+\delta _{\nu ,2n}\delta _{\mu ,2m-1}\right) \\ &{}- \sum \displaystyle \Biggl \{\beta L^2b_2\delta ^4\left[ (v_{\nu \mu }-v_{\nu +1\mu +1})^3\right. \\ &{}\left. +(v_{\nu \mu }-v_{\nu +1\mu -1})^3+(v_{\nu \mu }-v_{\nu -1\mu -1})^3\right. \\ &{}\left. +(v_{\nu \mu }-v_{\nu -1\mu +1})^3\right] \Biggr . \\ &{}\displaystyle \Biggl .+3\beta Lb_1\delta ^{2}\left[ (v_{\nu \mu }-v_{\nu +1\mu +1})^2\right. \\ &{}\left. \quad -(v_{\nu \mu }-v_{\nu +1\mu -1})^2\right. \\ &{}\left. -(v_{\nu \mu }-v_{\nu -1\mu -1})^2+(v_{\nu \mu }-v_{\nu -1\mu +1})^2\right] \Biggr . \\ &{}\displaystyle \Biggl .+2\beta \frac{b^2}{\ell ^2}\left( 4v_{\nu \mu }-v_{\nu -1\mu -1}\right. \\ &{}\left. -v_{\nu -1\mu +1}-v_{\nu +1\mu +1}-v_{\nu +1\mu -1}\right) \Biggr \} \\ &{}\left( \delta _{\nu ,2n-1}\delta _{\mu ,2m-1}+\delta _{\nu ,2n}\delta _{\mu ,2m}\right) , \\ \end{array}\right. } \end{aligned}$$
(16)

where \(\sum =\sum _{m,n=0}^{N}\) and we neglect all the terms of the order \(O(\delta ^6)\) and higher. The indices \(\nu \) and \(\mu \) for the displacements w are different from those of the displacements v, but we use the same indices just to not overload the formalism. Note that one has to keep in mind that some terms in Eq.16 are zero when the equations describe the dynamics of nodes at the boundaries (the equations of motion 16 do not have self-interaction terms).

Fig. 2
figure 2

The Z cell in the rest configuration

Full size image

3 Z Cell and multiscale approximation

In the following, we focus our analysis to the elementary cell, generating by periodicity the plane metamaterial, which will be called the Z cell hereinafter. The reference frame is the same pictured in Fig. 1. More in details, when every node is in its rest position, one of the 1-node has position vector \(\textbf{r}^{1}_{11}=(a,b)\), the other 1-node has position vector \(\textbf{r}^{1}_{22}=(2a,2b)\), whereas the 0-nodes are in the positions pointed out by the vectors \(\textbf{r}^{0}_{12}=(a,2b)\) and \(\textbf{r}^{0}_{21}=(2a,b)\). This rest configuration is outlined in Fig. 2, where the coordinates \((x^{k}_{\nu \mu },y^{k}_{\nu \mu })=(\nu a,\mu b)\) are specified, for \(\nu ,\mu =1,2\) and \(k=0,1\), and only the position vector \(\textbf{r}^{1}_{11}\) is showed to not overload the figure, but to figure out the reference frame in an easy way. The two 0-nodes have displacements \(w_{12}\) and \(w_{21}\) and the two 1-nodes have displacements \(v_{11}\) and \(v_{22}\). Hereinafter, we drop out the second index to simplify the notation and we define

$$\begin{aligned}{} & {} v_{1}{:}{=}v_{11}, \quad \quad v_{2}:=v_{22}, \end{aligned}$$
(17a)
$$\begin{aligned}{} & {} w_{1}{:}{=}w_{21}, \quad \quad w_{2}:=w_{12}. \end{aligned}$$
(17b)

To the aim of detecting slow and fast dynamical regimes, we introduce the following general scalings

$$\begin{aligned} \tilde{\beta }=2\varepsilon ^{-n}\beta , \quad \tilde{L}=\delta ^2\varepsilon ^{-\frac{m}{2}}L, \quad \quad n,m\in \mathbb {N}. \end{aligned}$$
(18)

The system of ODEs for the Z cell is

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{d^2{w}_{1}}{d\tau ^2}=&{}\displaystyle \frac{\tilde{L}^2}{a^2}\epsilon ^{m}(v_{1}-w_{1})^3,\\ \displaystyle \frac{d^2{w}_{2}}{d\tau ^2}=&{}\displaystyle \frac{\tilde{L}^2}{a^2}\epsilon ^{m}(v_{2}-w_{2})^3,\\ \displaystyle \frac{d^2{v}_{1}}{d\tau ^2}=&{}\displaystyle -\epsilon ^n\tilde{\beta }\frac{b^2}{\ell ^2}(v_{1}-v_{2})\\ &{}-\frac{3}{2}\epsilon ^{n+\frac{m}{2}}\tilde{\beta }\tilde{L}b_1(v_1-v_2)^2\\ &{}+\frac{\tilde{L}^2}{a^2}\epsilon ^{m}(w_{1}-v_{1})^3,\\ \displaystyle \frac{d^2{v}_{2}}{d\tau ^2}=&{}\displaystyle -\epsilon ^n\tilde{\beta }\frac{b^2}{\ell ^2}(v_{2}-v_{1})\\ &{}-\frac{3}{2}\epsilon ^{n+\frac{m}{2}}\tilde{\beta }\tilde{L}b_1(v_2-v_1)^2\\ &{}+\frac{\tilde{L}^2}{a^2}\epsilon ^{m}(w_{2}-v_{2})^3, \end{array}\right. } \end{aligned}$$
(19)

where we neglect all the terms \(O(\epsilon ^{n+m})\).

Following the strategy introduced by Manevitch in [74], we proceed by complexifying the problem introducing the following complex variables, for \(\nu =1,2\),

$$\begin{aligned} \displaystyle \psi _\nu&:=\displaystyle e^{-i\epsilon \tau }\left( \dot{w}_{\nu }+i\epsilon w_{\nu }\right) , \quad \quad \nonumber \\ \psi _\nu ^*&:=e^{i\epsilon \tau }\left( \dot{w}_{\nu }-i\epsilon w_{\nu }\right) ,\end{aligned}$$
(20a)
$$\begin{aligned} \displaystyle \phi _\nu&:=\displaystyle e^{-i\epsilon \tau }\left( \dot{v}_{\nu }+i\epsilon v_{\nu }\right) , \,\,\,\quad \quad \nonumber \\ \phi _\nu ^*&:=e^{i\epsilon \tau }\left( \dot{v}_{\nu }-i\epsilon v_{\nu }\right) , \end{aligned}$$
(20b)

where i is the imaginary unit.

Then, the ODEs (19) read at the first harmonic (we take all the terms multiplied by \(e^{i\epsilon \tau }\)) as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\displaystyle \frac{d{\psi _1}}{d\tau }+i\epsilon \psi _1+c.c.=\displaystyle i\frac{3}{4}\frac{\tilde{L}^2}{a^2}\epsilon ^{m-3}\\ &{}\quad \left[ 2(|\phi _1|^2\psi _1-|\psi _1|^2\phi _1)\right. \\ &{}\quad \left. +|\psi _1|^2\psi _1-|\phi _1|^2\phi _1+\phi _1^2\psi _1^*-\psi _1^2\phi _1^*\right] \\ &{}\quad +c.c.+h.h.,\\ &{}\displaystyle \frac{d{\psi _2}}{d\tau }+i\epsilon \psi _2+c.c.=\displaystyle i\frac{3}{4}\frac{\tilde{L}^2}{a^2}\epsilon ^{m-3}\\ &{}\quad \left[ 2(|\phi _2|^2\psi _2-|\psi _2|^2\phi _2)+|\psi _2|^2\psi _2\right. \\ &{}\quad \left. -|\phi _2|^2\phi _2+\phi _2^2\psi _2^*-\psi _2^2\phi _2^*\right] \\ &{}\quad +c.c.+h.h.,\\ &{}\displaystyle \frac{d{\phi _1}}{d\tau }+i\epsilon \phi _1+c.c.=\displaystyle i\tilde{\beta } \epsilon ^{n-1}\frac{b^2}{\ell ^2}\left( \phi _1-\phi _2\right) \\ &{}\quad \displaystyle +i\frac{3}{4}\frac{\tilde{L}^2}{a^2}\epsilon ^{m-3} \left[ 2\left( |\psi _1|^2\phi _1-|\phi _1|^2\psi _1\right) \right. \\ &{}\quad \left. +|\phi _1|^2\phi _1-|\psi _1|^2\psi _1+\psi _1^2\phi _1^*-\phi _1^2\psi _1^*\right] \\ &{}\quad +c.c.+h.h.+0.h.,\\ &{}\displaystyle \frac{d{\phi _2}}{d\tau }+i\epsilon \phi _2+c.c.=\displaystyle i\tilde{\beta } \epsilon ^{n-1}\frac{b^2}{\ell ^2}\left( \phi _2-\phi _1\right) \\ &{}\quad \displaystyle +i\frac{3}{4}\frac{\tilde{L}^2}{a^2}\epsilon ^{m-3} \left[ 2\left( |\psi _2|^2\phi _2-|\phi _2|^2\psi _2\right) \right. \\ &{}\quad \left. +|\phi _2|^2\phi _2-|\psi _2|^2\psi _2+\psi _2^2\phi _2^*-\phi _2^2\psi _2^*\right] \\ &{}\quad +c.c.+h.h.+0.h. \end{array}\right. } \end{aligned}$$
(21)

where c.c. stands for “complex conjugated” terms and h.h. stands for terms that contribute to the higher harmonics (until the third harmonic) and 0.h. are the terms that contribute to the 0-frequency harmonic. The terms of order \(O(\epsilon ^{n+\frac{m}{2}})\) contribute to the higher harmonics and 0-frequency terms. In order to ensure that the nonlinear and the linear terms do not blow up as \(\epsilon \rightarrow 0\), it is necessary to have

$$\begin{aligned} m\ge 3 \quad \quad \textrm{and}\quad \quad n\ge 1. \end{aligned}$$
(22)

As emphasised in [70], a formulation of mechanical problems is not fully adequate if it is not written in appropriate scales, where “appropriate scales” are those at which non-trivial nonlinear effects are clearly manifested. Therefore, in the following discussion we find those particular values of m and n satisfying the conditions (22) such that the system (21) describes the nonlinear dynamics regime for the Z-cell in which we can clearly capture the phenomena of energy transfer and localisations. To this aim, we have to begin by checking the right timescale, so we first perturb in time the system (21) following the methodology in [73].

Let us introduce the various timescales \(\tau _\ell =\epsilon ^\ell \tau \), \(\ell =0,1,...\) and consider the complex functions \(\psi _\nu \) and \(\phi _\nu \) as functions of the variables \(\tau _0\), \(\tau _1\),... . Differentiation w.r.t. \(\tau \) gives the following expansion

$$\begin{aligned} \frac{d(...)}{d\tau }= & {} \frac{\partial }{\partial \tau _0}(...)+\epsilon \frac{\partial }{\partial \tau _1}(...)+\epsilon ^2\frac{\partial }{\partial \tau _2}(...)\nonumber \\{} & {} \quad +...+\epsilon ^k\frac{\partial }{\partial \tau _k}(...). \end{aligned}$$
(23)

The functions \(\psi _\nu (\tau )\) and \(\phi _\nu (\tau )\) are expanded as asymptotic series via the small parameter \(\epsilon \)

$$\begin{aligned} \psi _\nu (\tau )= & {} \psi _{\nu 0}(\tau )+\epsilon \psi _{\nu 1}(\tau )+\epsilon ^2\psi _{\nu 2}(\tau )+\cdots \end{aligned}$$
(24a)
$$\begin{aligned} \phi _\nu (\tau )= & {} \phi _{\nu 0}(\tau )+\epsilon \phi _{\nu 1}(\tau )+\epsilon ^2\phi _{\nu 2}(\tau )+\cdots \end{aligned}$$
(24b)

Besides the initial conditions on the functions, for any fixed \(\nu \), \(\psi _{\nu 0}(\tau )\) and \(\phi _{\nu 0}(\tau )\), the functions \(\psi _{\nu k}(\tau )\) and \(\phi _{\nu k}(\tau )\) are supposed to satisfy zero initial conditions: \(\psi _{\nu k}(0)=0\), \(\phi _{\nu k}(0)=0\) with \(k=1,2,...\).

We highlight that the first harmonic can be written as \(e^{i\epsilon \tau }\psi _{\nu }=\dot{w}_{\nu }+i\epsilon w_{\nu }\) and \(e^{i\epsilon \tau }\phi _{\nu }=\dot{v}_{\nu }+i\epsilon v_{\nu }\), where \(\psi _\nu \) and \(\phi _\nu \) are the slow parts and \(e^{i\epsilon \tau }\) is the fast part of the solutions. For this reason, the functions \(\psi _\nu (\tau )=\psi _\nu (\tau _0,\tau _1,\tau _2,...)\) and \(\phi _\nu (\tau )=\phi _\nu (\tau _0,\tau _1,\tau _2,...)\) must not depend on the natural time \(\tau _0\) at the principal order in the perturbation \(O(\epsilon ^0)\), that is the equations

$$\begin{aligned} \frac{\partial \psi _{\nu 0}}{\partial \tau _0}=0 \quad \quad \textrm{and}\quad \quad \frac{\partial \phi _{\nu 0}}{\partial \tau _0}=0, \quad \quad \nu =1,2, \end{aligned}$$
(25)

must be satisfied. As a consequence, we have non-trivial PDEs at the order \(O(\epsilon )\) or higher.

Proposition 3.1

The system (21) describes the nonlinear dynamics for the Z-cell at the \(O(\epsilon )\) order perturbation if and only if \(m=4\) and \(n=2\).

Proof

See “Appendix A”. \(\square \)

Proposition 3.2

Fix \(m=4\), \(n=2\). If \(w_{\nu }\) and \(v_{\nu }\), for \(\nu =1,2\), are solutions of the system (19), then \(\psi _\nu \) and \(\phi _\nu \) given by (20a) and (20b) are solutions of system (21).

Proof

See “Appendix B”. \(\square \)

After Proposition 3.1 and Proposition 3.2, the system (21) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\displaystyle \frac{d{\psi _1}}{d\tau }+i\epsilon \psi _1=\displaystyle i\frac{3}{4}\frac{L^2}{a^2}\epsilon \\ &{}\quad \left[ 2(|\phi _1|^2\psi _1-|\psi _1|^2\phi _1)\right. \\ &{}\quad \left. +|\psi _1|^2\psi _1-|\phi _1|^2\phi _1+\phi _1^2\psi _1^*-\psi _1^2\phi _1^*\right] ,\\ &{}\displaystyle \frac{d{\psi _2}}{d\tau }+i\epsilon \psi _2=\displaystyle i\frac{3}{4}\frac{L}{a^2}\epsilon \\ &{}\quad \left[ 2(|\phi _2|^2\psi _2-|\psi _2|^2\phi _2)+|\psi _2|^2\psi _2\right. \\ &{}\quad \left. -|\phi _2|^2\phi _2+\phi _2^2\psi _2^*-\psi _2^2\phi _2^*\right] ,\\ &{}\displaystyle \frac{d{\phi _1}}{d\tau }+i\epsilon \phi _1=\displaystyle i\epsilon \tilde{\beta } \frac{b^2}{\ell ^2}\\ &{}\quad \left( \phi _1-\phi _2\right) +i\frac{3}{4}\frac{L^2}{a^2}\epsilon \left[ 2\left( |\psi _1|^2\phi _1-|\phi _1|^2\psi _1\right) \right. \\ &{}\quad \left. +|\phi _1|^2\phi _1-|\psi _1|^2\psi _1+\psi _1^2\phi _1^*-\phi _1^2\psi _1^*\right] ,\\ &{}\displaystyle \frac{d{\phi _2}}{d\tau }+i\epsilon \phi _2=\displaystyle i\epsilon \tilde{\beta } \frac{b^2}{\ell ^2}\\ &{}\quad \left( \phi _2-\phi _1\right) +i\frac{3}{4}\frac{L^2}{a^2}\epsilon \\ &{}\quad \left[ 2\left( |\psi _2|^2\phi _2-|\phi _2|^2\psi _2\right) \right. \\ &{}\quad \left. +|\phi _2|^2\phi _2-|\psi _2|^2\psi _2+\psi _2^2\phi _2^*-\phi _2^2\psi _2^*\right] . \end{array}\right. } \end{aligned}$$
(26)

Note that we leave out the c.c. and the 0.h. terms from the system (21).

After introducing the slow times \(\tau _1=\epsilon \tau _0\), \(\tau _2=\epsilon ^2\tau _0\),... where \(\tau =\tau _0\), in order to rule out trivial solutions and keep solutions which depend on slow times only, the solutions have to oscillate with small frequencies. In particular, these frequencies must be of the order of \(\epsilon \) and cannot be finite (see “Appendix B”). The system (26), at the order \(\epsilon ^0\), reads

$$\begin{aligned} \displaystyle \frac{\partial {\psi _{10}}}{\partial \tau _0}=0,\quad \displaystyle \frac{\partial {\psi _{20}}}{\partial \tau _0}=0,\quad \displaystyle \frac{\partial {\phi _{10}}}{\partial \tau _0}=0,\quad \displaystyle \frac{\partial {\phi _{20}}}{\partial \tau _0}=0, \end{aligned}$$
(27)

thus, \(\psi _{\nu 0}\) and \(\phi _{\nu 0}\) do not depend on \(\tau _0\) and depend on the slow times only, that is \(\psi _{\nu 0}=\psi _{\nu 0}(\tau _1,\tau _2,...)\) and \(\phi _{\nu 0}=\phi _{\nu 0}(\tau _1,\tau _2,...)\).

At the order \(\epsilon \), we have

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\displaystyle \frac{\partial {\psi _{10}}}{\partial \tau _1}+\frac{\partial {\psi _{11}}}{\partial \tau _0}+i\psi _{10}=\displaystyle i\frac{3}{4}\frac{L^2}{a^2}\\ &{}\quad \left[ 2(|\phi _{10}|^2\psi _{10}-|\psi _{10}|^2\phi _{10})+|\psi _{10}|^2\psi _{10}\right. \\ &{}\quad \left. -|\phi _{10}|^2\phi _{10}+\phi _{10}^2\psi _{10}^*\right. \\ &{}\left. \quad -\psi _{10}^2\phi _{10}^*\right] ,\\ &{}\displaystyle \frac{\partial {\psi _{20}}}{\partial \tau _1}+\frac{\partial {\psi _{21}}}{\partial \tau _0}+i\psi _{20}=\displaystyle i\frac{3}{4}\frac{L}{a^2}\\ &{}\quad \left[ 2(|\phi _{20}|^2\psi _{20}-|\psi _{20}|^2\phi _{20})\right. \\ &{}\quad \left. +|\psi _{20}|^2\psi _{20}-|\phi _{20}|^2\phi _{20}+ \phi _{20}^2\psi _{20}^*-\psi _{20}^2\phi _{20}^*\right] ,\\ &{}\displaystyle \frac{\partial {\phi _{10}}}{\partial \tau _1}+\frac{\partial {\phi _{11}}}{\partial \tau _0}+i\phi _{10}=\displaystyle i\tilde{\beta } \frac{b^2}{\ell ^2}\left( \phi _{10}-\phi _{20}\right) \\ &{}\quad \displaystyle {+}i\frac{3}{4}\frac{L^2}{a^2}\left[ 2\left( |\psi _{10}|^2\phi _{10}{-}|\phi _{10}|^2\psi _{10}\right) {+}|\phi _{10}|^2\phi _{10}\right. \\ &{}\quad \left. -|\psi _{10}|^2\psi _{10}+\psi _{10}^2\phi _{10}^*-\phi _{10}^2\psi _{10}^*\right] ,\\ &{}\displaystyle \frac{\partial {\phi _{20}}}{\partial \tau _1}+\frac{\partial {\phi _{21}}}{\partial \tau _0}+i\phi _{20}=\displaystyle i\tilde{\beta } \frac{b^2}{\ell ^2}\left( \phi _{20}-\phi _{10}\right) \\ &{}\quad \displaystyle {+}i\frac{3}{4}\frac{L^2}{a^2}\left[ 2\left( |\psi _{20}|^2\phi _{20}{-}|\phi _{20}|^2\psi _{20}\right) {+}|\phi _{20}|^2\phi _{20}\right. \\ &{}\quad \left. -|\psi _{20}|^2\psi _{20}+\psi _{20}^2\phi _{20}^*-\phi _{20}^2\psi _{20}^*\right] . \end{array}\right. } \end{aligned}$$
(28)

In order to avoid secular terms, we study the system

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\displaystyle \frac{\partial {\psi _{10}}}{\partial \tau _1}+i\psi _{10}=\displaystyle i\frac{3}{4}\frac{L^2}{a^2}\\ &{}\quad \left[ 2(|\phi _{10}|^2\psi _{10}-|\psi _{10}|^2\phi _{10})+|\psi _{10}|^2\psi _{10}\right. \\ &{}\quad \left. -|\phi _{10}|^2\phi _{10}+\phi _{10}^2\psi _{10}^*-\psi _{10}^2\phi _{10}^*\right] ,\\ &{}\displaystyle \frac{\partial {\psi _{20}}}{\partial \tau _1}+i\psi _{20}=\displaystyle i\frac{3}{4}\frac{L}{a^2}\\ &{}\quad \left[ 2(|\phi _{20}|^2\psi _{20}-|\psi _{20}|^2\phi _{20})\right. \\ &{}\quad \left. +|\psi _{20}|^2\psi _{20}-|\phi _{20}|^2\phi _{20}+\phi _{20}^2\psi _{20}^*-\psi _{20}^2\phi _{20}^*\right] ,\\ &{}\displaystyle \frac{\partial {\phi _{10}}}{\partial \tau _1}+i\phi _{10}=\displaystyle i\tilde{\beta } \frac{b^2}{\ell ^2}\left( \phi _{10}-\phi _{20}\right) \displaystyle +i\frac{3}{4}\frac{L^2}{a^2} \\ &{}\quad \left[ 2\left( |\psi _{10}|^2\phi _{10}-|\phi _{10}|^2\psi _{10}\right) +|\phi _{10}|^2\phi _{10}\right. \\ &{}\quad \left. -|\psi _{10}|^2\psi _{10}+\psi _{10}^2\phi _{10}^*-\phi _{10}^2\psi _{10}^*\right] ,\\ &{}\displaystyle \frac{\partial {\phi _{20}}}{\partial \tau _1}+i\phi _{20}=\displaystyle i\tilde{\beta } \frac{b^2}{\ell ^2}\left( \phi _{20}-\phi _{10}\right) \\ &{}\quad \displaystyle {+}i\frac{3}{4}\frac{L^2}{a^2}\left[ 2\left( |\psi _{20}|^2\phi _{20}{-}|\phi _{20}|^2\psi _{20}\right) {+}|\phi _{20}|^2\phi _{20}\right. \\ &{}\quad \left. -|\psi _{20}|^2\psi _{20}+\psi _{20}^2\phi _{20}^*-\phi _{20}^2\psi _{20}^*\right] . \end{array}\right. } \end{aligned}$$
(29)

Eventually, we look for solutions of (29) in the form of single-frequency exponentials, namely

$$\begin{aligned} \psi _{\nu 0}&=f_\nu e^{-i\left( 1-\tilde{\beta }\frac{b^2}{\ell ^2}\right) \tau _1}, \quad \phi _{\nu 0}=g_\nu e^{-i\left( 1-\tilde{\beta }\frac{b^2}{\ell ^2}\right) \tau _1}, \quad \nonumber \\ \nu&=1,2\,, \end{aligned}$$
(30)

hence, we get

$$\begin{aligned} \small {\left\{ \begin{array}{ll} &{}\displaystyle \frac{d{f_{1}}}{d\tau _1}+i\tilde{\beta }\frac{b^2}{\ell ^2}f_1=\displaystyle i\frac{3}{4}\frac{L^2}{a^2}\\ &{}\quad \left[ 2(|g_{1}|^2f_{1}-|f_{1}|^2g_{1})+|f_{1}|^2f_{1}-|g_{1}|^2g_{1}\right. \\ &{}\quad \left. +g_{1}^2f_{1}^*-f_{1}^2g_{1}^*\right] ,\\ &{}\displaystyle \frac{d{f_{2}}}{d\tau _1}+i\tilde{\beta }\frac{b^2}{\ell ^2}f_2=\displaystyle i\frac{3}{4}\frac{L^2}{a^2}\\ &{}\quad \left[ 2(|g_{2}|^2f_{2}-|f_{2}|^2g_{2})+|f_{2}|^2f_{2}\right. \\ &{}\quad \left. -|g_{2}|^2g_{2}+g_{2}^2f_{2}^*-f_{2}^2g_{2}^*\right] ,\\ &{}\displaystyle \frac{d{g_{1}}}{d\tau _1}+i\tilde{\beta } \frac{b^2}{\ell ^2}g_2=\displaystyle i\frac{3}{4}\frac{L^2}{a^2}\\ &{}\quad \left[ 2\left( |f_{1}|^2g_{1}-|g_{1}|^2f_{1}\right) \right. \\ &{}\quad \left. +|g_{1}|^2g_{1}-|f_{1}|^2f_{1}+f_{1}^2g_{1}^*-g_{1}^2f_{1}^*\right] ,\\ &{}\displaystyle \frac{d{g_{2}}}{d\tau _1}+i\tilde{\beta } \frac{b^2}{\ell ^2}g_1=\displaystyle i\frac{3}{4}\frac{L^2}{a^2}\\ &{}\quad \left[ 2\left( |f_{2}|^2g_{2}-|g_{2}|^2f_{2}\right) \right. \\ &{}\quad \left. +|g_{2}|^2g_{2}-|f_{2}|^2f_{2}+f_{2}^2g_{2}^*-g_{2}^2f_{2}^*\right] , \end{array}\right. } \end{aligned}$$
(31)

which is the ODEs system we will focus on in the sequel of this paper.

The system (31) possesses Hamiltonian structure (see “Appendix C”), and so there exists the Hamiltonian function \(\mathcal {H}\) such that

$$\begin{aligned} \frac{d{f_{\nu }}}{d\tau _1}= & {} \frac{\partial \mathcal {H}}{\partial f_\nu ^*}, \quad \frac{d{f^*_{\nu }}}{d\tau _1}=-\frac{\partial \mathcal {H}}{\partial f_\nu },\quad \nu =1,2, \end{aligned}$$
(32)
$$\begin{aligned} \frac{d{g_{\nu }}}{d\tau _1}= & {} \frac{\partial \mathcal {H}}{\partial g_\nu ^*}, \quad \frac{d{g^*_{\nu }}}{d\tau _1}=-\frac{\partial \mathcal {H}}{\partial g_\nu },\quad \nu =1,2, \end{aligned}$$
(33)

where

$$\begin{aligned} \begin{aligned} \mathcal {H}&=\frac{3}{8}\frac{L^2}{a^2} \left[ (f_1-g_1)^2 \left( f_1^*-g_1^*\right) ^2\right. \\&\left. +(f_2-g_2)^2 \left( f_2^*-g_2^*\right) ^2\right] \\&-\tilde{\beta }\frac{b^2}{\ell ^2} \left[ (|f_1|^2+ |f_2|^2)+g_1 g_2^*+g_1^* g_2\right] . \end{aligned} \end{aligned}$$
(34)

By introducing the total mass \(\mathcal {M}\) of the system as

$$\begin{aligned} \mathcal {M}=|f_1|^2+|f_2|^2+|g_1|^2+|g_2|^2, \end{aligned}$$
(35)

it is easy to check that \(\mathcal {H}\) and \(\mathcal {M}\) are two invariants of the motion. Then, the unknown \(f_\nu \) and \(g_\nu \) can be written in terms of the scaled mass \(M=\frac{\mathcal {M}}{4}\) and of the frequency variables \(\delta _\mu \), \(\mu =1,..,4\), as follows

$$\begin{aligned} \begin{aligned}&f_1=\sqrt{M}\cos \theta e^{i\delta _1}, \quad \quad \quad f_2=\sqrt{M}\sin \theta e^{i\delta _2},\\&g_1=\sqrt{M}\sin \theta e^{i\delta _3}, \quad \quad \quad g_2=\sqrt{M}\cos \theta e^{i\delta _4}. \end{aligned} \end{aligned}$$
(36)

Introducing the frequency gaps

$$\begin{aligned} \Delta _1=\delta _1-\delta _3, \quad \quad \Delta _2=\delta _2-\delta _4, \quad \quad \Delta _3=\delta _3-\delta _4, \end{aligned}$$
(37)

the Hamiltonian (34), in terms of these variables, takes the form

$$\begin{aligned} \begin{aligned} \mathcal {H}=&-\frac{b^2}{\ell ^2}\tilde{\beta }\left( 1+\cos \Delta _3 \sin 2\theta \right) \\&\quad +\frac{3}{32}\frac{L^2}{a^2}M\left( \cos 2\Delta _1+\cos 2\Delta _2\right) \\&\quad \left( 1-\cos 4\theta \right) -\frac{3}{16}\frac{L^2}{a^2}M\\&\quad \left[ 4\sin 2\theta \left( \cos \Delta _1+\cos \Delta _2\right) +\cos 4\theta -5\right] . \end{aligned} \end{aligned}$$
(38)

We claim that Hamiltonian (38) exhibits the features allowing the study of energy transfer and localisation whose existence we are going to detect. This purpose will be achieved in the following section through an analysis in the four-dimensional phase space \((\theta ,\Delta _1,\Delta _2,\Delta _3)\).

4 Phase space analysis

We aim to find conditions of existence of stationary and non-stationary localised excitations when resonant processes take place, that is we want to find for which values of the physical parameters energy localisations occur in the metamaterial. In the following, we fix the interspaces, \(a=b=\frac{10}{\sqrt{2}}\) [79], the scale, \(L=1\), and the intensity of the excitation, \(M=10\). We vary the parameter \(\tilde{\beta }=2\epsilon ^{-2}\frac{k_1}{k_0}\), that is we vary the ratio between the stiffness \(k_1\) and \(k_0\). The parameter \(\tilde{\beta }\) tunes the linear coupling between the oscillators and the characteristic scale L tunes the nonlinear coupling between the oscillators.

Following the Manevitch’s works [66,67,68,69,70, 74], we provide the following definitions which will be used in our analysis.

Definition 4.1

NNMs are the stationary points of the nonlinear Hamiltonian system (31).

Therefore, in order to find and investigate the NNMs, one has to search for the stationary points of the Hamiltonian system (31). Then, we study the 2D subspace of the phase space associated to a particular couple of oscillators. We observe that there are several energy levels which encircle the NNMs within this subspace. These curves correspond to non-stationary processes and the energy that the oscillators exchange increases from the closest to the furthest curve. Among these curves, one can individuate the LPT as the outer energy level, i.e. it is the maximum energy possible that two oscillators can exchange when they interact via weak nonlinear interaction.

Definition 4.2

The LPT corresponds to highly non-stationary resonant processes, equivalently the LPT is the outer curve encircling the NNMs in the phase plane.

The LPT can transform into a curve that separates the NNMs one from another and, when it breaks, the energy exchange is not possible anymore. This kind of curve is named a separatrix and it is defined below.

Definition 4.3

The separatrix is a boundary between domains with distinct dynamical behaviour (phase curves) in a dynamical system.

First of all, we find some stationary points, i.e. the NNMs, and we compute the value of \(\tilde{\beta }\) at which they change their nature (for instance, they are minima and then become saddle points).

For any fixed \(\theta \in \mathbb {R}\), the relations (36) describe simple oscillators, so we shall say that two oscillators are in-phase if there exist values of \(\delta _\nu \) such that they oscillate with the same phase.

Hereinafter, we fix \(\theta =\frac{\pi }{4}\), so that when \(\delta _1=\delta _2=\delta _3=\delta _4\) or when the phases \(\delta _j\) differ one from another by a value \(2\pi n\), \(n\in \mathbb {N}\), by (36), all the oscillators \(f_1\), \(f_2\), \(g_1\), \(g_2\) oscillate with the same phase and, as a consequence, the entire system is in-phase. Otherwise, one can choose values of the phases \(\delta _\nu \) such that we have at least a couple of oscillators that oscillate in anti-phase. For instance, when \(\delta _1=\delta _2=0\) and \(\delta _3=\delta _4=\pi \), we have \(f_1\) and \(f_2\), respectively \(g_1\) and \(g_2\), which oscillate in-phase, but every oscillator \(f_{\nu }\) is in anti-phase with every oscillator \(g_{\nu }\).

Therefore, we can have two situations:

  • the case in which \(\delta _\nu \) are equal one with another or they differ one with another only for a phase \(2n\pi \) with \(n\in \mathbb {N}\), so the entire system oscillates in-phase in a 4D phase space;

  • the case in which in a 2D phase subspace two oscillators are in-phase and in another 2D phase subspace two other oscillators are in anti-phase.

As a consequence, in the 4D phase space one cannot classify the NNMs as purely anti-phase, but one can individuate anti-phase NNMs in a 2D phase subspace.

In order to find the stationary points of the Hamiltonian \({\mathcal {H}}={\mathcal {H}}(\theta ,\Delta _1,\Delta _2,\Delta _3)\) given in (38), we solve the equations

$$\begin{aligned} \frac{\partial {\mathcal {H}}}{\partial \theta }=0, \quad \frac{\partial {\mathcal {H}}}{\partial \Delta _1}=0, \quad \frac{\partial {\mathcal {H}}}{\partial \Delta _2}=0,\quad \frac{\partial {\mathcal {H}}}{\partial \Delta _3}=0, \end{aligned}$$
(39)

then we compute the Hessian \(Hess({\mathcal {H}})\) and its eigenvalues to classify them. Because of the periodic structure of the phase space, we do not need to take into account all the stationary points. For \(\theta >0\), two of the stationary points \((\theta ,\Delta _1,\Delta _2,\Delta _3)\) are \(\left( \frac{\pi }{4},\pi ,\pi ,\pi \right) \) and \(\left( \frac{\pi }{4},\pi ,\pi ,0\right) \) corresponding to NNMs, respectively.

For the stationary point \(\left( \frac{\pi }{4},\pi ,\pi ,\pi \right) \) we have that, for \(\delta _1=2\pi \), \(\delta _2=\delta _3=\pi \) and \(\delta _4=0\), then \(\Delta _1=\Delta _2=\Delta _3=\pi \), so that the oscillators \(w_{1}\) and \(v_{2}\) oscillate in-phase, but they are in anti-phase with the oscillators \(w_{2}\) and \(v_{1}\) which, in turn, oscillate in-phase one with another.

For the stationary point \(\left( \frac{\pi }{4},\pi ,\pi ,0\right) \) a possible choice is \(\delta _1=\delta _2=\pi \) and \(\delta _3=\delta _4=0\), such that the oscillators \(w_{1}\) and \(w_{2}\) are in-phase, whereas they are in anti-phase with the oscillators \(v_{1}\) and \(v_{2}\), which in turn oscillate in-phase one with another.

The analysis via the second-derivative test shows that the eigenvalues of the Hessian matrix are \(\left( {-}\frac{4}{5}(3{+} \right. \left. \frac{5}{2}\tilde{\beta }), -\frac{3}{10},-\frac{3}{10},-\frac{\tilde{\beta }}{2}\right) \) in the stationary point \(\left( \frac{\pi }{4},\pi ,\pi ,\right. \left. \pi \right) \), such that they are associated to a local maxima for any \(\tilde{\beta }>0\). Then, this point is a local maximum in any 2D phase subspace. Therefore, the NNMs cannot bifurcate neither in the entire 4D space nor in any 2D subspace.

For the stationary point \(\left( \frac{\pi }{4},\pi ,\pi ,0\right) \), the eigenvalues of the Hessian matrix are \(\left( \frac{4}{5}(-3+\frac{5}{2}\tilde{\beta }),-\frac{3}{10},-\frac{3}{10},\frac{\tilde{\beta }}{2}\right) \) which correspond to a saddle point for any \(\tilde{\beta }>0\). Nevertheless, the eigenvalue corresponding to the \(\theta \)-dimension can change its sign at \(\tilde{\beta }=\frac{6}{5}\). As a result, since the eigenvalue \(\frac{\tilde{\beta }}{2}\) corresponds to the \(\Delta _3\)-dimension, in the 2D subspaces \((\theta ,\Delta _3)\), we have a local minimum for \(\tilde{\beta }>\frac{6}{5}\) and a saddle point for \(\tilde{\beta }<\frac{6}{5}\), although in the entire 4D space \((\theta ,\Delta _1,\Delta _2,\Delta _3)\) we have only saddle points. Thus, for \(\tilde{\beta }=\frac{6}{5}\), the in-phase NNMs (\(g_1\) and \(g_2\)) in the 2D phase subspace \((\theta ,\Delta _3)\) become unstable (Fig. 3a) and then, for \(\tilde{\beta }<\frac{6}{5}\), they bifurcate (Fig. 3b).

The 2D phase space \((\theta ,\Delta _3)\) of in-phase oscillations is obtained fixing \(\Delta _1=\Delta _2=\pi \) at the stationary point \(\left( \frac{4}{5}(-3+\frac{5}{2}\tilde{\beta }),\frac{\tilde{\beta }}{2}\right) \). We have a phase transition and bifurcation of NNMs in the 2D phase space \((\theta ,\Delta _3)\) for \(\tilde{\beta }<\frac{6}{5}\). Looking at the Z cell in Fig. 2, this means that the ratio of the stiffness \(k_1\) between the two oscillators \(v_{1}\) and \(v_{2}\) and the stiffnesses \(k_0\) between the two oscillators \(w_{1}\) and \(v_{1}\) (or \(w_{2}\) and \(v_{2}\)) is very small, \(\frac{k_1}{k_0}<\frac{3}{5}\epsilon ^{2}\). Subsequently the formation of NNMs and their bifurcations, the LPT modifies: for instance, its deformation is clear for \(\tilde{\beta }=0.92\), (Fig. 3c). At \(\tilde{\beta }=0.9002\), it becomes unstable and transforms in a separatrix (Fig. 3d). This separatrix separates the phase plane in two domains around the NNMs: the first includes all the circular curves which represent the periodic oscillations around the right-hand NNM, the second includes all the circular curves which represent the periodic oscillations around the left-hand NNM. This instability corresponds to a complete energy transfer between the oscillators: all the energy of an oscillator is surrendered to the other oscillator [66,67,68,69,70, 74]. For \(\tilde{\beta }=0.9\), the LPT breaks (see Fig. 3e and its zoom-in Fig. 3g) and we have energy localisation for \(\tilde{\beta }\le 0.9\), that is \(\frac{k_1}{k_0}\le \epsilon ^2 0.45\), at which NNMs in the 2D phase subspace \((\theta ,\Delta _3)\) drift apart and oscillators do not exchange energy anymore. At this point, all the energy is localised in just one of the oscillators (see Fig. 3f and its zoom-in in Fig. 3h). One notes that, the characteristic scale L is O(1), such that the dynamics takes place when the nonlinear coupling dominates the linear coupling.

Fig. 3
figure 3

The 2D phase space \((\theta ,\Delta _3)\) for \(\tilde{\beta }=1.2\), where NNMs become unstable (a), \(\tilde{\beta }=1.16\), where NNMs bifurcate (b), \(\tilde{\beta }=0.92\), where the LPTs is clearly deformed (c), \(\tilde{\beta }=0.9002\), where the LPT becomes a separatrix and there is the maximum energy exchange between the oscillators (d), \(\tilde{\beta }=0.90\), where the LPT breaks to move away the NNMs, (e) and its zoom-in (g). Finally, the last two figures are both for \(\tilde{\beta }=0.80\). In (f) it is clear that the NNMs do not exchange energy anymore, the zoom-in (h) shows that the energy is completely localised

Full size image

By a further discussion, we can corroborate the observations of the evolution of the LPT in the 2D subspace. First of all, we can compute analytically the value of \(\tilde{\beta }\) at which the LPT becomes a separatrix.

Keeping in mind the Definition 4.3, we observe that the LPT can be individuated in the 2D phase plane by some initial conditions at \(\tau _1=0\). Indeed, \(\theta (0)=0\) implies \(g_1(0)=0\) (see definition (36)) and, going backwards to the formulas (30), (24b) and (20b), we obtain \(v_1=0\) and \(\dot{v}_1=0\) when \(\tau =0\). Therefore, the oscillator \(g_1\) is initially at rest, while the oscillator \(g_2\) is excited.

Let us consider the reduced Hamiltonian in the 2D phase space

$$\begin{aligned} \begin{aligned} {{\mathcal {H}}}_\text {red}(\theta ,\Delta _3)&=-\frac{\tilde{\beta }}{2}+\frac{3}{40}\left( 3-\cos 4\theta \right) \\&\quad +\sin 2\theta \left( \frac{3}{10}-\frac{\tilde{\beta }}{2}\cos \Delta _3\right) . \end{aligned} \end{aligned}$$
(40)

Since, when \(\tau _1=0\) and for the initial condition \(\theta (0)=0\), the segment \((0,\Delta _3)\) must belong to the LPT, then the expression of the Hamiltonian on this segment is

$$\begin{aligned} {{\mathcal {H}}}_\text {red}(0,\Delta _3)=\frac{3}{20}-\frac{\tilde{\beta }}{2}, \quad \quad \tau _1=0, \end{aligned}$$
(41)

and, for any generic \(\theta (0)\) on the LPT, the expression of the Hamiltonian \(\mathcal {H}(\theta ,\Delta _3)\) on the LPT (at initial time \(\tau _1=0\)) satisfies the following condition

$$\begin{aligned} {{\mathcal {H}}}_\text {red}(\theta ,\Delta _3)={{\mathcal {H}}}_\text {red}(0,\Delta _3), \quad \quad \tau _1=0. \end{aligned}$$
(42)

Furthermore, the LPT becomes a separatrix when (see Fig. 3d)

$$\begin{aligned} \mathcal {H}_\text {red}\left( \frac{\pi }{4},0\right) =\mathcal {H}_\text {red}(0,\pi ), \end{aligned}$$
(43)

that is satisfied when \(\tilde{\beta }=0.9002\).

Later, we prove that the dynamics of the system on the LPT is described only by the evolution in time of the variable \(\theta (\tau _1)\). Indeed, by the numerical analysis and by varying the values of \(\tilde{\beta }\), we see that the profile of \(\theta (\tau _1)\) changes its shape at the same value of \(\tilde{\beta }\) at which the LPT transforms in the 2D subspace. Indeed, the reduction to the 2D phase space leads to the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{d\theta }{d\tau _1}=-\displaystyle \frac{1}{4}\tilde{\beta } \sin \Delta _3,\\ \displaystyle \sin 2\theta \frac{d\Delta _3}{d\tau _1}=\displaystyle \frac{3}{10}(\cos 2\theta +\frac{1}{2}\cos 4\theta )-\tilde{\beta }\cos 2\theta \cos \Delta _3. \end{array}\right. } \end{aligned}$$
(44)

Let us focus on the first equation of the system (44). By the condition (42), we express \(\sin \Delta _3\) as function of \(\theta \). Then, we obtain the following differential equation

$$\begin{aligned} \frac{d\theta }{d\tau _1}={\mp }\bar{\beta }\sqrt{1-\frac{9}{400\bar{\beta }^2}(2+\sin 2\theta )^2}, \quad \bar{\beta }=\frac{\tilde{\beta }}{2}, \end{aligned}$$
(45)

that is satisfied on the LPT [67] which, by separation of variables, gives

$$\begin{aligned}{} & {} \int \frac{d\tilde{\theta }}{\sqrt{1-\textrm{k}(2+\sin \tilde{\theta })^2}}={\mp }\bar{\beta }\int d\tau _1, \nonumber \\{} & {} \quad \tilde{\theta }=2\theta \frac{9}{400\bar{\beta }^2}=\textrm{k}. \end{aligned}$$
(46)

The integral in the left-hand side has as solution the Elliptic function, whereas the integration of the right-hand side yields \({\mp } \tilde{\beta }\tau _1\). Nevertheless, we do not compute explicitly the solution of (46), but we provide a numerical analysis of the evolution of its shape as the values of \(\tilde{\beta }\) decreases, as shown in Fig. 4. Following Manevitch’s works (see, for instance, [67]), we know that the LPT is described by non-smooth functions. In particular, we plot a saw-tooth periodic function for \(\tilde{\beta }=1.2\) (Fig. 4a).

Fig. 4
figure 4

The absolute value of the amplitude of the Elliptic function for different values of \(\tilde{\beta }\)

Full size image

Moreover, the numerical computations confirm that the LPT allows the maximum exchange of energy between the oscillators when \(\tilde{\beta }=0.9002\) (Fig. 4b), and it breaks when \(\tilde{\beta }=0.90\) (Fig. 4c), i.e. when \(\frac{k_0}{k_1}=\epsilon ^2 0.45\) (see Fig. 4).

Finally, the previous analysis does not need to be repeated for other characteristic scales L, due to the invariance of the Hamiltonian.

5 Numerical investigations on energy exchange

In this section, we show that a 2D metamaterial with fixed boundaries can be meant as the sum of Fermi–Pasta–Ulam–Tsingou (FPUT) 1D chains [75]. We investigate the occurrence of energy localisation by performing the well-known FPUT numerical experiment [76] generalised to the 2D case by the Runge–Kutta-45 algorithm (tolerance \(10^{-4}\)). Then, similarly to [76, 78], we think our problem in terms of normal modes depending on the time variable \(t\in {\mathbb {R}}_+\).

We add fixed boundaries at \(\mu =0\) and \(\mu =N+1\), such that \(v_{\nu 0}=w_{\nu 0}=0\) and \(v_{\nu N+1}=w_{\nu N+1}=0\), with \(\nu =0,...,N+1\), and at \(\nu =0\) and \(\nu =N+1\) such that \(v_{0\mu }=w_{0\mu }=0\), for \(\mu =0,..., N+1\). Actually, the metamaterial is composed by \((N+2)\times (N+2)\) nodes, but only the inner \(N\times N\) nodes have displacements different from zero. The potentials \(U_0\) and \(U_1\) defined in (8) and (9) are different from zero if the conditions (7) are encountered. Indeed, the boundary conditions are different from those provided in the previous section because the outer moving oscillators interact with the fixed ones. As a consequence, the ODEs we are going to integrate numerically are the \(N\times N\) equations (16), but the equations of the moving outer oscillators have self-interaction terms.

The initial conditions for the displacements \(v_{\nu \mu }\) and \(w_{\nu \mu }\), for \(1\le \mu \le N\) and \(1\le \nu \le N\), are set as follows: the initial positions are zero except those of the nodes with \(\nu =1\) which take the expression of the initial conditions provided in the FPUT experiment (see code in [76] and the formulas (47) and (48)), whereas the initial velocities of all the nodes are zero.

Moreover, since the oscillators move along the y-direction only, the Fourier transform is performed only for the discrete variable \(\mu \). Similarly to [75], we introduce the normal modes \(A_{\nu k}=A_{\nu k}(t)\) and \(B_{\nu k}=B_{\nu k}(t)\) for the \(N\times N\) moving nodes,

$$\begin{aligned} w_{\nu \mu }= & {} \sqrt{\frac{2}{N+1}}\sum _{k=1}^{N} A_{\nu k} \sin \frac{k\mu }{N+1}\pi ,\nonumber \\ \dot{w}_{\nu \mu }= & {} \sqrt{\frac{2}{N+1}}\sum _{k=1}^{N} \dot{A}_{\nu k} \sin \frac{k\mu }{N+1}\pi , \end{aligned}$$
(47)

and

$$\begin{aligned} v_{\nu \mu }= & {} \sqrt{\frac{2}{N+1}}\sum _{k=1}^{N} B_{\nu k} \sin \frac{k\mu }{N+1}\pi ,\nonumber \\ \dot{v}_{\nu \mu }= & {} \sqrt{\frac{2}{N+1}}\sum _{k=1}^{N} \dot{B}_{\nu k}\sin \frac{k\mu }{N+1}\pi , \end{aligned}$$
(48)

with frequencies

$$\begin{aligned} \omega _{k}=2\sin \frac{k\pi }{2(N+1)}. \end{aligned}$$
(49)

The boundary conditions are

$$\begin{aligned} A_{0k}&=B_{0k}=0,\quad \quad A_{N+1k}=B_{N+1k}=0, \quad \quad \nonumber \\ k&=1,...,N, \end{aligned}$$
(50)

and the initial conditions for the positions are set different from zero only for the \(\nu =1\), that is

$$\begin{aligned} A_{\nu k}(0)=B_{\nu k}(0)= {\left\{ \begin{array}{ll} 1, \quad \quad \textrm{if}\quad \nu =1,\\ 0, \quad \quad \textrm{if}\quad \nu \ne 1, \end{array}\right. } \end{aligned}$$
(51)

whereas, for every \(\mu ,\nu =1,..,N\),

$$\begin{aligned} \dot{A}_{\nu k}(0)=\dot{B}_{\nu k}(0)=0. \end{aligned}$$
(52)

The numerical integration does not involve the quadratic terms in (16) because they contribute to harmonics greater than the first harmonic as explained in Sect. 5.

Note that in (47) and (48) the subscripts \(\mu \) and \(\nu \) for the displacements w are different from those of the displacements v, indeed 0-nodes and 1-nodes alternate their positions in the metamaterial. In this respect, we can use the matrix formulation as follows

$$\begin{aligned} U(t)=&\begin{pmatrix} 0&{}\dots &{}\dots &{}\dots &{}\dots &{}\dots &{}\dots &{}0\\ \vdots &{}u_{1\,1} &{}u_{1\,2} &{} \dots &{}\dots &{} u_{1\,N-1} &{}u_{1\,N}&{}\vdots \\ \vdots &{}u_{2\,1}&{}u_{2\,2}&{}\dots &{}\dots &{}u_{2\,N-1}&{}u_{2\,N}&{}\vdots \\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \vdots &{}u_{N-1\,1} &{}u_{N-1\,2}&{}\dots &{}\dots &{}u_{N-1\,N-1} &{}u_{N-1\,N}&{}\vdots \\ \vdots &{}u_{N\,1} &{} u_{N\,2} &{}\dots &{}\dots &{}u_{N\,N-1}&{}u_{N\,N}&{}\vdots \\ 0&{}\dots &{}\dots &{}\dots &{}\dots &{}\dots &{}\dots &{}0 \end{pmatrix}\quad \nonumber \\ =&\begin{pmatrix} 0&{}\dots &{}\dots &{}\dots &{}\dots &{}\dots &{}\dots &{}0\\ \vdots &{}v_{1\,1} &{}w_{1\,2} &{} \dots &{}\dots &{} v_{1\,N-1} &{}w_{1\,N}&{}\vdots \\ \vdots &{}w_{2\,1}&{}v_{2\,2}&{}\dots &{}\dots &{}w_{2\,N-1}&{}v_{2\,N}&{}\vdots \\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \vdots &{}v_{N-1\,1} &{}w_{N-1\,2}&{}\dots &{}\dots &{}v_{N-1\,N-1} &{}w_{N-1\,N}&{}\vdots \\ \vdots &{}w_{N\,1} &{} v_{N\,2} &{}\dots &{}\dots &{}w_{N\,N-1}&{}v_{N\,N}&{}\vdots \\ 0&{}\dots &{}\dots &{}\dots &{}\dots &{}\dots &{}\dots &{}0 \end{pmatrix},\nonumber \\ \end{aligned}$$
(53)

where

$$\begin{aligned} u_{\nu \mu }=\sqrt{\frac{2}{N+1}}\sum _{k=1}^NU_{\nu k}\sin \frac{k\mu }{N+1}\pi . \end{aligned}$$
(54)

The entries of the matrix U(t) are the solutions of the nonlinear ODEs over the integration time and they are computed via the Runge-Kutta method. However, in the following discussion, we focus only on the energy contributing to the linear part of the dynamics by analogy with Fermi’s research work [75].

Proposition 5.1

If the masses of the metamaterial in study oscillate only along the y-direction and the moving masses satisfy

$$\begin{aligned} B_{\nu _1k}(t)=B_{\nu _2k}(t),\quad A_{\nu _1k}(t)=A_{\nu _2k}(t), \quad t>0, \end{aligned}$$
(55)

even if \(\nu _1\ne \nu _2\), then the kinetic and the potential energy contributing to the linear part of the equations of motion read

$$\begin{aligned} \mathcal {E}= & {} \frac{1}{2}\sum _{\nu ,k=1}^N\Bigg (\dot{U}_{\nu k}^2+4\frac{b^2}{\ell ^2}\tilde{\beta }\epsilon ^2\sum _{\begin{array}{c} n,m=1 \end{array}}^NU_{\nu k}^2\omega _k^2\nonumber \\{} & {} (\delta _{\nu ,2n}\delta _{k,2m}+\delta _{\nu ,2n-1}\delta _{k,2m-1})\Bigg ), \end{aligned}$$
(56)

i.e. the energy \(\mathcal {E}\) is the sum of the energy of N FPUT chains [75], except the 0-nodes do not have the potential contribution and the coupling parameter encloses the geometry of the metamaterial.

Proof

See “Appendix E”. \(\square \)

We highlight that the condition (55) holds only when \(t>0\), instead at \(t=0\) the initial conditions (51) and (52) are satisfied. Nevertheless, it easy to check that the energy \(\mathcal {E}\) defined in (56) holds even at \(t=0\) with the initial conditions (51) and (52). Moreover, by considering only the energy contributing the linear part of the dynamics, the conditions (55) implies that, for every fixed \(\mu =1,...,N\), the displacements satisfy \(w_{\nu _1\mu }=w_{\nu _2\mu }\) and \(v_{\nu _1\mu }=v_{\nu _2\mu }\), with \(\nu _1\ne \nu _2\).

We plot the time evolution of the energy (56) of all the modes in both the two cases with \(N=4\) and \(N=16\) moving oscillators. In all the plots, we put \(L=1\), \(\epsilon =0.1\), \(a=b=10/\sqrt{2}\) and \(\ell =10\).

In Fig. 5, we plot the energy \(\mathcal {E}\) of all the 4 modes in a metamaterial composed by 4 moving oscillators at fixed \(\tilde{\beta }=0.9\) and the integration time is \(t=190\). We set initial conditions different from zero only for the displacements \(u_{11}(0)\) and \(u_{12}(0)\), whereas the velocities are set to zero (i.e. \(\dot{u}_{11}(0)=0\) and \(\dot{u}_{12}=0\)) such that only the energy of the mode (1, 1) has initial energy different from zero. Indeed, the displacement \(u_{12}\) contributes with only the kinetic term to the energy \(\mathcal {E}\). After some time \((t>0)\), all the modes start sharing their energies, and we observe that both the energies of the modes (1, 1) and (1, 2) decrease (Fig. 5). As time goes on, the energy of the mode (2, 2) oscillates with maxima higher and higher, and simultaneously, the energy of the mode (1, 1) oscillates with maxima smaller and smaller. For instance, the mode (2, 2) gains the maximum of its energy when the energy of the mode (1, 1) has transferred about the \(75\%\) of its initial energy to the other modes. The most of the lost energy (\(\sim 97\%\)) has been surrendered to the mode (2, 2). Later, the energy of the mode (1, 1) starts oscillate with maxima higher and higher, whereas the the energy of the mode (2, 2) oscillates with maxima smaller and smaller. Finally, the energy of the mode (1, 1) gains back the most of its initial energy except the \(11\%\). This behaviour resembles the FPUT recurrence. The modes (2, 1) and (1, 2) which have only kinetic terms in the energy \(\mathcal {E}\) have similar behaviour, but they exchange the maximum energy possible. The mode (1, 2) gives away to and then gains back from the mode (2, 1) all the possible energy and this process is periodic. This resembles the FPUT super-recurrence [77]. Thus, it seems that the exchange of energy occurs in pairs between the modes. Probably, this is linked to the fact that two NNMs are stable and the other two are unstable in the phase space. Moreover, we underline that varying \(\tilde{\beta }\) (at least within the range \(0.9 \le \tilde{\beta }\le 1000\)), the trend of the energy \(\mathcal {E}\) does not change, since the modes exchange the energy in the same way described above. However, as \(\tilde{\beta }\) increases the recurrences occur in a time smaller and smaller and the energy into play is larger and larger. For instance, for \(\tilde{\beta }=1000\), the mode (1, 1) gains back almost its initial energy except the \(0.5\%\) just after an integration time \(t=5\).

Fig. 5
figure 5

Energy evolution in time of all the modes (1, 1), (1, 2), (2, 1) and (2, 2) for a metamaterial composed by 4 moving oscillators when \(\tilde{\beta }=0.9\). The mode (1, 1) is excited, whereas the other modes have zero energy at the beginning of the simulation (\(t=0\)). The integration time is \(t=190\) and length-step time \(\Delta t=0.5\)

Full size image
Fig. 6
figure 6

Case with 16 moving oscillators. Energy plot of all the modes with integration time \(t=190\) and length-step time \(\Delta T=0.5\)

Full size image

For the sake of completeness, we plot some modes of a metamaterial composed by 16 moving oscillators with \(\tilde{\beta }=0.9\) (see Fig. 6). At the beginning of the simulation (\(t=0\)), all the nodes on the first column of the metamatrial \((\nu =1)\) have initial conditions for the displacements different from zero. After some time, the excited mode (1, 1) gives way its energy, and after a time \(t=190\), it gains back its energy up to around \(37\%\). It is worth to highlight that there are some modes which are not excited at every time \(t\ge 0\) (for example, the modes (4, 3) and (4, 2)) and they are not plotted. Instead, we observe that the modes (4, 1) and (4, 4) with initial energy zero gain their energy when some other modes are loosing their energy (see, for instance, the modes (1, 1) and (3, 1)). Even for the metamaterial with 16 moving oscillators, we observe the same trend of the energy \(\mathcal {E}\) as \(\tilde{\beta }\) varies \((0.9\le \tilde{\beta }\le 100)\) and the same considerations for 4 moving oscillators hold as well.

Similarly to the outcomes obtained for the 2D toymodel via the phase space analysis in which the energy exchange takes place between two modes only, even in the numerical experiments we observe that the energy exchange may take place in pair between the modes in the metamaterial with 4 moving oscillators. However, without fixed boundaries and without further restrictions on the modes amplitude, the energy localisation occurs only for particular values of the stiffnesses. This result provides conditions for which FPUT recurrence and super-recurrence can be observed in a 2D metamaterial.

Analogously to the Fermi’s work on a chain of nonlinearly interacting oscillators, we would expect equipartition of energy, that is the energy introduced in some modes should drift into the other modes. Instead, just like the FPUT experiment, we observe that, after some period of time, the initially excited modes gain back a large percentage of their energies. This is due to the fact that the energy \(\mathcal {E}\), which contributes to the linear dynamics of the system, is affected by the terms of the energy which contributes to the nonlinear dynamics, that is the nonlinear terms cause localisation of energy instead of equipartition of energy. Moreover, we should keep in mind that the linear dynamics can be rediscovered in the linear approximation, i.e. when the nonlinear coupling between the oscillators approaches zero. Thus, we can say that the study of the energy \(\mathcal {E}\) allows us to know qualitatively how much the nonlinear interactions “disturb” the linear dynamics of the system.

Fig. 7
figure 7

Energy evolution in time of all the modes (1, 1), (1, 2), (2, 1) and (2, 2) for a metamaterial composed by 4 moving oscillators when \(\tilde{\beta }=0.9\) and the initial conditions are those which individuate the LPT in the 2D subspace. The integration time is \(t=190\) and length-step time \(\Delta t=0.5\)

Full size image

6 An insight on the energy exchange in the Z cell

In the numerical experiment on the Z cell performed in Sect. 5, we set the initial conditions (51) and (52) for which all the first column (\(\nu =1\)) of the material is excited, whereas the other two oscillators are at rest. With these initial conditions, the plot in Fig. 5 shows partial energy exchange between the two modes (1, 1) and (2, 2). The initial excited mode (1, 1) surrenders a certain quantity of its initial energy to the mode (2, 2). This phenomenon corresponds to the existence and instability of two NNMs in the phase plane. We have showed that the instability of these NNMs leads to the formation and subsequent instability of the LPT in the 2D subspace. On the LPT, the two unstable modes exchange the maximum energy possible. This means that, at the time \(t=0\), the LPT in the 2D subspace can be individuated by the initial conditions for which one of the two unstable mode is completely excited and the other one is at rest (see discussion in Sect. 4). Therefore, we repeat the same experiment in Sect. 5, with the same boundary conditions (50), but now we set the initial conditions for which only the displacement \(u_{22}(0)\) is different from zero, whereas all the other displacements and velocities are zero, as a consequence, at \(t=0\), only the mode (2, 2) is excited.

In Fig. 7, we observe that the energy of the mode (2, 2) oscillates with maxima smaller and smaller, whereas the energy of the mode (1, 1) reaches its maxima values around the half of the integration time. When the energy of the mode (1, 1) reaches its maximum, the energy of the mode (2, 2) looses around the \(99.5\%\) of its initial energy. At the end of the period of integration time, i.e. \(t=190\), the energy of the mode (1, 1) goes to zero, while the mode (2, 2) gains back all its initial energy. This phenomenon repeats itself periodically (Fig. 8) resembling a FPUT super-recurrence and it can be associated to the instability of the LPT in the 2D subspace.

Note that the other two modes (1, 2) and (2, 1) have the same initial conditions in both the two numerical experiments and their behaviour is the same in both Figs. 5 and 7. We suggest that these two modes are associated to the two stable modes in the phase space.

The numerical experiments on the Z cell with different initial conditions suggest that its nonlinear behaviour depends on which oscillator is excited and which one is at rest at the initial time.

Fig. 8
figure 8

Energy evolution in time of all the modes (1, 1), (1, 2), (2, 1) and (2, 2) when the integration time is \(t=380\) and length-step time \(\Delta t=0.5\) and the initial conditions are those which individuate the LPT in the 2D subspace. The energy exchange is periodic in time

Full size image

Finally, we aim to analyse deeper the connection between the occurrence of FPUT recurrence and super-recurrence with the instabilities of NNMs and LPTs in future research works, even for a system with number of oscillators bigger than 4.

7 Conclusions

A simplified model of plane metamaterial represented by a 2D mass–spring system with weakly nonlinear coupled oscillators seems to be suitable for understanding the formation of energy transfer and localisation. We have considered a toymodel composed by 4 oscillators in order to prove that weakly nonlinear coupling between them is a fundamental characteristic for internal resonant bandgap existence at short wavelengths (high frequencies). In this way, the working resonant bandgap of a metamaterial can be augmented by adding weakly nonlinear coupling between the oscillators besides the interaction with incident waves or excited host structures. The numerical investigation via a tailored FPUT code suggests that this result may be extended to a system with a finite number of oscillators (bigger than 4) and that the energy localisation may be observed for generic values of the stiffnesses by adding fixed boundaries, particular restrictions on the modes amplitude and proper initial conditions. These outcomes pave the road to other future research on resonant metamaterials.