Dynamics modeling method dedicated to system models with open- and closed-loop structures subjected to kinematic and task based constraints

Abstract

The paper presents a development of an automated computational procedure for constrained dynamics (CoPCoD) dedicated to derivation of dynamical models of mechanical systems, e.g. manipulators, both ground and space or mobile robotic systems, which can be composed of rigid and flexible links. They may be subjected to constraints, which are referred to as programmed, which may come from performance requirements, e.g. work or services a system is dedicated to. The CoPCoD structure offers systematic modeling of either open or closed loop constrained structures and results in computationally efficient numerical dynamical equations derivation. The CoPCoD development has its background in the generalized programmed motion equations (GPME) algorithm developed successfully for rigid models of mechanical systems subjected to high order nonholonomic constraints, however, the GPME was not fully automated for computer equation derivations. The two main motivations that underlie the CoPCoD development are to extend the GPME to flexible system models and make it fully automated to computer equation derivations for large classes of systems. The paper presents the general scheme of the CoPCoD architecture and examples which illustrate its application advantages.

1 Introduction

1.1 Background and literature survey

The literature on various aspects of research on rigid and flexible multibody systems is very rich. There is a lot of papers about writing, solving and simulation of dynamic equations of rigid and flexible multibody systems; see e.g. [1, 2] and references there. Also, there are multiple papers on designing control techniques for such systems. Depending upon the purpose of modeling, we can distinguish methods aimed to build validation models including nonlinear terms [3, 4], methods to derive preliminary design models, which due to their simplicity are attractive to control [5]. The control dedicated models often arise as various versions of linearized equations, small displacement assumptions are adopted for flexible multibody systems and link flexibility is approximated by discretized models using finite element methods or assumed mode methods; see e.g. [6]. The dynamics of the system is usually derived using the Euler–Lagrange formulation. As indicated in [7], there are cases, e.g. in space manipulation during debris capture, when there is a need to have a model for each sub-structure of a system such that it is valid for arbitrary boundary conditions.

Among models that take advantage of the sub-structure approaches, the transfer matrix method gained popularity [8]. Later, this approach was merged with the finite-element method and presented as the finite-element transfer matrix method [9]. Some extensions of this method were also developed for control design purposes and for rigid and flexible multibody systems [10]. However, the transfer matrix method has some limitations due to the inversion of sub-matrices, which are not always square or invertible, depending on the boundary conditions. It cannot be directly applied to tree-like structures, like a spacecraft composed of a rigid base and flexible appendages on it.

In many works various methods for derivation of linear or linearized models of flexible multibody system dynamics are presented. For example in [7], the approach is based on the two-port model of each body allowing the whole system model to be built by connecting the inputs/outputs of each body model. Boundary conditions of each body are taken into account through inversion of some input–output channels of its two-port model. This one model of the link can be built into an open or closed-loop mechanism. The method presented in [7] fills the gap between the transfer matrix method and the effective mass-inertia method.

The significant group of dynamic models in engineering applications origins from the multibody dynamics and control of rigid and flexible systems for which Newton–Euler and Lagrange based dynamics derivation methods are used. Among them, there are special methods dedicated to constrained systems in both analytical and computational approaches. As reported in [11], constrained system dynamical models constitute a significant class of models essential to engineering applications. They are used so videly, e.g. in motion analysis in robotics for multi-link industrial manipulators and robots, for ground, underwater, aerospace and space vehicle system dynamics, control, and performance analysis for variety of their missions, that computational methods for derivation of their dynamical models, and their solution methods, became separate research areas, see e.g. works [12, 13] and references there. A lot of application examples for multibody system dynamics models can be found in [14]. Reviewing derivation methods of dynamic models for mechanical systems, the first observation is that they are for systems subjected to position and first order constraints, which are material ones; see e.g. [15, 16] and references there. The task based constraints, control and performance constraints and other requirements available in equation forms are not merged into these models. Consequently, these models are derived using classical analytical dynamics methods, i.e. based upon the Lagrange approach and its modifications. Another approach to dynamics modeling and control approach is based upon the framework developed by Udwadia and Kalaba [17, 18]. This is an elegant apparatus for deriving constrained dynamics based upon the classical mechanics approach and it serves systems subjected to position and kinematic constraints. Also, there are many specialized computational packages for generation of constrained system dynamical models. Generally, they are either Newton–Euler equations or Lagrange equations based and dedicated to rigid multibody systems; see e.g. [19, 20]. The consequence of the derivation method applied to obtain constrained system models is that the resulting equations of motion may not be convenient for their final applications, e.g. they contain Lagrange multipliers which need to be eliminated for most model based controller designs. The second observation is that some of the proposed methods of motion equations derivation are specific and may be challenging for applications for systems with flexible components; see e.g. [21]. The good illustrations of the two observations mentioned above are works [22,23,24]. These works have had significant impact upon the insight into the constrained system structures and for the subsequent control design, like [24] where geometric properties of dynamic models were shown to be the key to model properties from stability and control points of view. However, constraint kinds considered there and presented results were for material constraints, position and kinematic ones. Also, new challenges in dynamic modeling and control designs emerged from interdisciplinary or specifically dedicated models as well as from requirements for system performance or their service mission demands. The new challenges were brought, for example, by underwater vehicles and spacecraft, see e.g. [25]. For the latter ones, long and lightweight structures require link flexibility incorporation into dynamic models as well as mission service and control requires formulation of task based constraints and some of them can be easily formulated by constraint equations. Usually such constraints, if formulated, are at position levels; see e.g. [26, 27]. Also, one more challenge arises for spacecraft modeling and simulation; this is to keep conserved quantities of motion like the linear and angular momentum. The linear and angular momenta can be considered the kinematic constraints and incorporated into constrained dynamics [28].

1.2 Formulation of the problem of interest for this investigation

In most dynamics derivation methods, of either approaches, systems subjected to position and velocity constraints are considered and the Lagrange approach is used. Other constraints are not handled but there are the ones, which are generated by designers, control engineers or system operators that have to be executed during a system operation, see e.g. [29,30,31,32]. For systems subjected to such constraints the preliminary results for obtaining computationally efficient dynamical models were presented in [11, 33]. Such constraints at the position level, referred to as programmed, were incorporated into a rigid-flexible system dynamics for open loop structures. The analytical dynamics background for the constrained dynamic models are works [34, 35], where the generalized programmed motion equations (GPME) are derived. The GPME proved to be effective to derive constrained dynamics, referred to as reference dynamics, for rigid system models in various parameter settings like generalized or quasi-coordinates. The GPME were employed to design a control strategy architecture for tracking predefined motions. Also, the GPME approach can be applied to variable mass and configuration systems [36]. However, The GPME depend heavily upon analytical dynamics calculations and the merit of this paper is to extend to multi-degree of freedom systems whose dynamics require computation.

1.3 Motivation and contribution of this study

This paper is motivated by two factors, being quite critical in designing constrained dynamics and controllers for programmed constraints execution. The first one is the specification of programmed constraints as demands for some work regimes, e.g. velocity of a manipulator end effector has to be modulated during the manipulator work. From the control points of view, incorporation of these constraints into the system dynamics can be advantageous. The second motivation refers to system structures, e.g. rigid or flexible parts with open- and closed-loop structures, for which one modeling method would be welcome. Finally, dynamics modeling should be proactive not reactive what means that its destination should be clear before but not after modelling [37].

The main contribution of the paper is development of the automated computational procedure for constrained dynamics (CoPCoD) of the flexibly supported systems. In contrast to the authors' earlier work, programmed constraints are defined as rheonomic. The presented approach is based on the GPME and preserves its properties, however is fully computationally automated. The basic one is that the constrained dynamics it produces is in the reduced state form, i.e. constraint reaction force are eliminated at the derivation level but not afterwards as in the Lagrange approach. This is the essential advantage of the CoPCoD which may serve directly to constrained motion analysis as well as to control design. The CoPCoD offers automation of the constrained dynamics generation for rigid and flexible system models with open- and closed-loop structures, and possibility of incorporation into these dynamics any position or first order material or non-material constraints, also these related to operation regimes. The credibility of the CoPCoD method is built by its development on the GPME’s. The GPME proved to be effective to constrained rigid multibody systems dyanmics and control. The CoPCoD enjoys all the GPME’s properties and is substantially extended to flexible structures with open and closed loops.

The paper presents the general structure of the CoPCoD and demonstrates the ease of its application in cases of complex kinematic structures, e.g. a tree structure with open and closed loop chains. Examples illustrate how the CoPCoD structure supports modeling and computation of complex structures.

1.4 Organization of the paper

The paper is organized as follows. After presenting the background and motivation of the paper, the general algorithm of CoPCoD for open- and closed-loop serial kinematic chains subjected to programmed constraints is presented in Sect. 2. In this section, models of a flexible base support, a flexible link and friction in joints are described. Further, in Sect. 3, the results of numerical simulations for two model examples representing open loop kinematic chain (OLKC) and closed loop kinematic chain (CLKC) structures are discussed. In simulations, the influence of joint and link imperfections, base support flexibility and material and programmed constraint forms on the reference dynamics are analyzed. The paper closes with conclusions and the list of references.

2 Architecture of the automated computational procedure for constrained dynamics (CoPCoD)

To develop a general structure of the automated Computational Procedure for Constrained Dynamics, referred to as the CoPCoD, let us consider systems of general structures that can be composed of open-loop kinematic chains (OLKC) (Fig. 1a) and closed-loop kinematic chains (CLKC) (Fig. 1b). Both kinds of systems are attached to the ground in $n_{e} \times n_{{sde_{s} }}^{(i)}$ points by means of spring-damping elements (${\text{sde}}_{s}$), where $n_{e}$ is the number of layers and $n_{{sde_{s} }}^{(i)}$ is the number of ${\text{sde}}_{s}$ in each layer.

Fig. 1

Multibody systems with the flexibly supported base: a OLKC system b CLKC system

The cut-joint technique is used when an analyzed structure consists of CLKC.

The kinematic chain $\alpha$ is built of $\left. {n_{{r_{l} }}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}}$ rigid and $\left. {n_{{f_{l} }}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}}$ flexible links. Flexible links are discretized by means of the Rigid Finite Element Method in the modified formulation [38]. In this method the rigid link is replaced by a system of $n_{{rfe_{l} }}^{(\alpha ,i)}$ rigid finite elements (rfe) interconnected by a system of $n_{{sde_{{_{l} }} }}^{(\alpha ,i)}$ spring-damping elements (sde).

2.1 Generalized coordinates and homogeneous transformation matrices

Motion of a system can be defined by a vector of generalized coordinates as follows:

$$ {\mathbf{q}} = \left( {q_{v} } \right)_{{v = 1, \ldots ,n_{dof} }} = \left\{ {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {{\mathbf{q}}^{{(b)^{T} }} } & {{\mathbf{q}}^{{(c)^{T} }} } \\ \end{array} } \right]^{T} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {{\text{for}}} & {{\text{OLKC}},} \\ {\left[ {\begin{array}{*{20}c} {{\mathbf{q}}^{{(b)^{T} }} } & {{\mathbf{q}}^{{(c_{1} )^{T} }} } & {{\mathbf{q}}^{{(c_{2} )^{T} }} } \\ \end{array} } \right]^{T} } & {{\text{for}}} & {{\text{CLKC}},} \\ \end{array} } \right. $$

(1)

where: $n_{dof}$ is number of generalized coordinates which describe a system motion, $n_{dof} = \left\{ {\begin{array}{*{20}c} {n_{dof}^{(b)} + n_{dof}^{(c)} \,\,\,\,\,\,\,\,\,\,\,\,} & {{\text{for}}} & {\text{OLKC,}} \\ {n_{dof}^{(b)} + n_{dof}^{{(c_{1} )}} + n_{dof}^{{(c_{2} )}} } & {{\text{for}}} & {\text{CLKC,}} \\ \end{array} } \right.$$n_{dof}^{(b)} ,\;\left. {n_{dof}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}}$ is number of generalized coordinates of the base and chain $\alpha .$

${\mathbf{q}}^{(b)}$ is a vector defining motion of flexibly supported base b,

$\left. {{\mathbf{q}}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}}$ is a vector describing motion of chain $\alpha$ with respect to base b.

In the case, when the system reference motion is analyzed, i.e. according to constraints imposed upon it, the vector of generalized coordinates is divided into independent and dependent ones, i.e.

$$ {\mathbf{q}} = \left( {q_{v} } \right)_{{v \in i_{{i_{c} }} \cup i_{{d_{c} }} }} = {\mathbf{q}}_{{i_{c} }} \cup {\mathbf{q}}_{{d_{c} }} , $$

(2)

where $i_{{i_{c} }} ,\,\,i_{{d_{c} }}$ are indices of the independent and dependent coordinates, respectively.

Motion of a link $\left. {\left( {\alpha ,i} \right)} \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}}$ with respect to the global reference frame ${\mathcal{F}}^{(0)}$ is described by the following vector:

$$ \left. {{\mathbf{q}}^{(\alpha ,i)} } \right|_{\begin{subarray}{l} \alpha \in \left\{ {c,c_{1} ,c_{2} } \right\} \\ i = 1, \ldots ,n_{l}^{(\alpha )} \end{subarray} } = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}^{{(b)^{T} }} } & {{\mathbf{q}}^{{(\alpha ,i - 1)^{T} }} } & {{\tilde{\mathbf{q}}}^{{(\alpha ,i)^{T} }} } \\ \end{array} } \right]^{T} , $$

(3)

where: $n_{l}^{(\alpha )}$ is the number of links (rigid and flexible) in chain $\alpha ,\;n_{l}^{(\alpha )} = n_{{r_{l} }}^{(\alpha )} + n_{{f_{l} }}^{(\alpha )} ,\;{\tilde{\mathbf{q}}}^{(\alpha ,i)}$ is a vector defining motion of link $\left( {\alpha ,i} \right)$ with respect to a preceding link $\left( {\alpha ,i - 1} \right)$ and ${\mathbf{q}}^{(\alpha ,0)} \in \emptyset .$

When the link $\left( {\alpha ,i} \right)$ is treated as flexible, its motion with respect to the preceding link is described by a vector:

$$ \left. {{\tilde{\mathbf{q}}}^{(\alpha ,i)} } \right|_{\begin{subarray}{l} \alpha \in \left\{ {c,c_{1} ,c_{2} } \right\} \\ i = 1, \ldots ,n_{l}^{(\alpha )} \end{subarray} } = \left[ {\begin{array}{*{20}c} {{\tilde{\mathbf{q}}}^{{(\alpha ,i,0)^{T} }} } & \cdots & {{\tilde{\mathbf{q}}}^{{(\alpha ,i,r)^{T} }} } & \cdots & {{\tilde{\mathbf{q}}}^{{(\alpha ,i,n_{rfe}^{(\alpha )} - 1)^{T} }} } \\ \end{array} } \right]^{T} , $$

(4)

where ${\tilde{\mathbf{q}}}^{(\alpha ,i,r)}$ is a vector defining motion of ${\text{rfe}}\,\left( {\alpha ,i,r} \right)$ with respect to the preceding ${\text{rfe}}\,\left( {\alpha ,i,r - 1} \right).$.

Homogeneous transformation matrices from a local frame of a link to the global reference frame ${\mathcal{F}}^{(0)}$ can be obtained in the following way:

$$ \left. {{\mathbf{T}}^{(\alpha ,i)} } \right|_{\begin{subarray}{l} \alpha \in \left\{ {c,c_{1} ,c_{2} } \right\} \\ i = 1, \ldots ,n_{l}^{(\alpha )} \end{subarray} } = {\mathbf{T}}^{(b)} \prod\limits_{j = 1}^{i} {{\tilde{\mathbf{T}}}^{(\alpha ,j)} } , $$

(5)

where: ${\mathbf{T}}^{(b)}$ is the transformation matrix from a frame ${\mathcal{F}}^{(b)}$ fixed at the flexibly supported base to the global reference frame ${\mathcal{F}}^{(0)}$ and ${\tilde{\mathbf{T}}}^{(\alpha ,j)}$ is the transformation matrix from a local frame of the link $\left( {\alpha ,i} \right)$ to a local frame of a preceding link in a kinematic chain.

The homogeneous transformation matrices of rfes from their local frames ${\mathcal{F}}^{(\alpha ,i,r)}$ to the global reference frame ${\mathcal{F}}^{(0)}$ are determined by:

$$ \left. {{\mathbf{T}}^{(\alpha ,i,r)} } \right|_{\begin{subarray}{l} \alpha \in \left\{ {c,c_{1} ,c_{2} } \right\} \\ i = 1, \ldots ,n_{l}^{(\alpha )} \\ r = 0, \ldots ,n_{rfe}^{(\alpha ,i)} - 1 \end{subarray} } = \left\{ {\begin{array}{*{20}c} {{\mathbf{T}}^{(b)} \prod\limits_{j = 0}^{r} {{\tilde{\mathbf{T}}}^{(\alpha ,i,j)} } \,\,\,\,\,} & {{\text{if}}\,\,i = 1,} \\ {{\mathbf{T}}^{(\alpha ,i - 1)} \prod\limits_{j = 0}^{r} {{\tilde{\mathbf{T}}}^{(\alpha ,i,j)} } } & {{\text{otherwise}}{.}} \\ \end{array} } \right. $$

(6)

2.2 Generalized Programmed Motion Equations (GPME) for systems subjected to position and velocity constraints

The constrained dynamics, referred to as the reference dynamics, is obtained based upon a dedicated method to constrained dynamics generation, i.e. upon the Generalized Programmed Motion Equations (GPME). The method developed for constrained rigid system structures subjected to arbitrary order nonholonomic constraints, which can specify motion demands and are called programmed, is detailed in [34, 35]. It enables verification of the system behavior when it is subjected to programmed constraints, e.g. vibrations that may accompany the desired motions specified by these constraints. It enables then defining and analyzing desired motions for performing servicing tasks. As detailed in [34, 35], the constraint equations imposed as control goals on system performance or as service tasks and can be presented in a general form as:

$$ {\mathbf{B}}\left( {t,{\mathbf{q}},{\dot{\mathbf{q}}},...,{\mathbf{q}}^{{{\mathbf{(}}p - 1{\mathbf{)}}}} } \right){\mathbf{q}}^{(p)} + {\mathbf{s}}\left( {t,{\mathbf{q}},{\dot{\mathbf{q}}},...,{\mathbf{q}}^{{{\mathbf{(}}p - 1{\mathbf{)}}}} } \right) = {\mathbf{0}}, $$

(7)

where: ${\mathbf{q}}^{(p)}$ is a $n_{dof}$-dimensional state vector, ${\mathbf{B}}$ is $\left( {n_{{d_{c} }}^{{}} \times n_{dof}^{{}} } \right)$ dimensional constraint matrix, $n_{dof} \ge n_{{d_{c} }}$, and ${\mathbf{s}}$ is a $n_{{d_{c} }}$-dimensional vector, $n_{{d_{c} }}$ is the number of dependent generalised coordinates.

The constraints can be material for $p = 0,1$, or programmed for $p \ge 1$. The programmed constraints are imposed by a designer or a control engineer to obtain a system desired performance, e.g. they can be imposed upon acceleration $p = 2$ or jerk $p = 3$, as well as for desired trajectories with $p = 1$. The constraints form (7) is the generalized constraint formulation and it encompasses the classical analytical constraint concept.

The GPME for rigid body models subjected to constraints (7) have the form:

$$ {\mathbf{M}}\left( {\mathbf{q}} \right){\mathbf{\ddot{q}}} - {\mathbf{h}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}}} \right) + {\mathbf{g}}\left( {\mathbf{q}} \right) = {\mathbf{Q}}\left( {t,{\mathbf{q}},{\dot{\mathbf{q}}}} \right), $$

(8.1)

$$ {\mathbf{B}}\left( {t,{\mathbf{q}},{\dot{\mathbf{q}}},...,{\mathbf{q}}^{{{\mathbf{(}}p - 1{\mathbf{)}}}} } \right){\mathbf{q}}^{(p)} + {\mathbf{s}}\left( {t,{\mathbf{q}},{\dot{\mathbf{q}}},...,{\mathbf{q}}^{{{\mathbf{(}}p - 1{\mathbf{)}}}} } \right) = {\mathbf{0}}, $$

(8.2)

where: ${\mathbf{M}}\left( {\mathbf{q}} \right)$ is mass matrix, ${\mathbf{h}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}}} \right)$ is a vector of centrifugal forces, ${\mathbf{g}}\left( {\mathbf{q}} \right)$ is a vector of gravity forces, ${\mathbf{Q}}\left( {t,{\mathbf{q}},{\dot{\mathbf{q}}}} \right)$ is a vector of generalized forces vector resulting from external actions which are not controls. The set of Eqs. (8.1) and (8.2) can be transformed to the form that uses directly functions for the kinetic and potential energies, as well as explicit forms of external forces on a system.

The GPME modified for flexible open-loop structures subjected to position constraints are detailed in [33].

For the development of a general structure of the automated CoPCoD, we take advantage of the form of the GPME that uses the energy and force functions. Also, the actual form of the CoPCoD can incorporate position and velocity constraints, both material and non-material into system dynamics. From engineering application points of view such constraints are the most significant ones. Modifications that are dedicated to motion description of rigid and flexible open and closed-loop substructures have to be substantiated. The modified new structure of the GPME for position and velocity constraints is introduced as follows

$$ \frac{{\partial R_{1} }}{{\partial \dot{q}_{v} }} + \sum\limits_{{w \in i_{{d_{c} }} }} {\frac{{\partial R_{1} }}{{\partial \dot{q}_{w} }}} \frac{{\partial \dot{q}_{w} }}{{\partial \dot{q}_{v} }} = 0,\;\;\;\;v \in i_{{i_{c} }} , $$

(9.1)

$$ {{\varvec{\Phi}}}(t,{\mathbf{q}}) = {\mathbf{0}}, $$

(9.2)

where now the function $R_{1}$ that collects the system energies and forces is composed of

$$ R_{1} = \left\{ {\begin{array}{*{20}l} {R_{1}^{(b)} + \,R_{1}^{(c)} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \hfill & {{\text{for}}} \hfill & {{\text{OLKC}},} \hfill \\ {R_{1}^{(b)} + \,\sum\limits_{{\beta \in \left\{ {c_{1} ,c_{2} } \right\}}} {R_{1}^{(\beta )} } } \hfill & {{\text{for}}} \hfill & {{\text{CLKC}},} \hfill \\ \end{array} } \right. $$

$$ R_{1}^{(b)} = \dot{E}_{k}^{(b)} - 2\sum\limits_{v = 1}^{{n_{dof}^{(b)} }} {\frac{{\partial E_{k}^{(b)} }}{{\partial q_{v}^{(b)} }}\dot{q}_{v}^{(b)} } + \sum\limits_{v = 1}^{{n_{dof}^{(b)} }} {\frac{{\partial E_{p}^{(b)} }}{{\partial q_{v}^{(b)} }}\dot{q}_{v}^{(b)} } + \sum\limits_{v = 1}^{{n_{dof}^{(b)} }} {\frac{{\partial R_{sup}^{(b)} }}{{\partial \dot{q}_{v}^{(b)} }}\dot{q}_{v}^{(b)} } , $$

$$ R_{1}^{(\alpha )} = E_{k}^{(\alpha )} - 2\sum\limits_{v = 1}^{{n_{dof}^{(\alpha )} }} {\frac{{\partial E_{k}^{(\alpha )} }}{{\partial q_{v}^{(\alpha )} }}\dot{q}_{v}^{(\alpha )} } + \sum\limits_{v = 1}^{{n_{dof}^{(\alpha )} }} {\frac{{\partial E_{p}^{(\alpha )} }}{{\partial q_{v}^{(\alpha )} }}\dot{q}_{v}^{(\alpha )} } + \sum\limits_{v = 1}^{{n_{dof}^{(\alpha )} }} {\frac{{\partial R_{{f_{l} }}^{(\alpha )} }}{{\partial \dot{q}_{v}^{(\alpha )} }}\dot{q}_{v}^{(\alpha )} } + \sum\limits_{v = 1}^{{n_{dof}^{(\alpha )} }} {f_{fric,v}^{(\alpha )} \,\dot{q}_{v}^{(\alpha )} } , $$

$E_{k}^{(b)} ,\,\,\left. {E_{k}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}}$ are kinetic energy terms of the flexibly supported base and the chains,

$E_{p}^{(b)} = E_{p,sup}^{(b)} + E_{p,g}^{(b)}$ is the potential energy of the base which can be calculated as a sum of spring deformations energy and the potential energy of the gravity forces,

$\left. {E_{p}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}} = E_{p,g}^{(\alpha )} + E_{{p,f_{l} }}^{(\alpha )}$ is the potential energy of the chain which can be expressed as a sum of spring deformations energy of flexible links and the potential energy of the gravity forces of links,

$R_{sup}^{(b)} ,\,\,\left. {R_{{f_{l} }}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}}$ are the Rayleigh dissipation functions of the flexibly supported base and the chains,

$\left. {{\mathbf{f}}_{fric}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}}$ is the vector of friction forces acting in the joints,

${{\varvec{\Phi}}}(t,{\mathbf{q}})$ are the programmed and kinematic constraint equations.

Thus, in order to derive the CoPCoD, it is required to determine the kinetic and potential energies, the Rayleigh dissipation functions and external forces for components of kinematic chains, as well as formulate the constraint equations.

2.2.1 Kinetic energy of the system

The kinetic energy of the system structure can be presented in the following forms:

$$ E_{k}^{(b)} = \frac{1}{2}{\text{tr}}\left( {{\dot{\mathbf{T}}}^{(b)} {\mathbf{H}}^{(b)} {\dot{\mathbf{T}}}^{{(b)^{T} }} } \right), $$

(10.1)

$$ \left. {E_{k}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}} = \frac{1}{2}\sum\nolimits_{{i \in I_{{r_{l} }}^{(\alpha )} }} {{\text{tr}}\left( {{\dot{\mathbf{T}}}^{(\alpha ,i)} {\mathbf{H}}^{(\alpha ,i)} {\dot{\mathbf{T}}}^{{(\alpha ,i)^{T} }} } \right)} + \frac{1}{2}\sum\nolimits_{{i \in I_{{f_{l} }}^{(\alpha )} }} {\sum\limits_{r = 0}^{{n_{rfe}^{(\alpha ,i)} - 1}} {{\text{tr}}\left( {{\dot{\mathbf{T}}}^{(\alpha ,i,r)} {\mathbf{H}}^{(\alpha ,i,r)} {\dot{\mathbf{T}}}^{{(\alpha ,i,r)^{T} }} } \right)} } , $$

(10.2)

where:

$\left. {{\mathbf{H}}_{{}}^{(\gamma )} } \right|_{{\gamma \in \left\{ {b,(\alpha ,i),(\alpha ,i,r)} \right\}}}$ is the pseudo-inertia matrix of the link,${\mathbf{H}}^{(\gamma )} = \left[ {\begin{array}{*{20}c} {h_{(yz)}^{(\gamma )} } & {h_{xy}^{(\gamma )} } & {h_{xz}^{(\gamma )} } & {h_{x}^{(\gamma )} } \\ {} & {h_{(xz)}^{(\gamma )} } & {h_{yz}^{(\gamma )} } & {h_{y}^{(\gamma )} } \\ {} & {} & {h_{(xy)}^{(\gamma )} } & {h_{z}^{(\gamma )} } \\ {{\text{sym}}.} & {} & {} & {m^{(\gamma )} } \\ \end{array} } \right],$$m_{{}}^{(\gamma )}$ is the mass of the link, $\left. {h_{\xi }^{(\gamma )} } \right|_{{\xi \in \{ x,y,z\} }}$ are the static moments of inertia, $\left. {h_{\xi }^{(\gamma )} } \right|_{{\xi \in \{ xy,xz,yz\} }}$ are the products of inertia, $\left. {h_{\xi }^{(\gamma )} } \right|_{{\xi \in \left\{ {(yz),(xz),(xy)} \right\}}}$ are the moments of inertia with respect to the planes of the local reference frame of the link, $I_{{r_{l} }}^{(\alpha )} ,\,\,I_{{f_{l} }}^{(\alpha )}$ are the indices of rigid and flexible links.

In Eq. (9.1) derivatives of the function $R_{1}$ components with respect to time and generalized coordinates require determining the following derivatives:

$$ \dot{E}_{k}^{(b)} = {\text{tr}}\left( {{\dot{\mathbf{T}}}^{(b)} {\mathbf{H}}^{(b)} {\mathbf{\ddot{T}}}^{{(b)^{T} }} } \right), $$

(11.1)

$$ \left. {\dot{E}_{k}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}} = \sum\nolimits_{{i \in I_{{r_{l} }}^{(\alpha )} }} {{\text{tr}}\left( {{\dot{\mathbf{T}}}^{(\alpha ,i)} {\mathbf{H}}^{(\alpha ,i)} {\mathbf{\ddot{T}}}^{{(\alpha ,i)^{T} }} } \right)} + \sum\nolimits_{{i \in I_{{r_{l} }}^{(\alpha )} }} {\sum\limits_{r = 0}^{{n_{rfe}^{(\alpha ,i)} - 1}} {{\text{tr}}\left( {{\dot{\mathbf{T}}}^{(\alpha ,i,r)} {\mathbf{H}}^{(\alpha ,i,r)} {\mathbf{\ddot{T}}}^{{(\alpha ,i,r)^{T} }} } \right)} } , $$

(11.2)

$$ \frac{{\partial E_{k}^{(b)} }}{{\partial q_{v}^{(b)} }} = {\text{tr}}\left( {{\mathbf{T}}_{v}^{(b)} {\mathbf{H}}^{(b)} {\dot{\mathbf{T}}}^{{(b)^{T} }} } \right), $$

(11.3)

$$ \left. {\frac{{\partial E_{k}^{(\alpha )} }}{{\partial q_{v}^{(\alpha )} }}} \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}} = \sum\limits_{{i \in I_{{r_{l} }}^{(\alpha )} }}^{{}} {{\text{tr}}\left( {{\mathbf{T}}_{v}^{(\alpha ,i)} {\mathbf{H}}^{(\alpha ,i)} {\dot{\mathbf{T}}}^{{(\alpha ,i)^{T} }} } \right)} + \sum\limits_{{i \in I_{{f_{l} }}^{(\alpha )} }}^{{}} {\sum\limits_{r = 0}^{{n_{rfe}^{(\alpha ,i)} - 1}} {{\text{tr}}\left( {{\mathbf{T}}_{v}^{(\alpha ,i,r)} {\mathbf{H}}^{(\alpha ,i,r)} {\dot{\mathbf{T}}}^{{(\alpha ,i,r)^{T} }} } \right)} } , $$

(11.4)

where $\left. {{\mathbf{T}}_{v}^{(\gamma )} } \right|_{{\gamma \in \left\{ {b,(\alpha ,i),(\alpha ,i,r)} \right\}}} = \frac{{\partial {\mathbf{T}}^{(\gamma )} }}{{\partial q_{v}^{(\gamma )} }}.$

The time derivatives of the transformation matrices are determined by the following formulas:

$$ \left. {{\dot{\mathbf{T}}}^{(\gamma )} } \right|_{{\gamma \in \left\{ {b,(\alpha ,i),(\alpha ,i,r)} \right\}}} = \sum\limits_{v = 1}^{{n_{dof}^{(\gamma )} }} {{\mathbf{T}}_{v}^{(\gamma )} \dot{q}_{v}^{(\gamma )} } , $$

(12.1)

$$ \left. {{\mathbf{\ddot{T}}}^{(\gamma )} } \right|_{{\gamma \in \left\{ {b,(\alpha ,i),(\alpha ,i,r)} \right\}}} = \sum\limits_{v = 1}^{{n_{dof}^{(\gamma )} }} {{\mathbf{T}}_{v}^{(\gamma )} \ddot{q}_{v}^{(\gamma )} } + \sum\limits_{v = 1}^{{n_{dof}^{(\gamma )} }} {\sum\limits_{w = 1}^{{n_{dof}^{(\gamma )} }} {{\mathbf{T}}_{vw}^{(\gamma )} \dot{q}_{v}^{(\gamma )} \dot{q}_{w}^{(\gamma )} } } , $$

(12.2)

where: $\left. {{\mathbf{T}}_{v,w}^{(\gamma )} } \right|_{{\gamma \in \left\{ {b,(\alpha ,i),(\alpha ,i,r)} \right\}}} = \frac{{\partial^{2} {\mathbf{T}}^{(\gamma )} }}{{\partial q_{v}^{(\gamma )} \partial q_{w}^{(\gamma )} }}.$

2.2.2 Potential energy of the system gravity force

The potential energy of the gravity force that acts on the chains can be presented as follows:

$$ E_{p,g}^{(b)} = m^{(b)} g\,{\mathbf{j}}_{2} {\mathbf{T}}^{(b)} {\tilde{\mathbf{r}}}_{C}^{(b)} , $$

(13.1)

$$ \left. {E_{p,g}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}} = \sum\limits_{{i \in i_{{r_{l} }}^{(\alpha )} }}^{{}} {m^{(\alpha ,i)} g\,{\mathbf{j}}_{2} {\mathbf{T}}^{(\alpha ,i)} {\tilde{\mathbf{r}}}_{C}^{(\alpha ,i)} } + \sum\limits_{{i \in i_{{f_{l} }}^{(\alpha )} }}^{{}} {\sum\limits_{r = 0}^{{n_{rfe}^{(\alpha ,i)} - 1}} {m^{(\alpha ,i,r)} g\,{\mathbf{j}}_{2} {\mathbf{T}}^{(\alpha ,i,r)} {\tilde{\mathbf{r}}}_{C}^{(\alpha ,i,r)} } } , $$

(13.2)

where g is the gravity acceleration, $\left. {{\tilde{\mathbf{r}}}_{C}^{(\gamma )} } \right|_{{\gamma \in \left\{ {b,(\alpha ,i),(\alpha ,i,r)} \right\}}}$ are position vectors of the mass center of the link, ${\mathbf{j}}_{2}$ is the second row of a reducing matrix ${\mathbf{J}} = \left[ {\begin{array}{*{20}c} {{\mathbf{j}}_{1} } \\ {{\mathbf{j}}_{2} } \\ {{\mathbf{j}}_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}r} \hfill 1 & \hfill 0 & \hfill 0 & \hfill 0 \\ \hfill 0 & \hfill 1 & \hfill 0 & \hfill 0 \\ \hfill 0 & \hfill 0 & \hfill 1 & \hfill 0 \\ \end{array} } \right]$.

The derivatives of Eqs. (13.1 and 13.2) with respect to the generalized coordinates are written as follows:

$$ \frac{{\partial E_{p,g}^{(b)} }}{{\partial q_{v}^{(b)} }} = m^{(b)} g\,{\mathbf{j}}_{2} {\mathbf{T}}_{v}^{(b)} {\tilde{\mathbf{r}}}_{C}^{(b)} , $$

(14.1)

$$ \frac{{\partial E_{p,g}^{(\alpha )} }}{{\partial q_{v}^{(\alpha )} }} = \sum\limits_{{i \in I_{{r_{l} }}^{(\alpha )} }}^{{}} {m^{(\alpha ,i)} g\,{\mathbf{j}}_{2} {\mathbf{T}}_{v}^{(\alpha ,i)} {\tilde{\mathbf{r}}}_{C}^{(\alpha ,i)} } + \sum\limits_{{i \in I_{{f_{l} }}^{(\alpha )} }}^{{}} {\sum\limits_{r = 0}^{{n_{rfe}^{(\alpha ,i)} - 1}} {m^{(\alpha ,i,r)} g\,{\mathbf{j}}_{2} {\mathbf{T}}_{v}^{(\alpha ,i,r)} {\tilde{\mathbf{r}}}_{C}^{(\alpha ,i,r)} } } \,. $$

(14.2)

2.2.3 Potential energy of spring deformations and the Rayleigh dissipation function of the base support

The flexible support of the base is modelled by means of spring-damping elements as shown in Fig. 2. Positions of the supports are described with respect to the base fixed frame. It is assumed that deformations of the spring-damping elements are small and the transformation matrix can be linearized.

Fig. 2

Flexible support of the base

The spring deformation energy and the Rayleigh dissipation function of the spring-damping elements are determined according to the following formulas:

$$ E_{p,sup}^{(b)} = \frac{1}{2}\sum\limits_{i = 1}^{{n_{e} }} {\sum\limits_{j = 1}^{{n_{{sde_{s} }}^{(i)} }} {\left( {{\mathbf{d}}_{{sde_{s} }}^{(i,j)} } \right)^{T} } {\mathbf{S}}_{{sde_{s} }}^{(i,j)} {\mathbf{d}}_{{sde_{s} }}^{(i,j)} } , $$

(15.1)

$$ R_{sup}^{(b)} = \frac{1}{2}\sum\limits_{i = 1}^{{n_{e} }} {\sum\limits_{j = 1}^{{n_{{sde_{s} }}^{(i)} }} {\left( {{\dot{\mathbf{d}}}_{{sde_{s} }}^{(i,j)} } \right)^{T} } {\mathbf{D}}_{{sde_{s} }}^{(i,j)} {\dot{\mathbf{d}}}_{{sde_{s} }}^{(i,j)} } , $$

(15.2)

where: ${\mathbf{d}}_{{sde_{s} }}^{(i,j)}$ is a vector of deformation of ${\text{sde}}_{s} \,(i,j),\;{\mathbf{d}}_{{sde_{s} }}^{(i,j)} = {\mathbf{J}}{\Delta }{\mathbf{r}}_{{E_{ij} }}^{(b)} = {\mathbf{J}}\left( {{\mathbf{T}}^{(b)} {\tilde{\mathbf{r}}}_{{E_{ij} }}^{(b)} - {\mathbf{r}}_{{E_{ij,0} }}^{(b)} } \right),\;{\mathbf{r}}_{{E_{ij,0} }}^{(b)}$ is a position vector of point $E_{ij}^{{}}$ in the undeformed state,

${\mathbf{S}}_{{sde_{s} }}^{(i,j)} = {\text{diag}}\left( {s_{{sde_{s} ,x}}^{(i,j)} ,s_{{sde_{s} ,y}}^{(i,j)} ,s_{{sde_{s} ,z}}^{(i,j)} } \right),\;{\mathbf{D}}_{{sde_{s} }}^{(i,j)} = {\text{diag}}\left( {d_{{sde_{s} ,x}}^{(i,j)} ,d_{{sde_{s} ,y}}^{(i,j)} ,d_{{sde_{s} ,z}}^{(i,j)} } \right)$ are matrices containing stiffness and damping coefficients of ${\text{sde}}_{s} \left( {i,j} \right).$

The derivatives of Eqs. (15.1) and (15.2) with respect to the generalized coordinates and velocities are written as follows:

$$ \frac{{\partial E_{p,sup}^{(b)} }}{{\partial q_{v}^{(b)} }} = \sum\limits_{i = 1}^{{n_{e} }} {\sum\limits_{j = 1}^{{n_{{sde_{s} }}^{(i)} }} {\left( {\frac{{\partial {\mathbf{d}}_{{sde_{s} }}^{(i,j)} }}{{\partial q_{v}^{(b)} }}} \right)^{T} } {\mathbf{S}}_{{sde_{s} }}^{(i,j)} {\mathbf{d}}_{{sde_{s} }}^{(i,j)} } , $$

(16.1)

$$ \frac{{\partial R_{sup}^{(b)} }}{{\partial \dot{q}_{v}^{(b)} }} = \sum\limits_{i = 1}^{{n_{e} }} {\sum\limits_{j = 1}^{{n_{{sde_{s} }}^{(i)} }} {\left( {\frac{{\partial {\dot{\mathbf{d}}}_{{sde_{s} }}^{(i,j)} }}{{\partial \dot{q}_{v}^{(b)} }}} \right)^{T} } {\mathbf{D}}_{{sde_{s} }}^{(i,j)} {\dot{\mathbf{d}}}_{{sde_{s} }}^{(i,j)} } , $$

(16.2)

2.2.4 Potential energy of spring deformations and the Rayleigh dissipation function of flexible links

The energy of spring deformations and the Rayleigh dissipation function of flexible links are written in the following forms:

$$ \left. {E_{{p,f_{l} }}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}} = \frac{1}{2}\sum\limits_{{i \in I_{{f_{l} }}^{(\alpha )} }} {\sum\limits_{j = 1}^{{n_{{sde_{l} }}^{(\alpha ,i)} }} {\left( {{\mathbf{d}}_{{sde_{l} }}^{(\alpha ,i,j)} } \right)^{T} } {\mathbf{S}}_{{sde_{l} }}^{(\alpha ,i,j)} {\mathbf{d}}_{{sde_{l} }}^{(\alpha ,i,j)} } , $$

(17.1)

$$ \left. {R_{{f_{l} }}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}} = \frac{1}{2}\sum\limits_{{i \in I_{{f_{l} }}^{(\alpha )} }} {\sum\limits_{j = 1}^{{n_{{sde_{l} }}^{(\alpha ,i)} }} {\left( {{\dot{\mathbf{d}}}_{{sde_{{_{{}} }} }}^{(\alpha ,i,j)} } \right)^{T} } {\mathbf{D}}_{{sde_{l} }}^{(\alpha ,i,j)} {\dot{\mathbf{d}}}_{{sde_{l} }}^{(\alpha ,i,j)} } , $$

(17.2)

where ${\mathbf{d}}_{{sde_{l} }}^{(\alpha ,i,j)}$ is a vector of deformation of $\begin{gathered} {\text{sde}}_{l} \,(\alpha ,i,j),\;{\mathbf{d}}_{{sde_{l} }}^{(\alpha ,i,j)} = {\tilde{\mathbf{q}}}^{(\alpha ,i,j)} ,\;{\mathbf{S}}_{{sde_{l} }}^{(\alpha ,i,j)} = {\text{diag}}\left( {s_{{sde_{l} ,\psi }}^{(\alpha ,i,j)} ,s_{{sde_{l} ,\theta }}^{(\alpha ,i,j)} ,s_{{sde_{{_{l} }} ,\varphi }}^{(\alpha ,i,j)} } \right), \hfill \\ {\mathbf{D}}_{{sde_{l} }}^{(\alpha ,i,j)} = {\text{diag}}\left( {d_{{sde_{l} ,\psi }}^{(\alpha ,i,j)} ,d_{{sde_{l} ,\theta }}^{(\alpha ,i,j)} ,d_{{sde_{l} ,\varphi }}^{(\alpha ,i,j)} } \right) \hfill \\ \end{gathered}$ are stiffness and damping matrices of ${\text{sde}}_{l} \,(\alpha ,i,j).$

The derivatives of Eqs. (17.1) and (17.2) with respect to the generalized coordinates and velocities are written as:

$$ \frac{{\left. {\partial E_{{p,f_{l} }}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}} }}{{\partial {\tilde{\mathbf{q}}}_{{}}^{(\alpha ,i,j)} }} = \sum\limits_{{i \in I_{{f_{l} }}^{(\alpha )} }} {\sum\limits_{j = 1}^{{n_{{sde_{l} }}^{(\alpha ,i)} }} {{\mathbf{S}}_{{sde_{l} }}^{(\alpha ,i,j)} {\tilde{\mathbf{q}}}^{(\alpha ,i,j)} } } , $$

(18.1)

$$ \frac{{\left. {\partial R_{{f_{l} }}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}} }}{{\partial {\mathbf{\dot{\tilde{q}}}}_{{}}^{(\alpha ,i,j)} }} = \sum\limits_{{i \in I_{{f_{l} }}^{(\alpha )} }} {\sum\limits_{j = 1}^{{n_{{sde_{l} }}^{(\alpha ,i)} }} {{\mathbf{D}}_{{sde_{l} }}^{(\alpha ,i,j)} {\mathbf{\dot{\tilde{q}}}}^{(\alpha ,i,j)} .} } $$

(18.2)

It can be seen that deformations and deformation velocities of ${\text{sde}}_{l} \,(\alpha ,i,j)$ are taken directly from the generalized coordinates vector and its derivative.

2.2.5 Generalized forces resulting from actions of friction torques and forces

The LuGre friction model [39] is used to describe friction phenomenon in joints. Planar models of revolute and prismatic joints with friction are presented in Fig. 3.

Fig. 3

Friction models in revolute a and prismatic b joints

The generalized forces vector of a chain $\alpha$ resulting from including friction in joints can be written as follows:

$$ \left. {{\mathbf{f}}_{fric}^{(\alpha )} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}} = \sum\limits_{{i \in I_{{r_{l} }}^{(\alpha )} }}^{{}} {{\mathbf{f}}_{fric}^{(\alpha ,i)} } + \sum\limits_{{i \in I_{{f_{l} }}^{(\alpha )} }}^{{}} {{\mathbf{f}}_{fric}^{(\alpha ,i,0)} } , $$

(19)

where ${\mathbf{f}}_{fric}^{(\alpha ,i)} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & \cdots & {f_{fric,j}^{(\alpha ,i)} } & \cdots & {\mathbf{0}} \\ \end{array} } \right].$

Forces $f_{fric,j}^{(\alpha ,i)}$ are non-zero elements containing friction forces acting on links $(\alpha ,i)$ and can be presented in the form:

$$ \left. {f_{fric,j}^{(\alpha ,i)} } \right|_{{\alpha \in \left\{ {c,c_{1} ,c_{2} } \right\}}} = \left\{ \begin{gathered} t_{f}^{(\alpha ,i)} \;{\text{for}}\,\,{\text{a revolute}}\,\,{\text{joint,}} \hfill \\ f_{f}^{(\alpha ,i)} \;{\text{for}}\,\,{\text{a prismatic}}\,\,\,{\text{joint}}{.} \hfill \\ \end{gathered} \right. $$

(20)

Friction torques and forces are calculated as follows:

$$ t_{f}^{(\alpha ,i)} = \mu^{(\alpha ,i)} \tilde{f}_{n}^{(\alpha ,i)} \frac{{d^{(\alpha ,i)} }}{2}, $$

(21.1)

$$ f_{f}^{(\alpha ,i)} = \mu^{(\alpha ,i)} \tilde{f}_{n}^{(\alpha ,i)} , $$

(21.2)

where: $\mu_{{}}^{(\alpha ,i)}$ is a friction coefficient,

$\tilde{f}_{n}^{(\alpha ,i)}$ is a normal force in a joint, $\tilde{f}_{n}^{(\alpha ,i)} = \left\{ {\begin{array}{*{20}c} {\sqrt {\left( {\tilde{f}_{x}^{(\alpha ,i)} } \right)^{2} + \left( {\tilde{f}_{y}^{(\alpha ,i)} } \right)^{2} } } & {{\text{for}}\,\,{\text{a revolute}}\,\,{\text{joint}},\,} \\ {\tilde{f}_{x}^{(\alpha ,i)} } & {\,{\text{for}}\,\,{\text{a prismatic}}\,\,{\text{joint}}{.}} \\ \end{array} } \right.$

$\tilde{f}_{x}^{(\alpha ,i)} ,\tilde{f}_{y}^{(\alpha ,i)}$ are joint forces, $d_{{}}^{(\alpha ,i)}$ is a diameter of the journal.

The joint forces can be determined, in each integration step of the dynamics equations of motion, using the recursive Newton–Euler algorithm.

Friction coefficients are calculated using the LuGre friction model from the following formula:

$$ \mu_{{}}^{(\alpha ,i)} = \sigma_{0}^{(\alpha ,i)} z_{{}}^{(\alpha ,i)} + \sigma_{1}^{(\alpha ,i)} \dot{z}^{(\alpha ,i)} + \sigma_{2}^{(\alpha ,i)} \dot{\tilde{q}}^{(\alpha ,i)} , $$

(22)

where: $\sigma_{0}^{(\alpha ,i)} ,\sigma_{1}^{(\alpha ,i)} ,\sigma_{2}^{(\alpha ,i)}$ are stiffness, damping and viscous friction coefficients, $z_{{}}^{(\alpha ,i)}$ is the state variable, $\dot{z}^{(\alpha ,i)} = \dot{\tilde{q}}_{{}}^{(\alpha ,i)} \left( {1 - \frac{{\sigma_{0}^{(\alpha ,i)} z_{{}}^{(\alpha ,i)} {\text{sgn}} \left( {\dot{\tilde{q}}_{{}}^{(\alpha ,i)} } \right)}}{{\mu_{k}^{(\alpha ,i)} + \left( {\mu_{s}^{(\alpha ,i)} - \mu_{k}^{(\alpha ,i)} } \right)\exp \left( { - \left( {\frac{{\dot{\tilde{q}}_{{}}^{(\alpha ,i)} }}{{\dot{\tilde{q}}_{S}^{(\alpha ,i)} }}} \right)^{2} } \right)}}} \right),$

$\mu_{s}^{(\alpha ,i)} ,\mu_{k}^{(\alpha ,i)}$ are static and kinetic friction coefficients, $\dot{\tilde{q}}_{S}^{(\alpha ,i)}$ is the Stribeck velocity.

2.3 Kinematic and programmed constraint equations

The GPME (9.1) needs to be supplemented by constraint equations composed of $n_{k}$ kinematic and $n_{p}$ programmed constraint equations which can be written in the following form:

$$ {{\varvec{\Phi}}}\left( {t,{\mathbf{q}}} \right) \equiv \left\{ {\begin{array}{*{20}l} {{{\varvec{\Phi}}}_{p} \left( {\mathbf{q}} \right) + {\mathbf{g}}_{p} (t) = {\mathbf{0}}} \hfill & {{\text{for}}\,\,{\text{OLKC}},} \hfill \\ {\left\{ \begin{gathered} {{\varvec{\Phi}}}_{k} \left( {\mathbf{q}} \right) = {\mathbf{0}} \hfill \\ {{\varvec{\Phi}}}_{p} \left( {\mathbf{q}} \right) + {\mathbf{g}}_{p} (t) = {\mathbf{0}} \hfill \\ \end{gathered} \right.} \hfill & {{\text{for}}\,\,{\text{CLKC,}}} \hfill \\ \end{array} } \right. $$

(23)

where ${{\varvec{\Phi}}}_{k} \left( {\mathbf{q}} \right),\;{{\varvec{\Phi}}}_{p} \left( {\mathbf{q}} \right)$ are kinematic and programmed constraints equations, ${\mathbf{g}}_{p} (t)$ is a vector of known time functions. The kinematic constraints come from closed chains modelling and are material constraints.

Time derivatives of the constraint Eqs. (23) lead to:

$$ {\dot{\mathbf{\Phi }}}\left( {t,{\mathbf{q}},\,{\dot{\mathbf{q}}}} \right) \equiv \left\{ {\begin{array}{*{20}l} {{{\varvec{\Phi}}}_{{p,{\mathbf{q}}}} \left( {\mathbf{q}} \right){\dot{\mathbf{q}}} + {\dot{\mathbf{g}}}_{p} (t) = {\mathbf{0}}} \hfill & {{\text{for}}\,\,{\text{OLKC}},} \hfill \\ {\left\{ \begin{gathered} {{\varvec{\Phi}}}_{{k,{\mathbf{q}}}} \left( {\mathbf{q}} \right){\dot{\mathbf{q}}} = {\mathbf{0}} \hfill \\ {{\varvec{\Phi}}}_{{p,{\mathbf{q}}}} \left( {\mathbf{q}} \right){\dot{\mathbf{q}}} + {\dot{\mathbf{g}}}_{p} (t) = {\mathbf{0}} \hfill \\ \end{gathered} \right.} \hfill & {{\text{for}}\,\,{\text{CLKC}},} \hfill \\ \end{array} } \right. $$

(24.1)

$$ {\mathbf{\ddot{\Phi }}}\left( {t,{\mathbf{q}},{\dot{\mathbf{q}}},\,{\mathbf{\ddot{q}}}} \right) \equiv \left\{ {\begin{array}{*{20}l} {{{\varvec{\Phi}}}_{{p,{\mathbf{q}}}} \left( {\mathbf{q}} \right){\mathbf{\ddot{q}}} + {\dot{\mathbf{\Phi }}}_{{p,{\mathbf{q}}}} \left( {\mathbf{q}} \right){\dot{\mathbf{q}}} + {\mathbf{\ddot{g}}}_{p} (t) = {\mathbf{0}}} \hfill & {{\text{for}}\,\,{\text{OLKC}},} \hfill \\ {\left\{ \begin{gathered} {{\varvec{\Phi}}}_{{k,{\mathbf{q}}}} \left( {\mathbf{q}} \right){\mathbf{\ddot{q}}} + {\dot{\mathbf{\Phi }}}_{{k,{\mathbf{q}}}} \left( {\mathbf{q}} \right){\dot{\mathbf{q}}} = {\mathbf{0}} \hfill \\ {{\varvec{\Phi}}}_{{p,{\mathbf{q}}}} \left( {\mathbf{q}} \right){\mathbf{\ddot{q}}} + {\dot{\mathbf{\Phi }}}_{{p,{\mathbf{q}}}} \left( {\mathbf{q}} \right){\dot{\mathbf{q}}} + {\mathbf{\ddot{g}}}_{p} (t) = {\mathbf{0}} \hfill \\ \end{gathered} \right.} \hfill & {{\text{for}}\,\,{\text{CLKC}},} \hfill \\ \end{array} } \right. $$

(24.2)

where: ${{\varvec{\Phi}}}_{{k,{\mathbf{q}}}} \left( {\mathbf{q}} \right) = \frac{{\partial {{\varvec{\Phi}}}_{k} }}{{\partial {\mathbf{q}}}},\;{{\varvec{\Phi}}}_{{p,{\mathbf{q}}}} \left( {\mathbf{q}} \right) = \frac{{\partial {{\varvec{\Phi}}}_{p} }}{{\partial {\mathbf{q}}}}$ are kinematic and programmed constraint matrices.

The vector of depended velocities calculated from Eq. (24.1) takes the form:

$$ {\dot{\mathbf{q}}}_{{d_{c} }} = {{\varvec{\Phi}}}_{{{\mathbf{q}},d_{c} }}^{ - 1} {{\varvec{\Phi}}}_{{{\mathbf{q}},i_{c} }}^{{}} {\dot{\mathbf{q}}}_{{i_{c} }} , $$

(25)

where: ${{\varvec{\Phi}}}_{{{\mathbf{q}},i_{c} }} ,\;{{\varvec{\Phi}}}_{{{\mathbf{q}},d_{c} }}$ are obtained the from the global constraint matrix ${{\varvec{\Phi}}}_{{\mathbf{q}}}^{{}} = \left[ {\begin{array}{*{20}c} {{{\varvec{\Phi}}}_{{k,{\mathbf{q}}}}^{{}} } \\ {{{\varvec{\Phi}}}_{{p,{\mathbf{q}}}}^{{}} } \\ \end{array} } \right]$ by selecting rows and columns corresponding to indices of the independent and dependent variables in vector q.

2.4 The computational procedure for constrained dynamics (CoPCoD) for systems subjected to constraints – the general form

Substituting components from Eqs. (11.1) – (11.4), (14.1), (14.2), (16.1), (16.2), (18.1), (18.2), (19), (24.1) and (24.2), to the GMPE Eq. (9.1), and performing all transformations, the CoPCoD underlying equations are obtained in the following matrix form:

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{{i_{c} }}^{{}} + {\mathbf{M}}_{{d_{c} }}^{{}} } \\ {{{\varvec{\Phi}}}_{{p,{\mathbf{q}}}} } \\ {{\overline{\mathbf{\Phi }}}_{{k,{\mathbf{q}}}} } \\ \end{array} } \right]{\mathbf{\ddot{q}}} = \left[ {\begin{array}{*{20}l} {{\mathbf{h}}_{{i_{c} }} + {\mathbf{Q}}_{{i_{c} }} + \Delta {\mathbf{Q}}_{{i_{c} }} + {\mathbf{h}}_{{d_{c} }} + {\mathbf{Q}}_{{d_{c} }} + \Delta {\mathbf{Q}}_{{d_{c} }} } \hfill \\ { - {\dot{\mathbf{\Phi }}}_{{p,{\mathbf{q}}}} {\dot{\mathbf{q}}} - {\mathbf{\ddot{g}}}_{p} (t)} \hfill \\ { - {\mathbf{\dot{\overline{\Phi }}}}_{{k,{\mathbf{q}}}} {\dot{\mathbf{q}}}} \hfill \\ \end{array} } \right], $$

(26)

where:

${\mathbf{M}}_{{i_{c} }} = \left( {{\text{row}}_{i} ({\mathbf{M}})} \right)_{{i \in i_{{i_{c} }} }} ,\;{\mathbf{M}}_{{d_{c} }} = \left( {\sum\limits_{{j \in i_{{d_{c} }} }}^{{}} {{\text{row}}_{j} \left( {\mathbf{M}} \right)\frac{{\partial \dot{q}_{j} }}{{\partial \dot{q}_{i} }}} } \right)_{{i \in i_{{i_{c} }} }} ,\;{\text{row}}_{i} ( \cdot )$ is the i-th matrix row,

$$ {\mathbf{M}} = \left\{ {\begin{array}{*{20}c} {{\mathbf{M}}^{(b)} + {\mathbf{M}}^{(c)} } & {{\text{for}}\,\,{\text{OLKC}},} \\ {{\mathbf{M}}^{(b)} + \sum\limits_{{\beta \in \left\{ {c_{1} ,c_{2} } \right\}}} {{\mathbf{M}}^{(\beta )} } } & {{\text{for}}\,\,{\text{CLKC}},} \\ \end{array} } \right. $$

$$ {\mathbf{M}}^{(b)} = \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{1,1}^{(b)} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right],\;{\mathbf{M}}_{11}^{(b)} = \left( {m_{i,j}^{(b)} } \right)_{{i,j = 1, \ldots ,n_{dof}^{(b)} }} ,\;m_{i,j}^{(b)} = {\text{tr}}\left\{ {{\mathbf{T}}_{i}^{(b)} {\mathbf{H}}^{(b)} {\mathbf{T}}_{j}^{{(b)^{T} }} } \right\}, $$

$$ {\mathbf{M}}^{(c)} = \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{1,1}^{(c)} } & \cdots & {{\mathbf{M}}_{1,j}^{(c)} } & \cdots & {{\mathbf{M}}_{{1,n_{l}^{(c)} + 1}}^{(c)} } \\ \vdots & \ddots & \vdots & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} & \vdots \\ {{\mathbf{M}}_{i,1}^{(c)} } & \cdots & {{\mathbf{M}}_{i,j}^{(c)} } & \cdots & {{\mathbf{M}}_{{i,n_{l}^{(c)} + 1}}^{(c)} } \\ \vdots & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} & \vdots & \ddots & \vdots \\ {{\mathbf{M}}_{{n_{l}^{(c)} + 1,1}}^{(c)} } & \cdots & {{\mathbf{M}}_{{n_{l}^{(c)} + 1,j}}^{(c)} } & \cdots & {{\mathbf{M}}_{{n_{l}^{(c)} + 1,n_{l}^{(c)} + 1}}^{(c)} } \\ \end{array} } \right], $$

$$ {\mathbf{M}}^{{c_{1} }} = \left[ {\begin{array}{*{20}l} {{\mathbf{M}}_{1,1}^{{\left( {c_{1} } \right)}} } \hfill & \cdots \hfill & {{\mathbf{M}}_{i,j}^{{\left( {c_{1} } \right)}} } \hfill & \cdots \hfill & {{\mathbf{M}}_{{1,n_{l}^{{^{{c_{1} }} }} + 1}}^{{\left( {c_{1} } \right)}} } \hfill & {\mathbf{0}} \hfill \\ \vdots \hfill & \ddots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill & \vdots \hfill \\ {{\mathbf{M}}_{i,1}^{{\left( {c_{1} } \right)}} } \hfill & \cdots \hfill & {{\mathbf{M}}_{i,j}^{{\left( {c_{1} } \right)}} } \hfill & \cdots \hfill & {{\mathbf{M}}_{{1,n_{l}^{{^{{c_{1} }} }} + 1}}^{{\left( {c_{1} } \right)}} } \hfill & {\mathbf{0}} \hfill \\ \vdots \hfill & \ddots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill & \vdots \hfill \\ {{\mathbf{M}}_{{n_{l}^{{c_{1} }} , + 1,1}}^{{\left( {c_{1} } \right)}} } \hfill & \cdots \hfill & {{\mathbf{M}}_{{n_{l}^{{c_{1} }} , + 1,j}}^{{\left( {c_{1} } \right)}} } \hfill & \cdots \hfill & {{\mathbf{M}}_{{1,n_{l}^{{^{{c_{1} }} }} + 1,n_{l}^{{c_{1} }} + 1}}^{{\left( {c_{1} } \right)}} } \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & \cdots \hfill & {\mathbf{0}} \hfill & \cdots \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ \end{array} } \right], $$

$$ {\mathbf{M}}^{{(c_{2} )}} = \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{1,1}^{{(c_{2} )}} } & {\mathbf{0}} & {{\mathbf{M}}_{1,2}^{{(c_{2} )}} } & \cdots & {{\mathbf{M}}_{1,j}^{{(c_{2} )}} } & \cdots & {{\mathbf{M}}_{{1,n_{l} }}^{{(c_{2} )}} } \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & \cdots & {\mathbf{0}} \\ {{\mathbf{M}}_{2,1}^{{(c_{2} )}} } & {\mathbf{0}} & {{\mathbf{M}}_{2,2}^{{(c_{2} )}} } & \cdots & {{\mathbf{M}}_{2,j}^{{(c_{2} )}} } & \cdots & {{\mathbf{M}}_{{2,n_{l} }}^{{(c_{2} )}} } \\ \vdots & \vdots & \vdots & \ddots & \vdots & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} & \vdots \\ {{\mathbf{M}}_{i,1}^{{(c_{2} )}} } & \cdots & {{\mathbf{M}}_{i,2}^{{(c_{2} )}} } & \cdots & {{\mathbf{M}}_{i,j}^{{(c_{2} )}} } & \cdots & {{\mathbf{M}}_{{i,n_{l} }}^{{(c_{2} )}} } \\ \vdots & \vdots & \vdots & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} & \vdots & \ddots & \vdots \\ {{\mathbf{M}}_{{n_{l} ,1}}^{{(c_{2} )}} } & \cdots & {{\mathbf{M}}_{{n_{l} ,2}}^{{(c_{2} )}} } & \cdots & {{\mathbf{M}}_{{n_{l} ,j}}^{{(c_{2} )}} } & \cdots & {{\mathbf{M}}_{{n_{l} ,n_{l} }}^{{(c_{2} )}} } \\ \end{array} } \right], $$

$$ {\mathbf{M}}_{{i,j}}^{{(\beta )}} = \sum\limits_{{l = \max \left\{ {i,j} \right\}}}^{{n_{l}^{{(\beta )}} }} {{\mathbf{M}}_{{i,j}}^{{(\beta ,l)}} } ,\;\left. {{\mathbf{M}}_{{i,j}}^{{(\beta ,l)}} } \right|_{{i,j = 1, \ldots ,l}} = \left( {m_{{n_{{dof}}^{{(\beta ,i - 1)}} + v,n_{{dof}}^{{(\beta ,j - 1)}} + w}}^{{(\beta ,l)}} } \right)_{\begin{subarray}{l} v = 1, \ldots ,\tilde{n}_{{dof}}^{{(\beta ,i)}} \\ w = 1, \ldots ,\tilde{n}_{{dof}}^{{(\beta ,j)}} \end{subarray} } ,\;m_{{i,j}}^{{(\beta ,l)}} = {\text{tr}}\left\{ {{\mathbf{T}}_{i}^{{(\beta ,l)}} {\mathbf{H}}^{{(\beta ,l)}} {\mathbf{T}}_{j}^{{(\beta ,l)^{T} }} } \right\}, $$

$$ {\mathbf{h}}_{{i_{c} }} = \left( {h_{i} } \right)_{{i \in i_{{i_{c} }} }} ,\;{\mathbf{h}}_{{d_{c} }} = \left( {\sum\limits_{{j \in i_{{d_{c} }} }}^{{}} {h_{j} \frac{{\partial \dot{q}_{j} }}{{\partial \dot{q}_{i} }}} } \right)_{{i \in i_{{i_{c} }} }} , $$

$$ {\mathbf{h}} = \left\{ {\begin{array}{*{20}c} {{\mathbf{h}}^{(b)} + {\mathbf{h}}^{(c)} } & {{\text{for}}\,\,{\text{OLKC}},} \\ {{\mathbf{h}}^{(b)} + \sum\limits_{{\beta \in \left\{ {c_{1} ,c_{2} } \right\}}} {{\mathbf{h}}^{(\beta )} } } & {{\text{for}}\,\,{\text{CLKC}},} \\ \end{array} } \right. $$

$$ {\mathbf{h}}^{(b)} = \left[ {\begin{array}{*{20}c} {{\mathbf{h}}_{1}^{(b)} } \\ {\mathbf{0}} \\ \end{array} } \right],\;{\mathbf{h}}_{1}^{(b)} = \left( {h_{i}^{(b)} } \right)_{{i,j = 1, \ldots ,n_{dof}^{(b)} }} , $$

$$ \,h_{i}^{(b)} = \sum\limits_{m = 1}^{{n_{dof}^{(b)} }} {\sum\limits_{n = 1}^{{n_{dof}^{(b)} }} {{\text{tr}}\left\{ {{\mathbf{T}}_{m}^{(b)} {\mathbf{H}}_{{}}^{(b)} \left( {{\mathbf{T}}_{m,n}^{(b)} } \right)^{T} } \right\}\dot{q}_{m}^{(b)} \dot{q}_{n}^{(b)} } } + 2\sum\limits_{m = 1}^{{n_{dof}^{(b)} }} {\sum\limits_{n = 1}^{{n_{dof}^{(b)} }} {{\text{tr}}\left\{ {{\mathbf{T}}_{m}^{(b)} {\mathbf{H}}_{{}}^{(b)} \left( {{\mathbf{T}}_{i,n}^{(b)} } \right)^{T} } \right\}\dot{q}_{m}^{(b)} \dot{q}_{n}^{(b)} } } , $$

$$ {\mathbf{h}}^{(c)} = \left[ {\begin{array}{*{20}c} {{\mathbf{h}}_{1}^{(c)} } \\ \vdots \\ {{\mathbf{h}}_{i}^{(c)} } \\ \vdots \\ {{\mathbf{h}}_{{n_{l}^{(c)} + 1}}^{(c)} } \\ \end{array} } \right],\quad {\mathbf{h}}^{{(c_{1} )}} = \left[ {\begin{array}{*{20}c} {{\mathbf{h}}_{1}^{{(c_{1} )}} } \\ \vdots \\ {{\mathbf{h}}_{i}^{{(c_{1} )}} } \\ \vdots \\ {{\mathbf{h}}_{{n_{l}^{{(c_{1} )}} + 1}}^{(c)} } \\ {\mathbf{0}} \\ \end{array} } \right],\quad {\mathbf{h}}^{{(c_{2} )}} = \left[ {\begin{array}{*{20}c} {{\mathbf{h}}_{1}^{{(c_{2} )}} } \\ {\mathbf{0}} \\ {{\mathbf{h}}_{2}^{{(c_{2} )}} } \\ \vdots \\ {{\mathbf{h}}_{i}^{{(c_{2} )}} } \\ \vdots \\ {{\mathbf{h}}_{{n_{l} }}^{{(c_{2} )}} } \\ \end{array} } \right],\quad {\mathbf{h}}_{i}^{(\beta )} = \sum\limits_{l = i}^{{n_{l}^{(\beta )} }} {{\mathbf{h}}_{i}^{(\beta ,l)} } $$

$$ \left. {{\mathbf{h}}_{i}^{(\beta ,l)} } \right|_{i = 1, \ldots ,l} = \left( {h_{{n_{dof}^{(\beta ,i - 1)} + v}}^{(\beta ,l)} } \right)_{{v = 1, \ldots ,\tilde{n}_{dof}^{(\beta ,l)} }} , $$

$$ \,h_{i}^{(\beta ,l)} = \sum\limits_{m = 1}^{{n_{dof}^{(\beta ,l)} }} {\sum\limits_{n = 1}^{{n_{dof}^{(\beta ,l)} }} {{\text{tr}}\left\{ {{\mathbf{T}}_{m}^{(\beta ,l)} {\mathbf{H}}_{{}}^{(\beta ,l)} \left( {{\mathbf{T}}_{m,n}^{(\beta ,l)} } \right)^{T} } \right\}\dot{q}_{m}^{(\beta ,l)} \dot{q}_{n}^{(\beta ,l)} } } + 2\sum\limits_{m = 1}^{{n_{dof}^{(\beta ,l)} }} {\sum\limits_{n = 1}^{{n_{dof}^{(\beta ,l)} }} {{\text{tr}}\left\{ {{\mathbf{T}}_{m}^{(\beta ,l)} {\mathbf{H}}_{{}}^{(\beta ,l)} \left( {{\mathbf{T}}_{i,n}^{(\beta ,l)} } \right)^{T} } \right\}\dot{q}_{m}^{(\beta ,l)} \dot{q}_{n}^{(\beta ,l)} } } , $$

$$ {\mathbf{Q}}_{{i_{c} }} = \left( {Q_{i} } \right)_{{i \in i_{{i_{c} }} }} ,\;{\mathbf{Q}}_{{d_{c} }} = \left( {\sum\limits_{{j \in i_{{d_{c} }} }}^{{}} {Q_{j} \frac{{\partial \dot{q}_{j} }}{{\partial \dot{q}_{i} }}} } \right)_{{i \in i_{{i_{c} }} }} , $$

$$ {\Delta }{\mathbf{Q}}_{{i_{c} }} = \left( {\sum\limits_{{k \in i_{{i_{c} }} \cup \,i_{{d_{c} }} }}^{{}} {\dot{q}_{k} \frac{{\partial Q_{k} }}{{\partial \dot{q}_{i} }}} } \right)_{{i \in i_{{i_{c} }} }} ,\;{\Delta }{\mathbf{Q}}_{{d_{c} }} = \left( {\sum\limits_{{j \in i_{{d_{c} }} }}^{{}} {\sum\limits_{{k \in i_{{i_{c} }} \cup \,i_{{d_{c} }} }}^{{}} {\dot{q}_{k} \frac{{\partial Q_{k} }}{{\partial \dot{q}_{i} }}} \frac{{\partial \dot{q}_{j} }}{{\partial \dot{q}_{i} }}} } \right)_{{i \in i_{{i_{c} }} }} , $$

$$ {\Delta }{\mathbf{Q}}_{{d_{c} }} = \left( {\sum\limits_{{j \in i_{{d_{c} }} }}^{{}} {\sum\limits_{{k \in i_{{i_{c} }} \cup \,i_{{d_{c} }} }}^{{}} {\dot{q}_{k} \frac{{\partial Q_{k} }}{{\partial \dot{q}_{i} }}} \frac{{\partial \dot{q}_{j} }}{{\partial \dot{q}_{i} }}} } \right)_{{i \in i_{{i_{c} }} }} , $$

$$ {\mathbf{Q}} = - \left( {{\mathbf{g}} + {\mathbf{f}}_{fl} + {\mathbf{f}}_{sup} + {\mathbf{f}}_{fric} } \right), $$

$$ {\mathbf{g}} = \left\{ {\begin{array}{*{20}c} {{\mathbf{g}}^{(b)} + {\mathbf{g}}^{(c)} } & {{\text{for}}\,\,{\text{OLKC}},} \\ {{\mathbf{g}}^{(b)} + \sum\limits_{{\beta \in \left\{ {c_{1} ,c_{2} } \right\}}} {{\mathbf{g}}^{(\beta )} } } & {{\text{for}}\,\,{\text{CLKC}},} \\ \end{array} } \right. $$

$$ {\mathbf{g}}^{(b)} = \left[ {\begin{array}{*{20}c} {{\mathbf{g}}_{1}^{(b)} } \\ {\mathbf{0}} \\ \end{array} } \right],\;{\mathbf{g}}_{1}^{(b)} = \left( {g_{i}^{(b)} } \right)_{{i,j = 1, \ldots ,n_{dof}^{(b)} }} ,\;g_{i}^{(b)} = m^{(b)} g\;{\mathbf{j}}_{2} {\mathbf{T}}_{i}^{(b)} {\mathbf{r}}_{C}^{(b)} , $$

$$ {\mathbf{g}}^{(c)} = \left[ {\begin{array}{*{20}c} {{\mathbf{g}}_{1}^{(c)} } \\ \vdots \\ {{\mathbf{g}}_{i}^{(c)} } \\ \vdots \\ {{\mathbf{g}}_{{n_{l}^{(c)} + 1}}^{(c)} } \\ \end{array} } \right],\quad {\mathbf{g}}^{{(c_{1} )}} = \left[ {\begin{array}{*{20}c} {{\mathbf{g}}_{1}^{{(c_{1} )}} } \\ \vdots \\ {{\mathbf{g}}_{i}^{{(c_{1} )}} } \\ \vdots \\ {{\mathbf{g}}_{{n_{l}^{{(c_{1} )}} + 1}}^{(c)} } \\ {\mathbf{0}} \\ \end{array} } \right],\quad {\mathbf{g}}^{{(c_{2} )}} = \left[ {\begin{array}{*{20}c} {{\mathbf{g}}_{1}^{{(c_{2} )}} } \\ {\mathbf{0}} \\ {{\mathbf{g}}_{2}^{{(c_{2} )}} } \\ \vdots \\ {{\mathbf{g}}_{i}^{{(c_{2} )}} } \\ \vdots \\ {{\mathbf{g}}_{{n_{l} }}^{{(c_{2} )}} } \\ \end{array} } \right],\quad {\mathbf{g}}_{i}^{(\beta )} = \sum\limits_{l = i}^{{n_{l}^{(\beta )} }} {{\mathbf{g}}_{i}^{(\beta ,l)} } ,\quad \left. {{\mathbf{g}}_{i}^{(\beta ,l)} } \right|_{i = 1, \ldots ,l} = \left( {{\mathbf{g}}_{{n_{dof}^{(\beta ,i - 1)} + v}}^{(\beta ,l)} } \right)_{{v = 1, \ldots ,\tilde{n}_{dof}^{(\beta ,l)} }} , $$

$$ g_{i}^{(\beta ,l)} = m^{(\beta ,l)} g\;{\mathbf{j}}_{2} {\mathbf{T}}_{i}^{(\beta ,l)} {\mathbf{r}}_{C}^{(\beta ,l)} , $$

${\mathbf{f}}_{fl}$ is a vector of generalized forces resulting from deformation of a flexible link,

${\mathbf{f}}_{sup}$ is a vector of generalized forces resulting from deformation of the support,

${\mathbf{f}}_{fric}$ is a vector of friction torques/forces

$$ {\overline{\mathbf{\Phi }}}_{{k,{\mathbf{q}}}} = \left\{ {\begin{array}{*{20}c} {\mathbf{0}} & {{\text{for}}\,\,{\text{OLKC}},} \\ {{{\varvec{\Phi}}}_{{k,{\mathbf{q}}}} } & {{\text{for}}\,\,{\text{CLKC}}.} \\ \end{array} } \right. $$

Equation (26) form a set of $n_{dof}$ differential algebraic-equations. It can be seen that the presented approach allows to obtain the dynamics free of the constraint reaction forces. Also, CoPCoD is structured into block architecture such that different systems can be modelled by selecting options provided by its blocks.

3 Examples of application of CoPCoD applications

In this section, two sample systems representing OLKC and CLKC structures are analysed. We demonstrate how the CoPCoD algorithm enables performing efficient numerical simulations. They provide information about the system model behaviour when the programmed constraints are imposed upon motion. It enables, in turn, constrained motion planning.

3.1 The OLKC manipulator model

As the first example, the programmed motion of the spatial OLKC manipulator model is analyzed. The manipulator possesses 5 degrees of freedom with respect to the base frame {b} (Fig. 4). It is assumed that link (1,2) can be flexible and flexibility of the ground is modelled by means of the $n_{{sde_{s} }}^{{}}$ spring-damping elements, where $n_{{sde_{s} }} = \sum\limits_{i = 1}^{{n_{e} }} {n_{{sde_{s} }}^{(i)} } .$

Fig. 4

The OLKC manipulator model and the programmed trajectory of its end-effector E

The local frames assigned to each link and generalized coordinates of the manipulator are presented in Fig. 5. The generalized coordinates vector consists of the following

$$ {\mathbf{q}} = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}^{{(b)^{T} }} } & {\underbrace {{\begin{array}{*{20}l} {\varphi^{(1,1)} } \hfill & {\psi^{(1,2)} } \hfill & {{\mathbf{q}}_{f}^{{(1,2)^{T} }} } \hfill & {\psi^{(1,3)} } \hfill & {x^{(1,4)} } \hfill & {x^{(1,5)} } \hfill \\ \end{array} }}_{{{\mathbf{q}}^{{(1)^{T} }} }}} \\ \end{array} } \right]^{T} . $$

(27)

where: ${\mathbf{q}}^{(b)} = \left[ {\begin{array}{*{20}c} {x^{(b)} } & {y^{(b)} } & {z^{(b)} } & {\psi^{(b)} } & {\theta^{(b)} } & {\varphi^{(b)} } \\ \end{array} } \right]^{T}$ contains generalized coordinates of the base,

Fig. 5

Local frames assigned to the particular links of the manipulator

${\mathbf{q}}_{f}^{(1,2)}$ is the vector containing generalized coordinates of rfes of the link (1, 2), ${\mathbf{q}}_{f}^{(1,2)} = \left\{ {\begin{array}{*{20}c} \emptyset & {n_{sde}^{(1,2)} = 0,} \\ {\left[ {\begin{array}{*{20}c} {\underbrace {{\begin{array}{*{20}c} {\psi_{{}}^{(1,2,1)} } & {\theta_{{}}^{(1,2,1)} } & {\varphi_{{}}^{(1,2,1)} } \\ \end{array} }}_{{{\tilde{\mathbf{q}}}^{{(1,2,1)^{T} }} }}} & \cdots & {\underbrace {{\begin{array}{*{20}c} {\psi_{{}}^{{(1,2,n_{sde}^{(c,2)} )}} } & {\theta_{{}}^{{(1,2,n_{sde}^{(c,2)} )}} } & {\varphi_{{}}^{{(1,2,n_{sde}^{(1,2)} )}} } \\ \end{array} }}_{{{\tilde{\mathbf{q}}}^{{(1,2,\,n_{sde}^{(c,2)} )^{T} }} }}} \\ \end{array} } \right]^{T} } & {n_{sde}^{(1,2)} > 0.} \\ \end{array} } \right.$

It is assumed that the end-effector E has to track the rectangle trajectory defined in ${\mathbf{y}}^{(P)} {\mathbf{z}}^{(P)}$ plane (Fig. 4) and it moves between adjacent corners of the rectangle within the scheduled time ${\Delta }t^{(E)} = 1\;{\text{s}}$. The change of the end-effector coordinates in this motion is described by a 5^th order polynomial:

$$ s_{E} (t) = \frac{{10\,{\Delta }s_{E} }}{{{\Delta }t_{E}^{3} }}\left( {t - t_{E,s} } \right)^{3} - \frac{{15\,{\Delta }s_{E} }}{{{\Delta }t_{E}^{4} }}\left( {t - t_{E,s} } \right)^{4} + \frac{{6\,{\Delta }s_{E}^{{}} }}{{{\Delta }t_{E}^{5} }}\left( {t - t_{E,s} } \right)^{5} , $$

(28)

where: ${\Delta }s_{E}^{{}} = s_{E,f}^{{}} - s_{E,s}^{{}} ,\;{\Delta }t_{E}^{{}} = t_{E,f}^{{}} - t_{E,s}^{{}} ,\;s_{E,f}^{{}} ,\,\,s_{E,s}^{{}}$ are positions of the end-effector at start $t_{E,s}^{{}}$ and final time $t_{E,f}^{{}}$ of its motion. According to the motion description specified for E, the programmed constraint equations have the following form:

$$ {{\varvec{\Phi}}}_{p} (t,{\mathbf{q}}) \equiv {\mathbf{J}}\left( {{\mathbf{r}}_{E} - {\hat{\mathbf{r}}}_{E} (t)} \right) = {\mathbf{0}}, $$

(29)

where: ${\mathbf{r}}_{E}^{{}} = {\mathbf{B}}^{(1,5)} \,{\tilde{\mathbf{r}}}_{E}^{(1,5)}$ is the calculated global position of the end-effector E at time t,

${\tilde{\mathbf{r}}}_{E}^{(1,5)}$ is the position of the end-effector defined in the local frame of the link $(1,5)$,

${\hat{\mathbf{r}}}_{E}^{{}} (t) = {\mathbf{B}}^{(P)} \,{\tilde{\mathbf{r}}}_{E}^{(P)} (t)$ is the required position of the end-effector expressed in the global reference frame,

${\mathbf{B}}^{(P)} = \left[ {\begin{array}{*{20}c} {{\mathbf{R}}^{(P)} } & {{\mathbf{r}}_{org}^{(P)} } \\ {\mathbf{0}} & 1 \\ \end{array} } \right]$ is the constant transformation matrix from the frame $\{ P\}$ to the global frame,

${\mathbf{R}}^{(P)}$ is the rotation matrix from $\{ P\}$ to {0},

${\mathbf{r}}_{org}^{(P)}$ is the position vector of the frame {P} origin with respect to the global coordinate system,

${\hat{\mathbf{r}}}_{E}^{(P)} (t)$ is the required position of the end-effector E expressed directly in the frame $\{ P\}$.

By differentiating (29) with respect to time, one obtains the constraint equations at the velocity and acceleration levels:

$$ {\dot{\mathbf{\Phi }}}_{p} (t,{\mathbf{q}},{\dot{\mathbf{q}}}) \equiv {\mathbf{J}}\left( {\sum\limits_{i = 1}^{{n_{dof}^{(1,5)} }} {{\mathbf{B}}_{i}^{(1,5)} {\tilde{\mathbf{r}}}_{E}^{(1,5)} {\dot{\mathbf{q}}}_{i}^{(1,5)} } - {\mathbf{B}}^{(P)} \,{\mathbf{\dot{\hat{r}}}}_{E}^{(P)} (t)} \right) = {\mathbf{0}}, $$

(30.1)

$$ {\mathbf{\ddot{\Phi }}}_{p} (t,{\mathbf{q}},{\dot{\mathbf{q}}},{\mathbf{\ddot{q}}}) \equiv {\mathbf{J}}\left( {\sum\limits_{i = 1}^{{n_{dof}^{(1,5)} }} {\left( {{\mathbf{B}}_{i}^{(1,5)} {\tilde{\mathbf{r}}}_{E}^{(1,5)} {\mathbf{\ddot{q}}}_{i}^{(1,5)} + \sum\limits_{j = 1}^{{n_{dof}^{(1,5)} }} {{\mathbf{B}}_{i,j}^{(1,5)} {\tilde{\mathbf{r}}}_{E}^{(1,5)} {\dot{\mathbf{q}}}_{i}^{(1,5)} {\dot{\mathbf{q}}}_{j}^{(1,5)} } } \right) + } \,{\mathbf{B}}^{(P)} \,{\mathbf{\ddot{\hat{r}}}}_{E}^{(P)} (t)} \right) = {\mathbf{0}}. $$

(30.2)

From Eqs. (30.1) and (30.2) and taking into account (24.1), (24.2), the following components can be identified:

$$ {{\varvec{\Phi}}}_{{p,{\mathbf{q}}}} = \left[ {\begin{array}{*{20}l} {{\mathbf{J}}\,{\mathbf{B}}_{1}^{(1,5)} {\tilde{\mathbf{r}}}_{E}^{(1,5)} } \hfill & \cdots \hfill & {{\mathbf{J}}\,{\mathbf{B}}_{i}^{(1,5)} {\tilde{\mathbf{r}}}_{E}^{(1,5)} } \hfill & \cdots \hfill & {{\mathbf{J}}\,{\mathbf{B}}_{{n_{dof}^{(1,5)} }}^{(1,5)} {\tilde{\mathbf{r}}}_{E}^{(1,5)} } \hfill \\ \end{array} } \right], $$

(31.1)

$$ {\dot{\mathbf{\Phi }}}_{{p,{\mathbf{q}}}} {\dot{\mathbf{q}}} = {\mathbf{J}}\sum\limits_{i = 1}^{{n_{dof}^{(1,5)} }} {\sum\limits_{j = 1}^{{n_{dof}^{(1,5)} }} {{\mathbf{B}}_{i,j}^{(1,5)} {\tilde{\mathbf{r}}}_{E}^{(1,5)} {\dot{\mathbf{q}}}_{i}^{(1,5)} {\dot{\mathbf{q}}}_{j}^{(1,5)} } } , $$

(31.2)

$$ {\mathbf{g}}_{p} (t) = {\mathbf{J}}\,{\mathbf{B}}^{(P)} \,{\mathbf{\ddot{\hat{r}}}}_{E}^{(P)} (t). $$

(31.3)

When the model with a fixed base is considered, additional constraint equations need to be defined as

$$ {{\varvec{\Phi}}}_{b} \left( {{\mathbf{q}}^{(b)} \,} \right) \equiv {\mathbf{q}}^{(b)} = {\mathbf{0}}. $$

(32)

Finally, equations of motion (26) for the OLKC manipulator model have the form

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{{i_{c} }}^{{}} + {\mathbf{M}}_{{d_{c} }}^{{}} } \\ {{{\varvec{\Phi}}}_{{p,{\mathbf{q}}}} } \\ {{{\varvec{\Phi}}}_{{b,{\mathbf{q}}}} } \\ \end{array} } \right]{\mathbf{\ddot{q}}} = \left[ {\begin{array}{*{20}l} {{\mathbf{h}}_{{i_{c} }} + {\mathbf{Q}}_{{i_{c} }} + \Delta {\mathbf{Q}}_{{i_{c} }} + {\mathbf{h}}_{{d_{c} }} + {\mathbf{Q}}_{{d_{c} }} + \Delta {\mathbf{Q}}_{{d_{c} }} } \hfill \\ { - {\dot{\mathbf{\Phi }}}_{{p,{\mathbf{q}}}} {\dot{\mathbf{q}}} - {\mathbf{\ddot{g}}}_{p} (t) - 2\alpha \,{\dot{\mathbf{\Phi }}}_{p} - \beta^{2} \,{{\varvec{\Phi}}}_{p} } \hfill \\ {{\mathbf{0}} - 2\alpha \,{\dot{\mathbf{\Phi }}}_{b} - \beta^{2} \,{{\varvec{\Phi}}}_{b} } \hfill \\ \end{array} } \right], $$

(33)

where $\alpha ,\;\beta$—the Baumgarte method parameters for solution stabilization, ${{\varvec{\Phi}}}_{{b,{\mathbf{q}}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{6 \times 6} } & {\mathbf{0}} \\ \end{array} } \right]$—the $6 \times n_{dof}^{(1,5)}$ constraint matrix resulting from (30.1), (30.2), ${\mathbf{I}}_{6 \times 6}$—identity matrix. In the case when the base support is flexible the constraint (32) and its derivatives are not included into (33).

In Table 1 mass parameters of the manipulator are provided. Friction parameters, stiffness, damping and other parameters are gathered in Table 2.

Table 1 Pseudo-inertia matrices of the manipulator links

Table 2 Parameters assumed for the manipulator and the mechanism models in simulations

The influence of the base support stiffness, link’s flexibility and friction in joints in the programmed motion performed by the manipulator is analyzed next. Also, forces acting in the joints are inspected. To facilitate the description of subsequent simulation results, the following notation shown in Fig. 6 is introduced. The 4th Runge–Kutta scheme with a constant step size equal to $10^{ - 5} \,{\text{s}}$ is applied to integrate the dynamic equations of motion. The Baumgarte method parameters for solution stabilization are selected to be $\alpha = 10^{3} ,\;\beta = 10^{2} .$

Fig. 6

The scheme of notation applied in the simulation results description

Figure 7 shows the trajectory and time courses of the end-effector. The starting point of the effector motion differs from the assumed point A. The elimination of disturbances resulting from an arbitrary initial configuration of the manipulator end effector is obtained during its transition from the starting point * to B. After this time, the effector moves along the edges of the ABCD rectangle. The effector is stopped at the corner points and then moves to the next point. Figure 8 shows the time course of the magnitude of constraint violations at the displacement level for all analyzed cases. A logarithmic scale on the vertical axis is introduced to increase the resolution of the presented results. Analyzing the results, it can be seen that during the motion from point B to points C, D, and A, violations of the programmed constraints do not exceed the value of $5 \times 10^{ - 3} \;{\text{m}}$. The constraint violations linearly decrease in about 2.2 s, and then they oscillate not exceeding the value of $5 \times 10^{ - 7} \;{\text{m}}$.

Fig. 7

The calculated trajectory of the end-effector and time courses of its coordinates

Fig. 8

Time courses of the magnitude of the programmed constraints violations at the displacement level

Time courses of the joint coordinates are presented in Fig. 9. These results show that the most significant influence on the manipulator motion comes from the flexibility of the base support and friction in joints. Comparing the plots for the manipulator with the rigid link (1,2) and ideal joints (${\text{S}}_{{\text{r}}} {\text{\_L}}_{{\text{r}}} \_{\text{J}}_{{{\text{nf}}}}$) with those for the flexible link (1,2) and frictionless joints (${\text{S}}_{{\text{r}}} {\text{\_L}}_{{{\text{fl}}}} \_{\text{J}}_{{{\text{nf}}}}$), one can conclude that they are close to each other.

Fig. 9

Time courses of the manipulator joint coordinates

Figure 10 displays plots of the time courses of force magnitudes acting in the joints. It can be seen that while the flexibility of the links does not have major impact on the manipulator motion, it has a significant effect on the forces generated in the joints.

Fig. 10

Time courses of the force magnitudes acting in each joint

In order to analyze the values of the axial and normal forces acting in the joints in the respected cases, the RMS (Root Mean Square) indicator is introduced

$$ {\text{RMS}} = \sqrt {\frac{1}{{t_{k} }}\int\limits_{0}^{{t_{k} }} {F(t)^{2} {\text{d}}t} } , $$

(34)

where: $t_{k}$ is the analysis time, $F(t)$ is the time course of the axial or normal forces.

Figure 11 allows us to analyze RMS values of the particular components of the joint forces.

Fig. 11

RMS values of the axial and normal forces acting in the joints

Analyzing the RMS values calculated for the axial and normal forces it can be observed that the highest values of the RMS are obtained for the case ${\text{S}}_{{\text{r}}} {\text{\_L}}_{{{\text{fl}}}} \_{\text{J}}_{{{\text{nf}}}} ,$, i.e. the link (1,2) is flexible, the support is rigid and friction in joints is neglected. The RMS values determined for this case are up to 8 times bigger than the others. Thus, it can be concluded that the link flexibility, in this case, does not have major impact on the manipulator motion, but may cause a significant increase of the joint loads.

The presented analysis of the system performance in programmed motion enables detailed verification and motion planning for constrained tasks.

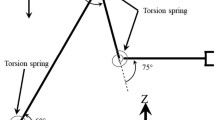
3.2 The RPSUP mechanism model

The RPSUP (R-revolute, P-prismatic, S-spherical, U-universal, P-prismatic joint) mechanism is the second example and it is the CLKC system model (Fig. 12). The goal of the simulation is to track programmed motion by the end effector E, which is a rectangular trajectory located on the plane ${\mathbf{y}}^{(P)} {\mathbf{z}}^{(P)}$ that is inclined to ${\mathbf{x}}^{(0)} {\mathbf{z}}^{(0)}$ plane at the angle $\alpha = 45^\circ$. This trajectory reflects some work regime on the end effector. The transformation matrix from the frame $\{ P\}$ to the global reference frame has the form:

$$ {\mathbf{B}}^{(P)} = \left[ {\begin{array}{*{20}c} {\cos \alpha } & { - \sin \alpha } & 0 & {x_{org}^{(P)} } \\ {\sin \alpha } & {\cos \alpha } & 0 & {y_{org}^{(P)} } \\ 0 & 0 & 1 & {z_{org}^{(P)} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right], $$

(35)

where $x_{org}^{(P)} ,\;y_{org}^{(P)} ,\;z_{org}^{(P)}$ are coordinates of the position vector ${\mathbf{r}}_{org}^{(P)}$ describing position of the frame $\{ P\}$ with respect to the global one. It is assumed that $x_{org}^{(P)} = 0.0384\,{\text{m,}}\;y_{org}^{(P)} = 0.2335\,{\text{m}},\;z_{org}^{(P)} = 0\,{\text{m}}.$

Fig. 12

The RPSUP mechanism with the programmed trajectory

In order to formulate the dynamic equations of motion of the mechanism using the CoPCoD algorithm, first it is necessary to remove the kinematic loop using the cut-joint technique. It is assumed that the cut-joint is located at the revolute joint R connecting the flexible link (1,3) with the slider (2,1). Local coordinate systems are assigned to the links as shown in Fig. 13. As a result, two systems of the OLKC types are obtained, for which the generalized coordinates vector results as:

$$ {\mathbf{q}} = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}^{{(b)^{T} }} } & {\underbrace {{\begin{array}{*{20}c} {\psi^{(1,1)} } & {x^{(1,2)} } & {\psi^{(1,3,0)} } & {\theta^{(1,3,0)} } & {\varphi^{(1,3,0)} } & {{\mathbf{q}}_{f}^{{(1,3)^{T} }} } \\ \end{array} }}_{{{\mathbf{q}}^{{(1)^{T} }} }}} & {\underbrace {{\begin{array}{*{20}c} {z^{(2,1)} } & {\psi^{(2,2)} } \\ \end{array} }}_{{{\mathbf{q}}^{{(2)^{T} }} }}} \\ \end{array} } \right]^{T} , $$

(36)

where: $\left. {{\mathbf{q}}^{(c)} } \right|_{c = 1,2}$ is a vector of generalized coordinates of c sub-chain, ${\mathbf{q}}_{f}^{(1,3)}$ is a vector containing generalized coordinates of the flexible coupler (1,3).

Fig. 13

Local frames assigned to the mechanism links

Next, applying the CoPCoD algorithm presented in the paper, the dynamic equations of motion of the mechanism are obtained as:

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{{i_{c} }}^{{}} + {\mathbf{M}}_{{d_{c} }}^{{}} } \\ {{{\varvec{\Phi}}}_{{p,{\mathbf{q}}}} } \\ {{{\varvec{\Phi}}}_{{k,{\mathbf{q}}}} } \\ {{{\varvec{\Phi}}}_{{b,{\mathbf{q}}}} } \\ \end{array} } \right]{\mathbf{\ddot{q}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{h}}_{{i_{c} }} + {\mathbf{Q}}_{{i_{c} }} + \Delta {\mathbf{Q}}_{{i_{c} }} + {\mathbf{h}}_{{d_{c} }} + {\mathbf{Q}}_{{d_{c} }} + \Delta {\mathbf{Q}}_{{d_{c} }} } \\ { - {\dot{\mathbf{\Phi }}}_{{p,{\mathbf{q}}}} {\dot{\mathbf{q}}} - {\mathbf{\ddot{g}}}_{p} (t) - 2\alpha \,{\dot{\mathbf{\Phi }}}_{p} - \beta^{2} \,{{\varvec{\Phi}}}_{p} } \\ { - {\dot{\mathbf{\Phi }}}_{{k,{\mathbf{q}}}} {\dot{\mathbf{q}}} - 2\alpha \,{\dot{\mathbf{\Phi }}}_{k} - \beta^{2} \,{{\varvec{\Phi}}}_{k} } \\ {\,\,\,\,\,\,\,\,\,\,\,\,{\mathbf{0}} - 2\alpha \,{\dot{\mathbf{\Phi }}}_{b} - \beta^{2} \,{{\varvec{\Phi}}}_{b} } \\ \end{array} } \right], $$

(37)

Equations (36) are additionally supplemented by closing constraint equations formulated for the revolute cut-joint R. In simulations, as in the case of the manipulator, the influence of the base support flexibility, the coupler flexibility, friction in the joints on the generated programmed motion courses and the forces acting in the joints are analyzed. Mass parameters of the mechanism links applied in simulation tests are presented in Table 3. Other parameters are gathered in Table 2.

Table 3 Pseudo-inertia matrices of the mechanism links

Runge–Kutta method is used to integrate dynamic Eqs. (36) with a constant step size $h = 10^{ - 5} \,{\text{s}}$. The applied Baumgarte method coefficient values are $\alpha = 500$, $\beta = 50$. Initial conditions for the dynamic analysis are obtained from solving the statics case. Figures 14 and 15 show the obtained end-effector E trajectory and the corresponding time courses of the end-effector coordinates.

Fig. 14

Motion along the programmed trajectory of the end-effector

Fig. 15

Time courses of the end-effector coordinates in programmed motion

Analyzing the solutions obtained from statics, it can be noticed that the application of the base support flexibility leads to the effector displacement with respect to the point A. Moreover, the coupler flexibility has no major effect on the effector position change at the initial time. Initial arbitrary location of the end effector is eliminated during its transition from the point A to B, and then the mechanism moves according to the programmed constraints. Some distortions of the trajectory for y-component of the end-effector displacement can be observed for the case of ${\text{S}}_{{\text{r}}} {\text{\_L}}_{{\text{r}}} \_{\text{J}}_{{{\text{nf}}}}$, in which the base support and the coupler are rigid and all joints are treat as ideal. These distortions are even greater at the velocity and acceleration levels (Fig. 16).

Fig. 16

Time courses of the y-components of velocity and acceleration of the end effector

Figure 17 displays magnitudes of the constraint violations for the kinematic and programmed constraints. The plots are presented using the logarithmic scale. Significantly large violations of the kinematic constraints can be observed for the case of ${\text{S}}_{{\text{r}}} {\text{\_L}}_{{\text{r}}} \_{\text{J}}_{{{\text{nf}}}}$ ($\left\| {{\tilde{\mathbf{\Phi }}}_{k} } \right\| = 4.39\,{\text{cm}}$ for $t = 2.014{\text{ s}}$), despite the use of the Baumgarte stabilization method with different parameter settings to eliminate these errors. However, these violations of the programmed constraints are at an acceptable level. One should also pay attention to the different nature of the time courses of violations of the programmed and kinematic constraints. Violations of the programmed constraints, except in the first case, are linear (in the sense of a logarithmic scale), while violations of the kinematic constraints are strongly non-linear. Figure 18 shows the time courses of joint coordinates for the analyzed cases.

Fig. 17

Constraint violations at the cut-joint R presented in the joint local frame

Fig. 18

Time courses of the displacements of the joint coordinates

Examining the calculated time courses, it can be seen that plots obtained for cases with rigid base support are close to each other. Also, the support flexibility impacts significantly courses of the joint coordinates (cases ${\text{S}}_{{{\text{fl}}}} {\text{\_L}}_{{\text{r}}} \_{\text{J}}_{{{\text{nf}}}}$, ${\text{S}}_{{{\text{fl}}}} {\text{\_L}}_{{\text{r}}} \_{\text{J}}_{{\text{f}}}$, ${\text{S}}_{{{\text{fl}}}} {\text{\_L}}_{{{\text{fl}}}} \_{\text{J}}_{{\text{f}}}$). Friction in joints also has noticeable impact on the overall mechanism motion. The flexibility of the coupler has the least influence on motion of individual links of the system. It is interesting because analyzing deformations of the coupler (Fig. 19) it can be concluded that they are large (for $t = 2\,{\text{s}}$ deformation of the coupler is around 4 cm for the cases with rigid support). On the other hand, links flexibility has visible impact on forces acting in joints. Figure 20 shows RMS values calculated for the normal and axial forces acting in each joint of the mechanism.

Fig. 19

Coupler deformations at selected time instants

Fig. 20

RMS values of forces acting in the joints

It can be seen that the highest values of the normal and axial forces are obtained for the case in which the coupler (1,3) is flexible. Links flexibility has significant impact on loading of the mechanism and cannot be neglected in numerical simulations.

4 Conclusions

The general modeling procedure for multibody systems with serial structures of the OLKC and CLKC types subjected to the programmed constraints is presented in the paper. It provides a systematically structured algorithm enabling derivation systems constrained dynamic models with rigid, flexible parts and supports, friction and arbitrary external load. It is based on the joint coordinates formalism and homogeneous transformation matrices. The CoPCoD produces the constrained dynamics, the so called reference dynamics, which enables detailed analysis of the system performance in the desired programmed motion. The underlying dynamics is derived using the GPME algorithm. In simulation tests presented in the paper, for both OLKC and CLKC system models, the influence of the model structure and its properties on the programmed motion were studied. Numerical experiments show that the CoPCoD allows obtaining solutions of the reference dynamics effectively. The computer generation of the model dynamics with the CoPCoD is suitable for various system structures. The presented results indicate how the base flexibility, friction in joints, adoption of rigid or flexible link models impacts motion of the system model. For example, link flexibility can affect motion of the mechanism if the deformation of the link is very large. In our example, the maximum deformations of flexible links are about 10% of the length of links, and their influence on motion of the analyzed systems are negligible. However, the link flexibility has a significant effect on the forces acting in the joints, and cannot be ignored in numerical simulations, even when deformations are small. The future works planned to CoPCoD upgrades to make it more powerful, will be focused on looking for reference dynamics for systems for which the programmed constraints are met with some tolerance, and additional constraints resulting from e.g. design requirements needs to be satisfied.