1 Introduction

Nonlinear energy sinks (NESs) are passive vibration absorbers, consisting of a small mass attached to the host system through a nonlinear spring and a damper [1,2,3]. Because of its nonlinear nature, the NES has a variable natural frequency, which increases its working bandwidth compared to conventional linear vibration absorbers, such as the tuned mass damper (TMD) [4]. Accordingly, in the case of broadband frequency vibrations, a small number of NESs can work more effectively than their linear counterpart, making the NES an attractive device in engineering.

Several types of NESs were proposed in the literature, apart from the classical one [3], which features a hardening polynomial stiffness. Examples are the vibro-impact NES [5,6,7], the rotating NES [8, 9] and the bistable NES [10,11,12]. A common feature of these various devices is the broad frequency bandwidth of operation. The NES proved to be effective in various tasks, such as mitigation of transient [2, 13, 14], forced [15,16,17,18] and self-excited oscillations [19, 20]; however, some limitations about its effectiveness for suppressing limit cycle oscillations were also disclosed [21, 22].

The NES is especially effective for suppressing vibrations of multi-degree-of-freedom (MDOF) mechanical systems with many vibration modes, each mode with its own shape and frequency [23]. Several studies illustrated that, under transient conditions, the NES mainly interacts with one vibration mode at a time. After dissipating most of the mechanical energy of one mode, the NES tunes to the subsequent mode, going from higher to lower frequency modes. This phenomenon is called resonance capture cascade (RCC) and is a consequence of the variable natural frequency property of the NES [2, 24,25,26,27].

The RCC phenomenon was first discovered in 2003 [24] by investigating the nonlinear normal modes (NNMs) of the undamped system. Recently, in [28], the energy transfer duration per vibration mode was analytically estimated. The implemented procedure exploited the slow invariant manifold (SIM), which is the set of fixed points of oscillation amplitudes for the fast timescale. In [28], the SIM was limited to a two-dimensional space by assuming one active mode at the time. In [29], the SIM was extended to a multi-dimensional space by simultaneously considering all the vibration modes of the primary system activated. This approach provided a better understanding of the RCC based on the so-called interaction points. Considering that only one mode of the primary system is activated, the interaction points indicate the points of the SIM most affected by slight activation of other modes. They proved to be able to explain the RCC, providing a different point of view than its interpretation based on the NNMs. The RCC was experimentally obtained in [26, 30].

Almost exclusively, all types of NES proposed in the literature present a hardening nonlinearity, in most cases cubic. The choice of a cubic restoring force is natural since it is probably the simplest and most studied type of nonlinearity (such as the Duffing oscillator [31]). Additionally, for any odd nonlinear function expanded in the Taylor series around the origin, a cubic term is the lowest-order nonlinear term, except for special cases. Furthermore, aiming at having a system with no linear component, the lowest order nonlinear term should be of hardening type to avoid a static instability in zero. Physical mechanisms utilized for generating nonlinear restoring force generally exploit geometrical nonlinearities, which usually can be reduced to hardening nonlinearities, in first approximation cubic. These involve transversely loaded strings [26, 32], springs [33, 34] or beams [35], magnets [36,37,38] or leafs springs [39]. Impact NES are one of the few types of NES whose restoring force is not reducible to a cubic term, but it is still of hardening type [5]. Between the few NES designs which are not strictly hardening, we mention the bistable NES [10, 11], the pendulum NES [40], the periodically extended NES [41] and other non-smooth NESs [42] with descending stiffness [43]. Nevertheless, none of them has a strictly softening restoring force.

Fig. 1
figure 1

a A simplified model of the nonlinear energy sink; b stiffness characteristics for hardening and softening stiffness; c relation between amplitude and natural frequency for the three different NESs considered

Full size image

Recently, a mechanism that can generate a large range of stiffness characteristics was proposed and realized in practice [30, 44, 45]. The mechanism relies on a mass in contact with an arbitrarily shaped surface through a compressed linear spring, placed orthogonally with respect to the mass displacement. The shape of this force profile, which can be either machined or 3D-printed, determines the total stiffness characteristic. In particular, this mechanism can be used to generate a softening restoring force. Alternative methods for obtaining a softening restoring force function exist, such as topology optimization [46,47,48], magnetic forces [36, 49] and metamaterials [48]. However, their effectiveness in real-world vibration control applications undergoing large vibrations is questionable since the displacement range for which the restoring force has a softening characteristic is usually limited [37].

Concerning the functionality of the NES, the possibility of freely choosing the restoring force function provides a significant advantage. In particular, the natural frequency of the conventional NESs (with hardening stiffness) increases with the NES’s vibration amplitude. As such, the NES dissipates the higher frequency modes of the host system more efficiently than the lower frequency modes. Referring to the RCC, the NES tunes first with higher modes and then with lower ones. However, lower vibration modes typically contain more energy and cause larger displacements. Therefore, it would be beneficial to design an NES that dissipates first the lower frequency modes and does it more efficiently. With this objective, this paper investigates an NES with a softening stiffness, which has a natural frequency that decreases for increasing vibration amplitude. By exploiting high-dimensional SIMs, it will be shown that the modal interaction between an MDOF and a softening NES inverts the order in which the modal energy is transferred from the host system to the NES during RCC. This sequential transfer will now be from low- to high-frequency modes and, as such, the phenomenon will be called inverted resonance capture cascade (IRCC).

The paper is structured as follows: in Sect. 2, the frequency–amplitude relations of hardening and softening NESs are investigated. In the following section, the expressions and stability of higher-dimensional SIMs are derived. Then, the SIMs for a two-DOF primary system are discussed in Sect. 4 and compared to numerical simulations where one of the two modes are constant. Section 5 observes the (inverted) RCC for both the previously considered two-DOF system and a four-DOF system. Finally, the conclusions are presented.

2 Frequency–amplitude plot of an NES with softening stiffness

Figure 1a shows a generic undamped NES. The variable natural frequency of an NES can be illustrated by considering the unforced NES and applying harmonic balancing. This consists of an unforced single-DOF oscillator, whose dynamics is described by:

$$\begin{aligned} m_{\text {a}}\ddot{x}_{\text {a}}+f_{\text {nl}}(x_{\text {a}}) = 0. \end{aligned}$$
(1)

Its steady-state solution is approximated by a Galerkin method, more precisely a projection on truncated Fourier series of a single harmonic [50, 51], \(x_{\text {a}}=A\sin (\omega T)\), where no assumption is made on \(\omega \). By then applying a standard harmonic balance technique [52] for frequency \(\omega \), Eq. (1) is transformed into:

$$\begin{aligned} \begin{aligned}&{\frac{\omega }{2\pi }\int _0^{\frac{2\pi }{\omega }}-m_{\text {a}}A\omega ^2\sin ^2(\omega T) dT} \\&\quad + \frac{\omega }{2\pi }\int _0^{\frac{2\pi }{\omega }} f_{\text {nl}}\left( A\sin (\omega T)\right) \sin \left( \omega T\right) d T=0 \\&\quad \Rightarrow m_{\text {a}}A\omega ^2 \sin (\omega T) \\&\quad - \frac{\omega }{2\pi }\int _0^{\frac{2\pi }{\omega }} f_{\text {nl}}\left( A\sin (\omega T)\right) \sin \left( \omega T\right) dT=0 \end{aligned} \end{aligned}$$
(2)

where the integral is the first harmonics from the truncated Fourier series. Three NESs are considered, which possess nonlinear restoring forces \(f_{\text {nl}}(x_{\text {a}})\) as depicted in Fig. 1b, namely one with a hardening stiffness \(x_{\text {a}}^3\), one with a softening stiffness \(\text {sgn}(x_{\text {a}})\root 3 \of {|x_{\text {a}}|}\) and, finally, one with a softening but saturating stiffness \(\arctan (20x_{\text {a}})\). The relation between frequency and amplitude is found by solving the integral in Eq. (2), which yields:

$$\begin{aligned} \begin{aligned}&f_{\text {nl}}(x_{\text {a}}) = x_{\text {a}}^3: {m_{\text {a}}}\omega ^2 = \frac{3A^2}{4} \\ {}&f_{\text {nl}}(x_{\text {a}}) = \text {sgn}(x_{\text {a}}) \root 3 \of {|x_{\text {a}}|}: {m_{\text {a}}}\omega ^2 = \frac{3 \Upgamma \left( \frac{7}{6}\right) }{\sqrt{\pi }\Upgamma \left( \frac{2}{3}\right) }\frac{1}{A^{\frac{2}{3}}} \\ {}&f_{\text {nl}}(x_{\text {a}}) = \arctan (20x_{\text {a}}): {m_{\text {a}}}\omega ^2 = 2\frac{\sqrt{400A^2+1}-1}{20A^2}, \end{aligned} \end{aligned}$$
(3)

where \(\Upgamma (\cdot )\) is the Gamma function. The frequency–amplitude plots are shown in Fig. 1c, considering a unit mass. The natural frequency of the NES with hardening stiffness is linearly proportional to the vibration amplitude, while it is inversely proportional for the NES with softening and saturating stiffness. For a hypothetical two-DOF host system, the natural frequencies are represented by dashed lines in Fig. 1c.

Generally speaking, the NES interacts with a natural frequency of the primary system when the line representing its natural frequency crosses the line of the natural frequency of the primary system. Consequently, the NES with hardening stiffness interacts with the higher mode of the primary system at a higher vibration amplitude than with the lower mode. The opposite holds for the NES with softening and saturating stiffness. This suggests that, assuming a sufficiently large energy content in the system, the NES with softening stiffness should dissipate the lower natural frequency earlier than the NES with hardening stiffness. Accordingly, the order of transfer of the vibration modes should also flip in the case of softening nonlinearity. This conjecture will be proved later on with a more rigorous approach.

The softening \(\text {sgn}(x_{\text {a}})\root 3 \of {|x_{\text {a}}|}\), and softening and saturating \(\arctan (20x_{\text {a}})\) functions are similar both in characteristic and frequency–amplitude relation. However, when approaching zero amplitude, \(\text {sgn}(x_{\text {a}})\root 3 \of {|x_{\text {a}}|}\)’s derivative, and accordingly its frequency, goes to infinity, while \(\arctan (20x_{\text {a}})\)’s derivative in zero is 20, i.e., its natural frequency tends to a constant value. Considering possible practical realizations of a softening NES, in [30, 41, 44] a device was presented that can tailor-make stiffness characteristics. It would not be able to achieve \(\text {sgn}(x_{\text {a}})\root 3 \of {|x_{\text {a}}|}\) because of its infinity derivative; therefore, to facilitate computation and future experimental works, the softening and saturation \(\arctan \) function will be used later on to showcase inverted resonance cascade, as its frequency–energy relation is very similar to the \(\text {sgn}(x_{\text {a}})\root 3 \of {|x_{\text {a}}|}\) function. Furthermore, the algorithm used to generate the multi-dimensional SIMs can better deal with the finite derivative of the \(\arctan \) function.

3 Slow invariant manifold for a generic primary system

Let us consider an n-DOF primary system with an attached NES, whose dynamics is modeled by the following system of differential equations

$$\begin{aligned}&\sum _{j=1}^nm_{hj}\ddot{x}_j+\sum _{j=1}^nc_{hj}\dot{x}_j+\sum _{j=1}^nk_{hj}x_j=0 \nonumber \\ {}&\quad \text {for } h=1,...,n,\,h\ne l\nonumber \\&\quad \sum _{j=1}^nm_{lj}\ddot{x}_j+\sum _{j=1}^nc_{lj}\dot{x}_j+\sum _{j=1}^nk_{lj}x_j+\varepsilon (\ddot{x}_{n+1})=0\nonumber \\&\quad \varepsilon \ddot{x}_{n+1}+c_{\text {a}}\left( \dot{x}_{n+1}-\dot{x}_l\right) + f_{\text {nl}}\left( x_{n+1}-x_l\right) =0, \end{aligned}$$
(4)

where \(m_{hj}=m_{jh}\), \(c_{hj}=c_{jh}\) and \(k_{hj}=k_{jh}\) are the terms of the primary system mass, damping and stiffness matrices, \(\varepsilon \) is the absorber mass, \(c_{\text {a}}\) is the absorber linear damping coefficient, \(x_{1}\) to \(x_n\) are the primary system’s coordinates and \(x_{n+1}\) the absorber’s coordinate. \(\varepsilon \) is assumed small with respect to the primary system masses. Also, this study does not consider the special case of internal resonances. The absorber is assumed to directly interact only with the \(l^{\text {th}}\) DOF of the primary system.

To perform a modal analysis of the primary system, we temporarily neglect the contribution of the absorber, reducing the system to

$$\begin{aligned} \textbf{M}\ddot{\textbf{x}}+\textbf{C}\dot{\textbf{x}}+\textbf{Kx}=\textbf{0}, \end{aligned}$$
(5)

where \(\textbf{M}\), \(\textbf{C}\) and \(\textbf{K}\) are \(n\times n\) matrices (the full system has dimension \(n+1\)). We decouple the primary system by adopting the transformation \(\textbf{x}=\textbf{Uq}\), where \(\textbf{U}\) contains the eigenvalues of \(\textbf{M}^{-1}\textbf{K}\), normalized such that \(\textbf{U}^{\text {T}}\textbf{MU}=\textbf{I}\), where \(\textbf{I}\) is the identity matrix. \(\textbf{U}\) is defined as

$$\begin{aligned} \textbf{U}=\left[ \begin{array}{ccc}u_{11}&{}\cdots &{}u_{1n}\\ \vdots &{}\ddots &{}\vdots \\ u_{n1}&{}\cdots &{}u_{nn} \end{array}\right] . \end{aligned}$$
(6)

To simplify the notation, the damping matrix \(\textbf{C}\) is assumed given by a linear combination of \(\textbf{M}\) and \(\textbf{K}\), such that the primary system is fully decoupled in modal coordinates. This simplification does not affect the generality of the results. After the modal analysis, the primary system dynamics is described by the differential equations

$$\begin{aligned} \ddot{q}_h+2\zeta _h\omega _h\dot{q}_h+\omega _h^2q_h=0\quad \text {for } h=1,...,n, \end{aligned}$$
(7)

where \(\omega _h\) and \(\zeta _h\) are the primary system’s natural angular frequencies and modal damping ratios.

By considering the coordinate transformation and that the NES is attached to the \(l^{\text {th}}\) DOF of the primary system, we reintroduce the absorber into the system. We then obtain the system of differential equations

$$\begin{aligned} \begin{aligned}&\ddot{q}_h+2\zeta _h\omega _h\dot{q}_h+\omega _h^2q_h=-u_{lh}\varepsilon \left( \ddot{z}-\sum _{j=1}^nu_{lj}\ddot{q}_j\right) \\ {}&\quad \text {for } h=1,...,n\\&\varepsilon \ddot{z}+c_{\text {a}}\dot{z}+ f_{\text {nl}}(z)=\varepsilon \sum _{j=1}^nu_{lj}\ddot{q}_j, \end{aligned} \end{aligned}$$
(8)

where \(z=x_l-x_{n+1}\). Next, we introduce the dimensionless damping parameter \(\zeta _{\text {a}}=c_{\text {a}}/\left( 2\varepsilon \omega _1\right) \), attaining

$$\begin{aligned} \begin{aligned}&\ddot{q}_h+2\zeta _h\omega _h\dot{q}_h+\omega _h^2q_h=-u_{lh}\varepsilon \left( \ddot{z}-\sum _{j=1}^nu_{lj}\ddot{q}_j\right) \\ {}&\quad \text {for } h=1,...,n\\&\ddot{z}+2\zeta _{\text {a}}\omega _1\dot{z}+\frac{f_{\text {nl}}(z)}{\varepsilon }=\sum _{j=1}^nu_{lj}\ddot{q}_j. \end{aligned} \end{aligned}$$
(9)

3.1 Slow invariant manifold and stability

Aiming at characterizing the behavior of the NES against impulsive excitations, we seek the SIM describing the slow dynamics of the system. Considering typical practical constraints, we assume that \(\varepsilon \) is a small parameter (\(\varepsilon \ll 1\)). To obtain the SIM, the dynamic variables are substituted by the complex variables of Manevitch \(A_h(T), B_j(T) \in \mathbb {C}\) [53]:

$$\begin{aligned} \begin{aligned} 2A_h(T)e^{i\omega _hT}&=q_h-i\dot{q}_h/\omega _h\\ 2B_j(T)e^{i\omega _jT}&=z_j-i\dot{z}_j/\omega _j \end{aligned} \end{aligned}$$
(10)

where the original variables are then substituted by:

(11)
(12)

where \(^*\) stands for complex conjugate and \(z_j\) is the contribution of mode j to z.

Deriving (10) w.r.t. time yields, after some steps [41]:

$$\begin{aligned} \begin{aligned} \ddot{q}_h + \omega _h^2q_h&= i2\omega _h\dot{A}_he^{i\omega _hT} \\ \ddot{z}_j + \omega _j^2z_j&= i2\omega _j\dot{B}_je^{i\omega _jT}. \end{aligned} \end{aligned}$$
(13)

The total relative acceleration of the NES is \(\ddot{z}=\sum _{j=1}^n \ddot{z}_j\). Substituting (11), (12) and (13) into (9) and applying harmonic balancing (keeping only terms of \(e^{i\omega _hT} \)) yield:

$$\begin{aligned}{} & {} 2\omega _h\dot{A}_h + 2\zeta _h\omega ^2_hA_h=\nonumber \\{} & {} \quad -u_{lh}\varepsilon (2 \omega _h\dot{B}_{h}-i\omega _{h}^2B_{h}-2u_{lh}\omega _h\dot{A}_{h}+iu_{lh}\omega ^2_hA_h)\nonumber \\{} & {} 2\omega _h \dot{B}_h - i\omega ^2_hB_h+2\zeta _a\omega _1\omega _hB_h \nonumber \\{} & {} \quad +iB_hG_{h}(|B_1|,...,|B_n|)=u_{lh}\left( 2\omega _h \dot{A}_h-i\omega _h^2A_h\right) \nonumber \\{} & {} \quad \text { for } h=1,...,n, \end{aligned}$$
(14)

where the term \(B_hG_{h}(|B_1|,...,|B_n|)\) in (14) is the Fourier coefficient for \(\omega _h\) of the multidimensional Fourier series. A multidimensional harmonic balancing method [52, 54, 55] is applied, which can deal with multi- and quasi-periodic vibrations. The first step is to separate the vibrations into distinct time variables:

$$\begin{aligned} T_{j} = \omega _{j}T \quad \text {for } j=1,...,n \end{aligned}$$
(15)

The multidimensional Fourier coefficient for \(\omega _h\) then is

(16)

The integral (16) is generally hard to solve analytically, except if the restoring force is assumed to have the following form:

$$\begin{aligned} f_{\text {nl}}\approx k_{\text {a}} \left( x_{n+1}-x_l\right) + \sum _{r=1}^g k_{\text {a}2r+1} \left( x_{n+1}-x_l\right) ^{2r+1}. \end{aligned}$$
(17)

The summation \( \sum _{r=1}^g k_{\text {a}2r+1} \left( x_{n+1}-x_l\right) ^{2r+1}\) indicates a generic polynomial series representation of the restoring force of the NES—which is assumed odd—excluding the linear term, and where \(2g+1\) is the highest polynomial order considered. This series can be an exact representation of the restoring force but can also be obtained from Taylor’s series expansion or least-squared fitting of the stiffness characteristic over a certain range. The polynomial series allows for an analytical expression under harmonic balancing [29] for the quasi-periodic vibrations of the NES, as the natural frequencies of the primary system are assumed incommensurate and remote. For now, no assumption will be made on \(f_{\text {nl}}\) to keep the generic nature of the equations, but Eq. (17) will be applied in the numerical examples further on.

Then, the dynamics in (14) are split into two time scales, a fast time \(\tau _0\) and a slow time \(\tau _1\):

$$\begin{aligned} \begin{aligned} A_h(T)&=A_h(\tau _0, \tau _1) \quad B_h(T)=B_h(\tau _0, \tau _1) \\ \quad \tau _0&= T , \, \tau _1=\varepsilon T \quad \frac{d}{dT} = \frac{\partial }{\partial \tau _0} + \varepsilon \frac{\partial }{\partial \tau _1} \end{aligned} \end{aligned}$$
(18)

By applying this procedure to (14) and collecting terms according to their order in \(\varepsilon \), we attain

(19)

where \(\xi _{h}=\zeta _h/\varepsilon \). To obtain the slow flow dynamics from Eq. (19), the (fast) time derivatives with respect to \(\tau _0\) will be assumed zero, leading to a steady-state solution in this time scale. An \(n+1\)-dimensional slow invariant manifold that governs the relation between \(A_{h}\) and \(B_j\), for \(j=1,...,n\) will be found. To verify the assumption that a steady-state motion exists, the stability in \(\tau _{0}\) will be obtained from Eq. (19) as well.

3.1.1 Slow invariant manifold

In the second and third equations of (19), derivatives of \(B_h\) with respect to \(\tau \) are set to zero, and \(A_{h}\) and \(B_{h}\) are defined as \(A_{h}=a_{h}e^{i\alpha _{h}}/2\) and \(B_{h}=b_{h}e^{i\beta _{h}}/2\). Then, the equations are split into their real and imaginary parts, yielding the following equations:

$$\begin{aligned}&2\frac{\partial a_h}{\partial \tau _1}=-2\xi _h\omega _ha_h + u_{lh}\omega _{h}b_h \sin (\beta _h-\alpha _h) \nonumber \\ {}&2a_{h}\frac{\partial \alpha _h}{\partial \tau _1}=-u_{lh}\left( -\omega _{h}b_h\cos (\beta _h-\alpha _h)+u_{lh}\omega _ha_h\right) \nonumber \\ {}&2\zeta _a\omega _1\omega _hb_h=u_{lh}\omega _h^2a_h \sin (\beta _h-\alpha _h) \nonumber \\ {}&\quad -\omega _h^2b_h+b_{h}G_h\left( b_1,...,b_n\right) \nonumber \\&\quad = u_{lh}\omega _h^2a_h \cos (\beta _h-\alpha _h)\nonumber \\&\quad \text { for } h=1,...,n. \end{aligned}$$
(20)

Subsequently, inserting the third into the first equations of (20), and squaring and adding the third and fourth equations yield the slow flow dynamics and slow invariant manifold, i.e.,

$$\begin{aligned} \frac{\partial a^2_h}{\partial \tau _1}&= -2\xi _h\omega _ha^2_h -2\zeta _a \omega _1b^2_h \nonumber \\ u_{lh}^2\omega _h^4a_h^2&=b_h^2\left( \left( \omega _h^2-G_{h}(b_1,...,b_n)\right) ^2+4\zeta _{\text {a}}^2\omega _1^2\omega _h^2\right) \nonumber \\&\quad \text { for } h=1,...,n. \end{aligned}$$
(21)

These form a system of differential equations and one of algebraic equations defining the SIM of the system. \(a_h\) indicates the amplitude of oscillation of the \(h^{\text {th}}\) mode of the primary system, while \(b_h\) indicates the component of the relative amplitude of oscillation of the absorber at \(\omega _h\) angular frequency. The differential equations of (21) imply that \(a_h\) will decrease if there is damping in the NES or modal damping in the primary system. The algebraic equations define the SIM that confines the relation between the modal amplitudes of the host system (\(a_1,...,a_n\)) and of the NES (\(b_1,...,b_n\)).

3.1.2 Stability

In order to obtain the SIM and slow flow dynamics, it was assumed that derivatives of \(B_h\) with respect to \(\tau _0\) were zero. To verify this assumption, the stability of \(B_h\) in \(\tau _0\) is determined by linearizing the last set of equations of (19) around the fixed points on the SIM obtained from (21), and determining the eigenvalues of the Jacobian matrix. As \(\partial A_h/\partial \tau _0=0\), \(A_h\) is not perturbed in this procedure. This procedure is common to determine the stability of SIMs [34, 41]. We obtain from the linearization

$$\begin{aligned} \left[ \begin{array}{c} \frac{\partial \varDelta \textbf{B}}{\partial \tau _0} \\ \frac{\partial \varDelta \textbf{B}^*}{\partial \tau _0} \\ \end{array} \right] = \underbrace{ \left[ \begin{array}{cc} \frac{\partial \textbf{f}}{\partial \textbf{B}} &{} \frac{\partial \textbf{f}}{\partial \mathbf {B^*}}\\ \frac{\partial \textbf{f}^*}{\partial \textbf{B}} &{} \frac{\partial \mathbf {f^*}}{\partial \mathbf {B^*}} \end{array} \right] }_\textbf{J} \left[ \begin{array}{c} \varDelta \textbf{B} \\ \varDelta \textbf{B}^* \\ \end{array} \right] , \end{aligned}$$
(22)

where \(^*\) stand for complex conjugate,

\(\varDelta \textbf{B}=[ \varDelta B_1,..., \varDelta B_n]^T\), \(\varDelta B_h=B_h-B_{h,\text {eq}}\), \(B_{h,\text {eq}}\) is the value of \(B_h\) in the fixed point, and \(\textbf{J}\) is the Jacobian. If the Jacobian has any eigenvalue with a positive real part, the fixed point is unstable. The Jacobian’s submatrices are defined as:

$$\begin{aligned} \begin{aligned} \frac{\partial \textbf{f}}{\partial \textbf{B}}&=\left[ \begin{array}{ccc} \frac{\partial f_1}{\partial B_1} &{} \dots &{} \frac{\partial f_1}{\partial B_n} \\ \vdots &{}\ddots &{}\vdots \\ \frac{\partial f_n}{\partial B_1} &{} \dots &{} \frac{\partial f_n}{\partial B_n} \end{array} \right] \quad \frac{\partial \textbf{f}}{\partial \mathbf {B^*}} =\left[ \begin{array}{ccc} \frac{\partial f_1}{\partial B^*_1} &{} \dots &{} \frac{\partial f_1}{\partial B^*_n} \\ \vdots &{}\ddots &{}\vdots \\ \frac{\partial f_n}{\partial B^*_1} &{} \dots &{} \frac{\partial f_n}{\partial B^*_n} \end{array} \right] \\ \frac{\partial \textbf{f}^*}{\partial \textbf{B}}&= \left( \frac{\partial \textbf{f}}{\partial \mathbf {B^*}}\right) ^* \quad \frac{\partial \mathbf {f^*}}{\partial \mathbf {B^*}} = \left( \frac{\partial \textbf{f}}{\partial \textbf{B}}\right) ^* \end{aligned} \end{aligned}$$
(23)

where \(f_h\) is a recollected version of the final equation of (19):

$$\begin{aligned} \begin{aligned} f_h&= \frac{1}{2\omega _h} \big ( -u_{lh}i\omega ^2_{h}A_h + i\omega _h^2B_h - 2\zeta _{\text {a}}\omega _{1}\omega _{h} \\&\quad -iB_{h}G_{h}(|B_1|,...,|B_n|) \big ) \\&\quad \text { for } h=1,...,n. \end{aligned} \end{aligned}$$
(24)

3.1.3 Interaction points

The SIM presented in Eq. (21) is very informative regarding the system’s slow dynamics since it can characterize the mutual effect of each modal vibration of the primary system on the NES. However, it is quite complex to visualize it because it exists in a 2n-dimensional space. In most studies about the SIM of NES, the SIM is limited to a single mode, which reduces it to a curve in a two-dimensional space. Indeed, this representation constitutes a good starting point for studying the effect of other modes on the one under study. With this purpose, in [29], the so-called interaction points were defined. Their meaning and implications are explained below.

Let us consider that only one mode of the primary system, \(a_h\), is activated. In this case, only \(b_h\ne 0\), while \(b_j=0\) for any \(j\ne h\). The SIM is then reduced to a line in the two-dimensional space \(a_h,b_h\). If any of the other modes \(a_j\) is activated (\(a_j\ne 0\), but small), then the SIM in the \(a_h,b_h\) will be affected, but only in a specific region around a point called interaction point \(b_h\)-\(b_j\).

The interaction point \(b_h\)-\(b_j\) can be found by considering the \(j^{\text {th}}\) equation of (21), and assuming that \(b_h\gg b_i\) for \(i\ne h\) (therefore including \(i=j\)). For illustration, we consider the example of a hardening and a softening stiffness, both locally approximated by a third-order polynomial (see Eq. (17)), such that \(G_h=\omega _{\text {a}}^2+\gamma _3\left( 3b_h^2+6b_j^2\right) /4\), with \(\omega _{\text {a}} = \sqrt{k_{\text {a1}}/\varepsilon }\), where \(\gamma _3>0\) for a hardening stiffness and \(\gamma _3<0\) for a softening stiffness.

This assumption reduces the \(j{\text {th}}\) equation of (21) to

$$\begin{aligned} b_j^2=\frac{u_{lj}^2\omega _j^4a_j^2}{\left( \omega _j^2-\omega _{\text {a}}^2-\gamma _{3}\frac{3}{2}b_h^2\right) ^2+4\zeta _{\text {a}}^2\omega _1^2\omega _j^2}. \end{aligned}$$
(25)

Equation (25) has a maximum for

$$\begin{aligned} b_h^2=\frac{2\left( \omega _j^2-\omega _{\text {a}}^2\right) }{3\gamma _{3}}. \end{aligned}$$
(26)

Since this value corresponds to the point where \(b_j\) is maximal, it is also the point where it has the largest effect on \(b_h\). By substituting Eq. (26) into the \(h{\text {th}}\) Eq. (21), we obtain

$$\begin{aligned} a_h^2=\frac{2\left( \omega _j^2-\omega _{\text {a}}^2\right) }{3\gamma _{3} u_{lh}^2\omega _h^4}\left( \left( \omega _h^2-\frac{\omega _{\text {a}}^2+\omega _j^2}{2}\right) ^2+4\zeta _{\text {a}}^2\omega _1^2\omega _h^2\right) . \end{aligned}$$
(27)

Equations (27) and (26) explicitly identify the interaction point \(b_h\)-\(b_j\) in the \(a_h,b_h\) space. If different polynomial orders are considered in the NES restoring force, the equations are not valid anymore, but the same procedure can be adopted.

We note that, for the case of a hardening NES (\(\gamma _{3}>0\)), a resonant point exists only if \(\omega _j>\omega _{\text {a}}\). Conversely, for a softening NES (\(\gamma _{3}<0\)), it exists only if \(\omega _j<\omega _{\text {a}}\). This observation is consistent with the fact that the NES can resonate with one mode only if the frequency backbone passes through its natural frequency. Therefore, if the mode has a natural frequency \(\omega _j\) larger than the linear natural frequency of the NES \(\omega _{\text {a}}\), only in the case of hardening NES the frequency backbone of the NES can reach \(\omega _j\). The opposite is valid for a softening NES. This implies that, for a hardening NES, \(\omega _{\text {a}}\) should be smaller or equal to the smallest natural frequency of the primary system (\(\omega _{\text {a}}\le \omega _1\)). Contrariwise, for a softening NES, \(\omega _{\text {a}}\) should be larger than the largest natural frequency of the primary system (\(\omega _{\text {a}}\ge \omega _n\)). In general, hardening NESs have \(\omega _{\text {a}}=0\).

Although the passages just presented do not demonstrate the existence of the interaction points, a numerical example presented in [29] illustrates their practical relevance for the case of a purely cubic NES. In the following of this work, they will be utilized to study the mutual effect of the amplitude of oscillation of different modes on the NES and to present the inverted RCC.

Fig. 2
figure 2

Two-DOF mechanical host system with an NES connected to the second mass

Full size image

4 Study for a two-DOF host system

4.1 System description

An undamped two-DOF chain of masses, with identical masses and stiffnesses, is considered as a host system, as illustrated in Fig. 2. The equations of motion with an NES attached to the second mass read:

$$\begin{aligned}{} & {} m\ddot{x}_1+2kx_1 - kx_2=0 \nonumber \\{} & {} m\ddot{x}_2-kx_1 + 2kx_2+\varepsilon \ddot{x}_{3}=0\nonumber \\{} & {} \varepsilon \ddot{x}_{3} +c_{\text {a}}\left( \dot{x}_{3}-\dot{x}_2\right) + f_{\text {nl}}(x_3-x_2) = 0 \end{aligned}$$
(28)

where, without loss of generality, we assume all dimensionless quantities, besides \(m=1\), \(k=1\), \(\varepsilon =0.02\) and \(\zeta _a\) = 0.05 (these numerical values are used throughout the whole study); \(f_{\text {nl}}(z)\) is the absorber’s restoring force. The natural frequencies are \(\omega _1=1\) and \(\omega _2=\sqrt{3}\), which exclude internal resonances. The modal mass normalized eigenvectors at the location of the second mass are \(u_{21}=\sqrt{2}/2\) and \(u_{22}=-\sqrt{2}/2\). A hardening and a softening restoring force will be compared, namely

$$\begin{aligned} \begin{aligned}&\text {Hardening:}\quad f_{\text {nl}}(z)=\varepsilon z^3 \\&\text {Softening:}\quad f_{\text {nl}}(z)=\varepsilon \arctan (20z). \end{aligned} \end{aligned}$$
(29)

In modal coordinates, the equations of motion are:

$$\begin{aligned} \begin{aligned}&\ddot{q}_1+2\zeta _1\omega _1\dot{q}_1+\omega _1^2q_1=u_{21}\varepsilon \left( 2\zeta _{\text {a}}\omega _1\dot{z}+\frac{f_{\text {nl}}(z)}{\varepsilon }\right) \\&\ddot{q}_2+2\zeta _h\omega _2\dot{q}_h+\omega _2^2q_h=u_{22}\varepsilon \left( 2\zeta _{\text {a}}\omega _1\dot{z}+\frac{f_{\text {nl}}(z)}{\varepsilon }\right) \\&\text {Hardening}: \ddot{z}+2\zeta _{\text {a}}\omega _1\dot{z}+z^3=\sum _{j=1}^nu_{lj}\ddot{q}_j\\&\text {Softening}: \ddot{z}+2\zeta _{\text {a}}\omega _1\dot{z}+\arctan (20z)=\sum _{j=1}^nu_{lj}\ddot{q}_j. \end{aligned} \end{aligned}$$
(30)

4.2 Slow invariant manifold

The SIM for the hardening NES, where \(n=l=2\) and \(\gamma _{3}=1\), is described by

$$\begin{aligned} \begin{aligned} u_{21}^2\omega _1^4a_1^2&=b_1^2\left( \left( \omega _1^2-\frac{\gamma _{3}}{4}\left( 3b_1^2+6b_2^2\right) \right) ^2+4\zeta _{\text {a}}^2\omega _1^4\right) \\ u_{22}^2\omega _2^4a_2^2&=b_2^2\left( \left( \omega _2^2-\frac{\gamma _{3}}{4}\left( 3b_2^2+6b_1^2\right) \right) ^2+4\zeta _{\text {a}}^2\omega _1^2\omega _2^2\right) , \end{aligned} \end{aligned}$$
(31)

while the SIM for the softening NES is given by

$$\begin{aligned} \begin{aligned} u_{21}^2\omega _1^4a_1^2&=b_1^2\left( \left( \omega _1^2-G_1(b_1,b_2)\right) ^2+4\zeta _{\text {a}}^2\omega _1^4\right) \\ u_{22}^2\omega _2^4a_2^2&=b_2^2\left( \left( \omega _2^2-G_2(b_1,b_2)\right) ^2+4\zeta _{\text {a}}^2\omega _1^2\omega _2^2\right) . \end{aligned} \end{aligned}$$
(32)

\(G_{1}\) and \(G_{2}\) can be obtained from solving the integral (16); however, an analytical solution to that integral cannot be obtained with standard techniques while numerically computing this integral is very slow. Therefore, for plotting the manifold and studying its stability, the integral is solved semi-analytically by exploiting a polynomial least square approximation. This approximation allows for a fast and converging continuation and stability computation of (32), similarly as in [29].

In the special case where there is only a single active mode, we have \(a_h\ne 0\), \(b_h\ne 0\), \(a_j=b_j=0\) where \(j \ne h\). Accordingly, an exact analytical expression for \(G_h(b_h)\) for the softening NES is found directly through harmonic balancing without resorting to a refitting of polynomial series. Solving the single integral (16) for that case:

(33)

4.3 SIMs with no activated other modes

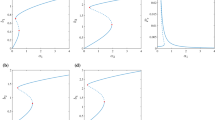
The case where only a single mode is active for a hardening NES has been extensively studied in the literature [11, 28,29,30, 33, 41, 56, 57]. The curves in Fig. 3a–b and c–d depict the SIMs for the hardening and softening stiffness, respectively. All SIMs have the same topology: three branches, of which the dashed middle one is unstable, separated by two folds. The left stable branch is suboptimal, as for this branch, the absorber relative displacement (\(b_h\)) is low; consequently, the decay will be slow, as indicated by the first equation of (21). (We remind that the host system damping is neglected, and the absorber relative velocity is the only source of energy dissipation.) The right branch has high absorber activity and, as such, enables fast energy decay. If the dynamics start on the right branch, the NES engages in efficient targeted energy transfer (TET). It was established in [28, 33, 57] that, to ensure TET, the initial energy of the primary system should be above the fold in the local maximum. For energy levels between the two folds, the TET triggering depends on the system’s initial conditions.

Fig. 3
figure 3

SIMs for the system in Eq. (30), assuming energy on a single mode of the primary system. a and b refer to the hardening case, c and d to the softening one; dashed lines indicate unstable solutions

Full size image

4.4 SIMs with slightly activated other mode and interaction points

Let us now consider the case of one mode of the primary system strongly activated and the other one only slightly.

4.4.1 Hardening stiffness

The SIMs for the hardening stiffness are shown in Fig. 4. To reduce the dimensionality of the problem (see Eq. (21)), Fig. 4a and b is obtained by assuming a constant \(a_2\), which allows 2-dimensional projections of the SIM. For \(a_2=0.01\), the projection of the SIM in the \(a_1,b_1\) space (Fig. 4a) exhibits the typical 3-branch curve with two folds, the stable left and right branch, and the unstable middle branch. It is practically identical to the SIM for a single activated mode in Fig. 3a.

Fig. 4
figure 4

Sections of the SIM for a hardening NES, to study the effect of slightly activated modes. a \(a_1-b_1\) SIM section for several constant \(a_2\); b the corresponding \(b_2/a_2-a_1\) curve; c \(a_2-b_2\) SIM section for several constant \(a_1\); d the corresponding \(b_1/a_1-a_2\) curve

Full size image
Fig. 5
figure 5

Sections of the SIM for a softening NES, to study the effect of slightly activated modes. a \(a_1-b_1\) SIM section for several constant \(a_2\); b the corresponding \(b_2/a_2-a_1\) curve; c \(a_2-b_2\) SIM section for several constant \(a_1\); d the corresponding \(b_1/a_1-a_2\) curve

Full size image

By slightly increasing the primary system’s second vibration mode’s amplitude \(a_2\), a tongue appears on the right branch of the SIM, which is the branch with the best dissipation performance. The tongue bends to the left for increasing \(a_2\), decreasing \(b_1\) for constant \(a_1\); the practical effect of this phenomenon is a reduction in the dissipation rate, which is proportional to \(b_1\). Thus, even a small amount of \(a_2\) will decrease the performance of the NES in dissipating \(a_1\). As expected, the tongue’s onset is on the interaction point \(b_1\)-\(b_2\), marked by a blue dot in Fig. 4a. To clarify this aspect, we note that the interaction point has coordinate \(a_1=1.02\)—as identified through Eq. (27)—that is the value of \(a_1\) for which \(b_2\) is maximal. This is illustrated by the curve in Fig. 4b, which resembles a resonance curve. From a purely analytic perspective, this means that \(b_2\) cannot be neglected in the first equation of (31). In practice, it means that energy of the host system’s second mode is pumped into the NES. As \(a_2\) increases, the peak in Fig. 4b, moves to the right, i.e., to higher \(a_1\) values; accordingly, the tongue in Fig. 4a moves upwards, also to higher \(a_1\) values.

The effect on \(a_2\) of small, but not negligible, \(a_1\) values is now studied through Fig. 4c and d, which are analogous to Figs. 4a and b, respectively, with the difference that now the second mode of the primary system is the one fully activated (\(a_2\ne 0\)), while \(a_1\) is small. Referring to the SIM in Fig. 4c for \(a_1=0.01\), we note that now the interaction point \(b_2\)-\(b_1\) is on the left branch, i.e., the branch with worse dissipation performance. The position of the interaction point suggests that increasing \(a_1\) will have a major effect on the left branch, which is less relevant concerning the absorber’s performance. This observation is fully confirmed by increasing \(a_1\); in fact, also this time, a tongue is generated in the vicinity of the interaction point, as expected. Additionally, even a small value of \(a_1\) lowers the left branch, and the branch becomes rapidly unstable (for \(a_1=0.15\)); accordingly, the required threshold \(a_2(0)\) to jump to the right branch and engage in TET decreases. In other words, a small \(a_1\) value improves the ability of the absorber to dissipate vibrations in the second mode. Regarding the relation between \(a_2\) and \(b_1\) illustrated in Fig. 4d, the peak of the curve now bends to lower \(a_2\) values for increasing \(a_1\), differently from the previous case, illustrated in Fig. 4b.

Thus, for hardening stiffness, a small amount of \(a_2\) (higher frequency mode) decreases the NES performance for \(a_1\) (lower frequency mode). Conversely, a small amount of \(a_1\) (lower frequency mode) increases the NES performance for \(a_2\). Later on, when the modes are both activated significantly, this will cause the resonance capture cascade effect, where the presence of a large amount of energy on the primary system’s second mode (large \(a_2\)) will drastically reduce \(b_1\), and thus the dissipation of \(a_1\), while the presence of a large amount of energy on the primary system’s first mode (large \(a_1\)) will force \(a_2\) to dissipate quickly. Only after \(a_2\) is dissipated and sufficiently low, the efficient right branch of the SIM in the \(a_1,b_1\) space is reinstated, and \(a_1\) is dissipated efficiently. This phenomenon explains the sequence from high-to-low modal dissipation by the NES, as thoroughly discussed in [29].

4.4.2 Softening stiffness

The SIMs for the softening stiffness case are depicted in Fig. 5. Comparing Fig. 5 with Fig. 4, we note different positions of the interaction points. In Fig. 5a and c, the interaction points are on the left and on the right branch, respectively, while in Fig. 4a and c they were positioned oppositely. This observation suggests that, for a softening nonlinearity, a small \(a_2\) value will improve energy dissipation on the first mode, while a small amount of energy on the first mode of the primary system (\(a_1\)) will reduce energy dissipation of the second mode, exactly the opposite of what occurs in the hardening case. This scenario is confirmed by the tongues illustrated in Fig. 5a and c. In both cases, the tongues are generated in correspondence with the interaction points. The same argumentation presented for the hardening case is valid also for the softening case but in an opposite way. In Fig. 5b and d, the trend of the NES amplitude for the slightly activated mode (respectively, \(b_2\) and \(b_1\)) is illustrated. The peak moves to the left when the slightly activated mode is the higher one, and to the right in the other case. The opposite was observed for the hardening case.

According to these observations regarding the SIM evolution for softening stiffness, a small amount of \(a_2\) (higher frequency mode) will increase the NES performance for \(a_1\) (lower frequency mode). Conversely, a small amount of \(a_1\) (lower frequency mode) will decrease the NES performance for \(a_2\) (higher frequency mode). Later, it will be shown that these modal interactions are the mechanism behind the inverted resonance capture cascade when both modes are significantly activated.

4.5 SIMs with strongly activated other modes

4.5.1 Effect on SIM

In Sect. 4.4, it was illustrated that a slightly activated other mode affects NES performance in dissipating the strongly activate mode. Now, we consider the case where both modes are significantly activated. The \(a_1-b_1\) and \(a_2-b_2\) sections of the SIM under strongly activated other modes for hardening stiffness are presented in Fig. 6a and b for modes 1 and 2, respectively. On the \(a_1-b_1\) section, the tongue protruding from the right branch eventually connects to the origin for increasing \(a_2\). A new suboptimal left branch appears that, for a large range of \(a_1\) (0\(-\)4.5), has a small \(b_1\), deteriorating the NES performance for suppressing vibrations of the first mode. Regarding the \(a_2-b_2\) section, strongly activating \(a_1\) not only makes part of the left branch unstable but also pushes the fold downwards. As such, the vibration threshold for \(a_2\) decreases significantly, improving the energy dissipation properties on the second mode for a wide range of \(a_2\). The SIM’s sections for the softening stiffness, shown in Figs. 6c and d, exhibit the opposite effect. The local maximum of the \(a_1-b_1\) SIM section is pushed down with increasing \(a_2\), which facilitates effective dissipation of the first mode’s vibration energy. Conversely, a new suboptimal branch is generated in the \(a_2-b_2\) SIM section for increasing \(a_1\), which deteriorates the dissipation performance of the second mode. In the next section, time series obtained from direct simulations are projected on the SIM to validate the relevance of its shape with respect to the system dynamics and NES performance.

4.5.2 Time simulation with constant modes

To validate the SIMs and the conclusions drawn from them, Eq. (30) is integrated in time with an ODE solver. To facilitate the comparison, one mode of the primary system is artificially kept constant by imposing the right-hand side of the first or the second equation of (30) equal to zero. Although this is a mathematical artifact, it enables us to validate the observations on the SIMs provided so far.

Fig. 6
figure 6

Sections of the SIM for hardening a,b and softening c, d NES, to study the effect of strongly activated modes. a \(a_1-b_1\) SIM section for several constant \(a_2\) (hardening NES); b \(a_2-b_2\) SIM section for several constant \(a_1\) (hardening NES); c \(a_1-b_1\) SIM section for several constant \(a_2\) (softening NES); d \(a_2-b_2\) SIM section for several constant \(a_1\) (softening NES)

Full size image
Fig. 7
figure 7

Modal amplitudes extracted from numerical simulations of Eq. (30), overlapped to the analytically obtained SIM. a,e hardening NES, b, f softening NES; a–d \(a_2\) artificially kept constant and \(a_1\) decreasing in time, e)–h \(a_1\) artificially kept constant and \(a_2\) decreasing in time; a, b, e, f sections of the SIM, c, d, g, h) evolution in time of modal amplitudes. Initial conditions for the hardening case are \(a_1(0)=3\) and \(a_2(0)=0.8\), while for the softening case \(a_1(0)=1\) and \(a_2(0)=1\). In each case, either \(a_1\) or \(a_2\) is kept constant

Full size image

Results regarding both hardening and softening NES are provided in Fig. 7. Figure 7a–d refers to the case of \(a_2\) constant, while Fig. 7e–h to \(a_1\) constant. \(a_h\) is obtained from \(q_h\) as \(a_h=\sqrt{q_h^2+\dot{q_h}/\omega _h}\) and \(b_h\) from z by applying band-pass filters to filter once around \(\omega _1\) and once around \(\omega _2\). Then \(b_h=\sqrt{z_h^2+\dot{z_h}/\omega _h}\) where \(z_h\) is a filtered version of z around \(\omega _h\). The filtering causes unavoidable quantitative errors, which do not alter the qualitative dynamical scenario.

As discussed before regarding the hardening stiffness, for \(a_2>0\), a new suboptimal branch is generated in the \(a_1-b_1\) SIM section, as illustrated in Fig. 7a. For \(a_2=0\), modal amplitudes extracted from the corresponding numerical simulation for \(a_1(0)=3\) are depicted on the SIM in a dotted black line, and for \(a_2=0.2\) in a dotted orange line. The corresponding time evolution of \(a_1\) and \(b_1\) is plotted in Fig. 7c and d with their corresponding colors. For \(a_2=0\), the system dynamics is attracted to the right branch of the \(a_1-b_1\) SIM section, and the time evolution of \(a_1\) shows that the dissipation of this modal energy takes approximately 1500 time units. At the same time, \(b_1\) is nearly constant until a sudden drop at about \(t=1500\), after which the dynamics converges to the SIM’s left branch, with a small \(b_1\) amplitude. When \(a_2=0.2\), the SIM is heavily distorted. The system converges to a SIM branch with very low \(b_1\) values, resulting in very poor energy dissipation. Evolution of \(a_1\) and \(b_1\) in time (orange lines in Fig. 7c and d) confirms this observation. We note a significant quantitative mismatch between the SIM and the \(a_1-b_1\) trend observed from simulations (orange lines in Fig. 7a), which is probably caused by the presence of (sub)harmonics in the absorber vibrations; nevertheless, the qualitative behavior is still confirmed.

As already discussed, the softening stiffness causes an opposite effect, as illustrated by the SIM section in Fig. 7b. In the figure, the dotted yellow and purple lines correspond to time integrations obtained for \(a_1(0)=1\), where either \(a_2=0\) (in yellow) or \(a_2=0.4\) (in purple). The time evolutions of the modal amplitudes are shown in Fig. 7c and d with their corresponding colors. In this case, the suboptimal left branch of the SIM is pushed down by increasing \(a_2\). For \(a_2=0\), the numerical simulation shows a stagnant decay. The inset in Fig. 7b illustrates that the dynamics is attracted to the left suboptimal branch of the SIM; this occurs because \(a_1(0)=1\) is below the local maximum of the SIM. By increasing \(a_2\) to 0.4, the left branch is pushed down and becomes partly unstable. Consequently, the system dynamics is attracted to the optimal right branch of the SIM, and the time evolution of \(a_1\) shows a rapid decay; \(b_1\) initially attains high amplitudes during the dissipation; then, its value drops as the system jumps to the left-most stable branch of the SIM.

We now study the effect of \(a_1\ne 0\) for energy dissipation of the second mode (\(a_2\)). The SIM sections for hardening stiffness are given in Fig. 7e. Modal amplitudes extracted from numerical simulations are superimposed to the SIM for the cases of \(a_1=0\) (black dotted line) and \(a_1=0.4\) (orange dotted line); initial conditions were set such that \(a_2(0)=0.8\). The time evolutions of the modal amplitudes \(a_2\) and \(b_2\) are depicted in Fig. 7g and h, respectively, with their corresponding colors. When \(a_1=0\) (black lines), \(a_2(0)=0.8\) is below the SIM’s local maximum, and the system dynamics converges to the suboptimal left branch, resulting in stagnant decay of \(a_2\) and small \(b_2\) values. Increasing \(a_1\) (\(a_1=0.4\)), this branch becomes unstable, and the dynamics converges to the optimal right branch, with corresponding rapid decay of \(a_2\) and high \(b_2\) values. As soon as the local minimum of the SIM section in Fig. 7e is reached, the system dynamics jumps to the left branch, resulting in small \(b_2\) values and a residual \(a_2\).

Again the opposite happens for the softening stiffness. Figure 7f shows the SIM and modal amplitudes from numerical simulations for the cases of \(a_1=0\) (yellow lines) and \(a_1=0.5\) (purple lines); initial conditions are set such that \(a_2(0)=1\). The time evolution of the modal amplitudes is represented in Figs. 7g and 7h with their corresponding colors. For \(a_1=0\), the system dynamics converges to the right branch of the SIM, while for \(a_1=0.5\), it goes toward a new suboptimal branch created from the fold of the modal interaction. Accordingly, Fig. 7g and h shows a fast decay for \(a_1=0\) and slow decay for \(a_1=0.5\).

To sum up the analysis performed in this section, our investigation reveals that for a hardening NES, a small amount of energy on the higher frequency mode is sufficient to degrade the dissipation performance of the lower frequency mode. On the other hand, vibration energy on the lower frequency mode does not negatively affect the energy dissipation of the higher frequency mode. In contrast, the opposite is true for a softening NES. In some sense, a hardening NES appears to prioritize energy dissipation of the higher frequency mode, while a softening NES prioritizes the energy dissipation of the lower frequency mode. In the next section, the complete system is simulated, and both modes will be able to interact and decay concurrently, which enables the triggering of the resonance capture cascade phenomenon.

5 (Inverted) resonance capture cascade

The full dynamical system in Eq. (28) is now simulated with both modes initially equally activated in terms of kinetic energy, i.e., \(a_1(0)=1\) and \(a_2(0)=1/\sqrt{3}\).

5.1 Hardening stiffness: RCC

At first, we consider the hardening NES. The result of the simulation is shown in Fig. 8. The vibrations of the physical coordinates \(x_1\) and z are shown in Figs. 8a and b. First high-frequency vibrations of the primary system decay and then low-frequency vibrations. The wavelet transformation of the NES relative displacement z illustrates that the NES engages sequentially with the vibration modes, from high to low frequency, the transition being at about \(t=90\). This phenomenon is called RCC and is well known to occur for the conventional hardening cubic-stiffness NES. RCC is even more clearly recognizable looking at the modal vibration content of the primary system, depicted in Figs. 8d and e, where first only the second mode (\(a_2\)) decays. At about \(t=90\), the first mode (\(a_1\)) engages in the cascade and start decaying. The modes in the NES show a high, near-constant amplitude in the second mode (\(b_2\)) before switching to the first one (\(b_1\)). The time evolution of the modal amplitudes is projected on the SIM sections \(a_1-b_1\) and \(a_2-b_2\) in Figs. 8f and g. On the \(a_1-b_1\) section, the numerical simulation (dotted orange line) first sits on the black SIM, where \(a_2=1\). Only once \(a_2\) is sufficiently decayed, the dynamics converges to the optimal right branch of the yellow SIM. On the \(a_2-b_2\) section, the system dynamics immediately converges to the optimal right branch. Once the branch is descended, the numerical simulations are attracted to the left branch.

In order to have a more comprehensive illustration of the RCC and its connection to the SIM, a 3-dimensional representation of the SIM is provided in Figs. 8h (\(a_1,a_2,b_1\)) and 8i (\(a_1,a_2,b_2\)); in the figures, the modal amplitudes collected from the numerical simulation are overlapped to the SIM. The curves clearly show how the SIM provides a consistent qualitative description of the system dynamics.

Fig. 8
figure 8

Time simulation of (28) where \(f_{\text {nl}}=\varepsilon z^3\) is the hardening NES stiffness, initial conditions such that \(a_1(0)=1\) and \(a_2(0)=1/\omega _2\). a first mass displacement \(x_1\); b absorber relative displacement z; c absorber relative displacement wavelet transform; d primary system’s modal amplitudes \(a_1\) and \(a_2\); e NES’s modal amplitude \(b_1\) and \(b_2\); f \(a_1-b_1\) SIM sections with overlapped modal amplitudes varying in time; g \(a_2-b_2\) SIM section with overlapped modal amplitudes varying in time; h, i 3-dimensional SIM representations with overlapped modal amplitudes varying in time

Full size image
Fig. 9
figure 9

Time simulation of (28) where\(f_{\text {nl}}=\varepsilon \arctan (20 z)\) is the softening NES stiffness, initial conditions such that \(a_1(0)=1\) and \(a_2(0)=1/\omega _2\). a first mass displacement \(x_1\); b absorber relative displacement z; c absorber relative displacement wavelet transform; d primary system’s modal amplitudes \(a_1\) and \(a_2\); e NES’s modal amplitude \(b_1\) and \(b_2\); f \(a_1-b_1\) SIM sections with overlapped modal amplitudes varying in time; g \(a_2-b_2\) SIM section with overlapped modal amplitudes varying in time; h, i 3-dimensional SIM representations with overlapped modal amplitudes varying in time

Full size image
Fig. 10
figure 10

Evolution of the modal amplitudes in time, for the four-DOF chain of masses, with an attached NES. a, b hardening NES, c, d softening NES. a, c evolution in time of the host system’s modal amplitudes, b, d wavelet transformation of the NES relative displacement

Full size image

5.2 Softening stiffness: IRCC

We now consider the case of a softening NES through a numerical simulation, whose results are provided in Fig. 9. The vibrations of the physical coordinates \(x_1\) and z (Fig. 9a and b) show an opposite picture compared to a hardening stiffness NES. The NES vibrates first with the lower frequency mode and then the higher frequency mode, which can be better seen in the wavelet transform of the NES of Fig. 9c. Accordingly, in the host system, the lower frequency mode is dissipated first. The same is observed in modal coordinates (Fig. 9d and e), where first \(a_1\) decays and \(b_1\) is large. Only once \(a_1\) is sufficiently small, \(a_2\) decays as well, thanks to increased \(b_2\) values. The SIMs and numerical simulations in Fig. 9f and g show good qualitative agreement; we note that the dynamics is first attracted to the right branch of the \(a_1-b_1\) SIM section (Fig. 9f) and to the left branch of the \(a_2-b_2\) section (Fig. 9g). Once the local minimum of the SIM is reached, the system dynamics jumps to the other branch. A more comprehensive view of the comparison between the SIM and the simulated dynamics is provided by the 3-dimensional representation of the SIM in Figs. 9h and i. Considering the main character of the dynamical phenomenon just described, i.e., that the NES first interacts with low-frequency modes, and then with high-frequency modes, this kind of motion is named inverted resonance capture cascade. Observe that the performance of both the softening and hardening NES is in the some order, the hardening NES dissipates the energy over about 370 time units, while the softening NES takes 310 time units. Finally, in Fig. 9c, an increasing frequency in the NES is observed after the RCC. This is because the NES loses synchronization with the modal frequencies of the host system at lower amplitudes. At these amplitudes, the NES reverts to its own natural frequency, which increases for decreasing amplitudes as seen in Sect. 2. For the cubic hardening NES, the frequency in the NES decreases after RCC, as it loses synchronization with the modes and jumps to a lower backbone of nonlinear mode, which has a decreasing frequency [26].

5.3 Four-DOF system

In order to further validate the existence and engineering relevance of the IRCC, we now consider a four-DOF host system. The system consists of an undamped chain of four unit masses attached to each other through identical unit springs; its dimensionless natural frequencies are 0.618, 1.1756, 1.618 and 1.9021. The NES is attached to the second mass. In practice, the system is an extension of the one shown in Fig. 2. First, we consider the case of a hardening NES, then a softening one. The system is studied solely through numerical simulations to validate the existence of the IRCC. The results of the numerical simulations are illustrated in Fig. 10. Figure 10a and b refers to the hardening NES, while Fig. 10c and d to the softening NES. In the figures, the decay in time of the host system’s modal amplitudes and the wavelet transformation of the NES relative displacement are illustrated for the two cases, respectively.

Referring to the hardening case, we observe (Fig. 10a) how, initially, modal amplitude \(a_4\) rapidly decreases, while \(a_1\), \(a_2\) and \(a_3\) do not decrease at all—they actually slightly increase, as also observed in [29]. As proved by the wavelet transformation in Fig. 10b, at the same time, the NES is tuned to the fourth mode. Once \(a_4\) reaches a small enough value, the NES starts oscillating according to the third mode, and simultaneously \(a_3\) rapidly decreases. After that, when also \(a_3\) has a small enough value, the NES tunes to the second mode, and the second vibration mode of the host system (\(a_2\)) is dissipated. Finally, the NES tunes to the first mode, completing the RCC. The higher the mode, the faster the dissipation because of the higher frequency involved.

We now consider the softening NES. Looking at the evolution of the modal amplitudes in time (Fig. 10c), the expected IRCC can be recognized. Namely, first \(a_1\) decays, then \(a_2\), after that \(a_3\) and finally \(a_4\). The mechanisms are analogous to the one observed for the hardening case but with an inverted order. The inverted cascade is even more evident from the wavelet transformation of the NES relative displacement (Fig. 10d). The NES vibrates according to the four modes of the primary system, from the first to the fourth one. The wavelet transformation shows that, initially, the NES vibrates also according to the fourth mode, although with a relatively small intensity, which causes a partial dissipation of the fourth mode concurrently to the first one. This effect is not part of the IRCC and is probably due to modal interactions, which are hard to predict but often present. Indeed, the larger the number of activated modes of the primary system, the more modal interactions are developed, even if the natural frequencies have irrational ratios. Modal interactions can be identified from the wavelet transformation of the NES relative displacement, both for the hardening and the softening cases (Fig. 10b and d). This phenomenon was also observed in [29]. To predict them analytically, modal interactions should be considered while obtaining the SIM. However, this significantly complicates its derivation and enlarges its dimension. It is, therefore, out of the scope of this study.

Regarding the performance of the NESs, while it was similar in the two-DOF case for the softening and hardening NES, here the softening NES is clearly superior, as it is better in dissipating the slower modes. The softening NES is able to dissipate all modes in just over 1600 time units, while in the hardening case, the host system still contains a significant amount of energy in the first mode even after 3000 time units. However, since neither NES was optimized, any comparison of their performance is limited in scope.

To verify the generality of the phenomenon, simulations of the system with an attached softening NES, having the restoring force function \(\text {sgn}\left( x_{\text {a}}\right) \root 3 \of {\left| x_{\text {a}}\right| }\) (see Sect. 2), were also performed. However, they did not exhibit any qualitative difference from the NES with a saturating restoring force considered in the rest of the paper. Therefore, the corresponding figure is omitted for the sake of brevity.

In summary, our analysis confirms that a hardening NES triggers an RRC, dissipating energy one-by-one from the highest to the lowest frequency mode, and reveals that a softening NES leads to an IRCC, where energy is dissipated from the lowest to the highest frequency mode.

6 Conclusions

This study unveiled the existence of the so-called inverted resonance capture cascade (IRCC), which indicates the subsequent engagement of an NES with the vibration modes of the host system, starting from the lowest frequency to the highest one. This phenomenon is opposite to the well-known RCC, where the NES engages first with the highest frequency mode and last with the lowest frequency one. The transition from the classical RCC to the IRCC is related to adopting a softening stiffness characteristic of the NES instead of a hardening one. The performed analysis exploits multi-dimensional SIMs obtained by combining harmonic balance with a multiple-scale technique. By comparing modal amplitudes extracted from numerical simulations, the relevance of the SIM to the system dynamics was validated considering a two-DOF primary system; the SIM enabled us to explain the dynamical phenomena involved. The IRCC was also illustrated for a four-DOF primary system.

From an engineering perspective, the IRCC provides several benefits with respect to the classical RCC. The main one is that low-frequency modes are usually the most dangerous from a structural point of view since they cause larger displacements than higher frequency modes. Thus, their quicker dissipation is an important benefit.

Several aspects were overlooked in this study, which should be further investigated. In particular, we noted that modal interactions and combinatorial resonances have an important role in the NES dynamics, which was not analyzed. However, observing the frequency content of NES from the simulations, these resonances do not seem to qualitatively affect the IRCC, as also observed in [29]. A more involved analytical approach is required for their analysis, which is out of the scope of this paper.

The practical realization of a softening NES poses specific challenges. Although previous studies addressed the realization of NESs with almost arbitrary stiffness forces [30, 36, 44,45,46,47,48,49], they were never utilized for real engineering applications, but only for academic studies; therefore, potential technical limitation might arise for their industrial exploitation.

In the present study, the IRCC was investigated from a purely phenomenological perspective, and no attempt to optimize its performance was made. Optimization is an important aspect that should be evaluated for assessing the real benefit of a softening NES. The optimization should also consider various shapes of the restoring force function. This is an essential step for comparing the performance of hardening and softening NESs.