A versatile strategy to compute nonlinear normal modes of flexible beams

Abstract

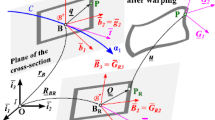
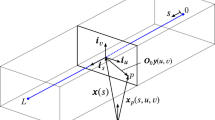
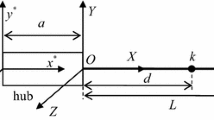
Flexible beams are usually modeled under the assumption of large displacement, finite rotation, but with small strains. Such hypothesis allows the equation of motion to be built using co-rotational finite elements. The co-rotational formulation decomposes the total motion of a structural element into two parts: a rigid body and an elastic (small) deformation. This way, a geometric nonlinearity caused by the large displacements and rotations of the beam’s cross sections can be efficiently modeled. The novelty of this paper consists in incorporating this modeling technique inside a standard method to compute nonlinear normal modes (NNMs). The resulting method becomes a dedicated one to the analysis of complex flexible beams, including those with nonuniform cross sections and with pre-deformations. Those cases are not easily incorporated by other methods in the literature. The harmonic balance method (HBM) is used here to approximate the periodic solutions of the system. The arc-length parametrization is used to perform the continuation with respect to the energy level. The alternating frequency-time (AFT) method is used to compute the Fourier coefficients of the nonlinear elastic forces computed from the co-rotational finite elements. Two examples are used to illustrate the performance of the proposed method: bi-clamped flexible beams with nonuniform cross sections and a flexible riser (offshore oil pipes) in catenary configuration.

Appendices

Appendix A: Nonlinear internal force computation and algorithm

The geometric nonlinearity of the model is concentrated in the nonlinear elastic force vector ${\textbf{f}}_{s}({\textbf{q}})$. As shown in Eqs. (27) and (28), this vector is defined for each finite element as the differentiation of the element’s stain energy ${\mathscr {V}}_e$ with respect to the element’s node displacements and the cross-section rotations, written with respect to the global coordinate system. However, since the stain energy defined by Eq. (15) is written with respect to the local coordinates, the chain rule is necessary to derive ${\textbf{f}}_{e,s}({\textbf{q}}_{e})$:

$$\begin{aligned} {\textbf{f}}_{e,s}({\textbf{q}}_{e}) = \frac{\partial {\mathscr {V}}_e}{\partial {\textbf{q}}_e} = \frac{\partial {\mathscr {V}}_e}{\partial \bar{{\textbf{q}}}_e}\frac{\partial \bar{{\textbf{q}}}_e}{\partial {\textbf{q}}_e} = {\textbf{B}}^{T}{\textbf{K}}_e\bar{{\textbf{q}}}_e \end{aligned}$$

(50)

In Eq. (50), it is implicit that the local coordinates are functions of the global ones, as shown through Eqs. (3)–(5). Also, the derivatives of the local coordinates with respect to the global ones were already defined in Eq. (13).

In order to evaluate the nonlinear elastic force vector through a computer code, the following steps should be taken for each element:

• 1. The global coordinates of the element ${\textbf{q}}_e$ should be selected from the coordinates of the entire structure from the mapping of the elements.

• 2. The element’s local coordinate $\bar{{\textbf{q}}}_e$ should then be calculated from the element’s global coordinates. To this end, the current length of element l must be first computed using Eq. (6). The element’s rigid body rotation angle $\beta$ must also be computed and it can be done either from Eq. (8) or from Eq. (9) by taking the arccosine or arcsine, respectively. It is assumed that the undeformed configuration of the beam is known, so that initial position of the element’s nodes 1 and 2 is known (i.e., $x_1$, $y_1$, $x_2$, $y_1$). This implies that the initial length $l_0$ and rotation of the element $\beta _0$ are also known. They can be computed using Eqs. (7) and (8), respectively, imposing $u_1 = u_2 = v_1 = v_2 = 0$ on the latter.

• 3. Knowing the current length l and rotation $\beta$, the matrix ${\textbf{B}}$ composed of the partial derivatives of the local coordinates with respect to the global ones can be computed using Eq. (14). Also, the element’s local coordinates $\bar{{\textbf{q}}}_e$ can be computed using Eqs. (3)–(5).

• 4. The element’s nonlinear elastic force ${\textbf{f}}_{e,s}$ can then be computed using Eq. (50). The element’s stiffness matrix was defined in Eq. (16) for the case of the IIE linear beam elements and can be computed in prior. Any other traditional linear beam element can also be used in this formulation, and the respective $3\times 3$ stiffness matrix can be constructed eliminating the lines and column of the full $6\times 6$ matrix that are related to the horizontal and vertical displacement of node 1 and the vertical displacement of node 2.

• 5. If necessary, the element’s tangent stiffness matrix can be also computed using Eq. (29), where the vectors ${\textbf{w}}$ and ${\textbf{z}}$ can be computed from their definition in Eqs. (11) and (12), respectively.

• 6. Once the element’s nonlinear elastic force ${\textbf{f}}_{e,s}$ has been computed for all elements that compose the flexible beam, the nonlinear elastic force of the entire structure ${\textbf{f}}_{s}$ can be constructed following the traditional finite element assembly from the element’s mapping.

Those steps were implemented in MATLAB and the code is presented follows:

Appendix B: Periodic solutions of Hamiltonian systems: reasons for phase and amplitude restrictions

When applied to a Hamiltonian systems, the harmonic balance equations defined by Eq. (39) are satisfied by two-dimensional families of periodic solutions. The system of algebraic equations is then underdetermined, since it has an infinite number of solutions. One of the dimension comes from the fact that the system is autonomous, meaning that any periodic solution can be shifted in time and continues to be a solution of the harmonic balance equations. By adding a phase restriction to the problem, the resulting algebraic equations are then satisfied by the one-dimensional families of periodic solutions, the nonlinear normal modes (NNMs) of the system. Since this one-dimensional solution branch corresponds to an infinite number of periodic solutions, the harmonic balance equations with only the phase restriction continue to be an underdetermined algebraic system. Therefore, to compute one periodic solution, an amplitude restriction is necessary.

Those restrictions are true even for the computation of linear normal modes (LNM). By imposing the Ansatz ${\textbf{q}} = e^{\lambda t}$ to the linear system ${\textbf{M}}\ddot{{\textbf{q}}} + {\textbf{K}}{\textbf{q}} = {\textbf{0}}$, an initial zero phase restriction is already imposed to the solution, and the classical eigenvalues problem that defines the LNMs is obtained. This eigenvalue problem also corresponds to an underdetermined system of algebraic equation since any multiple of the eigenvector is also an eigenvector, hence a solution. Then, to actually compute the LNM numerically, an amplitude restriction is necessary and it is usually realized through, for example, a mass normalization equation.

Later on, when performing the continuation of the periodic solution to compute the NNM, the parametrization restriction (arc length, orthogonal, local, etc.) in the predictor–corrector scheme already plays the role of an amplitude restriction since it indirectly restricts the distance between periodic solutions with different energy levels. Therefore, the additional amplitude restriction defined by Eq. (41) is not necessary to find the next periodic solution in the numerical continuation. But, when using a parametric restriction only, the energy of the solution, which corresponds to the free parameter of the continuation process, is not explicit, and a predefined interval for the continuation cannot be set upfront. With the explicit amplitude restriction, Eq. (41), not only one additional equation is added to the problem, but also the free energy parameter a. This is how the continuation of the periodic solution is implemented for example in the NLvib software supplied by Krack and Gross [26].

When using the strategy of adding a damping term $\lambda \dot{{\textbf{q}}}$ to the problem, as many authors do, the coefficient $\lambda$ is not a free parameter to the continuation since it must be always zero for a periodic solution to exist. Therefore, the interval of the free parameter in the continuation process cannot be initially set using this strategy. Nevertheless, the algebraic system becomes square, which can be beneficial regarding the numerical efficiency. Without an explicit free parameter in the continuation process, the continuation can still be done controlled by a fixed number of continuation steps, or by adding a conditional statement to be checked at every step of the continuation.

Although conceptually different, the amplitude restriction can also be associated with the continuation with the asymptotic numerical method (ANM) [45], since an arc length in which the Taylor series expansion of the solution branch is valid from a known periodic solution must be defined.