1 Introduction

In many power generation devices, including gas turbines, rocket engines, and industrial burners, combustion occurs in an enclosed space. In these devices, the heat release rate fluctuations may interact with the acoustic field in the combustor and vice versa. As a result, feedback may arise, and when this feedback is positive, there will be growth in acoustic fluctuations, which eventually saturates to limit cycle oscillations due to nonlinearities in the system. This phenomenon is known as thermoacoustic instability. The violent oscillations are usually harmful to combustion devices and can cause the extinction of the flame, or damage the hardware [1,2,3,4]. In the past few decades, lean-premixed-prevaporized (LPP) combustors are widely applied in the industry to reduce emissions. The flame is inherently more sensitive to perturbation when operating in fuel-lean conditions. Thus, the LPP combustors are more susceptible to thermoacoustic instability. Because of the wide application of LPP combustors, thermoacoustic instability has become a major concern in combustor design. Numerous studies in the past have focused on predicting the onset, evasion, or suppression of thermoacoustic instabilities.

Rayleigh first explained the emergence of thermoacoustic instability in 1878. He showed that when the acoustic oscillation is in phase with the fluctuations in unsteady heat release rate, energy is added to the acoustic field; hence the amplitude of acoustic pressure will grow [5]. The amplitude would keep increasing until limited by the nonlinear effects. To identify the regime where thermoacoustic instability occurs, investigating the feedback mechanism is of crucial importance [6]. In many cases, the propagation of acoustic waves is considered to be a linear phenomenon since the amplitude of pressure oscillations corresponding to the perturbations is relatively low when compared to the mean pressure in the combustor [7]. The flame, however, is more complex due to the inherent nonlinearities associated with the chemical reactions and transport processes of heat and momentum [8]. The response of the flame to the acoustic perturbation is also highly nonlinear, especially in a turbulent environment [7].

Traditionally, modeling of thermoacoustic instability aims to determine the response of the flame to acoustic perturbation. In the past few decades, several low-order models based on a quasi-linear approach were introduced. Among them, the most commonly used models are flame transfer function (FTF) [6, 9,10,11,12,13] and flame describing function (FDF) [6, 14,15,16]. FTF estimates the linear response of the flame to acoustic perturbations by either experiment or simulations. External velocity perturbation (\(u'\)) is introduced to the combustor by using actuators (speakers or linear actuators). Then, the response in the form of the fluctuation in the heat release rate (\(\dot{q}'\)) is measured and evaluated as a function of the forcing frequencies (\(\omega \)). The flame transfer function, F, is, then, defined as shown in Eq. (1), where \(\bar{\dot{q}}\) and \({\bar{u}}\) are the mean heat release rate and the mean velocity at a given condition.

$$\begin{aligned} F(\omega )~{=}~\frac{\dot{q}'(\omega )/\bar{\dot{q}}}{u'(\omega )/{\bar{u}}}~{=}~G(\omega )e^{i\varphi (\omega )} \end{aligned}$$
(1)

Once the FTF is estimated, the global dynamical behavior of a thermoacoustic system can be evaluated by incorporating the acoustic driving due to heat release rate fluctuations (obtained from FTF) into the acoustic field equations. However, established on classical linear stability analysis, FTF cannot capture the nonlinear effect of the thermoacoustic system. Thus, the amplitude of limit cycle oscillation, or triggering phenomenon in a subcritical Hopf bifurcation, cannot be estimated using FTF [17]. Subsequently, flame describing function (FDF) was introduced. Originated from theories of control systems [18] and introduced by Dowling et al. [6, 10], FDF extended the framework of FTF to the nonlinear regime. It defines the complex response of the flame as a function of both input frequency (\(\omega \)) and amplitude (\(|u'|\)), as shown in Eq. (2).

$$\begin{aligned} F(\omega ,|u'|)~{=}~\frac{\dot{q}'(\omega )/\bar{\dot{q}}}{u'(\omega )/{\bar{u}}}~{=}~G(\omega ,|u'|)e^{i\varphi (\omega ,|u'|)} \end{aligned}$$
(2)

The FDF approach considers the flame as a nonlinear module coupled to the linear acoustic system. Compared to FTF, FDF can predict the amplitude of limit cycle oscillation. However, FDF is based on a quasi-linear assumption, i.e., for a particular forcing, the flame only responds at the same frequency. In other words, the response of flame at the higher harmonic frequencies resulting from the forcing is ignored [19]. Thus, FDF may not be suitable for modeling complex behaviors that include non-harmonic responses, e.g. chaos, and intermittency. Moreover, in FDF, the flame is forced by acoustic perturbations at different frequencies and amplitude, which similar to FTF, does not include many aspects of the inherent physics of the flame dynamics [20]. For a long time, the conditions of a thermoacoustic system were considered either operational stable or unstable (limit cycle thermoacoustic oscillation). Correspondingly, FTF/FDF approaches mainly focus on finding out the unstable regime and the amplitude of periodic oscillation. However, experimental observations have shown that thermoacoustic systems can exhibit complex dynamical behaviors other than limit cycle oscillations [21,22,23]. Many of these behaviors can be identified from laminar thermoacoustic systems. Beyond limit cycle oscillation, Kabiraj et al. [24] observed a route to chaos through quasi-periodic oscillation in a laminar Rijke tube, which conforms Ruelle–Takens scenario. Various bifurcations in the same system were subsequently investigated [25], and complex behaviors including strange non-chaos were captured [26]. These findings were also supported by other groups. For example, in a separate study, Guan et al. [27] also identified an intermittency route to chaos in a laminar Rijke tube. Collectively, these studies show that even a simple thermoacoustic system can exhibit rich dynamics.

Inspired by the observations, the underlying physics of these complex behaviors in thermoacoustic systems attracts wide research interest. Existing approaches based on one-way coupling and forced response cannot provide plausible explanations for these phenomena. However, an alternative viewpoint based on synchronization is getting attention recently. Pawar et al. [28] showed that the onset of thermoacoustic instability is an outcome of the mutual synchronization between the unsteady heat release rate and acoustic fluctuations. Depending on the dynamical state of the system, the two signals can be either synchronized or de-synchronized. Later studies by Mondal et al. [29] found various synchronization states including phase locking, intermittent phase locking, and phase drifting. Moon et al. [30] presented a thermoacoustic system that consists of two coupled turbulent combustors, and investigated their mutual synchronization. Premraj et al. [31] investigated the effect of system parameters on the synchronization behaviors of coupled oscillators.

These researches paved the way for building new models for thermoacoustic systems using the framework of synchronization. Godvarthi et al. [32] found that while varying the coupling strength, a system of locally coupled grid of chaotic Rossler oscillators coupled globally to a chaotic Van der Pol oscillator can become self-organized and transition to periodic oscillations. Guan et al. [33] introduced a low order model consisting of two Van der Pol oscillators. Our recent work presented a phenomenological model based on the synchronization framework for modeling laminar thermoacoustic systems [20]. We use a pair of damped linear oscillators to represent the unsteady heat release rate and acoustic fluctuation, the two oscillators are nonlinearly coupled. By adjusting the coupling strength, the model can replicate the Hopf bifurcation in a laminar thermoacoustic system, capture the route to chaos, and predicts states including quasi-periodic oscillation, chaos, and strange non-chaos. In the present work, we attempt to extend the synchronization framework for thermoacoustic systems to the turbulent regime.

In turbulent combustors, turbulent reactive flow always generates low amplitude disordered acoustic fluctuations in the chamber. During stable operation, the sound is known as combustion noise. Traditionally, combustion noise is considered acoustic fluctuations and treated as background noise. However, recent studies [34,35,36] showed that combustion noise possesses high-dimensional chaotic fluctuations and exhibits multifractal characteristics. These studies indicate that combustion noise is dynamically complex and should not be considered pure stochastic fluctuation. Meanwhile, an intermittency state was also discovered presaging the transition from combustion noise to limit cycle oscillation [37, 38]. When increasing the flow rate in the combustor, intermittent bursts of periodic oscillations with high amplitude can appear randomly among low amplitude aperiodic oscillations. Upon increasing the flow rate further, the system will finally enter a regime of periodic oscillation. The transition is found to be a process in which the system gradually self-organizes and loses its multifractality, as order emerges from chaos [36, 39]. Meanwhile, several universal power laws were also identified [40,41,42]. These studies provide valuable early warning signals to evade combustion instability.

The main goal of this study is to extend our synchronization framework [20] for the laminar thermoacoustic system to the turbulent regime. Because the model is phenomenological, it should qualitatively replicate the observations from experiments. We expect the model to capture the transition from combustion noise to limit cycle oscillation through intermittency. Furthermore, the model should identify the self-organization and loss of multifractality in the transition. In our previous work [20], we showed that a pair of coupled oscillators with proper coupling strength can model the quasi-periodic route to chaos observed in laminar thermoacoustic systems. Based on that experience, in this work, we use a tuned pair of coupled oscillators to represent the simplified turbulent reactive flow. These two oscillators are then coupled with a third oscillator representing the acoustic field. We will show that, with proper coupling strength, this three-oscillator model can reflect the combustion dynamics arising in a turbulent combustor.

The rest of the manuscript is organized as follows: in Sect. 2, we introduce the model based on the synchronization framework; In Sect. 3, we introduce the experimental setup; In Sect. 4, we compare the dynamics observed in the model and the experiment. The results will show that the model can qualitatively replicate the transition from combustion noise to periodic oscillation in a turbulent thermoacoustic system. Power laws associated with self-organization and loss of multifractality are also captured.

2 Model construction

Our primary goal is to present a phenomenological, reduced-order model based on a synchronization framework for modeling the transition to thermoacoustic instability in a confined turbulent combustor. In our previous study [20], we proposed a synchronization-based model for a laminar combustor, where the acoustic field and the unsteady heat release rate were represented by a pair of nonlinearly coupled damped oscillators, each of which had a two-dimensional phase space. By varying the coupling strength between the two oscillators, the system could reproduce the route to chaos observed in a laminar combustor [24]. The system also captured multiple bifurcations and different dynamical states, including limit cycle oscillation, quasi-periodic oscillation, strange-non chaos [26], and chaos. Expanding on that work, this study considers the acoustic pressure and unsteady (turbulent) heat release rate as two nonlinearly coupled sub-systems. Unlike in a laminar combustor, a turbulent combustor’s heat release rate fluctuations exhibit chaotic behavior when the coupling between the unsteady heat release rate and the acoustic field is weak. In order to capture this, the unsteady heat release rate in the proposed model for the turbulent combustor is represented using a pair of coupled second-order differential equations (Eqs. 3–4). This system of differential equations with appropriate coupling strength exhibits chaotic dynamics in four-dimensional phase space. Hence, they can represent the chaotic oscillations corresponding to turbulent heat release rate. Here, we consider that the time series of \(y_2\) represents the unsteady heat release rate. Equations (3–4) are further coupled with Eq. 5 that represents the acoustic oscillator. Note that \(y_3\) represents the pressure fluctuations.

The system of oscillators has angular frequencies of \(\omega _1\), \(\omega _2\), and \(\omega _3\). We will use the symbol f to denote the frequency, which is related to angular frequency as \(\omega ~=~2\pi f\). The damping coefficients are \(\zeta _1\), \(\zeta _2\), and \(\zeta _3\).

$$\begin{aligned} \ddot{y}_1+\zeta _{1}\omega _1\dot{y}_1+\omega _1^2y_1~=~{C_{12}}(1-{y_2}^2) \dot{y}_1 \end{aligned}$$
(3)
$$\begin{aligned} \ddot{y}_2+\zeta _2\omega _2\dot{y}_2+\omega _2^2y_2~=~R_1C_{12}y_1^2+R_2C_{32}y_3^3 \end{aligned}$$
(4)
$$\begin{aligned} \ddot{y}_3+\zeta _3\omega _3\dot{y}_3+\omega _3^2y_3~=~C_{32}(1-y_2^2)\dot{y}_3-\dot{y}_3^3 \end{aligned}$$
(5)

We define \(C_{12}, C_{21}, C_{23}, C_{32}\) as the coupling strength. Furthermore, the relative strength of the mutual coupling is defined using the ratio of \(C_{ij}\)s, \(R_1~=~C_{21}/C_{12}\), \(R_2~=~C_{23}/C_{32}\). The presented reduced-order model is designed to replicate the dynamical states observed in a turbulent combustor exhibiting thermoacoustic instability. We leveraged knowledge gathered from past experiments to help guide the selection of various model parameters. For example, recent studies showed that the coupled interaction between the unsteady heat release rate and the acoustic field is asymmetric [43, 44]. Unsteady heat release rate exerts a stronger influence on the acoustic field than the converse, which implies \(C_{32}>C_{23}\) so that \(R_2<1\). We select the natural frequencies of the three oscillators (\(\omega _1\), \(\omega _2\), and \(\omega _3\)) such that the time series of pressure and heat release rate have a similar value and variational trend for the dominant frequency with a change in the control parameter as observed from experiments. To achieve this, we assign a fixed ratio between \(\omega _1\) and \(\omega _2\) (\(\omega _1~=~1.125 \omega _2\)), resulting in intended aperiodic oscillations when the heat release rate subsystem (Eq. 3–4) was weakly coupled to the acoustic oscillator (Eq. 5). Meanwhile, to ensure that the dominant frequency of \(\dot{q}'\) increases during the transition as observed in the experiment, we set a linear relationship between the natural frequency, \(\omega _2\) and the coupling strength \(C_{32}\) (\(\omega _2~=~2\pi C_{32}/20\)). The natural frequency of the acoustic field (\(y_3\)) is chosen to be constant (\(\omega _3~=~1.3\times 2\pi \)) since in the experiments, the dominant frequency of acoustic oscillations is more or less constant. The nonlinear terms \(C_{12}(1-y_2^2)\dot{y}_1\) and \(C_{32}(1-y_2^2)\dot{y}_3\) are inspired by Van der Pol oscillator. The other nonlinear terms, however, are manually selected to match the experimental observation, a more detailed description of this process is given in Sect. 4. In essence, we start with nonlinear terms with the lowest exponents and smaller degrees and increase the complexities of the terms until we qualitatively and statistically reproduce the dynamics observed in the experiments (nature of transitions in dynamics, the frequency profile, and the fractal characteristics of \(p'\)). The set of parameters we choose is not unique, and it is possible to use another set of better-optimized nonlinear terms with higher degrees and exponents to improve the model. Toward this, a data-driven optimization strategy will be designed in future work. The other parameter values used in Eqs. (3–5) are selected to be: \(\zeta _{1}~=~0.1\), \(\zeta _{2}~=~0.05\), \(\zeta _{3}~=~0.3\), \(C_{12}~=~1.62\), \(R_1~=~1.2\), and \(R_2~=~0.54\). In the study, since Eq. 3 and Eq. 4 form a subsystem that represents the unsteady heat release rate, \(C_{12}\) is fixed. Meanwhile, \(C_{32}\) is considered the control parameter which dictates the transitions between different dynamical states of the system. In an experimental turbulent thermoacoustic system, the control parameter is generally the Reynolds number of the flow, Re=\(\bar{u}L/\nu \), where L is the characteristic length scale of the burner and \(\nu \) is the kinematic viscosity of the unburned mixture. With the current model and the value of parameters mentioned above, the transition between various states was observed for the range of \(C_{32}\) from 14 to 18. The coupled equations (Eqs. 3–5) are solved using the 4th-order Runge–Kutta method in Matlab. Gaussian noise with variance \(\sigma =5\%\) is added to the time series. We note that for a fixed \(C_{32}\), the model outputs a normalized time series of heat release rate and pressure fluctuations.

As mentioned earlier, the primary goal of this work is to demonstrate that coupled oscillator models can reproduce combustion dynamics in a turbulent combustor. During the construction of the model, we intended to keep the nonlinear terms as simple (low-order) as possible while qualitatively reproducing the key dynamics observed in experiments. The current forms of nonlinear terms shown in Eqs. 3–5 and the values of various constants were chosen after manual optimization and satisfied the requirements. We note that, in general, a large number of possible forms of nonlinear terms can be selected. A robust method for identifying and optimizing the nonlinear terms will be a focus of our future work.

3 Experimental details

We primarily use the experimental data from Pawar et al. [28] as a benchmark to validate the model. The experimental study applies to a laboratory-scale turbulent combustor with a bluff body stabilized flame, where liquefied petroleum gas was burned with air. The incoming airflow first passes through a settling chamber. Then, it is premixed with the fuel and sent into the combustion section. The pressure fluctuation (\(p'\)) in the combustor is estimated using pressure transducers. The heat release rate (\(\dot{q}\)) is acquired by measuring the chemiluminescence intensity of CH* using a photo-multiplier tube (PMT), from which its fluctuations (\(\dot{q}'\)) are calculated. During the experiment, the fuel flow rate was kept constant at 25 slpm, while the air flow rate varied from 400 slpm to 940 slpm, covering Reynolds number (Re) range from \(1.09\times 10^5\) to \(2.12\times 10^5\). We note that an increase in flow rate (Re) increases the mean heat release rate (\(\bar{q}\)) of an unconfined (de-coupled from acoustics) turbulent flame due to decreased residence time [45]. Thus, it is appropriate to use heat release rate intensity \(\dot{q}'_{rms}/\bar{\dot{q}}\) as the statistical measure of fluctuations. However, the acoustic characteristics of the chamber remain unaffected by the Re. Thus, \(p'_{rms}\) is a good measure.

The measurements confirm that the combustor exhibited stable operation at low Re. However, the pressure and heat release rates fluctuate at a low amplitude due to the inherent turbulence. This regime refers to high-dimensional chaos [46]. As Re increases, the amplitude of pressure oscillation increases continuously. Meanwhile, among aperiodic oscillations, burst and periodic oscillations start emerging in a near-random fashion, which refers to the state of intermittency. When Re further increases, both pressure and heat release rates oscillate periodically and with significantly greater amplitude, corresponding to the onset of thermoacoustic instability.

We will use a second set of experimental data from Nair et al. [37] during our discussion on the power-law behaviors in the transition process (Sect. 4.5). This work used a swirl-stabilized burner. The rest of the configuration and experimental technique remained mostly unchanged. The details of this setup can be found in [37].

In experiments, the flow in the combustor is fully developed (constant turbulence intensity, \(u'_{rms}/{\bar{u}}\)) and hence, \(u'_{rms}\) grows linearly with Re (\(u'_{rms} \propto Re\)). In these experiments, the measured \(p'_{rms}\) and \(\dot{q}'_{rms}\), which increase with Re, are composed of the contribution from turbulence and the thermoacoustic instability. The former arises from the RMS of the fluctuations in flow velocity \(u'_{rms}\), and hence can be assumed to be proportional to Re. These turbulence-induced effects are apparent when one measures the pressure in a turbulent flow inside the combustor without the flame or heat release rate in an unconfined flame, thus no thermoacoustic effects. It is to be noted that the model presented in Eqs: 3–5, only accounts for the coupled dynamics between acoustics and heat release, thus discounts the increase in \(p'_{rms}\) and \(\dot{q}'_{rms}\) due to turbulence effects. Since these discounted effects are proportional to Re, and in our model, we assumed \(C_{32}~\text {is proportional to} Re\), the experiment equivalent of pressure and heat release rate from our models can be obtained as \(p' = y_3C_{32}\), and \(\dot{q}' = y_2C_{32}\).

4 Results and discussion

The presented synchronization-based three-oscillator model is expected to replicate some of the key features of a turbulent combustor. The model should capture the transition from combustion noise to periodic oscillation, during which the amplitude of pressure and heat release rate oscillation increase monotonically. It should also predict different synchronous states during the transition, which mostly depends on the synchronization states of the pressure and heat release rate. Moreover, in the regime of combustion noise, the model is expected to produce a multifractal behavior in pressure oscillations, which is the hallmark of a stable turbulent combustor. As the system transitions to thermoacoustic instability, self-organization is observed during experiments [40, 41] and the time series shows a scale-independent nature marked by power-law dynamics. We expect the model to be able to predict similar behavior.

In the following subsections, we will analyze the statistics and dynamics of the time series produced by the model and will qualitatively compare them with those of the experimental data. We note that the primary expectation from the model with predefined model parameters is to reproduce the experimental observations qualitatively. The quantitative similarity is not expected, which requires tuning the model parameters based on the experiments.

Fig. 1
figure 1

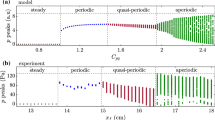
Time series obtained from the model and experiments at different dynamical states. Note that Gaussian noise with variance \(\sigma =5\%\) is added to the time series from the model. From left to right: model, experimental results from Pawar et al. [28] From top to bottom: combustion noise (a(i): \(C_{32}~=~11.05\), b(i): \(Re~=~1.6\times 10^4\)), intermittency (a(ii): \(C_{32}~=~14.95\), b(ii): \(Re~=~1.89\times 10^4\)), limit cycle oscillation (a(iii): \(C_{32}~=~19.7\), a(iii): \(Re~=~2.95\times 10^4\))

Full size image
Fig. 2
figure 2

a(i) and b(i): RMS of \(p'\) and \(\dot{q}'\) at different conditions from model and experiment. As \(C_{32}\) or Re increases, \(p'_{\textrm{rms}}\) increases monotonically. a(ii) and b(ii): dominant frequency of \(p'\) and \(\dot{q}'\) at different conditions from model and experiment. The dominant frequency of pressure and heat release rate when \(C_{32}\) or Re varies. As \(C_{32}\) or Re increases and the system transitions to periodic oscillation, both signals start to have the same dominant frequency

Full size image

4.1 The temporal transition from combustion noise to periodic oscillation

First, we will use the temporal dynamics and their statistics in assessing the model performance. As mentioned before, in the model, the control parameter is the coupling strength between the unsteady heat release rate and the acoustic oscillator \(C_{32}\). Increasing the coupling strength \(C_{32}\), the system transitions from chaos to periodic limit cycle oscillation through intermittency, a behavior also observed in experiments. Figure 1a (i, ii, iii) shows representative time series of the normalized pressure functions from the model at different \(C_{32}\). These plots also illustrate the changes in the morphology of the time series at different dynamical states. Figure 1b(i, ii, iii) shows a similar time series obtained from experiments ( [28]) at different Re, which clearly exhibit very similar qualitative behaviors. As shown in Fig. 1a(i), at low \(C_{32}\), the signal is disordered, and the overall amplitude of \(p'\) is small, which corresponds to the regime of combustion noise. In Fig. 1a(ii), as \(C_{32}\) increases, although the time series remains disordered, the amplitude of the time series increases, and intermittent oscillations appear. During intermittency, the signals are composed of aperiodic, low-amplitude fluctuations interspersed amongst periodic, high-amplitude fluctuations in a near-random fashion. The different parts of the signal have amplitudes with several different orders of magnitudes [37]. Previous studies proposed a route from combustion noise to thermoacoustic instability through intermittency [37], and hence it is important to determine the existence of an intermittency state in the model. When we further increase \(C_{32}\), as shown in Fig. 1a(iii) the time series becomes more regular and with a larger amplitude, the periodic oscillation has now become dominant. It indicates that the system has entered the regime of limit cycle oscillation. As mentioned earlier, we observe similar characteristics in the corresponding time series from the experiment, shown in columns Fig. 1b(i, ii, iii).

Fig. 3
figure 3

The power spectra density of \(p'\) at different conditions from model and experiment. As \(C_{32}\) or Re increases, the height of the peak increases significantly, where periodic oscillation becomes dominant

Full size image

4.2 The variation in the RMS and dominant frequency of the pressure and the heat release rate fluctuations

One of the hallmarks of thermoacoustic instability is the large increase in the amplitude of pressure and heat release rate fluctuations as the system transitions from combustion noise to the limit cycle oscillation. While this can be visualized qualitatively for three different \(C_{32}\) (model) and Re (experiment) in Fig. 1, we additionally compare the root mean square values of both pressure fluctuations (\(p'_{\textrm{rms}}\)) and heat release rate fluctuations (\(q'_{\textrm{rms}}\)) for a range of operating conditions (Fig. 2a(i) and b(ii)). Here we evaluate the \(\textit{RMS}\) of time series of a quantity, x(t) as \(x_\textrm{rms}~=~\sqrt{\frac{1}{M}\sum _{i=1}^{M} (x(t_i)-\bar{x})^2}\), where \(\bar{x}\) is the mean of x and \(M\) is the length of the time series. Our model predicts a continuous increase of \(p'_{\textrm{rms}}\) and \(q'_{\textrm{rms}}\) with an increase in the control variable, \(C_{32}\) (Fig. 2a(i)), a trend which is observed for experiments with turbulent combustor (Fig. 2b(i)). We next analyze the dominant frequency of the pressure and heat release rate signals, which is critical in determining the mode of oscillations in thermoacoustic instabilities. Figure 2a(ii) depicts the variations of dominant frequencies of \(p'\) and \(\dot{q}'\) with \(C_{32}\), predicted by the model. As we can see in the figure, initially at low \(C_{32}\) during the state of combustion noise, the two signals exhibit different dominant frequencies, which are far apart. But as \(C_{32}\) increases, the two dominant frequencies gradually merge, and finally, both signals have the same frequency during limit cycle oscillation (high \(C_{32}\)). This suggests that the two signals are synchronized with each other (we will quantify this process in the next subsection). Similar behavior of dominant frequency is also observed for experiments as Re is increased (Fig. 2b(ii)). Furthermore, we also compare the power spectral density (PSD) of \(p'\) at various \(C_{32}\) (model) and Re (experiment) in Fig. 3. They indeed show a similar trend in that, the peak of the dominant frequency becomes sharper in the spectrum as \(C_{32}\) or Re increases, and periodic oscillations become more dominant (seen in Fig. 1). The sharpened peak indicates that the energy is gradually concentrated to the dominant frequency from a previously broadband spectrum at low \(C_{32}\) or Re. We will quantify and discuss the behavior of spectral condensation in the later section.

4.3 Synchronization characteristics

As mentioned in Introduction, experimental studies have shown that the time series of \(p'\) and \(\dot{q}'\) exhibit a de-synchronous state during the state of combustion noise, in that the phase of their oscillation varies with time. The studies have also confirmed that these time series become phase synchronized as the system approaches the onset of combustion (thermoacoustic) instability. During limit cycle oscillation, \(p'\) and \(\dot{q}'\) become completely phase-locked or phase synchronized. The degree of synchronization between \(p'\) and \(\dot{q}'\) can be evaluated with the Phase Locking Value (PLV), which can be calculated using the Hilbert transform and the relation [47],

$$\begin{aligned} { PLV}~=~\frac{1}{M}\left| \sum _{j=1}^{M} e^{i\left( \phi _{p'}\left( t_{j}\right) -\phi _{\dot{q}'}\left( t_{j}\right) \right) }\right| , \end{aligned}$$
(6)

where \(\phi _{p'}(t_{j})\) and \(\phi _{\dot{q}'}(t_{j})\) are the instantaneous phase of the pressure and heat release rate fluctuations. PLV can vary between 0 to 1; a PLV value of 0 indicates that the two signals are desynchronized, and a PLV value of 1 corresponds to perfect phase synchronization. The PLV evaluated based on the experimental data [28] plotted in Fig. 4(b) shows low values of PLV at low Re (control parameter for the experiments) and at high Re, PLV approaches 1, suggesting phase synchronization. To assess if our model can predict such characteristics, we calculated the PLV from the model output and then plotted it as a function of the coupling strength, \(C_{32}\) in Fig. 4(a). The time series of \(p'\) and \(\dot{q}'\) are de-synchronized at a low \(C_{32}\) (combustion noise). Like experiments, the model also predicts an increase in PLV with \(C_{32}\) (control parameter for the model). Finally, PLV becomes almost 1 when \(C_{32}>17\), suggesting phase synchronization during limit cycle oscillations.

Fig. 4
figure 4

PLV between \(p'\) and \(\dot{q}'\) at different conditions from model (a) and experiment (b). In the regime of combustion noise, the phase locking value between \(p'\) And \(\dot{q}'\) is close to 0, which indicates the two signals are desynchronized. As periodic oscillation appears, PLV increases and stays close to 1, which corresponds to synchronization

Full size image

4.4 Loss of multifractality during transition

In a turbulent combustor, the observed flame dynamics are an outcome of the continuous interaction of multi-scale eddies in the flow with the chemical reaction. Such interaction leads to a broadband low amplitude oscillation in the heat release rate and pressure fluctuations, even in the de-synchronized states. Such broadband oscillations or combustion noise has been traditionally assumed to be stochastic and has been modeled as white or colored noise in many studies [46, 48,49,50]. However, recent studies have shown that combustion noise is not always stochastic, and it has features of higher-dimensional chaos [34, 51]. Furthermore, experimental data and analyses have also shown that the pressure fluctuations from combustion noise can be self-similar and exhibit multifractality [35, 36, 39]. Such behavior of multifractality is, indeed, a hallmark of turbulent flows [52,53,54] and turbulent flame dynamics [55,56,57]. In other words, combustion noise caused by turbulent reactive flows is dynamically complex and can be considered deterministic. More recent studies showed that the onset of thermoacoustic instability can be characterized as an order emerging from chaos via a state of intermittency [19]. During this transition, the system gradually loses its multifractality [36, 39]. Based on these observations, several techniques are proposed to determine the stability boundaries and to provide early warning signals (EWS) [36]. Since the proposed model aims to replicate the dynamics of turbulent combustors, it is critical to assess if it can reproduce the presence and loss of multifractality in pressure fluctuations in combustion noise and thermoacoustic instability (limit cycle oscillations), respectively.

In time series analysis, the fractal dimensions (D) are often used to characterize fractal behavior, where the value and the length of the data show a self-similarity associated with a power law, and D is the exponent of the scaling relation. Fractal nature also exists in many complex systems, e.g., time signals with complex dynamics can be self-similar in local fluctuations with multiple scales [58]. In a self-similar time series, the fractal dimension is related to the Hurst exponent (H) as \(D=2-H\) [59], which evaluates the long-term memory of the time series. However, in many systems involving broadband perturbations (e.g., turbulence), the scaling behavior can be more complex and may depend on the order of the structure function, giving rise to multifractality. A multifractal system, instead of one single Hurst exponent, requires a singularity spectrum consisting of a series of generalized Hurst exponents with multiple orders to describe its characteristics [60]. The singularity spectrum depicts the fractal behaviors of local fluctuations of different magnitudes. In our work, the generalized Hurst exponents are evaluated by multifractal spectrum \(f(\alpha )\) versus singularity exponent \(\alpha \) using the multifractal detrended fluctuation analysis (MFDFA) [61, 62]. In Appendix, we provide a brief description of MFDFA.

Fig. 5
figure 5

Multifractal spectrum at different dynamical states from the model (a) and experiment (b), as \(C_{32}\) or Re increases, the system transitions from combustion noise to periodic oscillation. In the regime of combustion noise, the multifractal profile exhibits a wide range spectrum, corresponding to a dynamically complex state. During the transition, the spectrum shrinks, indicating that the system gradually loses its multifractality

Full size image

Using MFDFA, the multifractal spectra \(f(\alpha )\) for pressure oscillations obtained from our model and previous experiment [28] are plotted as a function of \(\alpha \) in Fig. 5a and b, respectively. It is to be noted that the width of the spectrum quantifies the degree of multifractality of the time series. Figure 5a shows that at low \(C_{32}\) (combustion noise) the spectrum is indeed wide, suggesting strong multifractality and hence complexity. This behavior is also observed for experimental data at low Re (Fig. 5b). As \(C_{32}\) increases, the width of the spectrum shrinks, indicating that the system gradually loses its multifractality as it approaches thermoacoustic instability. At high \(C_{32}\), when the system exhibits limit cycle oscillations, the spectra condense to a point, and hence the multifractality has been lost. This reduction of width and the collapse of the multifractal spectrum can also be seen in experimental data as Re is increased (Fig. 5b).

4.5 Power law in self-organization

In this section, we will discuss the recent discoveries of scaling relations observed as a turbulent system transitions to thermoacoustic instabilities, and assess if the proposed coupled oscillator model can also produce such dynamics. Turbulent systems generally contain high-dimensional chaos, and their time series is naturally irregular and disordered. However, when turbulence is coupled to the other subsystems, through their inherent coupling, self-organization may occur, in that the underlying broadband nature is lost. One typical example is the turbulent Rayleigh-Bénard system, where the fluid motion is turbulent at a low-temperature gradient. However, fluid particles may move orderly at a high-temperature gradient and result in large-scale spatial patterns [63]. During self-organization, the positive feedback leads the disordered, chaotic system to transition to an ordered state, and regularly repeating patterns emerge both time-wise and space-wise. The initially disordered state is generally a superposition of a series of motions with a wide range of modes and a broadband energy spectrum. During self-organization, one or more modes gradually emerge and become dominant. Self-organization has been studied extensively in various turbulent systems including aeroelastic [64] and aeroacoustic [65] systems. In recent years, studies found that the transition from chaotic fluctuations to periodic oscillations in the turbulent thermoacoustic system is also a process of self-organization [39]. Several self-similar behaviors were subsequently identified, including the power laws of Hurst exponent [40] and spectral condensation [41]. To validate the proposed model, we will assess the scaling laws of the Hurst exponents and spectral condensation using the methodology reported by Pavithran et al. [40, 41]. Simultaneously, we will use the same measures on two sets of different experiments, bluff-body stabilized [28] and swirl-stabilized [37] combustors.

Fig. 6
figure 6

The spectral amplitude of the dominant mode (A) versus Hurst exponents (H) at different control parameters during the transition to thermoacoustic instability. Note that both A and H are plotted on a logarithmic scale, and A is normalized by the \(A_I\), which is the y-intercept of linear regression: \(\log (A)~=~n \log (H) + \log (A_I)\). We observed that an inverse power law, \(A/A_I\propto H^{n}\) with an exponent \(n=-2\) (dashed line) fits the data from both model and the two experimental studies. Experimental data are from the bluff-body-stabilized combustor by Pawar et al. [28], and swirl-flow combustor by Nair et al. [37]

Full size image
Fig. 7
figure 7

Scaling behaviors of spectral condensation from the model and experiments, which follows \(\log (P_0)=k \log ([\mu _{m}^{x} \mu _{n}^{y}]) +C\). Note that both \(P_0\) and \([\mu _{m}^{x} \mu _{n}^{y}]\) are plotted on a logarithmic scale, and \(P_0\) is normalized by \(P_{0 \mathrm min}\). Experimental data are from the bluff-body-stabilized combustor by Pawar et al. [28], and swirl-flow combustor by Nair et al. [37]. From left to right: \(\mu _{2}^{1} \mu _{0}^{0}\), \(\mu _{2}^{1} \mu _{0}^{1}\), \(\mu _{4}^{1} \mu _{4}^{1}\)

Full size image

As discussed in 4.4, the Hurst exponent relates to the fractal dimension and can vary between 0 and 1. Time series with \(H~=~0.5\) refers to uncorrelated random fluctuations. For the upper range (\(0.5<H<1\)), the time series is persistent with a long-term positive auto-correlation, i.e., a high value in the time series is likely to be followed by another high value. On the other hand, for \(0<H<0.5\), the time series is antipersistent, i.e., it tends to switch between high and low values. In recent studies [41, 42], an inverse power-law relation between the spectral amplitude of the dominant mode (A) and the Hurst exponent (\(H \propto A^n\)) was reported in turbulent systems that exhibit a transition from the chaotic state to periodic state and thus, self-organization. Interestingly, the exponent n was found to be almost constant and \(n\approx -2\) for a series of different systems, including aeroacoustic, aeroelastic, and thermoacoustic systems. Here, we calculated the Hurst exponent and spectral amplitude of the dominant mode during the transition from the data produced by the model. The results are compared with the experimental data from the bluff-body and swirl combustors, as shown in Fig. 6. We, indeed, observe a power law with an exponent close to − 2 for both the model and the experiments. Such agreement implies that the model is capable of capturing the underlying path in the transition to thermoacoustic instability in turbulent combustors.

Next, we investigate the model’s capability in capturing the self-organization using another measure reported in [40, 42]. In the regime of combustion noise, the time series is aperiodic, with a low amplitude, and show a broadband profile in the power spectrum. However, when the system undergoes limit cycle oscillation due to thermoacoustic instability, the time series become periodic, the amplitude increases significantly, and the natural frequency shifts slightly and becomes dominant in the power spectrum. During the transition, the profile of the power spectrum narrows from a broad peak centered around the natural frequency to a single sharp peak (Fig. 3). The measurement of spectral condensation quantifies how the power spectrum condenses during the transition by calculating the \(m^{th}\) moment of the power spectrum, evaluated as

$$\begin{aligned} \left[ \mu _{m}^{x} \mu _{n}^{y}\right]{} & {} =\left[ \int _{-\delta F}^{+\delta F} \frac{P(F)}{P_{0}}\left| \frac{F}{f_{0}}\right| ^{m} d F\right] ^{x}\nonumber \\{} & {} \quad \times \left[ \int _{-\delta F}^{+\delta F} \frac{P(F)}{P_{0}}\left| \frac{F}{f_{0}}\right| ^{n} d F\right] ^{y} \end{aligned}$$
(7)

\(\mu _m\) here is the \(m^{th}\) moment of the power spectrum, f is the frequency, \(f_0\) is the dominant frequency of time series, \(P_0=P(f_0)\) is the dominant peak of the power spectrum, and \(F=f-f_0\) is the modified frequency. \(\left[ \mu _{m}^{x} \mu _{n}^{y}\right] \) here are the products of higher-order moments of the power spectrum. In Fig. 7, we compare a few high-order moments statistics obtained from the model and the experiments. The figure shows that for all the moments, the model and the experiments do follow a similar behavior in that during the transition from combustion noise to periodic oscillation, the variation of \(\mu _{m}^{x} \mu _{n}^{y}\) follows a power law. The exponents of the power law are not the same constant across the model and the two experiments, primarily due to underlying coupling mechanisms. Nevertheless, the comparison confirms that the coupled oscillators can capture the underlying higher-order statistics of spectral condensation observed during the transition to the periodic states.

4.6 Summary and outlook

In this study, we introduced a phenomenological model for modeling turbulent thermoacoustic systems. The model is based on the synchronization framework, consisting of three oscillators. The first two oscillators are coupled nonlinearly at a fixed coupling strength and form a sub-system representing the unsteady heat release rate from the turbulent reactive flow. Meanwhile, the third oscillator represents the acoustic field. The acoustic field and the unsteady heat release are coupled with a variable coupling strength. The model can replicate the transition from stable operation to thermoacoustic instability in a turbulent combustor by adjusting the coupling strength. When the coupling strength is small, the model can produce chaotic oscillation with multifractal characteristics corresponding to combustion noise. As the coupling strength increases, the system loses multifractality and transitions to periodic oscillation with higher amplitude through intermittency. These behaviors are consistent with the experimental observations. Furthermore, we analyzed the self-organization behavior during the transition by calculating the scale of spectral condensation. The scale shows power laws similar to the ones reported in the experiments. In contrast to FTF/FDF, the developed model focuses on capturing the transition to thermoacoustic instability through intermittency. Currently, we have not tried to perform system identification and predict the unsteady regime or amplitude of oscillation in practical combustors. However, the model provides a new configuration for modeling thermoacoustic systems, which considers the unsteady heat release rate as an independent sub-system, instead of a quasi-steady response to the acoustic perturbation. With the help of data-driven methods, the model can be further improved and optimized for real combustors.