Abstract
Many dynamical systems such as gears, tire-pavement, automotive brakes, and cam-follower have clearance nonlinearity and excitation, which are periodic in nature. It is essential to accurately predict the steady-state response of these systems using contact-mechanics-based model for understanding their nonlinear dynamic behavior. Among the methods available to theoretically solve the system’s nonlinear governing equation(s), a semi-analytical technique such as the harmonic balance method (HBM) is preferred over numerical approaches for various reasons, including accuracy. An HBM formulation that can predict the fundamental, sub-, and super-harmonic solutions is presented here. As multiple variants of HBM exist in the literature, this work focuses on comparatively evaluating the most appropriate variant for the system under consideration. Since the system has multiple discontinuities in terms of contact stiffness and damping forces, these have to be smoothed precisely to be utilized in the HBM. Hence, a novel smoothing function was proposed and evaluated against other existing smoothing functions in literature based on various criteria. Next, the most applicable HBM variant was selected with reference to steady-state solutions from numerical methods. The predictions from the selected HBM variant were validated against the results furnished in the literature for a similar system. Finally, the nonlinear frequency response of the system with multiple discontinuities was estimated using the selected HBM and found to be in good agreement with numerical results.



















Similar content being viewed by others
Data availability
All necessary data needed to generate the results obtained in this study has been included in the article. The data sets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Abbreviations
- A, B :
-
Fourier coefficients
- b :
-
Backlash, m
- C :
-
Cosine component using Fourier fit
- c :
-
Damping coefficient, N s/m
- e :
-
Eccentricity, m
- F :
-
Contact force, N
- \(\varGamma ^{m}\) :
-
Smoothed contact force of case m
- f :
-
Frequency of q, rad/s
- G :
-
Center of mass
- g :
-
Gravitational acceleration, m/s\(^2\)
- I :
-
Mass moment, kg m\(^2\)
- H :
-
Horizontal reaction force at the follower support, N
- k :
-
Stiffness, N/m
- \(k_{\alpha }\) :
-
Stiffness of torsional spring, N/rad
- l :
-
Limit of \({\overline{q}}\), m
- L :
-
Length, m
- m :
-
Indexed variable
- \(m_\textrm{b}\) :
-
Mass of the follower, kg
- N :
-
Number of harmonics
- \(N_\textrm{a}\) :
-
Number of points in discrete-time
- n :
-
Indexed variable
- T :
-
Time period, s
- O :
-
Point of rotation
- Q :
-
Contact point
- q :
-
Response, m
- R :
-
Residue, N
- r :
-
Radius, m
- S :
-
Sine component using Fourier fit
- U :
-
Integration constant
- T :
-
Time period, s
- t :
-
Time, s
- V :
-
Vertical reaction force at the follower support, N
- w :
-
Width, m
- \(\alpha \) :
-
Angle between the follower and horizontal axis
- \(\chi _0\) :
-
Arm length of contact forces, m
- \(\epsilon \) :
-
Tuning parameter used in derivation of \(\varGamma ^v_s\)
- \(\gamma \) :
-
Factor of \({\mathcal {P}}\)
- \(\omega \) :
-
Frequency, rad/s
- \({\mathcal {P}}\) :
-
Periodicity number, a ratio of fundamental frequencies of the excitation to the frequency of the response
- \(\sigma \) :
-
Tuning parameter
- \(\psi \) :
-
External excitation, m
- \(\overline{( \ )}\) :
-
Normalized parameter
- \(\dot{( \ )}\) :
-
Time derivative, s\(^{-1}\)
- a:
-
Excitation
- b:
-
Parameter of the follower
- c:
-
Contact parameters
- d:
-
Contact damping
- g:
-
Parameter related to the gravity
- h:
-
Harmonic amplitude
- i:
-
Initial condition
- m:
-
Indexed variable
- n:
-
Natural parameter
- p:
-
Preload (torsion spring)
- s:
-
Contact stiffness
- z:
-
Zero-to-peak value
- \(\alpha \) :
-
Parameter of the torsional spring
- rms:
-
Root mean squared value
- sum:
-
Squared sum
- 0:
-
Mean component
- c:
-
Cos component of the response
- e:
-
Smoothed
- I:
-
Implicit smoothing
- s:
-
Sin component of the response
- \(\tilde{}\) :
-
Reference from literature
- DoF:
-
Degree of freedom
- HBM:
-
Harmonic balance method
- ODE:
-
Ordinary differential equation
- RMS:
-
Root mean square
References
Sundar, S., Dreyer, J.T., Singh, R.: Estimation of coefficient of friction for a mechanical system with combined rolling-sliding contact using vibration measurements. Mech. Syst. Signal Process. 58, 101 (2015)
Nayak, N., Lakshminarayanan, P.A., Babu, M.K.G., Dani, A.D.: Predictions of cam follower wear in diesel engines. Wear 260(1–2), 181 (2006)
Gäbel, G., Moldenhauer, P., Kröger, M.: Local effects between the tyre and the road. ATZ Worldw. 110(6), 70 (2008)
Lin, A.D., Kuang, J.H.: Dynamic interaction between contact loads and tooth wear of engaged plastic gear pairs. Int. J. Mech. Sci. 50(2), 205 (2008)
Kudra, G., Awrejcewicz, J., Szewc, M.: Modeling and simulations of the clutch dynamics using approximations of the resulting friction forces. Appl. Math. Model. 46, 707 (2017)
Massi, F., Baillet, L., Giannini, O., Sestieri, A.: Brake squeal: linear and nonlinear numerical approaches. Mech. Syst. Signal Process. 21(6), 2374 (2007)
Sundar, S., Dreyer, J.T., Singh, R.: Rotational sliding contact dynamics in a non-linear cam-follower system as excited by a periodic motion. J. Sound Vib. 332(18), 4280 (2013)
Sundar, S., Dreyer, J.T., Singh, R.: Estimation of impact damping parameters for a cam-follower system based on measurements and analytical model. Mech. Syst. Signal Process. 81, 294 (2016)
Li, X., Liang, Y., Zhao, G., Ju, X., Yang, H.: Dynamic characteristics of joint surface considering friction and vibration factors based on fractal theory. J. Vibroengineering 15(2), 872 (2013)
Feeny, B., Moon, F.C.: Chaos in a forced dry-friction oscillator: experiments and numerical modelling. J. Sound Vib. 170(3), 303 (1994)
Ge, Z.M., Ou, C.Y.: Chaos in a fractional order modified Duffing system. Chaos Solitons Fractals 34(2), 262 (2007)
Xu, L., Lu, M., Cao, Q.: Bifurcation and chaos of a harmonically excited oscillator with both stiffness and viscous damping piecewise linearities by incremental harmonic balance method. J. Sound Vib. 264(4), 873 (2003)
Tyler, J.C., Burton, R.A., Ku, P.A.: Contact fatigue under oscillatory normal load. ASLE Trans. 6(4), 255 (1963)
Gloerfelt, X.: Noise from automotive components, Aerodyn. noise from wall-bounded flows. 9–13 (2009)
Guo, Y., Eritenel, A.T.M.E.T., Parker, R.G.: Vibro-acoustic propagation of gear dynamics in a gear-bearing-housing system. J. Sound Vib. 333(22), 5762 (2014)
Rakvi, A.M.: Pavement condition evaluation using field data of surface deflection and tire-pavement noise. Ph.D. thesis, Rutgers The State University of New Jersey, School of Graduate Studies (2021)
Barthod, M., Hayne, B., Tébec, J.L., Pin, J.C.: Experimental study of gear rattle excited by a multi-harmonic excitation. Appl. Acoust. 68(9), 1003 (2007)
Ramesh, A., Sundar, S.: Estimation and study of drum brake noise using a comprehensive nonlinear vibroacoustic model. In: INTER-NOISE and NOISE-CON Congress and Conference Proceedings, vol. 261, pp. 5531–5540. Institute of Noise Control Engineering (2020)
Yella, A., Sundar, S.: Comparison of noise generated from simplex and duplex configurations of drum brake using non-linear vibro-acoustic models. In: INTER-NOISE and NOISE-CON Congress and Conference Proceedings, vol. 263, pp. 1415–1425. Institute of Noise Control Engineering (2021)
Shripad, K.M.R., Sundar, S.: Development of experimental vibro-acoustic transfer function for a system with combined rolling-sliding motion. In INTER-NOISE and NOISE-CON Congress and Conference Proceedings, vol. 263, pp. 1505–1515. Institute of Noise Control Engineering (2021)
Muraro, M.A., Koda, F., Reisdorfer, U., Jr., da Silva, C.H.: The influence of contact stress distribution and specific film thickness on the wear of spur gears during pitting tests. J. Braz. Soc. Mech. Sci. Eng. 34, 135 (2012)
Ramesh, A., Sundar, S.: Contributions of various non-linearities to the dynamic response of an automotive drum brake during typical braking: A theoretical study. Int. J. Non-Linear Mech. 137, 103808 (2021)
Morel, C., Morel, J.Y., Danca, M.F.: Generalization of the Filippov method for systems with a large periodic input. Math. Comput. Simul. 146, 1 (2018)
Arango, I., Taborda, J.A.: Continuation of nonsmooth bifurcations in Filippov systems using singular point tracking. Int. J. Appl. Math. Inform. 1(1), 36 (2007)
Kahraman, A., Singh, R.: Non-linear dynamics of a spur gear pair. J. Sound Vib. 142(1), 49 (1990)
Motallebi, A., Irani, S., Sazesh, S.: Analysis on jump and bifurcation phenomena in the forced vibration of nonlinear cantilever beam using hbm. J. Braz. Soc. Mech. Sci. Eng. 38(2), 515 (2016)
Wang, J., Wu, R.: The extended Galerkin method for approximate solutions of nonlinear vibration equations. Appl. Sci. 12(6), 2979 (2022)
Schnabel, R.B., Frank, P.D.: Tensor methods for nonlinear equations. SIAM J. Numer. Anal. 21(5), 815 (1984)
Magdy, M.A., Coowar, F.: Frequency domain analysis of power system forced oscillations. In: IEE Proceedings C (Generation, Transmission and Distribution), vol. 137, pp. 261–268. IET (1990)
Yan, H., Tsai, M., Hsu, M.: An experimental study of the effects of cam speeds on cam-follower systems. Mech. Mach. Theory 31(4), 397 (1996)
Yan, H.S., Tsai, M.C., Hsu, M.H.: A variable-speed method for improving motion characteristics of cam-follower systems 250–258 (1996)
Hugnell, A.B.J., Bjoerklund, S., Andersson, S.: Simulation of the mild wear in a cam-follower contact with follower rotation. Wear 199(2), 202 (1996)
Alzate, R., di Bernardo, M., Montanaro, U., Santini, S.: Experimental and numerical verification of bifurcations and chaos in cam-follower impacting systems. Nonlinear Dyn. 50(3), 409 (2007)
Taborda, J.A., Santini, S., Bernardo, M.D., Angulo, F.: Active chaos control of a cam-follower impacting system using FPIC technique. IFAC Proc. Vol. 42(7), 327 (2009)
Kim, T.C., Rook, T.E., Singh, R.: Effect of smoothening functions on the frequency response of an oscillator with clearance non-linearity. J. Sound Vib. 263(3), 665 (2003)
Cveticanin, L.: Stability of motion of the cam-follower system. Mech. Mach. Theory 42(9), 1238 (2007)
Comparin, R.J., Singh, R.: Non-linear frequency response characteristics of an impact pair. J. Sound Vib. 134(2), 259 (1989)
Al-Jawary, M.A., Abd-Al-Razaq, S.: Analytic and numerical solution for Duffing equations. Int. J. Basic Appl. Sci. 5(2), 115 (2016)
Lau, S.L., Zhang, W.S.: Nonlinear vibrations of piecewise-linear systems by incremental harmonic balance method. J. Appl. Mech. 59, 153 (1992)
Macki, J.W., Nistri, P., Zecca, P.: A theoretical justification of the method of harmonic balance for systems with discontinuities. Rocky Mt. J. Math. 1079–1098 (1990)
Kudryashova, E.V., Kuznetsov, N.V., Kuznetsova, O.A., Leonov, G.A., Mokaev, R.N.: Harmonic balance method and stability of discontinuous systems. In: Dynamics and Control of Advanced Structures and Machines, pp. 99–107. Springer, New York (2019)
Woiwode, L., Balaji, N.N., Kappauf, J., Tubita, F., Guillot, L., Vergez, C., Cochelin, B., Grolet, A., Krack, M.M.: Comparison of two algorithms for harmonic balance and path continuation. Mech. Syst. Signal Process. 136, 106503 (2020)
Johnson, K.L.: Contact Mechanics, vol. 1. Cambridge University Press, Cambridge (1987)
Eldred, L.B., Baker, W.P., Palazotto, A.N.: Kelvin-Voigt versus fractional derivative model as constitutive relations for viscoelastic materials. AIAA J. 33(3), 547 (1995)
Popov, V.L., et al.: Contact Mechanics and Friction. Springer, New York (2010)
Li, L., Singh, R.: Start-up transient vibration analysis of a vehicle powertrain system equipped with a nonlinear clutch damper. SAE Int. J. Passeng. Cars-Mech. Syst. 8, 726 (2015)
Liu, Z., Liu, Z., Zhao, J., Zhang, G.: Study on interactions between tooth backlash and journal bearing clearance nonlinearity in spur gear pair system. Mech. Mach. Theory 107, 229 (2017)
Suryawanshi, S., Sundar, S.: Nonlinear dynamics of system with combined rolling-sliding contact and clearance. Nonlinear Dyn. (2022). https://doi.org/10.1007/s11071-022-08127-6
Chiluveru, S.R., Tripathy, M., Mohapatra, B.: Accuracy controlled iterative method for efficient sigmoid function approximation. Electron. Lett. 56(18), 914 (2020)
Wolf, H., Kodvanj, J., Bjelovučić-Kopilović, S.: Effect of smoothing piecewise-linear oscillators on their stability predictions. J. Sound Vib. 270(4–5), 917 (2004)
Fay, T.H., Kloppers, P.H.: The Gibbs phenomenon for series of orthogonal polynomials. Int. J. Math. Educ. Sci. Technol. 37(8), 973 (2006)
Klaus, B., Physik, F.: Fitting in MATLAB. Fachbereich Phys. Univ, Osnabr (2003)
Nimmagadda, S., Economon, T.D., Alonso, J.J., da Silva, C.R.I.: Robust uniform time sampling approach for the harmonic balance method. In: 46th AIAA Fluid Dynamics Conference, p. 3966 (2016)
Xiao, S., Yan, S., Kassim, A.A.: Facial landmark detection via progressive initialization. In: Proceedings of the IEEE International Conference on Computer Vision Workshops, pp. 33–40 (2015)
Acknowledgements
We acknowledge the Science Engineering and Research Board (SERB), India (https://www.serbonline.in/) for partially supporting this research work under the Startup Research Grant (Grant No. SRG/2019/001172).
Funding
The authors have not disclosed any funding.
Author information
Authors and Affiliations
Contributions
MS was involved in software, methodology, validation, formal analysis, investigation, visualization and writing—original draft. SS was involved in conceptualization, methodology, validation, formal analysis, investigation, visualization, writing—review and editing, supervision, project administration.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
A: Values of parameters
B: Hyperbolic smoothing function
In reference to fig. B.1, assuming two continuous lines 1 and 2 (Eq. 18) that are taken from Eq. (4).
The family of hyperbolic curves for which lines 1 and 2 are asymptotic, given as Eq. (19),
Introducing a non-dimensional arbitrary constant \(\epsilon \) (tuning parameter) to define a point closer to the point of nonlinearity (b,0). Assuming Eq. (19) passes through a point \((b-\epsilon b,k_\textrm{c} \epsilon b)\), marked as *. On substituting the point \((b-\epsilon b,k_\textrm{c} \epsilon b)\) in Eq. (19), the value of u is given as,
A reduction in u by a factor of 2 as given by Eq. (21) improves the accuracy of smoothed function as shown in Fig. B.1.
Thus, the family of hyperbolas is given by,
On solving Eq. (22) for \(F_\textrm{s}\), Eq. (23) can be obtained.
Using curve with the positive sign as smoothed function (curve 1, as marked in Fig. B.1) and is given by,
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Shripad, K.M.R., Sundar, S. Semi-analytical solution for a system with clearance nonlinearity and periodic excitation. Nonlinear Dyn 111, 9215–9237 (2023). https://doi.org/10.1007/s11071-023-08350-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-023-08350-9


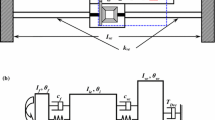
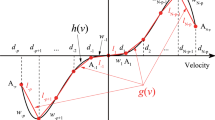
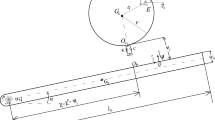

 lines from the nonlinear force
lines from the nonlinear force