Neural network-based reduced-order modeling for nonlinear vertical sloshing with experimental validation

Abstract

In this paper, a nonlinear reduced-order model based on neural networks is introduced in order to model vertical sloshing in presence of Rayleigh–Taylor instability of the free surface for use in fluid–structure interaction simulations. A box partially filled with water, representative of a wing tank, is first set on vertical harmonic motion via a controlled electrodynamic shaker. Accelerometers and load cells at the interface between the tank and an electrodynamic shaker are employed to train a neural network-based reduced-order model for vertical sloshing. The model is then investigated for its capacity to consistently simulate the amount of dissipation associated with vertical sloshing under different fluid dynamics regimes. The identified tank is then experimentally attached at the free end of a cantilever beam to test the effectiveness of the neural network in predicting the sloshing forces when coupled with the overall structure. The experimental free response and random seismic excitation responses are then compared with that obtained by simulating an equivalent virtual model in which the identified nonlinear reduced-order model is integrated to account for the effects of violent vertical sloshing.

1 Introduction

Vertical sloshing is a phenomenon that occurs in aircraft wing tanks when they are subjected to strong vertical acceleration. Gusts, turbulence and landing loads can cause fuel sloshing and subsequent coupling with aircraft structural dynamics, resulting in a significant increase in the overall system damping. The identification and study of such dissipative effects may enable the development of less conservative aircraft configurations in the future, allowing for increasingly lighter structures and reduced environmental impact. This paper deals with the development of nonlinear reduced-order models for vertical sloshing and is embedded in the European project H2020 SLOshing Wing Dynamics (SLOWD), which aims to characterize sloshing dynamics by combining experimental and numerical data to be used in the design of future aircraft (Ref. [1]). Vertical sloshing is not the only dynamic that fluids stowed in tanks can exhibit: lateral sloshing is another important type of dynamics, generally occurring with rotations and lateral motions of the tank (see Refs. [2,3,4,5]). It is generally characterized by the presence of standing waves that can contribute to coupling with the structure that integrates the tank. This, in aircraft structures, can also lead to changes in the aeroelastic stability margins (flutter). Specifically, the effects of lateral sloshing on aircraft aeroelastic flutter stability were considered in Refs. [6,7,8]. Sloshing lateral dynamics in tanks integrated in the wings have a limited effect on the aircraft’s dynamic characteristics and therefore play a minor role in structure size.

The focus of this work is on vertical sloshing, a phenomenon that exhibits a nonlinear high dissipative behavior that can potentially be used in aircraft sizing. Indeed, observing the fluid dynamics inside the tanks as a function of the vertical acceleration amplitudes, at very low excitation levels the free surface tends to remain flat. By increasing the level of vertical acceleration, some modes can become unstable depending on the oscillation frequency (Refs. [3, 9,10,11,12]). By reaching an even higher value of vertical acceleration, Rayleigh–Taylor instabilities are triggered (Ref. [9]), resulting in a chaotic flow regime with mixing of air and liquid (Ref. [13]). Previous experimental fluid–structure interaction campaigns in which a tank system was positioned at the tip of a beam, representing a wing, showed how this type of fluid behavior induces a considerably damped response of the structure (Refs. [14,15,16,17]). Indeed, turbulence, impacts and the continuous generation of the free surface result in an additional loss of energy. While the tank dynamics are extremely complex, these experiments demonstrated that the sloshing forces and the damping introduced to the structure are extremely repeatable when reproducing the same conditions. The sloshing dissipative behavior is further influenced by frequency and amplitude of oscillation when the tank is set in a harmonic motion. (Ref. [11, 12]). As a consequence, this phenomenon cannot simply be described by means of linear viscoelastic models in which the loss of energy depends only on the oscillation frequency [18, 19], such as fractional derivatives and finite states for the damping (see Ref. [20]). Nonlinear predictive models are therefore necessary to simulate the impact the sloshing forces have on the dissipation of the elastic energy. An equivalent mechanical model consisting of a bouncing ball capable to reproduce the impact mechanisms was proposed by Refs. [21, 22]). These models provide fast prediction of sloshing forces, but since they are obtained by fitting the sloshing forces—or its induced damping—of the free response of a single degree of freedom system, they do not generally provide consistent results when working at frequencies different from those used in their identification.

Dynamical systems identification techniques using data and machine learning approaches have been investigated to create a model capable of capturing the nonlinear dynamics of vertical sloshing. References [23, 24] already introduced the use of artificial neural network for real-time prediction of the sloshing loads in cargo containers. The dynamics to be modeled can be considered as a black box process. This leads to the identification of a surrogate model that makes use of only those signals that will be assumed as inputs and outputs regardless the knowledge of the internal dynamics. In addition, the collection of data adequately covering the input space is essential for the training of the model.

An experiment aimed at characterizing the dissipative behavior of vertical sloshing based on harmonic motion by varying the frequency and amplitude of the motion has already been carried out in Ref. [11]. The same configuration is used for this study to collect experimental data for the identification of a nonlinear reduced-order model (ROM) that takes advantage of neural network properties. Specifically, the data acquisition phase reflects an open-loop problem, where the process to be identified—vertical sloshing—is considered as an isolated system that enables to obtain data. The strategy employed to generate data for the training consists in imposing vertical displacements to the tank by means of an electromechanical shaker by slowly varying the frequency and output of the motion. The latter strategy will be referred to as variable frequency and amplitude (VFA). A sensitivity analysis on the neural network-based model constitutive parameters is then carried out to select the structure that most accurately describes the process to be identified. Two main types of models are considered for this analysis, that is, one strictly feed-forward and another recurrent, in which the output signal is fed to the model as additional input. Lastly, the present reduced-order model is validated in a complex fluid–structure interaction environment. In the new experimental setup, the same tank used to generate the training data is mounted at the free end of a cantilever beam. This particular setup will be referred to as the sloshing beam problem, and the experimental data generated for comparison and validation will be provided by free response and random testing. The comparison is carried out using a dynamic virtual simulation model that conforms to the closed-loop logic of the experiment, in which the numerical model of the beam interacts with the reduced-order model simulating the sloshing dynamics.

The paper is organized as in the following. The experiment used to generate the data for identifying the reduced-order model is presented in Sect. 2; the training procedure of the neural network-based model is presented in Sect. 3, where a sensitivity analysis performed in order to choose the best performing model is also described. Section 4 presents the sloshing beam problem, leveraging an introductory theoretical part and a second part in which the characteristics of the experimental setup realized to obtain the data to be used to validate the identified model are described. Lastly, Sect. 5 describes the simulation environment setup to obtain a virtual model equivalent to the sloshing beam experiment and the comparison results obtained. A concluding remarks section ends the paper.

2 Experimental test case of the isolated sloshing-tank

The first step in this work was to identify a data-driven ROM of vertical sloshing, which requires data from either a high-fidelity numerical model or an experimental model. The experimental setup presented in this section replicates that employed in Ref. [11] to characterize dissipation caused by vertical sloshing when a tank is set in harmonic motion.

Fig. 1

Experimental configuration of the isolated sloshing-tank

Fig. 2

Fragmentation of the free surface and impacts resulting from vertical sloshing dynamics

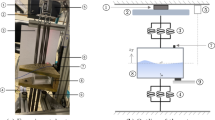
The experimental case study is shown in Fig. 1 and consists of a small-box-shaped Plexiglass tank partially filled with water, mounted over a controlled electrodynamic shaker, able to impose controlled seismic excitations. The height of the tank was designed to be $h = 27.2 \, mm$ in accordance with the limits of the shaker and the need to trigger the impacts of the liquid with the inner walls of the tank during its excitation that are mainly responsible for sloshing-induced dissipation. Tank base sides have dimensions $l_1 = 117.2 mm$ and $l_2 = 78.0 mm$. The quantification of the energy dissipated by the fluid was performed in Ref. [11] for three different filling level, 25%, 50% and 75% and for different values of the amplitude and frequency of the imposed harmonic motion. These last two parameters are strictly related to the unsteady boundary conditions that a vertically vibrating structure can impose to an interfacing tank. The operative ranges considered covered both the region of small perturbation where Faraday waves occur and the region characterized by the presence intense impacts between liquid and tank ceiling caused by high accelerations following the fragmentation of the free surface due to the Rayleigh–Taylor instability. Figure 2 shows the fragmentation of the free surface and the impacts of the liquid with the tank walls by means of the snapshots of two different acceleration and frequency pairs. It is worth noting that with the aim of identifying a black box model of the vertical sloshing system, it is not in the interest of this activity to describe the internal dynamics of the liquid (bubble generation, etc.) but only to get predictions of the interface forces as a function of the motion that can be imposed by an interfacing structure.

The dynamic load at the interface between shaker and tank is measured by two load cells (See Fig. 1), symmetrically placed along the mid-line of the long side of the tank base. The overall force exchanged by tank and shaker is the sum of the two load cells. Additionally, the system is equipped with two redundant accelerometers mounted on the upper closure side of the tank, and an accelerometer used by the shaker controller. Figure 3a shows, for the operating pair having acceleration and excitation frequency equal to 3g and 17Hz, respectively, the force data used for the dissipation evaluation performed in Ref. [11]. Specifically, Fig. 3a shows the trend over time of the sloshing force $f_S$, normalized by the purely inertial contribution $(m_l a \varOmega ^2)$, where $m_l$ is the mass of the liquid, while a and $\varOmega$ are the oscillation amplitude and frequency of the vertical imposed motion $w(t) = a \cos (\varOmega t)$. Note that the oscillation amplitude is linked to the acceleration amplitude through the excitation frequency. Figure 3b shows the hysteresis cycles obtained by plotting the variation of the normalized sloshing force with respect to the normalized vertical harmonic displacement imposed by the tank $w(t)/a$. The area enclosed by the hysteresis cycles represents the work $L_d$ done by the sloshing force $f_S$ in a vertical harmonic motion cycle at the specific amplitude–frequency pair (see Ref. [11]). It can be expressed as $L_d\big (\varOmega ,a\big ) = \oint f_{S} (\varOmega ,a) \, \, \textrm{d} w$ and has the meaning of the energy dissipated by the sloshing dynamics.

Fig. 3

Sloshing force and hysteresis cycle for the point (3g, 17Hz) and for the fill level case 50%

By deriving the hysteresis cycle for different amplitude and frequency pairs in the domain of interest, it was possible to obtain a map of the sloshing dissipated energy. In particular, Fig. 4 shows this result for the case with 50 % of filling level, highlighting the distribution of the non-dimensional dissipated energy $\varPhi _d = L_d/(m_l a^2 \varOmega ^2)$ as a function of non-dimensional frequency and amplitude, which are, respectively, defined as $\bar{\omega } = \varOmega /\sqrt{g/h}$ and $\bar{a} = a/h$ (see Ref. [11]).

More in general, the energy dissipated by the sloshing fluid $L_d$ can be expressed through the following non-dimensional analysis:

$$\begin{aligned} L_d = m_l a^2 \varOmega ^2 \varPhi _d \left( \bar{\omega }, \bar{a}, \alpha , Re, Bo, \lambda _1, \lambda _2,...\right) \end{aligned}$$

(1)

Besides the non-dimensional frequency $\bar{\omega }$ and amplitude $\bar{a}$, $L_d$ is dependent on the fill level $\alpha$, the Reynolds number $Re = v h/\nu$ ($\nu$ kinematic viscosity) that reflects viscosity effects, and the Bond number $Bo = \rho g h^2/\gamma$ ($\gamma$ surface tension) that reflects surface tension effects. Furthermore, the dissipated energy may also depend on the aspect ratios relative to the dimensions in the tank plane, referred to as $\lambda _1 = h/l_1$ and $\lambda _2 = h/l_2$, respectively. For vertical sloshing dynamics, the most important dimensionless parameters are the frequency $\bar{\omega }$ and the ratio between the amplitude of motion and the height of the tank $\bar{a}$. Capillarity may have an influence on dissipation, but numerical studies have shown that the dissipative capabilities during violent vertical sloshing phenomena are less sensitive to parameters more related to the physical properties of the fluid, such as Reynolds and Bond. (Ref. [25]). The liquid impacts with the tank roof that occur during these phenomena influence the dissipation, erasing memory effects of the sloshing dynamics at high oscillation amplitudes. Accordingly, the tank height h plays the key role since the ullage drives the amount of kinetic energy stored by the liquid that is dissipated during the impacts (Ref. [26]). The aspect ratios of the tank are much less important compared to the tank height (Refs. [11, 12]).

Fig. 4

Non-dimensional dissipated energy $\varPhi _d$

Therefore, the non-dimensional dissipated energy $\varPhi _d$ is represented as a nonlinear function of the frequency and amplitude of motion. Figure 4 shows that vertical sloshing provides considerable dissipation over 1g of acceleration, and that the highest dissipation, corresponding to the darkest area on the map, arises close to 4g of vertical acceleration and vertical displacement about the $25\%$ of the tank height. At high frequencies, the impact of sloshing on energy dissipation is reduced most likely due to surface tension and viscosity that may play a role in stabilizing the free surface. Similar results have also been found in Ref. [12].

2.1 Data collection for reduced-order model identification

The experimental setup presented in the previous section was used to generate a training and validation data set for the identification of a neural network-based ROM capable to predict the desired sloshing forces. To this end, two additional harmonic tests with variable frequency and amplitude (VFA) were performed by considering the case with 50 % filling level. These tests are performed setting an acquisition time of $480 \, s$ and $240 \, s$ and are employed for the collection of training and validation data. Similarly to Ref. [11], the vertical sloshing fluid is considered as an isolated system that receives as input a motion (or acceleration) imposed to the boundary by the electrodynamic shaker and returns as output a force. The excitation provided by the shaker, which is controlled in order to impose the vertical acceleration law denoted variable frequency and amplitude (VFA) $\ddot{w}= f(t) \left[ \cos (\int _0 ^t \varOmega (\tau ) \textrm{d}\tau )\right]$, was such as to suitably cover the non-dimensional frequency $\bar{\omega }$ and amplitude $\bar{a}$ domain of interest, following the path shown in Fig. 5. The choice of this path was dictated by the need to acquire the most representative data possible to describe the dissipation induced by vertical sloshing shown in Fig. 4 with a single time history.

Fig. 5

Path of the VFA harmonic tests considered for training and validation data collection

The time series needed for training the neural network were obtained by acquiring sensor measurements. In particular, from the accelerometers we obtain the signal associated with the motion imposed by the shaker, while from the load cells we obtain the force exchanged at the fluid–tank interface. Integrating the acceleration signal yields the velocity signal given by the vertical shaker motion shown in Fig. 6a. This signal assumes the role of the input of neural network model to be identified.

Fig. 6

Input–output time histories for data-driven ROM training process

On the other hand, load cells are used to acquire the force that is exchanged at the interface between the shaker and the tank. In this study, sloshing force is decomposed into two contributions: the inertial force according to the frozen fuel modeling (Ref. [7]) and the perturbation resulting from the relative motion of the fluid particles within the tank, hereafter denoted as dynamic sloshing force

$$\begin{aligned} f_S= & {} - m_l \, \ddot{w} + \varDelta f_{S_z} \end{aligned}$$

(2)

where $m_l$ is the overall fluid mass. As the inertial contribution $- m_l \, \ddot{w}$ is linear and conservative with respect to the input, it is convenient to identify directly the dynamic sloshing force $\varDelta f_{S_z}$. Therefore, in order to obtain the dynamic sloshing force in Fig. 6b, it is necessary to subtract from the force measured by the load cells the inertial contribution of the liquid $- m_l \ddot{w}$ and the supporting structure of the box which lies on top of the load cells. Figure 7a shows the input signal of the validation data set, obtained with the shorter VFA harmonic test (240 s long), in the frequency–amplitude domain. Figure 7b shows the trend of the dynamic sloshing force of the validation data set. The validation data shown in Fig. 7, although gathered in the same domain as the training data, have an important function in avoiding overfitting by filtering out any process and measurement-related noise.

Fig. 7

Input–output time histories for data-driven ROM validation

3 Identification of the neural network-based ROM for vertical sloshing

The identification of vertical sloshing is carried out by exploiting a neural network-based model that is divided into a nonlinear static approximator (i.e., memory-less) and an external dynamic filter bank (Ref. [27]). Filters are chosen as simple time delays, while the approximator is chosen as a fully connected neural network. A model of this kind is usually called time delay neural network (TDNN) and has the property to be a universal dynamic mapper (see Ref. [28]). It can either be purely feed-forward or present output feedback, resulting in a recurrent architecture. Two kinds of architecture were used to perform a sensitivity analysis on their constituent parameters, aimed at identifying the best performing model.

The first is a nonlinear finite impulse response (NFIR) model, which is feed-forward and has an inherently stable structure (Ref. [29]). Its static approximator receives as input the vertical velocity passing through the delay lines. The second one, indicated as nonlinear output error (NOE) model, has a recurrent structure, with the feedback of the predicted output. In this case, the approximator receives as input both the velocity and the predicted sloshing force (once passed through the delay lines). A disadvantage of output feedback is that stability cannot be demonstrated in general. In NOE models, prediction errors can accumulate over time, leading to lower accuracy or even instability of the model. On the other hand, the advantage of the output feedback models relies on a very compact description of the process as compared to those without output feedback like the NFIR model that generally requires a large number of regressors to fully capture the dynamics of the process. However, regardless the neural network architecture the appropriate number of delay lines cannot be determined a priori, generally leading to a trial-and-error approach to determine the number of delay lines and neurons (Ref. [30]). As a consequence, a sensitivity analysis is carried out varying the number of delay lines and neurons of the unique hidden layer considered in the neural network. The static approximator of both considered types of model is precisely a neural network having a hidden layer and an output layer. Normalized radial basis functions are employed as activation functions in all nodes of the hidden layer, while the output layer consists of a simple linear function (see Appendix A for more details). By using Gaussian activation functions, neural networks are ensured to be universal approximators (Ref. [28]).

The algorithm used consists of Levenberg–Marquardt backpropagation implemented in MATLAB®  through the trainlm function (Ref. [31]). Training employs a fitness function based on mean squared error (MSE) between the experimental sloshing forces and the ones provided by the network when feed with the experimental velocity. The networks learn directly from the training data shown in Fig. 6, while the validation data, shown in Fig. 7, are not involved in the process of estimating the network weights and biases. However, all the tested models underwent a training process that stops after the error rate on the validation data increase continuously for more than 6 epochs.¹ Sensitivity analysis is performed considering for NFIR models three different filter banks with 50, 60 and 70 delay lines for the input velocity and with a variable number of hidden layer neurons from 5 to 40, while for NOE models the only architectures that in our trials guaranteed stability are those having 2 delay lines for both velocity and predicted output and a number of hidden layer neurons equal to 10, 15 and 20. The results of the sensitivity analysis are shown in Fig. 8, in terms of the trend of MSE as the number of neurons and selected delay lines changed.

Fig. 8

Sensitivity analysis for NFIR and NOE models with varying number of neurons and number of delay lines

Each MSE displayed is equal to the average of the MSE computed on the training data and the validation data obtained at the end of the training process. Figure 8 shows that as the number of neurons increases, the NFIR models perform better than the few stable NOE models identified. As the convergence seems to be reached for the NFIR models after 35 neurons, the model with 70 tapped delay lines and 35 neurons is considered for being used in FSI simulations. The training process of a model like the one selected takes approximately 40 min before convergence, using a high-performance commercial computer with CPU parallel computing integrated in MATLAB®(see Ref. [31]). The architecture of this model is shown in Fig. 9.

Fig. 9

Architecture of the identified time delay neural network: NFIR model with 70 tapped delay lines and 35 hidden layer neurons

The selected network was then converted into a Simulink®  block to simulate it and obtain predictions for the output. Figure 10 shows the dynamic sloshing force (in red) that the network predicts when it is excited with a velocity equal to that used for the validation data set generation (see Fig. 7a), compared to the validation force (in black). From the comparison figure, it looks like the identified network is able to accurately replace the nonlinear behavior of sloshing.

Fig. 10

Comparison between the output predicted by the identified neural network and the experimental time history of the force used for the validation

It should be noted that NFIR models are heavier—in terms of the number of hyperparameters, such as weights—than NOE models, due to the larger number of delay lines. However, the selected NFIR model does not require excessive computational cost to perform FSI simulations (The time required to obtain the response results is around 3 s). Finally, by performing tests varying the frequency and amplitude of excitation in the domain of interest, the sloshing dissipated energy was evaluated based on the predictions provided by the neural network. The result is the non-dimensional dissipated energy map shown in Fig. 11 that is in good agreement with the experimental map in Fig. 4, corroborating the use of neural network-based ROM as a reliable digital twin of the vertical slosh dynamics.

Fig. 11

Non-dimensional dissipated energy map predicted by the neural network-based NFIR model

4 The sloshing beam problem

This section introduces the sloshing beam model, that is, a FSI problem in which the tank introduced in Sect. 2 is mounted at the tip of a cantilever beam. This model is used to validate the reduced-order model for sloshing identified in Sect. 2.1 for its application in sloshing integrated aeroelastic analyses (Ref. [32]). Specifically, the section consists of a first part that introduces the analytical formulation used to describe the problem of a structural system interfacing with vertical sloshing dynamics and a second part that describes the second experimental setup representing the sloshing beam problem. This is used to generate data to be used as a benchmark for the experimental validation of the identified model.

4.1 Analytical formulation of the sloshing beam integrated system

Fig. 12

Sloshing beam problem

Fig. 13

Layout of the experimental FSI problem

In this section, the mathematical formulation for the dynamic description of the sloshing beam system shown in Fig. 12 is presented. The problem consists of a cantilever beam characterized by a purely vertical linear displacement field, with a partially filled tank placed at its free end. The latter is assumed perfectly symmetrical with respect to the vertical plane passing through the elastic center. The structural transversal displacement for a one-dimensional bending beam $w(x,t)$ can be expressed as

$$\begin{aligned} w(x ,t) \simeq \sum _{n=1}^{N} \psi _n(x )q_n(t) \end{aligned}$$

(3)

where $\psi _n(x )$ is the n-th mode of vibration of the structure² and $q_n(t)$ is the n-th modal coordinate describing the body vertical displacement in time. This analysis uses a modal representation involving a finite number of modes N, which corresponds to describing the system in a limited frequency band. Considering the displacement representation defined in Eq. 3 for the beam dynamics, one has the following Lagrange equations of motion in terms of N modal coordinates $q_n(t)$:

$$\begin{aligned}{} & {} \textsf{M}\ddot{\textsf{q}} + \textsf{K}\textsf{q}= \textsf{g}(\textsf{q}) + \textsf{f}^{(ext)} \end{aligned}$$

(4)

where $\textsf{M}= \textrm{diag}(m_1, m_2, \dots m_N)$ and $\textsf{K}=\textrm{diag}(k_1, k_2, \dots k_N)$ are, respectively, the modal mass and stiffness diagonal matrices, whereas $\textsf{g}= [g_1, g_2,\dots ,g_N]^{\hbox {T}}$ is the vector of the generalized sloshing forces nonlinearly induced by the elastic motion $\textsf{q}$. The $\textsf{f}^{(ext)}$ is the vector of the current external forcing terms. The natural frequency of the n-th mode is indicated as $\omega _n = \sqrt{k_n/m_n}$.

The n-th component of $\textsf{g}$ is the projection of the liquid-induced internal pressure distribution $p_S$ on each n-th modal shape $\psi _n$ by integrating the inner product on the n-th tank wet surface ${\mathcal {S}}_{tank}$ as in the following ($\textbf{n}$ unit normal vector to ${\mathcal {S}}_{tank}$ and $\textbf{k}$ vertical unit vector)

(5)

By assuming a rigid tank identified by its geometrical center, Eq. 5 can be recast as:

$$\begin{aligned} g_n = f_S \, \psi _n (x_{T}) + m_S \, \varphi _n (x_{T}) \end{aligned}$$

(6)

where $f_S$ and $m_S$ are, respectively, the sloshing force and moment applied in the geometric center of the tank $x_{T}$, whereas $\varphi _n (x_{T})$ is the n-th modal rotation of the point $x_{T}$.

Assuming that the moment $m_S$ about the geometric center of the tank is negligible, and considering the decomposition of the sloshing force as in Eq. 2, Eq. 6 can be recast as:

$$\begin{aligned} g_n = - \sum _{k = 1}^{N} m_l \, \psi _n (x_{T}) \, \psi _k (x_{T}) \, \ddot{q}_k + \psi _n (x_{T}) \, \varDelta f_{S_z} \end{aligned}$$

(7)

It is worth to remind that the dynamic sloshing force $\varDelta f_{S_z}$ is a non-conservative force that is a nonlinear function of the history of the tank vertical displacement and corresponds to the output used for training the neural network in Sect. 3.

4.2 Experimental test case of the sloshing beam

The tank presented in Sect. 2, used to generate the data for the identification of the reduced-order model, is placed at the end of a cantilever beam in order to obtain a new experimental configuration, shown in Fig. 13, aimed at studying the interaction between the liquid stowed in the box and the beam. The vertical sloshing dynamics and the beam structural dynamics interface with each other, defining a closed-loop problem, through the motion imposed by the structure and the load provided by the liquid impacting with the internal walls of the tank. These two actions are measured by means of accelerometers and load cell sensors properly placed on the experimental system (see Fig. 13). The beam is $74 \, cm$ long, $10 \, cm$ large, $1 \, cm$ thick.

Table 1 shows the main modal quantities of the first three modes of vibration of the cantilever beam in the configuration with frozen liquid, defined as the case in which $\varDelta f_{S_z}=0$. In experimental practice, this reference configuration, useful for assessing the effects that sloshing induces on the system response, was realized by replacing the liquid with an equivalent non-sloshing mass. The experimental natural frequencies $f_n^{(exp)}$ are listed, as well as the numerical frequencies $f_n^{(num)}$ derived by a structural model updating process. In addition, the table also shows the experimental modal damping coefficients. The modal masses of the beam (with modes normalised to the unit value of the larger displacement) are also listed based on the numerical model obtained with the structural updating process.

Table 1 Experimental and numerical natural frequencies $f_n$, modal damping coefficients $\zeta _n$ and modal masses $m_n$ of the cantilever beam with frozen liquid at the free end

The sloshing beam presented in this section is used to obtain experimental reference data that can be used to validate the identified reduced-order model. Free response data as well as random seismic excitation at the root provided by the shaker are used to assess the identified ROM performances.

4.3 Free response analysis

Similarly to Refs. [14], a free response problem was considered in this work, where an initial displacement is assigned to the free end of the beam. With the release of the beam tip, the interaction between liquid and structure is triggered. The free response results are shown in Fig. 14 showing the effects induced by sloshing on the system response compared to the frozen case. A weight of 7 kg (see Fig. 13) was used to provide an initial vertical displacement of the beam tip of $1.46 \, cm$ that provides initial acceleration in line with the maximum acceleration provided during the training process. Figure 14 shows the time trends of the free acceleration response signals measured by the accelerometers for the frozen case in Fig. 14a and the sloshing case in Fig. 14b).

Fig. 14

Comparison between acceleration signals measured by the sensors in the case where the liquid is considered as frozen a and in the case where it is free to move (sloshing) b

The impacts of the liquid with the ceiling of the tank, which occur in the initial stages of the response, lead to considerable dissipation of energy, resulting in more damped responses than in the frozen case. This can also be appreciated from Fig. 15, in which two different instants of the sloshing beam response are shown. In particular, in the first instants of the response, the liquid impacts violently with the ceiling of the tank (see Fig. 15a) inducing considerable damping in the response. Once the initial phase of the response is over, the fluid transitions to a regime characterized by the presence of standing waves (see Fig. 15b).

Fig. 15

Frames of the sloshing beam free response in two different time instants

It is also possible to consider a further comparison by identifying the modal content from accelerometer responses. Indeed, by exploiting the modal filtering technique (see Ref. [33]) on the measured acceleration signals, the modal accelerations of the cantilever beam can be extracted. The comparison of the first three modal accelerations of the frozen case with that of the sloshing case is provided in Fig. 16. The interaction between sloshing and structural dynamics provides effects on damping the dynamics of the first mode of vibrations, while it is less effective on the second mode and looks to have a detrimental on the third mode.

Fig. 16

Comparison between modal accelerations of frozen a and sloshing b cases

4.4 Random analysis

In addition to the free response test, other experiments were conducted in which the same configuration presented in Sect. 4.2 is subjected to seismic excitation. To this end, the beam root is attached to the electromechanical shaker as described in Ref. [17].

Three 90s long experimental tests were performed, corresponding to three different levels of vertical random excitation, with a root-mean-square (RMS) acceleration value of $0.1 \, g$, $0.2 \, g$ and $0.4 \, g$. Figure 17 shows the three controlled accelerations imposed by the shaker at the beam root. More in details, Fig. 17a shows the trend of the acceleration signals over time (for a limited time window), while Fig. 17b shows their power spectral densities (PSD) as a function of the frequency, in which the inset plot shows a zoom on the PSD having RMS equal to $0.1 \, g$, compared with a black dashed curve representing the assigned theoretical Gaussian spectrum expressed as follows

$$\begin{aligned} S\left( f\right) \, = \, \frac{A}{{\sigma \sqrt{2\pi } }} \left[ e^{{{ - \left( {f - f_0 } \right) ^2 } / {2\sigma ^2 }}} + e^{{{ - \left( {f + f_0 } \right) ^2 } / {2\sigma ^2 }}}\right] \end{aligned}$$

(8)

where A is the amplitude, $\sigma$ is the standard deviation, and $f_0$ is the center of the distribution.

Fig. 17

Seismic excitations imposed by the shaker (RMS: $0.1 \,g$, $0.2 \,g$, $0.4 \,g$)

Sloshing response data are collected by means of accelerometers and load cells placed on the beam as shown in Fig. 13. Figure 18 shows the tank accelerations measured for each of the three considered RMS levels, in the case where the liquid is free to slosh. It is possible to appreciate that the seismic excitation imposed on the beam is amplified by the beam’s dynamics, leading to acceleration values that, for the case with RMS level equal to 0.4g, reach at most a value of $6 \, g$ at the tank location. This value is in line with the maximum acceleration covered by the identification process.

Fig. 18

Tank accelerations measured in the sloshing case, following the application of the shaker random excitations (RMS: $0.1 \,g$, $0.2 \,g$, $0.4 \,g$)

5 Results of the experimental validation

The neural network-based NFIR model identified in Sect. 3 is experimentally validated using the data obtained with the experimental setup presented in Sect. 4.2. In this section, the numerical procedure implemented in order to evaluate the performance of the model by comparison with experimental data is presented. The logic employed in this activity is to implement a digital twin of the experimental configuration in Fig. 13.

For this purpose, a simulation model was built in Simulink®, representing the sloshing beam problem as shown in Fig. 19.

Fig. 19

Simulink®  model representing the sloshing beam experiment

The block structure in Fig. 19a contains the modal description of the cantilever beam implementing Eq. 4, while the block sloshing detailed in Fig. 19b includes the neural network ROM architecture. It provides the dynamic sloshing forces $\varDelta f_{S_z}$ when it receives as input the history of the elastic velocity evaluated at the tank position $x_{T}$. The gains before and after the network in Fig. 19b (the blue block) allow, respectively, for the transformation of modal velocities in tank vertical velocity as $\dot{w}(x_T) = \sum _m \psi _m(x_{T}) \dot{q}_m(t)$, and the projection of the dynamic sloshing force on the modes of vibration to obtain the generalized sloshing forces $\psi _n (x_{T}) \, \varDelta f_{S_z}$.

The numerical model of the sloshing beam problem was used to replicate the same responses of the experimental setup presented in Sect. 4.2. The results used for the experimental validation of the surrogate model are shown next, starting with those related to the free response problem presented in Sect. 4.3.

Figure 20a shows the predicted numerical acceleration at the center of tank $x_{T}$ compared with that obtained by the corresponding experiment. On the other hand, Fig. 20b shows the comparison of time histories of the interface forces exchanged between the structure and the tank. The curves are practically superimposed for both acceleration at tank location and interface force. The duration of the beam release mechanism attenuates the modal response at higher frequencies. The difficulty in its quantification affects the discrepancy from experimental data in the first instants of the simulation. Figure 20c shows the comparison between the experimental dynamic sloshing force and that predicted numerically by the network. The two curves are in good agreement with each other, except for the first cycles of the response in which the load cells seem to need a small transient to recover the correct measurement of the sloshing forces following a strong impulsive excitation. By taking advantage of the modal filtering technique, it is possible to isolate the first mode of vibration from the experimental and numerical acceleration signals shown in Fig. 20a. Once the dynamics of the first mode of vibration has been isolated, the instantaneous damping ratio can be evaluated by considering the envelope through logarithmic decay. Then, since the envelope decreases monotonically, the damping can be parameterized as a function of the vertical acceleration of the tank as shown in Fig. 21 that provides the comparison between experimental and numerical instantaneous damping. Since the model is trained using harmonic input, it is limited in providing a perfect estimate of the damping at the very initial transient—first two cycles at high acceleration amplitudes—but the neural network-based ROM looks to provide perfect superimposition in the prediction of the nonlinear damping induced by slosh dynamics in the rest of the response. Indeed, when high vertical accelerations are involved triggering Rayleigh–Taylor instabilities and impacts with the tank ceiling, the system promptly reaches a steady regime. The difference at the first cycles—in which the NN model appears to be anyway conservative with respect to the experimental response in terms of damping—is likely to be linked with the time needed for the inertial forces to win the surface tension and fragment the free surface. The problem of introducing such an effect on the training process is still open.

Fig. 20

Comparison between network predictions and experiments for vertical acceleration of a tank, interface force and sloshing force

Fig. 21

Instantaneous damping ratio of the first mode of vibration as a function of the acceleration amplitude

Concerning random analysis, the seismic excitation is implemented by considering the model in the non-inertial frame of reference and modeling a generalized force $\textsf{f}^{(ext)}$ determined by the fictitious forces such as

$$\begin{aligned} f_n^{(ext)} = -\int _0^l \mu (x) \psi _n(x) \, \textrm{d}x \, a_s \end{aligned}$$

(9)

where $a_s$ is the controlled vertical acceleration imposed by the shaker at the beam root and $\mu (x)$ the beam linear density. On the other hand, the input to the neural network needs to be expressed in the inertial frame of reference and thus equal to $\dot{w}(x_T) + v_s$ where $\dot{w}(x_T)$ is the tank vertical velocity in the non-inertial frame of reference and $v_s$ the drag speed. Figure 22 compares the estimated and measured tank acceleration signals over time for each of the three considered seismic tests. Again, the experimental response measured in the sloshing case (blue curve) is compared with the acceleration predicted by the sloshing beam simulation (red dot-dashed curve) obtained considering the same $a_s$ as in Fig. 17(a). In order to compare the effects that sloshing has on the random response of the system over time, the response in the frozen case obtained numerically with the same experimental input (black dotted curve) is also represented. This is more representative of the experimental counterpart given the difficulty of assigning the same random signal for two different experimental tests. In the time intervals selected for the representation of the results, it can be noticed that the NFIR model identified in Sect. 3, once integrated into the equivalent virtual sloshing beam model, is able to return a reasonable estimate of the sloshing beam response. This is mainly due to the predominantly mono-harmonic nature of the random response, which is consistent with that of the VFA harmonic experimental data used to train the neural network. However, as can be seen from the inset plots in Fig. 22, the response is less accurate at low amplitudes. This may be related to the lack of zero crossings at some points, which, based on the training data used, may cause the model to fail in its predictions. However, the numerical response is very close to the experimental response when compared with the frozen case numerical response that still includes experimentally derived damping values. This is also corroborated in Fig. 23, which shows the comparisons of the power spectral densities (using Welch method, Ref. [34]) of the tank acceleration for the different RMS cases. In fact, the PSDs associated with the numerical frozen case (black) present a clearly higher peak than that of the sloshing curves (blue). Comparing these with the (red) curves obtained by simulating the sloshing beam with the integrated data-driven ROM, it can be noticed that qualitatively the identified ROM is able to return the same level of dissipation at the system resonance frequency.

Although it is quite clear that the damping level depends on the amplitude of the tank vertical oscillation, PSDs are next used to make an average estimate of the modal damping of the first vibration mode as a function of the intensity of the input random signal. To this end, for each of the curves in Fig. 23, a modal fitting procedure is implemented based on the least-squares rational function estimation method (Ref. [35]). Table 2 shows the obtained damping ratios, in which it can be noticed that the experimental case of sloshing turn out to provide similar to those predicted with ROM, emphasizing the capability of the identified model to adequately reproduce the dissipative behavior induced by vertical sloshing.

Fig. 22

Comparison between the numerical tank accelerations predicted by the virtual sloshing beam model with NFIR model and with frozen liquid and the experimental one measured in the sloshing case

Table 2 Comparison between estimated modal damping ratios

Fig. 23

Comparison between the PSDs of the tank acceleration predicted by the virtual sloshing beam model with NFIR model and with frozen liquid and those of the experimental sloshing case

6 Conclusions

In this paper, data-driven nonlinear system identification techniques were exploited to identify a neural network-based reduced-order model to describe vertical sloshing. An experimental setup with a box-shaped tank partially filled with water and placed on an electrodynamic shaker was considered for data generation. The experimental test chosen for data collection consisted of harmonic excitation covering the amplitude–frequency range of interest. The velocity signal and dynamic sloshing force were used, respectively, as input and output data for the training process of the network. To avoid overfitting in the training process, a validation data set, obtained by performing an additional experimental test with variable frequency and amplitude, was also considered. A neural network-based nonlinear finite impulse response model (NFIR), resulting from a sensitivity analysis aimed at finding the most performing network, was selected to construct the surrogate model for vertical sloshing.

Fig. 24

Radial basis function (RBF) network

In the second part of the article, an experimental validation procedure of the identified model as integrated to a flexible structure was presented. To this end, an experimental setup consisting of a cantilever beam with a tank mounted at its free end was realized. The latter is the same as that used to generate the training data. By performing free response and seismic tests, FSI experimental data were collected to be used as a benchmark for validating the nonlinear identified ROM when integrated in an equivalent virtual model to account for the effects of vertical sloshing. The comparisons for the free response case showed that the time histories of the numerical acceleration at the end of the beam and sloshing forces are in good agreement with the experimental data. The estimated instantaneous damping ratio validates the good capabilities of the identified model to accurately reproduce the dissipative behavior induced by vertical sloshing.

The random analyses also yielded good results and showed a satisfactory level of accuracy for the time response in each of the considered excitation cases. By comparing the damping coefficients estimated in the frequency domain, it was possible to assess the neural network capability to provide the same levels of dissipation as experimentally given by vertical sloshing in random FSI testing. Future developments of the presented approach will have to address the need to include different filling levels in the training process and allow the sloshing model to interact with structural dynamics that are not one-tone-dominant (e.g., the frequency of the first vibration mode).

Radial basis functions networks

This appendix describes the structure of the radial basis function (RBF) networks used in this work to build the reduced-order model of vertical sloshing.

According to the external dynamics strategy, the model to be identified consists of a neural network preceded by a bank of filters containing delay lines. Thus, the neural network must perform a nonlinear mapping between the p regressors in vector $\textsf{x}\, = \, [x_1 \, x_2 \, \cdots x_p]^T$ (given by the number of input signals and the considered delay lines) and the single output y, which represents the sloshing force. RBF networks allow this mapping by means of the following basis function formulation:

(10)

corresponding to the structure shown in Fig. 24. The output layer is made up by the so-called output neurons. (Since only one output is considered here, the layer is made of one output neuron.) On the other hand, each of the M nodes in the hidden layer realizes a Gaussian basis (or activation) function whose parameters are determined following the neural network training process. These functions return the following output:

(11)

where the center vector $\textsf{w}_i$ and inverse covariance matrix representing the distribution of the i-th basis function are the hidden layer parameters of the i-th RBF neuron. For the sake of simplicity, the inverse covariance matrix is assumed to be equal to the identity matrix . Moreover, the parameter $w_i$ weighs the output provided by the hidden neurons that are subsequently linearly combined to obtain the estimate of y. $w_0$ assumes the role of bias.

These parameters are determined following an optimization or training process in order to obtain an RBF neural network model enabling the prediction of an output $\hat{y}$ fitting the target physics at the best. The training of neural networks is generally performed using the backpropagation algorithm. This method consists of calculating the gradients of the output of the neural network with respect to its parameters (hence, its weights). The built-in functions of MATLAB^® enable the design and implementation of RBF networks (Ref. [31]). It also allows the use of a variant called normalized radial basis function (NRBF) network, which is the one used to build the nonlinear reduced-order model of vertical sloshing. This model is equivalent to the classic radial basis one, except that neurons output are normalized by the sum of the pre-normalized values (see Ref. [36]). In basis function formulation, the NRBF network can be written as

(12)

overcoming some of the shortcomings of RBF networks, such as the lowering of interpolating capabilities in the case of too small standard deviations. In addition, the extrapolation behavior of standard RBF networks, which tends to zero, is undesirable for many applications (Ref. [30]).