Constrained parameter-splitting perturbation method for the improved solutions to the nonlinear vibrations of Euler–Bernoulli cantilevers

Abstract

In this paper, a new method named constrained parameter-splitting perturbation method for improving the solutions obtained from the parameter-splitting perturbation method is proposed for solving the problems in some extremal cases, such as the strongly nonlinear vibration of an Euler–Bernoulli cantilever. The proposed method takes the advantages of both the perturbation method and the harmonic balance method. The idea is that the solution obtained by the parameter-splitting perturbation method is substituted into the equation of motion and then the accumulative error of the equation is minimized for determining the unknown splitting parameters under the constraints constructed under the frame of harmonic balance method. The forced vibration of an oscillator with cubic geometric nonlinearity and inertia nonlinearity and the forced vibration of a planar microcantilever beam with a lumped tip mass are studied as examples to reveal the efficacy of the proposed method. The inspection of the steady-state response including its stability is conducted by means of comparing the frequency-response curves obtained by the proposed method with those obtained by the numerical continuation method and harmonic balance method, respectively, to show the efficacy and the advantages of the proposed method. Meanwhile, the nonlinear ordering effect on the solutions of the proposed method is also studied by comparing the results obtained by using different nonlinear orderings in the systems. In the last, we found through convergence examinations that it is necessary to have corrections to the erroneous solution which are obtained by harmonic balance method and Floquet theory in stability analysis.

Appendixes

1.1 A Mathematical modelling of an inextensible Euler–Bernoulli cantilever beam carrying a tip mass

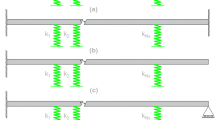
A planar and largely deflected cantilever beam carrying a lumped tip mass under a harmonic base motion is considered. The cantilever is assumed to be an isotropic and inextensible Euler–Bernoulli beam with an uniform cross section. The sketch of the simplified model under consideration is shown in Fig. 15.

Fig. 15

Simplified model of the cantilever carrying a tip mass. m, EI, M, L, g, s, u, v are the mass per unit length of the cantilever, the bending stiffness of the cantilever, the mass of the tip mass, the length of the cantilever, ground acceleration, the arclength coordinate, the axial displacement and transverse displacement, respectively

1.1.1 A.1 Extended Hamilton’s Principle

By using the extended Hamilton’s principle as in [2], the functional $\mathcal {I}$ is defined as

$$\begin{aligned} \delta \mathcal {I}=\int _{t_1}^{t_2}(\delta \mathcal {L}+\delta {W_{nc}})\,dt=0 \end{aligned}$$

(23)

where $t_1$, $t_2$, $\mathcal {L}$ and $W_{nc}$ are the initial time instant, the final time instant, the Lagrangian of motion of the cantilever and the work done by the non-conservative force. The Lagrangian of motion $\mathcal {L}$ of the cantilever beam and tip mass consists of two parts: $\mathcal {L}_{beam}$ and $\mathcal {L}_{tip}$.

$\mathcal {L}_{tip}$ is simplified as (1. since the tip mass is considered as a point mass, only the translational kinetic energy is considered; 2. the potential energy $V_{tip}$ only consists of gravitational potential energy as the concentrated mass is not deformable; 3. the gravitational potential energy is considered in the work done by the gravity force instead of considering in the potential energy since $-V_{tip}=W_{g}$)

$$\begin{aligned} \mathcal {L}_{tip}\equiv & {} T_{tip}-V_{tip}\nonumber \\= & {} \int _0^{L^+}\frac{1}{2}M{\big [}\dot{u}^2(s,t)+\dot{v}^2(s,t){\big ]}\delta (s-L)\,ds\nonumber \\ {}{} & {} \quad -0=T_{tip} \end{aligned}$$

(24)

where M is the mass of the concentrated tip mass and $\delta (\cdot )$ is the Dirac’s delta function. The Lagrangian of motion of the cantilever $\mathcal {L}_{beam}$ is defined as

$$\begin{aligned} \mathcal {L}_{beam}\equiv T_{beam}-V_{beam}=\int _0^L\ell _{beam}\,ds \end{aligned}$$

(25)

where $T_{beam}$ is the kinetic energy of the beam, $V_{beam}$ is the potential energy of the beam and $\ell _{beam}$ is the specific Lagrangian of the beam. The kinetic energy of the beam $T_{beam}$ consists of translational kinetic energy and rotational kinetic energy. The translational kinetic energy is given by

$$\begin{aligned} T_{t,beam}=\frac{1}{2}\int _0^Lm(\dot{u}^2+\dot{v}^2)\,ds \end{aligned}$$

(26)

where m is the mass per unit length of the beam and the rotational kinetic energy is given by

$$\begin{aligned} T_{r,beam}=\frac{1}{2}\int _0^LJ_z\omega _z^2\,ds \end{aligned}$$

(27)

where $J_z$ is the mass moment of inertia about z axis per unit length of the cantilever and it is defined as

$$\begin{aligned} J_z=\iint _A\rho \eta ^2\,d\eta {dz} \end{aligned}$$

(28)

in which $\rho$ denotes the mass density of the cantilever and A denotes the area of the cross section of the cantilever beam located at a distance s from the origin in the (x, y, z) coordinate system. As the cross section of the cantilever is uniform, $J_z$ is a constant. Hence, the total kinetic energy of the beam can be written as

$$\begin{aligned} T_{beam}=\frac{1}{2}\int _0^L{\big [}m(\dot{u}^2+\dot{v}^2)+J_z\omega _z^2{\big ]}\,ds. \end{aligned}$$

(29)

In our derivation, the gravitational potential energy is not include in the potential energy. The gravitational potential energy will be considered as work done of gravity force in $W_{nc}$ as in [2]. The potential energy V can be determined from the corresponding strain energy $U_{beam}$ for the cantilever beam considered here is given by

$$\begin{aligned} U_{beam}=\frac{1}{2}\int _0^L{\bigg [}\iint _A(\sigma _{11}\varepsilon _{11})\,d\eta {dz}{\bigg ]}\,ds \end{aligned}$$

(30)

where $\sigma _{11}$ denotes the normal stress in $\xi$ direction. In Eq. (30), it is assumed that the cantilever beam is an elastic structure with a linear stress–strain relationship and $\varepsilon _{22}=\gamma _{12}=0$. With Hooke’s law and neglecting Poisson’s effect, it gives $\sigma _{11}\approx {E\varepsilon _{11}}$, where E is Young’s modulus of the beam material. Substituting this relation and the expressions of strain component into Eq. (30), we obtain

$$\begin{aligned} V=U_{beam}=\frac{1}{2}\int _0^L{\bigg [}\iint _AE(-\eta \rho _z^2)^2\,d\eta {dz}{\bigg ]}\,ds \end{aligned}$$

(31)

Eq. (31) can be written as

$$\begin{aligned} V=\frac{1}{2}\int _0^LD_z\rho _z^2\,ds \end{aligned}$$

(32)

where $D_z=E\iint _A(-\eta \rho _z^2)^2\,d\eta {dz}$ is the bending stiffness of the beam. The total kinetic energy T is given by

$$\begin{aligned} \begin{aligned} T&=T_{beam}+T_{tip}=\int _0^L\ell _{beam}\,ds\\&\quad \;\; +\frac{1}{2}M{\big [}\dot{u}^2(L,t)+\dot{v}^2(L,t){\big ]}\\&\equiv \int _0^{L^+}\ell \,ds \end{aligned} \end{aligned}$$

(33)

in which $\ell$ is the specific Lagrangian of the whole system. As we discussed in the introduction of this section, the Lagrange multiplier $\lambda (s,t)$ is used to enforce the inextensionality constraint. With Eqs. 32 and 33 and the inextensionality constraint $(1+u')^2+v'^2=1$, we write the specific Lagrangian of the whole system $\ell$ as follows:

$$\begin{aligned} \ell= & {} \frac{1}{2}m(\dot{u}^2+\dot{v}^2)+\frac{1}{2}M(\dot{u}^2+\dot{v}^2)\delta (s-L)\nonumber \\{} & {} +\frac{1}{2}\lambda \big [1-(1+u')^2-v'^2\big ]\nonumber \\{} & {} +\frac{1}{2}J_z\omega _z^2-\frac{1}{2}D_z\rho _z^2. \end{aligned}$$

(34)

As mentioned above, the gravitational potential energy is considered as the work done by the gravity force, the variation of work done by the non-conservative force and gravity force is given by

$$\begin{aligned} \delta {W_{nc}}=\int _0^{L^+}\big [(Q_u-c_u\dot{u})\delta {u}+(Q_v-c_v\dot{v})\delta {v}\big ]\,ds \end{aligned}$$

(35)

where $Q_u$ is non-conservative force and gravity force projection in u direction, $Q_v$ is non-conservative force and gravity force projection in v direction, $c_u$ is the damping coefficient in u direction and $c_v$ is the damping coefficient in v direction. Substituting Eqs. (34) and (35) into Eq. (23) leads to

$$\begin{aligned} \delta \mathcal {I}= & {} \int _{t_1}^{t_2}\int _0^{L^+}{\big (}\delta \ell +Q_u\delta {u}-c_u\dot{u}\delta {u}\nonumber \\{} & {} \quad +Q_v\delta {v}-\dot{v}\delta {v}{\big )}\,dsdt=0 \end{aligned}$$

(36)

where $Q_u=-mg\sin (\theta )-Mg\sin (\theta )\delta (s-L)$, $Q_v=mg\cos (\theta )+Mg\cos (\theta )\delta (s-L)$ and base motion $v=\bar{v}+v_0\cos (\varOmega t)$. Following the procedures proposed in [2], the integro-differential equation representing the equation of motion of the system is then obtained as

$$\begin{aligned} \begin{aligned}&\bar{M}\ddot{v}+c_v\dot{v}+D_\zeta {v^{(4)}}=Q_v-D_\zeta {\big [}v'(v'v'')'{\big ]}'\\&\quad -\bar{M}v''\int _L^s\frac{\partial ^2}{\partial {t^2}}{\bigg [}\int _0^s\frac{1}{2}v'^2\,ds{\bigg ]}ds\\&\quad -\bar{M}v'\frac{\partial ^2}{\partial {t^2}}{\bigg [}\int _0^s\frac{1}{2}v'^2\,ds{\bigg ]}\\&\quad +\bar{M}g{\bigg [}(s-L)v''+v'+(s-L)\frac{3v'^2v''}{2}+\frac{v'^3}{2}{\bigg ]}\\&\quad +\bar{M}v_0\varOmega ^2\cos (\varOmega t). \end{aligned} \end{aligned}$$

(37)

where v is the displacement relative to the neutral axis; $v_0$ is the displacement amplitude of ground motion; the over dot represents the partial derivative with respect to time; the prime represents the partial derivative with respect to space; t is the time, m is the mass per unit length of the cantilever; M is the mass of the lumped mass; v is the transverse deflection of the harvester; $c_v$ is the damping coefficient of the harvester; $D_\zeta$ is the bending stiffness of the cantilever; $\bar{M}=\big [m+M\delta (s-L){\big ]}$ and $Q_v$ is the transverse loading.

1.1.2 A.2 Model reduction by Galerkin discretization

The linear eigenvalues and eigenvectors of the undamped free vibration of a uniform cantilever beam with or without lumping tip mass indicate the natural frequencies and mode functions of the linear structure, or called the linear natural frequencies and mode functions of the structure for short in the following analysis. The ith mode function of the system is given by Eq. (39) as shown in [34]. The characteristic equation of a uniform cantilever carrying a lumped tip mass is expressed by

$$\begin{aligned}{} & {} 1+\cos (\lambda L)\cosh (\lambda L)-\nu \lambda L{\big [}\cosh (\lambda L)\sin (\lambda L)\nonumber \\{} & {} -\cos (\lambda L)\sinh (\lambda L){\big ]}=0 \end{aligned}$$

(38)

where $\lambda$ is the characteristic root, L is the length of the cantilever and $\nu$ is the proof mass ratio expressed as $\nu =\frac{M}{mL}$. With the ith characteristic root, the ith mode function of a cantilever with uniform cross section and carrying a lumped tip mass is

$$\begin{aligned} \varPhi _i=\cos (\lambda _is)-\cosh (\lambda _is)+\chi {\big [}\sin (\lambda _is)-\sinh (\lambda _is){\big ]} \end{aligned}$$

(39)

where s is the arclength coordinate and $\chi$ is given as

$$\begin{aligned} \chi =\frac{\sin (\lambda _iL)+\mu \cosh (\lambda _iL)-\mu \cos (\lambda _iL)-\sinh (\lambda _iL)}{\cos (\lambda _iL) +\mu \sin (\lambda _iL)-\mu \sinh (\lambda _iL)+\cosh (\lambda _i L)} \end{aligned}$$

(40)

in which $\mu =-\nu \lambda L$.

In this paper, the above natural frequencies and the mode functions are adopted to formulate the equation of motion of the system. By Galerkin’s method, the transverse displacement of the cantilever in Eq. (37) is assumed in the following form

$$\begin{aligned} v(s,t)=\sum _i^N\varPhi _i(s)q_i(t). \end{aligned}$$

(41)

where N is a positive integer. A set of ordinary differential equations can then be formulated by Galerkin’s method. Finally, the modal coordinates $q_i(t) (i=1,2,\ldots ,N)$ can be determined by solving the ordinary differential equations with numerical method such as fourth-order Runge–Kutta method or analytical method such as HB method. Due to simplicity and the attention restriction to the examination of accuracy of stability analysis done by various analytical methods, only one mode function $\varPhi _i(s)$ is used in the Galerkin’s discretization procedure. Therefore, substituting Eq. (41) along with $N=1$ and the first ($i=1$) mode function into Eq. (37) and integrating with respect to s from 0 to L lead to the single-mode response of the simplified VEH

$$\begin{aligned} \mathbb {A}_1\ddot{q}+\mathbb {A}_2\dot{q}+\mathbb {A}_3q+\mathbb {A}_4q^3+\mathbb {A}_5(q\dot{q}^2+q^2\ddot{q})\!=\!\mathbb {A}_6\cos (\varOmega t) \end{aligned}$$

(42)

where the spatial integrals $\mathbb {A}_i\,(i=1,\ldots ,6)$ are given in the following and q is adopted instead of $q_1$ for simplicity.

$$\begin{aligned} \mathbb {A}_1&=\int _0^{L^{+}}\bar{M}\varPhi _i^2\,ds \end{aligned}$$

(43)

$$\begin{aligned} \mathbb {A}_2&=\int _0^Lc_v\varPhi _i^2\,ds \end{aligned}$$

(44)

$$\begin{aligned} \mathbb {A}_3&=\!\int _0^{L^{+}} EI\varPhi _i\varPhi _i^{(4)}\!-\!\bar{M}g\sin \theta \varPhi _i\big [(s\!-\!L)\varPhi _i''\!+\!\varPhi _i'\big ]\,ds\end{aligned}$$

(45)

$$\begin{aligned} \mathbb {A}_4&=\int _0^{L^{+}}EI\varPhi _i(\varPhi _i''^3+4\varPhi _i'\varPhi _i''\varPhi _i'''+\varPhi _i'^2\varPhi _i^{(4)})\nonumber \\&\quad -\bar{M}g\sin \theta \varPhi _i\bigg [(s-L)\frac{3\varPhi _i^2\varPhi _i''}{2}+\frac{\varPhi _i'^3}{2}\bigg ]\,ds \end{aligned}$$

(46)

$$\begin{aligned} \mathbb {A}_5&=\int _0^{L^{+}}\bar{M}\varPhi _i\varPhi _i''\int _L^s\int _0^s\varPhi _i'^2dsds\nonumber \\&\quad +\bar{M}\varPhi _i\varPhi _i'\int _0^s\varPhi _i'^2ds\,ds \end{aligned}$$

(47)

$$\begin{aligned} \mathbb {A}_6&=\int _0^{L^{+}}\varPhi _i\bar{M}a_{bm}\,ds \end{aligned}$$

(48)

where $i=1$. With the following definitions being $\hat{c}\equiv \frac{\mathbb {A}_2}{\mathbb {A}_1}$, $\hat{\alpha }\equiv \frac{\mathbb {A}_5}{\mathbb {A}_1}$, $\hat{\beta }\equiv \frac{\mathbb {A}_5}{\mathbb {A}_1}$, $\hat{\eta }\equiv \frac{\mathbb {A}_4}{\mathbb {A}_1}$, $\omega _0^2\equiv \frac{\mathbb {A}_3}{\mathbb {A}_1}$ and $\hat{F}\equiv \frac{\mathbb {A}_6}{\mathbb {A}_1}$, Eq. (42) can be deduced to be Eq. (1).

1.2 B Nth-order C-PSMS method for the primary resonance analysis of a harmonically forced second-order oscillator with general polynomial nonlinearity

1. Procedures for MTS analysis

A second-order oscillator with general polynomial nonlinearity is given as

$$\begin{aligned} \ddot{y}+c\varepsilon ^N\dot{y}+\omega _0^2y+\varepsilon {g({\varvec{\alpha }},y,\dot{y},\ddot{y})}=F\varepsilon ^N\cos (\varOmega {t}) \end{aligned}$$

(49)

where the means of the symbols are the same as those in Eq. (2). The solution to Eq. (49) and the scales of time are expressed as a power series of the perturbation parameter $\varepsilon$ as follows:

$$\begin{aligned} y(t;\varepsilon ,N)= & {} \sum _{i=0}^{N}\varepsilon ^iy_i(T_0,T_1,\ldots ,T_N)+O(\varepsilon ^{N+1}), \nonumber \\{} & {} \end{aligned}$$

(50)

$$\begin{aligned} T_i= & {} \varepsilon ^it,\,\,\,\,\,\,\,\,\,i=0,1,\ldots ,N \end{aligned}$$

(51)

The operators of time derivatives are given as

$$\begin{aligned} \frac{d}{dt} = \sum _{i=0}^{N}\varepsilon ^iD_i \end{aligned}$$

(52)

where $D_i=\partial /\partial {T_i}$. The derivatives of y are expressed as follows:

$$\begin{aligned} \frac{dy}{dt}= & {} \sum _{i=0}^{N}\varepsilon ^i\sum _{l=0}^{i}(D_ly_{i-l})+O(\varepsilon ^{N+1}) \end{aligned}$$

(53)

$$\begin{aligned} \frac{d^2y}{dt^2}= & {} \sum _{i=0}^{N}\varepsilon ^i\bigg [\sum _{j=0}^{i}D_j\bigg (\sum _{l=0}^{i-j}D_ly_{i-j-l}\bigg )\bigg ]+O(\varepsilon ^{N+1}) \nonumber \\ \end{aligned}$$

(54)

The nonlinearity $g({\varvec{\alpha }},y,\dot{y},\ddot{y})$ is a polynomial function of y, $\dot{y}$ and $\ddot{y}$, which can be written as

$$\begin{aligned} g({\varvec{\alpha }},y,\dot{y},\ddot{y})=\sum _{m=0}^{M}\alpha _my^{p_m}\dot{y}^{q_m}\ddot{y}^{n_m}, \end{aligned}$$

(55)

where

$$\begin{aligned}{} & {} y^p\dot{y}^q\ddot{y}^n= \bigg [\sum _{j_0+\ldots +j_N=p}\frac{p!}{j_0!\ldots {j_N!}}\prod _{k=0}^{N}(\varepsilon ^ky_k)^{j_k}\bigg ] \nonumber \\{} & {} \quad \bigg \{\sum _{j_0+\ldots +j_N=q}\frac{q!}{j_0!\ldots {j_N!}}\prod _{k=0}^{N}\bigg [\varepsilon ^k\sum _{l=0}^{k}\big (D_ly_{k-l}\big )\bigg ]^{j_k}\bigg \} \nonumber \\{} & {} \quad \bigg \{\sum _{j_0+\ldots +j_N=n}\frac{n!}{j_0!\ldots {j_N!}}\prod _{k=0}^{N}\bigg \{\varepsilon ^k\bigg [\sum _{j=0}^{k}D_j\nonumber \\ {}{} & {} \times \quad \bigg (\sum _{l=0}^{k-j}D_ly_{k-j-l}\bigg )\bigg ]\bigg \}^{j_k}\bigg \} \end{aligned}$$

(56)

where

$$\begin{aligned} \sum _{j_0+\ldots +j_N=p}=\sum _{j_0}\ldots \sum _{j_N}\,\,\,\,\,\text {such that}\,\,\,j_0+\ldots +j_N=p. \end{aligned}$$

(57)

2. Parameter splitting

Different from the classical MTS method, the natural frequency $\omega _0^2$ and the nonlinear coefficients $\alpha _m$ are expanded as power series of $\varepsilon$ as

$$\begin{aligned} \alpha _m= & {} \alpha _{m_0}\varepsilon ^0+\alpha _{m_1}\varepsilon ^1+\ldots \nonumber \\ {}{} & {} \quad +\alpha _{m_N}\varepsilon ^N,\,\,\,\,\,m=0,1,\ldots ,M \end{aligned}$$

(58)

$$\begin{aligned} \omega _0^2= & {} \omega _{00}^2\varepsilon ^0+\omega _{1}\varepsilon ^1+\ldots +\omega _{N}\varepsilon ^N \end{aligned}$$

(59)

The splitting parameters are defined as

$$\begin{aligned}{} & {} {{\varvec{\varTheta }}_{{\varvec{s}}}}\equiv \big \{\{\omega _{00}^2,\ldots ,\omega _{N}\},\{\alpha _{0_0},\ldots ,\alpha _{0_N}\},\nonumber \\{} & {} \quad \ldots ,\{\alpha _{m_0},\ldots ,\alpha _{m_N}\}, \ldots ,\{\alpha _{M_0}\ldots ,\alpha _{M_N}\}\big \} \end{aligned}$$

(60)

Substituting Eqs. (50)–(59) into Eq. (49), and equating the coefficients of $\varepsilon ^m\,\,\,(m=0,1,\ldots ,N)$ to zeros lead to $N+1$ differential equations given in the following.

Order $O(\varepsilon ^0)$:

$$\begin{aligned} D_0^2y_0+\omega _{00}^2y_0=0, \end{aligned}$$

(61)

order $O(\varepsilon ^1)$:

$$\begin{aligned}{} & {} D_0^2y_1+\omega _{00}^2y_1=-\omega _1y_0-2D_0D1y_0\nonumber \\{} & {} \quad -g({\varvec{\alpha }_0},y_0,D_0y_0,D_0^2y_0), \end{aligned}$$

(62)

where ${\varvec{\alpha }_0}=\{\alpha _{0_0},\alpha _{1_0},\ldots ,\alpha _{M_0}\}$, order $O(\varepsilon ^i)$:

$$\begin{aligned} \begin{aligned}&D_0^2y_i+\omega _{00}^2y_i=-2D_0D_iy_0-D_0\bigg (\sum _{l=1}^{i-1}D_ly_{i-l}\bigg )\\&\quad -\sum _{j=1}^{i-1}D_j\bigg (\sum _{l=0}^{i-j}D_ly_{i-j-l}\bigg ) -\sum _{t=1}^{i}(\omega _ty_{i-t}) \\&\quad -\sum _{m=0}^{M}\bigg \{\alpha _{m_{i-1}}\bigg (\sum _{j_{m0}+\ldots +j_{mN}=p_m}\frac{p_m!}{j_{m0}!\ldots {j_{mN!}}}\prod _{k=0}^{N}y_k^{j_{mk}}\bigg ) \\&\quad \bigg \{\sum _{h_{m0}+\ldots +h_{mN}=q_m}\frac{q_m!}{h_{m0}!\ldots {h_{mN}!}} \prod _{k=0}^{N}\bigg [\sum _{l=0}^{k}\big (D_ly_{k-l}\big )^{h_{mk}}\bigg ]\bigg \} \\&\quad \bigg \{\sum _{g_{m0}+\ldots +g_{mN}}+\frac{n_m!}{g_{m0}!\ldots {g_{mN}!}}\prod _{k=0}^{N}\bigg [\sum _{j=0}^{k}D_j \\&\times \quad \bigg (\sum _{l=0}^{k-j}D_ly_{k-j-l}\bigg )^{g_{mk}}\bigg ]\bigg \} \bigg \}\\&\quad +\delta (i-N)F\cos (\varOmega T_0) \end{aligned} \end{aligned}$$

(63)

where

$$\begin{aligned} \bigg (\sum _{k=0}^{N}kj_{mk}\bigg )\bigg (\sum _{k=0}^{N}kh_{mk}\bigg )\bigg (\sum _{k=0}^{N}kg_{mk}\bigg )=i-1. \end{aligned}$$

(64)

Equation (61) is a homogenous differential equation and the solution to it is

$$\begin{aligned} y_0=C(T_1,\ldots ,T_N)e^{i\omega _{00}T_0}+\text {c.c.} \end{aligned}$$

(65)

where $C(T_1,\ldots ,T_N)=Ae^{i\gamma }$ and c.c. stands for the complex conjugation. A is the response amplitude and $\gamma$ is the phase angle. They are functions of $T_1,\ldots ,T_N$. After that, Eqs. (62) and (63) can be solved in succession. The analytical approximation $y_a$ can be obtained easily. It is clear that $y_a$ is a function of the splitting parameters ${\varvec{\varTheta }}_{{\varvec{s}}}$. By eliminating the secularity and introducing the detuning of the excitation frequency, the modulations on response amplitude A and phase angle $\gamma$ can be deduced as two first-order differential equations. It should be noted that the elimination of secularity is different when different perturbation method is adopted. In our analysis, the MTS method is chosen. Therefore, the suppression on the secularity is conducted by setting the coefficient of the resonant term to be zero with the partial derivatives with respect to different time scales introduced in MTS method. If the someone adopted the method like Lindstedt-Poincaré method, the secularity is removed by the ‘strained’ frequency $\omega _1$ as shown in [1, 35,36,37]

3. Constraints

The constraints are constructed with Eqs. (11)-(13).

4. Determining the splitting parameters

Unlike the MTS method, the FRC and the response to Eq. (2) are still unknown as ${\varvec{\varTheta }}_{{\varvec{s}}}$ are unknowns. Therefore, the splitting parameters ${\varvec{\varTheta }}_{{\varvec{s}}}$ are determined by minimizing $R_e$ defined in Eq. (6) under the constraints introduced in Section 2 with Eqs. (9) and (10). The complete FRC can be obtained by varying the excitation frequency $\varOmega$ as it is by PSMS method in [4]. One technique is adopted to accelerate the computation of the FRC. The splitting parameters at $\varOmega =\varOmega _i$ are defined as ${\varvec{\varTheta }}_{{\varvec{s}}}^{(i)}$. The ${\varvec{\varTheta }}_{{\varvec{s}}}^{(i)}$ is adopted as the initial guess of the parameters when $\varOmega =\varOmega _{i+1}=\varOmega _i+\varDelta \varOmega$ during the minimization procedure. $\varDelta \varOmega$ is a small step of $\varOmega$.

1.3 C Constraints derivations

Derivation of the constraints given by Eqs. (9) and (10) is given in the following. The analytical approximation obtained by the PSP method can be expressed as a series with preservation of $m+1$ terms.

$$\begin{aligned} y_a=\sum _{k=0}^{m}A_k\cos [k(\varOmega t+\theta )]\equiv \sum _{k=0}^{m}A_k\cos (k\tau ) \end{aligned}$$

(66)

with $\tau =\varOmega t+\theta$.

Therefore,

$$\begin{aligned} \dot{y}_a= & {} \sum _{k=0}^{m}\{-A_k(k\varOmega )\sin [k(\varOmega t+\theta )]\}\nonumber \\= & {} \sum _{k=0}^{m}[-A_k(k\varOmega )\sin (k\tau )] \end{aligned}$$

(67)

$$\begin{aligned} \ddot{y}_a= & {} \sum _{k=0}^{m}\{-A_k(k\varOmega )^2\cos [k(\varOmega t+\theta )]\}\nonumber \\= & {} \sum _{k=0}^{m}[-A_k(k\varOmega )^2\cos (k\tau )] \end{aligned}$$

(68)

It should be noted that the dot represents the derivation with respect to time t in Eq. (13). Substituting Eqs. 67 and 68 into Eq. (13) leads to

$$\begin{aligned}{} & {} \sum _{k=0}^{m}[-A_k(k\varOmega )^2\cos (k\tau )]+c\varepsilon \sum _{k=0}^{m}[-A_k(k\varOmega )\sin (k\tau )]\nonumber \\{} & {} \quad +\omega _0^2\sum _{k=0}^{m}[A_k\cos (k\tau )]+\varepsilon {g({\varvec{\alpha }},y_a,\dot{y}_a,\ddot{y}_a)-F\varepsilon \cos (\varOmega t)} \nonumber \\ \end{aligned}$$

(69)

where $\varepsilon {g({\varvec{\alpha }},y_a,\dot{y}_a,\ddot{y}_a)}$ is given as

$$\begin{aligned} \varepsilon {g({\varvec{\alpha }},y_a,\dot{y}_a,\ddot{y}_a)}=\varepsilon \sum _{l=0}^{M}\alpha _ly_a^{p_l}\dot{y}_a^{q_l}\ddot{y}_a^{n_l} \end{aligned}$$

(70)

in which

$$\begin{aligned}{} & {} y_a^{p_l}\dot{y}_a^{q_l}\ddot{y}_a^{n_l}= \bigg \{\sum _{j_0+\ldots +j_m=p_l}\frac{p_l!}{j_0!\ldots {j_m!}} \prod _{k=0}^{m}\bigg [A_k\cos (k\tau )\bigg ]^{j_k}\bigg \}\nonumber \\{} & {} \quad \bigg \{\sum _{j_0+\ldots +j_m=q_l}\frac{q_l!}{j_0!\ldots {j_m!}} \prod _{k=0}^{m}\bigg [-A_k(k\varOmega )\sin (k\tau )\bigg ]^{j_k}\bigg \} \nonumber \\{} & {} \quad \bigg \{\sum _{j_0+\ldots +j_m=n_l}\frac{n_l!}{j_0!\ldots {j_m!}} \prod _{k=0}^{m}\bigg [-A_k(k\varOmega )^2\cos (k\tau )\bigg ]^{j_k}\bigg \} \nonumber \\ \end{aligned}$$

(71)

where

$$\begin{aligned} \sum _{j_0+\ldots +j_m=p_l}= & {} \sum _{j_0}\ldots \sum _{j_m}\,\,\,\,\,\text {such that}\,\,\,j_0+\ldots +j_m\nonumber \\ {}{} & {} =p_l. \end{aligned}$$

(72)

After trigonometric identities, Eq. (71) can be expressed as

$$\begin{aligned}{} & {} \varepsilon {g({\varvec{\alpha }},y_a,\dot{y}_a,\ddot{y}_a)}=\sum _{k=0}^{m}E_{s,k}\sin (k\tau )\nonumber \\{} & {} \quad +\sum _{k=0}^{m}E_{c,k}\cos (k\tau )+\text {higher order term with}\,\,k\nonumber \\{} & {} \quad \ge {m+1} \end{aligned}$$

(73)

where $E_{s,k}$ and $E_{c,k}$ are the sum of the coefficients in front of $\sin (k\tau )$ and $\cos (k\tau )$, respectively.

Preserving the first m terms in Eq. (13) leads to

$$\begin{aligned} r_e= & {} \sum _{k=0}^{m}[-A_k(k\varOmega )^2\cos (k\tau )]+c\varepsilon \sum _{k=0}^{m}[-A_k(k\varOmega )\sin (k\tau )]\nonumber \\{} & {} +\omega _0^2\sum _{k=0}^{m}[A_k\cos (k\tau )]+\sum _{k=0}^{m}E_{s,k}\sin (k\tau )\nonumber \\{} & {} +\sum _{k=0}^{m}E_{c,k}\cos (k\tau )-F\varepsilon \cos (\varOmega t) \end{aligned}$$

(74)

The amplitudes of like harmonics can be obtained by using orthogonality with $\int _{0}^{2\pi }\cos (i\tau )\cos (j\tau )d\tau =0$ (if $i\ne {j}$), $\int _{0}^{2\pi }\cos (i\tau )\sin (j\tau )d\tau =0$ (for any i, j) and $\int _{0}^{2\pi }\sin (i\tau )\sin (j\tau )d\tau =0$ (if $i\ne {j}$).

$$\begin{aligned}{} & {} \cos (k\tau )\,\,\text {term}: X_k=\frac{1}{\pi }\int _{0}^{2\pi }r_e\cos (k\tau )d\tau \end{aligned}$$

(75)

$$\begin{aligned}{} & {} \sin (k\tau )\,\,\text {term}: x_k=\frac{1}{\pi }\int _{0}^{2\pi }r_e\sin (k\tau )d\tau \end{aligned}$$

(76)

where $X_k$ and $x_k$ are the amplitudes of terms $\cos (k\tau )$ and $\sin (k\tau )$, respectively. Observing from Eq. (74), the forcing term $F\varepsilon \cos (\varOmega {t})$ also needs to be balanced. Therefore, specially, for the harmonics with $k=1$ we have

$$\begin{aligned}{} & {} X_1\cos (1\tau )+x_1\sin (1\tau )=X_1\cos (\varOmega {t}+\theta )\nonumber \\{} & {} \quad +x_1\sin (\varOmega {t}+\theta )=F\varepsilon \cos (\varOmega {t}) \end{aligned}$$

(77)

With trigonometric identities, it can be rewritten as

$$\begin{aligned}{} & {} X_1[\cos (\varOmega {t})\cos (\theta ) - \sin (\varOmega {t})\sin (\theta )] \nonumber \\{} & {} \quad +x_1[\cos (\varOmega {t})\sin (\theta ) \nonumber \\{} & {} \quad + \sin (\varOmega {t})\cos (\theta )]=F\varepsilon \cos (\varOmega {t}) \end{aligned}$$

(78)

As the above equation holds for any t. Therefore, it can split into two equations by collecting the coefficients of the terms $\cos (\varOmega {t})$ and $\sin (\varOmega {t})$. They are given in the following, respectively.

$$\begin{aligned}&\cos (\varOmega {t})\,\,\text {term}:\,\,X_1\cos (\theta )+x_1\sin (\theta )=F\varepsilon \end{aligned}$$

(79)

$$\begin{aligned}&\sin (\varOmega {t})\,\,\text {term}:\,\,-X_1\sin (\theta )+x_1\cos (\theta )=0 \end{aligned}$$

(80)

Summing the square of the above equations up leads to the following constraint.

$$\begin{aligned} X_1^2+x_1^2=(F\varepsilon )^2 \end{aligned}$$

(81)

For any $k\ne 1$, we have

$$\begin{aligned}{} & {} X_k\cos (k\tau )+x_k\sin (k\tau )=X_k\cos [k(\varOmega {t}+\theta )]\nonumber \\{} & {} \quad +x_k\sin [k(\varOmega {t}+\theta )]=0 \end{aligned}$$

(82)

As the above equation holds for any t. Therefore, it can split into two equations by collecting the coefficients of the terms $\cos (\varOmega {t})$ and $\sin (\varOmega {t})$. They are given in the following, respectively.

$$\begin{aligned}&\cos (\varOmega {t})\,\,\text {term}:\,\,X_k\cos (\theta )=-x_k\sin (\theta )=0 \end{aligned}$$

(83)

$$\begin{aligned}&\sin (\varOmega {t})\,\,\text {term}:\,\,X_k\sin (\theta )=x_k\cos (\theta )=0 \end{aligned}$$

(84)

Summing the square of the above equations up leads to the following constraint.

$$\begin{aligned} X_k^2=x_k^2 \end{aligned}$$

(85)

which turns into

$$\begin{aligned} X_k^2-x_k^2=0\,\,\text {(for any)}\,\,k\ne 1 \end{aligned}$$

(86)

From the above deductions, it is clear to see that the nonlinear algebraic equations adopted in the constraints are same of the nonlinear algebraic equations generated by using a classical HB method.

1.4 D Symbolic expressions

Expressions of $A_1$, $A_3$, $A_5$, $\varGamma _1$ and $\varGamma _2$ are given in the following.

$$\begin{aligned} A_1&= A \end{aligned}$$

(87)

$$\begin{aligned} A_3&= \frac{A^3 \varepsilon (\alpha _{0} -\beta _{0} \omega _{00}^2 - \eta _{0} \omega _{00}^2)}{32 \omega _{00}^2} -\frac{A^3 \varepsilon ^2 (16 \beta _{1} \omega _{00}^4 - 16 \alpha _{1} \omega _{00}^2 - 2 \alpha _{0} \omega _1 + 16 \eta _{1} \omega _{00}^4 - 3 A^2 \alpha _{0}^2)}{512 \omega _{00}^4} \nonumber \\&\quad -\frac{A^3\varepsilon ^2(2 \beta _{0} \omega _{00}^2 \omega _1 + 2 \eta _{0} \omega _{00}^2 \omega _1 + A^2 \beta _{0}^2 \omega _{00}^4 - 11 A^2 \eta _{0}^2 \omega _{00}^4 + 2 A^2 \alpha _{0} \beta _{0} \omega _{00}^2 + 14 A^2 \alpha _{0} \eta _{0} \omega _{00}^2 - 10 A^2 \beta _{0} \eta _{0} \omega _{00}^4)}{512 \omega _{00}^4} \end{aligned}$$

(88)

$$\begin{aligned} A_5&= \frac{A^5 \varepsilon ^2 (3 \alpha _{0}^2 - 10 \alpha _{0} \beta _{0} \omega _{00}^2 - 14 \alpha _{0} \eta _{0} \omega _{00}^2 + 7 \beta _{0}^2 \omega _{00}^4 + 18 \beta _{0} \eta _{0} \omega _{00}^4 + 11 \eta _{0}^2 \omega _{00}^4)}{3072 \omega _{00}^4} \end{aligned}$$

(89)

$$\begin{aligned} \varGamma _1&=-\frac{\varepsilon (3 \alpha _{0} + 3 \alpha _{1} \varepsilon + \beta _{0} \omega _{00}^2 - 3 \eta _{0} \omega _{00}^2 - 3 \varepsilon \eta _{1} \omega _{00}^2 + \beta _{1} \varepsilon \omega _{00}^2)}{8 \omega _{00}} \end{aligned}$$

(90)

$$\begin{aligned} \varGamma _2&=-\frac{\varepsilon ^2 (3 \alpha _{0}^2 + 2 \alpha _{0} \beta _{0} \omega _{00}^2 - 14 \alpha _{0} \eta _{0} \omega _{00}^2 - 5 \beta _{0}^2 \omega _{00}^4 + 6 \beta _{0} \eta _{0} \omega _{00}^4 + 11 \eta _{0}^2 \omega _{00}^4)}{256 \omega _{00}^3} \end{aligned}$$

(91)

The classical second-order MTS analytical approximation to Eq. (1) is given by

$$\begin{aligned}{} & {} q_a^{\text {2nd-order MTS}}=B_1\cos (\varOmega t-\gamma )\nonumber \\{} & {} \quad +B_3\cos [3(\varOmega t-\gamma )]+B_5\cos [5(\varOmega t-\gamma )] \end{aligned}$$

(92)

where

$$\begin{aligned}&B_1= A \end{aligned}$$

(93)

$$\begin{aligned}&B_3 = \frac{A^3(\hat{\alpha } -\hat{\beta }\omega _{0}^2 - \hat{\eta }\omega _{0}^2)}{32 \omega _{0}^2}\nonumber \\&\quad \quad -\frac{A^3(- 3 A^2 \hat{\alpha }^2 + A^2 \hat{\beta }^2 \omega _{0}^4 - 11 A^2 \hat{\eta }^2 \omega _{0}^4 + 2 A^2 \hat{\alpha }\hat{\beta } \omega _{0}^2 + 14 A^2 \hat{\alpha }\hat{\eta } \omega _{0}^2 - 10 A^2 \hat{\beta } \hat{\eta } \omega _{0}^4)}{512 \omega _{0}^4} \end{aligned}$$

(94)

$$\begin{aligned} \nonumber \\&B_5 = \frac{A^5 (3 \hat{\alpha }^2 - 10 \hat{\alpha } \hat{\beta } \omega _{0}^2 - 14 \hat{\alpha } \hat{\eta } \omega _{0}^2 + 7 \hat{\beta }^2 \omega _{0}^4 + 18 \hat{\beta } \hat{\eta } \omega _{0}^4 + 11 \hat{\eta }^2 \omega _{0}^4)}{3072 \omega _{0}^4} \end{aligned}$$

(95)